Uranium isotope compositions of the basaltic angrite meteorites and the chronological implications for the early Solar System

Abstract

Events occurring within the first 10 million years of the Solar System’s approximately 4.5 billion-year history, such as formation of the first solids, accretion, and differentiation of protoplanetary bodies, have determined the evolutionary course of our Solar System and the planetary bodies within it. The application of high-resolution chronometers based on short-lived radionuclides is critical to our understanding of the temporal sequence of these critical events. However, to map the relative ages from such chronometers onto the absolute time scale, they must be “anchored” to absolute ages of appropriate meteoritic materials using the high-precision lead–lead (Pb–Pb) chronometer. Previously reported Pb–Pb dates of the basaltic angrite meteorites, some of which have been used extensively as time anchors, assumed a constant ²³⁸U/²³⁵U ratio (= 137.88). In this work, we report measurements of ²³⁸U/²³⁵U ratios in several angrites that are distinct from the previously assumed value, resulting in corrections to the Pb–Pb ages of ≥1 million years. There is no resolvable variation in the ²³⁸U/²³⁵U ratio among the angrite bulk samples or mineral separates, suggesting homogeneity in the U isotopic composition of the angrite parent body. Based on these measurements, we recalculated the Pb–Pb age for the commonly used anchor, the D’Orbigny angrite, to be 4563.37 ± 0.25 Ma. An adjustment to the Pb–Pb age of a time anchor (such as D’Orbigny) requires a corresponding correction to the “model ages” of all materials dated using that anchor and a short-lived chronometer. This, in turn, has consequences for accurately defining the absolute timeline of early Solar System events.

The time from the formation of the first solids in the Solar System to the accretion and differentiation of protoplanetary embryos is less than approximately 10 million years (Ma) (ref. 1 and references therein), and these events have determined the evolutionary course of our Solar System and the planetary bodies within it. Knowledge of the precise timing of events during this period is critical to a broader understanding of how star systems and planetary bodies form and evolve. As such, precise and accurate geochronology, allowing the resolution of events occurring within this critical approximately 10 Ma interval, is required to understand this earliest sequence of events in the Solar System. A very limited number of chronometers can provide the sub-Ma precision necessary to resolve early Solar System events. These include the long-lived lead–lead (Pb–Pb) chronometer, and the short-lived chronometers such as ²⁶Al-²⁶Mg (t_1/2 approx. 0.72 Ma), ⁵³Mn-⁵³Cr (t_1/2 approx. 3.7 Ma), and ¹⁸²Hf-¹⁸²W (t_1/2 approx. 9 Ma). The Pb–Pb chronometer is based on two radioactive isotopes of uranium, utilizing the distinct decay schemes of ²³⁵U → ²⁰⁷Pb (t_1/2 approx. 704 Ma) and ²³⁸U → ²⁰⁶Pb (t_1/2 approx. 4.47 Ga) to calculate an absolute age of the sample. The short-lived or extinct radionuclide chronometers have parent isotopes with half-lives significantly shorter than the age of the Solar System; even though they were initially present in the solar nebula, they have fully decayed to their daughter isotopes at the present time. Chronology based on an extinct system relies on the assumption that the parent isotope was homogenously distributed in the solar nebula. The application of an extinct chronometer then requires that the abundances of the short-lived parent isotope at the formation times of two different objects be determined. With the knowledge of the half-life of the parent isotope, it is then possible to obtain relative time constraints between these two objects with high precision [uncertainties as low as a few tens of thousands of years have been reported for samples older than approximately 4.5 billion years (2)]. These relative ages can be mapped to an absolute time scale only if they can be anchored to an absolute date obtained with the long-lived but highly precise Pb–Pb chronometer. This can only be accomplished if there is an appropriate anchor, which is a meteoritic material for which a precise and accurate Pb–Pb age as well as the abundance of the short-lived parent isotope at that time has been determined. The inferred abundance of the short-lived parent isotope in the object to be dated is then compared to that in the anchor, based upon which an age can be calculated for that object relative to the known absolute Pb–Pb age of the anchor. Since this calculation does not yield an independent absolute age for the object, but one that is relative to the age of the anchor and is based on the assumptions that (i) the abundance of the parent radioisotope in the anchor is known for the time dated with the Pb–Pb chronometer and (ii) both the object and the anchor originated from a reservoir in which the parent radioisotope was initially homogeneously distributed, it is referred to hereafter as a “model age” and not an absolute age.

The Pb–Pb system is the only absolute dating technique able to resolve sub-Ma time differences. Because ²³⁸U and ²³⁵U decay to ²⁰⁶Pb and ²⁰⁷Pb, respectively, a known ²³⁸U/²³⁵U is required for age calculation, as shown in Eq. 1.

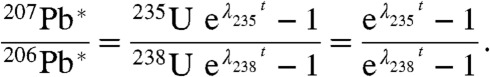[1]

Recent work has shown that the assumption of an invariant ²³⁸U/²³⁵U ratio in Solar System materials is no longer valid (3–6); the uranium isotopic compositions must be measured to obtain accurate Pb–Pb dates. As the high-resolution relative ages of early Solar System events based on extinct chronometers (such as ²⁶Al-²⁶Mg) must be anchored by precise and accurate absolute ages from Pb–Pb dating, determination of the uranium isotope compositions of meteoritic objects that serve as age anchors is particularly important, since this has implications for the accuracy of the model ages obtained using short-lived chronometers.

Previous studies have revealed inconsistencies between ages determined for the same meteoritic object by different high-resolution chronometers mentioned above (e.g., 1, 7). These discrepancies may be caused by a variety of reasons, including heterogeneous distribution of the short-lived radionuclides and resetting of different isotopic systems to different degrees by secondary processes. The assumption of an invariant ²³⁸U/²³⁵U ratio in Solar System materials could also be responsible for some of these discrepancies since it may result in erroneous Pb–Pb ages of the time anchors.

The accuracy of the model ages obtained using short-lived chronometers is ultimately dependent on the choice of an appropriate meteoritic material to serve as an age anchor. An ideal age anchor (i) originated from an isotopically uniform source reservoir, (ii) contains measureable quantities of the daughter products of multiple short-lived radioisotope systems (e.g., ²⁶Al-²⁶Mg, ⁵³Mn-⁵³Cr, and ¹⁸²Hf-¹⁸²W), (iii) cooled rapidly while those systems were still “live,” and (iv) has remained undisturbed by secondary alteration since the initial closure of these isotopic systems (7, 8).

Angrites are a small group of basaltic achondrites distinguished by ancient crystallization ages and unique geochemical and mineralogical characteristics (9). Several of these achondritic meteorites have been used in previous studies as age anchors for the short-lived chronometers (10–12). Currently known angrites define two distinct subgroups: the plutonic (coarse-grained) and quenched (fine-grained) angrites. Geochemical evidence suggests both subgroups originated from the same angrite parent body (APB) (13), but the crystallization of the quenched angrites predates that of the plutonic angrites by approximately 7 Ma (14).

The quenched angrites in particular can serve as suitable age anchors for multiple short-lived chronometers for a variety of reasons. First, these are igneous rocks that originated from crystallization of a melt and were therefore isotopically homogenized at the time of their original formation. Second, they formed early enough in the history of the Solar System that they are likely to contain measurable excesses of the daughter products of several short-lived radionuclides. Additionally, they crystallized and cooled rapidly at the time of their formation (ref. 13 and the references therein), so the isotope systems associated with both extinct and long-lived chronometers closed at effectively the same time in these samples. Among the quenched angrites, the D’Orbigny meteorite represents an especially attractive age anchor because it is relatively unmetamorphosed and has consequently remained unaltered by secondary processing (15). In several recent studies, the short-lived ²⁶Al-²⁶Mg, ⁵³Mn-⁵³Cr, and ¹⁸²Hf-¹⁸²W systems have been anchored to the Pb–Pb age of the D’Orbigny angrite (e.g., 10, 12, 16); thus, the model ages calculated based on these extinct chronometers inherently depend on the precision and accuracy of the Pb–Pb date of the D’Orbigny anchor. The previously reported highly precise absolute Pb–Pb age of 4564.42 ± 0.12 Ma for the D’Orbigny angrite (14) is based on an internal isochron from pyroxene separates and whole-rock fractions, but assumes a ²³⁸U/²³⁵U ratio of 137.88. In this work we report precise measurements of the ²³⁸U/²³⁵U ratio in several angrite samples, including D’Orbigny, and discuss the implications for obtaining precise and accurate ages for early Solar System events.

Results

The previously accepted consensus value for the ²³⁸U/²³⁵U ratio in the commonly used U isotope standards was 137.88 (as, in fact, was the case for all Solar System materials). However, the recent work of Richter et al. (17) and Condon et al. (18) has demonstrated that the uranium isotope compositions of these terrestrial standards vary, and they have ²³⁸U/²³⁵U ratios that are lower than this previously assumed consensus value by as much as 0.08%. In our work, the U isotope data are reported relative to the SRM950a standard, which has a measured ²³⁸U/²³⁵U ratio of 137.837 ± 0.015 (17) [in good agreement with the value reported by (18) for this same standard].

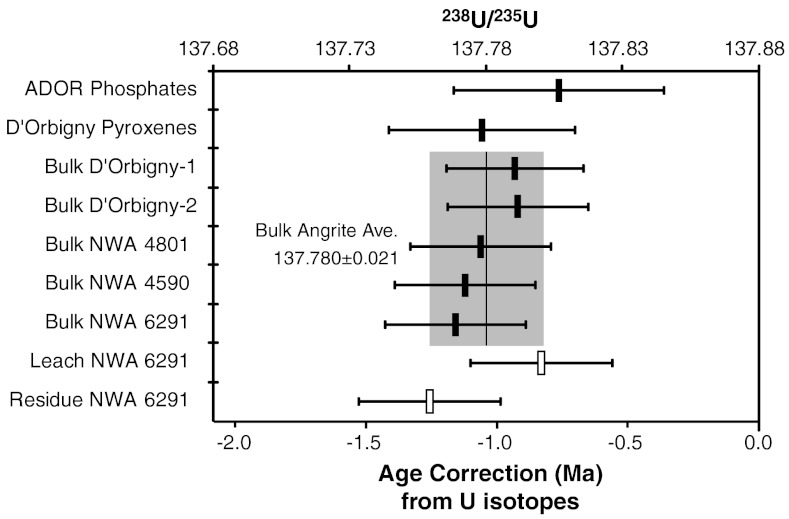
Uranium isotope ratios in a pyroxene separate and two whole-rock fractions of D’Orbigny, a phosphate separate from Angra dos Reis (ADOR), whole-rock fractions of NWA 4590, NWA 4801, and NWA 6291, as well as an acid leach (0.5 M HNO₃) and remaining residue from a second whole-rock fraction of NWA 6291 were determined during this study. All uncertainties reported here are 2 × standard deviation (2SD). We report a ²³⁸U/²³⁵U ratio of 137.778 ± 0.034 for the D’Orbigny pyroxene separate, 137.790 ± 0.025 for a whole-rock sample of D’Orbigny (Bulk D’Orbigny-1), and 137.791 ± 0.026 for another whole-rock sample of D’Orbigny (Bulk D’Orbigny-2). Whole-rock fractions of NWA 4590, NWA 4801 and NWA 6291 yielded ²³⁸U/²³⁵U ratios of 137.772 ± 0.026, 137.778 ± 0.026, and 137.769 ± 0.026, respectively. The 0.5 M HNO₃ acid leach of a second whole-rock sample of NWA 6291 yielded a ²³⁸U/²³⁵U of 137.800 ± 0.026, with the remaining residue having a ²³⁸U/²³⁵U of 137.759 ± 0.026. Finally, the ADOR phosphate separate has a ²³⁸U/²³⁵U ratio of 137.806 ± 0.039. The data are summarized in Fig. 1 and Table 1. The ²³⁸U/²³⁵U values obtained for the terrestrial standards BCR-2 and G-2, 137.800 ± 0.033 and 137.809 ± 0.026, respectively, are also shown in Table 1.

Fig. 1.

The ²³⁸U/²³⁵U ratio of the samples of this study (upper axis) and the associated age correction (lower axis) based on the measured U isotope ratio compared to the previously assumed value (²³⁸U/²³⁵U = 137.88). Uncertainties represent total 2SD uncertainties propagated from the uncertainties on the U isotope ratio measurements and the spike composition. The average value of bulk angrites is shown with a vertical line, with associated 2SD uncertainty in grey. This value represents the best estimate for the modern ²³⁸U/²³⁵U ratio of the angrite parent body.

Table 1.

U isotopic compositions of angrite samples and terrestrial standards

Sample	238U/235U	Measurement uncertainty 2SD	Spike uncertainty 2SD	Total uncertainty 2SD	N	238U intensity (V)	Age adjustment (Ma)
D’Orbigny pyroxenes*†	137.778	0.028	0.020	0.034	1	6.5	-1.06 ± 0.36
Bulk D’Orbigny-1†	137.790	0.010	0.020	0.025	3	18	-0.94 ± 0.26
Bulk D’Orbigny-2‡	137.791	0.010	0.021	0.026	3	12	-0.92 ± 0.27
ADOR phosphates*	137.806	0.033	0.020	0.039	1	2.5	-0.77 ± 0.40
Bulk NWA 4801‡	137.778	0.009	0.021	0.026	3	11	-1.07 ± 0.27
Bulk NWA 4590‡	137.772	0.004	0.021	0.026	3	17	-1.13 ± 0.27
Bulk NWA 6291‡	137.769	0.006	0.021	0.026	3	15	-1.17 ± 0.27
Leach NWA 6291‡	137.800	0.007	0.021	0.026	3	11	-0.83 ± 0.27
Residue NWA 6291‡	137.759	0.015	0.021	0.026	1	11	-1.26 ± 0.27
Terrestrial Std. BCR-2†	137.800	0.026	0.020	0.033	3	4
Terrestrial Std. G-2†	137.809	0.006	0.020	0.026	4	16
SRM950a†‡	137.837	0.015	0.021	0.026	28	2.5–20

The age adjustment is calculated based on the measured U isotope composition in comparison to the previously assumed consensus value for the ²³⁸U/²³⁵U ratio of 137.88.

N = number of repeat runs.

^*Using 10¹² Ω resistors on ²³³U, ²³⁵U, and ²³⁶U; 10¹¹ Ω resistors were used for measuring these isotopes in all other samples.

^†Using in-house ASU double-spike.

^‡Using IRMM-3636 double-spike.

Discussion

Whole-rock samples of the quenched and plutonic angrites as well as the angrite mineral separates analyzed in this study all have ²³⁸U/²³⁵U values that are indistinguishable from one another within the reported uncertainties. While the uranium isotope compositions of the leachate and residue of the second whole-rock fraction of NWA 6291 agree with each other within the uncertainties, the leachate appears to have a slightly but systematically higher ²³⁸U/²³⁵U ratio, most likely due to the addition of isotopically heavy terrestrial U contamination. This work underscores the need to remove terrestrial contamination from meteoritic materials, particularly those collected from hot deserts that tend to be more heavily altered by terrestrial weathering (19). The ²³⁸U/²³⁵U ratio of the NWA 6291 residual material after the 0.5 M HNO₃ acid leach is indistinguishable from that of a separate NWA 6291 whole-rock (which was washed with only a mild acid, 0.05 M HCl, prior to digestion). The uniformity among the samples suggests that ²³⁸U/²³⁵U variation did not exist on the APB or between angrite mineral phases at the current level of precision. Given this isotopic uniformity, an average of the ²³⁸U/²³⁵U ratios of the angrite whole-rock samples measured in this study (= 137.780 ± 0.021) provides the best estimate for the ²³⁸U/²³⁵U ratio of the APB, and thus of any meteorite originating from this parent body. Using this average value as the ²³⁸U/²³⁵U composition for the angrites and propagating uncertainties from both this U isotopic composition and the previously reported Pb–Pb dates, the corrected Pb–Pb age for each sample is calculated and shown in Fig. 2 and Table 2. Any sample that has been dated using a short-lived chronometer that utilizes any of these angrites as a time anchor requires an age adjustment of the same magnitude as that anchor.

Fig. 2.

Comparison of the Pb–Pb ages recalculated using the average ²³⁸U/²³⁵U ratio obtained from all angrite samples analyzed in this study with the previously reported Pb–Pb ages (see Table 2 for references). Recalculated age uncertainties include total 2SD uncertainties propagated from the uncertainties on the U isotope ratio measurements and the spike composition.

Table 2.

Recalculated Pb–Pb ages of the angrites, with propagated 2SD uncertainties

Sample	Previously reported Pb–Pb age (Ma)*	± (Ma)	Corrected Pb–Pb age (Ma)†	± (Ma)
D’Orbigny	4564.42‡	0.12	4563.37	0.25
Angra dos Reis	4557.65‡	0.13	4556.60	0.26
NWA 4590	4557.93§,¶	0.36	4557.81	0.37
NWA 4801	4558.06§	0.15	4557.01	0.27
NWA 2999∥	4561.79§	0.42	4560.74	0.47
NWA 6291	4560.10**	1.10	4560.21	1.05

^*These ages were calculated assuming a ²³⁸U/²³⁵U ratio of 137.88; the two exceptions are the ages recently reported for NWA 4590 by Amelin and Irving (26), which was corrected using the ²³⁸U/²³⁵U ratio measured for this sample by Amelin et al. (6), and NWA 6291 by Bouvier et al. (20) which used the U isotope composition measured in this sample (²³⁸U/²³⁵U = 137.769 ± 0.026).

^†These ages were calculated using the average ²³⁸U/²³⁵U ratio for the angrites reported here.

^‡Amelin (14).

^§Amelin and Irving (26).

^¶Amelin et al. (6).

^∥Paired with NWA 6291.

^**Bouvier et al. (20).

Recent analytical advances leading to significantly greater precision along with renewed interest have led to several investigations of the U isotopic compositions of meteoritic materials in recent years. While refractory calcium-aluminum-rich inclusions (CAIs) in the carbonaceous chondrite Allende have been shown to have large variability in ²³⁸U/²³⁵U ratios (3, 5), the measured ²³⁸U/²³⁵U ratios of bulk samples of several types of chondrites and achondrites are all within analytical uncertainty of one another, and have an average ²³⁸U/²³⁵U ratio ≈ 137.78 (3–6, 20–22). There are many other meteorite types that have not yet been measured, but the current data suggest that while the ²³⁸U/²³⁵U ratio of Solar System materials is resolvably distinct from the previously assumed value of 137.88, the extent of U isotopic variation among bulk meteorites is likely to be relatively small (i.e., smaller than the current level of precision of the U isotope measurements of ± 1 - 2ε units).

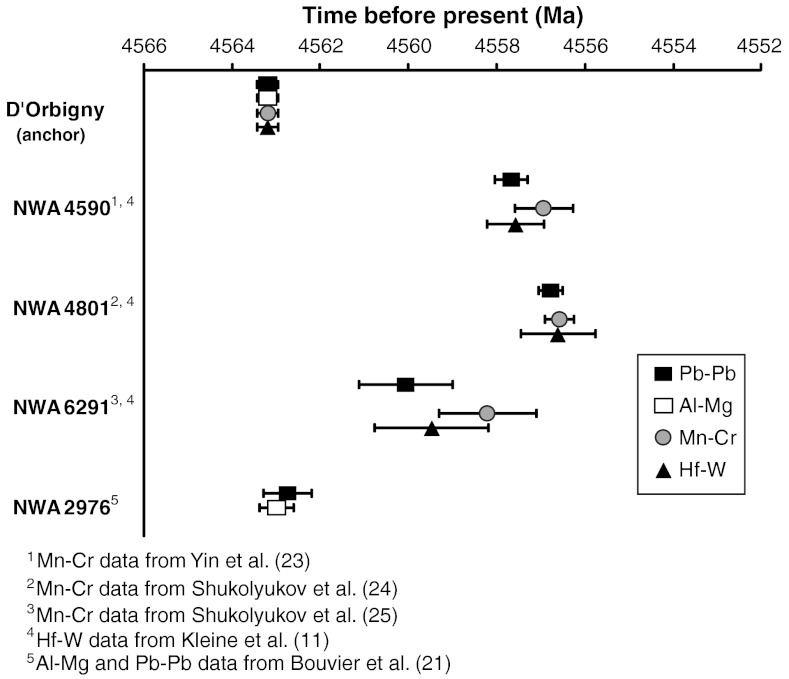
Obtaining the same ages (i.e., that agree within the uncertainties) for multiple high-resolution chronometers on an object in which one might expect similar closure temperatures for these chronometers is a critical step in unraveling the sequence of events in the early Solar System. If concordant ages are not obtained, and if there is not clear petrographic or geochemical evidence indicating possible reasons for discordance, the confidence in time constraints obtained from such chronometers is diminished. Measurement of ²³⁸U/²³⁵U ratio as part of the Pb–Pb dating procedure of samples, particularly those that can serve as time anchors, clearly has a significant implication for the accuracy of the reported dates. Moreover, this has a similarly major effect on the model ages obtained using other high-resolution chronometers based on extinct radionuclides that are anchored to these Pb–Pb dates, and could therefore impact the concordance of these various chronometers. An example of this is illustrated in Fig. 3, which shows the Pb–Pb ages (published previously in the literature; references shown in Table 2) recalculated using the measured U isotope compositions reported here for several angrites, as well as that for the unique achondrite NWA 2976 (21); these Pb–Pb ages are compared with high-resolution model ages for these samples calculated based on three extinct chronometers (Al-Mg, Mn-Cr and Hf-W; data for these chronometers are from refs. 23–25, shown in Fig. 3) using D’Orbigny as the time anchor. As can be seen in Fig. 3, there is now good agreement between the ages for these various objects using the Pb–Pb absolute chronometer and the three extinct chronometers; this would not have been the case for previously published Pb–Pb ages of the various angrites (determined using ²³⁸U/²³⁵U = 137.88; refs. 14 and 26) that were approximately 1 Ma older than shown here.

Fig. 3.

Corrected Pb–Pb ages of the angrites (shown in Table 2, and calculated using the average ²³⁸U/²³⁵U ratio of 137.780 ± 0.021 based on all angrite whole-rock samples analyzed here) and the unique achondrite NWA 2976 (calculated using its measured ²³⁸U/²³⁵U ratio; ref. 21) compared with relative ages based on short-lived chronometers (“model ages”) anchored to the corrected Pb–Pb age for D’Orbigny of 4563.37 ± 0.25 Ma. By definition, since D’Orbigny serves as the age anchor, the ages based on the short-lived chronometers for this sample are identical to its Pb–Pb age.

Finally, using the corrected age of D’Orbigny (4563.37 ± 0.25 Ma), the “canonical” Solar System initial ²⁶Al/²⁷Al ratio assuming that ²⁶Al was homogeneously distributed (27, 28), and the ²⁶Al/²⁷Al ratio at the time of crystallization of D’Orbigny (29), the age of the Solar System is calculated to be 4568.2 ± 0.4 Ma. This age is in good agreement with the Pb–Pb and Al-Mg internal isochron ages reported by Bouvier and Wadhwa (30) for CAI 2364-B1 from NWA 2364. While the Pb–Pb age of CAI 2364-B1 does not include U isotope measurement, the ²³⁸U/²³⁵U is estimated for it using its measured Th/U ratio and the correlation of the Th/U ratio with the U isotope composition in Allende CAIs (3). In comparison, high precision Pb–Pb internal isochron ages reported previously for other CAIs from Allende and Efremovka, and assuming a ²³⁸U/²³⁵U ratio of 137.88, are younger by approximately 1 Ma (28, 31, 32). A more recent determination of the internal isochron Pb–Pb age for another Allende CAI, however, does include measurement of its U isotope composition, and also has a somewhat younger age (4567.18 ± 0.50 Ma; ref. 6) compared to that of the NWA 2364 CAI. It is unclear at this time why this age discrepancy exists, but it is possible that Pb–Pb systematics in some CAIs have been disturbed by secondary processes (e.g., 33).

For obtaining the precise and accurate chronology of the early Solar System and understanding the time sequence of events during its first few millions of years, it is essential that the ²³⁸U/²³⁵U ratio be measured (and not assumed to be 137.88) when determining absolute Pb–Pb dates for meteoritic materials. This has been shown to be particularly important for refractory inclusions from the primitive chondrites in which large variations in the ²³⁸U/²³⁵U ratio (of up to approximately 3–4 per mil) have been reported (e.g., 3). This investigation demonstrates that while the ²³⁸U/²³⁵U ratio of the APB and meteorites originating from it is indeed also distinct from the previously assumed value of 137.88, it is uniform (at the current level of precision). Although the U isotope compositions of several other meteorite types remain to be measured, this study as well as some other recent investigations of the U isotope compositions of bulk sample of various undifferentiated and differentiated meteorites suggest that ²³⁸U/²³⁵U ratio in the early Solar System was homogenous on the scale of bulk samples.

Materials and Methods

Multiple fragments of the D’Orbigny meteorite were obtained, two from the Center for Meteorite Studies (CMS) at Arizona State University (ASU) and one from R. Carlson (Carnegie Institution of Washington). Whole-rock samples of NWA 4590, NWA 4801, and NWA 6291 were obtained from the CMS. Interior fragments of all meteorites were obtained for our analyses to avoid fusion crust and to minimize any terrestrial contamination. All chemical processing was performed under clean laboratory conditions in the Isotope Cosmochemistry and Geochronology Laboratory (ICGL) at ASU. One whole-rock sample of D’Orbigny (1.1612 g) was gently crushed with agate mortar and pestle, sieved, and 174 mg of clean pyroxenes were separated by hand-picking. This pyroxene separate was then agitated in an ultrasonic bath for 5 min in 0.05 M HCl. Other whole-rock samples of D’Orbigny (0.5969 g and 0.7281 g), NWA 4801 (0.6112 g), NWA 4590 (0.7375 g), and NWA 6291 (0.6454 g) were crushed and washed following the same procedure. The samples were completely dissolved in Savillex® beakers using a mix of concentrated HNO₃, HF, and HCl. An additional piece of NWA 6291 (0.3400 g) was leached with 0.5 M HNO₃ (ultrasonicated for 5 min), and the leachate (designated as “Leach”) was reserved for analysis. The residue remaining from this acid leaching (designated as “Residue”) was completely dissolved using a mix of concentrated HNO₃, HF, and HCl. Hand-picked phosphates (5.4 mg) from ADOR were provided by G. J. Wasserburg (Caltech) and were dissolved directly in 3 M HNO₃. Approximately 5% of each dissolved sample used in this study was reserved for trace element measurements. Uranium was separated from the remaining sample solutions for measurement of the ²³⁸U/²³⁵U ratio, following previously published procedures (3, 34).

Uranium isotope measurements were performed on a Thermo Finnigan Neptune multicollector inductively coupled plasma mass spectrometer (MC-ICPMS) in the ICGL. All samples were measured using a ²³⁶U∶²³³U double-spike to correct for instrumental mass bias. The ADOR phosphate separate, the D’Orbigny pyroxene separate, and one of D’Orbigny whole-rock samples were spiked with an in-house ASU double spike. The ASU double spike consists of an approximately 1∶1 ratio of ²³⁶U and ²³³U with the minor contributions of ²³⁵U and ²³⁸U subtracted during data reduction (²³⁶U/²³³U = 1.00496; ²³⁸U/²³³U = 0.000958; ²³⁵U/²³³U = 0.000108). The second D’Orbigny whole-rock sample, the whole-rock samples of NWA 4590, NWA 4801, and NWA 6291, as well as the leach and residue from NWA 6291 were spiked with the gravimetrically prepared IRMM-3636 double spike (35). Additional information regarding sample specifics and uranium double-spike information is given in the SI Text.