Accurate de novo structure prediction of large transmembrane protein domains using fragment-assembly and correlated mutation analysis

Abstract

A new de novo protein structure prediction method for transmembrane proteins (FILM3) is described that is able to accurately predict the structures of large membrane proteins domains using an ensemble of two secondary structure prediction methods to guide fragment selection in combination with a scoring function based solely on correlated mutations detected in multiple sequence alignments. This approach has been validated by generating models for 28 membrane proteins with a diverse range of complex topologies and an average length of over 300 residues with results showing that TM-scores > 0.5 can be achieved in almost every case following refinement using MODELLER. In one of the most impressive results, a model of mitochondrial cytochrome c oxidase polypeptide I was obtained with a TM-score > 0.75 and an rmsd of only 5.7 Å over all 514 residues. These results suggest that FILM3 could be applicable to a wide range of transmembrane proteins of as-yet-unknown 3D structure given sufficient homologous sequences.

Alpha-helical transmembrane proteins (TMPs) constitute roughly 30% of a typical genome and play critical roles in a diverse range of biological processes whereas many are also important drug targets. Despite the recent increase in the number of solved TMP crystal structures, coverage of TMP fold space remains sparse, particularly at high resolutions, with close to 300 unique structures deposited as of 2011 (1). Computational methods to predict TMP structure are therefore vital in helping to further our knowledge of the structure and function of these proteins.

To date, TMP structure prediction has been dominated by topology prediction. Machine learning-based predictors, trained and validated using topology data derived from structural data combined with evolutionary information, now achieve prediction accuracies in the range 80–90% (2, 3). Another approach, based on an experimental scale of position-specific amino acid contributions to membrane insertion free energy, achieves similar accuracy suggesting that predicting TMP topology from first principles is an achievable goal (4).

As with globular proteins, predicting the structure of TMPs by homology modeling is very effective particularly when TMP-specific methods are used (5); however, the paucity of solved structures means that homology modeling can only be applied to a minority of TMP families. With this in mind, a small number of de novo modeling approaches, which attempt to build 3D models for TMPs without the use of homology to known structures, have also been developed.

FILM (6), a modification of the globular protein structure prediction method FRAGFOLD (7, 8), attempts to assemble folds from supersecondary structural fragments taken from a library of highly resolved protein structures using simulated annealing. FILM differs from FRAGFOLD in the addition of a membrane environment potential, derived from the statistical analysis of 640 transmembrane helices, by measuring the relative frequencies of each amino acid at fixed distances from the membrane center. These values were transformed into energy-like terms by applying the inverse Boltzmann equation. FILM was shown to be able to predict the correct topology and conformation for four out of five small protein domains of up to 79 residues at a reasonable level of accuracy. The main limitation of FILM was that the potential function was unable to reproduce the compactness of large transmembrane helix bundles that are often not as compact as globular helical proteins. FILM2 improved upon the prediction of larger bundles by incorporating prediction of lipid exposure from variphobicity analysis (9) into the original FILM potential function allowing models of seven-helix bacteriorhodopsin and rhodopsin to be generated to within 6–7 Å rmsd of the native structures (10).

Like FRAGFOLD, Rosetta (11–13) assembles folds from fragments of known structures with local sequence similarity to the target. Again, statistical potentials and simulated annealing are used to find low energy structures. An adaptation of Rosetta, RosettaMembrane (14), added an energy function that described membrane intraprotein interactions at atomic level and membrane protein/lipid interactions implicitly while treating hydrogen bonds explicitly. This allowed the prediction of 12 small TMP domains of up to 150 residues to within 4 Å rmsd of the native structures suggesting that the essential physical properties that govern the solvation and stability of TMPs were being captured. A subsequent development allowed a small number of distance constraints to be applied to helix-helix packing arrangements, predicted from sequence (15–17) or identified from experimental data, allowing larger structures of between 90 and 300 residues with a diverse range of topologies to be predicted with reasonable accuracy (18). Results showed that only a single constraint was sometimes enough to enrich the population of near-native models; whereas, models within 4 Å of the native structure could be achieved in four cases.

The use of knowledge-based potentials derived from statistical analyses of known TMP structures has been the standard approach for de novo prediction of these proteins. Recently, however, significant progress has been made in inferring residue-residue contacts directly from evolutionary information, i.e., from the observation of correlated mutations in multiple sequence alignments (MSAs). Given a sufficiently accurate list of contacts, it has long been realized that the native fold of a protein can easily be deduced from this information alone (19, 20); however, accurate prediction of residue-residue contacts has been the bottleneck.

The main source of information exploited in contact prediction is that of correlated mutations observed between sites in aligned protein families. Although the causal link between residue-residue contacts and correlated mutations is not fully understood, the underlying hypothesis is that any given contact, critical for maintaining the fold of a protein, will constrain the physicochemical properties of the two amino acids involved. Should either or both contacting residues mutate, this is likely to disrupt the stability of the contact and, thus, reduce the stability of the native structure. In such a situation, one or both residues are more likely to mutate to a more physicochemically complementary amino acid pairing. Thus, pairs of residues seen to coevolve in tandem, therefore preserving their relative physicochemical properties, are likely to be proximate in the native structure.

Although many different approaches have been proposed for predicting contacts from sequence data (19–31), success has remained relatively modest (32). The major obstacle in contact prediction has been dealing with indirect coupling effects that arise where direct physical coupling between sites AB and BC result in apparent correlations between sites AC even though no direct interaction exists between AC. Lapedes et al. (33) related the problem of decoupling mutation correlations in MSAs to the inverse Ising problem in statistical physics and proposed a solution based on entropy maximization; however, it is only recently that practical solutions to the decoupling problem have been proposed (34–36) and applied to protein structure prediction (37).

Recently, we developed a new contact prediction approach called PSICOV (38) that makes use of sparse inverse covariance estimation (SICE) techniques to overcome effectively the indirect coupling effects that plague correlated mutation analysis of sequence alignments. When sufficient homologous sequences are available, results of using PSICOV to predict contacts from sequence alignments can be quite remarkable. In some cases, the accuracy of contact prediction can approach 80% even for long-range contacts (i.e., contacts separated by > 23 residues in the sequence).

We have already shown that contacts predicted using PSICOV are enough on their own to identify the native fold for medium-sized (< 200 residues) globular βα protein domains (39); however, it was apparent from this work that an ideal application for the approach would be in predicting the folds for alpha-helical TMP domains. Due to the geometric constraints of the helices and the architectural constraints provided by the lipid bilayer, the contacts predicted by PSICOV should be more than sufficient to identify correctly the native fold even for large TMPs.

With this in mind, we have modified the original FILM method by replacing the statistical potentials with a single scoring function based simply on predicted contacts and estimated probabilities. To show the power of PSICOV in predicting long-range contacts, we have deliberately avoided the use of knowledge-based potentials or other statistically derived scoring functions in FILM3. In this way, the predictions can be considered purely de novo, i.e., using only information derivable from the target sequence (and its homologues) to produce a 3D model.

Results

In this section, we describe the results of applying FILM3 to the 28 target sequences listed in Table 1. These targets have a diverse range of complex topologies, containing between four and twelve transmembrane helices, in addition to unusual features such as reentrant and interfacial helices. Furthermore, they are signficantly larger than those used in any previous TMP de novo modeling study having an average length close to 300 residues and a maximum of 531. Several targets also contained irregular regions within transmembrane helices that disrupt the backbone conformation and lead to deviations in helix direction whereas most displayed a wide distribution of helix tilt angles with respect to the membrane normal rather than idealized up-down helix packing. As PSICOV requires fairly large MSAs to be most effective, only targets with large numbers of homologous sequences were selected. As a result, the long-range (> 23 residue separation) top-L/2 (where L is the length of the protein) predicted contact precision values exceeded 0.4 in 64% of targets (Table 1).

Table 1.

Modeling targets. Topology indicates the number of transmembrane helices. Contact performance by PSICOV (38) is based on L/2 precision (i.e., top-L/2 predictions for a protein of length L)

						Top L/2 contact precision at sequence separation
PDB	Protein	Length	Topology	MSA size	Total	5–9	10–22	> 23
1fftC	Ubiquinol Oxidase	185	5	6805	0.215	0.125	0.056	0.237
1gzmA	Rhodopsin	329	7	38101	0.576	0.205	0.333	0.515
1ldiA	Glycerol uptake facilitator	254	6	3899	0.633	0.448	0.423	0.523
1pw4A	Glycerol-3-Phosphate Transporter	434	12	82032	0.596	0.202	0.432	0.587
1xqfA	Ammonia Channel	362	11	3177	0.670	0.469	0.667	0.571
2abmH	Aquaporin Z	227	6	4035	0.632	0.368	0.577	0.518
2b2fA	Ammonium transporter Amt-1	391	11	3188	0.694	0.500	0.674	0.577
2d2cN	Cytochrome b6f	202	4	37253	0.373	0.125	0.286	0.265
2d57A	Aquaporin-4	224	6	4082	0.602	0.400	0.359	0.487
2f2bA	Aquaporin Aqpm	245	6	3893	0.683	0.410	0.462	0.634
2feeB	ClC chloride transporter	441	10	3516	0.457	0.099	0.143	0.417
2nq2A	ABC transporter permease HI1471	308	10	8071	0.697	0.311	0.523	0.626
2nr9A	Protease GlpG	192	6	3979	0.536	0.265	0.269	0.433
2occA	Mitochondrial cytochrome c oxidase	514	12	165064	0.624	0.476	0.500	0.535
2onkC	Molybdate transporter ModBC	252	6	62736	0.646	0.306	0.429	0.488
2q7rA	FLAP protein	140	4	479	0.239	0.000	0.036	0.268
2qfiA	Zinc transporter YiiP	286	6	5418	0.194	0.192	0.175	0.111
2r6gG	Maltose transporter MalFGK	284	6	42217	0.615	0.145	0.543	0.500
2witA	Sodium-betaine symporter BetP	531	12	1803	0.407	0.146	0.149	0.313
2wswA	Carnitine transporter	508	12	1827	0.405	0.167	0.128	0.331
2ydvA	Adenosine receptor A2A	315	7	38924	0.595	0.197	0.276	0.532
2z73A	Rhodopsin	350	7	37139	0.636	0.169	0.359	0.534
3b9wA	RH50 protein	362	11	3211	0.489	0.229	0.606	0.407
3dhwA	Methionine importer MetNI	203	5	66018	0.343	0.128	0.105	0.349
3mk7A	Cytochrome c oxidase, cbb3 type	466	12	16147	0.308	0.130	0.250	0.291
3mktA	MDR efflux pump	460	12	10035	0.342	0.378	0.368	0.247
3pjzA	Potassium uptake protein TrkH	468	12	2598	0.472	0.341	0.448	0.366
3qnqA	Saccharide transporter component ChbC	432	10	1967	0.560	0.257	0.211	0.413

Table 2 summarizes GDT-TS, TM-score, and rmsd scores for all models; whereas, Table 3 gives model energies and corresponding TM-scores after the various stages of the FILM3 procedure. Fig. 1 illustrates some of the best predictions. Results indicate that all targets, except for three, achieved a TM-score > 0.5 indicating a correct overall fold. Of the models with a TM-score below 0.5, FLAP protein (PDB 2q7rA) correctly places 3 of 4 transmembrane helices while the fourth, which partially aligns in our model, is stabilized by interchain contacts in the native homotrimeric complex. Similarly, the zinc transporter YiiP (2qfiA) model is let down by poor contact prediction at the C terminus. In the native state, YiiP is a homodimer held together in a parallel orientation by four Zn²⁺ ions in a tetrahedral binding site at the interface of the C-terminal cytoplasmic domains. The transmembrane domain consisting of a bundle of six helices is, however, reasonably well modeled resulting in a TM-score of 0.58 for nonloop residues (Table 2). Sodium-betaine symporter BetP (2witA), a homotrimeric structure with a complex twelve helix topology, is also stabilized by significant interactions between monomers. These include interactions between amphipathic helix 7, which makes contact with helices 2, 3, 9, and 7 from the other two monomers, and a long osmosensing C-terminal helix that interacts with loop 2 and the C termini of the other monomers via a salt bridge. This helix is modeled poorly though the majority of the transmembrane helices are reasonably placed with respect to their native positions.

Table 2.

Summary of model quality. GDT-TS, TM-Score and rmsd values are calculated over all residue Cα atoms (Left) and nonloop Cα atoms only (Right)

	Over all residues			Over nonloop residue subset
PDB	GDT-TS	TM-score	RMSD	GDT-TS	TM-score	RMSD	Superposed residues	Length
1fftC	42.03	0.564	5.86	52.97	0.669	4.50	101	185
1gzmA	42.71	0.654	9.63	55.78	0.790	3.79	212	329
1ldiA	44.29	0.677	5.37	52.46	0.744	3.93	173	254
1pw4A	36.81	0.660	8.90	42.77	0.723	5.35	318	434
1xqfA	44.61	0.721	5.40	52.08	0.786	4.14	253	362
2abmH	52.42	0.726	4.64	59.85	0.796	3.34	165	227
2b2fA	38.68	0.689	6.02	43.59	0.728	5.27	269	391
2d2cN	41.34	0.568	7.77	51.99	0.692	4.38	113	202
2d57A	55.13	0.745	4.20	62.34	0.817	2.78	160	224
2f2bA	50.31	0.719	5.49	57.88	0.792	3.30	165	245
2feeB	32.94	0.629	8.85	36.00	0.651	8.77	309	441
2nq2A	42.29	0.653	5.98	46.17	0.671	5.68	222	308
2nr9A	41.28	0.570	6.98	52.69	0.678	4.83	121	192
2occA	41.25	0.753	5.72	49.56	0.833	3.95	339	514
2onkC	42.96	0.626	6.92	48.33	0.678	5.88	195	252
2q7rA	27.50	0.324	8.87	34.67	0.367	7.21	106	140
2qfiA	26.31	0.467	10.94	46.25	0.582	8.30	60	286
2r6gG	32.22	0.501	9.81	38.84	0.558	7.74	177	284
2witA	14.60	0.364	21.11	17.35	0.382	19.96	392	531
2wswA	24.31	0.503	14.12	29.54	0.563	12.45	391	508
2ydvA	40.56	0.668	7.29	46.52	0.724	6.08	237	315
2z73A	41.00	0.634	12.93	51.08	0.746	8.37	231	350
3b9wA	38.26	0.624	13.64	43.67	0.666	13.81	245	362
3dhwA	42.73	0.582	8.30	45.80	0.597	7.97	143	203
3mk7A	26.88	0.534	9.91	32.45	0.582	8.49	329	466
3mktA	39.02	0.689	6.75	43.77	0.730	5.44	317	460
3pjzA	39.74	0.718	6.05	49.36	0.797	4.54	272	468
3qnqA	27.95	0.532	10.23	36.11	0.626	7.55	261	432

Table 3.

Summary of model quality at each step in the FILM3 process. Energy and Template Modeling (TM) scores are shown for ensembles generated with and without Z-coordinate distance constraints, after recombination and after refinement

		Ensemble without Z-coordinate constraints		Ensemble with Z-coordinate constraints		After recombination		After refinement
Target	Native structure energy	Minimum energy	Best TM-score	Minimum energy	Best TM-score	Energy	TM-score	Energy	TM-score
1fftC	−25.7	−55.3	0.56	−56.2	0.60	−57.6	0.56	−50.7	0.56
1gzmA	−178.9	−214.7	0.65	−217.3	0.65	−222.9	0.66	−210.6	0.65
1ldiA	−92.8	−94.6	0.65	−95.3	0.67	−102.4	0.64	−95.0	0.68
1pw4A	−279.5	−315.5	0.63	−312.1	0.67	−335.7	0.65	−316.7	0.66
1xqfA	−147.9	−135.4	0.50	−130.9	0.69	−154.4	0.72	−142.1	0.72
2abmH	−82.9	−86.7	0.69	−86.3	0.70	−92.8	0.71	−88.7	0.73
2b2fA	−199.6	−172.6	0.66	−145.5	0.64	−183.6	0.68	−169.4	0.69
2d2cN	−41.6	−60.2	0.53	−60.1	0.49	−67.7	0.54	−55.3	0.57
2d57A	−83.8	−86.2	0.70	−87.4	0.71	−96.6	0.74	−89.2	0.75
2f2bA	−99.8	−103.0	0.72	−95.9	0.63	−108.2	0.70	−100.8	0.72
2feeB	−86.2	−103.9	0.59	−84.8	0.36	−105.9	0.61	−92.3	0.63
2nq2A	−161.9	−160.4	0.64	−133.0	0.61	−166.4	0.65	−160.2	0.65
2nr9A	−60.8	−73.5	0.66	−68.4	0.56	−76.3	0.56	−71.1	0.57
2occA	−233.7	−202.3	0.38	−215.2	0.54	−224.6	0.72	−217.2	0.75
2onkC	−117.0	−128.4	0.55	−130.1	0.63	−134.9	0.64	−128.8	0.63
2q7rA	−14.2	−24.3	0.25	−23.1	0.38	−24.5	0.40	−11.6	0.32
2qfiA	−39.2	−111.9	0.46	−92.2	0.38	−112.4	0.46	−100.8	0.47
2r6gG	−195.4	−200.8	0.50	−194.1	0.49	−203.2	0.51	−185.3	0.50
2witA	−141.1	−94.5	0.35	−90.6	0.36	−94.9	0.35	−79.7	0.36
2wswA	−140.0	−110.5	0.55	−105.9	0.42	−112.3	0.46	−99.9	0.50
2ydvA	−176.3	−213.7	0.64	−208.8	0.60	−218.9	0.65	−209.4	0.67
2z73A	−195.8	−223.7	0.59	−221.2	0.57	−224.3	0.62	−213.8	0.63
3b9wA	−111.9	−137.0	0.52	−112.2	0.60	−145.5	0.61	−137.9	0.62
3dhwA	−48.7	−83.6	0.58	−82.9	0.63	−85.0	0.56	−74.9	0.58
3mk7A	−167.4	−167.9	0.46	−168.5	0.42	−178.0	0.48	−149.2	0.53
3mktA	−160.1	−247.4	0.68	−250.6	0.70	−280.2	0.69	−269.1	0.69
3pjzA	−180.7	−174.1	0.68	−139.8	0.44	−178.1	0.70	−165.4	0.72
3qnqA	−132.0	−124.5	0.52	−123.2	0.39	−126.7	0.52	−117.2	0.53

Best TM-score indicates the TM-score for the minimum energy model.

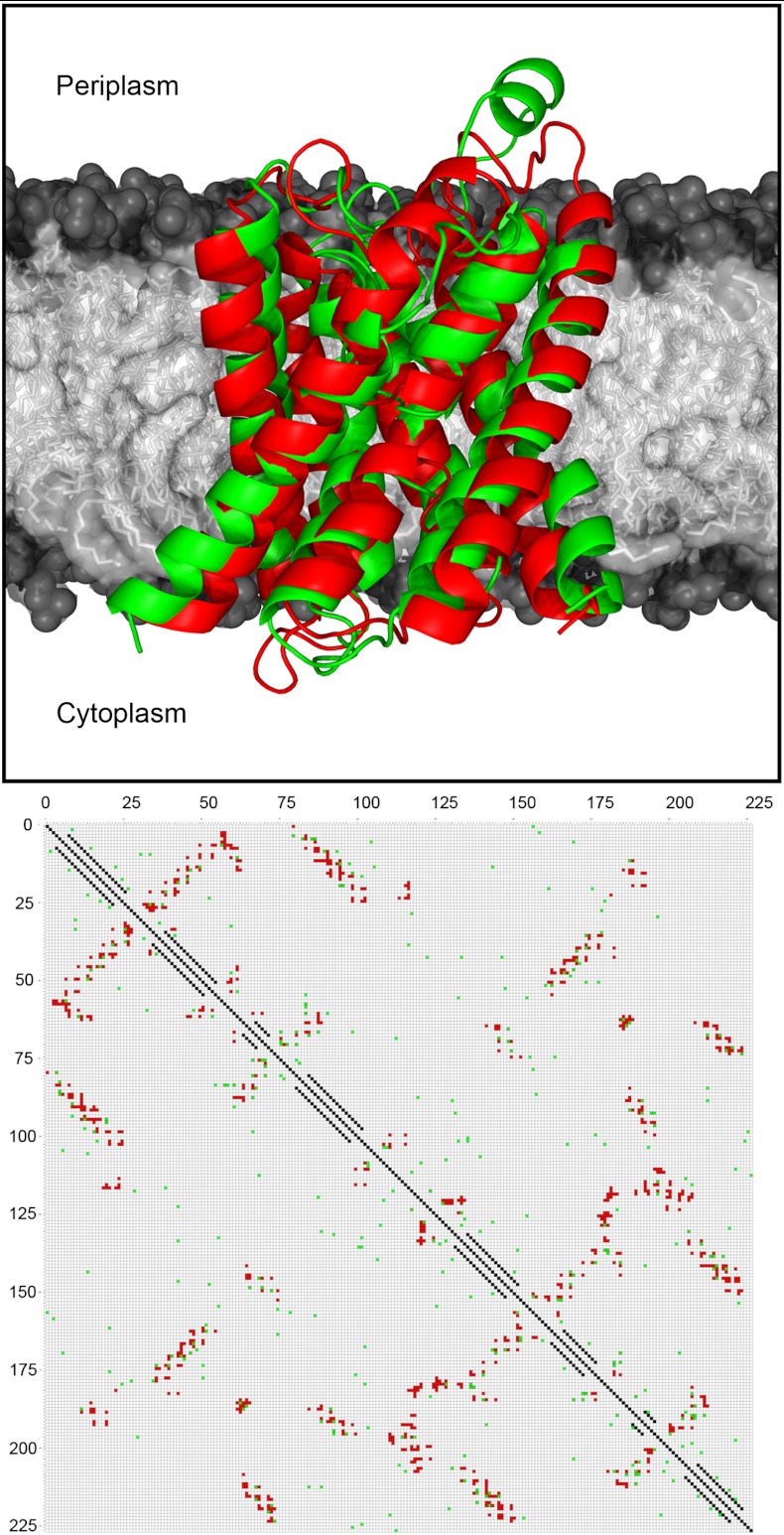
Fig. 1.

Prediction of TMP structures. Superposition between native (red) and models (green) of (A) Rhodopsin (1gzmA), (B) Cytochrome c oxidase (2occA), (C) Ammonium transporter Amt-1(2b2fA), (D) Aquaporin-4 (2d57A), (E) Ammonia channel (1xqfA), (F) MDR efflux pump (3mktA). The two black lines indicate the approximate position of the membrane.

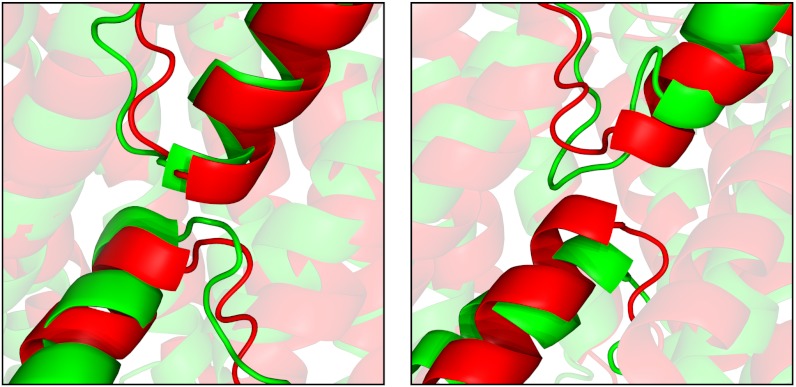
Of particular note were six models with TM-scores > 0.7 including cytochrome c oxidase (PDB 2occA) where 9 out of 12 transmembrane helices were perfectly placed (Fig. 1B) and, again, the less accurately placed helices all forming stabilizing interactions with additional chains in the native complex. The overall model has a global Cα rmsd of only 5.7 Å across all 514 residues, which indicates a globally correct native fold has been clearly identified. Targets belonging to the aquaporin superfamily fared very well with all six transmembrane helices accurately modeled (Fig. 1D). Additionally, the two reentrant helices containing the NPA motif, whose asparagine residue plays a vital role in water selectivity (40), are also accurately positioned adjacent to the central channel (2d57A, Fig. 2). Reentrant regions were also well modeled in the glycerol uptake facilitator (1ldiA, Fig. 2). Interfacial helices were generally positioned correctly, for example in rhodopsin (1gzmA), where it is essential for binding the G-protein transducin suggesting that, in general, they form important stabilizing contacts with adjacent transmembrane helices or loops in addition to their expected role in constraining interhelix distances (41). Other than its N terminus, a series of beta strands that may form a “lid” over the retinal binding site (42) but that is poorly conserved across the whole family resulting in low contact prediction performance for this region, rhodopsin produces an excellent model with a TM-score of 0.65, with only minimal deviations from the native helix axes (Fig. 1A) and a TM-score of 0.79 over nonloop residues. We note that Marks et al. (37) have recently used a similar combination of contact prediction and constraint satisfaction to achieve comparable performance on a 258 residue fragment of bovine rhodopsin (the fragment corresponding to the truncated 7TM_1 alignment found in Pfam). In their case, a TM-score of 0.5 (Cα rmsd of 4.8 Å over 171 residues) was achieved on this region though, notably, this was accomplished in the absence of predicted transmembrane topology information. The ammonia channel (1xqfA), a protein with a complex 11 transmembrane helix topology, also produces a good model with a TM-score of 0.72 while reproducing the significant helix tilt angles present in the native structure, particularly helix 11 that is tilted ≈45° and lies across the membrane-exposed side of the monomer (Fig. 1E).

Fig. 2.

Re-entrant helices in Aquaporin-4 (2d57A, Left) and Glycerol uptake facilitator (1ldiA, Right). Superposition between native (red) and models (green).

In two cases, topology predictions were incorrect due to under or over prediction of transmembrane helices. MEMSAT-SVM under predicted the ABC transporter permease (2nq2A) topology by two helices; whereas, the potassium uptake protein (3pjzA) topology was over predicted by one helix. In each case, the Z-coordinate constraints imposed by the missing or additional helices resulted in models with a number of misplaced transmembrane helices as FILM3 was constrained from finding the native structure; however, these models were easily detected, having higher energies than equivalent models generated without Z-coordinate constraints (Table 3) allowing correct models with TM-Scores of 0.64 and 0.68 to be generated from the conformations without Z-coordinate constraints. All models were also superposed with their native structures and carefully inspected to evaluate the correctness of topology using transmembrane helix locations. Aside from models with an incorrectly predicted topology or where interactions with additional chains appear to play a role in stabilizing the fold, only two additional chains with a TM-scores > 0.5, the carnitine transporter (2wswA, TM-score 0.503) and cytochrome oxidase CBB3 (3mk7A, TM-score 0.534), both twelve helix structures, contained a single transmembrane helix that did not clearly overlap with the corresponding helix in the native structure.

In general, ensembles generated with Z-coordinate constraints contained lower energy models in eight cases, six of which have a higher TM-score than the lowest energy model generated without Z-coordinate constraints (Table 3). In some cases, such as cytochrome c oxidase (2occA) and the ammonia channel (1xqfA), the improvement in TM-score is significant (> 0.15); however, in a further eight cases, models from ensembles generated with Z-coordinate constraints have a higher energy and higher TM-score than models from ensembles lacking the constraints. This suggests that the Z-coordinate constraints are useful for half of the targets but that the final objective function is ineffective at discriminating these additional cases where the energy is higher. Targets producing ensembles with higher TM-scores without the filter tended to have more complex topologies suggesting that the simple linearly extrapolated Z-coordinate approximation is insufficient in such cases. The benefits of the recombination step were more obvious, with higher TM-scores in 18 cases, whereas final refinement using MODELLER improved the recombined models in 22 cases (Table 3).

Discussion

TMP structure prediction remains a challenging problem and is particularly important in the context of the difficulties associated with experimentally determining structures for this class of protein. To address this, we have developed FILM3, a de novo folding method that is able to predict accurately the structures of large and complex TMP domains using a scoring function based solely on the estimated probabilities of residue-residue contacts predicted using PSICOV applied to large MSAs. We have validated this approach by generating models for 28 targets with a diverse range of complex topologies and an average length of over 300 residues with results demonstrating that mostly correct folds [TM-scores > 0.5 (43)] can be achieved in almost all cases.

These results clearly indicate that contacts predicted by PSICOV are indeed more than sufficient to identify correctly the native folds of even large TMP domains where large numbers of homologous sequences are available and that near-atomic resolution de novo structure prediction using FILM3 could well be an achievable goal in the future. We specifically wished to exclude statistical potentials or physics-based force fields in the current work to demonstrate the power of PSICOV in accurately predicting residue-residue contacts and the ability of FILM3 to generate native-like structures from this information alone; however, an obvious next step is to consider augmenting FILM3 with traditional knowledge-based potentials that should further increase performance towards the goal of near-atomic resolution modeling.

The fact that such high modeling accuracy can be obtained simply from evolutionary analysis of large sequence families is, nonetheless, remarkable. Also, as TMP families tend to be very large, FILM3 should be applicable to many TMPs of biomedical interest. From the results of this study, we can see that contacts predicted by PSICOV appear to yield sufficient precision where MSAs contain upwards of 400 sequences. Analysis of the current Pfam database (44) suggests that, even today, more than 500 single architecture transmembrane domain families exist with > 400 aligned family members and yet have no experimentally determined 3D structure. Also, as more sequence data arrives from next generation sequencing, this number will be expected to rise rapidly. Considering that only 50 polytopic alpha-helical TMP superfamilies have been structurally characterized to date (45), applying FILM3 to these Pfam domains has the potential to expand our knowledge of TMP fold space significantly.

Although our results demonstrate an impressive advance in de novo TMP modeling, it is clear that more sophisticated strategies will be required to overcome a number of current limitations. Modeling of extramembranous loops is substantially more challenging than transmembrane regions primarily due to sparsely or poorly predicted contacts as demonstrated by the average difference in TM-scores over all residues compared to secondary structure regions only (Table 2). Inherent loop flexibility, often essential for channel gating functionality, poses particular difficulties for contact-based folding methods and may be handled more effectively using an energy function with an appropriate solvation energy term. Notably, targets that are particularly well predicted such as cytochrome c oxidase and aquaporin family members tend to undergo relatively little conformational change upon activation as opposed to a number of transporters that exhibit distinct alternate conformations therefore requiring different sets of contacts to stabilize each state. In such cases, model quality appears to be limited by the inability to satisfy such multiple sets of contacts simultaneously. Another issue is the stabilization of chains via interactions between monomers in complexes that affected all of our poorest models. TMP complexes are thought to assemble in a rapid and orderly fashion allowing stabilizing interactions to form between adjacent chains. Clearly, without knowledge of these interactions, the FILM3 objective function will struggle to discriminate between appropriate conformations. Future modifications to PSICOV to allow contacts to be predicted between chains may enable membrane complexes to be folded by allowing the objective function to evaluate all inter- and intrachain contacts simultaneously (i.e., combined folding and docking).

Despite these shortcomings, FILM3 is clearly a powerful tool to allow complex TMP domains to be modeled entirely de novo to unprecedented levels of accuracy for domains of such sizes. These predicted models will hopefully prove valuable for directing experimental studies on TMP families where structural data is currently unavailable. Although the results here only cover TMP structure prediction, the high level of success on this difficult problem alludes to future promise in predicting the structure of globular protein domains using similar techniques. Indeed, recent work (37, 39) has already demonstrated that models for small globular proteins (size range 48–223 amino acids) can be generated to a comparably high degree of accuracy using a similar combination of contact prediction and constraint satisfaction, further demonstrating the immense value of contacts predicted by methods such as PSICOV when applied to large MSAs to de novo protein structure prediction.

Methods

Contact Prediction.

At the heart of FILM3 is PSICOV, a novel contact prediction method based on SICE (38). The method begins by computing a 21m by 21m sample covariance matrix using the observed single amino acid and amino acid pair occurrence frequencies observed in a MSA with m columns:

[1]

where f(A_iB_j) is the observed relative frequency of amino acid pair ab at columns ij, f(A_i) is the observed relative frequency of amino acid type a at column i, and f(B_j) is the observed frequency of amino acid type b at column j.

To identify directly coupled residue pairings, we apply the graphical Lasso approach of Banerjee et al. (46) as implemented by Friedman et al. (47) to the above empirical covariance matrix to determine a sparse inverse covariance matrix (Θ). To arrive at the final predictions of contacting residues for alignment columns i and j, the ℓ₁-norm is calculated for the 20 × 20 submatrix of Θ corresponding to the 20 × 20 amino acid types ab observed in the two alignment columns (contributions from gaps are ignored):

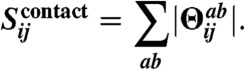[2]

To calculate a final score that has reduced entropic and phylogenetic bias, we correct the raw precision norms 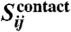as follows:

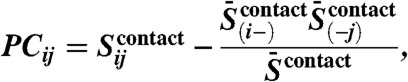[3]

where 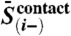is the mean precision norm between alignment column i and all other columns, 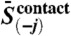is the equivalent for alignment column j, and 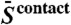is the mean precision norm across the whole alignment.

Finally, to estimate the precision or Positive Predictive Value for each predicted contact, the raw results from the original 150 globular protein test set for PSICOV were analyzed. For each target, PC_ij scores were first converted to Z-scores by subtracting the mean and dividing by the standard deviation of the scores obtained for that target. The Z-scores for all 150 targets were then pooled and the PPVs calculated for binned Z-score ranges. These binned PPVs were then fitted against a standard logistic function to give the following empirical formula for estimating PPVs from Z-scores:

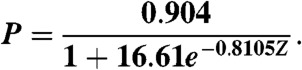[4]

Dataset Construction.

We selected 28 TMP families with structures in the PDB (http://www.pdb.org) (48) as our targets. Selection criteria were for the families to be large, to have multiple spanning transmembrane helices, a complex topology, and a fold that was independent of other chains (i.e., the transmembrane domains selected were reasonably compact when considered in isolation from the rest of their subunits). Alignments were generated automatically for each of the target proteins using the jackhmmer program that is part of the HMMER 3.0 package (http://hmmer.org) (49). For each of the 28 target sequences (derived from the Cα ATOM records in the relevant PDB files), three iterations of jackhmmer with an E-value threshold of 10^-6 (for profile inclusion and alignment output) and searching against the UNIREF100 data bank (50), were used to find and align a homologous sequence. In the final alignments, duplicate rows (i.e., sequences 100% identical over the length of the alignment) and columns with gaps in the target sequence were removed. Numbers of distinct sequences in each alignment ranged from 479 (FLAP protein) to 165,064 (mitochondrial cytochrome c oxidase). Further alignment statistics can be found in Table S1 though no obvious correlations could be seen between the eventual model quality and any of these statistics. At best, we surmise that the total number of observed substitutions is the principle factor in determining eventual prediction success.

Fragment Selection.

For each residue position in the target sequence, compatible supersecondary structural fragments were preselected from a fragment library generated from 224 highly resolved (< 1.5 Å) globular protein structures (Table S2). Using globular proteins ensures that the possibility of using homologous fragments can be excluded while allowing a large fragment library to be established because relatively few TMP structures have been resolved to high resolution. Fragments were selected by considering local sequence similarity (using standard PSI-BLAST PSSM tables) and compatibility of the fragment with predicted contacts using the contact-based objective function. In addition to supersecondary fragments, fixed-length fragments of nine residues were also considered. In both cases, fragments were not considered where there was disagreement with predicted secondary structure using PSIPRED version 3.2 (51) and MEMSAT-SVM (3). At each position in the target sequence, a list of the five best scoring supersecondary fragments and the 25 best nine-residue fragments is stored. A generic fragment list was also constructed from all dipeptide and tripeptide fragments from the library of highly resolved structures, though these smaller fragments were not preselected, i.e., they were chosen at random and uniformly throughout the simulation. During the simulation, a random change of conformation is effected by selecting a supersecondary fragment, a nine-residue fragment, or from the generic list of small fragments (the three types of fragment are sampled equally).

Secondary Structure and Topology.

Rather than using PSIPRED alone for fragment selection, as is the case for FRAGFOLD, in FILM3 we also made use of MEMSAT-SVM predictions of transmembrane helices. Predictions were combined using a simple consensus scheme (see SI Text) with scoring thresholds for the two methods optimized using 99 TMPs of known structure that had insufficient homologous sequences available to be used as prediction targets (Table S3). We further checked that these proteins had no detectable sequence homology to the targets (E-value < 0.001) or were members of the same OPM (45) superfamily. Raw residue preference scores for each method were used to determine the ensemble with strong transmembrane helix predictions overriding PSIPRED predictions. Where MEMSAT-SVM did not predict helix, the ensemble was constructed using helix, coil, or helix/coil depending on PSIPRED confidence, whereas sheet was only used in rare cases where PSIPRED confidence was high. Additionally, a small amount of coil was enforced in the center of predicted transmembrane loops if it did not already exist in the ensemble.

Objective Function.

FILM3 uses an objective function that is entirely based on distance restraints that are inferred only from the MSA and predicted transmembrane topology. PSICOV is first used to generate a list of predicted contacts from the target MSA along with precision estimates (P) for each contact. Where a contact is predicted, a constraint on the Cβ-Cβ distance (d) between the two given residues is applied according to the following energy-like objective function:

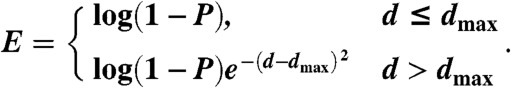[5]

A table of values for d_max can be calculated for each pair of amino acids in the target sequence. This table is calculated by tabulating the maximum Cβ-Cβ distance observed for each pair of sites that show significant covariation signals (P≥0.5) in the original 150-protein globular protein dataset used to benchmark PSICOV (38). For underrepresented amino acid pairs (n < 10), a default upper bound value of 10 Å was used for d_max. The complete table is presented in Table S4. The use of amino acid pair specific maximum contact distances has a small but measurable effect on overall model quality. For example, Fig. S1 shows the results of running FILM3 with the usual fixed cut-off distance of 8 Å compared to using Table S4. Over all 28 targets, the mean absolute TM-score improvement is 0.07, which is a useful but not critical improvement to overall prediction accuracy.

Although the above objective function is formulated as a pseudoenergy function, it is purely a mathematical transformation of the predicted contact probabilities and the degree of satisfaction of the implied distance constraints. The identification of the native protein fold, therefore, depends purely on the ability of PSICOV to predict accurately residue contacts from directly coupled correlated mutations observed in large MSAs.

Minimum Distance Constraints.

Predicted contacts provide only upper bounds on residue-residue distances, but some lower bound distances can also be inferred by other means. The most obvious of these are lower bound distance constraints of 4.5 Å between all pairs of Cα atoms (for sequence separations > 1). These constraints simply account for excluded volume effects (i.e., steric hindrance between residues). A further source of minimum distance constraints arises from our knowledge of the target protein’s transmembrane topology and the simple meandering nature of alpha-helical transmembrane protein folds. From this information alone, we can deduce approximate Z-coordinate values—the distance a residue lies from the center of the membrane—for residues in each transmembrane spanning segment.

By assuming the midpoint of each transmembrane helix is located at Z ≈ 0, Z-coordinates for residues along each helix can be inferred by simple linear extrapolation assuming a lipid bilayer thickness of 30 Å (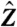 being a unit direction vector normal to the membrane plane). The residue Z-coordinates along each helix, no matter what its length, are assumed to vary linearly from +15 to -15 (-15 arbitrarily indicating the end of the helix close to the cytoplasmic facing plane of the bilayer). This simple assumption was used previously in the calculation of transmembrane potentials (6). More elaborate schemes for predicting residue Z-coordinates have been proposed (52), but we wished to avoid the use of knowledge-based machine learning methods as much as possible in this work; however, it is likely that more accurate predictions of Z-coordinates could be beneficial in further improving model quality.

We use the crudely predicted Z-coordinates for residues in transmembrane segments to provide additional minimum distance constraints as follows:

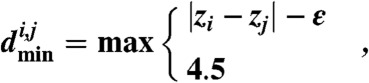[6]

where z_i is the estimated Z-coordinate for residue i, z_j the coordinate for residue j, and ε the estimated error in Z-coordinate prediction (assumed here to be 6 Å). These simple constraints encourage the protein to adopt a meandering topology according to the predicted transmembrane topology. Pairs of residues that cannot be close together because they are predicted to be at significantly different depths in the bilayer can therefore be prevented from coming close together in the FILM3 search process.

Minimum distance constraints are not actually included in the objective function but are, instead, applied immediately after a candidate move has been generated in the Monte Carlo procedure, i.e., any candidate conformation that violates any of the minimum distance constraints is immediately rejected and the previous conformation restored. This procedure is repeated until a conformation is generated that satisfies all of the minimum distance constraints after which the acceptance of the conformation is decided by the objective function and the standard Metropolis–Hastings criterion.

In cases where the predicted topology is incorrect or where the native protein fold is highly irregular and deviates substantially from a simple up-down alpha-helical bundle architecture, the Z-coordinate constraint filter will prevent FILM3 from arriving at a correct structure; however, these cases are easily detected by simply considering the final objective function value reached by the simulation. Simulations are run with and without Z-coordinate constraints, and the lowest energy models obtained from constrained and unconstrained simulations are then selected for the refinement stage.

Model Generation.

Generation of models is carried out in two phases: conformational searching and combinatorial refinement. Initial conformational searching is carried out using the standard FILM/FRAGFOLD approach (7), though with the standard simplified energy function replaced by the distance constraint function (Eq. 5). In addition, FILM3 uses Replica Exchange Monte Carlo (sometimes called parallel tempering) (53) to identify low energy conformations in place of simulated annealing. Nine replica conformations were used with a temperature ratio of 0.6 between each replica. The highest temperature is set by calculating the mean objective function change observed when 1,000 fragment swaps are made starting from a randomly generated chain conformation without minimum distance violations. After initial randomization, a total of 20 million fragment swaps are carried out divided equally between each replica and temperatures T_i and T_j exchanged between replica pairs with energies E_i and E_j with probability p given by an extension of the standard Metropolis-Hastings criterion:

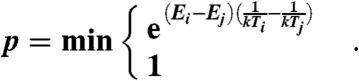[7]

To improve search performance further, a variable target function (54) is used where only contacts within a specified maximum sequence separation range were considered at each step. This range was linearly increased from six to m (the length of the protein) during the course of each simulation so that only local contacts with a sequence separation ≤ 6 are considered at the very beginning of the search, but all predicted contacts are considered near the end.

For each target, 100 independent runs were carried out each beginning with a randomly generated starting conformation with a further 100 runs per target carried out without Z-coordinate constraints.

Model Selection and Final Refinement.

Rather than simply selecting the final model with the lowest energy or selecting a model by clustering, a combinatorial refinement step was carried out using the final ensemble of models. In this step, the lowest energy model for the target was identified and the 100 lowest energy models fitted to it by rigid body superposition (selected from the pooled set of Z-coordinate constrained and unconstrained models) using the same objective function) (Eq. 5). Random segments were then selected from each model and simply transferred (without rotation or translation) onto the equivalent chain segment in the lowest energy structure to see if a lower energy model was produced. This greedy search procedure repeated until no further improvement in energy was observed. In this way, a final model could usually be found with an energy value lower than any of the 200 candidate structures. Very little variation in the final models was observed when this procedure was repeated using different random number seeds, which suggests that this greedy recombination procedure is robust. Consequently, only a single final model needs to be generated for each target protein. If the recombined model did not have a lower energy than any of the 200 candidate structures, then the lowest energy model of the 200 candidates was selected as the final model.

After combinatorial selection of a final model, the model coordinates were refined using MODELLER (55) mainly to produce reasonable loop and side chain conformations. The FILM3 model after recombination was simply used as a template for MODELLER but with additional secondary structure restraints applied to regions predicted to be alpha helical by PSIPRED and MEMSAT-SVM. No attempt was made to try to satisfy further contact-based distance constraints using MODELLER, but the predicted contacts from PSICOV could easily be converted into upper bound distance restraints for final refinement. The addition of distance restraints in final refinement might prevent the final refined models from ending up satisfying fewer of the predicted contacts than the unrefined models (see Table 3 and Tables S5 and S6).

The FILM3 software (free of charge to noncommercial users), plus sample data and scripts can be downloaded from http://bioinfadmin.cs.ucl.ac.uk/downloads/FILM3.

Model Quality Assessment.

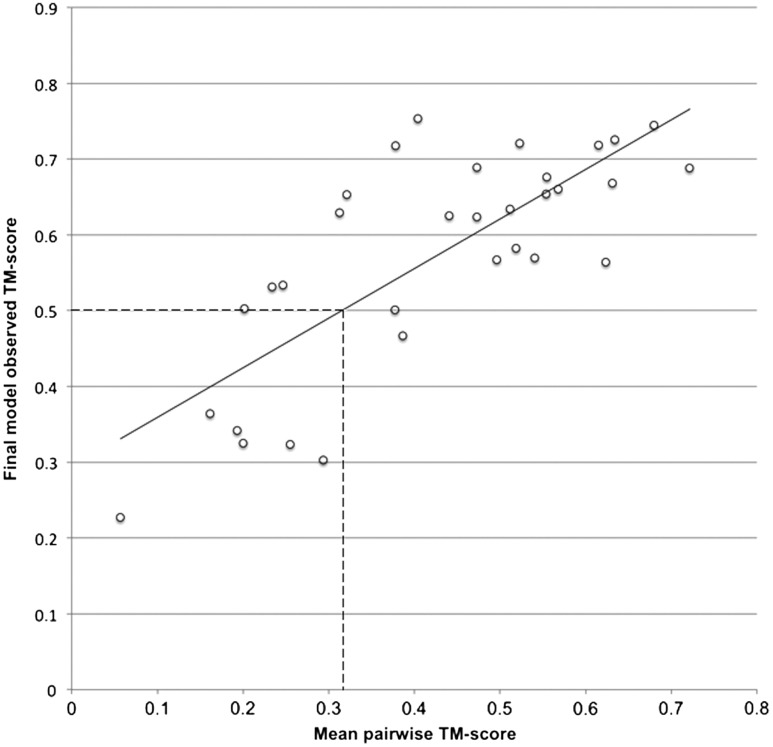
In protein structure prediction, it is clearly important to give users some guidance as to the likely quality of generated models. Although it is impossible to determine a priori how accurate a model is compared to the experimental structure, it is possible to provide guideline statistics that can discriminate between plausible and implausible models. For FILM3, the first source of model quality information comes from the estimated precision of contacts predicted by PSICOV. The results described here suggest that a minimum number of contacts (with precision ≥0.5) needed to generate a model with TM-score≥0.5 is 20 (1fftC, length 185 residues), though this threshold will depend on target length. Two targets with > 20 predicted contacts with precision > 0.5 produced models with TM-score < 0.5—in both cases, however, significant stabilization of the native fold is provided by additional chains. For a second means to determine expected model quality, it is possible to look at the degree of similarity between pairs of models in the generated ensemble. Where predicted contacts are insufficient to determine the global fold, an ensemble of generated structures will be expected to lack homogeneity. To demonstrate this, for each target (and an additional four targets where PSICOV contact precision was insufficient to generate correct models), we computed mean TM-scores across all pairs of models in the ensemble prior to recombination. The mean pairwise TM-score for each target showed a strong correlation with the observed TM-score of the final model (Pearson’s r = 0.77, Kendall’s τ = 0.54, Fig. 3) allowing the expected TM-score of the final model to be predicted using a linear regression fit. An estimate of local reliability for a model can also be derived, similarly, where the pairwise rmsd for each residue can be calculated from the initial ensemble of FILM3 models.

Fig. 3.

Observed TM-score of the final refined model plotted against mean pairwise TM-score of all 28 target structures and an additional 4 structures where poor quality contact predictions were used. A mean pairwise TM-score > 0.32 is likely to yield a final model with TM-score > 0.5.