A Muscle’s Force Depends on the Recruitment Patterns of Its Fibers

Abstract

Biomechanical models of whole muscles commonly used in simulations of musculoskeletal function and movement typically assume that the muscle generates force as a scaled-up muscle fiber. However, muscles are comprised of motor units that have different intrinsic properties and that can be activated at different times. This study tested whether a muscle model comprised of motor units that could be independently activated resulted in more accurate predictions of force than traditional Hill-type models. Forces predicted by the models were evaluated by direct comparison with the muscle forces measured in situ from the gastrocnemii in goats. The muscle was stimulated tetanically at a range of frequencies, muscle fiber strains were measured using sonomicrometry, and the activation patterns of the different types of motor unit were calculated from electromyographic recordings. Activation patterns were input into five different muscle models. Four models were traditional Hill-type models with different intrinsic speeds and fiber-type properties. The fifth model incorporated differential groups of fast and slow motor units. For all goats, muscles and stimulation frequencies the differential model resulted in the best predictions of muscle force. The in situ muscle output was shown to depend on the recruitment of different motor units within the muscle.

INTRODUCTION

Muscle models, in combination with electromyographic (EMG) recordings of muscle activity, are key components of dynamic simulations used to investigate musculoskeletal function during movement.¹⁰ The forces that a muscle produces during contraction can be estimated using phenomenological, Hill-based relations that describe how the force is influenced by factors including the muscle’s length, velocity, and activation.^19,57 However, Hill-type models commonly implemented in simulations of walking, running, and other movements have limitations. For example, whole muscles are typically represented as scaled-up fibers, driven by a single contractile element with average biochemical and mechanical properties. Estimates of the muscle forces derived from such models have rarely been validated, in part, due to the challenges associated with measuring the forces during natural behaviors. This is particularly the case for human muscles. Recently, several studies have attempted to validate scaled length–tension relationships for whole muscles, ⁶⁸ to simulate the three-dimensional geometry of muscles during contraction,⁷ and to qualitatively confirm the actions of select muscles predicted by simulations.²⁷ However, the accuracy with which traditional, Hill-type models predict muscle forces during in vivo activities remains untested.

Recent studies of motor unit recruitment suggest that existing Hill-type models may not adequately capture the complex relations between motor unit recruitment within a muscle, the EMG signals generated, and the resulting forces developed.³² Most mammalian skeletal muscles contain mixed populations of different muscle fiber types. The contractile properties of muscle fibers vary between fiber types,^8,12 so it is likely that the force developed by a whole muscle depends on the recruitment patterns and contractile properties of the different fibers within it.²¹ Some models have included different fiber-type properties; but these have been limited to the simulation of isometric contractions.^7,21 The recruitment of different muscle fiber-types is particularly relevant during dynamic movements.³² Despite this, most existing models used to simulate such movements have assumed that the contractile function of a whole muscle can be scaled up from a single fiber with little, or no regard for the patterns of motor unit recruitment or the properties of the different motor units recruited.

This study used a modified Hill-based approach to examine how the contributions of different constituent fibers influence the mechanical output of whole muscle. Specifically, we hypothesized that the fluctuations in force that occur during unfused and fused tetanic contractions would be better predicted by a model that activated fast and slow motor units independently than by a model that activated the whole muscle as a homogeneous block. Five different models were used to predict the forces generated during in situ nerve stimulation experiments. Four of the models were traditional Hill-type models that were assigned different fiber-type proportions, intrinsic activation dynamics, and force–velocity relations.^28,67,69 A fifth model was developed where contractile elements of different fiber types could be activated independently. The activation patterns to drive this fifth model were derived from the fast and slow components of the EMG signals recorded from these muscles.³⁶ Performance of the models was evaluated in a system where the muscle forces could be measured directly, and this was not possible in man; therefore, the models were tested against the measured muscle forces from a mammalian model, the goat. This study tested the models for fixed length contractions of the muscle– tendon unit. However, the models’ implementation is potentially just as suitable for dynamic contractions in vivo.

MATERIALS AND METHODS

Muscle models were tested using physiological data measured in situ from five goats (Capra hircus; age 17.2 ± 52 months; mass 25.4 ± 1.7 kg, mean ± SEM) at Harvard University’s Concord Field Station. All surgical and testing procedures followed IACUC approval.

Nerve Stimulation Experiments

The data used to test the models form part of a larger study; full details for the 3-day procedures have been reported elsewhere.³⁶ In brief, on day 1 the medial and lateral gastrocnemius muscles (MG and LG) were each instrumented with bipolar silver-wire EMG electrodes (0.1 mm enamel insulated silver: California Fine Wire, Grover Beach, CA) and with a pair of 2 mm sonomicrometry crystals (Sonometrics Inc., London, ON, Canada) aligned along the fascicle direction within the muscle belly. The sonomicrometry crystals were used to estimate length changes of the muscle fascicles, based on the transmission time of acoustic signals between the piezoelectric crystals.^5,23,25 A custom-fabricated “E”-shaped tendon buckle was also attached to the common gastrocnemius tendon.⁴¹ In vivo measures of locomotor activity were recorded on day 2. On day 3, a second surgical procedure was done, and in situ nerve stimulation experiments were performed. Tri-polar nerve cuffs were placed around the branches of the tibial nerve that innervate the MG and LG. A second “E”-shaped tendon buckle was mounted on either the medial or lateral portion of the tendon, proximal to the common buckle, by separating tendons by blunt dissection and more distally by separating the collagen fibrils with a scalpel. The goat’s hindlimb was then secured in a stereotactic frame whereby the femur and tibia were fixed with bone pins and the foot was strapped to an adjustable plate that, when unlocked, allowed rotation at the ankle. The goat was maintained at 0.5–1.0% isoflurane anesthesia for the duration of the testing. The goat was ultimately euthanized with an intravenous injection of sodium pentobarbitol.

Contractile measurements were made on the MG and then the LG with nerve stimulations applied during in situ tests. A heating pad was used to maintain a constant muscle temperature of about 34 ± 0.7 °C (mean ± SD, N = 5). Initial investigation determined the threshold stimulus voltage that resulted in the greatest twitch force. Subsequent twitches were stimulated using a 1.5 times threshold pulse that was 2 ms in duration. The ankle flexion–extension angle was adjusted in the stereotactic frame, then fixed for each contraction, resulting in contractions that were isometric for the muscle–tendon unit. The active and passive force–length relationship was measured using tetanic stimulation (at 40 Hz stimulation frequency) for a range of different ankle angles (and thus muscle lengths). The ankle was subsequently fixed at the angle that resulted in maximum tetanic force at the tendon. A series of tetanic contractions were then measured at stimulation frequencies of 5, 10, 20 and 40 Hz. The 20 and 40 Hz tests were no more than 0.5 s in length, and a 2-min rest was given between all tetanic contractions to minimize muscle fatigue.

Analog signals were conditioned for the EMG (P511J amplifiers, Grass, West Warwick, RI), sonomicrometry (model 120–1000, Triton Technology Inc, San Diego, CA), and tendon forces (bridge amplifier, Vishay 2120, Micro-Measurements, Raleigh, NC). Analog signals were acquired on a 16-bit analog-todigital convertor (NI 6259, National Instruments, Austin, TX), and recorded at a 5000 Hz sample rate. Fascicle length changes measured via sonomicrometry were corrected for the sound velocity of muscle at 34 °C and the offset introduced by the epoxy of the lens of each crystal.²⁴

Muscle Contractile Parameters

Contractile characteristics of the muscles, including activation, force–length and maximum intrinsic speed, were estimated from the experimental data. The EMG signals were analyzed to obtain time-varying information about the motor recruitment strategies, which are encoded by frequency properties of the signal. The intensity of the EMG signals was calculated using wavelet analysis, a time–frequency decomposition technique that has been described extensively.^36,60,64 The total intensity was calculated across the frequency band 101–1857 Hz using a filter-bank of non-linearly scaled wavelets and is a close approximation to the power of the signal.³⁶ The intensities of the EMG across high-frequency (240–423 Hz) and low-frequency (82–247 Hz) bands were used to identify the myoelectric activity from faster and slower motor units, respectively, and were calculated from specific wavelets that had been optimized to the EMG intensity spectra from these motor units in the goat.^29,36

A muscle’s activation level represents the capacity of the muscle to actively develop force, and it reflects the Ca²⁺ concentration within the sarcoplasm. We converted EMG intensities to activation states as a function of time, denoted by a(t), for the whole muscle and for the fast- and slow-motor units using methods that we have described previously.³⁶ Briefly, EMG intensities were converted to activations using transfer functions formed by sets of three first-order differential equations. The transfer functions were characterized for these same goats, and they were validated in a previous study by correlating the predicted activation states with the measured isometric force³⁶ (from the same data as in this study: r = 0.98–0.99). The transfer functions incorporate both a timing offset, to accommodate electromechanical delay, and coupled differential equations that describe the differing activation and deactivation rates and the rise in activation that persists after the action potentials in the EMG have passed. The muscle activations were normalized, â(t); to the maximum activity of the whole muscle that occurred across all tetanic contractions.

Force–length properties were determined for these goats as a function of fascicle strain. The resting fascicle length was defined as the passive fascicle length at the ankle angle that yielded maximum force. Force–length properties, F̂(l); were normalized to the maximum isometric force and were averaged for the five goats.

The maximum unloaded shortening velocities, v₀ (muscle lengths s⁻¹), were estimated for the fast- and slow-fibers in two ways. First, the following relation for locomotor muscles in terrestrial species was used, derived from a literature survey of 59 species from 88 papers (coefficient of determination, r² = 0.75; Hodson-Tole and Wakeling, personal communication):

$$v_0=71.1{\tau }_{\text{a}}^{-0.74}$$ (1)

τ_a is the time to maximum twitch force (ms), and was estimated for these goats as 52.9 and 98.6 ms for the fast- and slow-fibers, respectively.³⁶ This relation yielded v₀ values of 3.59 and 2.74 s⁻¹ for the fast and slow fibers, respectively. A variant of each muscle model was evaluated using faster v₀ to test the sensitivity of the muscle force predictions to the choice of v₀. No data currently exist for v₀ for larger mammals at physiological temperatures; however, v₀ for the mouse, rat and cat at physiological temperatures range between 4.8 and 7.3 s⁻¹ for slow fibers^3,13,52 and 9.2–24.2 s⁻¹ for faster fibers.^{2,11,13,14,17,38,39,46,52} Larger animals have lower v₀,^16,49,55 and v₀ would be slightly less at the depressed temperature of 34 °C during these in situ experiments. Therefore, we additionally selected v₀ values of 5 and 10 s⁻¹ for the slow and fast fibers, respectively. For the purposes of this study, fiber velocity was measured relative to the passive fiber length that resulted in the maximum isometric force, and thus velocity was equivalent to the fiber strain rate.

Muscle Models

Five muscle models were used to estimate the muscle force (see summary of parameters in Tables 1, 2). Models A–D are described in the following sections, and they shared the following features. The activation state was determined from the total EMG intensity, and the total muscle force F_m was given by:

$$F_{\text{m}}=c_1\left[{\widehat{F}}_{\text{f}}+{\widehat{F}}_{\text{p}}(l)\right]cos\beta ,$$ (2)

where F̂_f is the active component of the muscle fiber force, F̂_p(l)is the passive component of the force– length relationship, β is the pennation angle (assumed constant for the isometric contractions in this study), and c₁ scaled the fiber force to the whole muscle force.^3,43,57

TABLE 1.

Parameters used in the equations for the muscle models.

Parameter	Definition	Source
â(t)	Activation state of fibers	Derived from measured EMG36
c1	Scalar to calculate actual from normalized force	Measured
c2/c3	Ratio that scales activation between fast and slow components	Calculated
Fm	Muscle force	Calculated
F̂p(l)	Normalized, passive force–length relation	Measured
F̂a(l)	Normalized, active force–length relation	Measured
F̂(v)	Normalized, force–velocity relation	Literature
k	Curvature of force–velocity relation	Literature
l	Fascicle length	Measured
v	Fascicle velocity	Derived from l
v0	Maximum shortening velocity	Literature
β	Pennation angle	Measured
τa	Force-rise time	Measured36

TABLE 2.

Key parameters used in the five muscle models.

Model	Force–velocity curvature, k	Maximum unloaded shortening velocity, v0	Activation state
Homogeneous, A	kslow + (kfast − kslow)p	v0;fastp + v0;slow (1 − p)	â(t)
Hybrid, B	Composite from Hill28	v0;fast	â(t)
Orderly, C	kslow + (kfast − kslow)p	v0;slow + (v0;fast − v0 slow)â(t)	â(t)
Reverse, D	kslow + (kfast − kslow)p	v0;fast + (v0;fast − v0 slow)â(t)	â(t)
Differential, E	kfast	v0;fast	âfast(t)
	kslow	v0 slow	âslow(t)

Subscripts “fast” and “slow” denote properties from fast or slow muscle fibers.

Models (A–C) were similar to those currently used for biomechanical simulations of human and animal movement. In these models the normalized, active component of the muscle fiber force F̂_f was given by the expression⁵⁷:

$${\widehat{F}}_{\text{f}}=\widehat{a}(t){\widehat{F}}_{\text{a}}(l)\widehat{F}(v),$$ (3)

where â(t) is the time-varying level of activation, normalized to a maximum of 1, and F̂_a(l) is the active force–length relationship, normalized to a maximum of 1. The fascicle lengths fluctuate during contractions, so both length, l, and velocity, v, are time-varying in addition to â(t):

When a muscle fiber contracts, its force depends on the contraction speed. The force diminishes to zero for very rapid contractions, and increases to 150% its isometric levels for lengthening contractions. This force–velocity relationship, F̂(v) was normalized to an isometric value of 1 and was given by:

$$\widehat{F}(v)=\frac{\left(1-\frac{v}{v_0}\right)}{\left(1+\frac{v}{v_{0}k}\right)}\text{for}v\le 0$$ (4)

$$\widehat{F}(v)=1.5-0.5\lfloor \frac{\left(1-\frac{v}{v_0}\right)}{\left(1-\frac{7.56v}{v_{0}k}\right)}\rfloor \text{for}v>0$$ (5)

where v is the contractile velocity of the fiber and v₀ is its maximum intrinsic speed.^33,57 Constant k describes the curvature of the force–velocity curve and depends on muscle fiber type.⁴² The curvature for the faster fibers of locomotor muscles in terrestrial species (k = 0.29) is significantly flatter than for slower fibers (k = 0.18), as determined from a literature survey of 59 species from 88 papers (Hodson-Tole and Wakeling, personal communication). Values of v₀ and k were chosen for the different muscle models as follows.

Homogeneous model A assumed that the muscles contained fibers with homogeneous properties. v₀ was taken from the maximum intrinsic speeds of the different fiber types weighted by their fractional cross-sectional areas. The curvature k was assumed to be the same for all fibers, and was assigned an intermediate value between the fast and slow fiber limits⁶⁹:

$$k=k_{\text{slow}}+(k_{\text{fast}}-k_{\text{slow}})p$$ (6)

where p is the fractional area occupied by the fast muscle fibers.⁶⁷ Because p is not yet known for the goat, we analyzed two variants of the models, with p = 0.75 and p = 0.5 to bracket the range of fast-fiber proportions in the gastrocnemii reported from six different species.^1,35

Hybrid model B was the same as homogeneous model A except that v₀ represented the fastest fibers and k was calculated from the composite force–velocity relation taken from a combination of fast and slow fibers with forces proportional to their fractional fiber area following Hill.²⁸ This assumption resulted in a greater curvature than calculated using Eq. (6).

Orderly recruitment model C assumed that as the level of activation increases, the active muscle takes the intrinsic properties of progressively faster fiber types. These ideas stem from the classic observations of orderly recruitment during steady stretch reflexes²⁶ and follow previous approaches,^56,58 but here v₀ was activation dependent and was scaled to equal that of the slowest fibers at the lowest (near zero) activation levels:

$$v_0=v_{0,\text{slow}}+(v_{0,\text{fast}}-v_{0,\text{slow}})\widehat{a}(t)$$ (7)

For this model, k was calculated using Eq. (6), and the muscle fiber force F_f was calculated using Eq. (3).

Reverse recruitment model D assumed that as the level of activation increases, the active muscle takes the characteristics of progressively slower fiber types. This may be appropriate during direct electrical stimulation to the nerve where the larger diameter axons from the faster motor units are the most excitable,^51,54 but is not expected to occur in vivo. For this reverse recruitment model, k was calculated using Eq. (6) and v₀ was activation dependent in an opposite manner to model C:

$$v_0=v_{0,\text{fast}}-(v_{0,\text{fast}}-v_{0,\text{slow}})\widehat{a}(t)$$ (8)

Differential recruitment model E contained fast and slow contractile elements in parallel that could be independently activated. The activation levels for the fast and slow elements, â_fast(t) and â_slow(t); respectively, were determined from the EMG intensity at the high- and low-frequency bands.³⁶ The total muscle force F_m for this model was given by:

$$F_{\text{m}}=c_1\left[c_2{\widehat{F}}_{\text{f},\text{fast}}+c_3{\widehat{F}}_{\text{f},\text{slow}}+{\widehat{F}}_{\text{p}}(l)\right]cos\beta$$ (9)

where c₂ and c₃ scaled the relative contribution of the fast and slow elements, respectively, and F̂_f;fast and F̂_f;slow are the normalized forces from fast and slow fibers, respectively, as determined from Eq. (3) using fiber-specific values of â(t); v₀ and k (Table 2). The ratio c₂/c₃ partially reflects the lower EMG intensities that would be expected from action potentials with higher spectral frequencies, and a value of 10 was used.

Statistics

The models were run 800 times (5 models × 5 goats × 2 muscles × 4 stimulation frequencies × 2 choices of p × 2 sets of v₀). For each run, the coefficient of determination, r², was calculated between the predicted force and the measured tendon force, and these datawere used as the dependent variable in an ANOVA. Model type, goat (random), muscle, stimulation frequency, fiber-type proportion and selection of v₀ were used as factors. Differences were considered significant at the α = 0.05 level. Values are reported as mean ± SEM

RESULTS

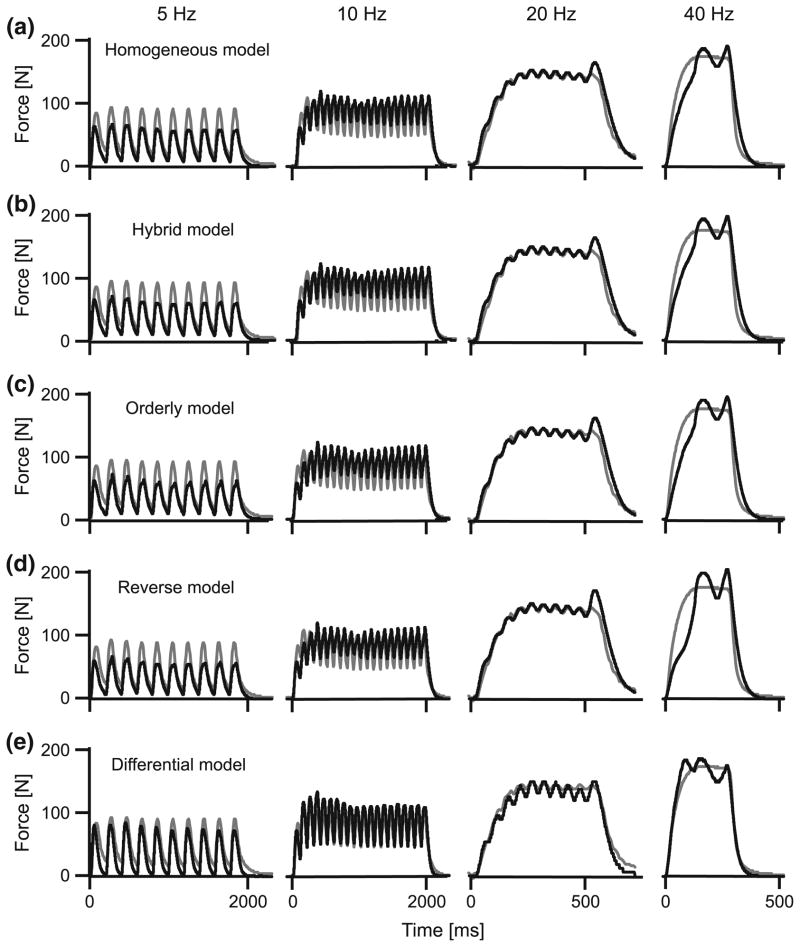
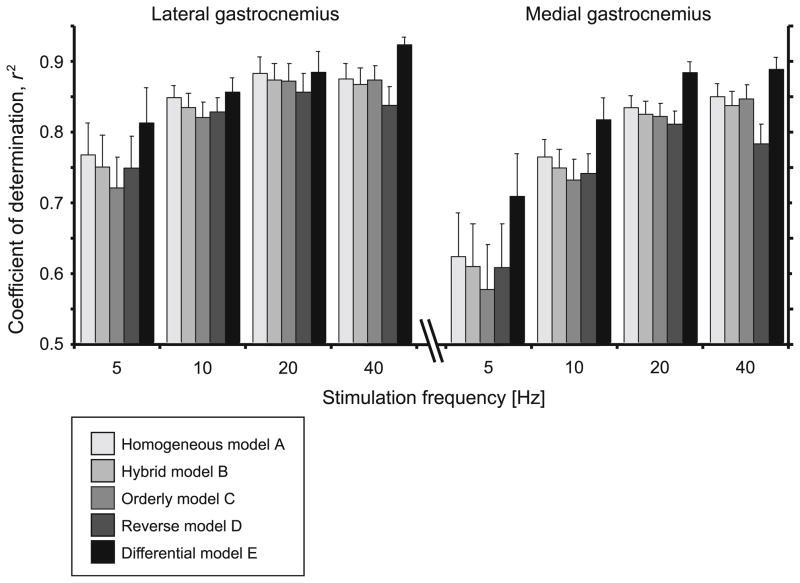
All models captured the salient features of the measured muscle forces, generating oscillating forces at the low (5–10 Hz) stimulation frequencies and fused tetanic contractions for the highest (40 Hz) stimulation frequency (Figs. 1–3). However, the models varied in their ability to reconstruct the force traces, particularly the force rise and the force relaxation. These differences were most apparent for the low frequency stimulations (5 Hz) where the rise and fall characteristics play a major role in the force trace. The models generally performed better for the higher stimulation frequencies (Figs. 3, 5). The differential model E performed best for all stimulation frequencies and both muscles (Figs. 4, 5).

FIGURE 1.

Composite traces of muscle force for a series of contractions in the medial gastrocnemius at a range of stimulation frequencies. Measured forces are shown in gray, and predicted forces are shown in black. The forces were modeled using differential model E, with v₀ estimated at 5 and 10 s⁻¹ (a) or 2.74 and 3.59 s⁻¹ (b) for the slow and fast-fibers, respectively, and with fast fibers comprising 75% of the muscle.

FIGURE 3.

The performance of the different muscle models across a range of stimulation frequencies for the lateral gastrocnemius. Measured tendon forces are shown in gray, and predicted forces are shown in black. The forces were modeled with v₀ estimated at 5 and 10 s⁻¹ for the slow and fast-fibers, respectively, and with fast fibers comprising 75% of the muscle.

FIGURE 5.

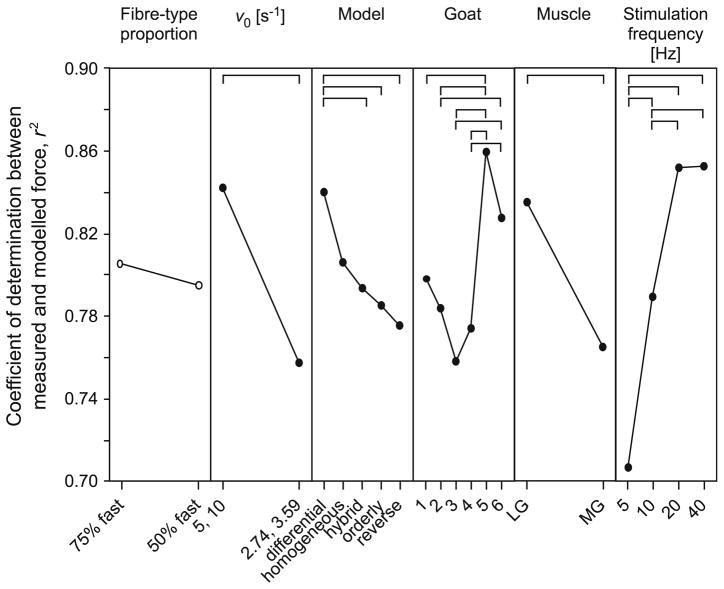
The main effects of model parameters and experimental factors on the coefficient of determination. Points show the main effects (least-squares adjusted means) from the ANOVA. Where a factor had a significant effect on the coefficient of determination, the points are shown by filled circles; open circles denote no significant effect. Post hoc Tukey tests identified specific differences within each category, and they are denoted by the horizontal bars.

FIGURE 4.

The performance of the different muscle models for the different stimulation frequencies and muscles. Bars show the mean + SEM values (N = 20) pooled from the different goats, fiber-type proportions and choices of v₀.

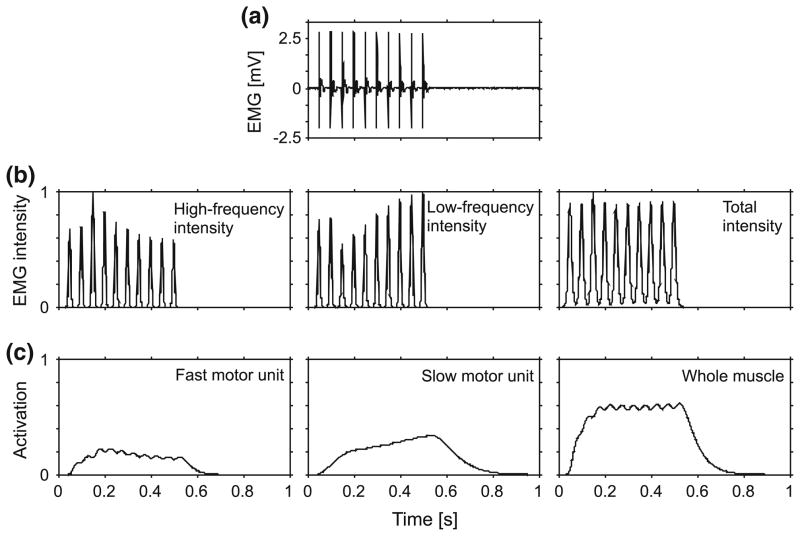
Model E accounted for fluctuations in the EMG intensity from the fast and slow motor units (Fig. 6), and this modification improved its performance (Fig. 4). During contractions, we measured oscillations in both fascicle length and whole muscle force. The fascicles oscillated in length as they worked against the series compliance of the tissue (internal and external tendon), showing substantial variations in strain (standard deviation 0.075) and shortening strain rate (standard deviation 0.704 s⁻¹) across trials. The peak twitch forces for the 5 Hz stimulus trains, for instance, showed no systematic trend over the course of the stimulus (linear regression, p = 0.728) and had a standard deviation of 9.5% (from the second peak onwards, relative to the mean peak force). Considerable and independent fluctuations also occurred in the intensity of the MU action potentials in the high- and low-frequency bands as determined from wavelet analysis (Fig. 6b), though the MU action potentials in each train had similar amplitudes (Fig. 6a). The time course of the activation levels similarly varied between the different types of motor unit; in the example shown in Fig. 6c, the fast MU activation level fluctuated with each stimulus, and gradually decreased over the contraction, whereas the slow MU activation level increased gradually over the course of the contraction.

FIGURE 6.

EMG and activation states for the medial gastrocnemius during a tetanic contraction stimulated at 20 Hz. Raw EMG is shown in panel a. EMG intensity is shown for the high (240.5–422.9 Hz) and low (82.4–247.0 Hz) frequency bands (b), corresponding to the fast- and slow-motor unit activity, respectively. The intensities were normalized to their maximum values during these supramaximal stimuli. The activation profiles are shown for the fast- and slow-motor units, and a general activation for the whole muscle (c).

ANOVA showed that there were significant differences in the outputs from the different models, and that model outputs were dependent on the choice of v₀, muscle, stimulation frequency, goat and most importantly the type of model used (p<0.001; Fig. 5). Selecting v₀ of 5 and 10 s⁻¹ rather than the slower values estimated for the goat resulted in a better reconstruction: r² = 0.843 ± 0.007 as compared to 0.758 ± 0.009 (mean ± SEM, N = 400 each group). The models generated a better fit for the LG muscle than for the MG muscle: r² = 0.836 ± 0.007 as compared to 0.766 ± 0.009 (mean ± SEM, N = 400 each group). The fiber-type proportion selected for the model did not significantly influence the model outputs.

DISCUSSION

Activation Parameters to Drive Muscle Models

This study was based on the premise that EMG signals from muscles contain information about motor recruitment patterns, and that extracting this information for use in muscle models will result in better predictions of whole muscle force. Several approaches, differing both in the experimental design and the signal analysis, have been used in previous studies to extract information about motor unit recruitment. These approaches have yielded different rates of success in resolving such information.^20,62,64 The specific approach used in this study involved wavelet analysis of fine-wire EMG, and this approach has been previously adapted and validated for the gastrocnemii muscles of goats.³⁶ The main difference between the differential model E and the models A–D is that the differential model was independently driven by the active states of fast- and slow-motor units, as determined from information encoded in the high- and low-frequency bands of the EMG. The fact that the differential model resulted in the best predictions of time-varying force (Fig. 4) is a compelling indication that differential recruitment of fast and slow motor units was encoded in the EMG, it was successfully resolved, and it is an important determinate of the mechanical function of the muscles.

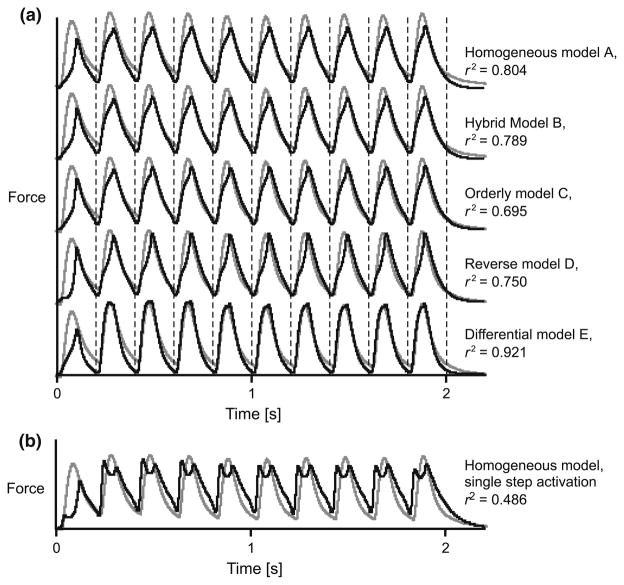
We used a three-step function to estimate the activation state from the EMG intensity,³⁶ and this differs from previous studies that have used a single first-order differential equation.⁶⁹ While the purpose of this study was not to evaluate different methods for calculating the active state of the muscle, Fig. 2 shows that the predicted muscle force is influenced by how activation is calculated. Using a single bilinear first-order differential equation to estimate activation only allows the activation to increase while the EMG intensity is positive⁶⁹ (Fig. 2b; all other parameters being the same as model A). This is limiting, since action potentials may exist for about 3 ms while the force rise during twitch may last up to 100 ms.³⁶ Using the three-step transfer functions in this study, activation persisted after the action potentials decayed³⁶ (models A–E), and this resulted in a substantial improvement in the predicted muscle forces (Fig. 2b).

FIGURE 2.

Forces for a 5 Hz train of twitches in the medial gastrocnemius, calculated using different muscle models. Models A–E are shown in panel a. For comparison, a homogeneous model in which a single-step first-order ordinary differential equation was used to calculate the activation is shown in panel b. Measured tendon forces are shown in gray, and predicted forces are shown in black. Vertical lines show the times of each stimulus. The forces were modeled with v₀ estimated at 5 and 10 s⁻¹ for the slow and fast-fibers, respectively, and with fast fibers comprising 75% of the muscle. The coefficient of determination, r², is shown for each model with respect to the measured force.

The models in this study assumed that the muscle activation, force–velocity and force–length properties were independent, typical of Hill-type models. However, it is known that activation depends on muscle length,^4,15,53 and that activation in turn affects the force–length and force–velocity properties.^9,45,50 Additionally, muscle forces are modulated by history-dependent effects⁴⁷ and fatigue.¹⁸ In the future, the models presented here could be further refined to incorporate these coupling and history-dependent effects. The results from this study demonstrate how muscle model predictions depend on the mechanics of the active motor units.

The models in this study incorporated a number of scaling constants. Constant c₁, which was used for all models (Eqs. 2, 9), scales the force from a normalized value to the force actually produced. Hence, c₁ reflects the maximum isometric force that the muscle can develop. The correlation analysis we used to evaluate the models is independent of the scale of the measured and predicted forces, and thus the choice of c₁ does not affect the conclusions. Constants c₂ and c₃ scale the relative contributions from the fast- and slow-components of the differential model E (Eq. 9). A number of factors potentially influence the ratio c₂/c₃, and these include the fiber-type proportion within the muscle, the proximity of the different types of fibers to the recording electrodes, and the transformation between EMG intensity and the predicted active state of the different types of motor unit. Due to uncertainty in the former two factors, the selection of c₂/c₃ was based on some simplifying assumptions about the transfer of action potential amplitude. Faster motor units have action potential conduction velocities and thus EMG frequencies typically 2–3 times greater than slower motor units.^32,36,64,65 If an action potential from a faster motor unit scales in time inversely proportional to its conduction velocity, its Fourier transform would be 1/2 to 1/3 in magnitude, and it would have 1/4 to 1/9 the power, compared to the action potential from a slower motor unit. Thus the intensity of the high-frequency signal from the faster motor units must be scaled to obtain an equivalent measure of active state. We used a value of 10 for c₂/c₃ to reproduce this effect. Specifying this ratio more precisely is an avenue for future investigation. We found that fiber-type proportion had only a small effect on the performance of the models (Fig. 5), and this may have been related to our choice of c₂/c₃.

Intrinsic Properties of the Modeled Fibers

The five muscle models differed in their force– velocity relations and in how the active state of the muscle fibers was calculated (Table 2; Fig. 5). These differences significantly influenced the accuracy of the predictions of whole muscle force. Force–velocity relations depend on the proportion of fast and slow fibers that affect the curvature and maximum shortening velocity (Eq. 6–8). Two sets of estimates for v₀ were used. The first set was calculated from the measured twitch rise times for the goats. It is possible that this set underestimated v₀, perhaps due to the experimental challenges of detecting motor unit twitch dynamics from whole muscle twitches,³⁶ or due to errors in extrapolating the values from a relation that was derived from smaller species (Eq. 1). A second set of greater values for v₀ was chosen to bracket the expected range of v₀ that likely occurred in these muscles. From the ANOVA, the model outputs were not sensitive to the choice of the fiber-type proportion, but were sensitive to the choice of v₀. A possible explanation is as follows: despite the limb being held isometrically in a stereotactic frame, the fibers showed oscillations in length and velocity due to elastic compliance within the muscle–tendon unit. The force–length and force–velocity properties of the muscle thus modulated the predicted muscle force. The force–velocity modulation is greatest when the absolute velocity is a greater proportion of v₀ (Eqs. 4, 5). Thus, models with higher values of v₀ showed smaller force modulations due to the reduced force–velocity effect, and this resulted in better fits to the measured forces. Models A–D differed in their predictions of muscle forces despite having the same activation profiles. This further demonstrates that the models were sensitive to the force–velocity properties that were used.

During the trains of stimuli there were fluctuations in the muscle force that were not a function of systematic processes, such as fatigue. These fluctuations occurred despite a constant stimulus voltage, indicating that the force was not always maximal and thus not all the motor units were activated for each twitch. This interpretation is consistent with our findings that the maximal muscle forces measured from goats in vivo, during nearly isometric phases of contraction, exceeded the muscle forces that we could elicit in situ. Our nerve-cuff design and implementation evolved and improved throughout the study; nonetheless, the recorded data do show fluctuations in motor unit recruitment. These fluctuations enabled this study, since they allowed the alternative models of motor recruitment to be tested on these data. Had all the motor units been recruited for each stimulus, then this evaluation of the different models would not have been possible.

The models predicted force more accurately for the goat LG than for the MG (Figs. 4, 5), perhaps due to variations in the muscle architecture and the intrinsic properties of the motor units. For example, differences in the degree of fascicle rotation during contraction may have contributed to minor differences in model performance. It was assumed that the effect of fascicle rotations on tendon force could be ignored, since the only evidence for fascicle rotations in the LG and MG comes from man, where differences between the muscles are <5°.^40,63 If the models are used to predict forces for muscles that are less pennate, or parallelfibered, in architecture, such that the fascicle rotations during contraction are less, or even non-existent, then the models are likely to better predict the tendon force. Differences in the motor unit twitch profiles between the LG and MG have also been reported, in both man and goats,^36,59 and may reflect differences in activation-relaxation dynamics that affect the accuracy of the predicted muscle force.

Motor Unit Recruitment and the Differential Muscle Model

Muscle models used for biomechanical simulations typically assume an orderly recruitment of motor units, based on classic neurophysiological studies.²⁶ However, different types of motor units can be differentially activated for different mechanical tasks.^22,34,37,61 It has been suggested, for example, that faster fibers may be utilized for power production at high contraction speeds. Indeed, we have previously shown that the recruitment of faster fibers significantly correlates with the strain rates of the fibers in both rats and man.^31,66 It has also been suggested that faster fibers are recruited for contractions that require fast rates of force development and relaxation.^6,30,48

There was fluctuation in the motor recruitment patterns during in situ stimulations, despite the constant nerve excitation. These recruitment patterns produced fluctuations in the activity levels of the different motor units, and these features were only captured in the activation input to differential model E. The fluctuations in recruitment were not apparent from the raw EMG or the total intensity traces, but were only apparent after the EMG signals had been resolved into their time–frequency components (Fig. 6). This illustrates the utility of the wavelet techniques for identifying patterns of motor recruitment from the EMG. The ability of differential model E to respond to the activation dynamics of the different types of motor units resulted in improved model performance. The sensitivity of the models to the activation-relaxation dynamics is illustrated by the fact that the models show a poorer fit where the stimulation rates are low (Figs. 4, 5) and where the activation dynamics are more important; this result parallels similar observations in the cat soleus.⁴⁴ Differential model E showed the greatest improvement relative to the traditional models at the lowest stimulation frequencies (Fig. 4) due to its enhanced ability to predict the activation-dependant fluctuations from the different motor units.

CONCLUSION

This study showed that a muscle model comprised of parallel fast- and slow-components that could be independently activated generated better predictions of whole muscle force than traditional Hill-type models (e.g., Fig. 2). This in situ study examined the muscle forces during contractions that were isometric for the muscle–tendon unit, where the fiber strains and strain rates may be much more limited than during free movement. These contractions form a particularly challenging data set for discriminating among the different models because they involve limited fascicle velocities. By contrast, a larger change in recruitment patterns is expected to exist across a range of locomotor behaviors in vivo,³² and a model that accommodates varying motor unit recruitment is expected to perform substantially better. Nonetheless, the differential model performed the best in this study and demonstrated that motor unit recruitment is an important feature of muscle force. This has largely been ignored in prior implementations of Hill-type muscle models.We expect that even greater improvements in muscle force prediction will be realized when the models are compared over a wide range of locomotor tasks in vivo.