An efficient multi-locus mixed model approach for genome-wide association studies in structured populations

Abstract

Population structure causes genome-wide linkage disequilibrium between unlinked loci, leading to statistical confounding in genome-wide association studies. Mixed models have been shown to handle the confounding effects of a diffuse background of large numbers of loci of small effect well, but do not always account for loci of larger effect. Here we propose a multi-locus mixed model as a general method for mapping complex traits in structured populations. Simulations suggest that our method outperforms existing methods, in terms of power as well as false discovery rate. We apply our method to human and Arabidopsis thaliana data, identifying novel associations in known candidates as well as evidence for allelic heterogeneity. We also demonstrate how a priori knowledge from an A. thaliana linkage mapping study can be integrated into our method using a Bayesian approach. Our implementation is computationally efficient, making the analysis of large datasets (n > 10000) practicable.

INTRODUCTION

With the increasing availability of genomic polymorphism data, genome-wide association studies (GWAS) are becoming the default method for investigating the genetics of quantitative traits. Typically, GWAS are carried out using single-locus tests to identify associations between polymorphisms and traits in either case-control populations or cohorts. However, both designs are subject to confounding by population structure, leading to an inflation of test statistics and a high false positive rate^1,2. Several methods have been proposed to deal with this issue, including genomic control³, structured association⁴, principal components analysis⁵, and mixed linear models⁶. Genomic control scales the test statistics uniformly so that the observed median test statistic equals the expected one. Even though this approach reduces the inflation of test statistics globally, it does not change the rank of the polymorphisms, as they are subject to the same correction. In the structured association and principal component analysis approaches, population structure is taken into account by including covariates in the association model representing the cluster memberships and principal component loadings of the individuals, respectively. While these approaches are expected to perform well when the population structure is simple, they may perform poorly when the structure is more complex, e.g., when individuals display a continuum of relatedness⁷. A further improvement has been made with the use of mixed linear models, which are based on the insight that confounding will be caused by the genetic background of causal variants in the presence of population structure. The mixed model controls for this through a random polygenic term having a covariance structure described by a relationship matrix so that correlation in phenotype mirrors relatedness⁸, as predicted by Fisher's classical model⁹. This approach has been shown to perform well in plants, animals and humans^6,10,11,12 and methods have been developed to allow the analysis of large GWAS datasets in a reasonable amount of time^11,13,14.

All these approaches are based on single-locus tests combined with some kind of diffuse genomic background. For complex traits controlled by several large-effect loci, this may not be appropriate, especially in presence of population structure¹² (indeed, a substantial inflation of single-locus test statistics can be expected for complex traits even in the absence of population structure¹⁵). Explicit use of multiple cofactors in the statistical model is an obvious alternative, and is indeed standard in traditional linkage mapping, where both “Multiple QTL Mapping” and “Composite Interval Mapping” have been shown to outperform simple interval mapping^16,17. In GWAS, the case for including multiple loci is arguably even stronger, as the confounding effects of background loci may be genome-wide (due to linkage disequilibrium) rather than just local (due to linkage)¹⁸. Thus, while conditioning on known causative factors in GWAS has typically been done on a local scale, to help identify multiple alleles and clarify complex associations^12,19,20, we believe that it should be done on a genome-wide basis. As illustrated in Fig. 1, a conditional analysis at a genome-wide scale may well have higher power and lower false discovery rate (FDR) than single-locus approaches. Similarly, in the context of human genetics, it has been suggested that conditioning on major effects loci, like the MHC, may improve power¹¹.

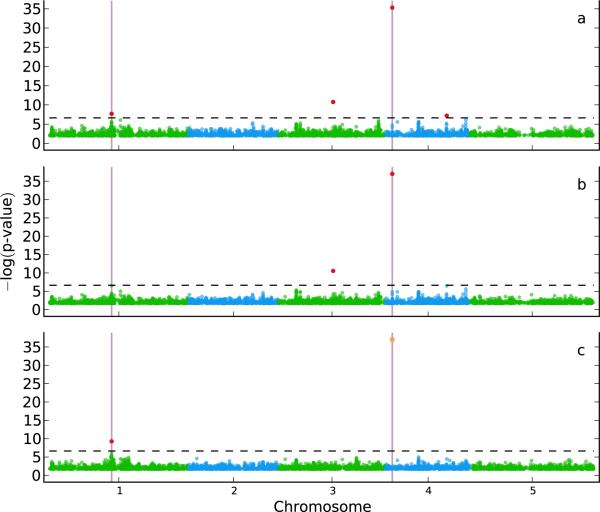
Figure 1.

A GWAS for a simulated trait with two causal SNPs (marked by vertical lines), randomly chosen from a real A. thaliana SNP dataset²⁸. Random error was added to the trait to fix the heritability at 25%. (a) A single-SNP linear regression scan detects four significantly associated SNPs (at a Bonferroni-corrected threshold of 0.05; dashed horizontal line) marked in red. Half of these SNPs are false positives and the other half true positives, leading to a false discovery rate (FDR) of 50% and a power of 100%. (b) A single-SNP mixed-model^11,14 scan eliminates one false positive but also one true positive, leading to a similar (50%) FDR while decreasing the power to 50%. (c) Adding the most significant SNP as a cofactor to the mixed model (marked in orange) recovers the second causal SNP while eliminating the last false positive, leading to the perfect case of a FDR of 0% and a power of 100%.

However, automatically including cofactors is challenging when the number of predictors is large compared to the number of observations. This is particularly problematic for GWAS, where the number of polymorphisms can reach millions, but the number of phenotyped and genotyped individuals is rarely more than tens of thousands. Such “large p, small n” problems are very challenging: the model space is usually too large to explore exhaustively, and the maximum number of polymorphism that can be fitted at a time must be lower than the number of individuals. In addition, identifying the causative polymorphisms by fitting more than one polymorphism at a time is complicated by the presence of linkage disequilibrium. Several approaches have been proposed to address these issues, including stepwise regression²¹ and penalized regression with different penalty functions, such as ridge regression, normal exponential-, elastic net and LASSO^{22,23,24,25,26}. These approaches have been shown to perform better than single locus approaches, but most are either computationally infeasible in GWAS²⁷, or do not explicitly address the problems posed by population structure. As an alternative, we propose using a simple stepwise mixed-model regression with forward inclusion and backward elimination, which, despite being limited in terms of exploring the model space, has the advantage of being computationally efficient and therefore applicable to GWAS. To handle the population structure issue effectively we make use of an approximate version of the mixed model^11,14, where re-estimate the genetic and error variances at each step of the regression (see Methods). As the variance attributed to the random polygenic term decreases when cofactors are added to the model, we propose to use the heritable variance estimate as a criterion to stop the forward inclusion; and then to perform a backward elimination from the last forward model for a more thorough exploration of the model space. We evaluate various model-selection criteria through simulations, which also suggest that the proposed multi-locus mixed-model (MLMM) method performs well in terms of false discovery rate and power. Finally, we demonstrate the utility of our approach by applying it to human and A. thaliana data.

RESULTS

Simulations

GWAS data were simulated by adding phenotypic effects to real genotypic data from A. thaliana²⁸ under two different scenarios: a two-locus model, and a 100-locus model. For the latter, additivity was assumed, whereas for the former, different types of interactions were explored. For details, see Methods.

We compared our proposed MLMM method with three other mapping methods: a single-locus approximate mixed model that corrects for population structure, but does not take other major loci into account (MM)^11,14; a stepwise linear model that takes other major loci into account, but does not correct for population structure (SWLM); and a single-locus linear model that does neither (LM). The four methods were compared in terms of their statistical power and their false discovery rate (FDR). For single-locus methods, SNPs were considered detected if their p-values were below the defined threshold; while for the multi-locus methods, the detected SNPs were those belonging to the most complex model whose cofactors' marginal p-values were all below the defined threshold.

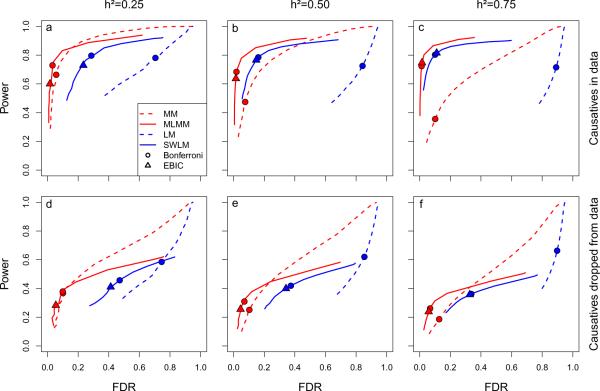
The results for the 100-locus model are shown in Fig. 2 and Supplementary Figs. 1–4, and can be summarized as follows. First, methods that use a kinship term to correct for population structure always outperform comparable methods that do not (MM and MLMM vs LM and SWLM, respectively). There is simply too much structure in these data for it to be ignored without paying a very heavy price in terms of increased FDR (Supplementary Fig. 1). Second, multi-locus methods generally outperform comparable single-locus methods (SWLM and MLMM vs LM and MM, respectively) as long as the causative sites themselves are included in the data (Fig. 2a–c). The advantage increases with increasing heritability because, under our simulation scheme, increased heritability implies more loci of large effect, and hence greater confounding (Supplementary Figs. 1–2). If the causative sites themselves are excluded from the data, the single-locus mixed-model (MM) may have greater power than the multi-locus version (MLMM), but only at the cost of greatly increased FDR (Fig. 2d–f).

Figure 2.

Power and false discovery rate (FDR) in the 100-locus model simulations for four different mapping methods: linear model (LM), stepwise linear model (SWLM), mixed-model (MM), and multi-locus mixed-model (MLMM). For the purpose of computing power and FDR, a causal SNP was considered detected if a SNP within 25kb on either side was declared significant (results for other window sizes are given in Supplementary Fig. 3), and only causal SNPs that were in principle detectable (i.e., that were marginally significant at a Bonferroni-corrected threshold of 0.05 in a simple linear model were considered. For clarity, only the backward path of the multi-locus methods (SWLM and MLMM) is shown: a comparison between forward and backward paths is given in Supplementary Fig. 4. Circles and triangles denote the best-fitting model according to the Bonferroni and EBIC model-selection criteria, respectively. Three phenotypic heritabilities were used in the simulations: 0.25 (a, d), 0.50 (b, e), and 0.75 (c, f). Power and FDR was estimated with (a–c) and without (d–f) the causal loci included.

The 2-locus simulations allowed us to examine the advantages of including cofactors in the mixed model under several scenarios of population structure and/or epistasis (for details, see Methods). Regardless of the scenario considered, MLMM consistently performed at least as well as the other methods when restricted to small FDR (Supplementary Fig. 5, see also Fig. 1). When there are two random randomly chosen causal sites, the improvement in power observed for MLMM compared to the single marker MM is almost entirely attributed to increased power to detect the second causal site (Supplementary Fig. 6).

A serious problem when employing multi-locus models is knowing how many loci to include. We propose two model-selection criteria: the extended Bayesian information criteria (EBIC)²⁹, and the multiple-Bonferroni criterion (mBonf) defined as the largest model whose cofactors all have a p-value below a Bonferroni-corrected threshold (we used 0.05). Our simulations show that both criteria are consistent in bounding the FDR for the MLMM method regardless of the simulation scenario, EBIC being slightly more stringent than mBonf (Fig. 2 and Supplementary Fig. 5). In addition, the genome-wide p-values in the models selected by both criteria were uniformly distributed, demonstrating the ability of mixed models to control confounding by population structure in a multi-locus setting (Supplementary Fig. 1). Furthermore, both criteria perform appropriately in extreme scenarios where there is no detectable signal in the data, as when an external confounding variable interacts non-linearly with a single causal locus¹⁸. In this case, MLMM with one of the proposed criteria correctly selects a model without any SNPs whereas the other methods tested would identify false positives only (Supplementary Fig. 5). In summary, MLMM, with the conservative FDR provided by the proposed model-selection criteria, consistently outperforms the other methods in all scenarios we have simulated.

For completeness, we also compared MLMM to other single-locus mixed model implementations, the exact mixed-model³⁰ and the approximate mixed-model with compression¹⁴, as they have been shown to perform better than the approximate method used above. These did indeed perform slightly better than the approximate method in our simulations, but were still far from the performances achieved by MLMM (Supplementary Fig. 7).

Application to humans

To illustrate the feasibility as well as the utility of MLMM, we applied it to a previously published dataset of metabolic traits in the Northern Finland Birth Cohort (NFBC1966)³¹. The data were previously reanalyzed to demonstrate the utility of the mixed-model¹¹, and we used the same settings for the mixed model estimation here. The SNPs identified using MLMM are listed in Table 1. As predicted by our simulations, EBIC was more stringent than mBonf, resulting in the selection of models that were either similar to, or nested within, the models selected by mBonf. Focusing on the less conservative mBonf criterion, we identify all the associations previously detected using the single-locus mixed-model¹¹ and nine additional associations. Of the latter, three were located near genes previously reported using the same data³¹ (two in the TOMM40- APOE cluster for low density lipoprotein (LDL) and one in MTNR1B for glucose (GLU), while four were located in gene regions not previously reported with this dataset (HNF4A for high density lipoprotein (HDL), SMEK2 for systolic blood pressure (SBP), and two in the TOMM40-APOE cluster for C-reactive protein (CRP)). The remaining two were additional SNPs in genes that had already been identified (CETP for HDL, and CRP for CRP). The detected association in HNF4A for HDL (rs1800961) — a gene region not previously reported with this dataset — has been replicated in two meta-analyses based on 30,714 and 99,900 individuals respectively^32,33.

Table 1.

SNPs identified in multi-locus mixed-model analysis of the NFBC1966 traits

				p-value		Previously identified by
SNP	Chr.	Position	Gene	EBIC	mBonf	Sabatti et al.31	Kang et al.11
Associated with mmol/l TG
rs673548	2	21091049	APOB		5.1 × 10−8	Y	Y
rs1260326	2	27584444	GCKR	1.5 × 1O−10	7.9 × 10−11	Y	Y
rs10096633	8	19875201	LPL	1.6 × 10−8	2.4 × 10−8	Y	Y
Associated with mmol/l HDL
rs1532085	15	56470658	LIPC	9.2 × 10−12	8.0 × 10−12	Y	Y
rs3764261	16	55550825	CETP	2.7 × 10−32	3.7 × 10−23	Y	Y
rs7499892	16	55564091	CETP		9.5 × 10−8	N	N
rs255049	16	66570972	LCAT	1.3 × 10−8	4.8 × 10−8	Y	Y
rs1800961	20	42475778	HNF4A		1.5 × 10−7	N	N
Associated with mmol/l LDL
rs646776	1	109620053	CELSR2	4.2 × 10−16	4.2 × 10−16	Y	Y
rs693	2	21085700	APOB	7.1 × 10−12	7.1 × 10−12	Y	Y
rs11668477	19	11056030	LDLR	1.0 × 10−9	1.0 × 10−9	Y	Y
rs157580	19	50087106	TOMM40-APOE	2.2 × 10−17	2.2 × 10−17	Y	N
rs405509	19	50100676	TOMM40-APOE	1.3 × 10−12	1.3 × 10−12	N	N
Associated with mmol/l CRP
rs2369146	1	157934819	CRP	4.5 × 10−9	2.8 × 10−9	N	N
rs2794520	1	157945440	CRP	1.1 × 10−29	6.6 × 10−30	Y	Y
rs2650000	12	119873345	HNF1A	1.3 × 10−12	1.0 × 10−12	Y	Y
rs8106922	19	50093506	TOMM40-APOE		1.6 × 10−12	N	N
rs439401	19	50106291	TOMM40-APOE		2.2 × 10−9	N	N
Associated with mmol/l GLU
rs560887	2	169471394	G6PC2	2.2 × 10−13	2.2 × 10−13	Y	Y
rs2971671	7	44177862	GCK	3.2 × 10−9	3.2 × 10−9	N	Y
rs3847554	11	92308474	MTNR1B	4.7 × 10−11	4.7 × 10−11	Na	N
Associated with SBP
rs782602	2	55702813	SMEK2		1.4 × 10−7	N	Nb

Models were selected using either extended BIC (EBIC) or the multiple Bonferroni criterion (mBonf). Phenotype abbreviations are TG, triglyceride; HDL, high-density lipoprotein; LDL, low density lipoprotein; CRP, C-reactive protein; GLU, glucose; SBP, systolic blood pressure.

^aThis SNP was not reported by Sabatti et al., but they reported two other SNPs located in the same gene.

^bKang et al. did not report this association because they used a p-value threshold slightly more stringent then the Bonferroni-corrected threshold of 0.05 used for mBonf.

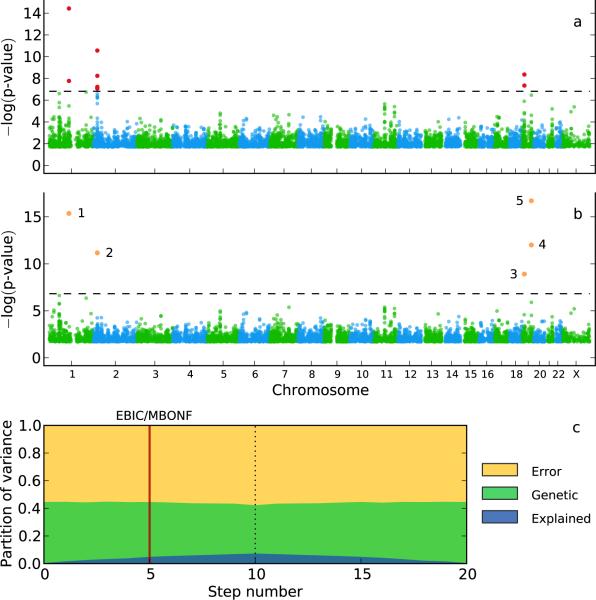
Multiple significant SNPs within or near a single gene suggest either allelic heterogeneity or the presence of an untyped causal variant that is partially tagged by multiple SNPs (or both). In the case of the associations located in the TOMM40-APOE cluster (for both LDL and CRP), we observed a dramatic decrease of the p-values for the two selected SNPs when they were both included in the model (Fig. 3 and Supplementary Fig. 8), which presumably explains why they were not identified using the single-locus mixed-model. This type of situation expected when loci mask each other, for example by when alleles of compensatory effect are correlated, as appears to be the case here (R² = 0.33 and R² = 0.25 for LDL and CRP respectively).

Figure 3.

GWAS for low-density lipoprotein (LDL) in the NFBC1966 dataset. (a) A single-locus mixedmodel identifies seven SNPs in three genes (marked in red; Bonferroni-corrected threshold of 0.05; dashed horizontal line). (b) A multi-locus mixed-model (MLMM) identifies five SNPs in four genes (marked in orange, and numbered in the order they were included in the model). (c) Partition of variance at each step of MLMM (10 forward and 10 backward) into variance explained by: the SNPs included in the model (blue); kinship (green); and noise (yellow).

Fig. 3 also shows the percentage of variance explained by the SNPs included into the model as well as the percentages of unexplained genetic and residual variance at the different steps of MLMM for LDL (for the other phenotypes, see Supplementary Fig. 9). It is notable that most of the heritable phenotypic variation remains unexplained.

Application to A. thaliana

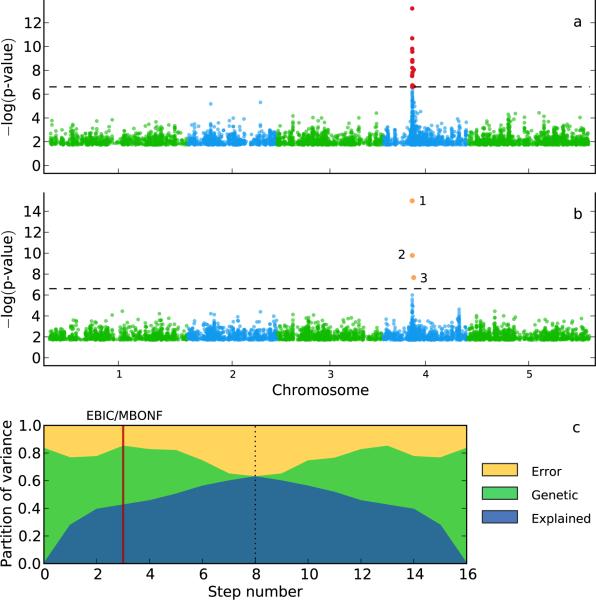
Sodium accumulation in the leaves of A. thaliana has been shown to be strongly associated with genotype and expression levels of the Na⁺ transporter AtHKT1;1³⁴. In particular, a SNP (chr4:6392280) located in the first exon of the gene has a highly significant association (p-value = 6.33 × 10⁻¹⁴ using an approximate mixed-model). We reanalyzed these data using MLMM and found that the sole SNP previously reported³⁴ only explains part of the signal in the region (Fig. 4).

Figure 4.

GWAS for Na⁺ accumulation in A. thaliana. (a) A single-locus mixed-model identifies a strong peak of significantly associated SNPs on chromosome 4 (marked in red; Bonferroni-corrected threshold of 0.05; dashed horizontal line). (b) Multi-locus mixed-model (MLMM) identifies three SNPs (marked in orange, and numbered in the order they were included in the model). (c) Partition of variance at each step of MLMM (8 forward and 8 backward) into variance explained by: the SNPs included in the model (blue); kinship (green); and noise (yellow).

Instead, the optimal model obtained with MLMM (according to both EBIC and mBonf) included three SNPs, which together explained 42.3% of the phenotypic variation. This model included the previously reported SNP, which explained 27.7% of the variation, and a second SNP only 22kb away from the gene, suggesting that there might be multiple causal variants in the gene. To further investigate the associations in this particular region, we applied our method locally, i.e. using only the 508 SNPs located within 100kb of the gene. Using the EBIC, six SNPs were included in the model, all within 25kb of AtHKT1;1, explaining 52.6% of the phenotypic variation (Supplementary Fig. 10), leaving 20.5% as unexplained heritable fraction of the total variance. As noted above, this suggests either allelic heterogeneity or the presence of one or more untyped causal variants. However, since largest possible fraction of variance explained by a single binary SNP (which would have a minor allele frequency of 0.32) is 47.6%, we conclude that there is evidence for allelic heterogeneity.

DISCUSSION

The problem of population structure in GWAS is best viewed as one of model mis-specification. When carrying out single-locus tests of association, we are using the wrong model unless the trait is actually due to a single locus. Ignoring the genetic background may be defensible in some circumstances, but is clearly not when causative alleles are correlated across loci due to population structure and/or selection¹², resulting in biased estimates of effect sizes. The problem has long been recognized by animal breeders, who developed a mixed linear model to reduce the bias⁸. This approach works well, but assumes that the phenotypic covariance between individuals can be predicted by their relatedness, as estimated by genome-wide SNPs. As demonstrated by Fisher close to 100 years ago⁹, this approximation is reasonable if the genetic background is sufficiently smooth, but it is easy to see that loci of relatively larger effect may make it invalid¹⁸. We therefore propose to extend the mixed model for GWAS to include multiple loci, in parallel to what is routinely done in QTL linkage mapping^16,17.

Our proposed method includes significant effects in the model via a forward-backward stepwise approach, while re-estimating the variance components of the model at each step. If the fixed effects included are real, they can reduce the unexplained heritable variance and effectively lower the restraints posed by the mixed model on other markers which correlate with population structure. As demonstrated by simulations, our implementation (MLMM) displays promising performance in terms of power and FDR in comparison with a single marker scan and a stepwise linear regression, especially when applying a conservative threshold which can be achieved with one of the proposed model-quality criteria. In particular, MLMM performed much better than the other methods tested for structured samples and traits involving several loci with moderate to large effect.

Applying MLMM to real data from humans and A. thaliana, we identified interesting novel associations as well as evidence for allelic heterogeneity. Indeed, as it includes multiple loci in the model, MLMM helps identify evidence for allelic heterogeneity as well as interactions, although it is difficult to exclude that multiple associated SNPs within a region are due to partial linkage disequilibrium with an untyped causal variant^12,18,20. However, with the rapid development of DNA sequencing³⁵, it is increasingly likely that causal variants will be typed. As seen in our simulations, all tested methods, and especially MLMM, will benefit greatly from this. While applied here to quantitative traits, MLMM can also be applied to diseases. Indeed, it is possible to analyze a disease phenotype with an approximate mixed-model by considering a binary quantitative response corresponding to the case-control status¹¹. Finally, MLMM partitions the phenotypic variance into genetic, random and explained variance at each step, suggesting a natural stopping criteria (genetic variance of 0) for including cofactors. This allows the user to obtain estimates of the explained and unexplained heritable variance, as well as give insights into the trait architecture.

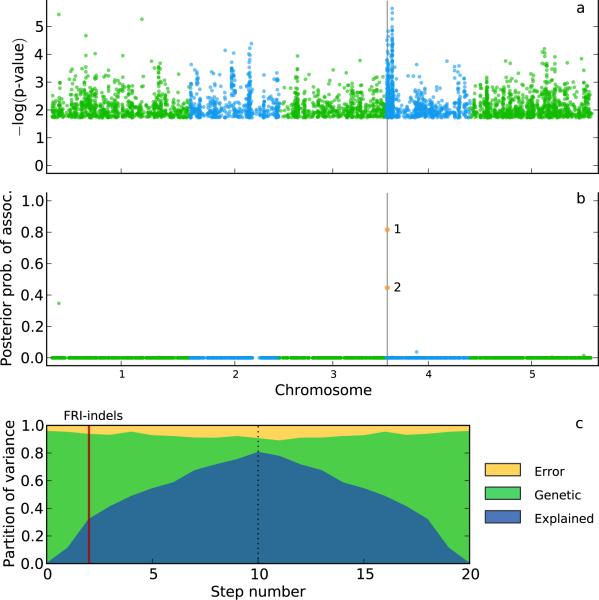
MLMM is far from a panacea, however. The greedy forward-backward inclusion of SNPs is clearly limited in exploring the huge model space. More sophisticated algorithms, like LASSO³⁶, are worth exploring. However, as other penalized methods, LASSO assumes independence between markers, which is obviously not appropriate for structured data. This might cause LASSO to give a large effect size to a marker that is in LD with many other markers, whereas a mixed model would down-weight such markers. A potential improvement on this would be use LASSO in conjunction with a mixed-model²⁶. While this approach is potentially very promising, it is currently too computationally demanding for GWAS datasets. Another promising approach is resample model averaging³⁷, which has been applied successfully to joint linkage association analysis³⁸. However, it is important to realize that the problem is fundamentally very hard. For example, we have previously shown that linkage disequilibrium between two known causal alleles of the A. thaliana flowering locus FRIGIDA (FRI) and the genomic background give rise to a very complicated pattern of association in a GWAS of FLOWERING LOCUS C (FLC) expression¹². None of the methods tested in this paper identify the causal sites—not surprisingly because there are many spurious one- and two-locus models that fit the data better than those involving the true causal loci. In cases like this, we think it is unlikely that progress will be made without independent data to help us prioritize variants. Since MLMM is based on a linear model it can easily be extended for Bayesian analysis^39,40 and allow for the integration of prior information into the model. Indeed, returning to the FLC example, by placing a 100-fold prior on all markers within 10kb of FRI we allow MLMM to include the two known causal variation as the first two cofactors in the model, demonstrating how prior knowledge can help identifying causal loci, and improving the model (Fig. 5).

Figure 5.

An example of Bayesian multi-locus mixed-model (MLMM) for the analysis of FLOWERING LOCUS C (FLC) expression in A. thaliana. (a) An approximate mixed-model scan for FLC expression, marking the FRIGIDA gene with a vertical grey line. (b) The posterior probability of association scan after the Bayesian MLMM has included two loci into the model, which incidentally are the two previously identified causative indels. (c) Partition of phenotypic variance for each forward inclusion (10 steps) and backwards elimination (10 steps after the dotted line). The vertical red line marks the model with the two causative indels in the model.

METHODS

Data

Both A. thaliana and human data were used for the examples. The genotype data for A. thaliana included 1,307 individuals genotyped at 214,051 SNPs using a 250K Affymetrix SNP chip²⁸. The two A. thaliana phenotype datasets used were: (i) sodium levels averaged over 6 replicates of 342 accessions³⁴, and (ii) FLOWERING LOCUS C (FLC) expression measured in 166 accessions¹². For FLC expression the genotype data used was the same as used by Atwell et al., which is a subset of the 1,307 individuals and contains 216,130 markers, including three indels within or near the FRIGIDA (FRI) gene. As priors we gave every marker which were within 10kb from the FRI gene a 100 fold greater prior over the base prior. We then scaled them so that the sum of the priors over all the SNPs was 1.

The human dataset used was the 1966 North-Finland Birth Cohort NFBC1966 composed of 5,402 individuals having both phenotypic and genotypic data³¹. Phenotypic data consisted of 10 quantitative traits, and genotypic data in 368,177 SNP markers. We were able to obtain the exact same dataset, i.e. 5,326 individuals and 331,475 SNPs after filtering, as used in¹¹. The proportion of missing genotypes was < 1% which we imputed with its corresponding average per SNP to speed up the mixed model computations.

Simulations

Using the A. thaliana genotypic data²⁸, we simulated two types of traits; simple ones controlled by one or two causal loci, and complex ones controlled by 100 loci. For the simple traits, two randomly chosen SNPs or one randomly chosen SNP and one binary latent variable were used to generate phenotypes using the three phenotypic models (additive, “and/or”, “xor”) described in Supplementary Table 1. The latent binary variable was designed by splitting the accessions in half on the basis of their latitude of origin, which we refer to as the latent north-south variable, to generate some substantial covariance between the phenotypes and population structure. An additional random deviation was added, drawn from a multivariate normal distribution having a mean of zero and a scaled identity matrix as covariance to fix the trait heritability to 0.1. 1,000 phenotypes were simulated for each simulation type (i.e., two causative SNPs or one causative SNP and the latent binary variable), phenotypic model, and phenotypic heritability. For complex traits, we used an additive model with 100 randomly sampled SNPs having effect sizes drawn from an exponential distribution with a rate of 1. An additional random deviation was added, drawn from a normal distribution with a mean of zero and scaled identity matrix as covariance matrix to fix the trait heritability to 0.25, 0.5, and 0.75. For each phenotypic heritability, 500 phenotypes were simulated. All simulated phenotypes have been analyzed with the four methods presented in the main text. For completeness, another single-locus approximate mixed-model has been used to analyze the phenotypes simulated under the 100-locus model. To control some potential population structure confounding that was not accounted for by the random term, this approach uses as covariates the ten first principal components from a principal component analysis of the standardized genotypic data. As no obvious difference was observed between this extra approach and the approximate mixed-model, only the latter was presented in the results (Supplementary Fig. 11).

Linear mixed model

Following Fisher's⁹ polygenic model and adopting similar notation as in Yang et al.⁴¹, the phenotypic value of the i'th individual can be written as

$$y_i=\mu +\sum _{j=1}^m{x}_{ij}{a}_j+e_i,$$

where m is the total number of causal loci, x_ij is the genotype (re- coded in numerical terms) of the j'th causal locus to the i'th individual, a_j is the effect size of the j'th locus, and e_i is the error. If we assume a large number of the independent causal loci are and that their effects are drawn from a Gaussian distribution (Fisher's infinitesimal model) we can sum them up and approximate them with a Gaussian random variable. We therefore model the trait using a mixed model⁸, where the phenotype can be written in vector notation as

$$\mathbf{y}=X\beta +\mathbf{g}+\mathbf{e},$$

where β are the effect sizes of fixed effects (e.g. SNPs), g is a vector of random polygenic effects and has distribution $\mathbf{g}~N(0,{\sigma }_g^2{K}^{\ast })$ and e is the residual (error) and has distribution $\mathbf{e}~N(0,{\sigma }_e^{2}I)$. Here K* denotes the adjusted kinship matrix, where the loci included as fixed effects are excluded from the kinship matrix estimation. If M ⪢ n, where M is the number of causal loci and n is the number of individuals, then K* ≈ K. Different assumptions lead to different kinship matrices that can be used for the mixed model as described in the Supplementary Note.

Multiple loci mixed model (MLMM)

We used forward-backward stepwise linear mixed model regression, where the variance components ${\widehat{\sigma }}_g^2$, and ${\widehat{\sigma }}_e^2$ are estimated before each step. The variance estimates are used to obtain generalized least square (GLS) effect size estimates and F-test p-values for each SNP. The most significant SNP is then added to the model as a cofactor for the next step, and the p-values for all cofactors are re-estimated together with the variance components. As a stopping criteria for the forward regression, we suggest stopping when the ${\widehat{\sigma }}_g^2∕\text{Var}\left(\mathbf{y}\right)$ estimate is close to zero, or when a maximum number of forward step is reached. After stopping the forward stepwise regression a backward stepwise regression is performed by dropping the least significant cofactor in the model at each step. The variance component and p-values of all cofactors again re-estimated at each step. For the variance components estimation at each forward and backward step, the markers included as cofactors in the model can be excluded from the kinship matrix calculation, although we did not do this since their effect on the kinship is arguably negligible.

We make use of the Gram-Schmidt process⁴¹ which makes each step as fast as the first one when M ⪢ n (i.e. the number of SNPs is much greater the number individuals). At each step we obtain the QR-decomposition of the cofactor matrix to obtain the $\mathcal{Q}$ matrix and use it to calculate the marginal inverse variance matrix

$$M^{-\frac{1}{2}}=(I-\mathcal{Q}\prime \mathcal{Q})\prime V^{-\frac{1}{2}},$$

where $V={\sigma }_g^{2}K+{\sigma }_e^{2}I$ is the covariance matrix estimated at each step.

We explored several model selection criteria to select the most appropriate model. The classic Bayesian information criterion (BIC) is too tolerant in the context of GWAS, allowing for too many loci in the model and is therefore not recommended. As an alternative, we used the extended BIC, initially defined by Chen and Chen²⁹ as the BIC penalized by the model space dimension. We also propose and define a new criterion, the multiple Bonferroni criterion (mBonf) which selects the model with most loci for which all have p-values below the Bonferroni threshold. This criteria enables the user to specify the p-value threshold if one wants to allow for a higher false discovery rate (FDR) or restrict to a lower one. The computational complexity of our implementation is described in the Supplementary Note.

Employing priors on loci

As described in³⁹ it is possible to employ priors on loci in a Bayesian model, where the Bayes factor is calculated for each locus. Calculating the Bayes factor is however not always easy, as it requires integrating out the model parameters which have some specified prior distributions. In our case the model parameters of interest are the effect sizes of the loci in the model. A rough approximation can be achieved using the Schwarz criterion which allows us to avoid having to define priors on the effect sizes and evaluate the integral⁴². We define the approximate Bayes factor (ABF) as

$$\log ABF=\log P(D\mid \beta ,M_1)-\log P(D\mid \beta ,M_0)-\frac{1}{2}(d_1-d_0)\log n,$$

where n in the number of individuals, D is the observed data, M_i is the i'th model and d_i the degree of freedom in the i'th model. Using this approximation together with a prior probability π for the locus being causal we define the approximate posterior probability of association (APPA) as

$$\mathrm{APPA}=\frac{\mathrm{ABF}\cdot \pi }{1-\pi (1+\mathrm{ABF})}.$$

We note that this quantity should be treated more as a score than a probability, as it is a rough estimate of the actual probability.