On-line apnea-bradycardia detection using hidden semi-Markov models

Abstract

In this work, we propose a detection method that exploits not only the instantaneous values, but also the intrinsic dynamics of the RR series, for the detection of apnea-bradycardia episodes in preterm infants. A hidden semi-Markov model is proposed to represent and characterize the temporal evolution of observed RR series and different pre-processing methods of these series are investigated. This approach is quantitatively evaluated through synthetic and real signals, the latter being acquired in neonatal intensive care units (NICU). Compared to two conventional detectors used in NICU our best detector shows an improvement of around 13% in sensitivity and 7% in specificity. Furthermore, a reduced detection delay of approximately 3 seconds is obtained with respect to conventional detectors.

I. INTRODUCTION

Apnea-bradycardia (AB) episodes are common on preterm infants. These episodes are defined as a respiratory pause, accompanied with a fall in heart rate, and are associated with short-term morbi-mortality and neurological impairment during childhood [1], [2]. AB episodes may be aggravated in the presence of infection, hypoxia or intracranial pathologies. Preterm infants suffering from frequent AB episodes are monitored in neonatal intensive care units (NICU), where the detection of AB triggers a set of nursing therapeutic actions.

In current NICU monitors, AB episodes are detected by processing a single variable extracted from the electrocardiogram (ECG): the cardiac cycle length (RR) [3], [4], [5]. However, a recent work has shown that other features extracted from the ECG, such as R-wave amplitude and QRS complex duration, also show significant changes before and after the episode [6]. Typically, AB episodes are detected when the cardiac cycle length is higher than a predefined fixed threshold (usually 600 ms) or when it is higher than a relative threshold (usually 33% of the base rhythm), for more than 4 s [3].

The aim of this work is to propose an AB detector that exploits not only the instantaneous values, but also the dynamics of the RR series. An approach based on a hidden semi-Markov model (HSMM) is thus presented, with different pre-processing methods. The rest of this paper is organized as follows: the next section introduces the phases of learning and evaluation of HSMM to perform the event detection, as well as the pre-processing methods applied (quantification and integration of delayed version of the observation) and the evaluation methodology. The evaluation of the proposed detector on simulated and real signals is described in Section III. Discussion of the results obtained are exposed in Section IV. Finally, the conclusions and future works are outlined in the last section.

II. METHODS

A. Hidden Semi-Markov Models

An HSMM is similar to a classic hidden Markov model (HMM), but the main difference is that the unobserved process is semi-Markov in the sense that a change to a future hidden state depends on both the current state and the time spent on this state. These models have already been applied successfully in the bioengineering field [7], [8].

An HSMM is characterized by a number of M states and the set of parameters λ ≜ {a_ij, b_i, π_i, p_i}, where a_ij is the transition probability between states i and j (a_ii = 0), b_i is the probability of emission of observations, π_i is the probability of the initial state and p_i is the probability of duration for state i. In this work, the Bayesian information criterion (BIC) [9] is used to calculate M. Additionally, b_i and p_i are represented by a Gaussian distribution: b_i(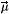,Σ) and p_i(μ_d, σ_d), where 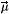and Σ correspond to the center and covariance matrix of observations and μ_d and σ_d are the mean and the standard deviation of the duration of each state. In order to avoid negative durations, Gaussian distributions for p_i(μ_d, σ_d) are always positive (truncated in zero).

The main interest in the application of an HSMM to biomedical series processing is that it can better represent the temporal evolution of a variable through parameters p_i. Indeed, the Gaussian law used in the proposed HSMM for p_i provides a better representation of the time spent in a given physiological state than the implicit geometric law of HMM, in particular when the duration on a given state is relatively long. In a previous work, we have shown the advantages of the HSMM approach, with respect to classic HMM, for the detection of cardiac ischemia episodes [8].

In this paper, K HSMM are used to represent K different observation dynamics, associated with distinct physiopathological states or events, to be discriminated. A learning phase is firstly applied to each model, in order to estimate each λ^k, ∀k ∈ {1, 2, …, K}, from the sequences of observations, provided in a learning dataset. During this phase, λ^k is initialized from the parameters of the equivalent HMM, in which the Viterbi algorithm is used to to estimate p_j(μ_d, σ_d). Additionally, a_ij and π_i are initialized with uniform probabilities and b_i(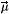, Σ) is initialized by a Gaussian mixture model where the center of each Gaussian, which corresponds to the barycenter of each state in the observation space, have been initialized by the K-means algorithm. The Viterbi algorithm, extended to HSMM, is subsequently applied to obtain the final value of λ^k, through an expectation-maximization stage. Learning is achieved when the log-likelihood

$${\mathcal{L}}^k=logP(O_{1:T}\mid {\lambda }^k)$$ (1)

converges to a maximum value, where P(O_1:T |λ^k) is the probability that the observation sequence O_1:T = O₁, O₂, …, O_T is generated by the model with parameters λ^k.

Once the learning phase is completed, the K HSMM are applied in a test phase to a set of observations on a specific dataset, in order to perform event detection. In this case, the log-likelihood for instant t and model k,

$${\mathcal{L}}_t^k=logP(O_{t-T+1:t}\mid {\lambda }^k)$$ (2)

is determined using a sliding window of length T. On-line detection of event α(α ∈ {k}) is finally performed when the following equation is verified:

$${\mathcal{L}}_t^{\alpha }-{\mathcal{L}}_t^k>{\delta }^{\alpha ,k}\forall k\in \{1,2,\dots ,K\}-\{\alpha \}$$ (3)

where δ^α,k are fixed thresholds that have to be optimized.

B. Quantization of observations

A quantization phase of the observations is proposed in this work to improve the detection performance of the HSMM approach. This quantization phase is justified, since i) HSMM are constituted of a discrete number of states M representing the dynamic range of the observations and ii) inputs to the proposed detector are the result of an automatic ECG segmentation phase that may produce segmentation errors.

Two quantization methods are applied: uniform, characterized by a constant quantization step Δ_QU and non uniform, characterized by a quantization step 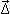_QNU, which depends on the distribution of the signal. Vector 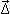_QNU is found by comparing the cumulative sum of values of the normalized histogram with respect to a threshold δ_QNU. Different values of Δ_QU and δ_QNU have been tested to obtain the value that maximizes detection performance. Variables noted with UQ and with NUQ indicate its uniform and non uniform quantization, as for RR_UQ and RR_NUQ.

C. Integration of delayed versions of the observation

Here, we explore the possibility of increasing the observability of the system while maintaining the same number of sources. In this sense, an observation matrix is constructed, integrating the original and a delayed version of the observed time-series. This observation matrix may be represented as:

$$\mathbf{O}=\left[\begin{array}{c}{O}_{t-T+1:t}\\ O_{t-\tau -T+1:t-\tau }\end{array}\right]$$ (4)

where τ is the predefined time delay. In the case of the RR series, the application of such a time-delay presents also a physiological argument, since it is known that the RR interval is modulated by the autonomic nervous function, with different dynamics for the sympathetic and parasympathetic systems. Different values of τ have been tested to optimize detection performance. These observation matrices will be represented in bold in this paper, such as RR.

D. Evaluation methodology

The proposed HSMM detection approach was firstly evaluated with simulated signals in order to optimize its structure and evaluate the impact of the different preprocessing methods in a controlled way. It was then evaluated with real signals acquired in NICU, in which AB episodes have been manually annotated.

1. Evaluation on simulated signals

Synthetic time series were generated with the FitzHugh-Nagumo model, described by the following differential equations [10]:

$$\begin{array}{l}\frac{dv}{dt}=3(v-\frac{1}{3}{v}^3+r+I)\\ \frac{dr}{dt}=-\frac{1}{3}(v-a+0.8r)\end{array}$$ (5)

Variables v and r are in a “rest” value until a perturbation is introduced into variable I. This induces an excursion in the phase space on variables v and r, before returning to their resting values. The simulated series have a size of 400 s and a perturbation I =−0.2 is introduced during the interval [300, 305] s. Parameter a was modified according to a uniform distribution in the interval a1 ~ 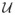(0.58, 0.62) and a2 ~ 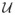(0.78, 0.82) to generate series presenting two slightly different different dynamics. Moreover, the simulated series were divided by its maximum value, in order to generate signals with similar amplitudes. Gaussian white noise was added to the series to obtain a signal to noise ratio SNR = 5 dB. Responses generated with a1 and a2 are thus difficult to differentiate by only analyzing their instantaneous values (such as with a threshold-based detector).

Three synthetic datasets will be used for the learning phase:

• LSFN1: comprising 80 segments at “rest” (before the perturbation) generated with a1 (40 segments) and a2 (40 segments).

• LSFN2: with 40 segments from the beginning of the perturbation and generated with a1.

• LSFN3: represented by 40 segments from the beginning of the perturbation and generated with a2.

All these segments have a duration of T = 10 s.

Once the HSMM have been trained, they are applied to a test dataset consisting of 400 synthetic signals of 400 s each: 200 of these signals were generated with parameter a1 and 200 with parameter a2. Equations 2 and 3 where applied as the online detection approach, with a sliding window of size T = 10 s.

2. Evaluation on real signals

RR series were extracted from the ECG of 32 preterm infants with frequent AB episodes as described in [6], [11]. RR series were uniformly resampled at 10 Hz. 233 bradycardia episodes were manually annotated from 148 RR series. Two datasets were constructed for the learning phase:

• LS1: composed of 30 segments taken randomly and including an AB event, taken at the beginning of the bradycardia with duration of T = 7 s.

• LS2: consisting of 300 segments at rest, taken randomly from the series, with duration of T = 7 s.

The length of these segments (7 s) corresponds to the average time measured from the beginning of the bradycardia to the peak RR value within the bradycardia episode. In order to reduce the variability of the first sample of the series, the mean, determined within 5 s before the start of each segment, was removed for all segments. This is particularly important for the estimation of the first state (π_i) of the models.

The evaluation of the models trained from real signals was performed on a test set containing the totality of the 148 RR series (series duration = 26.25 ± 11.37 minutes) with 233 bradycardia episodes. The online HSMM detector is applied to these series as described in the previous section, with a sliding window of size T = 7 s.

3. Performance evaluation

For both simulated and real signals, true positives (TP), true negatives (TN), false positives (FP) and false negatives (FN) were determined for each sample by comparing the obtained detections with the available annotations. TP occur when a detection falls within a 20 s window, centered at a given annotation. Even if this window seems particularly large, we justify this choice by the fact that we are also evaluating the detection delay as an important marker for the selection of the optimal detection method.

Detection performance was evaluated by estimating the sensitivity (SEN = TP=(TP + FN)) and specificity (SPC = TP=(TN + FP)) of each detector, for different detection thresholds, and represented by means of ROC curves. The detection delay (dd) is also determined, and defined as the time elapsed between the annotation instant and the detection. Detection results were evaluated using the shortest distance to perfect detection (SDPD) according to Eq. 6. Detection delay results are presented in mean ± SD.

$$\mathit{SDPD}=min\sqrt{{(1-\mathit{SEN})}^2+{(1-\mathit{SPC})}^2}$$ (6)

III. RESULTS

A. Simulated signals

This experience is particularly interesting, since, as described earlier, a simple threshold-based detection would be unable to discriminate the series produced with a1 from those produced with a2. Only the series generated with a1 were analyzed, as those generated with a2 do not provide additional information for our purpose of validation.

K = 3 HSMM were employed to model each learning dataset: HSMM with set λ^k to model LSFNk, k ∈ {1, 2, 3}. The BIC criterion was applied in each case to estimate the number of states per model: M^k. A sliding window of size T = 10 s was used to obtain the observation sequence and calculate the log-likelihoods 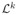. Two thresholds (δ^2,1 and δ^2,3) were used to detect the perturbation generated with a1 as in Eq. 3. Detection results for simulated signals are shown in Table I. Optimal parameters were: τ = 5 s, Δ_UQ = 25 and δ_QNU = 0.003.

TABLE I.

Sensibility, specificity and detection delay by evaluating SDPD (Eq. 6) for simulated signals

Variable	SEN (%)	SPC (%)	dd (s)
v	89.29	97.98	2.09 ± 0.07
vUQ	93.26	97.85	1.41 ± 0.24
vNUQ	92.14	96.19	0.16 ± 3.12
v	90.25	97.61	1.73 ± 1.40

B. Real signals

K = 2 HSMM models were used to detect AB episodes. Each parameter set λ^k, was estimated to reproduce the dynamics of LSk, k ∈ {1, 2}. Only one threshold is thus used, λ^1,2. M^k was determined using the BIC criterion. A T = 7 s sliding window was used to construct O_t−T+1:t and to determine ${\mathcal{L}}_t^k$. The detection of an AB episode is obtained by applying Eq. 3.

ROC curves are shown in Fig. 1 and its respective mean detection delays are shown in Fig. 2. Optimal parameters were: τ = 0, 67 s, Δ_UQ = 1300 and δ_QNU = 0.05. Conventional detection methods are also shown as a reference. In these figures, the point where SDPD occurs is shown with character “x”. Table II lists the obtained SEN, SPEC and dd at the SDPD point (represented with the “x” symbol in figures 1 and 2), for the detection of AB episodes.

Fig. 1.

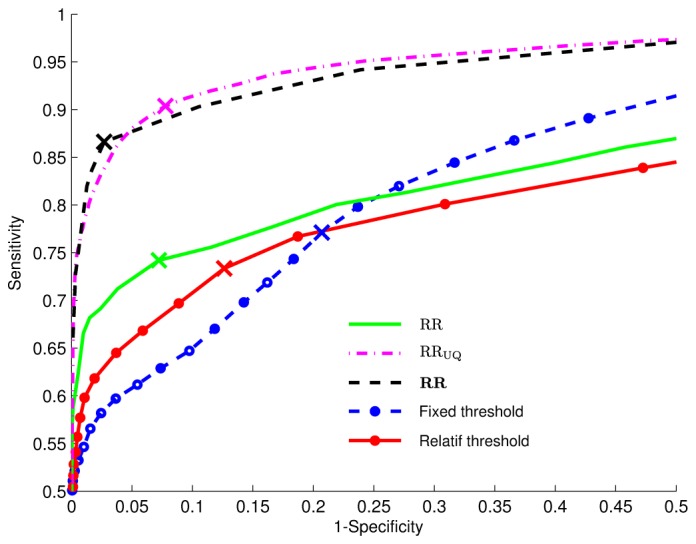
ROC curves for AB event detection.

Fig. 2.

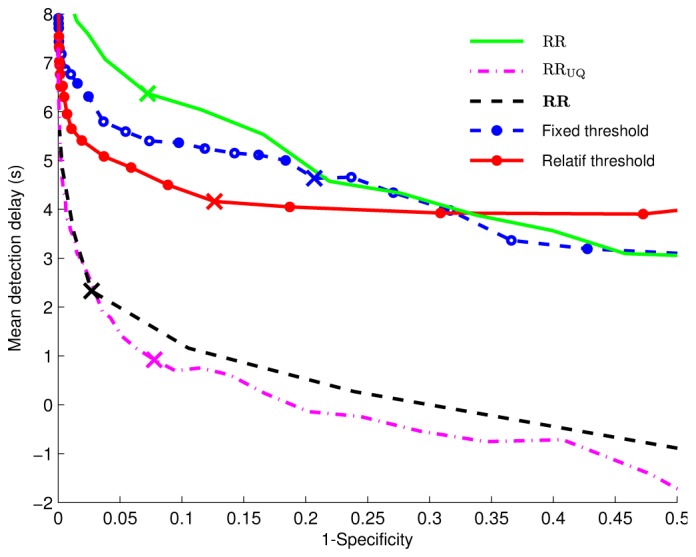
Mean detection delay of AB episodes.

TABLE II.

Sensibility, specificity and detection delay by evaluating SDPD (Eq. 6) for real signals

Variable	SEN (%)	SPC (%)	dd (s)
RR	74.20	92.77	6.37 ± 7.83
RRUQ	86.63	97.30	2.33 ± 3.15
RRNUQ	89.98	94.67	1.93 ± 3.34
RR	90.38	92.23	0.92 ± 3.56
Fixed thresh	77.11	79.31	4.63 ± 5.04
Adaptative thresh	73.35	87.36	4.16 ± 8.79

IV. DISCUSSION

Results on simulated signals show that the detection performance is improved when the quantization step is applied (see table I). The best detection performance and the minimum mean detection delay were obtained when a uniform quantization is applied (v_UQ), followed by the non uniform quantization version (v_NUQ). These results confirm the utility of the proposed HSMM approach, and measure the impact of the quantization step and the integration of a delayed version of the observables, on detection performance.

The introduction of a time-delayed version of the signal may improve obsevability by synchronizing different effects that modify the same variable, which are not necessarily in phase. The gain in performance depends on i) the existence of such kind of effects on the available series and ii) the appropriate optimization of τ (which is considered constant). The gain obtained from simulated data is rather low, but results from real signals show the benefit of the approach.

Detection results from real signals (Fig. 1 and 2 and table II) show that modeling the dynamics of RR series by HSMM provides an improved detection performance, when compared to conventional detection methods (fixed or relative threshold detections). In addition, the application of the proposed preprocessing methods (RR_UQ, RR_NUQ and RR), further improves this performance and reduces the mean detection delay. These results indicate that our approach detects, on average, more than 2 s earlier than conventional detectors.

V. CONCLUSIONS AND FUTURE WORKS

In this paper, the difficult problem of exploiting the dynamics of biomedical time series for the early-detection of pathological events was addressed. A detection approach, based on an HSMM and combining different pre-processing methods, was proposed and evaluated using simulated and real signals. Results obtained from synthetic signals demonstrate the interest of the proposed approach, and the fact that the detection is mainly based on the difference of the temporal dynamics of the events under consideration.

On real data, the performance of the proposed approach for the detection of AB episodes has shown to be higher than classical methods, while minimizing the detection delay. The usefulness of the quantization phase and of the integration of delayed versions of the observation into the HSMM was also evaluated and showed to improve the detection performance. This is an important result, as the minimization of the delay from the beginning of the AB episode to the application of the therapy by the nurse is one of the main goals in this clinical field.

The main advantage of the approach proposed in this paper is its simplicity, opening the possibility of an embedded implementation into a mobile device. Future works are directed towards the multivariate extension of this method, in order to integrate other features extracted from the preterm infant’s ECG, such as the R-wave amplitude, the QRS complex duration, the PR interval and P-wave morphology. This approach may also improve detection performance and reduce the detection delay.