Trimodal low-dose X-ray tomography

Abstract

X-ray grating interferometry is a coherent imaging technique that bears tremendous potential for three-dimensional tomographic imaging of soft biological tissue and other specimens whose details exhibit very weak absorption contrast. It is intrinsically trimodal, delivering phase contrast, absorption contrast, and scattering (“dark-field”) contrast. Recently reported acquisition strategies for grating-interferometric phase tomography constitute a major improvement of dose efficiency and speed. In particular, some of these techniques eliminate the need for scanning of one of the gratings (“phase stepping”). This advantage, however, comes at the cost of other limitations. These can be a loss in spatial resolution, or the inability to fully separate the three imaging modalities. In the present paper we report a data acquisition and processing method that optimizes dose efficiency but does not share the main limitations of other recently reported methods. Although our method still relies on phase stepping, it effectively uses only down to a single detector frame per projection angle and yields images corresponding to all three contrast modalities. In particular, this means that dark-field imaging remains accessible. The method is also compliant with data acquisition over an angular range of only 180° and with a continuous rotation of the specimen.

In X-ray phase-contrast imaging, contrast is generated by the refraction of X rays as they pass the object under study, and not, as in conventional radiography, by the differences in absorption between the constituents of the object.

Because the real part of the refractive index of hard X rays for light materials is several orders of magnitude higher than its imaginary part (which describes absorption), X-ray phase-contrast methods can reveal structures that usually remain invisible in conventional absorption contrast, for example, different types of soft biological tissue. However, the angles by which X rays are refracted when passing through macroscopically sized objects remain so small that a sophisticated apparatus is needed to exploit phase contrast.

For these reasons, although some X-ray phase-contrast methods had already been developed decades ago (1, 2), the full potential of these methods was recognized only with the availability of modern synchrotron radiation sources and microfocus X-ray generators for the laboratory. A variety of X-ray phase-contrast methods based on these sources was developed in the second half of the 1990s (3). In addition to providing the high contrast of a phase-sensitive method, some of them have the additional advantage of giving access to yet another complementary image modality, i.e., scattering (“dark-field”) contrast. This is notably the case for analyzer-based imaging (4, 5).

Starting in the early 2000s, X-ray grating interferometry (XGI) (6, 7) emerged as an additional multimodal X-ray imaging technique with particular benefits. It gives access to differential phase contrast (DPC) at ultrahigh sensitivity (density differences down to 0.5 mg/cm³ can be routinely resolved) (8, 9). XGI also provides dark-field images of the sample that reveal the presence of scattering structures on the nanoscale (10).

A grating interferometer is largely achromatic and can thus be efficiently used with X rays that have a broad spectral distribution (11, 12). Another important advantage of XGI over many other X-ray phase-contrast methods is that radiation from a low-brilliance X-ray source can be efficiently used (13). These features are unique properties that make XGI compatible with laboratory X-ray imaging systems and increase its efficiency on synchrotron imaging stations.

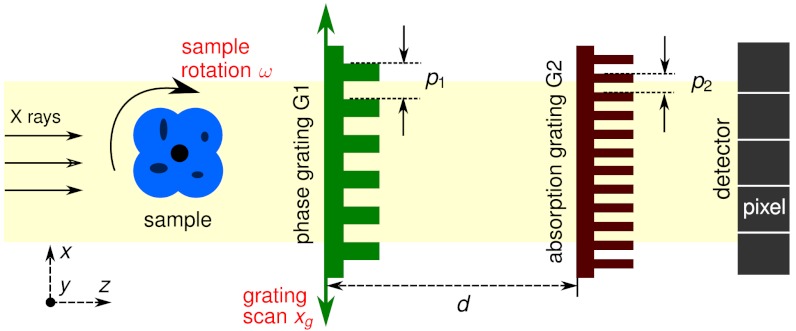
The key element of an XGI setup (Fig. 1) is a diffraction grating G1 in transmission geometry that induces a periodic modulation into the X-ray wavefront. Because the period p₁ of this grating is much larger than the X-ray wavelength, its diffraction orders overlap almost completely and form regular interference patterns in planes downstream of G1. An object placed in the beam will cause local modifications of these patterns. A second grating G2, placed before the detector, can be used to encode these modifications into intensity variations on the detector pixels.

Fig. 1.

Schematic representation of an X-ray grating interferometer setup. The phase grating (G1) and the absorption grating (G2) are positioned between the sample and the detector. G2 is placed at a distance d from G1 at which the interference pattern generated by G1 exhibits the maximum contrast.

The DPC and dark-field signals (as well as the absorption image) can be extracted from the raw interferograms with different approaches. Among these methods, the “phase-stepping” technique, which consists of recording and analyzing a series of interferograms (three or more) for different relative transverse positions of the two gratings (7, 11, 14), has several advantages. It does not affect the spatial resolution of the imaging system as in single-shot approaches (15, 16) and it does not have stringent requirements on the period matching of the gratings, which is a limitation in the reverse projections (RP) method (17). It should also be noted that, with the RP method, which uses a linear combination of two interferograms taken at sample positions 180° apart, the dark-field signal cannot be accessed. On the other hand, because at least three exposures are needed per final projection, the phase-stepping method may be slower and may deliver more dose to the sample than other methods.

In this paper we present and demonstrate, through simulated and experimental data, advanced phase-stepping methods, here called sliding window methods, which provide phase and scattering tomographies of quality comparable to the existing phase-stepping methods while significantly decreasing (up to a factor of 5) the acquisition time and the dose delivered to the sample.

Sliding Window Phase Stepping

A schematic representation of an X-ray grating interferometer is shown in Fig. 1 (11). In a phase-stepping tomography measurement, the scan of one of the gratings is combined with the rotation of the sample. Each raw interferogram recorded during a tomographic scan of this kind is taken at a different transverse position x_g of the grating and/or a different position ω of the sample. Thus, these interferograms can be represented by points in the (ω,x_g) coordinate system.

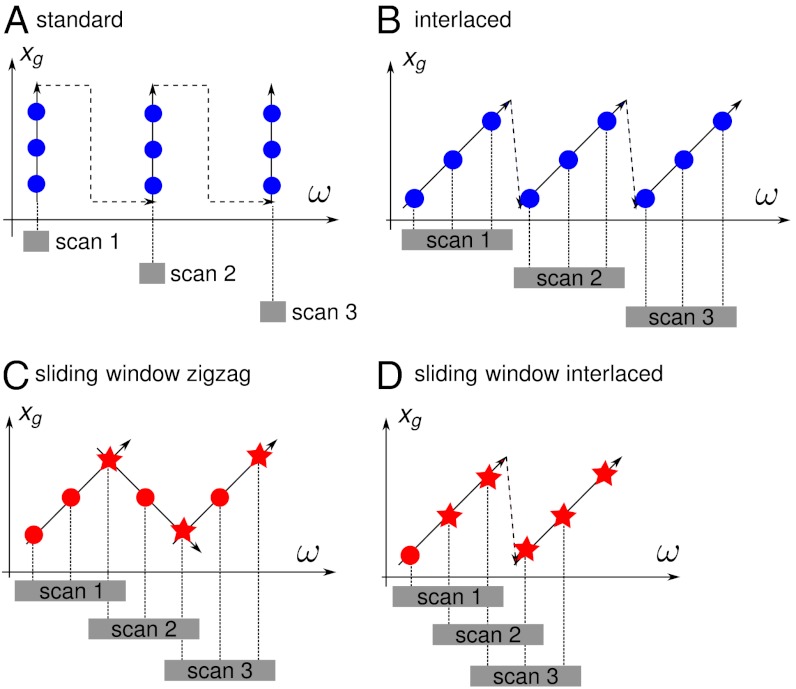
Fig. 2A illustrates the standard phase-stepping tomography acquisition scheme. All interferograms of one phase-stepping scan are recorded at a fixed angular position ω of the sample, which is rotated only between subsequent phase-stepping scans. A first improvement over this scheme, especially in view of clinical applications of grating interferometry, was the interlaced phase-stepping method (14) (Fig. 2B). In this method, interferograms of the same phase-stepping scan are recorded at slightly different angular positions of the sample, which introduces a tangential averaging of the features far from the rotation center. This improves the quality of local region-of-interest (ROI) reconstructions, where features in the external region (outside of the field of view of the detector) would otherwise disturb the signal in the ROI. Moreover, the interlaced method makes phase stepping compatible with a continuous rotation of the tomography axis.

Fig. 2.

Phase-stepping methods represented in the (ω,x_g) coordinate system. Each colored dot or star represents an interferogram recorded by the detector. Interferograms represented by stars are used in more than one phase-stepping scan. (A) Standard phase stepping. (B) Interlaced phase stepping (14). (C) SWZ method: One point of each scan is reused in the next scan. (D) SWI method: All but one point in each scan are reused in the next scan.

Although interlaced phase stepping is a significant improvement over the standard method, it shares with the latter an important limitation: The number of interferograms recorded during these tomography scans must be P times the number N of desired projections, i.e., P × N, where P≥3 is the number of steps per phase-stepping scan.

The sliding window methods presented in this paper, i.e., the sliding window zigzag (SWZ) and sliding window interlaced (SWI) methods, significantly reduce this number *. The basic idea is that a single interferogram, instead of being used in the processing of only one phase-stepping scan, can be used to calculate more than one final projection. This enables data acquisition with effective undersampling in the (ω,x_g) coordinate space while the quality of the reconstructed images remains largely unaffected. In other words, even if each phase-stepping scan still contains P interferograms, the actual number of interferograms recorded during a sliding window full tomography can be much less than P × N.

In the SWZ scheme, interferograms are recorded not only when the grating moves in the forward direction but also when it goes back to its initial position, as illustrated in Fig. 2C. In the zigzag method, one out of P interferograms is used for the processing of two phase-stepping scans, which reduces the effective number of interferograms recorded per phase-stepping scan to P - 1. In this way, the number of interferograms actually collected is reduced to R_SWZ = (P - 1) × N + 1. Because the number of projections N is usually large, this can be approximated by (P - 1) × N. For example, if P = 3, then R_SWZ = 2 × N, i.e., the same number of interferograms as needed in the RP method.

With the second method presented in this paper, the SWI method (Fig. 2D), the number of interferograms recorded in the tomography scan can be further reduced. The SWI method consists in an efficient analysis of the interlaced phase-stepping scans. In fact, if interferograms are recorded with the interlaced scheme, each group of P consecutive interferograms is recorded at P different positions of the grating and can therefore form a phase-stepping scan. In this way, P - 1 interferograms of each phase-stepping scan can be reused in the processing of the next phase-stepping scan and the number of interferograms needed to obtain N projections goes down to the minimum value of R_SWI = N + P - 1 ≈ N.

Thus, compared to existing phase-stepping schemes, sliding window methods yield the same number of final projections but with significantly fewer interferograms recorded during the scan, and, consequently, a lower dose deposited in the sample and shorter acquisition time. Likewise, for the same dose delivered to the sample, sliding window methods provide a finer angular sampling of the final projections, which increases the quality of the reconstructions.

The image signals in the sliding window methods (DPC, absorption, and dark-field) are extracted with the same algorithm as in standard phase stepping (10), based on Fourier analysis, which does not require linearization of the phase-stepping curve (assumed to be sinusoidal).

Because SWZ and SWI are based on interlaced phase stepping, they are compatible with continuous movement of the sample and they reduce artifacts caused by the presence of features outside of the field of view. Blurring at outer portions of the field of view might be observed with acquisition schemes based on interlaced phase stepping, as with all continuous rotation methods.

In the following, these properties of the sliding window methods are demonstrated with numerical simulations and experimental results. The latter have been obtained in both local and global tomography on biological and paleontological samples.

Numerical Simulations

We first demonstrate the potential of the sliding window methods with numerical simulations. The simulated slice is a pure phase (nonabsorbing) modified version of the Shepp–Logan phantom with a distribution of real-valued refractive index n = 1 - δ and zero absorption (Supporting Information). The size of the simulated noise-free slice is 2,048 × 2,048 pixels and the pixel size is 5 μm. Four DPC sinograms, corresponding to the acquisition methods shown in Fig. 2, have been generated from this slice from the same number of 1,700 interferograms. The parameters used in the simulation are listed in Table 1 (more details on the simulation can be found in the Supporting Information).

Table 1.

Parameters of simulation and experiments

	Energy (keV)	p1 (μm)	h1 (μm)	d (mm)	e (μm)	w (pixels)	t (s)
Simulation	23.0	4.80	29.5	480	5	800	-
Rat heart	23.0	4.78	29.5	481	7.5	700	1.5
Rat eye	23.0	4.78	29.5	481	5	2,048	1
Amber	35.0	4.78	45	404	5	2,048	2

p₁ and h₁ indicate, respectively, the period and the height of the phase grating G1, made of Si. The period of absorbing Au structures on the absorption Au grating G2 was p₂ = 2.4 μm and their height was h₂ = 50 μm. d is the distance between G1 and G2, e the effective pixel size, w the width of the detector field of view, and t the exposure time.

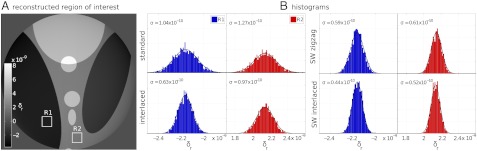
In order to compare the different acquisition schemes in local tomography, the sinograms were truncated and an ROI of 800 pixels in diameter was reconstructed. The reconstruction obtained with the SWI method is shown in Fig. 3A. The complete set of reconstructions with the different schemes can be found in the Supporting Information. The histogram analysis on the ROI reconstructions is shown in Fig. 3B. For each ROI reconstruction, we calculated the histograms of the two regions R1 and R2 of 50 × 50 pixels indicated in Fig. 3A.

Fig. 3.

Comparison of tomographic slices obtained with the different methods, using the same number of simulated noiseless interferograms for each method. (A) ROI of the simulated slice reconstructed with the SWI method; the simulated slice and the ROI reconstructions obtained with the other acquisition schemes are shown in SI. (B) Histograms of the two regions R1 and R2 indicated by rectangles in A. The y axis of the histogram is the number of pixels per histogram bin; the plotted range is from 0 to 200 for the histograms of R1 and 0 to 250 for the histograms of R2. The standard deviation σ of the Gaussian curve obtained by fitting the peaks is reported in the graphs. The value of σ is significantly reduced (of up to 50%) and consequently the contrast-to-noise ratio is substantially increased with the sliding window methods (because the histogram peak positions—i.e., the contrast—are unchanged between the different methods, the peak widths are a direct measure of the contrast-to-noise ratio obtained with the different methods.).

Angular undersampling in tomography generally generates image noise and edge artifacts. The strength and position of the undersampling artifacts depend on the features in the sample (inside and outside the ROI) and on the angular sampling. For a dataset with a given number of interferograms, these artifacts are smoothed out by grouping different viewing angles in a single projection as in the interlaced scheme (14) and by SW methods, compared to standard acquisition. This can be seen with the histograms analysis: the width of the histogram peak, which should be infinitely narrow in absence of noise and artifacts, is narrower in the histogram extracted from the slice obtained with the interlaced method than in the histogram extracted from the slice obtained with the standard acquisition scheme. By effectively increasing the angular sampling density, sliding window methods further improve the reconstructions and significantly reduce the image noise, as can be seen in Fig. 3B. The best results are given by the SWI method, which increases the angular sampling density by a factor of P (here, P = 4) with respect to the standard and interlaced acquisition schemes and gives gray level distributions in R1 and R2 with significantly reduced standard deviation (50% less) than the standard method.

Although this particular study has been performed on a phase object, similar results, showing the superiority of the sliding window methods on the other schemes, can be obtained for the dark-field and absorption signals.

Experimental Results

We validated the results of the numerical simulations with experimental measurements. The experiments were performed at the beamline ID19 of the European Synchrotron Radiation Facility (Grenoble, France) (19) using a monochromatic beam obtained via a Si (111) double crystal monochromator. The interferometer was located 150 m from the source. Its characteristics and the other experimental parameters are reported in Table 1.

The detector was a scintillator/lens-coupled CCD camera with 2,048 × 2,048 pixels. The effective pixel size and the field of view varied between measurements (Table 1).

We measured three samples: two soft-tissue biological specimens (a heart and an eye of a rat) and a fossil (an insect in opaque amber). The samples were placed approximately 100 mm upstream of G1. The rat organs were placed in cylindrical containers filled with formalin 10% solution. They had been extracted from a male Fischer rat (Charles River Laboratories) after sacrifice of the animal for another experiment ^†. The samples were immersed in a water tank to avoid strong refraction at the sample-to-air interface.

All tomography scans were performed over 180°. The exposure time per interferogram depended on the sample (see Table 1), but for each sample it was the same for the two methods.

Phase Tomography on Soft-Tissue Biological Specimens.

The rat organs were chosen to validate the SWI method in phase tomography. The internal anatomical structures of these samples, which exhibit very little absorption and dark-field contrast, can be visualized with high sensitivity in the phase tomographies obtained with the grating interferometer.

The heart was measured in ROI tomography to evaluate the performance of the SWI method under these conditions. The phase tomograms were reconstructed from 750 DPC projections. In tomography performed with the standard acquisition scheme, these projections were retrieved from 750 × 5 = 3,750 interferograms and in the SWI tomography they were retrieved from only 750 interferograms. The dose delivered to the sample with the SWI method was thus only 20% of the dose delivered to the sample with the standard method.

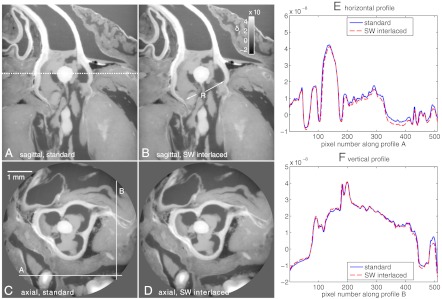
Sagittal views of the phase tomograms obtained with the standard and SWI methods are displayed in Fig. 4 A and B, respectively. In the sagittal slices the root of the aorta is indicated with the letter “R.” Axial slices at the position indicated by the dashed line in Fig. 4A are shown in Fig. 4 C (standard) and D (SWI). These slices highlight the anatomy of the aortic valve, and especially its tricuspid structure. Profiles have been extracted from the axial slices along the solid lines shown in Fig. 4C. These profiles are plotted in Fig. 4 E and F. The results show that, despite the huge difference in dose delivered to the sample during the tomography scan, standard and SWI methods provide phase reconstructions of very similar quality.

Fig. 4.

Sagittal (Top) and axial (Bottom) views of phase tomograms of a rat heart. A and C show images obtained with the standard method and B and D show images obtained with the SWI method. (E) and (F) Display profiles extracted from the standard and SWI axial slices along the lines shown in C. The two reconstructions show very similar quality despite the high difference in dose delivered in the two tomography scans (the SWI scan was obtained with only 20% the dose than of the standard phase-stepping scan).

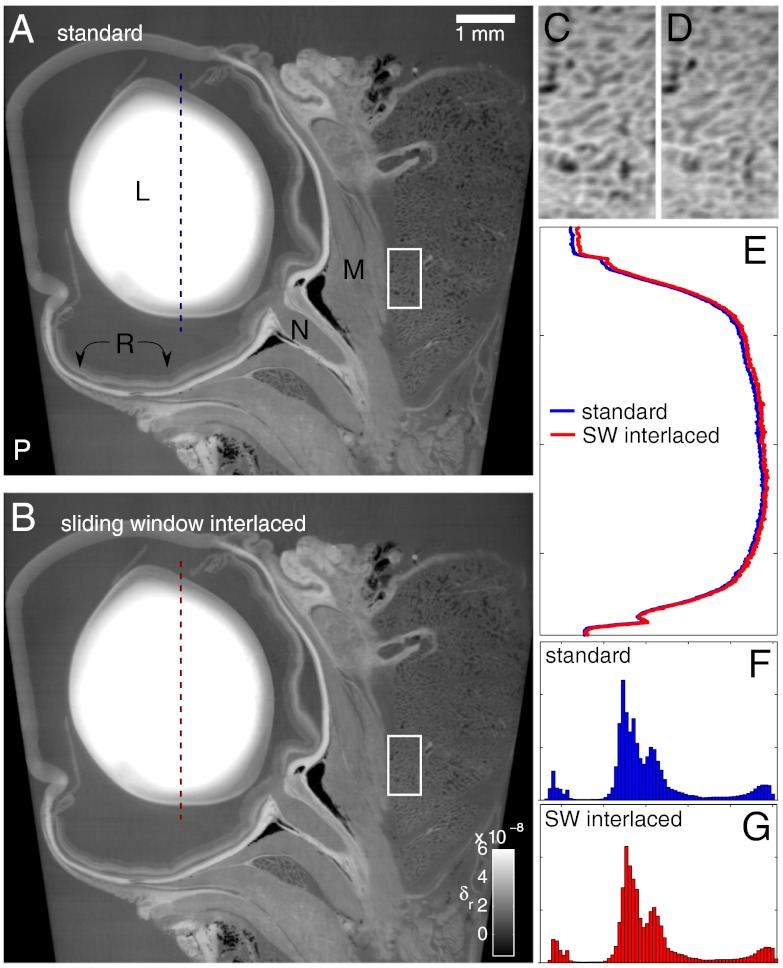
The second example is a tomography of an eye of a rat. In this case, the sample was fully within the field of view of the detector. The volumes were reconstructed from 750 DPC projections obtained from phase-stepping scans performed in four steps. The dose delivered to the sample during the tomography acquired with the SWI method was four times less than the dose delivered to the sample with the standard acquisition scheme. Fig. 5 shows sagittal slices obtained with the two acquisition schemes. The lens is indicated with the letter “L” and is the feature with the highest density. The presence of a gradient in the refractive index of the lens (the density decreases far from the center of the lens as shown in the profile plots displayed in Fig. 5E) is a known property of the eye lens that has an influence on both the refractive power and the aberrations of the lens (20). The optic nerve and the extraocular muscles (labeled with the letters “N” and “M,” respectively) can be clearly distinguished in the tomograms. The retina (“R”) was probably damaged during the extraction.

Fig. 5.

Sagittal views of phase tomograms of a rat eye obtained with the standard (A) and SWI (B) acquisition schemes; the dose delivered to the sample during the tomography performed with standard stepping was four times higher than the dose given to the sample during the SWI scan. Some of the anatomical features in the images are labeled with capital letters; see main text. The plastic container is indicated with the letter “P.” C and D show enlarged views of the regions indicated by rectangles in A and B, respectively. The profile plots in E show the refractive index in the lens—the δ_r values in this plot go from 0 to 1 × 10^-7. The histograms of the entire sagittal slices are shown in F and G. The δ_r values in the x axis go from -2 × 10^-8 to 8 × 10^-8. The y axis of the histograms represents the frequency of appearance of the gray levels in the slices; its range is the same for the two plots.

As observed in the previous example, the reconstructions obtained with the two acquisition schemes show very similar quality despite the great difference in deposited dose and number of interferograms taken. This is also confirmed by the similar gray level distribution in the two slices shown in the histograms of Fig. 5 F and G.

Fig. 5 C and D show enlarged views of the regions indicated by rectangles in Fig. 5 A and B. Both acquisition schemes allow to clearly resolve high density (bright) septa that have a thickness of approximately 30 μm.

The density resolution (resolution in δ) in the axial slices has been computed as the standard deviation of the gray levels in homogeneous ROIs of 50 × 50 pixels. The δ resolution in the standard and SWI volumes was very similar despite the drastic difference in dose and number of images: δ resolutions of 4.7 × 10^-10 and 4.9 × 10^-10 were obtained, respectively, with the standard and SWI acquisition schemes (note that similar values have been measured in ref. 9). δ values can be converted into Hounsfield units for the phase signal (HU-P) as described in ref. 21; this conversion makes phase tomography data taken at different conditions comparable to each other. The rescaling to HU-P yields a resolution of 1.3 HU-P in the SWI dataset and a resolution of 1.4 HU-P in the volume obtained with the standard method. These values are significantly better than the values measured with a conventional X-ray generator (21).

Slightly poorer δ resolution values have been obtained in the measurements of the heart, which were performed in local tomography: A δ resolution of 7.5 × 10^-10 and 6.2 × 10^-10 was measured with the standard and SWI method, respectively. Note that a better δ resolution is observed with the SWI method because it reduces the artifacts produced by the structures in the external region. For this dataset, a conversion to HU-P is not possible because a reference region with water is not present in the image.

Dark-Field Tomography of a Fossil.

From its first implementations up to this day, grating interferometry has been mainly exploited for imaging biological soft-tissue samples (8, 9, 16, 17, 21). However, other classes of samples, such as paleontological specimens, can also benefit from the high sensitivity of the phase and dark-field signals provided by this technique. The tremendous potential of X-ray phase-contrast imaging is already widely used to visualize inner structures in fossils, mostly in the form of in-line phase contrast (22). However, there are still features that cannot be revealed in phase contrast. Some of these can be made visible with the dark-field signal from the grating interferometer. This is demonstrated here with dark-field tomograms of a fossilized insect in opaque amber. The specimen, a Cretaceous maimetshid wasp from opaque amber of the Charentes region (France), was measured in local tomography and was recently described as a female of Guyotemaimetsha enigmatica (23).

In the experiments described so far, we compared standard and SWI phase-stepping tomography for the same number of projection angles and a different dose delivered to the sample. Now, tomographic scans performed with the two methods are compared for the same dose delivered to the sample. A total of 1,500 interferograms were collected in each tomographic scan with phase-stepping scans performed in four steps. From the 1,500 interferograms, 1,500/4 = 375 projections were retrieved with the standard method and 1,500 projections were retrieved with the SWI method.

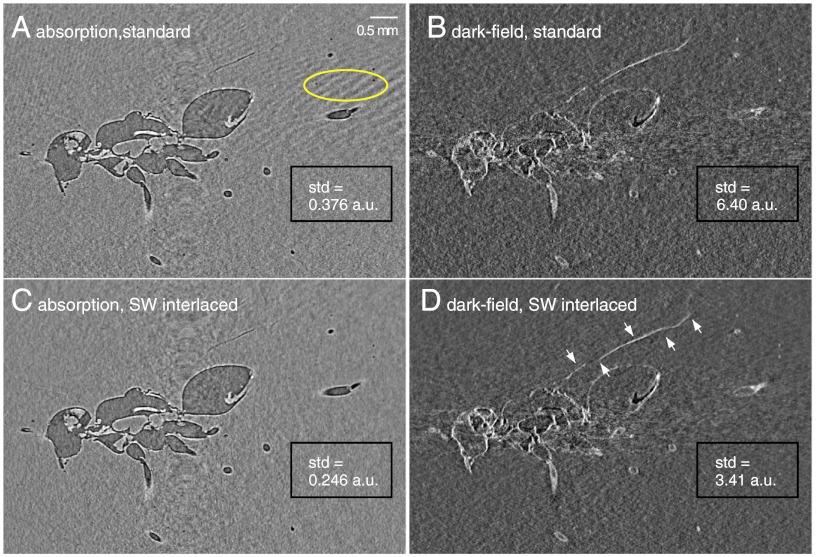
Fig. 6, Left shows tomographic sagittal slices of the fossil in “absorption” mode. Due to the low density of amber, the high degree of transverse coherence of the X-ray beam, and the long sample-to-detector distance of approximately 500 mm, these images exhibit also in-line phase contrast. Fig. 6, Right shows tomographic slices at the same position and from the same dataset, but in dark-field contrast. In the absorption/in-line-phase-contrast data the wing of the insect is not fully revealed. However, with the dark-field signal, which reveals details smaller than the spatial resolution of the detector (24), the wing of the insect can be clearly imaged in all its length; see arrows in Fig. 6D. The sagittal phase slice of the fossil, calculated from the same dataset, is shown in the Supporting Information.

Fig. 6.

XGI tomograms in absorption and in-line phase contrast (Left) and dark-field (Right) of an insect in opaque amber. Dark-field images show details that are not fully revealed in the absorption/phase-contrast data, such as the wing of the insect, indicated by arrows in D. The tomograms in the Top were obtained with the standard phase-stepping method, those in the Bottom with the SWI method. The dose and number of raw interferograms were the same for both methods. For both absorption and dark-field signals, the image noise is significantly reduced using the SWI method as shown by the standard deviation (std) of the gray levels in the uniform region at the bottom right of the images.

The advantages of the SWI method over the standard acquisition scheme are evident in Fig. 6. The images at the top, obtained with the standard acquisition scheme, show artifacts from angular undersampling (for example, see region at the right of the absorption image in Fig. 6A marked by an oval), which are not present in the images obtained with the SWI method; moreover, they show higher image noise. The image noise has been evaluated in a uniform region of 370 × 200 pixels at the bottom right of the images indicated by rectangles in Fig. 6. The standard deviations of the gray levels in these regions reported in Fig. 6 confirm the result from the numerical simulation that, at the same delivered dose, the SWI method reduces the image noise in the tomographic reconstructions.

Conclusion

By increasing the effective angular sampling density, the sliding window methods presented in this paper give a substantially improved contrast-to-noise ratio in grating-based tomography over the standard phase-stepping approach commonly used today. The results demonstrate this improvement both for phase contrast and for scatter-contrast (dark-field) tomography.

Moreover, because of the efficient acquisition and processing scheme represented by the sliding window methods, phase and dark-field tomographies of the investigated sample can now be obtained by effectively recording only one interferogram per set of final DPC, dark-field, and absorption projection image using the SWI method.

In addition to demonstrating the improvement in image quality that sliding window methods brings to dark-field tomography, the study on the fossilized insect highlights the potential of grating interferometry for applications in paleontology. The high dark-field contrast from the wing of the insect also suggests the exploitation of the dark-field signal in the investigation of sharply localized features in other application areas, e.g., cracks in biological or man-made materials.

We would like to point out that, although the results shown in this paper have been obtained with synchrotron radiation, sliding window phase stepping can be implemented at any phase-stepping interferometer, including laboratory X-ray systems or neutron sources.

Sliding window phase stepping is easy to realize, implies no additional requirements on the alignment of the gratings, is compatible with continuous tomography scans, performs well in local tomography, and gives access to three image modalities, with a simple algorithm. These advantages, together with the dose reduction, make it a substantial improvement for low-dose, fast phase-contrast, and scatter tomography based on X-ray grating interferometry.