Impact of branching on the elasticity of actin networks

Abstract

Actin filaments play a fundamental role in cell mechanics: assembled into networks by a large number of partners, they ensure cell integrity, deformability, and migration. Here we focus on the mechanics of the dense branched network found at the leading edge of a crawling cell. We develop a new technique based on the dipolar attraction between magnetic colloids to measure mechanical properties of branched actin gels assembled around the colloids. This technique allows us to probe a large number of gels and, through the study of different networks, to access fundamental relationships between their microscopic structure and their mechanical properties. We show that the architecture does regulate the elasticity of the network: increasing both capping and branching concentrations strongly stiffens the networks. These effects occur at protein concentrations that can be regulated by the cell. In addition, the dependence of the elastic modulus on the filaments’ flexibility and on increasing internal stress has been studied. Our overall results point toward an elastic regime dominated by enthalpic rather than entropic deformations. This result strongly differs from the elasticity of diluted cross-linked actin networks and can be explained by the dense dendritic structure of lamellipodium-like networks.

The cytoskeleton is an interconnected network of filamentous polymers and regulatory proteins. The cell’s integrity, deformability, and capacity to change shape come from the mechanical properties of these organized assemblies of filaments. Both the flexibility of the filaments themselves and their relative organization give the assembly its mechanical properties. We are interested in unraveling the link between mechanical properties and microscopic architecture in actin cytoskeleton networks. In cells, the actin filaments are organized by a large variety of proteins into different types of structures, depending on their location in the cell and their function (1). For example, in cell motility, actin polymerization drives protrusion of the leading edge of a crawling cell (2) within two organelles, lamellipodia and filopodia, based on two different actin polymerization machineries (3, 4). In lamellipodia, which are broad, flat protrusions, actin filaments assemble into a dendritic network through the branching protein complex Arp2/3 (4, 5). The polymerization of actin filaments at their barbed ends generates the driving force that extends the cell membrane forward. In filopodia, which are long finger-like protrusions filled with bundled actin filaments, processive actin barbed-end assembly is induced by formins at the tip (6). Actin is also present in the cortex, a cross-linked structure found beneath the plasma membrane, where it ensures cell integrity and mechanical support. These actin meshworks predominantly contribute to the cell’s ability to sense the micromechanical environment properties and to transmit compressive and tensile stresses. Their mechanical properties are crucial to determine the distance over which cellular response can be triggered by mechanical cues (7).

Polymer networks have elastic properties that directly rely on the individual behavior of their polymer chains and their relative organization. Actin filaments are semiflexible polymers: in all networks found in the cell, their typical length is less or comparable to their persistence length, i.e., they do not form loops and are nearly straight. As a consequence, the elasticity of their networks arises from two contributions: an entropic one that originates in the thermal fluctuations of individual filaments and an enthalpic one that comes from mechanical deformations of the filaments themselves (Fig. 1A). In entropic elasticity, filaments resist extension by the decrease in the number of available configurations. Near full extension, as the available conformations are drastically reduced, the filaments resist strongly to further extension. This phenomenon appears even at small strains in networks formed from semiflexible polymers, as they are already close to extension. Networks formed from such polymer stiffen when subjected to increasing stress, a behavior called nonlinear elasticity, typical of biological networks (8). Cross-linked actin networks exhibit this kind of entropic elasticity with a strong stress-stiffening (9, 10). Enthalpic elasticity comes from the mechanical deformation of the molecular links between monomers within the filament. Two regimes of enthalpic elasticity have been identified, one dominated by filament bending, the other by compression or stretching of the filaments (11–13). In enthalpic elasticities, the above-mentioned mechanism responsible for stress stiffening is absent. However, the enthalpic buckling of filaments subjected to an important force can lead to stress-softening, as was observed in dense branched networks (1).

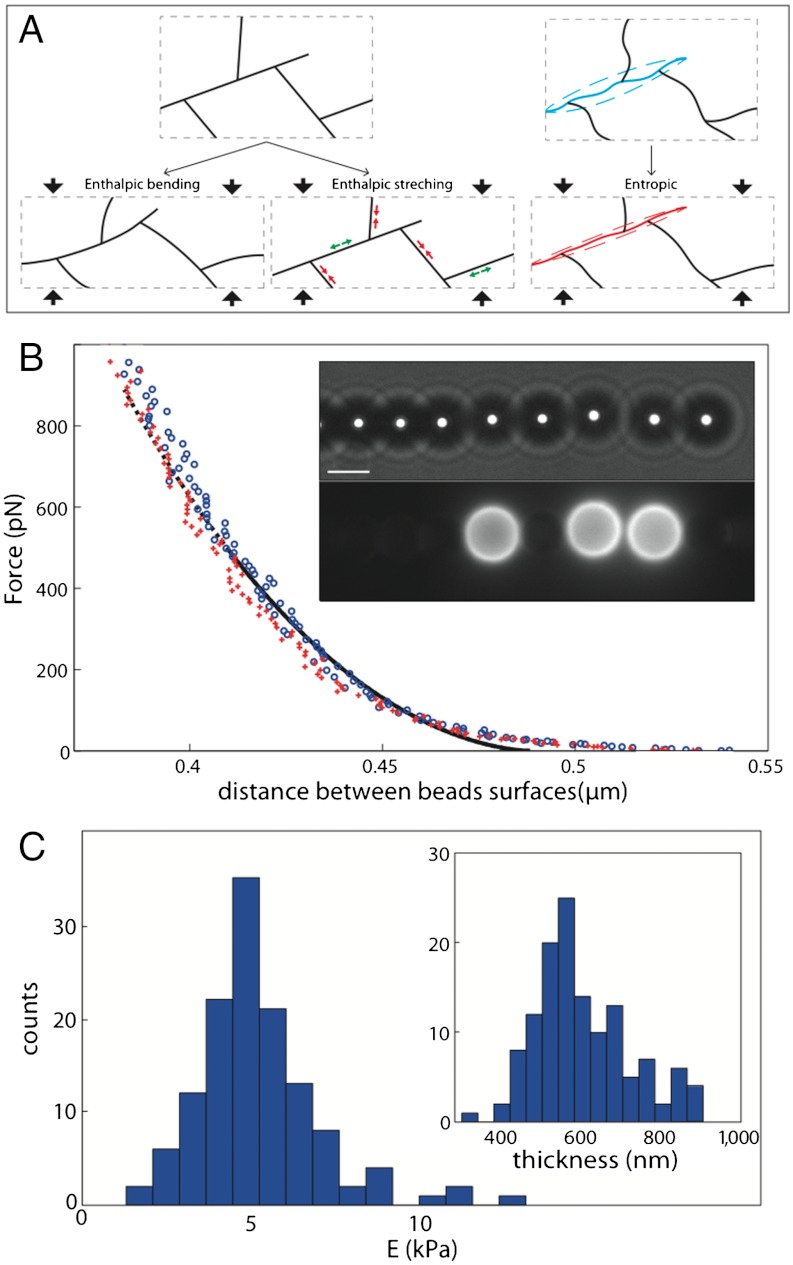
Fig. 1.

Modes of deformation and principle of measurements. (A) Schematic of enthalpic (Left) and entropic (Right) deformations of Arp2/3 branched filaments. The deformation of the box is vertical and the material is considered incompressible. (B) Typical force-distance curve. Blue circle: compression; red crosses: decompression; black lines: Hertzian fit modified for finite thickness (plain: range of the fit; dotted: extrapolation to the whole range of distance). Inset: bright-field and fluorescent images of a chain. Three beads are covered by actin gel as shown by the fluorescent image. Scale bar, 4 μm. (C) Histogram of Young’s moduli extracted from one experiment (129 probed gels) at [gelsolin] = 90 nM and [Arp2/3] = 180 nM. Mean value is 5.2 kPa; standard deviation is 1.9 kPa. Inset: Histogram of thicknesses; mean value is 650 nm; standard deviation is 130 nm.

Here we present a new technique that allows the collection of large amounts of data on the mechanical properties of actin networks. We study actin organized in structures comparable to the lamellipodium. The actin network is directly assembled in dendritic gels around superparamagnetic colloids, and mechanical measurements are based on magnetic dipolar attraction between colloids. The network growth occurs from the surface of the colloids and requires a limited number of proteins including actin, the Arp2/3 complex and a capping protein (14, 15). Due to this assembly process, we can probe denser and more organized actin networks than those that have been measured by macro- or micro-rheology. Previous experiments based on these techniques have used purified actin filaments either entangled or cross-linked by various proteins, forming loose networks (16). Measurements have been performed on branched actin networks grown form a surface via the Arp2/3 complex, as in our experiments (17, 18). These experiments are delicate, as they use macroscopic force sensor such as AFM and micropipette, which prevents the authors from studying a large range of parameters. On the contrary, in our experiment, each pair of colloids is a measurement device by itself, which allows us to carry out orders of magnitude more measurements than those allowed previously. We have thus studied the mechanical properties of gels with different histories and architectures by tuning the growth conditions. Using reconstituted medium allows us to modify the growth concentration of two proteins crucial for the architecture of the network: Arp2/3 complex, which induces the formation of new branches, and gelsolin, which regulates the length of filaments by capping the growing end. Hence we aim to establish the relationship between the growth process, the architecture, and the mechanics of actin networks.

Results

In this work, dendritic gels of actin grow around superparamagnetic colloids. We use a minimal set of proteins (14, 15): F-actin, gelsolin, Arp2/3 complex and cofilin, and colloids covered with the VCA domain of the protein neuronal Wiskott–Aldrich Syndrome protein (N-WASP). The polymerization is localized at the surface of magnetic beads. The formation and the integrity of the gel are checked by fluorescence microscopy using labeled actin. Specifically we let the gel grow for 15 min before stopping the polymerization by dilution in a buffer containing phalloidin. We thus obtain a stable configuration in which actin filaments do not polymerize (due to dilution, the actin concentration becomes smaller than the critical concentration for polymerization) and do not depolymerize (due to the stabilization of the filaments by phalloidin). These gels are stable for at least one hour. No evolution of the gels thickness or fluorescence was observed during the time course of an experiment. The mean fluorescence in the shell is measured for each actin gel, and gives an estimation of the actin concentration in the networks of the order of 170 μM (Materials and Methods).

Under a uniform magnetic field, each colloid acquires a magnetic moment that depends on the magnetic field intensity, and the only force applied to the colloids arises from dipolar interaction between neighboring beads. As a consequence, the colloids self-organize in chains parallel to the field and do not migrate (Fig. 1B). The dipolar forces between colloids in chains have already been used successfully to measure colloidal forces (19) and actin-polymerization induced forces (20). Increasing the magnetic field increases the attractive dipolar force between the colloids (21) and induces deformation of the gels present on the colloids. The relative displacement of the beads is measured by video microscopy as a function of field strength, and a force-distance profile is reconstructed from these measurements (Fig. 1B). The main advantage of this technique is that each pair of beads is a sensor by itself and tens of force-distance curves can thus be recorded within half an hour in one sample.

To provide a well-defined surface of contact during the deformation of the actin shells, we mix actin-covered beads with nonadhesive bare beads (BSA-coated) and only consider actin gels facing bare beads (see SI Text and Fig. S1 for a typical experiment between two actin-covered beads). As the surface of the gel is spherical, the area in contact with the neighboring bead increases when the gel is deformed. This situation is a typical problem of contact mechanics described by the Hertz contact theory. The experimental force-distance curves are fitted by a modified Hertzian model that takes into account the finite thickness of the elastic medium (22). Both the elastic modulus and the thickness of the gel are used as adjustable parameters.

A typical force-distance curve showing the deformation of an actin gel is given in Fig. 1B. The difference between the loading (compression) and unloading (decompression) curves is minimal. The fit is in good agreement with the experimental curves, except for the largest distances between colloids (SI Text). Fig. 1C shows the histogram of elastic modulus obtained from 129 different actin gels grown at our reference concentrations of proteins (180 nM Arp2/3 and 90 nM gelsolin). The mean value of the elastic modulus is 5.2 kPa and has a standard deviation of only 1.9 kPa. Thanks to the large number of measurements in one sample (between 50 and 150 gels are probed in one experiment), the confidence interval at 95% for the mean elastic modulus is 10% of the mean. Reproduction of the same experimental conditions introduces new uncertainties, and the standard deviation between the mean elastic modulus of different experiments is on the order of 20%, which is still much lower than published values on comparable branched actin networks.

Our measurements are in good agreement with values provided by Chaudhuri et al. and Marcy et al. on dendritic actin gels grown from a surface with the same Arp2/3 machinery (17, 18), but differ strongly from measurements on cross-linked networks. This discrepancy can be explained by stronger actin concentration (23) and the different architectures of the networks. Our measurements are also compatible with the values measured in single cells and in tissues. Typical Young’s moduli range from 650 Pa for liver to tens of kPa for muscle (7). On single cells in culture, typical values scatter between 0.1 and 40 kPa (24).

Elasticity and Architecture.

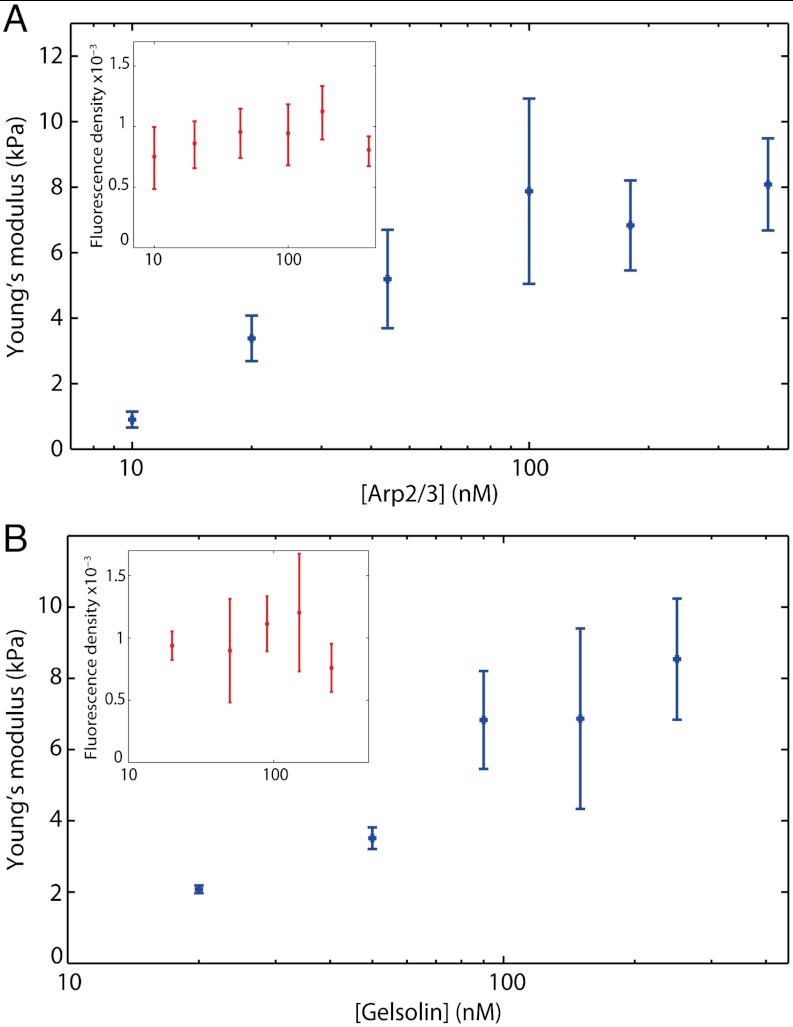
As the architecture of the gels is tightly linked to the growth process, varying the concentration of the branching and capping proteins in the polymerization medium changes the architecture of the studied networks. We carry out measurements in which the concentration of one protein is varied while all the others are kept constant. At constant gelsolin (90 nM) we investigate a range of Arp2/3 concentrations from 10 nM to 400 nM. Note that lower values induce formation of fractured gels. Likewise, at constant Arp2/3 (180 nM), we investigate a range of gelsolin concentrations from 20 nM to 250 nM. In this case, lower values induce formation of gels that are too thin to be probed. Each point is reproduced at least three times for a total of 200–400 measurements for each condition. The actin concentration around the beads is estimated from the fluorescence measurements for the different concentrations of Arp2/3 and gelsolin (Fig. 2, insets). The variation of actin density is at most a factor of 1.6 for gelsolin variation and 1.5 for Arp2/3 variation. Such a weak actin density variation with branching has already been observed in similar networks (25). Meanwhile, the gels strongly stiffen as the concentration of branching protein increases (from 1 kPa at 10 nM to 8 kPa at 100 nM), and the Young’s modulus levels off at a concentration above 100 nM (Fig. 2A). The increase in capping also strongly stiffens the network (from 2 kPa at 20 nM to 7 kPa at 90 nM) before plateauing (Fig. 2B). Thus, the increase of the capping and branching protein concentrations during the assembly process, while having weak effect on the actin density, induces a drastic stiffening of the actin networks. These dependences on protein concentrations will be discussed in light of existing models of polymer network elasticity in the discussion section.

Fig. 2.

Architecture of gels influences Young’s modulus. Evolution of the Young’s modulus with [Arp2/3] at [gelsolin] = 90 nM (A) and with [gelsolin] at [Arp2/3] = 180 nM (B). Each point represents the mean of 200–400 probed gels obtained from at least three reproductions of the same conditions. The error bars represent the 95% confidence interval on the mean elastic modulus. Inset: evolution of fluorescence density with [Arp2/3] and [Gelsolin], giving an estimate of actin concentration in the networks.

Rigidification by Phalloidin.

To further investigate the link between microscopic and macroscopic mechanical properties of the network, we study the role of the rigidification of filaments induced by phalloidin. We thus conduct experiments in the presence or in the absence of phalloidin. In the latter case, as the gel grows, the shape of the gels in already-formed chains can become nonspherical. Consequently, we adapt the protocol by stopping the magnetic field in between each measurement and only analyzing the newly-formed pair of beads, reduced to 22 in five different samples. A typical force distance curve is given in Fig. S2. We obtain a Young’s modulus around half the value of the phalloidin-stabilized sample (3.4 ± 0.6 kPa, compared to 5.9 ± 0.8 kPa).

We then compare these networks measurements to the flexibility of individual filaments. The persistence length of actin filaments varies from 18 μm for actin stabilized by phalloidin to 9 μm for (ADP) actin with no phalloidin (26). In solution, cofilin strongly increases the bending flexibility of the filaments it interacts with. The persistence length of actin in presence of excess cofilin has been measured to be 2.2 μm (27). In our case, the concentration of cofilin is lower and the tension applied to the filaments both during the network growth and deformation may perturb the interaction of cofilin with actin filaments (28). Hence, in our experiments without phalloidin, the persistence length of actin filaments is comprised between 2.2 and 9 μm. For actin filaments in the presence of both cofilin and phalloidin, no value of the persistence length was present in the literature. We thus performed the measurements at the concentrations used in the colloidal-chain experiments and found a persistence length of 16.2 ± 1.4 μm (Materials and Methods and Fig. S3).

The stabilization by phalloidin therefore stiffens the network by a factor of approximately 2 while increasing the persistence length of individual filaments by a factor of 2 to 8 (depending on the interaction of cofilin with the filaments). The experimental dependence of the network elasticity on the persistence length is therefore linear or less.

Influence of Time Growth.

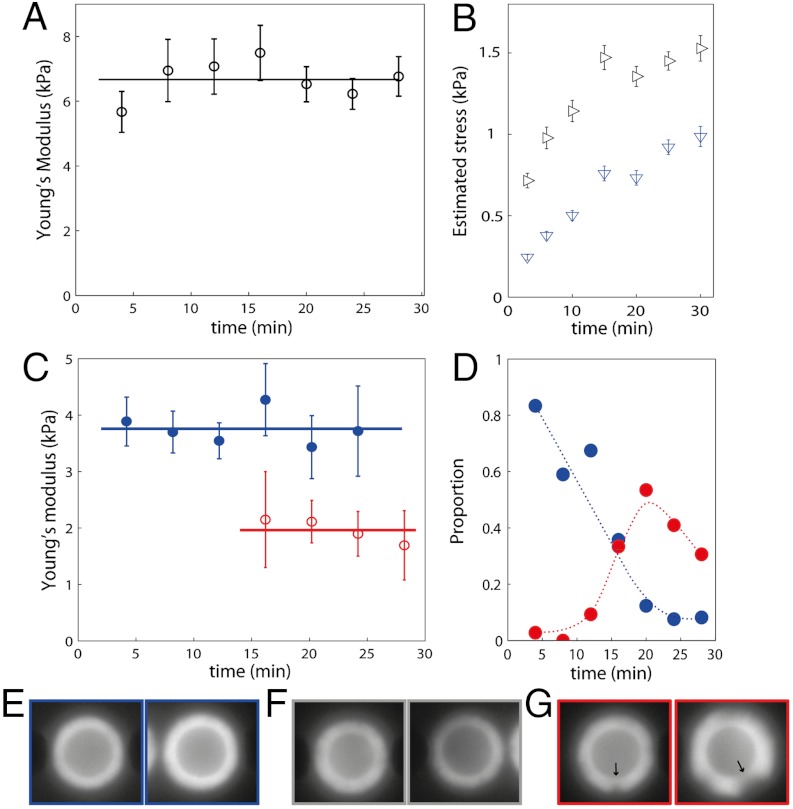
Because polymerization of the actin gels proceeds from the surface of the bead, the older network is pushed away from the surface by the new polymerizing network. The external layer of the growing gel is therefore tangentially stretched while the inner layers are radially compressed (29). The tangential stress can lead to the development of a notch and ultimately to the fracture of the gel (30). Here, studying gels at different growth times gives indications of the internal stress dependence of the mechanics of branched actin networks. Specifically, polymerization is stopped by dilution in phalloidin after different growth times from 4–30 min. We test two concentrations of Arp2/3 (44 and 400 nM) while gelsolin is kept constant (90 nM). The high Arp2/3 concentration results in a situation where very few gels break. In this case, the elastic modulus evolves slightly while the mean thickness of the gel significantly increases up to 25 min after the initiation of polymerization (Fig. 3A). We estimate the average tangential and radial stresses in our experiments by using the calculations of Noireaux et al. (29) with the elastic modulus and thickness measured for each gel in our experiments. We compute that the average tangential stress changes from 700 Pa after 3 min of polymerization to 1,500 Pa after 30 min, while the average radial stress changes from 250 Pa to 1,000 Pa (Fig. 3B). In the same time, the measured elastic modulus evolves slightly from 5.7 ± 0.6 kPa to 6.6 ± 0.6 kPa. This result signals a weak stress-stiffening when compared to measurements on cross-linked networks.

Fig. 3.

Effect of gel growth. (A) Evolution of the Young’s modulus with growth time at [Arp2/3] = 400 nM and [gelsolin] = 90 nM. (B) Corresponding evolution of the estimated mean tangential (black horizontal triangles) and radial (blue Down triangles) stresses. (C) Evolution of Young’s modulus with growth time at [Arp2/3] = 44 nM and [gelsolin] = 90 nM: blue close circles, homogenous gels; red open circles, broken gels. The lines are the mean value. (D) Proportion of homogenous gels (blue) and broken gels (red) as a function of growth time in all probes gels (including the undetermined ones). The dotted lines are guides for the eye. (E–G) Classification between homogenous (E), undetermined (F), and broken (G) gels. In (G), the arrows indicate failures in the gel. The images are 8 × 8 μm.

In the low Arp2/3 case, the majority of gels are unbroken 12 min after the start of polymerization, while very few remain intact after 20 min of growth (Fig. 3D). During the analysis each gel is classified either homogenous or broken, based on fluorescent images (Fig. 3 E–G). For some gels the classification is ambiguous and those gels are disregarded. We obtain two curves of the Young’s modulus as a function of growth time for broken and unbroken gels (Fig. 3C). Similar to the high Arp2/3 case, the elasticity of homogenous gel exhibits no significant evolution, although its thickness and thus its internal stress increases (from 320 Pa at 4 min to 650 Pa at 12 min). After the gels break, the elastic modulus is divided by a factor of two (2.0 kPa ± 0.5 for broken gels compared to 3.8 kPa ± 0.4 for unbroken gels). After the appearance of the first notch, stresses in the gel due to geometrical constraints are released although the gel is still not detached and a stress could remain. The measurements at different growth times thus indicate a weak stress-stiffening of the probed gels: the Young’s modulus does not evolve significantly with time even though the radial internal stress is increased four times and its maximum variation corresponds to a factor of two when a large part of the internal stress is released.

Discussion

In this paper, we study the relationship between network architecture and elasticity of lamellipodium-like actin networks. We report, for the first time, the dependence of the elasticity of such networks on the concentration of capping and branching proteins. We show a strong stiffening of the networks when either capping or branching concentrations are increased. The more Arp2/3 is present, the more branched the networks are. This results in a weak increase of the actin density within the network whereas the networks strongly stiffen. When [Arp2/3] is increased further, the Young’s modulus reaches a plateau, which can be attributed to a saturation of Arp2/3 activation by the VCA present on the colloids. We also look at the effect of the protein gelsolin, which caps growing ends of the filaments. We find a four-fold stiffening of the networks when gelsolin concentration is increased from 20 to 90 nM. Increasing the concentration of gelsolin will increase the rate of capping and thus reduce the length of the actin filament from the branching point to its capped end. This reduced length will decrease the connectivity of the network and thus induce its softening (31). Additionally, due to the semiflexibility of the filaments, the orientation of adjacent strands remains correlated; shorter strands will induce shorter long-range correlation, which will also result in the softening of the network (12). Both these effects would point to a softening when the concentration of gelsolin increases, in contrast to the observed stiffening. Nevertheless, the protein gelsolin has also been shown to reduce the distance between branches in reconstituted systems (25, 32). The major mechanical effect of increasing gelsolin is neither the decreasing connectivity nor the decrease of the filaments total length but rather the reduction of the distance between branching points.

The various mechanical models that describe the elasticity of semiflexible polymer networks are built on different microscopic origins of elasticity. They are all based on the same parameters: the persistence length of the filaments, l_p, the mesh size of the network, ξ, and a characteristic length of the network, L. In cross-linked networks, L is the distance between crosslinks. The mesh size ξ for this type of polymer is given by ξ ∼ (a c_A)^-1/2 where a is the size of the actin monomer and c_A the actin concentration (33, 34). The entropic elasticity model has been used to interpret dilute actin network rheology. In this model, the elastic modulus reads E ∼ kT ξ^-2 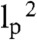L^-3 (23), where kT is the thermal energy. For models where the elasticity arises from the enthalpic bending of the filaments, the elastic modulus has been proposed to scale as E ∼ kT ξ^-2 l_p L^-2 (13, 35). However, the elastic modulus of this mode of deformation may be overestimated, due to its nonaffine nature: the deformation is localized in some parts of the gel. When the elasticity comes from the enthalpic stretching, the modulus can be rewritten from (13) as E ∼ kT ξ^-2 l_p a^-2. A regime in which enthalpic bending and enthalpic stretching are coupled has also been found in 3D simulations with an intermediate dependence on L (13). In the following discussion we will interpret our experimental results in light of these models.

In our experiments we found a weak dependence (linear or less) of network elasticity on persistence length. An entropic origin would lead to a quadratic dependence of the elasticity to l_p, which is far from our measurements. Instead, this result strongly suggests a dominant enthalpic contribution to the origin of elasticity in the branched actin networks.

As pointed out by Bausch and Kroy, the identification of the characteristic length L is delicate (16). An obvious choice for cross-linked networks is the mean distance between two crosslinks. In the case of lamellipodium-like networks, the characteristic length, L, can be chosen as the distance between branching points. Raising the concentration of Arp2/3 is expected to increase the number of branches and thus to decrease L. More precisely, measurements of the polymerization kinetics show that the number of free barbed ends, and thus of branches, is proportional to the Arp2/3 concentration at low values (36). It has also been observed by microscopy that the distance between branching points is smaller with more Arp2/3 complexes (37). We measure a ten-fold stiffening of branched actin networks when the concentration of Arp2/3 is increased ten-fold, while actin concentration in the shell varies only by a factor of 1.5. This stiffening is too strong to be attributed to the variation of actin concentration because the dependence of the elastic modulus on the actin concentration is linear in all the models described above. We thus interpret most of the dependence between E and [Arp2/3] as the consequence of the decrease of L. Our results are not compatible with a purely entropic regime that exhibits a strong dependence on L (E ∼ L^-3). Our results are more in agreement with enthalpic modes of deformation, especially the coupled bending stretching regime. The already mentioned plateau above 100 nM [Arp2/3] could also be due to a crossover to a purely enthalpic stretching mode, in which the elasticity is independent of L.

The crossovers between the entropic and both enthalpic regimes of elasticity in semiflexible networks have been studied theoretically as a function of filament length and distance between crosslinks (31). Decreasing the distance between crosslinks modifies the origin of elasticity from entropic to enthalpic stretching, as the thermal fluctuations of the filaments become negligible. Similarly, in cross-linked networks, reducing the length of the filaments changes the origin of the elasticity from entropic stretching to enthalpic bending. Indeed, as the length of the filaments decreases, the connectivity of the network decreases until filaments are not connected in a unique network anymore. Just above this transition, the network is loosely connected and the softest mode of deformation is the mechanical bending of the filaments. Typical rheological experiments on actin networks are carried out at concentrations around 10–20 μM, and their elasticity has been shown to be entropic (10). Actin networks grown from a surface by Arp2/3 are more concentrated: we estimated a concentration of 170 μM in our experiments, giving a mesh size of 60 nm [ξ ∼ (a c_A)^-1/2 with a = 2.7 nm/monomer]. These branched networks are also less connected than cross-linked networks, even at the same concentration, as each node connects three strands instead of four. Hence, both the concentration and the connectivity of branched actin networks may explain an important enthalpic contribution to their mechanics.

The last result of this study is the evolution of elasticity during growth and after gel breakage. While in our experiments, the continued growth of the gels results in a buildup of internal stress, no significant increase in the elastic modulus is measured. Comparing intact gels with internal stresses on the order of one kPa to fractured gels with a released stress, a softening of a factor of two is measured. This effect is comparable to the nonlinear effects seen by Chaudhuri and colleagues in similar branched networks where the elastic modulus varies by a factor of less than three at similar stresses (from 0.9 kPa at stress below 10 Pa to 2.5 kPa at 600 Pa, with a maximum of 4 kPa at 250 Pa) (18). These reduced stress-stiffening effects on dense branched networks are markedly different from what is observed in dilute cross-linked actin networks: stiffening as large as two orders of magnitude has been reported (10). Such a strong stress-stiffening is considered a signature of the entropic elasticity, since small strain drastically reduces the available configurations in nearly extended polymers. On the contrary, the enthalpic elasticities originating from the mechanical bending or extension and compression of polymers do not present this kind of intrinsic nonlinearity. The observed weak stress-stiffening of the networks is in agreement with the measured dependence of E on l_p and [Arp2/3] that converge into a strong enthalpic contribution to the elasticity of actin branched networks.

Conclusion

We have developed a new technique based on the dipolar attraction of superparamagnetic colloids to probe the mechanics of actin gels assembled around colloids. As each pair of beads is a sensor by itself, this method allows us to carry out tens of measurements in one sample. Using this method, we investigate dense dendritic actin networks resembling the ones found in lamellipodium of a crawling cell. We found elastic moduli in the range of 1–10 kPa, in good agreement with published values on similar reconstituted systems and compatible with cells and tissues elasticity. The massive parallel measurements allowed by our technique enable the investigation of the impact on network elasticity with variations of capping and branching concentrations, individual filament flexibility, and internal stress. All these dependencies point toward an elasticity of branched actin networks whose main contribution arises from mechanical bending, stretching, and compression of individual filaments. This type of elasticity does not exhibit strong stress-stiffening, in contrast to entropic elasticity, which is the main contribution to elasticity in cross-linked actin networks.

The increase in capping and branching concentrations stiffens the networks while only changing the actin concentration slightly within the network. This is direct evidence of the strong dependence between the branched networks architecture and elasticity. More precisely, the dominant effect of the architecture on the elasticity is the reduction of the distance between branching points when concentration of branching or capping is increased. The concentrations of branching (10–100 nM) and capping proteins (20–100 nM) at which we find strong variations of the elastic modulus are compatible with intracellular regulation. These findings indicate that a cell can modulate its cytoskeleton elasticity by intracellular regulation of the branching dynamics.

Materials and Methods

Materials.

The superparamagnetic colloids (Dynabeads M-450 Epoxy 4 ± 0.02 μm diameter measured in a chain) are purchased from Invitrogen (Carlsbad, CA). VCA domain of the human WASP protein (GST tagged), Arp2/3 protein complex from bovine brain, gelsolin recombinant human protein and cofilin1 recombinant human protein are purchased from Cytoskeleton (Denver, CO, USA). Rabbit muscle G actin and fluorescent G actin (alexa 488 and 594) have been provided by M-F Carlier’s lab (Gif sur Yvette, France). All other chemicals are from Sigma-Aldrich (St Louis, MO, USA).

Sample Preparation.

Colloids are coated by VCA: 3.5 μL of beads stock solution (volumic fraction 0.013) are diluted in 47 μL of milliQ water, washed twice with X buffer (Hepes 10 mM, KCl 100 mM, CaCl₂ 0.1 mM, MgCl₂ 10 mM) and then mixed with VCA (23 μM) in X buffer. After one hour of incubation, 5 μL of BSA 10% is added for passivation (15 min). By centrifugation the suspending medium is replaced by X buffer with 0.1% of BSA, and the volumic fraction of beads is 0.1%. Bare beads are coated with 1% BSA following the same protocol.

G-actin is polymerized at 29 μM (including 5% labeled monomers) using KME (KCl 2 M, MgCl₂ 20 mM, EGTA 4 mM). The gel growth occurs at 6.5 μM of actin, 6.5 μM of cofilin, 20–250 nM of gelsolin, 10–400 nM of Arp2/3, and 0.01% VCA covered beads (Hepes 6 mM, ATP 1.8 mM, DTT 6.2 mM, Dabco 140 μM, KCl 80 mM, CaCl₂ 100 μM, MgCl₂ 6 mM, and EGTA 42 μM at pH 7.8).

The polymerization is stopped between 3 –30 min by a 10 times dilution in X buffer with 20 μM phalloidin. Actin-covered colloids are then concentrated and bare beads are added at the same volumic fraction of 0.01%. The sample is introduced in homemade chambers (22 ∗ 1 ∗ 0.25 mm³) coated with BSA.

Magnetic Setup.

The setup is mounted on an Axio A1 inverted microscope from Zeiss (Carl Zeiss, Germany) with an oil-immersion 100x objective (NA = 1.4) and equipped with X-cite XPS-120 lamp for fluorescence. The magnetic field is generated by two coaxial coils (SBEA, Vitry, Fr) with mu metal core (length 40 mm, diameter 26–88 mm, 750 spires). The coils are powered by a bipolar operational power supply amplifier 6A/36V (Kepco, Flushing, NY) controlled by Labview software (National Instruments, Austin, TX). The maximum field generated is 100 mT with a gradient less than 0.1 mT·mm^-1 over the sample. The chains are formed with a constant field of 3 mT and the acquisition goes from 1 mT to 80 mT in 5 s. The CCD camera is a Coolsnap ES² (Roper Scientific, Ottobrunn, Germany) used at a frame rate of 27 Hz. The measurement of the tension used to control the field is synchronized with the frame acquisition. After each measurement, a fluorescent image (δt = 100 ms) of the chain is acquired.

Fluorescence Measurements.

The fluorescence density is the average value of fluorescence on the thickness of the shell in an angular sector of π/3 perpendicular to the chain (the thickness is extracted from mechanical analysis detailed below). An estimation of the actin concentration in the shell is obtained by measuring the fluorescence intensity of known concentrations of labeled G-actin between the slide and the coverslip with 4 μm beads as spacers.

Experiment Analysis.

Image analysis is carried out using Image J (NIH) and data processing using Matlab (MathWorks, MA). The center of each particle is determined by a weighted mean of gray levels giving a precision of 20 nm.

The attractive dipolar force between two particles reads F_d = 3 μ₀m²/(2πd⁴), where μ₀ is the permittivity of the empty space, m the magnetic moment of the particles, and d the distance between their center. Also, m = VHχ_m, with V the volume of the particle, H the magnetic excitation, and χ_m the magnetic susceptibility measured by Fonnum et al (38). The force on one gel is calculated by the sum of the force between the pair of beads and their first neighbors.

To fit force indentation curves, we use the relationship for Hertzian contact modified to take into account the finite thickness of the elastic medium (incompressible bonded sample, ref. 22):

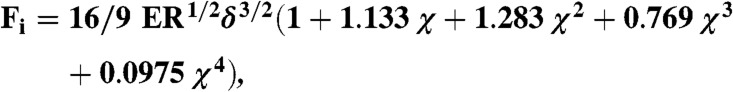where F_i is the force, E the Young’s modulus, R the equivalent radius, δ the indentation, and χ = δ^1/2R^1/2/h^-1, with h being the thickness of the gel. The Poisson ratio was assumed to be 0.5 (39). The indentation is the distance between beads compared to their distance when gels are undeformed. Both the elastic modulus and the thickness of the gel were used as adjustable parameters. The equivalent radius is calculated as 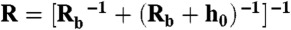, with R_b being the radius of the beads and h₀ being the thickness of the shell evaluated at small forces. All estimations of the fit were conducted from 0 –500 pN to allow comparisons between different gels. The strain rate is 0.01 Hz, and the mean stress is around 500 Pa.

It should be noted that when a contacting sphere deforms an elastic shell, the stress and strain applied during deformation are not homogenous in the elastic medium. The strain is maximum at the center of the area of contact, and minimal at the rim. On an axis spanning the center of the two spheres, it is highest at the surface of contact and decreases inside the medium (40). It is therefore difficult to characterize the nonlinear behavior of elastic materials using spherical contacts. Hence, the elastic properties measured in this study should be considered to be an average over different stresses and strains acting on the network.

We check for each curve the maximum indentation to ensure that the correction for finite thickness is accurate and that the area of contact calculated from Hertz theory is valid, and therefore, that quantitative comparison between the mechanics of different architecture networks is reliable (SI Text).

To compute the mean elastic modulus and the 95% confidence interval of each experimental condition, we aggregated the mean and standard error of each of 3–4 repetitions of the same condition and used a random effect meta-analysis (41).