Conscious updating is a rhythmic process

Abstract

As the visual world changes, its representation in our consciousness must be constantly updated. Given that the external changes are continuous, it appears plausible that conscious updating is continuous as well. Alternatively, this updating could be periodic, if, for example, its implementation at the neural level relies on oscillatory activity. The flash-lag illusion, where a briefly presented flash in the vicinity of a moving object is misperceived to lag behind the moving object, is a useful tool for studying the dynamics of conscious updating. Here, we show that the trial-by-trial variability in updating, measured by the flash-lag effect (FLE), is highly correlated with the phase of spontaneous EEG oscillations in occipital (5–10 Hz) and frontocentral (12–20 Hz) cortices just around the reference event (flash onset). Further, the periodicity in each region independently influences the updating process, suggesting a two-stage periodic mechanism. We conclude that conscious updating is not continuous; rather, it follows a rhythmic pattern.

The external world is in a state of continuous flux. The brain needs to track these changes and update its conscious representations to keep up with reality. This updating takes time and can be prone to systematic errors, as demonstrated, for example, by the flash-lag effect (1–4) (FLE). In FLE, a briefly presented stationary object (flash) near a moving object is misperceived to lag behind (1–4) or the moving stimulus is misperceived to be ahead (5, 6). This spatiotemporal illusion is classically taken to reflect the efficiency of updating and has been used to study the dynamics of conscious updating (3, 7, 8). The mechanisms underlying the FLE remain unclear, with various processes, such as motion extrapolation (1, 2), postdiction (3, 4), differential neuronal latencies (9–11), empirical experience (12), and attention (13–16) proposed to explain or modulate the misperception. Our study is not intended to address this debate, but we exploit the uncontroversial relation between FLE and conscious updating (3, 7, 8, 13–16) to determine whether the updating process is continuous or periodic.

Our perceptual experience of continuous external changes in the world appears seamless. Hence, it is intuitive to assume that object representations in awareness are updated continuously. However, a seamless appearance is not a guarantor of a continuous process: for example, a movie appears continuous even though it is based on discrete images displayed periodically. Discrete processing in perception is an idea that has been espoused and discarded several times (17–25). However, recent studies indicate that at least some aspects of perception, such as the detection of a perithreshold stimulus, rely on discrete or periodic sampling (26–28). Here, we ask whether one of the highest levels of perception, namely conscious updating, is periodic as well.

Results

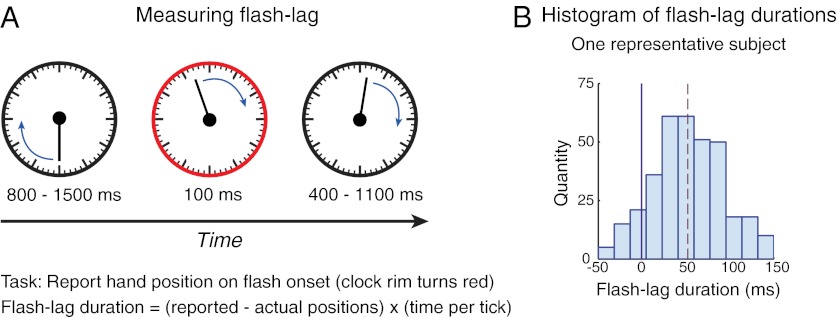
To test our hypothesis, we measured the flash-lag effect as an index of the efficiency of conscious updating on each trial: we asked observers to report the perceived location of a moving stimulus at the onset of a brief flash (Fig. 1A). The mean flash-lag duration (FLD, the misperception in milliseconds) across observers was 27 ms (±8 ms, SEM), and its SD across trials was 54 ms (±5 ms, SEM; Fig. 1B). This large SD in FLD is consistent with previous observations, where it has also been noted that the variability is unaffected by low-level stimulus features, thus implicating high-level processes as a source of the variability (5). Whereas previous studies (1–16) have focused on the mean FLD (that is, the illusion itself), we are concerned here with explaining its deviation across trials. Does this variability arise due to internal and/or external sources of noise imposed on a constant and continuous process or does the variability reflect an inherent periodicity in the updating process, with updating being more efficient at some time points than at others?

Fig. 1.

FLE and its dependence on ongoing oscillations. (A) Measuring flash lag. Stimulus was a clock measuring 4° in diameter presented at fixation, with a single hand rotating at 1 Hz. After a variable time, the rim briefly turned red (100 ms). The observer reported the hand position at this flash onset. The difference between the reported and veridical positions is the flash-lag duration (FLD), which reflects the efficiency of updating representations (Materials and Methods) (B) Histogram of FLD of one representative observer. Dashed line indicates mean flash-lag duration. We find large within-observer variance in FLD (mean SD across 13 participants = 54 ± 5 ms). This study tested whether a periodic process underlies part of this observed variability.

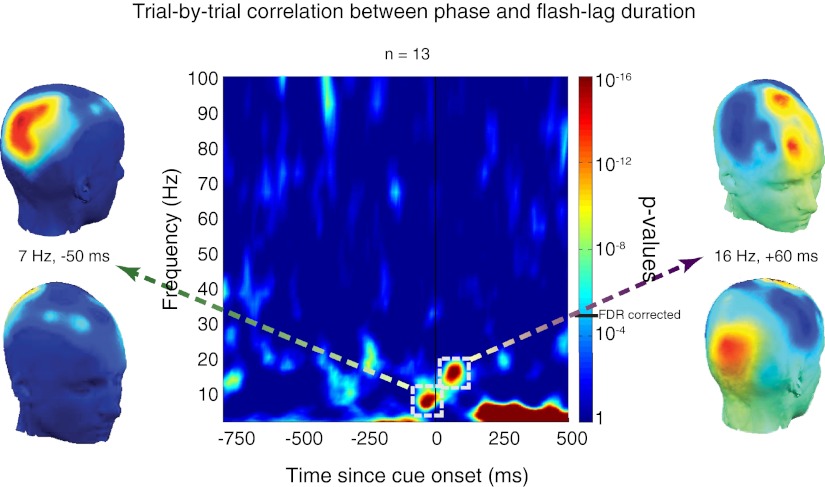
We concurrently measured the phase of ongoing EEG oscillations, and sought to determine whether this marker of periodic neuronal fluctuations (19, 29–31) was correlated with FLD on a trial-by-trial basis. Because phase is a circular variable and FLD a linear variable, we computed circular-to-linear correlations (32) between them (Fig. 2). A strong correlation, where longer and shorter FLDs are correlated with opposite phases, would imply that the updating process is cyclical. To determine whether these correlations were reliable we compared them with bootstrapped correlations. We estimated the distribution of correlations under the null hypothesis (no systematic relation between phase and FLD) by iteratively computing correlations between the observed trial-by-trial FLD and random phases. The proportion of values in this null-hypothesis distribution that were (by chance) above the observed correlation value gave us an indication of the significance of this correlation (i.e., P values). We found strong correlations (P < 10⁻¹⁴) between phase and FLD in the θ band (5–10 Hz) in occipital electrodes (with a peak at 7 Hz, 50 ms before the presentation of the flash) and also in the high-α, low-β band (12–20 Hz) in frontocentral electrodes (with a peak at 16 Hz, 60 ms after flash presentation). Because we compared phase–FLD correlations at all time points and frequencies, we corrected for multiple comparisons using the false discovery rate (FDR) (33) procedure, setting the α at a conservative 10⁻⁴. The strong correlations observed in the two regions were significant even when multiple comparisons were taken into account. To further confirm these findings we applied an alternative, independent analysis driven by information theory and pioneered by Schyns and colleagues (34) to our data. We found that trial-by-trial phase encodes significantly more information about the corresponding trial-by-trial FLD than does random phase (chance) at around the same time-frequency points as those discovered by the correlation method reported above and with the same topographical distribution (SI Text and Fig. S1). These results suggest that the state of neural oscillations at specific frequency bands and regions just around flash onset predicts how quickly object representations are updated: updating is more efficient at some phases of the oscillatory cycle than others.

Fig. 2.

Circular-to-linear correlations. We computed circular-to-linear correlations between the trial-by-trial FLD and the corresponding phase of EEG oscillations at all frequencies and time points, for each electrode and subject. We then averaged these correlations across all electrodes and subjects at each time-frequency point. These correlations were compared statistically with bootstrapped circular-to-linear correlations between FLD and random phase averaged across subjects. We plot P values of these comparisons at all frequencies and time points. P values were corrected for multiple comparisons using the false discovery rate procedure at a conservative α value (10⁻⁴), represented on the color bar by a black horizontal line (FDR corrected). Correlations with P values above this threshold were deemed significant. FLD was strongly correlated (P < 10⁻¹⁴) with phase at occipital (peak at 7 Hz, 50 ms before flash onset) and frontocentral (peak at 16 Hz, 60 ms after flash onset) electrodes.

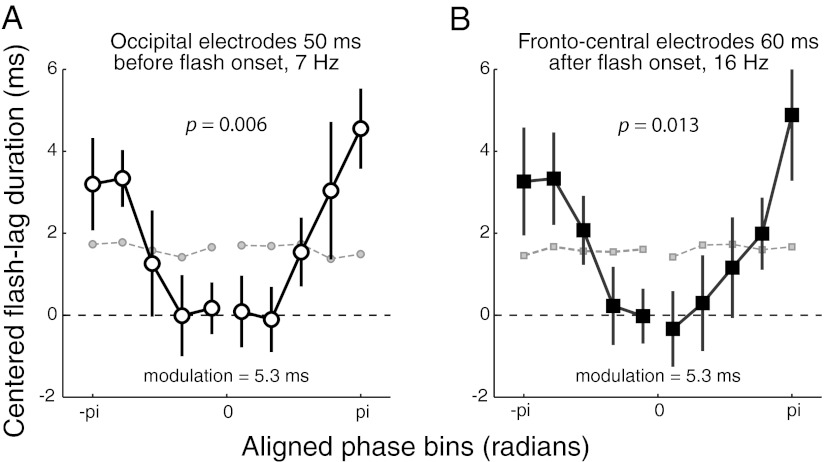
Next, we quantified the relation between oscillatory phase and FLD. The trial-by-trial FLDs were binned according to phase (at the time-frequency points with the most significant correlation; 11 phase bins for each region). After aligning the phase bins such that the bin with the shortest FLD was at the center (corresponding to the preferred phase for that observer and electrode in that region), the FLDs within each bin were averaged. If phase has a systematic effect on FLD, FLD should be slower and slower as phase gradually differs from the central bin. Also, the phase opposite to the preferred phase should have the longest FLD. This is precisely what we observed: a one-way repeated measures ANOVA indicated that oscillatory phase significantly affected FLD (occipital electrodes: F(9,120) = 2.71, P = 0.006; frontocentral electrodes: F(9,120) = 2.47, P = 0.013; Fig. 3). We then used a sine function approximation (a sine fit to the data) to determine how much of the variability in FLD was accounted for by phase. We found that each region—occipital cortex before flash presentation and frontocentral cortex just after flash onset—each accounted for 5.3 ms of the variability in FLD (Fig. 3). In other words, depending on the phase of the oscillatory activity around flash presentation in one of these regions, updating was faster or slower by as much as 5.3 ms on that trial.

Fig. 3.

Relationship between FLD and phase. Graphs plot the contribution of phase to FLD at occipital (A) and frontocentral (B) regions. FLDs were binned according to phase values (11 bins). Phases across electrodes and observers were then aligned such that the preferred phase, the phase with the fastest FLD, was centered (0 phase). Data for this bin are not shown, as they cannot be interpreted (they are by definition the lowest value of the curve, due to realignment). However, as predicted by the periodicity hypothesis, FLD increased as phase increasingly differed on either side of this central bin. Error bars are 1 SEM. We verified that the obtained near-sinusoidal curves were not an artifact of our realignment procedure by computing 100 bootstrapped baseline curves with FLD values shuffled across trials and plotting the average of these iterations (gray markers connected by dashed lines). These baseline curves are flat, suggesting that the phase–FLD correlations observed in the original data were not an artifact. To quantify these correlations, we fit a sine function to these data. The extent of the variability in FLD across trials explained by phase is equal to twice the amplitude of this sine fit: 5.3 ms in each region. We performed one-way repeated measures ANOVA on each phase–FLD plot, revealing a significant effect of phase on FLD (occipital electrodes F(9,120) = 2.72, P = 0.006; frontocentral electrodes F(9,120) = 2.47, P = 0.013). We also compared the amount of FLD explained by phase in each region (5.3 ms) to the modulation explained by chance as determined by the bootstrap procedure described above. We found that the observed modulation was highly significant (occipital electrodes, P = 1.54 × 10⁻¹⁰ and frontal electrodes, P = 2.53 × 10⁻¹¹).

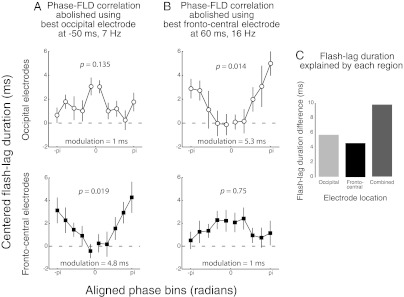
Given that the two regions explain similar amounts of variability in FLD, it is possible that a unique process underlies the effects observed in both regions; or it might be that the two effects are independent of each other. We assessed these possibilities in two ways. First, we compensated, using a sine function approximation fit to the phase-binned FLD (described above and in Materials and Methods), the oscillatory effect in one region. We did this by subtracting the amount of FLD predicted by phase in that region, as determined by the sine approximation, from each trial. We then reevaluated the phase–FLD relation in the other region using the corrected FLD values. As expected, the phase–FLD correlation was lost in the region used to predict the FLD compensation (Fig. 4 A, Upper and B, Lower). However, the phase–FLD correlation remained intact in the other region (Fig. 4 A Lower and B, Upper). That is, this procedure ascertained that the contributions of the two regions were independent of each other. Thus, overall, about 10 ms of the variability in FLD could be explained by oscillatory phase on any given trial. This conclusion was confirmed by a second analysis. We considered the trials with the best and worst phases in a given region and time-frequency point and subtracted the average FLD of the former from the latter, giving us an estimate of the variability in FLD explained by phase in that region. This estimate was about 5 ms for each region (Fig. 4C), consistent with the results from the sine fit procedure described above. Then we determined the variability explained when the phases of both regions were simultaneously considered: we selected only those trials that had the best phase in both regions and those with the worst phase in both regions. We subtracted the average FLD of the former from the latter. If the two regions were driven by the same underlying mechanism, we would expect the variability explained by both regions to be the same as the duration explained by each region (that is, about 5 ms). However, if the explanatory power of phase in the two regions is independent of each other, then the variability explained when phases of both regions are simultaneously considered should be the sum of the durations explained by each region (that is, 10 ms), which is what we found (Fig. 4C). These results confirm that conscious updating depends on periodic processes implemented independently in two regions at different frequency bands.

Fig. 4.

Testing independence. (A and B) We compensated for the contribution of phase to FLD in one area (A, occipital and B, frontocentral). This procedure abolishes the phase–FLD correlation in that area. However, the effect of phase in the other area remains. This finding suggests that the two areas explain different parts of the variability in FLD. Variability explained by phase is indicated in each plot. We performed one-way repeated-measure ANOVAs on each phase–FLD plot. P values are indicated at the Top of each graph. Error bars are 1 SEM. (C) We determined the amount of FLD explained by the phase of each region separately and then computed the amount explained by the phase of both regions considered together. Both regions combined explain as much as the sum of the FLD explained by each region separately, suggesting that each region contributes independently to the explanation of the variability in FLD.

Discussion

We used the flash-lag illusion (1–4) to assess the temporal dynamics of the conscious updating process (3, 7, 8). We tested the hypothesis that updating is periodic and found that periflash phase of ongoing oscillations in occipital and frontocentral regions influenced the speed of the updating process. We also found that the two regions explained different portions of the variability in the updating process. Combined, they explained about 10 ms of the variability on a trial-by-trial basis. These results imply that the updating process is periodic in nature.

It has implicitly been assumed that visual processing, including conscious perception, is continuous. However, the idea of discrete perception has been floated repeatedly (17–25) without gaining much traction. The broad proposal is that visual perception is periodic in nature (23, 35), with more efficient processing at certain time points than at others and that there are discrete “perceptual moments,” where events falling within a specific temporal window are combined to form a conscious percept (18). Convincing experimental evidence has been hard to come by (23). However, recent studies indicate that at least some aspects of perception rely on discrete or periodic sampling (22, 24, 26–28, 35). For example, detecting a perithreshold stimulus is driven by an intrinsic periodicity in attention (28, 35). Similarly, recent findings have suggested that perceptual illusions such as the continuous wagon-wheel illusion can be attributed to discrete temporal processing of motion information (22–25). Here we showed that one of the highest levels of perception—conscious updating—is periodic.

In this study, FLE served as a useful tool in testing various hypotheses about the updating process. However, the current results do not shed light on the underlying mechanisms of the illusion (nor were they intended to do so). Several mechanisms have been forwarded to account for the flash-lag effect and the logic continues to be debated. The motion extrapolation hypothesis (1, 2) suggests that the position of a moving object is compensated for using predictive mechanisms, whereas that of a stationary object’s (the flash) is not, leading to flash lag. Postdiction (3, 4), on the other hand, argues that information before the flash is not considered. It proposes that the flash resets the motion integration system, which then uses information from the period right after the flash (extending to about 80 ms postflash) to compute motion, leading to a discrepancy in the localization of moving and stationary objects. The differential neuronal latencies hypothesis (9–11) suggests that signals from moving and stationary objects are processed at different rates resulting in flash lag. The empirical experience (12) hypothesis suggests that perception of moving and static objects is a consequence of perceptual and behavioral experience with the world, perhaps over evolutionary time. This experience might underlie differences in their perception. Finally, it has been posited that attention (13–16) could explain or modulate the misperception in flash lag. The flash is thought to attract attention and shifting attention back to the moving object takes time. This time-consuming process might contribute to the misperception. In fact, attention might be understood as an underlying cause or component of the other proposed mechanisms. For example, attention drawn to the flash might trigger the postdictive mechanisms of the visual system, or attention might cause differential processing latencies between attended (moving) and unattended (stationary) stimuli. Nevertheless, all of the proposed mechanisms noted above are compatible with either a continuous or periodic updating process. Our study was not intended to address this debate and indeed does not arbitrate between these. We merely used the uncontroversial relation between FLE and conscious updating (3, 7, 8, 13–16) to explore the dynamics of the updating process and reveal its periodic nature.

On the basis of the current results, it appears that updating conscious representations may involve two distinct stages with distinct intrinsic periodicities. One possible, although speculative, interpretation is that the two stages correspond respectively to attentional capture and conscious access. First, part of the variability in updating might be driven by a θ-band (5–10Hz) periodicity in attentional capture (28) by the flash (13). It has been shown that, under conditions of sustained attention, phase of θ oscillations before the onset of a perithreshold stimulus predicts whether it is subsequently perceived (28). In our study, the observers were asked to attend to the clock continuously. The phase of θ oscillations might thus affect how quickly the flash captured attention. This interpretation resonates with the notion that attention plays a significant role in FLE (13–16). Following this stage, the conscious updating itself, wherein features of each object in the incoming stream are suitably extrapolated (1, 2), integrated (3, 4), or tagged for further processing (9–11, 13–16) might depend on the state of high-α low-β oscillations in frontocentral areas. Together, the two effects would determine the efficiency of object updating in awareness.

Materials and Methods

Participants and Stimuli.

Fifteen observers, aged 21–38 y, with normal or corrected-to-normal vision participated in this experiment. Data from 2 observers were discarded due to excessive eye blinks (leading to the rejection of more than 15% of trials). Stimuli were generated using MATLAB with the Psychtoolbox extensions. A single “clock,” measuring 4° in diameter, was used to measure the flash-lag effect. The clock had 60 tick marks as in a standard clock with 12 “major” ticks and 48 “minor” ticks. The clock had a single hand revolving around the center at the rate of 1 Hz (Fig. 1A). On each trial, initiated by a key press, the clock was presented at fixation and the hand started revolving from a random tick mark. The rim of the clock turned red for 100 ms, at a random time, between 800 and 1,500 ms after trial onset. The hand continued to revolve for another 500–1,200 ms, depending on when the flash was presented and hence for a total of 2 s on each trial (two revolutions of the hand per trial). The participants were asked to report the hand position at the onset of the flash. They did so at the end of the trial by rotating the hand of a “response” clock to the perceived position. Observers were allowed to discard a trial if they were not confident of their response or if they had failed to see the onset of the flash. These trials were then immediately replaced with trials with the same parameters as the discarded trials, but interspersed randomly among the remaining trials. An experimental session consisted of three blocks, each lasting 15 min. The participants completed as many trials as possible in that period. Each participant completed, on average, 385 trials.

EEG Acquisition.

Sixty-four–channel EEG was recorded with a BioSemi EEG system at 1,024 Hz, which was subsequently downsampled to 256 Hz. Artifacts were rejected manually, including deleting trials with eye blinks and movements (determined from electrooculogram recordings). Epochs of EEG activity between −2,000 to +750 ms relative to flash onset were created and analyzed for each trial.

EEG Analysis.

We applied a time-frequency transform (akin to a Morlet wavelet transform, using the EEGLAB “timefreq” function) to each epoch to obtain the phase of EEG activity in each of the 64 electrodes at various frequencies and time points. The frequencies ranged from 2 to 100 Hz in 50 logarithmically spaced steps with the number of cycles used for phase analysis progressively increasing from 1 cycle applied at 2 Hz to 15 cycles at 100 Hz. Circular-to-linear correlations (31) were then computed on this trial-by-trial phase information and the corresponding trial-by-trial flash-lag durations for each electrode, time point, frequency, and subject. These values were then averaged across all electrodes and subjects. Baseline (“null hypothesis”) values were obtained by a bootstrap analysis where the same circular-to-linear correlation was performed, but with randomly determined phase values for each observer. Ten thousand such bootstrap computations were performed for each subject. We then obtained the mean and SD of these baseline values across subjects. P values were then computed by comparing the real correlations (averaged across electrodes and observers) to a reconstructed bootstrap distribution combining the means and SDs of bootstrap distributions across observers. To correct for multiple comparisons across all time points and frequencies, the FDR (33) procedure was used (setting the α to 0.0001). Note that because, as a critical first step, we were interested in determining whether there was any measurable effect of phase on FLD, we pooled (averaged) data across all electrodes and subjects to obtain our results (Fig. 2). Therefore, in our omnibus analysis, we did not compare across electrodes and hence did not have to correct for comparisons across electrodes.

Quantifying the Effect of Phase on FLD.

Strong correlations between phase and FLD were observed in occipital electrodes 100–0 ms before flash onset in the 5- to 10-Hz band and in frontocentral electrodes 40–120 ms after flash onset in the 12- to 20-Hz band. To quantify these correlations, we considered the time point and frequency where the correlation was the strongest in each region (the point in each region with the lowest P value): 7 Hz, 50 ms before flash onset in occipital electrodes (P₁, P_z, P₂, PO₃, PO_z, PO₄, O₁, O_z, and O₂) and 16 Hz, 60 ms after flash onset in frontocentral electrodes (AF₃, AF_z, AF₄, F₁, F_z, F₂, FC₁, FC_z, and FC₂). FLDs (centered on the mean value for each observer) were then binned by phase (11 bins). The bins were then realigned for each observer and electrode such that the bin with the fastest FLD was centered and was relabeled as 0 phase (the corresponding central value is not displayed in Fig. 3, as it is not interpretable due to realignment). The FLDs within each bin were then averaged across electrodes and observers. A systematic relation between phase and FLD should be revealed as an increase of FLD on both sides of the minimum. In both regions of interest, one-way repeated measures ANOVA were conducted to test for this possibility. To ensure that the resulting phase–FLD curve was not an artifact of the above aligning procedure, we computed bootstrapped baseline values. The same binning and realigning procedure was performed 100 times but with FLD values shuffled across trials on each repetition, such that a given FLD is associated with a different phase each time. If the aligning procedure itself resulted in a “U”-shaped curve with FLD values increasing on either side of a centered minimum, we would observe the same in the bootstrapped values as well. To determine the amount of variability explained by phase, a sine fit was applied to each observer’s data, where the amplitude of the sine was allowed to vary (period was fixed at one cycle, and phase was set such that it was a sine wave: 0 FLD at 0 phase). The phase–FLD modulation is twice the amplitude of the best fitting sine. The average of this value across observers is the extent of variability explained by phase in that region.

Testing Independence Between Occipital and Frontocentral Correlations.

Phase of occipital and frontocentral oscillations around flash onset explains 5.3 ms, each, of the variability in FLD. These two effects could be the same (arising from a common source or occipital correlations driving the later frontocentral correlations) or they might represent two distinct independent processes. We tested these alternatives in two ways. First, as above, we picked the peak time-frequency point for the correlations in each region: (i) 7 Hz, 50 ms before flash onset in the occipital region and (ii) 16 Hz, 60 ms after flash onset for the frontocentral region. We then picked the “best” electrode in each region for these parameters. The best electrode was defined as the electrode that had the strongest phase–FLD correlation; using the best electrode ensures that there is no undercompensation. Then, for the occipital region, we abolished the effect of phase on FLD as follows: for each trial, we determined the phase of EEG activity in the best occipital electrode at the specified time-frequency point. We then subtracted the duration predicted by this phase, derived from the sine fit described earlier, from that trial’s FLD. We then recomputed the effect of phase on FLD in both regions using these corrected FLDs, as described earlier. This procedure abolishes the effect of occipital phase on FLD (Fig. 4A, Upper). If the correlations in the two regions are not independent, then the above procedure should eliminate the phase–FLD correlation in both regions. However, we found that the correlation remains intact in the frontocentral electrodes (Fig. 4A, Lower). We repeated the procedure by abolishing the effect of frontocentral phase on FLD (Fig. 4B, Upper) and examining its effect on the phase–FLD correlation in the occipital electrodes. Once again, abolishing the effect in frontocentral regions (by design) does not eliminate the effect in the occipital regions (Fig. 4B, Lower). We performed a second test of the hypothesis. Once again, we took the best electrode in each region. To assess the effect of phase, we compared trials with the optimal and the worst phases for each electrode. The difference in FLD between these two kinds of trials provides an estimate of the extent of variability explained by phase in each region. Then we selected only those trials that had the optimal phase in both electrodes. Similarly, we selected trials that had the worst phase in both electrodes. The difference in FLD between these two kinds of trials gives us the variability explained when phase of both regions was simultaneously taken into account. If the effects in the two regions were driven by the same underlying mechanism, we would expect this difference to be the same as the duration explained by each region. However, if they are independent of each other, then this difference should be the sum of the durations explained by each region, which is what we found (Fig. 4C). These results suggest that the two regions drive independent effects, indicating that two distinct mechanisms contribute to the rhythmicity of conscious updating.