Behavioral Estimates of the Contribution of Inner and Outer Hair Cell Dysfunction to Individualized Audiometric Loss

Abstract

Differentiating the relative importance of the various contributors to the audiometric loss (HL_TOTAL) of a given hearing impaired listener and frequency region is becoming critical as more specific treatments are being developed. The aim of the present study was to assess the relative contribution of inner (IHC) and outer hair cell (OHC) dysfunction (HL_IHC and HL_OHC, respectively) to the audiometric loss of patients with mild to moderate cochlear hearing loss. It was assumed that HL_TOTAL = HL_OHC + HL_IHC (all in decibels) and that HL_OHC may be estimated as the reduction in maximum cochlear gain. It is argued that the latter may be safely estimated from compression threshold shifts of cochlear input/output (I/O) curves relative to normal hearing references. I/O curves were inferred behaviorally using forward masking for 26 test frequencies in 18 hearing impaired listeners. Data suggested that the audiometric loss for six of these 26 test frequencies was consistent with pure OHC dysfunction, one was probably consistent with pure IHC dysfunction, 13 were indicative of mixed IHC and OHC dysfunction, and five were uncertain (one more was excluded from the analysis). HL_OHC and HL_IHC contributed on average 60 and 40 %, respectively, to the audiometric loss, but variability was large across cases. Indeed, in some cases, HL_IHC was up to 63 % of HL_TOTAL, even for moderate losses. The repeatability of the results is assessed using Monte Carlo simulations and potential sources of bias are discussed.

Introduction

Hearing loss, as revealed by abnormally elevated pure tone audiometric thresholds, is a frequent pathology (e.g., Johansson and Arlinger 2003; Kochkin 2001). The observed threshold shift for a given hearing-impaired listener and frequency region can have multiple contributions. It may reflect selective or combined dysfunction of the middle ear, the inner ear, and/or the central auditory system. Differentiating the relative importance of the various contributors is becoming critical as more specific treatments are being developed (Mills 2006). In this study, a behavioral method is applied to assess the relative contribution of inner (IHC) and outer hair cell (OHC) dysfunction to the individualized audiometric loss of patients with mild to moderate cochlear hearing loss.

Threshold shifts in subjects with cochlear hearing loss may occur as a result of two mechanisms (Moore 2007). First, dysfunction of the OHCs may impair the active mechanism of the cochlea, resulting in reduced basilar membrane (BM) responses for a given sound level. Hence, abnormally high sound levels are required to evoke just detectable BM responses. Secondly, dysfunction of the IHCs or their related structures and/or processes (e.g., stereocilia transduction, synaptic vesicle release, etc.) may require abnormally high BM responses at neural threshold, which also require sound levels higher than normal (e.g., see Fig. 1 of Lopez-Poveda et al. 2009). These two mechanisms may occur simultaneously, each contributing a different proportion to the measured threshold shift. For this reason, some authors (e.g., Jepsen and Dau 2011; Moore and Glasberg 1997) have conveniently expressed the total loss, HL_TOTAL, in decibels, as:

1

where HL_OHC and HL_IHC denote the relative contribution of the two mechanisms (in decibels) to the total loss. IHC and OHC dysfunction may occur as a result of physical injury to cellular structures, like stereocilia damage caused by acoustic trauma (Liberman and Dodds 1984; Liberman and Mulroy 1982; Liberman et al. 1986), or share a common physiological cause, like a reduced endocochlear potential associated with dysfunction of the stria vascularis (Schmiedt 1996). For convenience, however, it is commonly assumed that the different causes may be modeled as a loss of auditory sensitivity associated with IHC and/or OHC dysfunction, hence by Eq. (1) (e.g., Bondy et al. 2004; Jepsen and Dau 2011; Moore and Glasberg 1997, 2004).

Anatomical evidence suggests that treatment with kanamycin (Liberman and Dodds 1984), exposure to intense sounds (McGill and Schuknecht 1976) or aging (Wright et al. 1987) produce proportionally greater loss of OHCs than IHCs. Furthermore, models of loudness perception for patients with cochlear hearing loss (Moore and Glasberg 1997, 2004) suggest that typical loudness matching functions can be predicted assuming that HL_OHC is 80 % of HL_TOTAL for mild (40 dB) losses and 70 % of HL_TOTAL for moderate to severe (50–80 dB) losses (p. 304 of Moore and Glasberg 1997). Altogether, these observations have contributed to the common notion that even though IHC and OHC dysfunction likely coexist, HL_OHC is typically greater than HL_IHC [reviewed by Møller (2000) and Moore (2007)]. This notion is implicit in some of the models that have been used to estimate the initial dynamic-range gain prescription of nonlinear hearing aids (e.g., Bondy et al. 2004; Moore et al. 1999).

There is, however, evidence that the amount of OHC and IHC dysfunction and hence the relative proportion of HL_OHC and HL_IHC may vary widely across listeners with identical total hearing loss. For example, acoustic trauma produces more damage to IHC than to OHC stereocilia despite cell counts sometimes suggest comparable or greater OHC loss (Figs. 4 and 9 of Liberman and Dodds 1984). Second, after noise-induced hearing loss, the growth of auditory nerve fiber responses with increasing sound level is inconsistent with a common pattern of greater OHC dysfunction. Instead, individual rate-level functions encompass a wide range of shapes indicative of mixed IHC and OHC dysfunction of varying magnitude (Heinz and Young 2004). A third piece of evidence is that subjects with similar hearing loss can show very different cochlear input/output (I/O) functions as inferred using psychoacoustical methods (e.g., Jepsen and Dau 2011; Lopez-Poveda et al. 2005; Plack et al. 2004). Fourth, hearing-impaired listeners with identical hearing loss can show very different loudness-growth functions (Marozeau and Florentine 2007). The reason for the observed differences is uncertain, but the relationship between hair cell dysfunction and loudness growth (e.g., Jürgens et al. 2011; Moore and Glasberg 1997, 2004) makes it tempting to conjecture that it may reflect different amounts of IHC and OHC dysfunction across listeners. Lastly, human anatomical studies also show that IHC and OHC cell counts can vary largely across individuals (e.g., McGill and Schuknecht 1976; Wright et al. 1987). Altogether, this evidence suggests that HL_OHC may be greater than HL_IHC on average but not necessarily for every individual. Therefore, individualized estimates of HL_IHC and HL_OHC could be particularly useful when fitting hearing aids. For example, the applied dynamic range of compression may be critical for perceiving speech in noise (e.g., Glasberg and Moore 1992).

The aim of the present study was to estimate the proportion of the audiometric loss that can be attributed to OHC and IHC dysfunction (HL_OHC and HL_IHC, respectively) in listeners with mild-to-moderate cochlear hearing loss, paying particular attention to individualized results. The approach was based on comparisons of the characteristics of behaviorally inferred cochlear I/O curves of normal hearing (NH) and hearing impaired (HI) listeners. The former were taken from previous reports (Johannesen and Lopez-Poveda 2008, 2010; Lopez-Poveda and Johannesen 2009). The basic assumption was that cochlear gain is reduced by OHC dysfunction but not by IHC dysfunction; hence, HL_OHC may be equated to the reduction in maximum cochlear gain as inferred from the difference between I/O curves for NH and HI listeners.

Methods

Approach and Assumptions

The Assumed Model of IHC and OHC Dysfunction

The approach is based on the fundamental assumption that the nonlinear I/O response characteristics of the BM are altered by OHC dysfunction but not by IHC dysfunction. Despite its lacking direct support, this assumption seems reasonable because distortion product otoacoustic emissions (DPOAEs) are directly related to BM nonlinearity (e.g., Rhode 2007), and there is evidence that selective IHC damage does not affect the DPOAE levels (Trautwein et al. 1996). The issue is how to quantify HL_OHC and HL_IHC from comparisons of the estimated BM I/O curve of a given HI listener with the average I/O curve of NH listeners for a corresponding frequency region.

The proposed approach is based on the model depicted in Figure 1 from Plack et al. (2004). Consider Figure 1A first. The thin, dark continuous lines illustrate two idealized BM I/O curves for a basal site of a healthy cochlea. One of them is for a tone with a frequency equal to the characteristic frequency (CF) (on-CF condition) of the cochlear site in question, and the other one is for a tone with a frequency well below the CF (off-CF condition). (Note that the two lines partially overlap with thicker, gray lines that will be described later.) The on-CF I/O curve has three sections: a linear segment (slope = 1 dB/dB) at low levels, followed by a compressive segment (slope < 1 dB/dB) at moderate levels, followed by a linear segment at higher levels. The off-CF I/O curve is assumed to be linear. These shapes are idealized but are broadly consistent with that of basal I/O curves for on- and off-CF tones (e.g., Ruggero et al. 1997) and serve to illustrate the point. Let v₀ be the BM response (in units of, say, velocity of vibration) required to evoke a threshold sound sensation and L₀ and L₁ the levels of the on- and off-CF tones, respectively, required to produce BM responses at threshold. If it is assumed that a pure tone is detected by monitoring the response of nerve fibers innervating the cochlear region of maximum sensitivity to the tone frequency, then L₀ is the absolute threshold for a tone at the CF.

FIG. 1.

Presumed idealized on- and off-CF cochlear I/O curves for NH listeners (thin lines) and listeners with different types and degrees of hearing loss (thick lines). A Pure OHC dysfunction. B Pure IHC dysfunction. C Mixed IHC and OHC dysfunction. D Severe IHC dysfunction. See main text for a detailed explanation and symbols definitions.

The thick gray lines in Figure 1A illustrate presumed BM I/O curves for the same on- and off-CF tones after partial, pure OHC dysfunction. The diagram is based on the assumption that this type of dysfunction reduces the maximum cochlear gain and thus BM sensitivity to low level sounds but does not affect the compression exponent. This assumption is supported by recent psychoacoustical data (e.g., Lopez-Poveda et al. 2005; Plack et al. 2004). Let 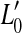be the absolute hearing threshold in this condition, that is, the sound level required for an on-CF tone to evoke the BM response at absolute threshold, v₀. In this case, the total audiometric loss for a CF tone, HL_TOTAL, defined as the shift in absolute threshold (), is equal to the reduction in maximum cochlear gain, ΔG, defined here as the magnitude of the horizontal shift of the low-level, linear portion of the I/O curve. Note also that pure OHC dysfunction does not change the BM response to the off-CF tone or the BM response at the detection threshold (v₀), and thus, the level L₁ at threshold remains unaltered ().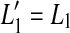

The shaded area in Figure 1A illustrates the region of undetectable BM responses, that is, the region where BM responses fall below v₀ for any stimulus. Assuming that BM I/O curves can be inferred using psychoacoustical methods (see below), the shaded area illustrates conditions for which the shape of BM I/O curves cannot be determined because corresponding BM responses are undetectable. To illustrate this, I/O curves for the HI conditions (thick gray lines) are represented only above their corresponding shaded area.

Figure 1B illustrates the consequences of pure IHC dysfunction in idealized form. For convenience, IHC dysfunction is illustrated here assuming that the threshold BM excitation required to evoke a sound sensation increases from v₀ to 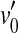. It is also assumed that pure IHC dysfunction does not alter the shape of the BM I/O curves. Note, however, that the range of undetectable BM responses (shaded area) extends vertically and hence BM I/O curves for on- and off-CF tones may be measured for a narrower range of input sound levels. The measurable portions of the two I/O curves are illustrated by thick gray lines. Note that absolute threshold increases from L₀ to 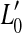as a result of the increase in BM response for threshold, 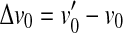. Unlike OHC dysfunction, pure IHC dysfunction also increases the level of the off-CF tone required to produce a just-detectable BM response from L₁ to 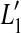. By virtue of the linear relationship between sound level and basal BM responses for the off-CF tone, such an increase, denoted ΔL₁, is equal to Δv₀ when the latter is expressed in decibels. It is important to note that the relationship between BM response and level is compressive for the on-CF tone, and therefore, both ΔL₁ and Δv₀ differ from HL_TOTAL.

Figure 1C illustrates the consequences of mixed IHC and OHC dysfunction. This is a straightforward combination of the cases illustrated in Figure 1A and B. It is important to note, however, that in this particular case, HL_TOTAL can be expressed as the sum of ΔG and ΔL₁. This is possible only because the on-CF I/O curve shows a compression threshold that allows estimating ΔG by extrapolation of the low-level linear segment of the HI I/O curve (dashed line). If a compression threshold was not observed in the measurable portion of the on-CF I/O, then ΔG would be indeterminate. The latter condition is illustrated in Figure 1D. In this case, Δv₀ (associated here with “severe” IHC dysfunction) is so large that it brings 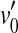well above the BM excitation at the compression thresholds of the NH I/O curve or of I/O curves for damaged cochleae with pure OHC dysfunction (thin dashed lines). As a result, HL_TOTAL is fully due to IHC dysfunction regardless of any concomitant OHC dysfunction. Furthermore, it would not be possible, to estimate ΔG from the behaviorally inferred portion of the I/O curve.

This latter example also serves to illustrate the difference between estimating structural and functional IHC and OHC damage. The distinction is important. While structural IHC and OHC damage coexist in the example of Figure 1D, in functional (or perceptual) terms, however, HL_TOTAL is fully due to IHC damage. In this particular case, a technique designed to assess structural damage would give a misleading functional estimate. The technique proposed here is designed to estimate the functional rather than the structural damage of each hair cell type (see below).

Definition of HL_OHC and HL_IHC

Based on the preceding analysis, HL_OHC was defined here as the reduction in maximum cochlear gain, ΔG, that can be calculated from the shift in the compression threshold, or kneepoint, of the on-CF I/O curve of a HI listener (K_HI) relative to the average compression threshold for a group of NH listeners . For the model depicted in Figure 1, it can be mathematically shown that:

2

where c is the compression exponent (i.e., the slope over the compressive region of the I/O curve). Using Eq. (1), HL_IHC is defined as the difference between HL_TOTAL and HL_OHC.

These definitions deserve some discussion and clarification. First, some authors have defined HL_IHC as ΔL₁ (Fig. 1B) and inferred HL_OHC using Eq. (1) (Jürgens et al. 2011). The latter definition, however, would lead to erroneous conclusions in cases like those illustrated in Figure 1D, where HL_TOTAL is much greater than ΔL₁, thus suggesting important HL_OHC, even when HL_TOTAL is solely due to IHC dysfunction. Another difficulty with the latter definition would be that the I/O curve for the off-CF tone is linear only for basal cochlear sites but not for apical sites (e.g., Lopez-Poveda et al. 2003; Lopez-Poveda and Alves-Pinto 2008; Plack and Drga 2003; Rhode and Cooper 1996). Therefore, it is likely that for apical cochlear sites, ΔL₁ may depend not only on IHC dysfunction but also on the active cochlear mechanism, thus on the functional status of OHCs. The chosen definitions of HL_OHC and HL_IHC are not affected by these shortcomings.

A second comment is that the present definition of HL_OHC (and HL_IHC) somewhat limits the applicability of our procedure, as it requires that a compression threshold exists in the measurable portion of estimated on-CF I/O curves of NH and HI listeners. If this were not the case, then HL_OHC would be indeterminate, as shown in Figure 1D. Fortunately, earlier reports suggest that the compression threshold may be estimated from behaviorally inferred I/O curves for the majority of NH and HI listeners with mild to moderate losses (e.g., Lopez-Poveda et al. 2003, 2005; Plack et al. 2004). This is also supported by the present data (see below).

Thirdly, it is important to stress that the compression exponent, c, is assumed to be independent (uncorrelated) with HL_TOTAL. This is supported by direct BM recordings (e.g., Fig. 3 in Ruggero et al. 1996), by recent psychophysical studies (Jepsen and Dau 2011; Lopez-Poveda et al. 2005; Plack et al. 2004) and by the present data. BM I/O curves inferred from auditory nerve responses, however, are not so clear cut (e.g. Heinz et al. 2005).

Lastly, it must be emphasized that HL_OHC and HL_IHC are the presumed contributions of OHC and IHC dysfunction to the audiometric loss of HI listeners (in decibels) and do not necessarily correspond with the degree of physical damage or loss of each cell type.

Methods to Estimate Cochlear I/O Curves

All experimental methods were approved by the Ethical Review Board of the University of Salamanca.

Cochlear I/O curves were inferred from temporal masking curves (TMCs). An attempt was made to apply the standard version of the TMC method (Nelson et al. 2001; Lopez-Poveda et al. 2003) for all HI listeners. Sometimes, however, it was not possible to measure a linear reference TMC. In those cases, I/O curves were obtained using the variant TMC method of Lopez-Poveda and Alves-Pinto (2008). The fundamentals of these methods may be found in the original publications and will not be repeated here. The adequacy of these methods to infer cochlear I/O curves in NH and HI listeners will be discussed below.

Listeners and Test Frequencies

HI listeners were included in the study only if they had absolute thresholds ≥15 dB HL [i.e., 15 dB above the ANSI (2004) absolute thresholds for young listeners without hearing deficits] for at least one frequency within the audiometric test range (125 Hz to 10 kHz), and they had no sign of middle-ear pathology, as judged from their clinical record and from a tympanometry test. A total of 18 HI listeners participated in the study. Their ages ranged from 20 to 74 years. Their sexes, ages, and audiograms are shown in Figure 2. Listeners were paid for their participation.

FIG. 2.

Absolute thresholds (in decibels SPL) for pure tones of 300 ms of duration for the test ear [L (ex symbol), left; R (circle), right] of all listeners, as indicated by the text at the top of each panel. The sex (M male, F female) and age (in years) of each listener are shown between brackets. The thick gray line illustrates ANSI (2004) reference thresholds for NH listeners. Error bars show a 15-dB range above reference NH threshold. Note that the absolute thresholds of S1 were obtained using insert rather than circumaural earphones, and this is why the reference thresholds in the top left panel are different. Vertical dashed lines illustrate the test frequencies used for each listener.

Some listeners were tested for more than one frequency, making a total of 26 cases. The number of test frequencies per subject depended on the listener’s time availability. Test frequencies (depicted by the vertical dashed lines in Fig. 2) were chosen quasi-randomly, with the aim to cover a wide range of losses across participants at the test frequencies. Hearing losses at the test frequencies ranged from 12 to 64 dB HL. Table 1 shows the listeners’ absolute thresholds [in decibel sound pressure level (SPL)] for pure tones at the test frequencies and for durations of 10, 110, and 300 ms.

TABLE 1.

Individual absolute thresholds (decibel SPL) for tone durations of 10 ms (probe signals), 110 ms (maskers) and 300 ms (∼absolute threshold), respectively (n/a not available)

		Threshold (dB SPL)
Subject number	Frequency (kHz)	300 ms	110 ms	10 ms
S1	2	15	19	40
	4	42	44	55
S2	1.5	40	42	47
S3	0.75	65	65	71
	4	68	67	68
	6	45	47	48
S4	1	45	50	52
	3	67	n/a	67
S5	4	57	54	56
S6	2	19	14	23
S7	1	22	21	32
S8	4	36	36	37
	6	56	57	62
S9	4	62	62	64
S10	2	18	20	25
	6	34	36	38
S11	0.5	41	45	51
	1	51	52	59
S12	1	25	28	32
	4	38	38	43
S13	0.5	43	33	44
S14	4	33	34	37
S15	0.75	42	45	50
S16	4	63	59	65
S17	2	36	37	41
S18	0.5	42	39	54

TMC Stimuli and Procedure

TMCs were measured for probe and masker frequencies equal to the test frequency (on-frequency condition). An additional TMC was measured for a 4-kHz probe and 1.6-kHz masker. The latter TMC was used as a linear reference. Probe level was fixed at 9 dB SL (i.e., 9 dB above the individual absolute thresholds for the probe). A linear reference TMC could not be measured for some listeners (S4, S5, S11, and S15), presumably because their hearing loss at 4 kHz was so high that the required masker levels were outside the output level range of the equipment. In these cases, an additional on-frequency TMC was measured for a probe level of 15 dB SL to infer I/O curves using the variant TMC method (Lopez-Poveda and Alves-Pinto 2008). The time interval between masker offset to probe onset ranged from 5 to 100 ms in 5-ms steps with an additional interval of 2 ms. Masker and probe durations were 110 and 10 ms, respectively, including 5-ms cosine-squared onset and offset ramps. The probe had no steady state portion.

Stimuli were generated digitally and delivered through an RME Fireface 400 sound card operating at a sampling rate of 44.1 kHz and a digital-to-analog conversion resolution of 24 bit. Stimuli were presented through circumaural Sennheiser HD-580 headphones to all listeners except S1, who was studied using Etymotic ER-2 insert earphones. SPLs were calibrated by placing the headphones (or earphones) on a Kemar equipped with a Zwislocki DB-100 coupler connected to a Brüel & Kjaer 2238 sound level meter. Calibration was performed at 1 kHz only, and the obtained sensitivity was used at all other frequencies.

Masker levels at masking threshold were measured using a two-interval, two-alternative, forced-choice adaptive procedure with feedback. Two sound intervals were presented to the listener in each trial. One of them contained the masker only and the other contained the masker followed by the probe. The probe was presented in the first or the second interval at random. The subject was asked to indicate the interval containing the probe. The time period between stimulus intervals in a given trial was 500 ms. The initial masker level was set sufficiently low that the listener always could hear both the masker and the probe. The masker level was then changed according to a two-up, one-down adaptive procedure to estimate the 71 % point on the psychometric function (Levitt 1971). An initial step size of 6 dB was used, which was decreased to 2 dB after three reversals. A total of 12 reversals were measured for each run. Threshold was calculated as the mean of the masker levels at the last 10 reversals for a run. A measurement was discarded if the standard deviation (SD) of the last 10 reversals exceeded 6 dB. Three threshold estimates were obtained in this way, and their mean was taken as the masker level at masked threshold. If the SD of these three measurements exceeded 6 dB, a fourth threshold estimate was obtained and included in the mean. Measurements were made in a double-wall sound attenuating booth. Listeners were given at least 2 h of training on the TMC task before data collection began.

Absolute thresholds for the probe tones, the masker tones, and for a pure tones with a duration of 300 ms were obtained in a similar manner but with a two-down, one-up adaptive procedure. The latter were regarded as absolute hearing thresholds and are shown in Figure 2 and Table 1.

Inference of Cochlear I/O Curves from TMCs

For listeners for whom it was possible to obtain a linear reference TMC, I/O curves were obtained using the standard TMC procedure (Nelson et al. 2001). That is, an I/O curve was inferred by plotting the levels of the linear reference TMC against the levels of the on-frequency TMC for the frequency of interest, paired according to masker-probe time gaps (Nelson et al. 2001). For listeners for whom TMCs were measured for more than one test frequency, the same linear reference TMC was used to infer I/O curves for all test frequencies (Lopez-Poveda et al. 2003).

To obtain smooth I/O curves, TMCs were fitted with the following functions, and the masker levels predicted by the fitted functions were used instead of the measured masker levels throughout the analysis. The linear reference TMC was fitted with a double exponential function [Eq. (1) in Johannesen and Lopez-Poveda (2008)]. On-frequency TMCs were fitted with a function that consisted of the sum of the double exponential function used to fit the linear reference TMCs plus a second-order Boltzmann function. The parameters of the double exponential function were held fixed to the values found when fitting the linear reference TMC; only the parameters of the second-order Boltzmann were allowed to vary freely when fitting the on-frequency TMCs. This procedure incorporated the main assumptions of TMC method for inferring I/O curves, namely, that the slope of linear reference TMC is affected only by the post-cochlear recovery from the internal effect of the masker (described here by the double-exponential function) while the slope of the on-frequency TMC is affected both by the post-cochlear recovery from the internal masker effect and by compression of the masker (described here by the double exponential function and the second order Boltzmann function, respectively) (Nelson et al. 2001). The same double exponential function was used for the linear reference and the on-frequency TMC of a given subject to incorporate the additional assumption that the recovery rate was independent of masker frequency and cochlear region (Lopez-Poveda et al. 2003; but see the Discussion). Therefore, the resulting I/O curve may be roughly described as a vertically flipped double Boltzmann function rotated 90 º anticlockwise with a maximum potential slope of 1 dB/dB.

For listeners for whom it was not possible to measure a linear reference TMC (S4, S5, S11, and S15), I/O curves were inferred using a variant TMC method (Lopez-Poveda and Alves-Pinto 2008). On-frequency TMCs for probe levels of 9 and 15 dB SL were fitted with a second-order Boltzmann function and the masker levels predicted by the fitted functions, rather than observed masker levels, were used throughout the analysis. It was assumed that (1) a 6-dB increase in probe level produced a corresponding 6-dB increase in cochlear excitation and (2) the two TMCs were affected by the same cochlear I/O curve, the slope of which was estimated as the ratio of the observed increase in masker level to the increase in probe level (6 dB). For each time interval, the slope estimate was assigned to the mean masker level for the two conditions. The I/O curve was then found by integrating the slopes. For further details of this method and its underlying assumptions, see Lopez-Poveda and Alves-Pinto (2008).

NH Reference TMCs and Compression Threshold Definition

The present approach for estimating HL_OHC required compression threshold and compression exponent reference values for NH listeners [Eq. (2)]. These were inferred from behaviorally inferred I/O curves previously published by Johannesen and Lopez-Poveda (2008) and Lopez-Poveda and Johannesen (2009). These data were chosen because they were obtained by the present authors using nearly identical methods and procedures to those employed in the present study. A total of 30 I/O curves for test frequencies between 500 Hz and 6 kHz and for 15 NH listeners were included in the analysis. These TMCs were re-analyzed using identical procedures to those described above for analyzing the new TMCs for HI listeners.

Compression threshold was defined as the input level at which the slope of each I/O curve was equal to 0.5 dB/dB, when decreasing from a higher value at lower input levels. This definition was arbitrary but convenient because it allowed obtaining a compression threshold for a large number of NH and HI I/O curves after trying various other slope criteria from 1 to 0.4 dB/dB. An attempt was made to obtain a compression threshold for all NH and HI I/O curves. A value was included for further analysis only when the corresponding I/O curve had at least one (and typically two) data point for input levels lower than the compression threshold. The compression exponent was arbitrarily defined as the average slope of the fitted I/O curves over the range of input levels where the I/O slope was <0.5 dB/dB. The accuracy of these definitions and their implications on the results will be discussed below.

Monte Carlo Simulations and Repeatability Analysis

Compression threshold estimates were likely vulnerable to variations of masker levels at masked thresholds. This variability may affect HL_OHC estimates when obtained repeatedly in the same listener. Monte Carlo simulation methods were used to assess the repeatability of the results. The masker levels for each experimental condition were assumed to conform to a Gaussian distribution whose mean and SD were equal to the measured values. For each test frequency, one hundred pairs of on-frequency and linear reference TMCs were simulated by generating random masker levels according to the observed masker level statistics. I/O curves were then inferred and analyzed using the methods described above. As a result, a distribution of compression threshold values (N = 100) was obtained for each case and retained for further analysis. Nonparametric methods were applied to describe and analyze the resulting distributions, as described below.

This Monte Carlo analysis was applied to the NH and HI cases for which a compression threshold could be obtained a priori with the standard TMC method, which were the great majority. For these cases, the median compression thresholds of the simulation distributions will be reported instead of the values obtained directly from the analysis of the mean TMCs. [Indeed, a high correlation between the two was observed both for NH (r = 0.95, N = 22, p < 0.0001) and HI listeners (r = 0.99, N = 18, p < 0.0001).] Monte Carlo methods were not applied to the few cases that were analyzed using the variant TMC method on the assumption that the variant and the standard TMC methods produce comparable degrees of variability in HL_OHC estimates.

Results

Temporal Masking Curves

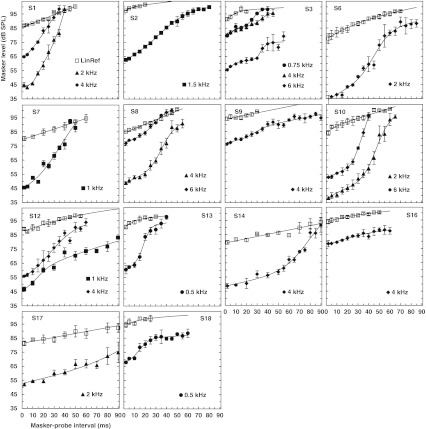
Figure 3 illustrates TMCs for 14 HI listeners for whom it was possible to obtain a linear reference TMC. Each panel illustrates data for a different listener, as indicated at the top of each panel. Open symbols illustrate linear reference TMCs (for f_P = 4 kHz and f_M = 1.6 kHz.). Filled symbols illustrate on-frequency TMCs for different probe frequencies, as indicated by the legend of each panel. Lines illustrate function fits to the TMCs. Lines are sometimes shown for masker-probe time intervals beyond the range of the experimental data (e.g., S2, S3, S6, S9, S12, and S18). These illustrate cases where the linear reference TMC was extrapolated to allow inference of cochlear I/O curves over a wider range of output levels.

FIG. 3.

TMCs for all listeners for whom cochlear I/O curves could be inferred using the standard TMC method (i.e., for those listeners for whom a linear reference TMC could be measured). Open squares illustrate the linear reference TMCs (masker and probe frequencies were 1.6 and 4 kHz, respectively). Corresponding lines illustrate fits with a double-exponential function. Filled symbols illustrate on-frequency TMCs, that is, TMCs for which the masker and probe frequencies were equal, as indicated by the legends. Corresponding lines illustrate fits with the sum of a double exponential function and a second-order Boltzmann function. Error bars illustrate ±1SD intervals around the mean. The probe level was always 9 dB SL.

Some of the on-frequency TMCs in Figure 3 show a shallow segment for short masker-probe time intervals followed by a steeper segment at longer intervals (e.g., S8, S10, and S14). Other TMCs showed a steep segment for short time intervals followed by a shallower segment at longer intervals (e.g., S12 at 1 kHz and S18). For one subject (S6), on-frequency TMCs showed three segments with different slopes: a shallow segment for short intervals, a steeper segment for intermediate intervals, and a shallower segment for long intervals. In all these cases, the shallow segments had slopes that were broadly comparable to the slope of the linear reference TMCs (open symbols) over the corresponding range of masker-probe time intervals. Finally, some on-frequency TMCs showed a single segment whose slope was comparable (e.g., S16) or steeper (e.g., S1) than the slope of the linear reference TMC.

The TMCs for listener S3 deserve special attention. First, the fit to the linear reference TMC was good, but its slope over the extrapolated section was markedly shallower than that suggested by the first four data points. Additionally, the 6-kHz on-frequency TMC had an atypical shape, with masker levels leveling off around 75 dB SPL for long masker-probe time intervals. This shape likely reflected a procedural artifact, since masker levels were calculated using at least three threshold estimates below the maximum system output (105 dB SPL) even though the experiment called for levels above the maximum output several times (i.e., if the exceedingly high levels had been measured and included in the mean, they would have likely raised the mean masker levels over the plateau). Nevertheless, these TMCs were retained for further analysis because the described features did not have an effect on the compression threshold estimate, which was around 65 dB SPL at 6 kHz (see below).

Figure 4 illustrates 12 on-frequency TMCs for the four listeners (S4, S5, S11, and S15) for whom it was not possible to obtain a linear reference TMC. Two TMCs are shown per test frequency: one for a probe level of 9 dB SL (filled symbols) and one for a probe level of 15 dB SL (open symbols), as indicated by the legends. The shapes of these TMCs were broadly similar to that of the on-frequency TMCs of Figure 3. Note that for listener S5, masker levels were unusually variable even after 5 h of training on the TMC task. This listener reported difficulty concentrating on the task.

FIG. 4.

On-frequency TMCs for all listeners for whom cochlear I/O curves were obtained using the variant TMC method (i.e., for those listeners for whom a linear reference TMC could not be measured). Filled and open symbols illustrate on-frequency TMCs for probe levels of 9 and 15 dB SL, respectively. Different symbols illustrate TMCs for different test frequencies, as indicated by the legends. Error bars illustrate ±1SD intervals around the mean. Continuous lines illustrate fits with a second-order Boltzmann function.

Except for the two cases highlighted (S3 in Fig. 3 and S5 in Fig. 4), the shapes of all these TMCs were consistent with the broad range of TMC shapes reported in previous studies (e.g., Jepsen and Dau 2011; Jürgens et al. 2011; Lopez-Poveda et al. 2005; Nelson et al. 2001; Plack et al. 2004; Rosengard et al. 2005; Stainsby and Moore 2006). The interpretation of these shapes has been amply discussed in the relevant earlier publications and will not be repeated here.

I/O Curves

Figure 5 shows the I/O curves for all 26 HI cases (dark symbols). The text at the top of each panel gives the subject number, followed by his/her audiometric loss at the test frequency (in decibel HL), followed by the test frequency, and followed sometimes by the letter ‘v’ when the I/O curve was inferred using the variant rather than the standard TMC method. Panels are broadly organized for increasing frequency from top to bottom (500 Hz to 6 kHz) and for increasing hearing loss from left to right. Dotted lines illustrate linear responses with a slope of 1 dB/dB. Each panel also shows a NH reference I/O curve for a frequency equal (or close) to the test frequency [data from Johannesen and Lopez-Poveda (2008) and Lopez-Poveda and Johannesen (2009)]. These NH I/O curves are shown for reference only and were not used in the following analyses. These reference I/O curves were calculated from the fitted TMCs for test frequencies of 0.5, 1, and 4 kHz in the following way. First, the compression threshold was calculated for each individual I/O curve and the mean value was obtained. Next, each I/O curve was shifted horizontally so that all I/O curves had their compression threshold at the mean value. Finally, all I/O curves were shifted vertically to the mean output value for an input level of 50 dB SPL and averaged. Therefore, any vertical displacement between the NH and HI I/O curves could be the result of this normalization and is not necessarily an informative result; the horizontal displacement between the two curves, by contrast, does allow a reasonable judgment of the compression threshold shift of a HI I/O curve with respect to the average NH. Another reason that the vertical displacement between NH and HI I/O curves is not informative is that output levels for the latter are unreliable. For I/O curves obtained with the variant TMC method output level is arbitrary (Lopez-Poveda and Alves-Pinto 2008). For I/O curves obtained with the standard TMC method, output levels equal the levels of the linear reference TMCs. These levels depend on the individual sensitivity of HI listeners to the 1.6 kHz masker in the 4 kHz cochlear place, and this may vary largely as a result of reduced frequency selectivity at 4 kHz or even small (undetectable) middle-ear losses.

FIG. 5.

Inferred I/O curves (filled diamonds) for all listeners and frequencies. Each panel shows data for one test frequency and one listener. Panels are roughly ordered for increasing hearing loss from left to right and increasing frequency from top to bottom. Hearing loss (in decibels), and test frequency are shown after the listener’s identifier at the top of each panel. The letter “v” indicates that the I/O curve was obtained using the variant (as opposed to the standard) TMC method. Gray circles and associated error bars depict compression thresholds and their fifth percentiles, respectively. Continous lines illustrate function fits to the data (see text for details). Dotted lines illustrate linear responses (slope of 1 dB/dB) with zero gain. Dashed and dashed-dotted lines illustrate NH reference I/O curves for 0.5, 1, and 4 kHz as shown by the legend in A (data from Johannesen and Lopez-Poveda 2008; Lopez-Poveda and Johannesen 2009). Note that only one of these three reference lines is shown in each panel. Gray squares and associated error bars illustrate NH median compression thresholds and their 95th percentiles, respectively.

Many of the HI I/O curves approached linearity at low input levels and were compressive (slope < 1 dB/dB) at moderate input levels. More rarely, I/O curves approached linearity also at very high input levels (e.g., Fig. 5M). This two- or three-segment shape was common of I/O curves for frequency regions with low or moderately low hearing losses. For regions with higher losses (i.e., right-most panels), by contrast, I/O curves sometimes became almost linear (e.g., Figs. 5J, W). In summary, for a given frequency region (i.e., for each row in Fig. 5), the overall trend was for the low-level linear segment of the I/O curves to shift to the right of the NH reference I/O curves in direct proportion to the amount of hearing loss (i.e., the shift increased when going from left to right in Fig. 5). This is consistent with a greater reduction of maximum cochlear gain with increasing hearing loss reported by earlier studies (e.g., Jepsen and Dau 2011; Plack et al. 2004).

Compression Thresholds

Test frequencies were different for HI (0.5, 0.75, 1, 1.5, 2, 3, 4, and 6 kHz) and for NH listeners (0.5, 1, 2, 4, and 6 kHz). This made it impossible to infer HL_OHC from direct comparisons of the compression thresholds at matching frequencies. To facilitate such comparisons, data were clustered as belonging to three frequency regions: low-frequency, which included data at 500 Hz; mid-frequencies (∼1 kHz), which included data for test frequencies between 0.75 and 1.5 kHz; and high frequencies (∼4 kHz), which included data for test frequencies ≥2 kHz.

A compression threshold could be obtained in 23 out of the 30 I/O curves available for NH listeners (Table 2). The Monte Carlo-simulated compression threshold distributions for these individual cases were combined to obtain a global NH reference distribution. Table 2 gives relevant percentiles of the resulting global distribution for each frequency region. Median compression threshold values and their corresponding 95th percentiles (K₅₀ and K₉₅ in Table 2) are depicted as gray squares and associated error bars in Figure 5. Note that the present compression thresholds estimates differ slightly from those in Figure 10 of Johannesen and Lopez-Poveda (2008), where most of the present NH TMCs were originally published. Several reasons explain the slight differences. First, the present values are based on a re-analysis of the original TMCs using different fitting functions. Second, the present mean values were calculated including some additional TMCs published by Lopez-Poveda and Johannesen (2009). Third, the I/O slope criterion for compression threshold is different here (0.5 dB/dB) than that in the study of Johannesen and Lopez-Poveda (2008) (0.4 dB/dB). Lastly, here the average rather than the minimum compression exponent was used.

TABLE 2.

Reference values and distributions for NH listeners

kHz	N (M)		Compression threshold percentiles					Gain loss percentiles
			K5	K25	K50	K75	K95	ΔG5	ΔG25	ΔG50	ΔG75	ΔG95	c
0.5	7 (9)	3.1	33.8	41.9	48.5	54.2	58.7	−6.9	−2.8	0	3.0	7.9	0.26
1	5 (9)	8.0	31.9	35.8	39.2	44.2	54.8	−6.5	−2.9	0	4.2	10.7	0.25
4	11(12)	4.5	35.7	40.7	44.9	50.3	56.3	−7.3	−3.4	0	2.8	6.9	0.22

N number of cases for which a compression threshold could be measured, M number of cases available for analysis, mean absolute threshold (dB HL), K compression thresholds (dB SPL), ΔG maximum gain loss (dB) (i.e., with respect to the median compression threshold) assuming HL_TOTAL = 0 dB (subscripts 5, 25, 50, 75, and 95 denote corresponding percentiles), c mean compression exponent (dB/dB) across all NH and HI cases

A compression threshold could be obtained for 22 of the 26 HI cases. Their values are given in Table 3 and are depicted as gray circles in Figure 5. Figure 5 also illustrates the fifth percentiles of the compression threshold distributions for those cases analyzed using standard TMC methods. There were four HI cases for which a compression threshold could not be obtained. S5 at 4 kHz was one of them. This case was excluded from the analysis because the I/O curve (Fig. 5R) was regarded as unreliable; specifically, its low-level “linear” segment was supported by a single data point in the TMCs (see S5 panel in Fig. 4), and this could be an artifact of the abovementioned listener’s reported difficulty in performing the task. Two other exceptions were S11 at 1 kHz (Fig. 5J) and S16 at 4 kHz (Fig. 5W). For these cases, a compression threshold could not be obtained because the slopes of these I/O curves were always greater than the compression threshold criterion (0.5 dB/dB), a result that is indicative of severe OHC dysfunction. The last exceptional case was S1 at 4 kHz (Fig. 5U). In this case, the I/O curve was compressive over the full range of input levels that could be measured (resembling the on-frequency thick gray line of Fig. 1B), and its slope was close to normal. Indeed, a compression threshold could not be measured because the slope was always less than the 0.5 dB/dB criterion. Altogether, these results suggest that this might be a case of pure IHC dysfunction.

TABLE 3.

Data and results for all HI cases

S#	Sex	Age	kHz		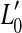K50	K5	HLTOTAL	HLIHC	HLOHC	p	Conclusion
S1	M	41	2	12	45.8	39.8	7.6	7.4	0.2	0.51	Uncertain
			4	37	n/m		32.5				IHC
S2	M	61	1.5	35	67.1	62.8	27	6.0	21.0	0.38	OHC
S3	M	67	0.75	57	85.9	82.5	49	13.7	35.3	1.00	IHC + OHC
			4	59	86.1	84.3	54.5	23.3	31.2	1.00	IHC + OHC
			6	36	62.5	59.7	31.5	18.5	13.0	1.00	IHC + OHC
S4v	M	66	1	38	68.9		30	7.6	22.4		Uncertain
			3	64	88.2		59.6	25.6	34.0		IHC + OHC
S5v	F	60	4	49	exc.		44.5
S6	F	27	2	16	47.2	37.6	11.5	10.3	1.2	0.72	Uncertain
S7	M	20	1	16	51.1	44.9	8	−0.9	8.9	0.00	OHC
S8	M	31	4	28	57.9	53.1	23.6	14.1	9.5	1.00	IHC + OHC
			6	47	84.4	77.4	42.6	12.7	29.9	0.97	IHC + OHC
S9	M	46	4	53	80.5	76.2	48.5	21.6	26.9	0.99	IHC + OHC
S10	M	23	2	15	50.5	43.6	10.6	6.8	3.8	0.40	OHC
			6	24	59.9	56.8	19.5	8.5	11.0	0.77	Uncertain
S11v	M	42	0.5	31	75.6		27.9	7.9	20.0		Uncertain
			1	45	n/m		37				OHC
S12	M	38	1	19	54.0	41.9	11	−0.1	11.1	0.17	OHC
			4	29	57.2	52.9	24.5	15.6	8.9	0.98	IHC + OHC
S13	F	59	0.5	34	63.7	54.5	30.9	18.9	12.0	1.00	IHC + OHC
S14	F	56	4	24	58.0	51.0	19.5	10.0	9.5	0.90	IHC + OHC
S15v	M	57	0.75	34	71.9		26	1.4	24.6		OHC
S16	M	74	4	55	n/m		50.5				IHC + OHC
S17	M	35	2	33	64.8	52.5	28.6	13.8	14.8	0.94	IHC + OHC
S18	F	51	0.5	32	70.9	66.2	28.9	11.6	17.3	0.93	IHC + OHC

S# subject number, v cases studied with the variant TMC method, 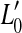absolute threshold (dB HL), K₅ and K₅₀ 5th and 50th percentiles of the compression threshold (dB SPL), respectively, HL_TOTAL, hearing loss relative to the mean of the NH cases (i.e., 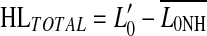), p probability that HL_IHC was significant and repeatable, n/m not measurable, exc. excluded

Estimates of the Relative Degree of OHC and IHC Dysfunction

Equation (2) was used to estimate the maximum gain loss for all NH and HI cases. Separate calculations were carried out for each of the three frequency regions considered in the analysis. 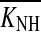was set equal to the median of the global compression thresholds distribution for all NH cases (K₅₀ in Table 2). The compression exponent, c, was found uncorrelated with absolute threshold (not shown), a result that is consistent with earlier studies (e.g., Jepsen and Dau 2011; Plack et al. 2004) and further supported the model depicted in Figure 1. Therefore, c was set equal to the mean value for all NH and HI cases (given in Table 2). Note that K_HI actually was a distribution for those cases for which Monte Carlo-simulated compression threshold distributions were available (see Methods). Therefore, for those cases, Eq. (2) was used to obtain a distribution of gain loss estimates, which was used to assess the repeatability of the results (see below).

HL_IHC was obtained as the difference between HL_TOTAL and gain loss (Eq. 1). It is important to note that HL_TOTAL was expressed with respect to the mean absolute threshold of the present NH group (shown in Table 2), which differed from 0 dB HL. In other words, our NH group did not have normal hearing according to ANSI (2004). The reason is unknown. Maybe the stimuli or the methods employed here for estimating absolute thresholds differed from those used to set the ANSI (2004) values or our NH group was not fully representative of the NH population. Indeed, the age range of our NH listeners (20–39 years) exceeded the 18–30 year range specified by ANSI (2004).

The resulting gain loss (HL_OHC) and HL_IHC estimates are given in Table 3 (the median HL_OHC is given for those cases for which Monte Carlo simulations were obtained). Note that the two values add up to HL_TOTAL. HL_IHC and HL_OHC were very small (<2 dB) for only three and two of the 22 HI cases, respectively, suggesting that pure OHC or IHC dysfunction was rare. The remaining 17 cases were consistent with mixed IHC and OHC dysfunction. Monte Carlo simulations suggested, however, that compression threshold, and so gain loss, fluctuated idiosyncratically for all NH and HI cases as a result of the variability in TMC masker levels. Therefore, a more rigorous statistical analysis was carried out to assess the significance and precision (reproducibility) of the HL_OHC and HL_IHC estimates given in Table 3.

Figure 6 illustrates the nature of the analysis by plotting individualized absolute threshold in decibel HL against cochlear gain loss. Each panel illustrates the results for a different frequency region, as indicated at the top. Open and filled symbols illustrate results for all NH and HI cases, respectively, for whom a compression threshold could be measured. Triangles depict results inferred using the variant TMC method. Compact boxplots are for cases analyzed with the standard TMC method and illustrate gain loss distributions with circles depicting median values; boxes and whiskers are shown only when their sizes were larger than the corresponding circle. The horizontal dotted lines at 15 dB HL show the criterion boundary between normal and impaired hearing. [Note that the filled symbol under the dotted line in Figure 6C is for a HI listener (S1) with a normal absolute threshold at 2 kHz.] The solid diagonal line in each panel of Figure 6 illustrates the condition where hearing loss equals gain loss. Assuming that the latter is caused solely by OHC dysfunction, cases that fall along the diagonal would be interpreted to suffer from pure OHC dysfunction. The diagonal lines were based on the present NH cases, and so they are vertically displaced by the mean absolute threshold of the NH cases. The thick vertical line illustrates cases with no gain loss but some hearing loss. Based on the present definitions of HL_OHC and HL_IHC, it depicts a condition of pure IHC dysfunction. Finally, the shaded area represents the possible range of cases where hearing loss exceeds the 95 % confident interval of gain loss (illustrated by the dashed diagonal lines discussed below). Therefore, cases that fall into this region are interpreted to suffer from mixed IHC and OHC dysfunction.

FIG. 6.

Absolute thresholds for NH (open symbols) and HI (filled symbols) listeners as a function of the distribution of cochlear gain loss (or HL_OHC) estimates. The latter are shown as compact boxplots with circles illustrating median values and thick and thin lines illustrating 50 and 99 % ranges, respectively. Boxplot distributions are only shown when they are greater than the corresponding symbol. Triangles are for cases for whom gain loss was inferred using the variant TMC method and so they are not accompanied by boxplot distributions. Each panel illustrates the results for a different test frequency range, as indicated at the top. The horizontal dotted line at 15 dB HL illustrates the boundary between normal and impaired hearing. The thick vertical line illustrates a presumed condition of pure IHC dysfunction. The solid diagonal line and its two parallel short-dashed lines illustrate a presumed condition of pure OHC dysfunction with 95 % confidence interval, respectively, based on data for the NH cases. The shaded area illustrates presumed conditions of mixed IHC and OHC dysfunction.

Figure 6 shows that median gain losses were not exactly zero for several NH cases. While seemingly paradoxical, this result was not surprising considering that gain loss increases with increasing absolute threshold and that absolute threshold was not zero for the NH cases (Fig. 6). Indeed, median gain loss was highly correlated with absolute threshold [r > 0.84 (p < 0.05) for each and every one of the three frequency regions after removing the outlier data point at 1 kHz at ∼0 dB HL]. Gain losses, however, varied across the NH cases even after allowing for individual differences in absolute threshold. Assuming that absolute threshold occurred for identical BM responses across our NH cases, such variability was used to set the significance criterion for pure OHC dysfunction. Absolute threshold was subtracted from the individual gain loss distributions of the NH cases and the results combined to obtain a reference distribution of gain loss for an absolute threshold of 0 dB HL. Such a distribution encompassed within- and across-case variability. Its relevant percentiles are given in Table 2. By adding an individual’s absolute threshold (in decibel HL) to the 5th and 95th percentiles, the critical values for pure OHC dysfunction (at 95 % significance level, single-tailed test) were obtained. These are illustrated by the two parallel dashed diagonal lines in Figure 6. Any value within the shaded area and outside the interval of pure OHC dysfunction was regarded as indicative of statistically significant IHC dysfunction.

Let us first analyze the results for the 18 HI cases for which Monte Carlo simulations were obtained. For some of these cases, individual gain loss distributions fully fell inside or outside the 95 % confidence interval of pure OHC dysfunction. For other cases, however, individual gain loss distributions partially overlapped with the 95 % confidence interval of pure OHC dysfunction. The p values in Table 3 give the proportion of each gain loss distribution (each boxplot) that fell outside the area of pure OHC dysfunction. [Note that (1 − p) would give the proportion of each distribution that fell inside the 95 % confidence interval of pure OHC dysfunction.] The type of dysfunction was classified using those p values according to the following criteria:

• p ≥ 0.9 means that more than 90 % of the gain loss estimates would be indicative of significant IHC dysfunction and hence was defined as the statistical criterion for significant IHC dysfunction. The relevant cases were regarded as indicative of pure IHC dysfunction or mixed dysfunction depending on the relative proportion of HL_IHC and HL_OHC.

• p ≤ 0.5 means that more than 50 % of the individual gain loss estimates would be indicative of pure OHC dysfunction. Therefore, this was set as the statistical criterion for pure OHC dysfunction.

• 0.5 < p < 0.9 means that more than 50 % but <90 % of the individual gain loss estimates would be indicative of significant IHC dysfunction. In other words, estimates would typically but not consistently reflect statistically significant IHC dysfunction. These cases were classified as uncertain.

According to these criteria, of the 18 HI cases shown in Table 3 for which p values were obtained, four of them were indicative of significant and repeatable pure OHC dysfunction; 11 cases were indicative of significant and repeatable IHC dysfunction, none of which was indicative of pure IHC dysfunction; and the three remaining cases were uncertain.

The Monte Carlo statistical analysis was not carried out for the four cases analyzed with the variant TMC method (denoted as “v” in Table 3 and triangles in Fig. 6). Assuming, however, that variability was comparable for the variant and the standard TMC methods, one of the four cases would be consistent with significant mixed dysfunction (triangle in Fig. 6C), one would be consistent with pure OHC dysfunction (triangle next to the diagonal in Fig. 6B), and two would be typically consistent with mixed dysfunction but were classified as uncertain (triangles on the dashed lines of Fig. 6A and B).

It is noteworthy that Figure 6 only illustrates cases for which a compression threshold could be measured, something unlikely for cases with severe pure IHC dysfunction or severe (or total) OHC dysfunction (Fig. 1D). Recall that there were indeed three (out 26 HI cases) for which it was not possible to obtain a compression threshold (described in the preceding section). One of them was indicative of severe pure IHC dysfunction (Fig. 5U), and two were indicative of severe OHC dysfunction (Figs. 5J and W). For the latter, gain loss was roughly estimated as the horizontal shift of the nearly linear I/O curve and the compression threshold for NH listeners. The I/O curve was extrapolated if necessary. For one case (S11 at 1 kHz, Fig. 5J), such distance was approximately equal to HL_TOTAL (38 vs. 37 dB), which was indicative of pure severe OHC dysfunction. For the other case (S16 at 4 kHz, Fig. 5W), HL_TOTAL was significantly greater (50.5 dB) than the estimated gain loss (30 dB), which was indicative of severe OHC dysfunction mixed with additional IHC dysfunction. These conclusions are shown in Table 3.

In summary, of the 26 I/O curves obtained behaviorally for 18 HI listeners, six were indicative of pure OHC dysfunction (or mixed with mild, non-significant IHC dysfunction), 13 were indicative of mixed IHC and OHC dysfunction, 1 could be indicative of pure IHC dysfunction, 5 were typically but not consistently indicative of mixed dysfunction, and 1 was excluded from further analysis.

Dependence of HL_IHC and HL_OHC on Absolute Threshold

The relationship of HL_OHC and HL_IHC with absolute threshold is shown in Figure 7A and B, respectively. Data are shown for the NH and HI groups. Clearly, HL_OHC and HL_IHC increased on average with increasing absolute threshold. The trends were reasonably well described by the following linear regression equations:

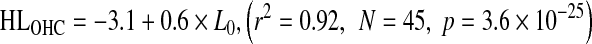3

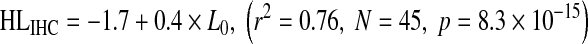4

where HL_OHC and HL_IHC are in decibels, L₀ is the absolute threshold in decibel HL, N is the number of data points, r² is the variance predicted by the regression functions, and p is the probability of this result occurring by chance.

FIG. 7.

A Correlation between HL_OHC and absolute threshold. B Correlation between HL_IHC and absolute threshold. C Correlation between HL_IHC and HL_OHC dysfunction. Filled and open symbols illustrate results for NH and HI listeners, respectively. Different symbols illustrate results for different test frequencies, as indicated by the legend in A.

Equations (3) and (4) suggest that, on average, HL_OHC and HL_IHC amount to 60 and 40 % of the hearing loss, respectively. The vertical offsets reflect that the NH group did not have mean hearing loss of 0 dB HL, as discussed above. Note, however, that there is significant individual variability around the regression lines and hence that the above average percentages do not hold individually, as will be shown in the next section.

Figure 7C shows that HL_IHC increased with increasing HL_OHC and that the trend can be described as:

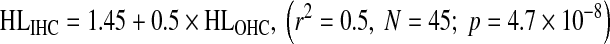5

This shows that HL_IHC and HL_OHC are rather poorly correlated. Therefore, for any given case, it is not possible to calculate one from the other unless the total hearing loss is known.

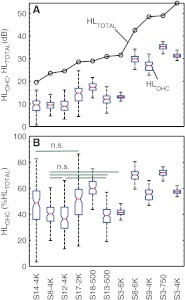
Variability in the Percentage of HL_OHC and HL_IHC

Figure 8 shows the distributions of HL_OHC estimates, expressed both in decibels (Fig. 8A) and as percent of HL_TOTAL (Fig. 8B), for the 11 cases with mixed loss analyzed using the standard TMC method (Table 3). Cases are ordered for increasing HL_TOTAL from left to right. As expected from the “population” trends described in the preceding section, HL_OHC (in decibels) tended to increase with increasing HL_TOTAL also for this case group (Fig. 8A). Strikingly, however, the percent of HL_OHC was not constant across cases (Fig. 8B). Median values ranged from 36.4 % (S12 at 4 kHz) to 72 % (S3 at 750 Hz) with an average value of 52 %. Except for the case pairs illustrated with horizontal bars in Figure 8B, all other pairwise comparisons of percent HL_OHC revealed statistically significant differences across cases (two-sided, Wilcoxon rank sum test, p < 0.05). This demonstrates that the average trends of Figure 7 do not hold individually; in other words, that HL_OHC and HL_IHC may contribute different proportions to HL_TOTAL for each case. Indeed, the proportion of HL_OHC and HL_IHC was reversed for some cases with comparable audiometric losses: compare, for instance, the percentage of HL_OHC for S13 (∼39 %) and S18 (∼60 %) at 500 Hz.

FIG. 8.

Variability of HL_OHC across the cases with mixed IHC and OHC dysfunction studied using the standard TMC method (see Table 3). Cases are identified on the abscissa by subject number and test frequency and are ordered for increasing HL_TOTAL from left to right. A Distributions of HL_OHC estimates (boxplots) and HL_TOTAL (circles), both in decibels. Red lines depict median values; blue boxes and whiskers depict 50 and 99 % ranges, respectively. B Distributions of HL_OHC estimates expressed as percent of HL_TOTAL. Pairwise comparisons revealed statistically significant differences (two-sided Wilcoxon rank sum test, p < 0.05) across all case pairs except for those pairs indicated by the horizontal lines (n.s. not significant).

Discussion

The present study aimed at estimating the relative contribution of IHC and OHC dysfunction to individualized audiometric losses. Theoretically, this may be assessed from the reduction of maximum cochlear gain and that this may be safely estimated only from the compression threshold shifts of cochlear I/O curves relative to NH references [(Eq. (2)]. This approach was applied to 26 behaviorally inferred I/O curves for 18 listeners with mild-to-moderate cochlear hearing loss. Results indicated that six of the 26 cases suffered from pure OHC dysfunction (or OHC dysfunction mixed with a non-significant IHC dysfunction component), one probably suffered from pure IHC dysfunction, and 13 suffered from statistically significant mixed IHC and OHC dysfunction. For five other cases, cochlear gain loss estimates typically (but not consistently) suggested mixed IHC and OHC dysfunction. One last case was excluded from the analysis. The incidence of each type of dysfunction is broadly consistent with that reported in recent computational modeling studies (Jepsen and Dau 2011; Jürgens et al. 2011).

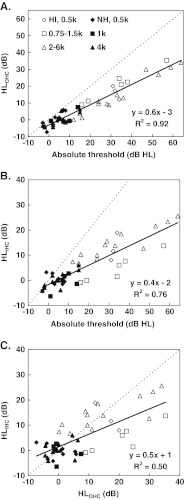
The present data also suggested that HL_OHC and HL_IHC contribute, on average, approximately 60 and 40 % to the total audiometric loss. These values are broadly in line with previously reported estimates: HL_OHC was ∼65 % of HL_TOTAL based on TMC data (Plack et al. 2004), ∼80 % based on loudness models (Moore and Glasberg 1997, 2004), and ∼66 % based on models of the effect of acoustic trauma on auditory nerve responses (Bruce et al. 2003). If anything, the present data suggest that IHC dysfunction contributes more to the audiometric loss than suggested by previous reports. Most importantly, however, the present data show that the percentages of HL_IHC and HL_OHC vary largely across cases. Indeed, in some cases, HL_IHC contributed ∼63 % to the total audiometric loss, and that two cases with comparable audiometric losses showed reversed HL_IHC and HL_OHC percentages (Fig. 8).

It is important to stress that the present study was designed to assess the functional consequences of IHC and OHC damage on audiometric loss rather than the extent of physical injury to each cell type or its physiological causes. Indeed, as it has been discussed earlier when describing Figure 1D, the proportion of the total hearing loss attributed to IHC or OHC dysfunction (HL_IHC and HL_OHC, respectively) need not reflect a corresponding proportion of physical injury to each cell type. To make that kind of inferences, one would require having regression statistics between behaviorally inferred I/O curves and anatomical (e.g., cell or stereocilia counts) data for human, which to the best of our knowledge are not available. On the other hand, estimates of functional damage may be more useful for optimizing treatment (Mills 2006) or for the design and programming of auditory models and auditory prostheses than estimates of structural damage (e.g. Bondy et al. 2004; Bruce et al. 2003; Jepsen and Dau 2011; Jürgens et al. 2011; Moore and Glasberg 1997, 2004).

On the importance of the mathematical function used to fit the I/O curves

The present results depend on the accuracy of the NH reference compression threshold, which is influenced by the selection of the function chosen to fit the derived I/O curves. In previous studies, I/O curves were typically fitted with a third order polynomial (e.g., Johannesen and Lopez-Poveda 2008, 2010; Nelson et al. 2001) or a three-section function with linear slopes for low and high input levels (e.g., Jürgens et al. 2011; Lopez-Poveda et al. 2003; Plack et al. 2004). Alternatively, TMCs were fitted with a linear-sigmoidal function from which I/O curves were inferred (e.g., Lopez-Poveda et al. 2005). These functions tend to force a compression threshold even when this is not clearly supported by the data. Specifically, the slope of a third-order polynomial is bound to be the same for values of the input variable below and above the inflection point of the polynomial. Therefore, when fitted to I/O curves, third-order polynomials may force a compression threshold when data suggest a linear segment at high input levels and a compressive segment at mid level but little or no sign of a linear segment at low levels. Something similar occurs when sigmoids are fitted to TMCs that show a steep segment for short masker-probe intervals followed by a shallower segment for longer intervals but no sign of a shallower segment for short intervals. As for three-section functions, they sometimes “force” a low-level linear segment in the I/O curve even when this is not supported by the data, which almost certainly influences the compression threshold value. The second-order Boltzmann function employed here reduces this source of bias insofar as its slopes for low and high input values are independent of each other and may differ from linearity.

On the possible bias in the behavioral NH reference compression thresholds

A compression threshold could not be obtained for four of nine NH listeners at 1 kHz (Table 2). The I/O curves in question showed a compressive segment at moderate levels but no linear segment at low input levels, which suggests that the compression thresholds were below the range of input levels that could be measured for these listeners. These missing estimates may have biased the NH reference compression threshold at 1 kHz to a value higher than the actual mean value, something that could have led to underestimating HL_OHC and overestimating HL_IHC. It is likely, however, that this bias effect was small. Assume, for example, that these listeners had a compression threshold 10 dB lower than the lowest measurable input level on their individual I/O curves. Including these arbitrarily guessed compression threshold estimates for the four listeners in question would decrease the mean compression threshold by only 1.5 dB, which would not change the main results of the above analysis. It is unlikely that the results at 0.5 and 4 kHz were affected by a similar bias because compression thresholds estimates were obtained for virtually all listeners considered at each of these two frequencies (Table 2).

On the validity of the presumed model for HI listeners

The present approach was based on the model depicted in Figure 1. This model is supported by experimental (e.g., Plack et al. 2004) as well as computational modeling (e.g., Jepsen and Dau 2011) evidence and is commonly used to interpret TMCs (e.g., Jürgens et al. 2011; Lopez-Poveda et al. 2003; Nelson et al. 2001; Plack et al. 2004). An assumption of this model is that basal BM responses to off-CF tones (which are used as linear reference TMCs) are independent of OHC dysfunction. This seems reasonable in light of existing physiological evidence (e.g., Robles and Ruggero 2001). However, an extreme situation where large portions of the OHC or IHC population are missing or physically altered might influence the mechanical properties of the cochlear partition (e.g., by altering the mass/stiffness ratio), which might, in turn, alter the passive motion of the BM. Such a situation is unaccounted for by the model of Figure 1 or the present interpretation of TMCs. The present study, however, did not include listeners with severe or profound hearing loss and so it is unlikely that the results were affected by the effect in question.

On the accuracy of the TMC methods of estimating gain loss

The accuracy of the present results depended on the validity of the assumptions of the standard and the variant TMC methods for inferring cochlear I/O curves. A critical assumption of the variant TMC method is that cochlear responses are linear over the range of probe levels considered by the method (Lopez-Poveda and Alves-Pinto 2008). This assumption likely holds true for NH listeners (Lopez-Poveda and Alves-Pinto 2008) and for listeners with pure OHC dysfunction (Fig. 1A) but may not hold for cases with significant IHC dysfunction (Figs. 1B and D). IHC dysfunction presumably increases the BM response at threshold and so can bring the internal excitation of the 9 and/or the 15 dB SL probes within the compressive region of the BM response. If this had happened for the six cases analyzed with the variant TMC method (denoted by ‘v’ in Table 3), then the internal probe excitation would have increased by <6 dB when increasing probe level from 9 to 15 dB. Therefore, the resulting behavioral I/O curves would be unreliable. For example, if identical degrees of compression had affected the probe and the masker, then the inferred I/O curves would wrongly suggest linear cochlear responses. Failure to meet the assumption in question, however, would not alter the overall conclusions of the study. Indeed, two of the six cases in question (S5 at 4 kHz and S11 at 4 kHz) were already omitted from the main analysis (Figs. 6 and 7) because a compression threshold could not be obtained. Even if the remaining four data points (triangles in Fig. 6) were also omitted from the analysis, it would have little impact on the conclusions.

As for the standard TMC method, a critical assumption is that the rate of recovery from forward masking is independent of masker frequency and masker level. This assumption is controversial, as there is evidence in support of (e.g., Lopez-Poveda and Alves-Pinto 2008) and against it (e.g., Stainsby and Moore 2006; Wojtczak and Oxenham 2010). The latter includes evidence that recovery from a high-level (92 dB SPL) linear reference masker can be slower than recovery from the equivalent on-frequency masker, and this can lead to overestimated compression by as much as a factor of two (Wojtczak and Oxenham 2010). Most of the linear reference TMCs in the present study had levels above 92 dB SPL (Fig. 3) and so, if the assumption in question did not hold, “true” cochlear I/O curves would be twice as steep as suggested by Figure 5 over the whole range of levels. This would imply that the present HL_OHC and HL_IHC estimates could be biased.

It is not possible to assess the impact of this potential bias on individual results without guessing which cases would or would not fail to meet the equal-recovery assumption. The average trend, however, may be assessed by analyzing the effects of doubling the slope of all I/O curves on the gain loss estimates. Doubling the slope of the I/O curves would double the compression exponent, c, from the present average value of 0.25 (Table 2) to 0.5 dB/dB. Hence, it would be unreasonable to maintain the present criterion slope for compression threshold, which was 0.5 dB/dB. Indeed, for consistency, it would seem reasonable to double it. As a result, individual compression thresholds would hardly change from the values reported here. (This is not unreasonable considering that the compression threshold could even be defined as the point of maximum change in the slope of the raw on-frequency TMCs). Even if they did change, though, the change would be approximately equal for the NH and HI cases, and so the compression threshold difference 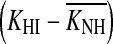[Eq. (2)] would remain roughly equal to the present values. Anyhow, HL_OHC would still change as a result of changing the compression exponent. Using Eq. (2), it is possible to show that for a constant 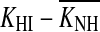doubling c from 0.25 to 0.5 dB/dB would reduce HL_OHC to two thirds of the present estimates; that is, HL_OHC would decrease from 60 to 40 % of the total hearing loss. In summary, failure of the equal-recovery-rate assumption would lead to steeper I/O curves, which in turn would lead to smaller HL_OHC and greater HL_IHC. That is, the contribution of IHC dysfunction to audiometric loss could be more significant than reported here.

A further assumption of the present approach is that it is reasonable to directly compare the I/O curves of NH and HI listeners inferred with either of the two TMC methods (as in Fig. 5). Evidence exists that noise-exposed auditory nerve fibers show slower recovery from stimulation than control fibers (Scheidt et al. 2010). Insofar as auditory nerve adaptation contributes to forward masking (e.g., Meddis and O’Mard 2005; Relkin and Turner 1988), this phenomenon could influence the slope of the TMCs. Each I/O curve, however, was inferred by “comparison” of two TMCs measured in the same HI ear. Therefore, the phenomenon in question could affect the present approach only if it had a different effect on the two TMCs to be compared. It is unlikely that this was the case for I/O curves inferred using the variant TMC method because this method involved comparing two TMCs for identical conditions except for the probe and masker level. As for the standard TMC method, the phenomenon in question could be important if it produced different recovery rates for the linear reference and the on-frequency TMC. This might be the case, for instance, if hearing loss was different across test (probe) frequencies and the recovery rate varied with hearing loss. To the best of our knowledge, there is no evidence in support of the latter. Indeed, psychoacoustical evidence suggests that recovery rates are identical when compared over matching masker levels (e.g., Table 3 in Jürgens et al. 2011; Figure 3 in Plack et al. 2004).

In summary, the accuracy of the present results depends on the validity of the assumptions of the TMC methods, some of which are controversial. Further research is necessary to verify those assumptions. Existing evidence suggests HL_IHC might actually be more frequent and/or significant than reported here.