Improved Electrically Evoked Auditory Steady-State Response Thresholds in Humans

Abstract

Electrically evoked auditory steady-state responses (EASSRs) are EEG potentials in response to periodic electrical stimuli presented through a cochlear implant. For low-rate pulse trains in the 40-Hz range, electrophysiological thresholds derived from response amplitude growth functions correlate well with behavioral T levels at these rates. The aims of this study were: (1) to improve the correlation between electrophysiological thresholds and behavioral T levels at 900 pps by using amplitude-modulated (AM) and pulse-width-modulated (PWM) high-rate pulse trains, (2) to develop and evaluate the performance of a new statistical method for response detection which is robust in the presence of stimulus artifacts, and (3) to assess the ability of this statistical method to determine reliable electrophysiological thresholds without any stimulus artifact removal. For six users of a Nucleus cochlear implant and a total of 12 stimulation electrode pairs, EASSRs to symmetric biphasic bipolar pulse trains were recorded with seven scalp electrodes. Responses to six different stimuli were analyzed: two low-rate pulse trains with pulse rates in the 40-Hz range as well as two AM and two PWM high-rate pulse trains with a carrier rate of 900 pps and modulation frequencies in the 40-Hz range. Responses were measured at eight different stimulus intensities for each stimulus and stimulation electrode pair. Artifacts due to the electrical stimulation were removed from the recordings. To determine the presence of a neural response, a new statistical method based on a two-sample Hotelling T² test was used. Measurements from different recording electrodes and adjacent stimulus intensities were combined to increase statistical power. The results show that EASSRs to modulated high-rate pulse trains account for some of the temporal effects at 900 pps and result in improved electrophysiological thresholds that correlate very well with behavioral T levels at 900 pps. The proposed statistical method for response detection based on a two-sample Hotelling T² test has comparable performance to previously used one-sample tests and does not require stimulus artifacts to be removed from the EEG signal for the determination of reliable electrophysiological thresholds.

Introduction

For patients with a profound hearing loss, a cochlear implant (CI) can be used to restore a sense of hearing. Nowadays, cochlear implantation is common for very young hearing-impaired children, where implantation before the age of 1 year provides a high chance of good integration into the mainstream school system. Fitting of CIs, i. e., adjusting it to the sensitivity of the electrode–nerve interface, is difficult in such young children, as conscious feedback about the perceived loudness of the stimulation is not available, and behavior-based fitting at this age is challenging. For automatic fitting of CIs, several types of objective measures have already been evaluated, e. g., compound action potentials and electrically evoked auditory brainstem responses (EABRs). Unfortunately, both measures result in electrophysiological thresholds that do not allow the reliable prediction of behavioral T levels, which severely limits their use for automatic fitting (Cafarelli Dees et al. 2005; Miller et al. 2008).

For acoustic stimulation, auditory steady-state responses (ASSRs) can be used to predict hearing thresholds in adults (Rance et al. 1995) and infants (Rance and Rickards 2002; Luts et al. 2006; Alaerts et al. 2010), where correlations with behavioral thresholds exceed 0.95. ASSRs are stationary responses to repeated stimuli such as clicks (Galambos et al. 1981), tone-bursts (Stapells et al. 1984), amplitude, or frequency-modulated sine tones and beats (Hall 1979; Picton et al. 2003) or modulated noise (Purcell et al. 2004). Response amplitudes in awake adults are the largest around 40 Hz, where responses can be modeled as the superposition of middle latency responses (MLRs) and auditory brainstem responses (ABRs) (Galambos et al. 1981; Bohórquez and Özdamar 2008), but responses can also be easily detected for other modulation frequencies, e. g., in the 20 and 80-Hz range (Cohen et al. 1991). A thorough review of ASSRs can be found in Picton (2010).

ASSRs can also be evoked by electrical stimulation. In guinea pigs, stationary responses to direct electrical stimulation with sinusoidally amplitude-modulated stimuli can be measured that exhibit response characteristics similar to those of acoustically evoked responses (Jeng et al. 2007, 2008). In CI users, electrically evoked auditory steady-state responses (EASSRs) can be evoked by unmodulated low-rate pulse trains (Hofmann and Wouters 2010). Response properties in the 40 and 80-Hz range are similar to those of acoustically evoked responses, and electrophysiological thresholds derived from amplitude growth functions for pulse trains in the 40-Hz range have a very high correlation with behavioral T levels for 40 pps.

Although the results presented in Hofmann and Wouters (2010) are encouraging, the implementation of an automatic fitting procedure for CIs in young children based on EASSRs still poses a number of methodological challenges: (1) the correlation between electrophysiological thresholds and behavioral T levels at clinically used pulse rates such as 900 pps is too low, (2) the used statistical methods for response detection are sensitive to any residual stimulus artifacts potentially resulting in erroneously detected responses, (3) the used response detection methods require the removal of stimulus artifacts as they cannot distinguish between neural response and stimulus artifacts, and (4) responses have mostly been recorded to bipolar stimulation, while, in clinical practice, most CIs are fit in monopolar mode.

The objectives of the present study were (1) to improve the correlation between electrophysiological thresholds and behavioral T levels at 900 pps by using modulated high-rate pulse trains that should account for some of the temporal effects such as neural refractoriness, adaptation, and summation, (2) to develop and evaluate the performance of a new statistical method for response detection which is robust in the presence of residual stimulus artifacts after artifact removal, and (3) to assess the ability of this statistical method to determine reliable electrophysiological thresholds even without any stimulus artifact removal at all.

Materials and methods

Subjects

The same six subjects as in Hofmann and Wouters (2010) took part in the experiments (Table 1). They were taking part voluntarily and signed an informed consent form. All experiments were approved by the medical ethics committee of the University Hospitals Leuven (approval number B32220072234).

TABLE 1.

List of subjects tested

Subject	Sex	Sex age	Experience	Deafness	Implant	Side	Etiology	Electrode pairs
S1	M	57	8	32	CI24R(CS)	R	Progressive	7/3	21/17
S2	M	37	10	<2	CI24R(CS)	R	Unknown	7/2	13/ 8
S3	M	42	15	<2	CI24R(CS)	R	Unknown	14/9	20/15
S4	M	62	6	<2	CI24M	L	Progressive	9/4	15/10
S5	F	53	14	6	CI24R(CS)	R	Unknown	10/5	21/16
S6	M	61	12	<2	CI24R(CS)	L	Congenital progressive	9/4	21/16

Sex: M male, F female; side of implantation: R right, L left

Age and experience with CI: at the time of testing (in years); deafness: duration of profound deafness before implantation (in years); implant: cochlear nucleus implant type; electrode pairs: active and reference stimulation electrodes

Experimental setup

A similar seven-channel stimulation and recording setup as in Hofmann and Wouters (2010) was used. The recording electrode placement was slightly modified by moving the two active electrodes located on the left and right forehead (F₇ and F₈) to the central contour left and right of the vertex (C₅ and C₆).

Stimulus construction

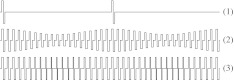
The electrical stimuli were trains of symmetric biphasic pulses with an interphase gap of 8 μs. Three different stimulus types have been used (Fig. 1): (1) unmodulated low-rate pulse trains with a constant phase width of 40 μs and a constant amplitude, (2) amplitude-modulated (AM) high-rate pulse trains with a carrier rate of 900 pps and a constant phase width of 40 μs, and (3) phase-width-modulated (PWM) high-rate pulse trains with a carrier rate of 900 pps and a constant amplitude. The amplitude of the AM high-rate pulse trains was modulated sinusoidally in current units (cu) between the behavioral T level of the subject for a constant-amplitude high-rate pulse train at the same carrier pulse rate and the desired stimulus intensity. The phase width of the PWM high-rate pulse trains was modulated sinusoidally between 25 and 40 μs. In the following, the term modulation frequency is also used for the pulse rate of low-rate pulse trains. The desired modulation frequency and carrier pulse rate were rounded to a multiple of the recording epoch rate of 2.93 Hz. Power-up pulses were inserted between the stimulus pulses if the time between pulses was longer than the maximum period possible for the implant, i. e., 13 ms for Cochlear Nucleus implants. Multiple epochs were grouped into stimulation sweeps of 64 epochs, after which stimulus polarity was inverted to account for the slow-delay component of the electrical artifacts (Hofmann and Wouters 2010).

FIG. 1.

Stimulus types used in the described experiments: (1) unmodulated low-rate pulse trains with constant phase width and amplitude, (2) AM high-rate pulse trains with constant phase width, and (3) PWM high-rate pulse trains with constant amplitude.

For each subject, the same two bipolar BP+3 or BP+4 stimulation electrode pairs as in Hofmann and Wouters (2010) were selected (Table 1). For each of these stimulation electrode pairs, the behavioral dynamic range (BDR) was determined for unmodulated pulse trains with a phase width of 40 μs at 40 and 900 pps as well as for the AM or PWM high-rate pulse trains. The behavioral threshold (T level) and comfort levels (C level) were chosen as the stimulus intensities between inaudible and very soft and between good and loud on a loudness scale of inaudible, very soft, soft, good, loud, very loud, and intolerable, respectively.

Stimulus and recording artifacts

EASSR recordings are contaminated with artifacts from the electrical stimulus pulses, radio frequency (RF) transmission, and muscle movements. Unless removed, these artifacts could cause the erroneous detection of neural responses with one-sample tests (see below) and could distort response properties such as shape, amplitude, and phase. A comprehensive discussion of artifact sources related to the electrical stimulation can be found in Hofmann and Wouters (2010).

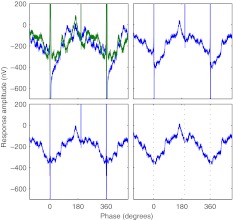
Based on the artifact removal procedure described in Hofmann and Wouters (2010), artifacts introduced by the stimulus pulses and RF transmission were removed in three steps (Fig. 2). In the first step, sweeps of alternating pulse polarity were averaged. This resulted in the removal of the slow-decay component of the stimulus artifacts and a reduction in peak stimulus artifact amplitude (Hofmann and Wouters 2010).

FIG. 2.

Example of stimulus artifacts removal. Response amplitude as a function of time for subject S6, active stimulation electrode 9, BP + 4, low-rate pulse train at C level, modulation frequency 44 Hz, recording electrode P3, averaged period plotted two times for clarity; artifacts of stimulus and power-up pulses can be seen at 0°, 198°, and 360°. Top left: raw recorded responses to cathodic-first (blue) and anodic-first (green) stimulus polarities. Top right: average of both stimulus polarities. Bottom left: inversely filtered average. Bottom right: filtered average with stimulus interpolation; dotted lines: positions of stimulus and power-up pulses.

In the second step, the distortions of the EEG signal introduced by the recording setup were compensated. The stimulus artifacts are superimposed on the neural response and occur synchronously with the stimulus and power-up pulses. With Cochlear Nucleus implants, RF transmission coincides with the stimulus and power-up pulses and is switched off in between. These artifacts are strictly time-limited to the first several hundred microseconds after such a pulse and may contain a DC offset from the RF transmission especially for electrodes close to the transcutaneous inductive RF link and from slight asymmetries of the stimulus pulses. During a recording, the recorded signal is modified by the filters in the medical amplifier and RME sound card used for recording. Besides filtering of the neural response and protecting the amplifier from saturation, these filters also distort the stimulus artifacts. In our specific setup, the combination of both filters corresponded to a fourth-order Butterworth filter with high-pass characteristics. As this filter removed the DC component from the recorded signal, electrodes with artifacts containing a high DC offset were most affected, resulting in artifacts of significantly longer duration.

To compensate for this distortion, an inverse filter constructed from the filter coefficients of the recording setup was used to restore the original signal before filtering. For the RME sound card, the filter coefficients were determined with the help of a digital function generator Fluke PM5138A. The function generator was set up to generate a sine wave in single burst mode in response to an external trigger pulse. The output of the function generator and the trigger signal were recorded with the RME sound card. With custom software, the recorded function generator output was referenced relative to the onset of the trigger pulse, averaged over multiple cycles, and transformed to the frequency domain. For stimulation frequencies between 0.01 and 1 kHz, the transfer function of the filter in the RME sound card was sampled from the frequency bins corresponding to the stimulation frequencies. A third-order Butterworth low-pass filter model was fit to the data to determine the filter coefficients. In the last step, the remaining strictly time-limited stimulus artifacts were removed by the approximation of the neural responses during the artifact duration (Hofmann and Wouters 2010).

Additionally, epochs with artifacts caused by muscle movements were removed from the analysis. Recording artifact rejection levels were adjusted in a way that about 5% of the recorded epochs were rejected. Rejection was based on the peak-to-peak amplitudes after the processing steps described above. Epochs were rejected synchronously across all recording electrodes so that the covariance of the EEG between recording electrodes was not affected. Only recording electrodes actually used in the further analysis were considered for recording artifact rejection.

EEG analysis

After the removal of stimulus and recording artifacts, a fast Fourier transform (FFT) was used to calculate the complex frequency spectrum separately for each epoch, with a resulting frequency resolution of 2.93 Hz. For each epoch, the response amplitude and phase were obtained from the complex frequency bin corresponding to the modulation frequency. The mean response amplitude and phase were calculated by vector-averaging of the response bins of the individual epochs.

To determine the significance of a response, a two-sample Hotelling T² test was used on multiple measurements with different modulation frequencies to compare the response bins for the same recording electrode and stimulus intensity. To increase statistical power, response bins for multiple recording electrodes and measurements were combined and checked with a modified two-sample Hotelling T² test as described below. Additionally, a one-sample Hotelling T² test was employed to check for the influence of stimulus artifacts on the response detection. A significance level of p < 0.05 was used for all tests.

Apparent latency (group delay) was used to determine the delay introduced by the auditory system (John and Picton 2000). The phase value of the mean response as obtained from the FFT had the initial phase of the stimulus subtracted and was then negated to obtain phase delay. Apparent latency was determined from the regression of phase delay versus modulation frequency by dividing the slope of the regression line by 2π.

Response detection

One-sample tests

To detect stationary EEG activity synchronous with the stimulation, different methods are available (Picton et al. 2003). All of these methods are based on a comparison of the assumed response, the signal, with the spontaneous EEG activity not linked to the stimulation, the noise. Stationary neural responses can be detected in the time, spectral, and complex domains. Time domain techniques and spectral domain techniques are both based on time-domain averaging together with statistical tests to determine the presence of a stationary neural response. For the spectral domain, an F-test can be used on the averaged response to compare the FFT response bin corresponding to the modulation frequency with the noise level calculated from adjacent frequency bins.

For the complex domain, the recorded signal is divided into epochs which contain an integer number of modulation cycles, and each epoch is transformed to the frequency domain. Several different one-sample tests are then available that try to reject the null hypothesis that the complex response bins corresponding to the modulation frequency contain only spontaneous EEG activity (Dobie and Wilson 1996). The magnitude squared coherence (MSC) statistic compares the power of the average response bin to the average power of the individual response bins. The phase coherence statistic only considers the phase of the response bins and is essentially a variant of MSC with equal amplitudes. The one-sample Hotelling T² test compares the average real and imaginary components of the response bin against the variation of the same response bin across epochs. When real and imaginary response components are assumed to have the same variance, this test is called the circular T² test and is equivalent to the MSC statistic. All of these different tests have about the same statistical power and can be used interchangeably (Dobie and Wilson 1996).

Problems with one-sample tests in the frequency and complex domains

For analysis of EASSRs in the frequency and complex domains, any residual artifacts after stimulus artifact removal will also contain a component that will appear in the frequency bin corresponding to the modulation frequency (Wilson and Ghassemlooy 1993) and that may be erroneously interpreted as a neural response by one-sample tests. This problem is more prominent in the present experiments with modulated high-rate pulse trains by two factors: (1) the high-rate pulse trains introduce about ten times more stimulus artifacts into the recording than the low-rate pulse trains used in Hofmann and Wouters (2010), and (2) for threshold detection with such stimuli, response amplitudes are expected to be close to noise level and are therefore excessively affected by any residual stimulus artifacts. As long as one cannot be sure that the stimulus artifacts are completely removed from the recordings, one-sample tests that only check for the existence of a response will only be of limited use for stimulation with modulated high-rate pulse trains as these tests are unable to distinguish between any left-over stimulus artifacts and the potential neural response.

Two-sample tests

One way to distinguish between stimulus artifacts and neural responses is to evaluate the behavior of both with changing modulation frequency.

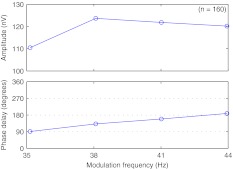
For unmodulated low-rate pulse trains in the 40-Hz range, the neural response amplitudes and phase delays for different modulation frequencies are shown in Figure 3. Neural response amplitudes are similar from 35 to 45 Hz, with a peak around 38 to 41 Hz and only minor attenuation for lower and higher modulation frequencies. Response phase delay changes linearly with modulation frequency, which is caused by the constant latency of the evoked neural response per frequency range (Picton et al. 2003).

FIG. 3.

EASSR median amplitude and phase delay for unmodulated low-rate pulse trains. Five subjects, stimulation at 75% BDR, reference electrode CZ, active electrodes contralateral mastoid (TP9 or TP10), and back of the head (P3, OZ, and P4). Analysis of data from Hofmann and Wouters (2010).

The stimulus artifacts are primarily caused by the electrical stimulus pulses. Both the artifacts of unmodulated low-rate pulse trains and AM or PWM high-rate pulse trains have a frequency component at the modulation frequency (Wilson and Ghassemlooy 1993). For AM or PWM high-rate pulse trains, the amplitude and phase of this frequency component are independent of modulation frequency, with an amplitude that depends only on modulation index and a phase that depends only on the initial phase of the stimulus. Stimulus artifacts would therefore have a phase delay of 0°, or, if the artifact source was sampled with reverse polarity, 180°.

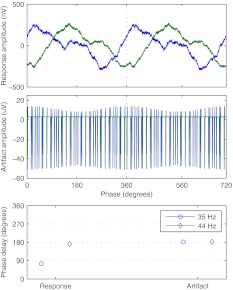
An example for PWM high-rate pulse trains can be seen in Figure 4. For modulation frequencies of 35 and 44 Hz, phase delays of the neural responses differ by about 100°, while they are the same for the stimulus artifacts independent of modulation frequency.

FIG. 4.

Example of neural response and stimulus artifacts for different modulation frequencies. Subject S2, active stimulation electrode 13, BP + 4, recording electrode TP9, PWM high-rate pulse train at C level; top: time-domain signal of the neural response; middle: time-domain signal of the stimulus artifacts; bottom: phase delay for both neural response and stimulus artifacts.

To use the phase dependency on modulation frequency for response detection, two measurements with different modulation frequencies are required for each stimulus condition. Additionally, statistical tests that are able to compare two responses need to be employed. For two measurements with different modulation frequencies but otherwise equal stimulation parameters, the test needs to detect response bin phase changes with modulation frequency, or more generally, that the response bin is not the same for the two modulation frequencies. Suitable tests for this task are two-sample tests which try to reject the null hypothesis that the response bins are the same independent of modulation frequency. For the experiments described here, a two-sample variant of the Hotelling T² test as detailed in Appendix A was used which compares the difference of two response bins against the variation of the same response bins across epochs.

One-sample Hotelling T² test

A one-sample Hotelling T² test was used additionally to the two-sample Hotelling T² test to check for the influence of any residual stimulus artifacts. To achieve a similar statistical power as with the two-sample Hotelling T² test, responses at different modulation frequencies were combined into one sample set by compensating for the phase difference between them. The mean response phase difference between modulation frequencies for one subject, stimulation electrode pair, and stimulus type was determined to be the average of all phase differences of the significant responses across all intensities with significance determined by the two-sample Hotelling T² test.

Increasing statistical power

The Hotelling T² test is a generalization of Student’s t statistic, which basically compares the mean 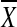and the standard error SE:

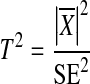As the standard error is inversely proportional to the square root of the sample set size, a larger sample set size will lead to increased statistical power. Such an increase can also be achieved by the combination of information from different sample sets, e. g., from multiple recording electrodes or from multiple measurements, as long as the sample sets have the same expected mean. Increasing statistical power is also possible by including additional degrees of freedom by combining sample sets with different expected means, e. g., from multiple frequency bins corresponding to harmonics of the modulation frequency.

For the experiments described here, two different kinds of sample sets were combined: sample sets from multiple recording electrodes of the same measurement and sample sets from multiple measurements with different stimulus intensities.

For the combination of recording electrodes, only electrodes with reasonable response growth were used. If necessary, the polarity of the recording electrodes was corrected so that the response dipole was sampled with the same polarity from all electrodes. To account for the covariance of the EEG recorded from multiple recording electrodes at the same time, the size of an equivalent sample set consisting of independent samples was determined by Monte Carlo simulation as described in Appendix B and was used instead in the statistical tests.

To increase the sample set size even further, multiple measurements with adjacent stimulus intensities were also combined. With neural responses that exhibit linear behavior in phase and amplitude with small changes in stimulus intensity, the combination of measurements with different stimulus intensities corresponds to a linear interpolation between the individual measurements. This will result in a new virtual measurement with statistical power higher than that of the individual measurements alone.

Threshold determination

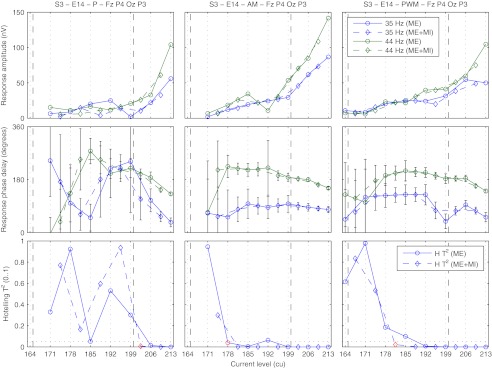
Electrophysiological thresholds were obtained using different methods by analyzing the influence of stimulus intensity on the response properties. Four different ways for the determination of thresholds from the curves of the Hotelling T² statistic against stimulus intensity were compared: with the one-sample or the two-sample Hotelling T² test as described above, and with or without stimulus artifact removal, i. e., with the length of artifact interpolation for stimulus and power-up pulses set to zero. To increase statistical power, multiple recording electrodes (ME) and multiple recording electrodes and multiple measurements with different stimulus intensities (ME + MI) were combined. For the Hotelling T² test calculated from sample sets that consisted of multiple measurements with different stimulus intensities, the effective stimulus intensity was assumed to be the mean of the individual stimulus intensities in current units. With decreasing stimulus intensity, the first two consecutive non-significant response differences on the ME + MI curve were taken as a lower limit beneath which no further analysis was done. The first significant response difference with higher stimulus intensity, on either the ME or ME + MI curve, was used as the estimated electrophysiological threshold. An example can be seen in Figure 5. This procedure ensured the reliable estimation of electrophysiological thresholds from response growth functions with very low response amplitudes even in the presence of a noisy measurement.

FIG. 5.

Example for the determination of electrophysiological thresholds from response growth functions. Subject S3, active stimulation electrode 14, BP + 4, recording electrodes FZ, P4, OZ, and P3; left, middle, right column: low-rate (P), AM, and PWM high-rate pulse trains, respectively; top, middle, bottom row: response amplitude, phase delay, and results of the Hotelling T² test for the combination of multiple recording electrodes (ME, solid lines) and multiple recording electrodes and stimulus intensities (ME + MI, dashed lines); dashed vertical lines: behavioral T levels for 900 and 40 pps; error bars: possible change in phase delay that could be introduced by the noise in the response bin based on the standard error of the response bin across epochs and recording electrodes corrected for channel covariance; dotted horizontal lines: significance level of p < 0.05; red markers: determined electrophysiological thresholds.

Additionally, as a fifth method, electrophysiological thresholds were derived from the number of significant responses per stimulus intensity. For each subject and stimulus type, bootstrapping (Wichmann and Hill 2001a,b) was used to fit a sigmoid function to the percentage of significant responses p per stimulus intensity s, with the maximum percentage of significant responses P, midpoint slope M, and midpoint intensity S.

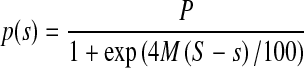The threshold was determined as the intensity at the intersection of p = 0 and the straight line through S and P/2 with slope M. Only significant responses from the recording electrodes at the contralateral mastoid and the back of the head were used for the fitting.

Experiments

EASSRs were evaluated in six subjects with each two stimulation electrode pairs selected as described in section “Stimulus construction.”

All measurements for one subject and stimulation electrode pair were done in one session to minimize the influence of external factors such as differences in state of arousal, recording electrode position, and electrode impedance between measurements. Each measurement consisted of 768 epochs of 0.34 s, resulting in a total length of 262 s. One session was formed by orthogonal measurements with two modulation frequencies, three stimulus types, and around eight stimulus intensities, resulting in a session duration of about 4 h. The six measurements with the same stimulus intensity were grouped into blocks of about 30 min. Inside each block, measurements with the same stimulus type were done consecutively to minimize the effects of external factors on the two-sample Hotelling T² test.

Measurements were conducted at modulation frequencies of 35 and 44 Hz, with the three stimulus types as described in section “Stimulus construction” and on eight evenly spaced decreasing current levels between the C level for modulated 900 pps pulse trains and below T level for unmodulated 900 pps pulse trains. To reduce total session time, measurements were omitted when at least two measurements with higher stimulus intensity did not show any responses even after the combination of multiple recording electrodes and multiple measurements with different stimulus intensities as described above. During the recording, each measurement was visually inspected for the amount of recording artifacts. In the case of more than 5% of the epochs exceeding peak-to-peak amplitudes of 100 μV, the measurement was repeated with the same parameters, and the epochs of the individual measurements were combined into one measurement. To increase the precision of the determined electrophysiological thresholds, additional measurements at intermediate stimulus intensities were performed in about 2% of the cases.

Phase delay and apparent latency

Phase delays and apparent latency were determined from the ME response growth functions used for threshold determination. The dependency of phase delay on modulation frequency was evaluated with a Wilcoxon signed rank test. A linear model was used to check whether the stimulus type or intensity would affect the latency of the responses.

Number of significant responses

For each subject and stimulation electrode pair, the percentage of significant responses per stimulus intensity and stimulus type was determined. A Wilcoxon signed rank test was used to check for differences in the percentage of significant responses across subjects between modulation frequencies per stimulus type. Finally, the detection of significant responses per recording electrode relative to all measurements with at least one significant response at C level was analyzed.

Response amplitudes

The distribution of significant response amplitudes was analyzed per recording electrode, and the median response amplitude was compared with the noise level in the FFT response frequency bin. Additionally, the response amplitudes per stimulus type at 35 Hz were compared with the ones at 44 Hz with the help of a Wilcoxon signed rank test.

Harmonic spectrum

The averaged complex spectrum across all significant responses of all subjects on all recording electrodes was determined and analyzed for differences because of modulation frequencies and stimulus type. The amplitudes of the response components at the second harmonic frequency were compared with the response components at the fundamental frequency, and the harmonic composition of the responses was evaluated by the calculation of the total harmonic distortion (THD) for the response component amplitudes at the fundamental frequency A₁ and the harmonics A₂ to A₁₀.

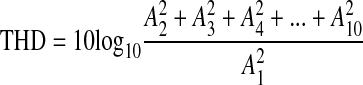THD calculation included the amplitudes of all frequency components independent of the significance of the frequency bins used.

Electrophysiological thresholds

Electrophysiological thresholds were derived from the recorded responses for the five different analysis methods as described in section “Threshold determination,” and it was evaluated whether they could determine thresholds for all recordings. For the combinations of stimulus type and analysis method that did not result in missing thresholds, the influence of analysis method and stimulus type on the electrophysiological thresholds was analyzed with a Wilcoxon signed rank test. For the different stimulus types, the correlation coefficients and mean differences between electrophysiological thresholds in current units and behavioral T levels for unmodulated pulse trains at 40 and 900 pps were calculated.

Results

Phase delay and apparent latency

The mean phase delay at 35 Hz was 81.0° (SD = 56.3°), with a significant mean increase of 131.3° to 203.2° (SD = 56.2°) for 44 Hz (p < 0.01, z = −3.1). Across all stimulus types and stimulus intensities, a mean apparent latency of 41.5 ms (SD = 10.1 ms) was obtained. No significant influence of stimulus type (p = 0.60) or stimulus intensity (p = 0.06) on apparent latency could be found.

Number of significant responses

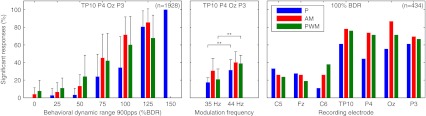
The percentage of significant responses across all subjects for different stimulus intensities, modulation frequencies, and recording electrodes can be seen in Figure 6.

FIG. 6.

Percentage of significant responses for different stimulus intensities, modulation frequencies, and recording electrodes. For subjects with a CI in the right ear, electrodes C5, P4, and TP10 were swapped with electrodes C6, P3, and TP9, respectively. Error bars denote the standard deviation across all subjects and stimulation electrode pairs. Left: bar plot for the number of significant responses measured at recording electrodes TP10, P3, OZ, and P4, grouped by stimulus intensity (n = 1,928). Middle: bar plot for the number of significant responses measured at recording electrodes TP10, P3, OZ, and P4, grouped by modulation frequency (n = 1,928). Right: bar plot for the number of significant responses grouped by recording electrode at C level (n = 434), the bars show the percentage of significant responses per electrode relative to all measurements with at least one significant response.

For recording electrodes at the contralateral mastoid and the back of the head, the left plot shows the increase in significant responses with rising stimulus intensity (n = 1,928 from six subjects on two stimulation electrode pairs, three stimulus types, two modulation frequencies, four recording electrodes, and, on average, seven stimulus intensities).

For the same recording electrodes, the middle plot shows the difference in significant responses between the two modulation frequencies. There were fewer detected responses at 35 than at 44 Hz, with a significant relative decrease in the percentage of detected responses of −38% for low-rate pulse trains (p < 0.01, z = −2.9, SE = 7.7%) and −45% for PWM high-rate pulse trains (p < 0.01, z = −2.8, SE = 9.6%). The decrease for AM high-rate pulse trains was not significant (p = 0.11, z = −1.6).

The right plot shows the percentage of significant responses per recording electrode at C level (n = 434 from six subjects on two stimulation electrode pairs, three stimulus types, two modulation frequencies, and at least one recording electrode with significant responses in about 85% of the measurements). Significant responses could be reliably obtained from electrodes at the contralateral mastoid or the back of the head (65% to 73% averaged across all stimulus types), but only in some cases from the forehead and central positions (24% to 27%).

Response amplitudes

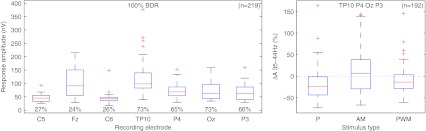
The left plot of Figure 7 shows a box plot of the mean response amplitudes to stimulation at C level per recording electrode for all subjects (n = 219 from six subjects on two stimulation electrode pairs, three stimulus types, two modulation frequencies, and seven recording electrodes; significant responses in about 45% of the measurements). Reliable responses could be obtained from the recording electrodes at the contralateral mastoid and the back of the head, with median response amplitudes of 99 nV (interquartile range (IR) = 57 nV) and 65 nV (IR = 41 nV), respectively. Noise levels at the contralateral mastoid and the back of the head were about 1,160 and 690 nV, respectively, which got reduced to 35 and 22 nV after time-domain averaging. This resulted in a median signal-to-noise ratio (SNR) of the neurological response independent of the recording electrode of about −21 dB.

FIG. 7.

Response amplitudes for different recording electrodes and modulation frequencies. For subjects with a CI in the right ear, electrodes C5, P4, and TP10 were swapped with electrodes C6, P3, and TP9, respectively. Left: box plot for the amplitudes of significant responses at C level per recording electrode for all subjects (n = 219), percentages show the number of significant responses per electrode relative to all measurements with at least one significant response. Right: box plot of the pairwise response amplitude differences between 35 and 44 Hz relative to the mean amplitude of both frequencies for different stimulation modes measured at recording electrodes TP10, P3, OZ, and P4 (n = 192).

The right plot shows the relative difference between the significant responses at 35 and 44 Hz recorded at the contralateral mastoid and the back of the head (n = 192 from six subjects on two stimulation electrode pairs, three stimulus types, and four recording electrodes; significant responses at both frequencies in about 20% of the measurements). While there was a tendency for median response amplitudes at 35 Hz to be lower than at 44 Hz, this was not significant for any stimulus type (p = 0.07, z = −1.8 for low-rate, p = 0.33, z = −1.0 for AM and p = 0.66, z = −0.44 for PWM high-rate pulse trains).

Harmonic spectrum

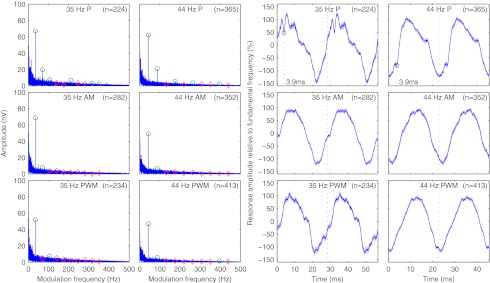
Figure 8 shows the mean response spectra and associated time domain signals for all significant responses for different modulation frequencies and stimulus types from the contralateral mastoid and the back of the head. While spectral composition did not change with modulation frequency, there were visible differences in harmonic content between responses to low-rate and modulated high-rate pulse trains. Responses to low-rate pulse trains had a richer harmonic spectrum (50% to 60% of the first ten harmonics were significant) than responses to modulated high-rate pulse trains (20% to 30%). Low-rate pulse trains caused responses with second harmonics at about −10.6 dB of the response component at the fundamental frequency for 35 Hz and about −9.4 dB for 44 Hz, resulting in THDs of −9.5 and −8.9 dB for 35 and 44 Hz, respectively. For modulated high-rate pulse trains, the second harmonics were barely significant or not significant at all at levels <−17.6 dB, resulting in THDs of <−16.8 dB.

FIG. 8.

Average frequency and time domain representation of the neurological response for different modulation frequencies and stimulus types at recording electrodes TP9, TP10, P3, OZ, and P4. Left: mean amplitude spectra; green and red markers: significance of response components at fundamental frequency and second to tenth harmonics, p < 0.05/10; frequency domain resolution, 0.046 Hz. Right: mean responses; green markers: peak electron volt of the EABR; time domain resolution, 0.083 ms.

Electrophysiological thresholds

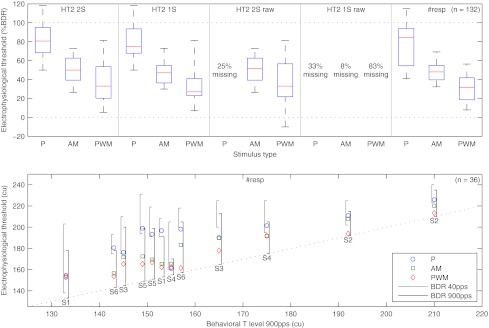
Box plots of the electrophysiological thresholds derived from the recorded responses for the five different analysis methods as described in section “Threshold determination” can be seen in the top plot of Figure 9 (n = 132, six subjects, two stimulation electrode pairs, and 11 combinations of stimulus type and analysis method that did not result in any missing electrophysiological thresholds). There was no difference between the thresholds derived from the two-sample and one-sample Hotelling T² test for all stimulus types applied to recordings with stimulus artifact removal (p = 0.15, z = −1.5), no difference between the thresholds of the two-sample Hotelling T² test for the modulated high-rate pulse trains applied to recordings either with or without stimulus artifact removal (p = 0.45, z = −0.76) and also no difference between the thresholds of the one-sample or two-sample Hotelling T² test with artifact removal and the thresholds derived from the sigmoid functions fit to the number of significant responses (p = 0.74, z = −0.33, and p = 0.29, z = −1.1, respectively). For recordings without stimulus artifact removal, it was not possible to obtain all electrophysiological thresholds from the two-sample Hotelling T² test for low-rate pulse trains (failing in 25% of the cases) and from the one-sample Hotelling T² test for all stimulus types (33%, 8%, and 83% for low-rate, AM, and PWM high-rate pulse trains, respectively).

FIG. 9.

Electrophysiological thresholds derived from response growth functions and number of significant responses. Top: box plot of electrophysiological thresholds across subjects for the five different analysis methods relative to the behavioral dynamic range at 900 pps (n = 132); HT2 2S and HT2 1S: thresholds derived from the response growth functions with a two-sample and one-sample Hotelling T² test, respectively; #resp: thresholds derived from the sigmoid functions fit to the number of significant responses; raw: thresholds derived from recordings without stimulus artifact removal; percentage missing: some electrophysiological threshold could not be determined. Bottom: individual electrophysiological thresholds derived from the sigmoid functions fit to the number of significant responses versus behavioral T levels at 900 pps (n = 36); left and right brackets: behavioral dynamic range at 40 and 900 pps, respectively; overlapping cases have been slightly shifted for clarity.

The bottom plot of Figure 9 shows the comparison of the individual electrophysiological thresholds derived from the sigmoid functions fit to the number of significant responses with the behavioral T levels at 900 pps. Thresholds for the three stimulus types were significantly different from each other (P–AM, p < 0.01, z = −2.6, and AM–PWM, p < 0.01, z = −3.0). Mean differences between electrophysiological thresholds and behavioral T levels at 900 pps were 77% BDR (SD = 25% BDR), 49% BDR (SD = 12% BDR), and 31% BDR (SD = 15% BDR) for low-rate, AM, and PWM high-rate pulse trains, respectively. When calculated in current units, these differences were 30 (SD = 13), 18 (SD = 6.1), and 12 cu (SD = 6.6 cu) for behavioral T levels at 900 pps and 3.5 (SD = 6.0), −8.0 (SD = 13), and −15 cu (SD = 15 cu) for behavioral T levels at 40 pps.

To estimate the inter-subject variability of the difference between electrophysiological thresholds and behavioral T levels, electrophysiological thresholds and behavioral T levels across the two stimulation electrode pairs were averaged per subject. With the intra-subject variability removed in this way, standard deviations of the differences between electrophysiological thresholds and behavioral T levels decreased to 12, 4.8, and 5.6 cu for behavioral T levels at 900 pps and to 4.8, 9.6, and 12 cu for behavioral T levels at 40 pps. To estimate the sensitivity of the electrophysiological thresholds to differences between behavioral T levels across stimulation electrode pairs within a subject, the inter-electrode differences between the two electrophysiological thresholds and the two behavioral T levels were calculated per subject. The differences between the electrophysiological thresholds were on average −0.8 (SD = 15), 3.2 (SD = 7.6), and 4.0 cu (SD = 6.9 cu) lower than the differences between the behavioral T levels at 900 pps and 1.5 (SD = 7.9), 5.6 (SD = 19), and 6.3 cu (SD = 21 cu) lower than the differences between the behavioral T levels at 40 pps.

Across all subjects and stimulation electrode pairs, electrophysiological thresholds for low-rate pulse trains were more correlated with behavioral T levels at 40 pps than with behavioral T levels at 900 pps (r₄₀ = 0.96 and r₉₀₀ = 0.80). This was not the case for AM (r₄₀ = 0.80 and r₉₀₀ = 0.96) or PWM high-rate pulse trains (r₄₀ = 0.72 and r₉₀₀ = 0.96), which both had higher correlations with behavioral T levels at 900 pps than the low-rate pulse trains. When calculated with the intra-subject variability removed as described above, all correlations between electrophysiological thresholds and related behavioral T levels were significant with p < 0.01. The correlation between electrophysiological thresholds for PWM high-rate pulse trains and behavioral T levels at 40 pps was not significant with p = 0.09, and the other correlations were significant with p < 0.05.

Discussion

Stimulus artifact removal

Artifacts resulting from bipolar stimulus and power-up pulses could be completely removed in all subjects and on all electrodes even at pulse rates up to 900 pps. On recording electrodes close to the RF transmission coil that exhibited recording artifacts with a high DC offset, compensation of the filtering done by the recording equipment restored the original strictly time-limited stimulus artifacts. In contrast to Hofmann and Wouters (2010) where no inverse filtering was employed, no recording electrodes had to be excluded from analysis because of non-removable excessive stimulus artifacts.

Phase delay and apparent latency

With a difference in response phase of 131.3° for the two selected modulation frequencies, response detection performance of the two-sample Hotelling T² test was comparable to the one-sample Hotelling T² test. For cases where one cannot be sure of complete artifact removal and where the use of a one-sample test is therefore not an option, the trade-off between phase difference and response amplitude should be explored further. On the one hand, selection of modulation frequencies further apart will result in larger differences in phase which could lead to better detectability of neural responses. On the other hand, this will also increase the mismatch of the underlying electrically evoked middle latency response (EMLR) spectrum and the modulation frequencies, which could lead to response attenuation.

The mean apparent latency of 41.5 (SD = 10.1 ms) is in line with Hofmann and Wouters (2010), where apparent latencies of 35.6 (SD = 5.3ms) were found for EASSRs to low-rate pulse trains between 35 to 47 pps. For acoustically evoked ASSRs to tone bursts, similar latencies of 33.3 (SD = 8.6 ms, 35 to 55 Hz), and 41.1 ms (SD = 5.7 ms, 29 to 54 Hz) were reported by Stapells et al. (1984, 1987), respectively.

Number of significant responses

EASSRs could be reliably recorded for low-rate pulse trains as well as AM and PWM high-rate pulse trains. At stimulus intensities around and above C level, no significant difference in the number of detected responses between the different stimulus types could be found. At lower stimulus intensities, relatively more responses to modulated high-rate pulse trains were detected compared with low-rate pulse trains. At C level, the percentage of significant responses at a modulation frequency of 35 Hz was significantly lower than at 44 Hz for low-rate and PWM high-rate pulse trains but not for AM high-rate pulse trains. With acoustically evoked ASSRs, maximum response amplitudes in awake adults to different stimuli such as clicks, tone bursts, or AM sine tones can be recorded at modulation frequencies around 40 Hz (Galambos et al. 1981; Stapells et al. 1984, 1987; Picton et al. 1987), but no precise frequency–amplitude relationship in this frequency range is known. For the two-sample Hotelling T² test, more research is needed to be able to select the modulation frequencies with the least attenuation. For the one-sample Hotelling T² test, modulation frequencies close to 40 Hz should provide optimal response amplitudes.

Response amplitudes

Overall, response amplitudes for AM and PWM high-rate pulse trains had a shallower response-growth function and resulted in larger response amplitudes at lower stimulus intensities than for low-rate pulse trains. This confirms the non-significant trend seen in the EMLR data of Davids et al. (2008), where response amplitudes for single pulses where slightly lower than for 2-ms pulse trains with rates between 500 and 3,600 pps. As SNRs between stationary and spontaneous EEG activity were very similar across the recording electrodes that allowed reliable response detection, each of the recording electrode sites at the contralateral mastoid or the back of the head seems to be equally suited for recording EASSRs. Nevertheless, response amplitudes were larger at the contralateral mastoid than at the back of the head, which hints at a better sampling of the dipoles in the brainstem and auditory cortex responsible for the response and should be taken into account when comparing responses across recording electrodes. Responses to stimuli at a modulation frequency of 35 Hz had a tendency to be lower in amplitude than the ones at 44 Hz, which was consistent with the results for the number of significant responses per modulation frequency.

Harmonic spectrum

Responses to low-rate pulse trains seemed to feature larger THDs than responses to modulated high-rate pulse trains, with most of the additional response energy at the second harmonic of the modulation frequency. EASSRs to low-rate pulse trains should be very similar to acoustically evoked ASSRs to click trains. They can be regarded as a superposition of repeated transient responses to the single clicks when evoked with modulation frequencies in the 40-Hz range (Bohórquez and Özdamar 2008). In this case, the spectrum of the stationary response can be explained as the product of a dirac comb with the spectrum of the transient response, i. e., it is equal to the sampling of the transient spectrum at the modulation frequency and its harmonics. Spectral analysis of MLRs shows a maximum around 40 Hz, with a smaller peak around 90 Hz corresponding to the observed second harmonic (Suzuki et al. 1983; Kavanagh and Domico 1986). Similar observations can also be made for acoustically evoked ASSRs to modulated sine tones, with a peak around 80 to 90 Hz (Picton et al. 2003). For the continuous excitation by modulated high-rate pulse trains, the resulting response spectrum was dominated by the spectrum of the periodic stimulus changes, with nearly all response energy at the modulation frequency. While there were differences in spectral composition between low-rate and modulated high-rate pulse trains, the time domain representations looked very similar, differing only in a clearly visible peak eV of the EABR that could be seen at about 3.9 ms after the onset of the stimulus pulse for low-rate pulse trains.

Increasing statistical power

The combination of multiple recording electrodes and multiple measurements with different stimulus intensities resulted in improved detection rates and increased robustness against recording artifacts. In multi-electrode recordings with 47 recording electrodes and AM stimuli in the 80-Hz range described in Picton et al. (2003), a multi-electrode F-test was not better than a single-electrode F-test on the recording electrode with the highest SNR. That result might have been specific to 80 Hz responses as they are thought to be predominantly generated by a single brainstem source with the resulting simple scalp topography. The improved detection rates in this study could also be related to the way in which the information of multiple recording electrodes was combined, as the assumption of a common underlying response with an amplitude and phase independent of the recording electrode should provide higher statistical power than the mere combination into one measure with additional degrees of freedom.

Additional improvements in detection time for responses to super-threshold stimuli might be possible by the integration of response components at multiples of the modulation frequency, although significant response components at these frequencies could only be observed for low-rate pulse trains. In Cebulla et al. (2006), q-sample tests that included up to six harmonics of the modulation frequency performed consistently better for detection than one-sample tests. In Stürzebecher et al. (1999), different variants of q-sample tests based on phase coherence and magnitude squared coherence were evaluated in Monte Carlo simulations and on real near-threshold ABR data, with tests based on amplitude and phase together performing the best. Besides using q-sample tests, multiple sample sets can also be evaluated separately and combined afterwards, e. g., with the Stouffer method (Dimitrijevic et al. 2001).

Electrophysiological thresholds

Electrophysiological thresholds could be reliably obtained with the two-sample Hotelling T² test, which was not affected by stimulus artifacts that had similar artifact components at the modulation frequencies. The one-sample Hotelling T² test gave comparable results but required the complete removal of stimulus artifacts from the analyzed signal.

The determination of electrophysiological thresholds from the two-sample Hotelling T² test applied to recordings without artifact removal was possible in all cases for the AM and PWM high-rate pulse trains. For the low-rate pulse trains, it failed in 25% of the cases. This was caused by different artifact components at the modulation frequencies, as the stimulation at 35 and 44 Hz used three and two power-up pulses between stimulus pulses, respectively. For low-rate pulse trains with carefully balanced power-up pulses, it seems likely that it should also be possible to determine reliable electrophysiological thresholds without stimulus artifact removal.

The one-sample Hotelling T² test did not give reliable results for any of the stimulus types when applied to recordings without stimulus artifact removal. For PWM high-rate pulse trains, the test detected significantly fewer thresholds than for AM high-rate pulse trains. This was probably caused by the differences in modulation index between the AM and PWM high-rate pulse trains, resulting in a stronger artifact component at the modulation frequency for the PWM high-rate pulse trains at lower stimulus intensities. See below for a discussion of the modulation indices of the stimulus types.

The electrophysiological thresholds derived from the sigmoid functions fit to the number of significant responses from the recording electrodes at the contralateral mastoid and the back of the head did not differ significantly from the thresholds described above. This method seems to be a feasible alternative to the direct derivation of thresholds from the curves of the Hotelling T² statistic and does not need statistical methods to combine multiple recording channels or special techniques to alleviate the influence of individual noisy measurements on the determined thresholds.

While electrophysiological thresholds for low-rate pulse trains were on average 30 cu above behavioral T levels at 900 pps, this difference dropped to 18 and 12 cu for AM and PWM high-rate pulse trains, respectively. Similar reductions in electrophysiological thresholds were reported by Kileny (2011) for pilot experiments comparing EMLRs to short high-rate pulse trains with responses to single pulses, with reductions in electrophysiological thresholds of 20 cu (about 50% BDR), and 10 cu (about 30% BDR) in two subjects. The electrophysiological thresholds found here slightly underestimated the differences between the corresponding behavioral T levels of the two stimulation electrode pairs within the same subject by on average 1.5, 3.2, and 4.0 cu for low-rate, AM, and PWM high-rate pulse trains, respectively, although none of these differences were significant.

The difference between the electrophysiological thresholds of the AM and PWM high-rate pulse trains can be explained in part by the differences in modulation index between the two stimulus types. While the modulation index of the PWM high-rate pulse trains with variable phase widths between 25 and 40 μs was fixed at 0.23, the modulation index of the AM high-rate pulse trains was dependent on stimulus intensity. Across all subjects, amplitude modulation indices decreased from 0.15 to 0.51 at C level down to 0.10 to 0.26 at the estimated electrophysiological thresholds. Compared with the PWM high-rate pulse trains, the AM high-rate pulse trains had equal or lower modulation indices at all corresponding electrophysiological thresholds. Galvin and Fu (2009) measured the minimum perceptible modulation index for different stimulus intensities on a linear behavioral dynamic range (LBDR) scale defined in linear microamperes. At a stimulus intensity of 5% LBDR, Galvin and Fu (2009) found a mean minimum perceptible modulation index of 0.4. When converting the electrophysiological thresholds of the AM and PWM high-rate pulse trains used here to their stimulus intensity definition, mean electrophysiological thresholds were at 3% LBDR for the AM and −1% LBDR for the PWM high-rate pulse trains. As the minimum perceptible modulation index increases with decreasing stimulus intensity, the minimum perceptible modulation indices at these electrophysiological thresholds should therefore have been similar or higher than 0.4, which is higher than the actual modulation indices found here. This could indicate that the electrophysiological thresholds were located around the stimulus intensity where the modulation started to become barely perceptible and that the lower modulation indices of the AM compared with the PWM high-rate pulse trains at lower stimulus intensities were the reason for the higher electrophysiological thresholds of the former.

The variance of the differences between electrophysiological thresholds and behavioral T levels gives an indication of the predictability of the latter from the former. Standard deviations were low for corresponding behavioral T levels (6.0 to 6.6 cu) and high for unrelated behavioral T levels (13 to 15 cu). If only the inter-subject variability was considered, similar results could be obtained, with low standard deviations for corresponding behavioral T levels (4.8 to 5.6 cu) and high standard deviations for unrelated behavioral T levels (9.6 to 12 cu). This was also true for the intra-subject variability of the differences between stimulation electrode pairs, with low standard deviations for corresponding behavioral T levels (6.9 to 7.9 cu) and high standard deviations for unrelated behavioral T levels (15 to 21 cu).

Thresholds for low-rate and modulated high-rate pulse trains correlated very well with the corresponding behavioral T levels, with correlation coefficients of r = 0.96 for all three stimulus types. Correlations coefficients were lower between electrophysiological thresholds and unrelated behavioral T levels, with correlation coefficients of r = 0.80 for thresholds of low-rate pulse trains and behavioral T levels at 900 pps and r = 0.72 and r = 0.80 for thresholds of modulated high-rate pulse trains and behavioral T levels at 40 pps. For low-rate pulse trains and behavioral T levels at 40 pps, the correlation coefficient is similar to the one found in Hofmann and Wouters (2010). For acoustically evoked MLRs, correlations between electrophysiological and behavioral thresholds are high (Kileny and Shea 1986), as are correlations between electrophysiological thresholds derived from EMLRs and behavioral T levels for the same stimulus (Kileny and Kemink 1987). The differences in correlation between behavioral T levels and electrophysiological thresholds for low-rate and modulated high-rate pulse trains can be partly explained by the degree that these different stimulus types account for temporal effects that occurred in response to the 900 pps unmodulated pulse trains used for the determination of the behavioral T levels.

Future improved stimuli should be as close as possible to the clinical stimulus used for behavioral T level estimation. They must contain an easily recognizable modulation even at low stimulus intensities and should match the clinical stimulus in pulse rate and stimulation mode.

With the recording equipment used here, no reliable monopolar EASSR recordings could be obtained as stimulus artifacts for monopolar stimulation exceeded the dynamic range of the RME sound card of about ±200 μV. This caused non-linear signal distortions because of clipping and ringing of the anti-aliasing filters inside the RME sound card at the edges of the clipped artifacts. Additionally, the distortions introduced by the filters of the recording equipment could not be removed as the unclipped signal was not available for inverse filtering. In a future study, these problems could be solved by the use of a DC amplifier with a higher dynamic range. Monopolar high-rate pulse trains might also have stimulus artifacts that are longer than the maximum duration of 1.1 ms where stimulus artifacts can still be successfully removed at 900 pps. On the one hand, these artifacts would make it impossible to determine response properties such as amplitude, phase, and latency and would prohibit the use of one-sample tests for response detection. On the other hand, we expect that it will still be feasible to obtain reliable electrophysiological thresholds with the proposed statistical method based on a two-sample Hotelling T² test.

Summary and future work

The results of this study show (1) that EASSRs to modulated high-rate pulse trains account for some of the temporal effects at 900 pps and result in improved electrophysiological thresholds that correlate very well with behavioral T levels at 900 pps, (2) that the proposed statistical method for response detection based on a two-sample Hotelling T² test has comparable performance to previously used one-sample tests, and (3) that stimulus artifacts do not need to be removed from the EEG signal for the determination of reliable electrophysiological thresholds if a two-sample Hotelling T² test is used for response detection.

For the goal of automatic fitting of CIs in young children, reliable detection of EASSRs to monopolar stimulation is still a challenge, and electrophysiological thresholds need to be determined for modulation frequencies in the 80-Hz range as ASSRs around 40 Hz are attenuated in small children (Picton et al. 2003).

Appendix

A implementation of Hotelling T² test

One measurement with complex frequency bins B corresponding to the modulation frequencies was represented by a matrix D defined as

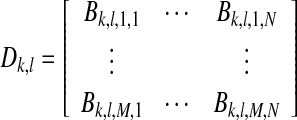1

with the number of modulation frequencies K, number of measurements L, number of epochs M, and number of recording electrodes N. Different sample sets with the same modulation frequency were combined into a matrix X with dimensions M × O

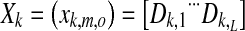2

and normalized into a matrix 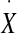obtained by column-wise division with the standard deviation S

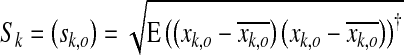3

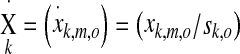4

For the Hotelling T² test, 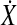was reshaped into a two-column matrix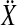

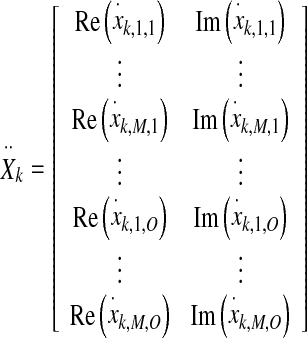5

that contained the real components in the first and the imaginary components in the second column. The Hotelling T² statistic and the probability of the incorrect rejection of the null hypothesis p was determined from the difference of the means 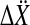of sample sets for two different frequencies in 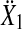and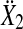

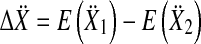6

and the pooled covariance matrix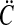

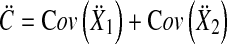7

with the cumulative density function of the 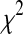distribution 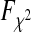, and correction factor r as

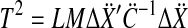8

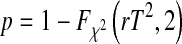9

B determination of r by Monte Carlo simulation

The Hotelling T² test expects independent samples which is not necessarily true for the EEG recorded from multiple electrodes at the same time. This was mitigated by the calculation of the size of an equivalent sample set of independent samples, represented by the correction factor r which was determined by Monte Carlo simulation.

The dependencies between the recording electrodes were modeled by the covariance matrices for the real and imaginary components C_re and C_im.

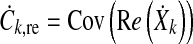10

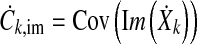11

Correlated random matrices 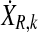were calculated from independent normally distributed random data matrices P and Q with dimensions M × O and zero mean by applying the Cholesky decomposition to the covariance matrices

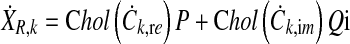12

For 10,000 trials with different matrices P and Q, Eqs. 5 to 8 were used to characterize the distribution of 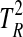for normally distributed random data with the specified covariance matrices and to determine the cumulative density function 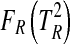. Least squares approximation was then used to determine the correction parameter r for the 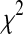cumulative density function 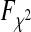with two degrees of freedom by

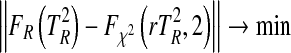13