Random Forests for Genomic Data Analysis

Abstract

Random forests (RF) is a popular tree-based ensemble machine learning tool that is highly data adaptive, applies to “large p, small n” problems, and is able to account for correlation as well as interactions among features. This makes RF particularly appealing for high-dimensional genomic data analysis. In this article, we systematically review the applications and recent progresses of RF for genomic data, including prediction and classification, variable selection, pathway analysis, genetic association and epistasis detection, and unsupervised learning.

1. Introduction

High-throughput genomic technologies, including gene expression microarray, single nucleotide polymorphism (SNP) array, microRNA array, RNA-seq, ChIP-seq, and whole genome sequencing, are powerful tools that have dramatically changed the landscape of biological research. At the same time, large-scale genomic data presents significant challenges for statistical and bioinformatic data analysis as the high dimensionality of genomic features makes the classical regression framework no longer feasible. As well, the highly correlated structure of genomic data violates the independent assumption required by standard statistical models. Many biological mechanisms involve gene-gene interactions or gene networks, but it is not realistic to pre-specify the interaction effects, especially high-order interactions, in statistical models for high-dimensional data. Generally, a small portion of genomic markers are associated with phenotypes, and performing variable selection for high-dimensional, correlated, and interactive genomic data is complex and requires sophisticated methodology.

Regularized statistical learning methods such as penalized regression, tree-based approaches, and boosting have recently been developed to handle high-dimensional problems. Random forests (RF) [1] is one of the most popular ensemble learning methods and has very broad applications in data mining and machine learning. Random forests is a nonparametric tree-based ensemble approach that merges the ideas of adaptive nearest neighbors with bagging [2] for effective data adaptive inference. The greedy nature of one-step-at-a-time node splitting enables trees (and hence forests) to impose regularization for effective analysis in “large p, small n” problems and the “grouping property” of trees [3] enables RF to adeptly deal with correlation and interaction among variables. RF can also be used to select and rank variables by taking advantage of variable importance measures. Thus, these properties of RF make it an appropriate tool for genomic data analysis and bioinformatics research. In this article, we review applications of RF to genomic data, including prediction, variable selection, pathway analysis, genetic association, and epistasis detection.

2. Results

2.1. RANDOM FORESTS

The basic unit of RF (the so-called base learner) is a binary tree constructed using recursive partitioning (RPART). The RF tree base learner is typically grown using the methodology of CART (Classification and Regression Tree) [4], a method in which binary splits recursively partition the tree into homogeneous or near-homogeneous terminal nodes (the ends of the tree). A good binary split pushes data from a parent tree-node to its two daughter nodes so that the ensuing homogeneity in the daughter nodes is improved from the parent node. RF are often a collection of hundreds to thousands of trees, where each tree is grown using a bootstrap sample of the original data. RF trees differ from CART as they are grown nondeterministically using a two-stage randomization procedure. In addition to the randomization introduced by growing the tree using a bootstrap sample of the original data, a second layer of randomization is introduced at the node level when growing the tree. Rather than splitting a tree node using all variables, RF selects at each node of each tree, a random subset of variables, and only those variables are used as candidates to find the best split for the node. The purpose of this two-step randomization is to decorrelate trees so that the forest ensemble will have low variance; a bagging phenomenen. RF trees are typically grown deeply. In fact, Breiman’s original proposal [1] called for splitting to purity. Although it has been shown that large sample consistency requires terminal nodes with large sample sizes [5], empirically, it has been observed that purity or near purity (small terminal node sample sizes) is often more effective when the feature space is large or the sample size is small [6]. This is because in such settings, deep trees grown without pruning generally yield lower bias. Thus, Breiman’s approach is generally favored in genomic analyses. In such cases, deep trees promote low bias, while aggregation reduces variance.

The construction of RF is described in the following steps:

1. Draw ntree bootstrap samples from the original data.

2. Grow a tree for each bootstrap data set. At each node of the tree, randomly select mtry variables for splitting. Grow the tree so that each terminal node has no fewer than nodesize cases.

3. Aggregate information from the ntree trees for new data prediction such as majority voting for classification.

4. Compute an out-of-bag (OOB) error rate by using the data not in the bootstrap sample.

2.2. RANDOM SURVIVAL FORESTS

RF has traditionally been applied to classification and regression settings. Random survival forests (RSF) [7] is a new extension of RF to right-censored survival data. RSF is derived using the same principles underlying RF and enjoys all its important properties. As in RF, tree node splits are designed to promote homogeneity. In survival settings this corresponds to maximizing survival differences between daughter nodes. The predictor and key deliverable of RSF is the ensemble estimate for the cumulative hazard function (CHF). The ensemble CHF can be calculated for each sample in a data set, and summing this ensemble over the observed survival times yields the predicted outcome referred to as ensemble mortality, a measure of mortality for a patient that has been shown to be an effective predictor of survival.

One of the first popular software implementations of RF was the Breiman and Cutler Fortran code http://www.stat.berkeley.edu/~breiman/RandomForests. Later this code was ported to the R-package randomForest [8]. RSF can be implemented using the R-package randomSurvivalForest [9]. Both RF and RSF are open source and freely available from the Comprehensive R Archive Network (CRAN). A new R-package randomForestSRC to be released soon unifies RF and RSF and will enable users to analyze all three settings of survival, regression and classification. We note that the R-package party [10] also provides a unified forest treatment, although the approach makes use of conditional trees and is different than Brieman’s RF.

2.3. MEASURES OF VARIABLE IMPORTANCE: RANKING

An important feature of RF is that it provides a rapidly computable internal measure of variable importance (VIMP) that can be used to rank variables. This feature is especially useful for high-dimensional genomic data. Two commonly evaluated importance measures are node impurity indices (such as the Gini index) and permutation importance. In classification, the Gini index importance is based on the node impurity measure for node splitting. The importance of a variable is defined as the Gini index reduction for the variable summed over all nodes for each tree in the forest, normalized by the number of trees.

Permutation importance (“Breiman-Cutler” importance) is the most frequently applied importance measure for RF. To calculate a variable’s permutation importance, the given variable is randomly permuted in the out-of-bag (OOB) data for the tree (the original data left out from the bootstrap sample used to grow the tree; approximately 1−.632 = .368 of the original sample), and the permuted OOB data is dropped down the tree. The OOB estimate of prediction error is then calculated. The difference between this estimate and the OOB error without permutation, averaged over all trees, is the VIMP of the variable. The larger the permutation importance of a variable, the more predictive the variable [1].

Modified VIMP measures have been proposed for genomic data. For example, the use of subsampling without replacement in place of bootstrapping has been proposed for settings where variables vary in their scale of measurement or their number of categories [11]. A conditional permutation VIMP was proposed to correct bias for correlated variables [12]. A maximal conditional chi-square importance measure was developed to improve power to detect SNPs with interaction effects [13].

Although there are many successful applications using permutation importance, a criticism is that it is a ranked based approach. Ranking is far more difficult than the variable selection problem, which simply seeks to select a group of variables that when combined are predictive, without imposing a ranking structure. Nevertheless, because of the complexity in biological systems, ranked gene lists based on RF or RSF which consider correlation and interaction effects are still a vast improvement from univariate ranked gene lists based on t-test’s or Cox proportional hazard modeling using one variable at a time. However, caution is needed when interpreting any linear ranking because it is in general likely that multiple sets of weakly predictive features are jointly predictive. This appears to be an unresolved problem of ranking and further studies are needed.

2.4. STEPWISE PROCEDURES FOR VARIABLE SELECTION

Although RF and RSF are capable of modeling a large number of predictors and achieving good prediction performance, finding a small number of variables with equivalent or better prediction ability is highly desired because it is not only helpful for interpretation but also easy for practical usage. Diaz-Uriarte and Alvares [14] described a backward elimination procedure using RF for selecting genes from microarray data. This method consists the following steps: (1) fit data by RF and rank all available genes according to permutation VIMP; (2) iteratively fit RF, and at each iteration remove a proportion of genes from the bottom of the gene importance ranking list (default 20%); (3) select a group of genes when RF reaches the smallest OOB error rate; (4) estimate the prediction error rate using the .632+ bootstrap method [15] to mitigate selection bias. The authors applied their method to ten microarray data sets and in each instance were able to find a small set of genes yielding an accurate predictor. The web-based tool GeneSrF and the R-package varSelRF are two software procedures that can be used to implement the method.

A similar variable elimination procedure based on random forests, named the gene shaving method (GSRF) [16], was proposed earlier than varSelRF. There are two major differences between GSRF and varSelRF. First, GSRF re-computes the VIMP after each backward gene elimination. Second, the best subset of genes is determined by both OOB error rate and the prediction error rate from an independent test data set. Thus, GSRF needs at least two data sets for implementation, which may limit its applications for real data.

It was shown that the classification error in varSelRF is not an optimal choice for dealing with unbalanced samples for SNP data from genome-wide association studies (GWAS). Calle et al. [17] suggested an improvement for varSelRF by replacing misclassification error (the default value used in RF classification) with AUC as the measure of predictive accuracy.

Genuer et al. [18] developed another heuristic strategy of variable selection using RF. It follows the basic workflow of varSelRF. It first ranks all features by VIMP. However, instead of eliminating 20% of the genes each time, it directly removes unimportant variables by setting a threshold for the minimum prediction value from CART fitting. The procedure keeps m important variables. Then nested RF are implemented, starting from the most important variable and increasing the number of variables in a stepwise fashion until all m variables are entered. The final model is selected on the basis of OOB error.

All the variable selection methods described above have good empirical performance, but one concern is that all implicity adopt a ranking approach, and as mentioned, ranking is a far more challenging issue than variable selection. Another concern is that each of these methods rely on VIMP measures, which have two major drawbacks: (1) VIMP is tied to the type of prediction error used; and (2) developing formal regularization methods based on VIMP is challenging as it has remained impenetrable to detailed theoretical study due to its complex randomization.

2.5. MINIMAL DEPTH FOR VARIABLE SELECTION

Recently Ishwaran et al. [3] described a new paradigm for forest variable selection based on a tree-based concept termed minimal depth. This novel method was designed to capture the essence of VIMP but without its problems such as the need to rank variables. With forests, one finds that variables that split close to the root node have a strong effect on prediction accuracy, and thus a strong effect on VIMP. Noising up test data (as done to calculate VIMP) leads to poor prediction and large VIMP in such cases because terminal node assignments will be distant from their original values. In contrast, variables that split higher in the tree have much less impact because terminal node assignments are not as perturbed. This observation motivated the concept of minimal depth, a measure of the distance of a variable relative to the root of the tree for directly assessing the predictiveness of a variable.

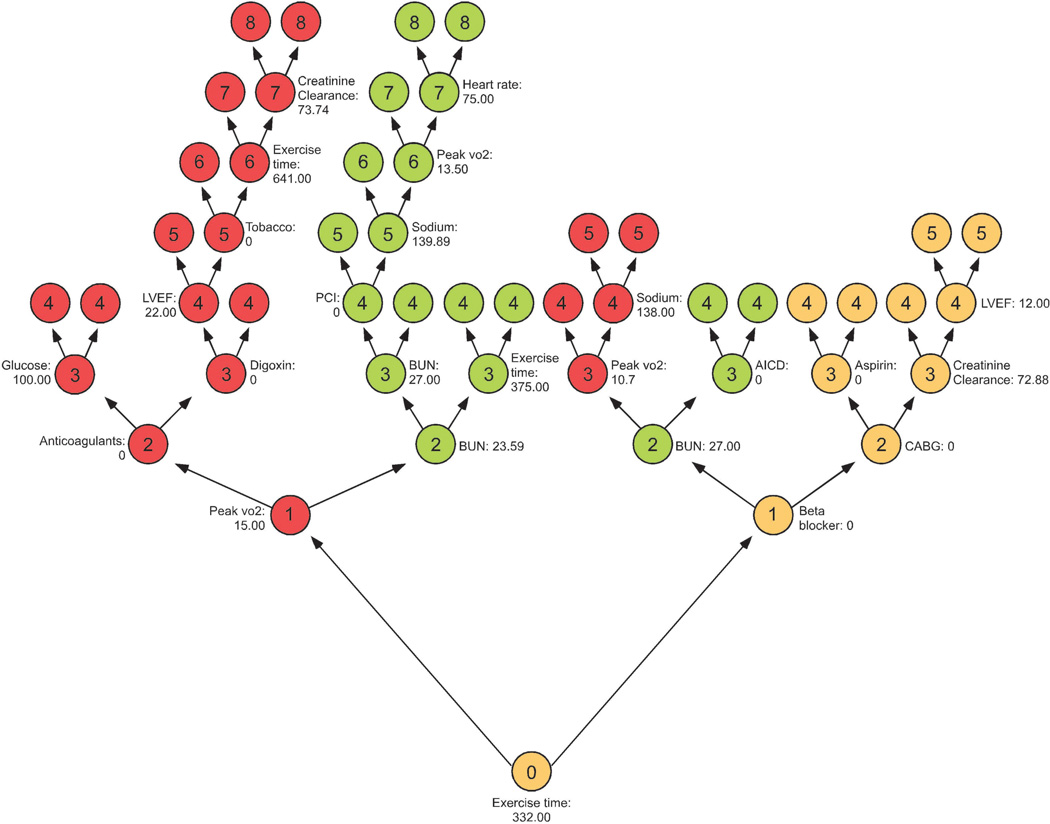
This idea can be formulated precisely in terms of a maximal subtree. The maximal subtree for a variable v is the largest subtree whose root node is split using v (i.e., no parent node of the subtree is split using v). The shortest distance from the root of the tree to the root of the closest maximal subtree of v is the minimal depth of v. A smaller value identifies a more predictive variable. Figure 1 illustrates this concept. Shown is a single tree highlighting three variables found to be predictive from an analysis involving cardiovascular disease (the tree has been inverted with the root node displayed at the bottom). The three key variables are: peak VO2 (red), BUN (green), and exercise time (orange). Maximal subtrees are indicated by color; node depth is indicated by an integer located in the center of a tree node. For example, the root node is split using exercise time; thus its maximal subtree is the entire tree and its minimal depth is 0. For BUN and peak VO2, there are two maximal subtrees on each side of the tree. The closest to the root node is on the left side for peak VO2 with minimal depth, 1. For BUN, both subtrees have depth 2; its minimal depth is 2.

Figure 1.

Illustration of minimal depth.

Due to randomization, it is not hard to construct examples where minimal depth could be misleading in a single tree. For example, if by chance the mtry variables selected for the root node are all noisy (unrelated to the outcome), then we would end up with a noisy variable having a minimal depth 0. However, such pathologic scenarios occur infrequently over a forest of trees and their effects washed out when we aggregate. Hence, when applying applying minimal depth, the forest averaged depth for a variable is used.

There are several advantages to working with minimal depth. First, it is independent of the way prediction error is measured. Thus, minimal depth side steps the controversial issue of selecting the measure used to assess performance. In survival settings, there is controversy whether the C-index, a ranked based method, is preferable to measures based on the Brier score [19, 20]. In classification, it is now recognized that misclassification error may be sub-optimal in RF analyses involving unbalanced samples [17]; a common occurence seen in many genomic data settings. See [21] for a comprehensive review of methods for comparing model performance. A second advantage is that unlike VIMP, the minimal depth distribution can be worked out in closed form and from this a rigorous threshold value for selecting variables can be computed efficiently in high-dimensional settings. Specifically, one can rapidly calculate the mean minimal depth under the null of no association with the outcome. Those variables with forest averaged minimal depth exceeding the mean minimal depth threshold are treated as noisy and are removed from the final model. In this manner, mean minimal depth thresholding bypasses the need to rank variables. Finally, because minimal depth is based on generic tree concepts, it is a general approach that applies to all forests and not just survival forests. The systematic evaluation of minimal depth using simulation and real data has been done as well as the comparison with permutation importance [22].

In ultra-high dimensional settings, mean minimal depth thresholding becomes ineffective. One promising extension is called variable hunting. In this approach, forward stepwise regularization is combined with minimal depth thresholding. Briefly, the procedure works as follows. First, the data are randomly subsetted, and a number of variables are randomly selected. A forest is fit to these data, and variables are selected using minimal depth thresholding. These selected variables are used as an initial model. Variables are then added to the initial model in order of minimal depth until the joint VIMP for the nested models stabilizes. This defines the final model. This whole process is then repeated several times. Those variables appearing the most frequently up to the average estimated model size from the repetitions are selected for the final model [3, 22].

2.6. RF PREDICTION

Prediction is often a primary goal of genomic data analyses. For example, one often needs to predict disease status such as tumor subtype using genomic markers. RF is a particularly appropriate tool and has been broadly used to predict clinical outcomes under various high-throughput genomic platforms.

Wu et al. [23] compared RF with linear discriminant analysis (LDA), quadratic discriminant analysis (QDA), k-nearest neighbor (KNN) classifier, bagging and boosting classification trees, and support vector machine (SVM) for separating early stage ovarian cancer samples from normal tissue samples based on mass spectrometry data. RF outperformed the other methods in terms of prediction error rate. Lee et al. [24] presented a comprehensive comparison of RF to LDA, QDA, logistic regression, partial least square (PLS), KNN, neural network, SVM, and other classification methods using seven microarray gene expression data sets. RF was shown to have the best performance among all tree-based methods. RSF displayed favorable results compared with supervised principal components analysis, nearest shrunken centroids, and boosting for five microarray gene expression data sets with survival outcomes [3].

These empirical results suggest that RF (and RSF) are capable of accurate prediction; on par with state-of-the art methods. However, while these results are certainly encouraging, we believe that the next wave of comparative analyses involving RF should be of a theoretical nature focusing on rates of convergence. Such studies should look at both traditional large sample settings, n → ∞, as well as settings in which the feature space is allowed to increase, p → ∞. The latter setting is especially important as it represents the high-dimensional scenario of high-throughput genomic data. It is in large p problems that RF is especially known to excel (in lower dimensional problems, the differences between RF and conventional methods are less dramatic) and studying the theoretical properties in such cases could lead to a much deeper understanding of RF, and ways of improving it in genomic applications.

We note that different modified versions of RF have been proposed to improve prediction performance, especially for high-dimensional data. “Enriched random forest” assigns weights to the predictors based on adjusted p-values from t-tests. It has achieved competitive prediction results on a benchmark experiment involving ten microarray datasets [25]. Chen et al. [26] proposed pathway-based predictors instead of individual genes for cancer survival prediction using RSF, and this method had advantages in both prediction accuracy and interpretations. However, these results are empirical based. Again, we believe that analyses focusing on theoretical properties such as rates of convergence should lend deeper insight into ways for improving RF.

RF has broad applications for biological questions from a prediction perspective. Protein-protein interactions (PPIs) play an essential role for pathway signaling and cell functions. PPI prediction is an important field in bioinformatics and structure biology. A recent study demonstrated that RF is more effective at predicting PPIs compared with other methods by integrating available biological knowledge [27].

Binding sites prediction from sequence annotation is another important area for structural bioinformatics. RF has been successfully applied to predict protein-DNA binding sites [28], protein-RNA binding sites [29], protein-protein interaction sites [30], and protein-ligand binding affinity [31]. Based on sequence information, RF was shown as a promising tool for predicting protein functions [32].

MicroRNAs (miRNAs) are post-transcriptional regulators that target mRNAs for translational repression or target degradation. RF was implemented to classify real or pseudo miRNA precursors using pre-miRNAs like hairpins, and it achieved high specificity and sensitivity [33]. Glycosylation is one of the post-translational modifications (PTMs) for protein folding, transport, and function. Hamby and Hirst [34] utilized RF to predict glycosylation sites based on pairwise sequence patterns and observed improved accuracy.

Amino acid sequence information can be linked to phenotypes. Segal et al. [35] applied RF to predict HIV-1 replication capacity based on the amino acid sequence from reverse transcriptase and protease. One of the two co-receptors CCR5 and CXCR4 is crucial for HIV-1 to enter the host cells. Prediction of the co-receptor usage by HIV-1 is important in deciding personalized treatment for patients.

Building computational models for predicting drug responses for cancer cell lines is another RF application [36]. These procedures include feature selection using RF variable importance for proteomic or gene expression profiling and the construction of RF regression for continuous chemosensitivity measurement.

2.7. PATHWAY ANALYSIS

Instead of conducting statistical tests on each individual gene, pathway analysis takes advantage of prior biological knowledge and examines the gene expression patterns of a group of genes; for example, genes grouped by metabolic pathways or biological functions. Gene Set Enrichment Analysis (GSEA) is one of the earliest approaches that tackles this problem, and it has been widely used by the research community. Although many analytical strategies have been proposed for pathway analysis and have achieved good power for detecting association signals, the question of how to properly model both the data correlation structure and gene interactions within a pathway remains challenging. Because of its properties, RF is an appropriate tool to capture complex data patterns and biological activities in pathways.

Pang et al. [37, 38] first applied RF on pathway level gene expression data for categorical and continuous phenotypes. RF classification and regression was performed for each pathway using all available samples. The OOB error rate and percent variance explained were used as metrics to rank pathways for classification and regression respectively. The pathway ranking list provided based on predictability is informative, but it is difficult to determine statistical significance for each tested pathway. In another approach, the learner of functional enrichment (LeFE) algorithm utilizes gene importance scores and a permutation framework to test pathways [39]. Specifically, LeFE combines each candidate pathway gene expression matrix with a negative control gene set, in which genes are randomly selected from outside of the pathway, into a composite gene matrix. A random forest is constructed from the composite matrix, and gene importance scores are then collected. LeFE runs t-tests to compare importance scores from candidate pathways and the control gene set. A permutation-based p-value is given to the pathway by repeating the steps from random selection of the control set. The authors of LeFE noted that pathway ranking by predictive power of RF could be biased due to the sample size difference between pathways since prediction favors large gene sets. LeFE is able to correct size bias through permutation procedure, but the trade-off is that the method is computationally intensive.

Pathway testing by RF was extended to censored survival outcomes using random survival forests for both gene expression data and SNP data [40, 38]. An interesting two-stage application of RF pathway analysis was described in Chang et al. [41]. The first stage is to apply RF to identify SNP pathways related to glioblastoma multiforme by OOB error rate smaller than 50%, and then varSelRF package is used to select a SNP subset within each pathway that passed the threshold for further validation.

2.8. GENETICS ASSOCIATION AND EPISTASIS DETECTION

Modern genome-wide association (GWA) studies can now test disease association with common genetic variations using millions of SNPs across the human genome. Employing large sample sizes, sometimes involving hundreds to thousands of study subjects, GWA studies have successfully identified new disease loci for complex diseases. However, the genetic variants identified by single marker association tests account for only a small proportion of the overall heritability. The rationale and design of GWA studies for common variants is an explanation for missing heritability of complex diseases, but understanding genetic architecture of complex diseases needs more efficient statistical modeling techniques to test joint effects of multiple genetic variants and gene-gene and gene-environment interactions, which are difficult to study due to the ultra-high dimensionality of genetic markers, linkage disequilibrium (LD) between SNPs, and small interaction effects. The capability of RF to prioritize SNPs, considering both marginal and interaction effects, is especially appealing for GWA data.

The major application of RF for GWA data is to rank SNPs according to VIMP. Permutation VIMP measures can show a bias when strong linkage disequilibrium exists between SNPs. For example, when two risk SNPs in LD, including one causal SNP and one surrogate SNP, are assigned to the same tree, the prediction accuracy of the tree can remain relatively unchanged when the causal SNP is randomly permuted if the surrogate SNP is higher up along the branch. The consequence is that the VIMPs of both SNPs will be diminished. One solution for correcting this bias is permuting a variable conditional on another correlated variable [12]. Another proposed strategy is revising RF to only include SNPs with LD lower than the pre-defined threshold in a same tree [42]. Nicodemus et al. [43] performed simulation studies to compare conditional permutation VIMP with standard permutation VIMP. The authors suggested that conditional VIMP is more appropriate to identify the causal SNPs from a group of correlated ones in small-scale studies, while standard permutation VIMP may be a better choice for large-scale screening studies. Gini VIMP is more biased on correlation compared with permutation VIMP, and it favors SNPs with large minor allele frequencies [43, 44]. Thus, Gini VIMP is not recommended for ranking SNPs in GWA studies.

Epistasis or gene-gene interaction is one of the essential elements in understanding the genetic architecture of common diseases. The term epistasis can have several different meanings in genetic studies such as functional epistasis, compositional epistasis, and statistical epistasis. Wang et al. [45] recently pointed out that interaction parameters in statistical modeling should be jointly interpreted with main effects for discovering biological interactions. RF and other tree-based methods have an advantage over traditional parametric modeling of interactions, which are generally taken to mean the product of two variables in a model, whereas in trees the notion of an interaction is more broad, meaning the ability to model the outcome differently over subgroups defined by the partition of the data space induced by the tree. This more general notion is better suited to handle biological interactions from pathways and gene networks which are unlikely to be represented in terms of simple cross product terms of variables. For a more comprehensive review of methods to detect gene-gene interactions, we refer to the papers of Cordell [46].

Lunetta et al. [47] conducted one of the earliest simulation experiments to evaluate the power of RF to screen SNPs with interaction effects in genetic association studies. The simulation results proved that RF VIMP outperformed Fisher’s exact test when risk SNPs were allowed to interact. When risk SNPs did not interact, the performance of RF and the Fisher exact test were comparable. Motivated by GWAS data, a freely available software package named Random Jungle (RJ) was specifically designed and optimized for large-scale SNP data [48]. Cordell and Schwarz et al. performed a real data illustration using 89,294 and 275,153 SNPs respectively for Crohn’s disease association studies [46, 48]. Although it may be computationally feasible to run RJ with whole genome level SNPs, filtering, dimension reduction, and other regularized methods are still necessary for RF and other related tree approaches to capture moderately associated SNPs and interactions. Jiang et al. [49] proposed a two-stage analysis method to identify interactions. A sliding window sequential forward feature selection algorithm using RF classification error was applied in the first stage to select a small number of SNPs. Then p-values were generated by a chi-square distribution test for three-way interactions of the candidate SNPs. De Lobel et al. [50] also performed RF screening at the first stage. The popular gene-gene interaction detection method, Multifactor Dimensionality Reduction (MDR), was then applied for an exhaustive search among the filtered SNPs for two-way interactions.

For interaction detection, RF has been compared with other available algorithms using simulated and real data. Carcia-Magarinos et al. [51] evaluated RF, CART, and logistic regression (LR) in 99 simulated scenarios involving different sample size, missing data, minor allele frequencies, and other factors. RF was more powerful in detecting true association, especially in pure interaction models. Molinaro et al. [52] compared RF with Monte Carlo logic regression (MCLR) and MDR. For RF modeling, VIMPs were used as statistics, with p-values obtained from permutation tests. RF also achieved the best power in simulation studies.

Although the main purpose of genetic association studies is to discover the functional role of genetic variants in the etiology of diseases, genetic profile-based disease risk prediction has become more and more important for personalized medicine. Most SNPs found by GWA studies are associated with only a small increased risk of disease indicating that each SNP has only a small predictive value. Integrating the joint and interaction effects of genetic variants and environmental factors is necessary for assessment of the risk of disease. Bureau et al. [53] applied RF on 42 SNPs from the asthma susceptibility gene ADAM33 to achieve 44% misclassification rate. Sun et al. [54] used 287 tagged SNPs and 17 risk factors as predictors and utilized RF to attain a successful prediction for coronary artery calcification. Xu et al. [55] showed that the prediction performance for severe asthma exacerbations in children using 160–320 SNPs by RF is better than using top 10 SNPs alone.

2.9. PROXIMITY AND UNSUPERVISED LEARNING BY RANDOM FORESTS

RF proximity is determined by examining the terminal node membership of the data. If sample i and sample j both fall within the same terminal node of a given tree, the proximity between i and j is increased by one. Summing over all terminal nodes in a forest produces the proximity matrix, which represents the degree of similarity between sample points. Unsupervised learning by RF cannot be implemented without modification, as RF requires an outcome for tree growing. A proximity solution proposed by Breiman is to artificially create a two-class problem and then apply two-class RF to the artificial problem. One treats the original data as class “1” and then a synthetic data set all having class labels of “2” is created. The synthetic data is created by randomly sampling from the product of the marginal distributions of the original variables or by uniformly sampling from the hyper-rectangle containing the observed data. Unsupervised RF learning can be implemented using the R-package randomForest. After transforming the RF proximity matrix to a dissimilarity matrix, it opens the door to many clustering and visualization approaches for detecting data structures.

Shi et al. [56] successfully used RF unsupervised learning for tumor class discovery based on immunohistochemical tumor maker expression. A RF dissimilarity matrix obtained from 307 clear renal cell carcinoma patients and eight protein markers was used as input for partitioning around medoid (PAM) clustering to separate patients into two groups. In terms of tumor recurrence between the two groups, the RF method was better than Euclidean distance based PAM clustering. Similar analyses were performed on histone markers of prostate cancer [57]. Shi and Horvath [58] further investigated the properties of RF dissimilarity using simulations and recommended that randomly sampling from the product of the marginal distributions of the variables to generate synthetic data is suitable for general settings.

Another use of the proximity matrix is for missing data imputation. Data imputation by weighting the frequency of the non-missing values with proximity values was illustrated in Breiman and Cutler’s RF manual. Schwarz et al. [59] modified supervised imputation to unsupervised imputation for SNP data by creating synthetic data for class 2, but the proposed method is difficult to implement due to the difficulty in accessing phased haplotype information from public domains such as HapMap. Recently Stekhoven and Buhlmann introduced another method of imputation by predicting missing values using RF trained on non-missing data [60]. The RSF software [9] also uses a different approach in which missing data is sampled randomly as the tree is grown. This approach was found to be as effective as proximity based imputation, but has the advantage that it can be applied to test data [7], something that cannot be done with proximity imputation.

3. DISCUSSION

The complexity and high-dimensionality of genomic data requires flexible and powerful statistical learning tools for effective statistical analysis. Random forest has proven to be an effective tool for such settings, already having produced numerous successful applications. However, rigorous theoretical work of RF is still needed. Its effectiveness in the non-standard small sample size and large feature space setting is still not fully understood and could reveal many insights into how to improve forests. We believe a theoretical analysis should focus on asymptotic rates of convergence. The results from such work should seek to answer practical questions, such as determining optimal tuning values for RF parameters, such as mtry and nodesize and it should seek to provide ways to modify forests for improved prediction performance. Furthermore, trees and forests provide a wealth of information about the data not typically available with other methods. For example, proximity is a unique way to quantify nearness of data points in high dimensions. Such values could be one target for further study. Interactions between variables could be explored by studying the splitting behavior of variables. Ishwaran et al. [3] suggested higher order maximal subtrees as a way to explore higher order interactions between variables. Such analyses could be a starting point for peering inside the black-box of RF and discovering ways of utilizing forests for even more successful applications to genomic data analysis.

Highlights.

• We review the applications and recent progresses of random forests for genomic data analysis.

• We review the methods for variable selection by random forests and random survival forests.

• We review the classification and prediction of random forests using high-dimensional genomic data.

• We review the genetic association and epistasis detection using random forests on GWA data.