Relating Memory To Functional Performance In Normal Aging to Dementia Using Hierarchical Bayesian Cognitive Processing Models

Abstract

Determining how cognition affects functional abilities is important in Alzheimer’s disease and related disorders (ADRD). 280 patients (normal or ADRD) received a total of 1,514 assessments using the Functional Assessment Staging Test (FAST) procedure and the MCI Screen (MCIS). A hierarchical Bayesian cognitive processing (HBCP) model was created by embedding a signal detection theory (SDT) model of the MCIS delayed recognition memory task into a hierarchical Bayesian framework. The SDT model used latent parameters of discriminability (memory process) and response bias (executive function) to predict, simultaneously, recognition memory performance for each patient and each FAST severity group.

The observed recognition memory data did not distinguish the six FAST severity stages, but the latent parameters completely separated them. The latent parameters were also used successfully to transform the ordinal FAST measure into a continuous measure reflecting the underlying continuum of functional severity.

HBCP models applied to recognition memory data from clinical practice settings accurately translated a latent measure of cognition to a continuous measure of functional severity for both individuals and FAST groups. Such a translation links two levels of brain information processing, and may enable more accurate correlations with other levels, such as those characterized by biomarkers.

Introduction

Relating cognitive to functional impairment has been a relatively understudied area in Alzheimer’s disease (AD) research. Yet it is practically important in terms of understanding outcomes in clinical trials as well as in predicting the degree of impairment in functional capabilities from objective cognitive testing in clinical practice.

The usual way of relating cognition to function has been to look at their inter-correlations. An alternative approach is to create a model that posits the form of the relationship between the degree of impairment in functional capabilities and the processes underlying a given cognitive task. Recently, we applied a methodology combining hierarchical Bayesian statistical methods with psychological measurement models of the processes underlying memory (Hierarchical Bayesian Cognitive Processing, HBCP). Such models may provide useful insights into the cognitive ability being studied. They can also simultaneously estimate parameters for groups and individuals, automatically make inferences for missing data, and integrate multidimensional data, such as biomarkers, cognitive and functional measures plus covariates, into a single construct.

The delayed recognition memory task may help relate cognitive and functional changes because its performance requires memory storage and executive function processes. The task involves studying a list of items (usually words or pictures) one or more times, then after a few minutes or longer, presenting these studied (old) items intermixed with a list of non-studied (new) items. The subject is asked to discriminate the old from the new items.

Signal detection theory (SDT) is used to model recognition memory as composed of underlying memory and decision-making processes.^1–3 Decision-making is an executive function, which helps individuals perform various functional abilities.

The Functional Assessment Staging procedure (FAST) is a valid and internationally used measure of the degree of impairment in functional capabilities for persons with AD, in which the functional stages have been correlated with cognitive impairment.^4,5 Because of their use in clinical practice and research, it is useful to explore how different degrees of functional incapacity relate to an SDT model of delayed recognition memory using clinical data.

Methods

FAST Staging Procedure

At each patient visit, a trained physician interviewed either the patient or a reliable informant using the FAST procedure^5,6 to stage the patient’s degree of functional incapacity into one of 16 stages (7 major stages, 1–7, with 11 sub-stages, 6a-e, and 7a-f).⁷

Patients with no subjective functional impairment and no objectively evident functional impairment are classified as FAST stage 1, and will be referred to as NCI (no cognitively related functional impairment). Patients who subjectively have greater difficulty in cognitively related functional abilities but still perform completely normally are classified as FAST stage 2. FAST stage 2 patients will be referred to as SCI (subjective cognitively related functional impairment). Patients who have impairment in cognitively related, executive level functional abilities, such as using a calendar to prospectively keep appointments, but have no impairment in instrumental activities of daily living (complex activities of daily life, such as marketing properly, managing personal finances properly, and preparing meals for guests, in one’s accustomed manner), are classified as FAST stage 3. FAST stage 3 patients will be referred to as MCI (mild cognitively related functional impairment). FAST stage 4, 5 and 6 patients have functional deficits that correspond to the levels of mild, moderate and moderately severe dementia respectively, and are classified by their degree of impairment in instrumental and basic activities of daily living.

Cognitive Testing

At each visit, patients are tested with a cognitive battery derived from the Consortium to Establish a Registry for AD (CERAD), consisting of Trails A and B—measures of sequencing, processing speed and set-shifting, FAS letter fluency—a measure of phonemic fluency, working memory and rule application, Ishihara number naming test—a measure of object recognition that minimizes use of semantic memory, CERAD drawings—a measure of simple object recognition, planning, organization and visual constructional praxis, and the MCI Screen—a measure of rule application, working memory, rehearsed delayed recall and recognition memory, unrehearsed delayed recall, judged comparisons and self estimation of memory ability.^8–10 The MCIS was the only cognitive test involved in relating cognition to function.

Clinical Sample

The data came from a primary care and a cognitive disorders clinic, and included all assessments of 280 patients followed every 3–6 months for up to six years. The number of patients assessed one or more times in any given FAST stage varied from 26 to 163. If one sums the number of patients assessed per FAST stage over the six stages, the total is 514, which is greater than the 280 patients in the study. This is because each patient can contribute data to one or more FAST stages. There was a total of 1,514 FAST stage assessments for the 280 patients studied.

Because the data are repeated measures, there are potential confounding effects on task performance due to practice and reliability. However, these potential confounds have been shown to be small, and are therefore unlikely to influence the present study’s results (MCIS inter-rater and test-retest reliability = 0.83⁹; wordlist effect size < 0.009 standard deviations¹¹).

Patients with AD or a related disorder (ADRD) underwent standardized evaluation, including MRI, laboratory tests, medical history and physical examination, and were diagnosed according to published criteria for AD, Lewy body disease, cerebrovascular disease, and Frontal Temporal Lobe disease.^12–16 Patients were followed every 3–6 months from 2002 to 2007. Table 1 shows the numbers of patients and patient-assessments by FAST stage, along with its description.

Table 1.

Number of Study Patients and Patient Assessments In Each FAST Stage

FAST Stage	Patients		Assessments		FAST Stage
	N	%	N	%	Severity	Description
1	159	15%	288	19%	Normal	no subjective or objective, cognitively related functional decline
2	163	10%	308	20%	Normal/SCI	subjective decline in cognitively related functional capacity
3	26	36%	129	9%	MCI	objective impairment in cognitively related complex functions without impairment in instrumental ADLs*
4	75	28%	436	29%	Mild Dementia	impaired instrumental ADLs*
5	47	7%	189	12%	Moderate Dementia	impaired judgment related to proper selection of clothing for social and weather conditions
6	44	4%	164	11%	Mod-Severe Dementia	impaired basic ADLs*
All	514	100%	1514	100%		*ADLs: activities of daily living

Delayed Recognition Memory Task

The delayed recognition memory task was performed after the MCIS delayed free recall task. The examiner reads aloud to the patient the 10 study list words (old) intermixed with 10 unstudied words (new), one at a time, and the patient is asked to decide whether the word was old or new. In SDT, correct identifications of old and new words are called hits and correct rejections; incorrect identifications of old and new words are called misses and false alarms.

Construction of New Wordlists for the MCIS

Ten pairs of equivalent wordlists have been constructed to minimize practice effects, minimize inter-item associability, and parallel the original CERAD Wordlist. Eight of the 10 pairs are used with the MCIS test. Each time a patient is tested, the MCIS algorithm randomly selects a pair of old and new wordlists from the available pool without replacement. This means the patient has to take the MCIS test 9 times before being exposed to the same pair of wordlists. The wordlists were designed so that: 1) the items of the old and new wordlists are similar; (2) words are one or two syllables; (3) their frequency, range, and diversity statistics resemble those of the original CERAD Wordlist; 4) the words in each list are not easily associable (low semantic associability);¹⁷ 5) the residual semantic similarities among list words are comparable to those of the CERAD wordlist; ¹⁸ 6) neither homophones (e.g., bare/bear) nor words ending in the same phoneme (e.g., plain/airplane) are allowed in a wordlist.¹⁹

Hierarchical Bayesian Cognitive Processing (HBCP) Model for Delayed Recognition Memory

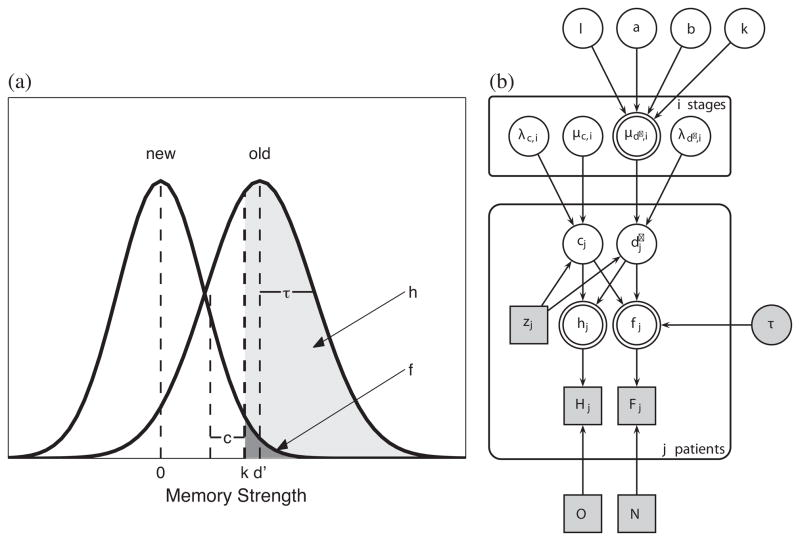
Figure 1 shows the SDT model of the memory strength distributions for old and new list words (left figure) that was incorporated into the HBCP model (right figure). Each presented word evokes a memory strength, which the subject compares to their criterion level, k, for decision-making. The model predicts that a subject will respond to a word that evokes a memory strength > k as an old word, whereas a word that evokes a memory strength ≤ k is responded to as a new word. The discriminability, d′, is the difference between mean memory strengths of old and new list words, and indicates the memory gain from studying the old list words. The hit rate is the area, h, of the old word distribution, and lies above k. The false-alarm rate is the area, f, of the new word distribution, and also lies above k. The response bias, c, for a subject is the distance between their criterion memory strength level, k, and the midpoint of their discriminability, d′. These measures of response bias and discriminability have been proposed to be independent.³ Because recognition memory experiments have found that the standard deviations of the old and new word distributions differ by about 25%,²⁰ we incorporated this unequal-variance assumption into the SDT model.

Figure 1.

(a) Signal Detection Theory (SDT) Model.

The SDT model shows the memory strength distributions for old (studied) and new (unstudied) list words, along with parameters, k (subject’s response criterion), d′ (discriminability), c (response bias), h (hit rate), and f (false-alarm rate). See Methods for details.

(b) The Hierarchical Bayesian Cognitive Processing (HBCP) Model.

This HBCP model generates each patient’s observed response data (Hj, Fj) from their cognitive processes of discriminability and response bias. It also models the continuum of functional severity underlying the discrete FAST stages. See Methods for details.

Model Extension for Group and Individual Differences

Unlike previous SDT applications to recognition memory data of ADRD patients, individual differences were modeled by introducing a parameter reflecting the six functional severity levels (FAST stages 1–6), which influenced the response bias, c_j, and discriminability, d′_j of each subject, j. Each subject’s discriminability and response bias parameters were therefore drawn from the distribution of values generated by the subject’s FAST stage group. In this way, the HBCP model allows different parameter values for individuals with the same FAST stage.

Model Extension for Predicting Changes in Discriminability

Discriminability, d′, between old and new words was modeled by a psychophysical function that made d′ a function of FAST stage severity. For FAST stage i, mean discriminability is:

$${\mu }_{d^{\prime }i}=k+\left(\frac{l}{\left(1+a\times e^{(b\times i)}\right)}\right)$$

k corresponds to baseline discriminability, l corresponds to the potential change in discriminability across FAST severity levels, and a and b are parameters that control the shape of the psychophysical function. A sigmoid form of the psychophysical function was selected because the changes in discriminability between each of the FAST stages from 1 to 6 are nonlinear (see Figure 3). The term in the denominator, ae^(bi), can approach “0” nonlinearly as one progresses from FAST stage 1 to 6, which maximizes the value of the numerator, l, at FAST stage 6. Thus, the change in mean discriminability from baseline at FAST stage 1 will be maximal at FAST stage 6, and approach it non-linearly. This approach goes beyond simply testing for a significant difference in discriminability between FAST stages, and models how discriminability changes with functional severity.

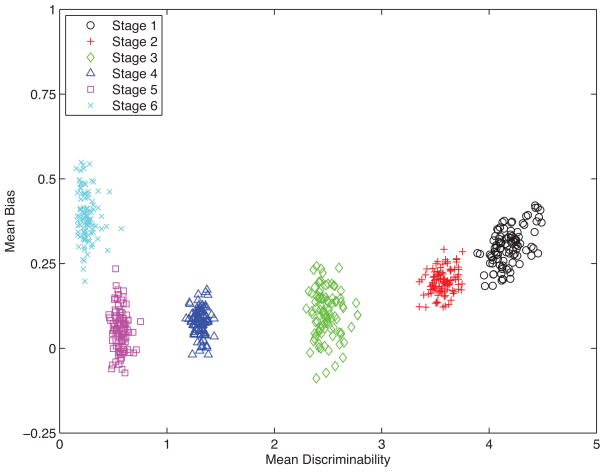
Figure 3. Joint Posterior Predictive Group-Level Discriminability and Response Bias Parameter Distributions per FAST Stage.

The joint posterior group-level distributions of these latent cognitive processing parameters (discriminability and response bias) completely separate the six FAST stages, whereas the observed behavioral data do not. See Results for details.

HBCP Graphical Model Implementation

We implemented the aforementioned hierarchical SDT model in the form of a Bayesian graphical model, a formalism widely used in statistics and computer science.^21,22 In graphical models, nodes correspond to variables, and their interdependencies show the causal relationships between the variables. In particular, graphical models show how unobserved variables (i.e., parameters) generate observed variables (i.e., data). Details and tutorials for the use of graphical models are available.^23,24 The practical advantage of graphical models is that sophisticated and general-purpose Markov chain Monte Carlo (MCMC) algorithms exist that can sample from the full joint posterior distribution of the parameters conditional on the observed data. In Bayesian statistics, the posterior is the probability distribution of unobserved values (often parameters) that results after a prior distribution has been updated by data.²⁵

It is easiest to understand the HBCP graphical model in Figure 1 by starting with the j^th patient’s discriminability and response bias parameters (d′_j and c_j nodes). These parameters generate the j^th patient’s predicted hit, h_j, and false-alarm, f_j, rates, according to the SDT model. The hit rate is h_j = Φ([d′_j/2] − c_j), and the false alarm rate is fj = Φ (−([d′_j/2]+ c_j )/τ), where τ = 0.8, coming from the unequal variance assumption. Based on these hit and false alarm rates and the O = 10 old and N = 10 new words presented to each patient during the recognition task, the j^th patient produces H_j observed hits and F_j observed false alarms, which follow binomial distributions parametrized by hit and false alarm rates, and by their number of old and new words presented (H_j ~ Binomial[h_j,O], F_j ~Binomial[f_j,N]). Each FAST stage, i, has its own set of Gaussian distributions for the discriminability (d′) and response bias (c) parameters, which are controlled by their mean, μ, and precision, λ (λ = 1/σ²) variables. These FAST stage group distributions are implemented using an indicator variable, z_j, which takes the value, 1,2,… 6 according to the j^th patient’s FAST stage. For this patient, j, their discriminability is distributed as d_j~Gaussian(μ_d′,zj, λ_d′,zj) and their response bias is distributed as c_j~Gaussian(μ_c,zj, λ_c,zj). Finally, the psychophysical function determines the mean discriminability of FAST stage, i, (μ_d′i node), which then updates the subject’s discriminability, d′_j.

Bayesian Inference Generated By The HBCP Graphical Model and Clinical Data

Graphical HBCP modeling was performed using WinBUGS software.²⁶ This software uses a range of MCMC computational methods to obtain samples from the posterior distributions of the relevant parameters.²⁷ To perform all analyses, 10,000 posterior samples were collected, following a burn-in of 1000 samples (samples collected, but not used to approximate the posterior distribution of interest), using multiple chains to check convergence.

Results

HBCP Grahical Model Fit

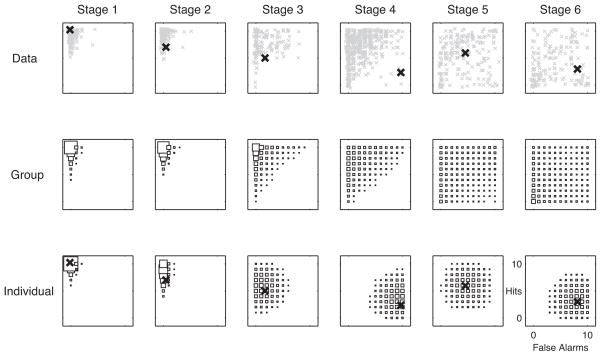
Posterior predictive distributions assess the descriptive adequacy of a Bayesian model by predicting what the data’s distribution should be.²⁵ A poor fitting model will produce inaccurate posterior predictive distributions of the data. Figure 2 shows a posterior predictive analysis for the implemented HBCP model. Rows 1–3 correspond to the 1) observed delayed recognition data (y-axis = Hits, x-axis = False Alarms); 2) group-level (FAST stage) model inferences; and 3) individual-level model inferences, showing one patient per FAST stage, with their mean value marked as an “X”. The hollow black squares show the distribution of predicted hits and false alarms for each FAST stage (column). For Row 1, the gray xs are the patient observed hits and false alarms. For Row 2, the hollow black squares show the posterior predictive distribution of hits and false alarms at the group level (FAST stage); each square’s area is proportional to its predictive mass. Comparison of Rows 1 and 2 indicates that the group-level predictions match the observed data fairly closely, which is consistent with a well fitting model. For Row 3, the hollow black squares show the posterior predictive distribution of hits and false alarms for a selected patient in each FAST stage; each square’s area is proportional to its predictive mass for that patient in that FAST stage.

Figure 2. Hit and False Alarm Distributions per FAST Stage: Observed vs. Group-and Individual-Level Posterior Predictions.

The predicted, individual-level data (row 3) model individuals better than group-level predictions (row 2). See Results for details.

Note that the posterior predictive distributions of the individuals selected for FAST stages 4–6 represent outliers for their FAST stage groups. The use of an individual who is an outlier for a given group illustrates the point that one can simultaneously examine both the group and individual posterior predictive distributions. It also illustrates the point that the distribution of the individual outlier patient is different from that of the group and is more informative than simply using the group distribution for that individual. Specifically, one can see that the HBCP model’s posterior predictive distribution of hits and false alarms for any given selected individual outlier patients is a much better fit than the group level predictions in Row 2. The HBCP model’s ability to characterize these individuals well, while simultaneously describing group-level performance well, highlights an important advantage of the hierarchical approach for modeling individual differences.

Assessing Discriminability, Response Bias and Changes As ADRD Progresses

Figure 3 shows the joint posterior distributions of the discriminability and response bias parameters for each FAST stage. As the degree of functional impairment increases from FAST stages 1 (black circles) to 5 (purple squares), discriminability between old and new list words decreases, and response bias shifts towards misses and false alarms being equally likely. However response bias during FAST stage 6 (light blue xs) shifts back towards that seen in normal aging patients (FAST 1), who make more misses than false alarms.

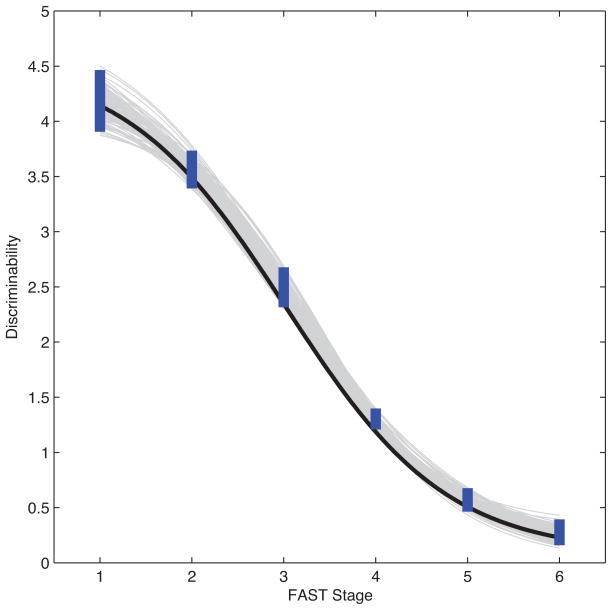
Figure 4 shows the fit of the modeled relation between discriminability and the degree of impairment in functional capabilities (FAST stage). MCMC sampling of the discriminability values, d′_I, generated by the psychophysical function were used to estimate mean discriminability (black curve) and its 95% credible interval (thick blue lines) per FAST stage. The uncertainty of predicted discriminability was also estimated by random sampling of the d′ parameter values from their associated posterior distributions (gray curves). Both measures of uncertainty showed that the predicted discriminability of each FAST stage was reliably predicted by the continuous measure of severity of functional impairment modeled by the psychophysical function.

Figure 4. Modeling the Underlying Continuum of Functional Impairment.

The psychophysical function that uses the discriminability cognitive processing parameter to model the continuum of functional impairment underlying the discrete FAST stage values fits well. See Results for details.

Discussion

The HBCP model of delayed recognition memory showed that decision-making—an executive function modeled by response bias—shifts towards unbiased responding during SCI and MCI (FAST 2–3). A surprising result was the shift back to biased responding similar to NCI individuals (FAST 1) during moderately severe dementia (FAST 6). FAST stage 6 patients have severe memory impairment, so that the memory strength distributions for the old and new wordlists will be similar. This loss of discriminability means that there is no memory signal to make a decision between old and new list words. However, judgment becomes more severely impaired as dementia severity progresses from FAST stages 4 to 6. This decline in judgment may shift the FAST stage 6 patient’s decision-making criterion, k, to the right. This shift would give a response bias, c, similar to that seen in NCI (FAST 1).

A potentially useful clinical application is that delayed recognition memory tasks can be used to create a continuous measure of severity of functional impairment that reliably predicts FAST staging, which is an ordinal measure. A continuous measure of functional impairment allows one to compute rate of functional decline, which can be used, for example, to determine if a treatment has delayed disease progression.

The relatively good fit between discriminability, d′, and the FAST stages, as shown in Figure 4, means that the psychophysical function used to model this relationship will help with interpolation, generalization and prediction of the severity of functional impairment. In other words, this psychophysical function lets one trace out trajectories of functional decline with respect to discriminability, and map these trajectories into statements about memory task performance.

The HBCP model presented here demonstrates how one can simultaneously evaluate clinically relevant groups (i.e., FAST stage groups) as well as individuals within each group. The individual-level fits (see row 3, Figure 2) show that one can predict the distribution of an individual’s recognition memory performance better than that obtained by the individual’s group-level predictions. This is particularly useful for patients who may belong to a distinct subset of the distribution.

The HBCP model presented here also shows how latent processes of memory and executive function that are not directly measurable, can be usefully estimated from the delayed recognition memory response data. These latent parameters separated the group-level values for FAST stages 1 and 2 (see Figure 3), whereas the observed recognition memory data did not (see Row 1, Figure 2). This improved separation of the FAST stages illustrates an important advantage of generative HBCP models over discriminative statistical methods.

HBCP models accurately translated a latent measure of cognition into a continuous measure of the degree of impairment in functional capabilities, This translational ability may facilitate better understanding of the relations between cognition, function and other levels of brain information processing, including those measured by biomarkers at molecular, structural and electrophysiological levels. In this regard, our future studies will examine how this continuous measure of functional severity relates to ADRD diagnosis, quantitative MRI volumetric data, apolipoprotein E genotype, cerebrospinal fluid levels of Abeta42, phospho-tau and total tau, plus affective states such as depression, and behavioral states such as agitation, aggression and psychosis.