Dynamically Applied B₁⁺ Shimming Solutions for Non-Contrast Enhanced Renal Angiography at 7.0 Tesla

Abstract

The purpose of this study was to detail a strategy for performing non-contrast enhanced renal angiography (rMRA) studies at 7.0 Tesla. It is demonstrated that with proper B₁⁺ management, these studies can be successfully performed at ultrahigh fields within local specific absorption rate (SAR) constraints. An inversion prepared gradient echo acquisition, standard for non-contrast rMRA studies, required RF pulse specific B₁⁺ shimming solutions to be dynamically applied to address the field dependent increases in both B₀ and B₁⁺ inhomogeneity as well as to accommodate limitation in available power. By using more efficient B₁⁺ shimming solutions for the inversion preparation and more homogeneous solutions for the excitation, high quality images of the the renal arteries were obtained without venous and background signal artifacts while working within hardware and safety constraints. Finite difference time domain simulations confirmed in vivo measurements with respect to B₁⁺ distributions and homogeneity for the range of shimming strategies employed, and allowed the calculation of peak local SAR values normalized by input power and B₁⁺. Increasing B₁⁺ homogeneity was accompanied by decreasing local SAR per Watt and increasing local SAR per [B₁⁺]², which must be considered, along with body size and respiratory rate, when finalizing acquisition parameters for a given individual.

Introduction

The goal of this work was to investigate the ability to perform non-contrast enhanced (non-CE) renal magnetic resonance angiography (rMRA) studies at 7 Tesla. The potential advantage of performing these studies at 7T includes increased vessel conspicuity, which would benefit multiple clinical applications including the evaluation of patients with renal insufficiency or failure, uncontrolled hypertension, and preoperative evaluation of renal vascular anatomy. The subset of patients with renal insufficiency or failure poses a unique clinical challenge in that their renal impairment may preclude the use of gadolinium-based contrast agents due to the possibility of developing nephrogenic systemic fibrosis (NSF)(1,2), a debilitating and potentially fatal disease (3). Besides these important concerns about NSF, there is a decreasing effectiveness of approved gadolinium based contrast agents at ultra high field (UHF) (> 3 Tesla). In particular, the relatively constant –or decreasing– R1 relaxivity of Gadolinium-DTPA with increasing field strength coupled with increasing T2* signal losses (4) reduce the potential advantages of performing studies at UHF when using first pass CE renal MRA methods, which is another reason to avoid the use of gadolinium to perform rMRA at 7 Tesla.

A common strategy to acquire non-CE renal angiography involves the use of an inversion magnetization preparation followed by a delay and data acquisition relying on in-flow enhancement of the vasculature. The inversion delay time (TI) is chosen to maximally suppress background signal from the parenchyma and venous blood. Performing these studies at 7 Tesla may have the potential to improve the visualization of the first and second order branches as well as more distal arteries compared to lower field strengths and CE acquisitions (5). Along with the increased SNR expected at 7 Tesla, the longer T1s will result in longer inversion delays for background suppression. Thus, better in-flow enhancement is expected. Previous studies at lower fields have shown similar techniques to compare with contrast-enhanced studies at identifying significant renal artery stenosis (6,7) and at evaluating the post transplantation vasculature(8).

Several challenges, however, must be overcome before the potential advantages of performing non-contrast enhanced renal angiography at 7 Tesla can be realized. One of the main difficulties comes from the fact that with increasing field strength inhomogeneities in the electromagnetic magnetic fields also increase. These spatial inhomogeneities are, for a large part, the result of constructive and destructive interferences between complex B₁ vectors (9). These interferences become especially severe at 7 Tesla as the dimensions of the torso are larger than the average RF wavelength in biological tissues (∼12 cm) at the corresponding Larmor frequency (∼ 300 MHz). While the large discrepancies between the spatial phase patterns of the complex receive B₁ (B₁^-) field of each element in a receive coil array can be handled with various multi-channel image reconstruction strategies (e.g. root of sum-of-squares (RSOS),(10)) no similar solution is available for transmit B₁ (B₁⁺). The challenge for B₁⁺ results from the fact that the transmit complex B₁⁺ fields of all coil elements are merged in a unique B₁⁺ vector during RF transmission. It is possible, however, to alter the final B₁⁺ field generated with a multi-channel transmit array driven by independent RF amplifiers, and different B₁⁺ shimming strategies have been employed to optimize transmit fields in targeted regions in both head (9,11,12) and body (13,14) applications. The optimization strategy depends on the size, shape, and location of each target of interest, and optimal B₁⁺ shimming solutions may vary for each individual RF pulse within an acquisition sequence. This was demonstrated by Hetherington et al. in the head (15), where different B₁⁺ shimming solutions, aiming at optimizing B1⁺ homogeneity within different ROI's, were used for performing outer volume suppression and spectroscopic localization. Multiple B₁⁺ shimming solutions within one MR sequence were also employed in the present study for achieving non-CE renal MRA, however, the limited achievable peak B₁⁺ realized at 7 Tesla in the body together with the requirement of obtaining a rapid transmit B₁ field estimation over 16 channels necessitated a different approach.

In this paper, initial technical and methodological challenges of performing non-CE renal MRA at 7 Tesla were investigated. If possible, it would be ideal to perform all imaging under a homogeneous transmit B₁ distribution, but in many instances this is impractical at UHF where there is typically a tradeoff between the goals of obtaining, with B₁ shimming, high B₁⁺ efficiency and high B₁⁺ homogeneity. In out initial investigations, it was determined that achieving a uniform B₁⁺ distribution over the renal arteries as a whole would come at the cost of drastically reduced RF efficiency which in turn would greatly reduce the ability to suppress background signals within the limits of available RF power. Thus, an alternative approach had to be developed. Our results demonstrate that by appropriately designing B₁ shimming solutions weighing towards B₁⁺ efficiency or B₁⁺ homogeneity, effective background suppression can be realized while maintaining a relatively uniform vessel signal even in the context of limited resources in maximum RF power. The rapid, single breath hold B₁⁺ calibration scan used in this study, critical for B₁⁺ shimming, demonstrates that a low flip angle based B₁⁺ approximation can be used in the torso to effectively adjust B₁⁺ shimming solutions under various constraints.

Methods

System and imaging setup

The system used in this study consisted of a 7 Tesla, 90cm bore magnet (Magnex, Oxford, UK) with a 32 receive channel console (Siemens Medical Solutions, Erlangen, Germany), using whole body gradients and a 16-channel transceiver RF coil array built in-house. The RF transmit path of each coil element was equipped with a broadband T/R switch and preamplifier (Varian Inc, Palo Alto, CA). For RF transmission, 16 × 1 kW amplifiers (CPC, Hauppauge, NY) were used to drive a previously described 16 channel strip-line transceiver array made out of two plates (anterior and posterior) carrying 8 transceiver elements each (14,16). The phase and gain of the low voltage input of the 16 amplifiers were modulated by a remotely controlled multi channel RF phase and gain unit (CPC, Hauppauge, NY). In practice, applying a B₁⁺ shimming solution consists of multiplying by a scalar V_k the low voltage RF input of each channel k and of applying a phase offset φ_k on the same channel with k=1,2,3,…,16. In addition to the standard MR console RF power monitoring system of forward and reflected power for one channel, a similar, developed in-house 16-channel RF power monitoring system was used as previously described (16).

In vivo data were obtained in healthy volunteers who signed an Institutional Review Board-approved consent form. With subjects lying in a supine position, the two 8-transceiver array plates were positioned in such a way that the center of the coil elements along the Z axis approximately coincide with the center of the long axis of the kidneys. The transmit B₁⁺ phases typically used at the beginning of an imaging session and for initial scout images are referred to as the “geometric transmit phase setting”. This set of phases was obtained by assigning a transmit B₁ phase for each of the 16 channels based on RF coil geometry approximating the azimuthal angle of each element with respect to center of the body. After moving the table in the bore (with the RF coil center set at the magnet iso-center), multi-axial scout images were obtained to verify that the kidneys were properly positioned along the Z axis with regards to the RF coil. Phase map based B₀ shimming was then performed over an imaging volume encompassing both kidneys (17). For visualization of the renal anatomy and to assist in planning the B₁⁺ calibration scan, breath-hold, T1-weighted gradient echo acquisitions were performed in the coronal and axial planes:450 mm FOV, 150 ms TR, 3.7 ms TE, 242×384 acquisition matrix, 5 mm slice thickness, 20° nominal flip angle and GRAPPA acceleration of 2.

Angiography Sequence

The non-CE acquisition relied on a respiratory triggered turbo-flash (TFL) sequence consisting of a slab selective adiabatic inversion and a frequency selective fat saturation followed by a small flip angle gradient-echo readout. Planning of the axial imaging and inversion volumes are shown in Figure 1a following the strategy presented by Liu et al (8). The imaging parameters for the respiratory triggered angiography sequence included the following: 3.8 ms TR, 1.76 ms TE, 1000 ms TI, 8° nominal flip angle, GRAPPA acceleration of 2. Depending on the size of the individual and long-axis extent of the kidneys, the FOV, slice thickness and matrix sizes varied, in order to cover both kidneys within a stack of 72 slices, with the following ranges: field of view 300-380 mm, slice thickness of 1.0-1.3 mm and in-plane resolution of 1.1 × 1.0 to 1.2 × 1.1 mm². The duration of the acquisition window was adjusted based on the respiratory cycle and the length of the end-expiratory quiescent period allowing for 55 to 73 phase encodes per trigger. The approximate acquisition time for this sequence was 9 minutes.

Figure 1.

(a) Planning of the axial imaging (dashed box) and inversion (hashed area) volumes. (b) Sequence diagram of the respiratory triggered angiography sequence. B1S1 and B1S2 refer to two dynamically applied B1+ shimming solutions and their relative placement with respect to the RF pulses in the sequence.

In order to provide satisfactory angiograms at 7 Tesla, the adiabatic inversion RF pulse and the small flip angle excitation RF pulse present drastically different requirements in term of |B₁⁺| homogeneity and |B₁⁺| peak value. For the inversion RF pulse, which is responsible for suppressing the background signal, the main limiting factor is the available peak value of |B₁⁺| because an adiabatic threshold needs to be attained to ensure spin inversion; |B₁⁺| homogeneity however is not necessary critical as adiabatic inversion pulses provide a uniform inversion as long as |B₁⁺| equals or exceeds this threshold. Thus, a first B₁⁺ shimming solution (B1S1), to be applied on the inversion pulse (and on the fat saturation pulse), was optimized to provide a tradeoff favoring transmit efficiency over homogeneity (further details on B₁⁺ shimming calculation will be found in the next section). To improve inversion performance even further, i.e. to reduce the adiabatic |B₁⁺| threshold, the standard adiabatic inversion pulse on the system, a 10 ms HS1, was modified to a 20-25 ms HS4 which requires a lower peak |B₁⁺| (18). Verification of the inversion slab coverage was achieved by running a rapid single-slice coronal rMRA perpendicular to the inversion volume. In contrast to the inversion pulse, the spatial distribution of the flip angle for a conventional excitation pulse directly determines signal intensity in the final images. Thus, it is critical to homogenize as much as possible |B₁⁺| in the target of interest and, at the same time, avoid areas with little or no |B₁⁺| that would result in artifactual defects mimicking occluded vessels in the reconstructed angiograms. To satisfy these needs, a second B₁ shimming solution (B1S2) was employed which focused on |B₁⁺| homogeneity. Note that the small flip angle used for the excitation pulse makes it possible to apply B₁⁺ shimming solutions with low transmission performance without hitting the maximum achievable |B₁⁺|. The format of each B₁⁺ shimming solution consisted of a table of RF phases and gains for the 16 channels which were uploaded in the RF control unit memory before starting the angiography acquisition. The imaging sequence was programmed to then sequentially send TTL triggers to the RF control unit before the inversion pulse and before the first excitation pulse (Figure 1b) to switch to the next B₁ shimming table. All B₁ shimming tables being pre-loaded into the phase and gain controller RAM, real-time switching between tables during the MR sequence takes approximately 5 μs. From the acquired 3D source data, axial 40 mm thin slab maximum intensity projections (MIPs) were generated before manual cropping and full volume coronal MIPs were generated after manual cropping. All images used for angiography were reconstructed as root sum of squared magnitude images (from the 16 receive channels) using the standard reconstruction software of the scanner.

B₁⁺ shimming

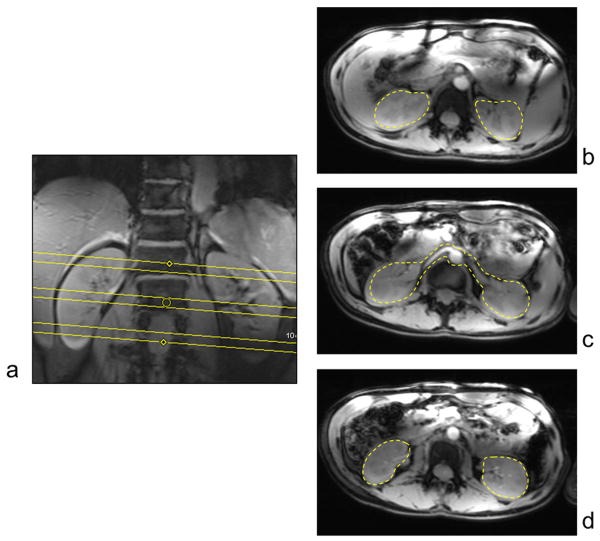
Prior to the angiographic acquisition described above, subject dependent B₁⁺ shimming was performed to address the transmit B₁ challenges. Complex B₁⁺ maps were estimated for each of the 16 channels using a fast, low flip angle, multichannel B₁⁺ calibration scan (19) allowing for completing the entire calibration acquisition over three slices in a single breath hold (20): 300 mm × 420 mm rectangular FOV, 18 ms TR, 3.5 ms TE, 57 × 128 acquisition matrix and 8 mm slice thickness. The total time for the calibration scan was 18 s including separate acquisitions transmitting through each channel individually, transmitting through all channels simultaneously and with all RF channels blanked. The calibration data was acquired in oblique axial views, angled to accommodate the spatial shift typically observed along the foot head direction between the center of the right and left kidneys. The center slice was positioned to approximately cover both the left and right renal arteries, while the other two slices covered the upper and lower poles of both kidneys, Figure 2a. Contoured regions of interested (ROI) were manually drawn on the three calibration slices to define a multi-ROI spatial target for subsequent B₁⁺ shimming computations: on the center slice, a single ROI was drawn, encompassing the two renal arteries and the parenchyma of both kidneys, while on the upper and lower slices two ROIs were drawn, one around each kidney, Figure 2b. From here onward, the union of all the aforementioned manually drawn ROIs will be collectively referred to as the ROI utilized for B₁⁺ shimming computation.

Figure 2.

(a) The three slice, subject dependent, single breath-hold, B1+ shimming calibration data was acquired in oblique axial views angled to best cover both kidneys. The center slice (c) was positioned to approximately cover both the left and right renal arteries, while the other two slices covered the upper (b) and lower (d) poles. Contoured regions of interested (ROI) were manually drawn on the three calibration slices to define a multi-ROI spatial target for subsequent B₁⁺ shimming computations. The union of all the regions are collectively referred to as the ROI utilized for B₁⁺ shimming computation in the text.

As indicated in the angiography sequence section, different optimization criteria were used to calculate B₁⁺ shimming solutions. The two ends of the spectrum of B₁⁺ optimizations utilized for B₁⁺ shimming can be described as follows. One end of the spectrum, aiming at a uniform |B₁⁺| distribution, consists of minimizing the Inhomogeneity Coefficient (IC) defined as the ratio of the standard deviation to the mean of |B₁⁺| through the targeted ROI: IC = std(|B₁⁺|) / mean(|B₁⁺|), where B₁⁺ is the sum of the 16 complex valued B_1,k⁺ of each channel k [k : 1 → 16] with B₁⁺ = Σ_kB_1,k⁺. This algorithm was used to compute B1S2 applied on the excitation pulse. The other end of the spectrum, aiming at minimizing the RF power required for a given average flip angle, consists of maximizing B1 efficiency (B₁Eff) defined as the ratio of the magnitude of the sum (B₁MOS) to the sum of the magnitude (B₁SOM) of B_1,k⁺, i.e. B₁Eff = B₁MOS / B₁SOM with B₁SOM = Σ_k|B_1,k⁺| and B₁MOS = |Σ_kB_1,k⁺| (9,13). Used alone, however, B₁Eff maximization often resulted in highly heterogeneous B1⁺ shimming solutions where areas of very high B1 efficiency (B₁Eff close to 100%) were juxtaposed to areas almost completely devoid of B1⁺ (data not shown). To avoid such excessive local |B1⁺| minima, a tradeoff algorithm was used to compute B1S1 (applied on the inversion pulse), where B₁Eff maximization was constrained to a user definable upper limit of a min-max ratio defined as R = (max(|B₁⁺|)-min(|B₁⁺|))/mean(|B₁⁺|). In practice, if the min-max constraint is completely relaxed, the tradeoff solution equates to a straight B1 efficiency solution. After the computation and application of each B1⁺ shimming solution, a quick (few seconds) small flip angle test, consisting of a simple GRE acquisition, was obtained and compared against the image pattern predicted by the B₁ shimming algorithm. These calculated B₁⁺ shimming solutions were compared against the geometric transmit phase setting.

The various optimization criteria detailed above can be performed by varying the phase (φ_k), magnitude (V_k) or both magnitude and phase of each of the transmit channels. An advantage in modulating the phase-only, while keeping an even magnitude through all channels, is to avoid B₁ shimming solutions where most of the total RF power is distributed on only a few channels, potentially increasing the risk of exceeding local SAR limits especially when a high average flip angle is sought. Hence, in practice, the majority of B₁⁺ shimming used for body applications by our group is accomplished using phase-only optimization. On the other hand, a larger degree of freedom is expected in principle when modulating both the phase and magnitude, which is especially desirable to achieve a homogeneous excitation. As mentioned previously, the B₁⁺ shimming requirement for the low flip angle excitation (B1S2) was for a homogeneous field. Because of the small flip angles required for excitation, the corresponding RF pulses had a dramatically lower peak B₁⁺ requirement reducing the potential of excessive local SAR resulting from the distribution of RF power through only a few channels. Therefore, for the small flip angle excitation only (B1S2), we investigated both phase-only and magnitude+phase solutions.

In order to compare transmit performance between different B₁⁺ shimming solutions, 2D |B₁⁺| maps were obtained with the actual flip angle (AFI) imaging sequence, a gradient echo technique using a constant flip angle with two interleaved TRs (21). While it has been shown that 2D AFI measurements are intrinsically biased (22) and do not directly provide an absolute quantification of B₁⁺ fields, they offer the substantial advantage of being short enough to be acquired in a single breath hold, allowing for the rapid measurement of relative |B₁⁺| for comparing different optimization strategies. The AFI sequence parameters included: FOV = 350 mm, TR1/TR2 = 20/120 ms, 3.0 ms TE, 2 averages, 96×128 acquisition matrix, 5 mm slice thickness, nominal flip angle 50 degrees, GRAPPA acceleration 3 with an acquisition time of approximately 13 s.

B₁⁺ related computations were run in Matlab (The Mathworks, Natick, MA). All B₁⁺ shimming calculations were performed using routines written in-house making use of functions provided by the Matlab Optimization Toolbox to perform iterative non-linear constrained optimization. All Matlab tools were made available in a user friendly, HTML based, graphic interface using the web browser functionality of Matlab. B₁⁺ shimming was performed with the goal of managing the B₁⁺ magnitude profile without concern for actual B₁⁺ spatial phase distribution; thus, B₁⁺ targets were always defined as magnitude B₁⁺, even though all computations were done using B_1,k⁺ maps in the complex domain. The non-linear constrained optimization algorithms included one minimized function and one (or two) additional constraints. The corresponding combinations used for the four B1+ shimming solutions detailed in this study are summarized in Table 1.

Table 1.

Minimized functions and constraints for B₁⁺ shimming algorithms

		Magnitude+Phase	Phase-Only
		Homogeneous	Homogeneous	Efficiency	Tradeoff
Minimized function§†	IC = std(|B1+|) / mean(|B1+|)	X	X
	−B1Eff = −B1MOS/B1SOM			X	X
Constraint†	[(max(|B1+|)−min(|B1+|)) / mean(|B1+|)] ≤ R¶				X
	[Max(Vk) / Min(Vk)] ≤ 4	X
	Vk=1 for all channels k=1,2,…,16		X	X	X

^§The practical implementation in Matlab of maximizing (B1Eff) consisted of minimizing (−B1Eff)

^†For all B₁⁺ shimming algorithms, B₁⁺ values are only considered for the voxels included within the B₁⁺ shimming ROI. Other pixels are ignored.

^¶R is a positive scalar chosen by the user. Smaller values of R tend to decrease both IC and B1Eff

RF power calibration

A centric k-space ordered, single shot, small flip angle, saturation prepared turbo-FLASH (TFL) acquisition was used for absolute power calibration, by varying the voltage of the saturation pulse, immediately followed by a train of fast GRE readout as described by Vaughan et al. (23). With this technique, when the preparation pulse attains 90 degrees in a given area, the corresponding signal approaches the level of the background noise in the reconstructed image. Parameters for the TFL acquisition included: FOV = 450 mm, TE = 1.2 ms, acquisition matrix = 144×192, 8 mm slice thickness, nominal flip angle 20 degrees, GRAPPA acceleration of 2 with an acquisition time of approximately 0.2 s. This power calibration was performed for each B₁⁺ shimming solutions and the voltage of each RF pulse was individually adjusted within the sequence, accordingly.

SAR Modeling

XFDTD, a finite difference time domain (FDTD) solver was used to evaluate B₁ and E-fields in the torso in a whole body model (REMCOM, Pittsburgh, PA). The focus was on evaluating the transmit B₁⁺ distributions and peak local SAR under various B₁⁺ shimming solutions in the target region.

When multiple B₁⁺ shimming solutions were used, a combined peak local 10 g average SAR per Watt was obtained by taking the maximum value of a weighted sum of each simulated, B₁⁺ shimming specific, volumetric SAR data. The weights were derived from the fraction of the power applied during each B₁⁺ shim solution within the angiography sequence, taking into account the shape, duration and magnitude of the corresponding RF pulses. The final peak local SAR was determined, for an individual and for a specific B₁⁺ applied shimming strategy, by multiplying the total average power delivered in-vivo with the combined peak local 10 g average SAR per Watt derived from the simulations time averaged over the mean TR. Because the sequence is respiratory triggered, the average respiratory rate affects the average TR and thus the final SAR values.

Power Monitoring

Safety for all subjects was ensured by monitoring forward and reflected power, individually on all channels, using a previously described home-built system (16). Limits on allowable time averaged transmit power (TAP) were based on the knowledge of the combined peak local 10 g averaged SAR values from simulation and local SAR guidelines provided by the International Electromechanical Commission (IEC) (24). The normal and first level operating modes suggested by the IEC for local SAR in the torso are 10 W/kg and 20 W/kg, respectively.

Results

Anatomic Imaging

Figure 3a shows the coronal image of the kidneys using the transmit phases based on coil geometry. This image demonstrates the typical pattern or destructive interferences observed in vivo with the default setting. Despite the observed signal heterogeneity, similar images acquired in the axial plane were sufficient for planning the B₁⁺ calibration data in the angiography studies. If the origin of the renal arteries could not be observed with the default geometric transmit phase setting, then a previous B₁⁺ shim solution from another study was used as a starting point. Figure 3b shows the same coronal slice after acquiring a dataset with a local B₁⁺ shim setting (13). The local shim was implemented with two regions of interest, one around each kidney, drawn on a single axial slice. While this most basic B₁⁺ shimming algorithm provides reasonable gradient echo images in the kidney, it was not sufficient for obtaining the homogeneity or efficiency required for imaging the more complex anatomy of the renal arteries. Using the same acquisition parameters with the exception of a smaller FOV (240 mm) and thinner slices (2 mm), a higher resolution T1-weighted image shows the high contrast of the vessels in the kidney, Figure 3c.

Figure 3.

Coronal anatomic images from a volunteer using (a) the default geometric transmit phase setting and (b) a local B₁⁺ phase shim optimized over two regions of interest in the axial plane; one around each kidney. (c) A high resolution version of (b) demonstrating excellent contrast between structures in the kidney and the vessels.

B₁⁺ Mapping

The relative 2D AFI B₁⁺ maps for geometric, efficiency and homogeneous B₁⁺ phase sets are shown for the same individual in Figure 4a-c. All B₁⁺ maps were generated while using the same transmit power. B₁⁺ profiles along the course of the renal artery are shown in Figure 4d. While the efficiency solution greatly increases the average B₁⁺ performance through the kidney, the transmit field is still relatively inhomogeneous with a notable region of low B₁⁺ through the right renal artery. With the homogeneous solution, transmit B₁ is more uniform throughout the target region at the cost of efficiency.

Figure 4.

The relative 2D AFI B₁⁺ maps from the same individual are shown for (a) geometric, (b) efficiency and (c) homogeneous B₁⁺ phase sets. All B₁⁺ maps were generated while using the same transmit power. (d) Relative B₁⁺ profiles along the course of the renal artery for the different shim solutions.

Angiography

Low flip angle GRE acquisitions are shown in Figure 5a-c at the middle slice location of the B₁⁺ shimming acquisition after applying various transmit phase sets. The region in this slice used for B₁⁺ shimming is shown in Figure 5a. As demonstrated in the relative B₁⁺ maps in Figure 4, the efficiency solution results in higher B₁⁺, as indicated by the brighter signal intensity, compared to the homogeneous solution. However, the arrow at the location of the right renal artery clearly shows the absence of B₁⁺ when pure transmit efficiency was the goal. The impact of using a single B₁⁺ shim solution for all RF pulses in the angiography acquisition, that is when B1S1 and B1S2 are the same, can be observed in the volumetric MIPs in Figure 5d through 5g. With the straight efficient B₁⁺ solution, Figure 5d and 5e, the contrast between the distal arteries and the background parenchyma is better than that of the homogeneous solution, Figure 5f and 5g. Meanwhile, the homogeneous solution allows continuous visualization of the arteries with more uniform signal intensity without the signal void observed in the efficiency solution.

Figure 5.

Low flip angle GRE acquisitions at the middle slice location of the B₁⁺ shimming acquisition with (a) geometric, (b) efficiency and (c) homogeneous phase sets. The broken yellow curve in (a) identifies the location of the B₁⁺ shimming ROI located at the position of the central slice of the calibration dataset. The resulting axial (d) and coronal (e) volumetric MIPs are shown when using the efficiency solution for both B1S1 and B1S2 in the angiography sequence. The resulting axial (f) and coronal (g) MIPs are shown after using the homogeneous solution for both B1S1 and B1S2 in the angiography sequence.

Figure 6 demonstrates angiography results from several volunteers with various B₁⁺ shimming strategies. Figure 6a shows the axial thin MIPs and the coronal cropped volumetric MIPs from a small individual where a phase-only homogeneous solution was used for both B1S1 and B1S2. As opposed to Figure 5g, where the same shimming strategy was used, this acquisition shows improved background suppression due mainly to the reduced size of the subject in this example where anterior-posterior dimension was 15.4 cm compared to 21.6 cm for the subject in Figure 5g. However, even with improved performance, residual parenchymal and venous signal reduce the ability to visualize the renal arterial vessels when using a homogenous solution for B1S1 and B1S2. Improved results in a larger individual, anterior-posterior dimension of 21.6 cm, are shown in figure 6b where a completely relaxed min-max constraint was used to maximize efficiency for B1S1 and a phase-only homogeneous solution was used for B1S2. The angiography results of the final two subjects shown in Figure 6c and 6d were acquired using a tradeoff between efficiency and homogeneity with an R of 1.5 for B1S1 and a magnitude+phase homogeneous solution for B1S2. These individuals had anterior-posterior dimensions of 18.4 and 18.3 cm, respectively. In addition, the inversion slab was overprescribed in these last two cases to accommodate for residual B₀ inhomogeneities which can have a large impact on the positioning and effectiveness of the selective inversion especially on kidneys with a larger extent in the cranial-caudal direction.

Figure 6.

Thin axial MIPs (left column) and cropped volumetric coronal MIPs (right column) from multiple volunteers with various B₁⁺ shimming strategies: (a) both B1S1 and B1S2 run with a phase-only homogeneous solution, (b) B1S1 efficiency solution and B1S2 phase-only homogeneous, (c-d) B1S1 tradeoff solution R=1.5 and B1S2 magnitude+phase homogeneous.

Simulations

Electromagnetic simulations allowed the different shim strategies to be evaluated in terms of transmit B₁ efficiency and homogeneity (Figure 7) and SAR (Figure 8). Figure 7 demonstrates that homogeneity decreases with increased efficiency. This is further detailed in Table 2 which summarizes the mean, standard deviation and inhomogeneity coefficient (IC) of the B₁⁺ normalized by the square root of the net input power for the multiple shimming solutions within the multi-slice optimization ROI.

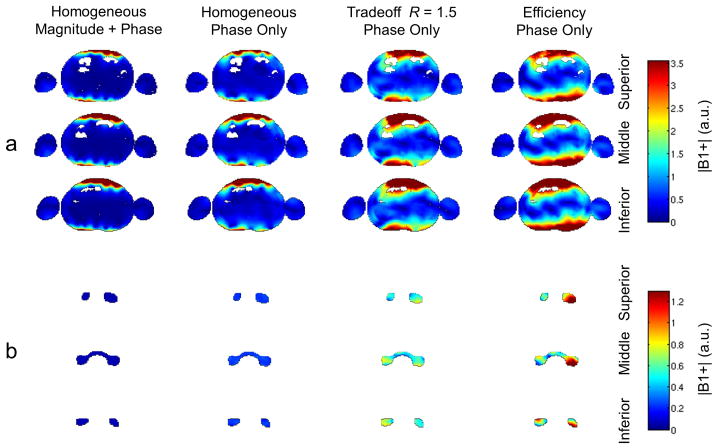
Figure 7.

Relative transmit B1 maps from FDTD simulations of the four B₁⁺ shimming strategies employed in this work. Similar to in vivo, three slices were used to calculate the B₁⁺ shim solutions. (a) The relative transmit B1 maps across each of the three slices. (b) the relative transmit B1 maps across each of the ROIs from each slice. Simulations demonstrate a similar behavior in B₁⁺ performance to the in vivo measurements demonstrated in Figure 4. Of particular note is the drop out of B₁⁺ in the region of the right renal artery shown in the middle slice of the phase-only efficiency solution.

Figure 8.

The axial sections of the simulation at the level of the peak local SAR are for 4 different B1+ shim solutions: (a) magnitude+phase homogeneous, (b) phase-only homogeneous, (c) phase-only tradeoff R=1.5, and (d) phase-only efficiency. The spatial location of the peak SAR varies depending on the specific solution employed.

Table 2.

SAR and transmit B1 shimming results from simulation.

		Magnitude+Phase	Phase-Only
		Homogeneous	Homogeneous	Tradeoff	Efficiency
|B1+|/W½	Mean	0.0566	0.223	0.558	0.827
	SD	0.0014	0.017	0.130	0.363
	IC	0.073	0.077	0.233	0.439
Local SAR	SAR / W	1.202	0.259	0.508	0.358
	SAR / B12	375.0	5.21	1.63	0.522

The simulated electric fields allowed the calculation of local 10 g average SAR per Watt throughout the entire body model. The axial sections, at the level of the peak local SAR, are shown in Figure 8 for each of the shim solutions. It is notable that the spatial location of the peak SAR varies depending on the specific solution employed. The local SAR and SAR normalized per [B₁⁺]² are reported in Table 2. When normalized by the average B₁⁺ over the shim ROI, the SAR/[B₁⁺]² increases dramatically for the less efficient and more homogeneous solutions.

Local SAR

For the acquisitions conducted in this study, the average predicted combined peak local 10 g average SAR was 10.13 ± 3.78 W/kg with a range of 6.91 to 14.33 W/kg. The majority of the power was applied during B1S1, ranging from 83% to 93%. The large range was primarily a result of the widely varying power required for B1S2 as it depended on the B₁⁺ shim solution, the number of echoes acquired per respiratory cycle, and the nominal flip angle. The number of echoes acquired per cycle was in turn dependent on respiratory cycle duration (3.61± 0.68) and the requirement to restrict data acquisition to the quiescent period at end expiration.

Time Averaged Power Limit

A limit on time averaged power in the body was set at 2.0 Watts per channel. The angiography acquisition with the highest local 10 g average SAR (14.33 W/kg) was close to this limit using near maximum power for B1S1 with a tradeoff solution and much lower power for B1S2 with a magnitude+phase homogeneous solution. If any single channel exceeded the prescribed limit, all amplifiers were disabled immediately. With respect to the studies conducted to date, there have been no reports of local or global heating based on standard exit interviews completed by study participants.

Discussion

Non-contrast enhanced rMRA can play an important role in the evaluation of the renal vasculature without the need for exogenous contrast agents or ionizing radiation. The potential of improved vessel visualization and characterization when running these studies at higher fields is a result of prolonged longitudinal relaxation rates and increased SNR. In the T1w images, the high signal in the vasculature can already be observed simply from in-flow effect (Figure 3c). However, the ability to image the complete arterial vasculature of the kidney while suppressing the background signal is more challenging as the target anatomy covers a relatively large region of interest, typically across regions which experience large destructive interferences and B₀ inhomogeneities. The major impediments to performing successful studies at 7T were B₁⁺ inhomogeneity and limitations in the achievable peak B₁⁺. Depending on the specific choices of B₁⁺ shim and an individual subjects respiratory rate, local SAR can also be an issue if high SAR, low efficiency B₁⁺ shimming solutions are used. By using a 16 channel transmit array coil combined with RF pulse dependent B₁⁺ optimization, non-contrast enhanced renal angiography was successfully performed. Implementation of the multi-shim acquisition strategies were performed with real-time power monitoring on all channels to ensure adherence to current guidelines on local SAR.

B₁⁺ Shimming Methods

In general, gradient echo anatomic imaging was relatively robust with respect to the B₁⁺ shimming solution. For example, in Figure 3, B₁⁺ shimming was performed using a local shim approach using two ROIs drawn around the kidneys from a single axial slice. While this solution provided high quality anatomic images it was insufficient for angiographic studies which had more demanding requirements in terms of peak B₁⁺ and B₁⁺ homogeneity.

For the non-contrast rMRA acquisitions, tailoring the optimization constraints to fit the characteristics and function of each RF pulse was critical. As shown in Figure 5, the use of a single solution results in compromised image quality either as uneven visualization of the vasculature or incomplete suppression of the background signal. Using a homogeneous solution for both inversion as well as excitation resulted in the inability to achieve signal nulling throughout the kidneys, Figure 5g and 6a. As shown by simulation (Figure 7) and relative B₁⁺ plots measured in vivo (Figure 4), the homogeneous solutions are less efficient than the tradeoff or pure efficiency solutions. This lack of efficiency results in two significant problems: 1) the power to reach the adiabatic condition for the inversion pulse can simply not be realized with the hardware available in this study except in extremely small individuals and 2) even if enough power was available, local SAR limits would most likely be exceeded. The second point can be further appreciated by again observing the B₁⁺ normalized SAR performance for the different solutions presented in Table 2 where, for the phase optimized homogeneous solution, the SAR/[B₁⁺]² is nearly 3-fold the value of the tradeoff and 10-fold higher than the straight efficiency solution. This issue is even more pronounced with the magnitude+phase homogeneous solution where a four-fold decrease in B₁⁺/W^1/2(0.0566 / 0.223) and nearly 5-fold increase in SAR/W (1.202 / 0.256) create a situation where the penalty to achieve anything but the smallest flip angles is unreasonable.

In the data acquired with the magnitude+phase homogeneous solution (Figure 6c and 6d), the power effectively used for excitation was, at most, minimally increased compared to the phase-only solution despite of the fact that, based on simulations shown in Table 2, it should have been increased about 16-fold to maintain the same B₁⁺ magnitude. Increasing the power 16-fold was not an option for three reasons: 1) the required power was simply not available, 2) any increase in power would be a multiplier on the already 5-fold increase SAR/W as shown in Table 2, and 3) sufficient SNR was available even with the predicted lower flip angles to provide reasonable angiograms. Anecdotally, this solution produced improved results, although arguably insignificantly improved. Further studies investigating the role of the magnitude+phase solution are required to determine if the decreased efficiency and dramatic increases in normalized SAR are worth the modest improvement in homogeneity compared to the phase-only solution.

In general, the impact of reduced RF efficiency is much less significant for the excitation RF pulse of the gradient echo readout than for the inversion pulse. Even when using the magnitude+phase homogenous solution, the percent of the total power used by the excitation pulses was maximally 17% of the total power delivered during an acquisition. The contribution of the excitation pulses can even be further mitigated by reducing the number of profiles acquired during each inversion prepared shot by increasing the parallel imaging reduction factor. A factor of 2 was used in most of the scans in this study with the goal of decreasing the total acquisition window to minimize motion artifacts. However, higher reduction factors are possible to further decrease sensitivity to motion during the respiratory cycle and to further mitigate B₁⁺ shimming solutions which have a higher SAR/ [B₁⁺]².

The combination of the homogeneous solution for excitation and the tradeoff solution for inversion, whether constrained by R or with the min-max criteria fully relaxed, provides the flexibility needed to accommodate a much larger range of patient geometries. Every geometry, including torso dimensions, kidney size and kidney location, results in different patterns of destructive interferences which can be more or less favorable for a given B1+ shimming solution. Background suppression was reasonable when using the efficiency solution in some individuals. However, even though an adiabatic inversion pulse was used, local minima in B₁⁺ can result in incomplete inversion at some locations causing variable background suppression and venous contamination as seen in figure 6b, which can obscure the smaller vessels in the kidney. When using the tradeoff solution with a variable R, the operator has some control over these local minima. On one hand, as these local minima are reduced with decreasing R, the efficiency decreases, while on the other hand reducing the regions which fail to be inverted given that sufficient power is available. In the current application, R was chosen empirically based on the predicted efficiency and spatial distribution of the combined B₁⁺ shimming calibration data. In general, for an R of 1.5, relatively uniform inversion was possible as can be seen in the MIPs shown in Figure 6c and 6d, reducing both background signal and local venous contamination. Further optimization tools are under active development, aiming to automatically determine the R value of the tradeoff solution taking into consideration limits on available power as well as constraints on local SAR (based on XFDTD models), while avoiding residual spots of weak |B₁⁺| (25).

Inversion Pulse

The RF pulse chosen for inversion in these studies was an adiabatic hyperbolic secant (HSn) pulse with n=4. With increasing “n”, the peak power requirements decrease as the amplitude envelope of the pulse flattens (18). Values of “n” larger than 4 were also tried to further minimize the peak B₁⁺ requirements, however the drop of adiabaticity near the edges of the pass band resulted in banding artifacts in the background signal therefore their use was discontinued (results not shown).

Along with “n”, there is the bandwidth time product of the HSn pulse we label R as in Garwood et al. (18). In this study, an R of 20 was used resulting in an inversion bandwidth between 800 and 1000 Hz when using pulse durations of 25 and 20 ms, respectively. The bandwidth time product also influences the required peak power and thus SAR; for a given HSn pulse the required peak power is proportional to R. Choosing an HS4, R=20 inversion pulse was a compromise in both band pass performance and bandwidth. With a bandwidth of 1000 Hz, the spatial selectivity of this inversion pulse was still affected by the relatively large B₀ variations across the planned volume even after performing localized phase map based B₀ shimming. Typically, the effect of residual B₀ inhomogeneities resulted in warping and stretching of the slab selective inversion which, if tightly prescribed, resulted in missing part of the kidneys. These challenges were addressed by overprescribing the inversion slab accomplished by stretching it in the foot-head direction. Based on the limitations of the coil coverage, this overprescribed inversion was equivalent to implementing a non-selective pulse, effectively reducing planning issues especially when attempting to accommodate the B₀ inhomogeneities across larger kidneys as in Figs. 6c and 6d. While the potential exists to saturate the in-flowing blood thus decreasing the available signal for imaging in the renal arteries, this has not been observed in the presented results. Most likely, non-selective inversion strategy would not be appropriate with large circumventing volume transmit coils used on most lower field clinical scanners, however the transmit B₁ profile along the Z axis of the local transceiver array used in this study serves to limit the foot-head extent of the applied RF, even when a non-selective inversion is used, thus greatly minimizing the potential saturation of the in-flowing blood.

Future Directions

Improvements in the current approach could be realized building upon the developments discussed in this study. For example, the systems default chemical shift selective saturation was used for lipid suppression with the same B₁⁺ shimming solution used for inversion. While the quality of the lipid suppression was not explicitly investigated, as this pulse was not designed to be insensitive to B₁⁺ variations. While a composite saturation pulse optimized for B₁⁺ insensitivity or an adiabatic half passage pulse would be more appropriate in the current application at 7T, it should be mentioned that the presence of residual lipids were not a prominent issue when generating the cropped volumetric MIPs. Also, if suppression of the subcutaneous lipids is the goal, then the challenge to achieve lipid suppression will lie as much with B₀ shimming as it would with a B₁⁺ insensitive saturation. In addition, to optimize lipid suppression for the subcutaneous signals, B₁⁺ shimming would need to be performed over a different ROI than that used for optimizing the inversion and excitation pulses as used in the current study.

At ultrahigh fields, there is often a challenge to obtain the required peak B₁⁺ needed for a given application with sufficient homogeneity while not exceeding SAR limits. Limitations of peak B₁⁺ can potentially be addressed through hardware solutions and/or RF pulse design. Potential hardware solutions include the use of larger RF amplifiers and more efficient delivery of RF to the subject by optimizing the transmit chain and coils. However, using solely the B₁⁺ optimization strategies presented in this study, the potential advantage of increased power delivered to the subject would be limited due to proportionately higher local E-fields and thus SAR. B₁⁺ optimization strategies which implicitly include local SAR in the solutions would improve the ability to use increases in the amount of available power (26). These B₁⁺ optimization strategies could be employed in combination with RF pulse optimization (27,28). For example, VERSE can be used to decrease the peak power requirements of the adiabatic pulses used for inversion, however this advantage is accompanied by undesirable off-resonance characteristics (29). The tradeoff between different hardware configurations and optimization strategies will need to be evaluated in the context of this application in future studies to better define the best approach.

In our current implementation, it takes at least about 12 to 15 minutes to complete the B₁⁺ shimming procedure, which includes: positioning oblique axial slices on scout images (∼2min), fast 16-channel B₁⁺ mapping acquisition (∼18s), raw data transfer on an external PC (∼1min), data format conversion and B₁⁺ map computation (∼2min30s), manual drawing of ROIs (∼2min), B₁⁺ shimming calculation (about 10 to 20s for each solution), transferring and applying B₁⁺ shimming solution to the RF control unit (∼20s), running quick test images to verify B₁⁺ shimming success (∼3s acquisition per solution). However, most of the time described above is spent on data transfer on a standard external PC, followed by data conversion, computation and graphical display in maltab. Therefore, the B₁⁺ shimming procedure described in this study will be dramatically shortened when these methods are integrated directly on the scanner console (no data transfer) with calculation modules compiled in C-language.

Conclusion

Performing non-contrast rMRA studies at ultrahigh field depends on the ability to manage multiple challenges including inhomogeneity in B₀ and B₁⁺, limitations in peak power and the potential for local heating currently characterized by local SAR. By using a 16 channel TEM/stripline transceiver surface array coil driven by 16 independent RF amplifiers with individual phase and gain control, subject dependent B₁⁺ shimming solutions within anatomically selected regions of interest could be determined. The benefits of optimizing B₁⁺ for efficiency, homogeneity and a tradeoff between the two were investigated both experimentally and in simulation. Solutions with increased homogeneity were also less efficient while simultaneously exhibiting an increase in normalized local SAR. Therefore, due to limits in both available power and local SAR, using solely a homogeneous solution was not a realistic option especially as subject size increased. By dynamically applying B₁⁺ shim solutions which match the requirements of each RF pulse in the angiography sequence, high quality rMRA results in a variety of subject geometries could be generated with the current acquisition methods, hardware and within SAR constraints.

Further studies focusing on the optimal use of the various B₁⁺ shimming solutions still need to be performed. In addition, the potential role of RF design and optimization strategies which specifically address the limiting factor of peak local SAR need to be investigated. Once optimized, these methods will be compared against non-contrast enhanced SSFP acquisitions performed at lower field strengths to determine if the improved SNR and prolonged longitudinal relaxation times associated with increased static magnetic field strength can indeed yield superior diagnostic information.