Working with capacity limitations: operations management in critical care

Abstract

As your hospital's ICU director, you are approached by the hospital's administration to help solve ongoing problems with ICU bed availability. The ICU seems to be constantly full, and trauma patients in the emergency department sometimes wait up to 24 hours before receiving a bed. Additionally, the cardiac surgeons were forced to cancel several elective coronary-artery bypass graft cases because there was not a bed available for postoperative recovery. The hospital administrators ask whether you can decrease your ICU length of stay, and wonder whether they should expand the ICU to include more beds For help in understanding and optimizing your ICU's throughput, you seek out the operations management researchers at your university.

Introduction

Increasing demand for critical care has made capacity limitations commonplace in the ICU [1]. These limitations occur when there are no available ICU beds for patients with critical illness, leading to delays in ICU admission that have important clinical and economic consequences. Admission delays can result in the boarding of critically ill patients in the emergency department or in other hospital units, which is associated with increased morbidity and mortality [2,3]. Admission delays can also result in decreased revenue for hospitals, as they may force hospitals to cancel elective surgeries or transfers from outside hospitals.

These problems have forced the critical care community to develop innovative ways to address capacity constraints and improve throughput. Yet these problems are not unique to the ICU, or even unique to healthcare in general. Limited capacity and the resulting problems of waiting times and throughput losses exist in many processes, ranging from financial services to automotive production. The academic field of operations management is specifically designed to address these issues. The purpose of the present review is to provide a brief overview of operations management and to present a set of case studies from work environments other than hospitals, thereby exposing readers to operations management and its potential application to critical care.

What is operations management?

Working with capacity limitations

Many operations - in particular, service processes such as restaurants and airlines - have high fixed costs. These fixed costs typically reflect the cost of maintaining a certain capacity availability, where capacity is defined as the maximum number of customers that can be served per unit of time. Examples of fixed costs include the wages required to pay labor or the cost of machinery for production. Yet while costs in services tend to be fixed, revenue increases proportionally to the number of customers served per unit time - also referred to as throughput. This scenario creates an economic incentive to operate the process at a high level of utilization, where utilization is defined as the ratio of the number of customers served (the throughput) to the maximum number of customers that we could serve (the capacity).

Consider the following simplified example. A service has a fixed cost of $1,000 per day and obtains $20 per customer served. The operation thus breaks even at 50 customers served per day. At 60 customers per day, the service obtains $200 in profits per day. At 70 customers, the process obtains $400 in profits. In other words, increasing the number of customers served from 60 to 70 (a 16.7% increase) leads to a 100% increase in profits. The marginal (additional) cost of service is zero while the marginal revenue is high. Maximizing utilization becomes a key priority.

Understanding the problem

By definition, utilization cannot exceed 100%. The money-seeking manager is thus tempted to seek almost 100% utilization. And high utilization, in and by itself, is not a problem. To see this, assume in an example process that customers arrive exactly once every 5 minutes (12 customers arrive per hour). Further, assume that it takes us exactly 4 minutes to serve each customer (thus, we could serve up to 15 customers per hour). The resulting utilization in this process would be 12/15 = 80%. We might be tempted to call this a 20% underutilization and seek additional demand to improve our profitability.

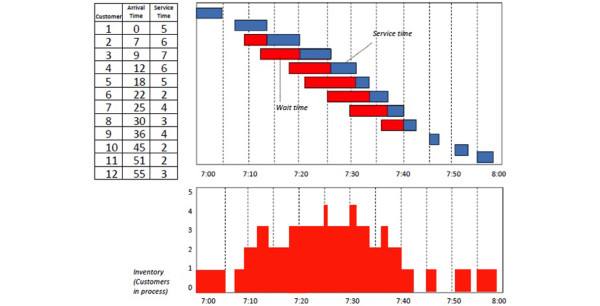
This strategy, however, would ignore an important reality of service delivery - variability. Customers are not widgets in an assembly line. The amount of service time depends on the particular needs of the customer at hand. Furthermore, the arrival times of individual customers may not be known in advance. These sources of uncertainty create a stochastic effect on our process. Consider the data shown in Figure 1. Just as before, 12 customers arrive per hour. This time, however, the arrival times are random. Similarly, we again take 4 minutes, on average, to serve a customer. Yet some customers get served quickly while others take longer. Although the mean demand and capacity remain constant, Figure 1 reveals that what previously appeared as an underutilized process is in reality a rather busy place. Indeed, some customers (for example, the fifth and sixth customers) spend much more time waiting than they spend in service. We also observe that the number of customers in the process at any one time goes as high as four (three waiting, one being served). Contrast this with the previous deterministic scenario, where each customer is served immediately upon arrival.

Figure 1.

Waiting time example. In this example a sample process takes an average of 4 minutes and 12 customers arrive randomly per hour. Time (minutes) is presented on the y axis. Top: the total process time, with the service time in blue and the wait time in red. Bottom: the number of customers in the process at any one time.

Variability is the enemy of operations. An 80% utilization of an automated assembly line with limited or no variability might be underutilized; an 80% utilization of a time-critical service in the presence of variability is asking for trouble. The example in Figure 1 assumed that customers would patiently wait in line until it is their turn to be served. But it is easy to conceive of settings in which customers might not be able or willing to wait. The branch of operations management that mathematically analyzes the interplay between process flows, utilization, and variability is referred to as queuing theory. Various mathematical models exist to inform the capacity planning in such an environment. For example, one might ask for the amount of capacity that is needed (the number of people to be hired, or the equipment to be purchased) so that customers get served in a given expected wait time.

One of the most prominent findings in this line of work is the insight that the average waiting time increases dramatically at higher levels of utilization. Specifically, the average waiting grows proportionally to a formula: utilization/(1 - utilization). This finding has substantial practical implications. For example, for a utilization of 80%, the ratio of 0.8/(1 - 0.8) equates to 4. For a utilization of 90%, this ratio grows to 0.9/(1 - 0.9) = 9. A 10% increase in utilization can therefore more than double the waiting time. This detrimental effect on the process's responsiveness needs to be kept in mind when we accept more demand in an attempt to increase utilization. Similar mathematical models exist for the case in which waiting is not possible. For example, one can predict the percentage of customers that will be lost due to capacity shortfalls when customers are unwilling or unable to wait.

Better, not more

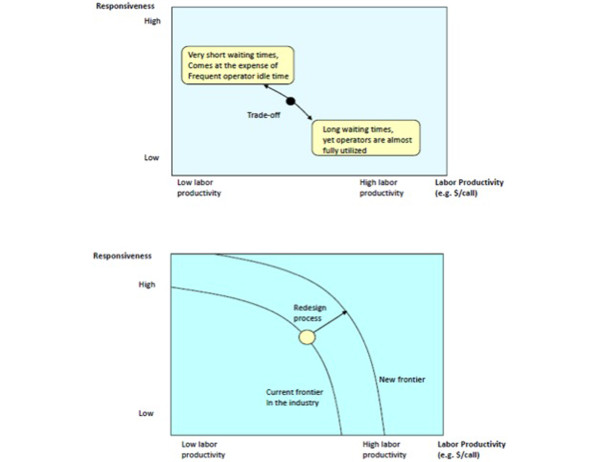
Our waiting time example illustrates the fundamental tradeoff between the efficiency of a process as measured by its utilization and its responsiveness as measured by its waiting time. The waiting time is reduced as more resources are added. Operations management tools - in particular, queuing theory - can help to find the right positioning along the efficiency-responsiveness frontier. But operations management can do more than just tradeoff one desirable process characteristic against another. Operations management is also about innovation. By creating an innovative process redesign, the aim is to shift out the frontier instead of simply supporting the optimal position on the current frontier (Figure 2). The process becomes better.

Figure 2.

Interaction of process responsiveness and productivity. Top: the tradeoff between responsiveness and productivity in a given process. Bottom: how process redesign can improve both responsiveness and utilization.

New frontiers might be reached by overcoming inefficiencies in the present process design (often referred to as waste) or by creating the flexibility to better cope with variability. Industrial pioneers such as Henry Ford reached new frontiers by redefining the production of physical goods. As work was increasingly divided, crafts-men were replaced by less skilled workers. Production processes were perfected over the subsequent decades, culminating in the legendary Toyota Production System that is now widely regarded as the gold standard for excellent operations [4,5]. The Toyota Production System emphasizes the need to continuously improve a process, driving out the so-called seven sources of waste: excess production, waiting times, transport steps, excessively long activity times, inventory, rework (fixing quality problems), and unnecessary motions. Work flows are optimized, capacity levels are chosen to match demand, activities are standardized, and protocols are implemented to standardize work, to reduce defects, and improve productivity.

Example 1: focus - the US Airline industry and the emergence of Southwest Airlines

The US Airline industry is a tough place in which to compete, and many airlines have experienced financial losses and bankruptcies. An interesting exception is Southwest Airlines, which has created a number of efficiency-related innovations in the air travel process and in turn has been rewarded with outstanding growth and profitability. Many of these innovations reflect the company's decision to focus on specific market segments and operational processes. For example, Southwest Airlines offers only economy-class seating, has a standardized check-in process, flies only one type of aircraft, and minimizes extraneous amenities such as meals and entertainment. Such focus has led to substantial process improvements by reducing both customer-related and process-related variability. Consequently, Southwest Airlines can achieve high levels of utilization and improved service times, while being able to command only marginally lower fares compared with their competitors (Figure 3).

Figure 3.

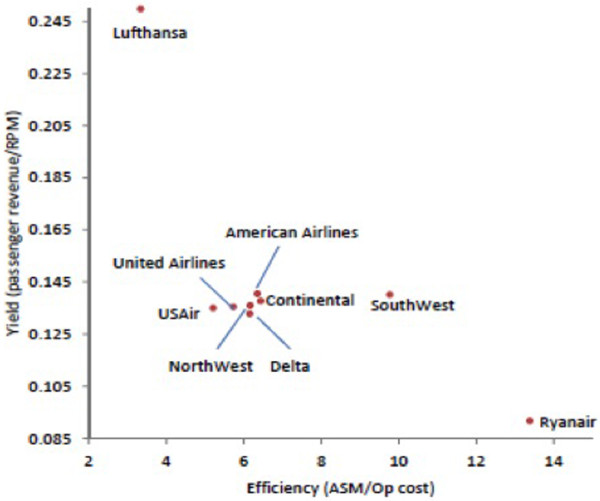
Productivity comparison in the US airline industry. Compared with other US airlines, Southwest Airlines achieves similar yields with greater efficiency. Lufthansa and Ryanair are added as non-US illustrative benchmarks. ASM, available seat mile; RPM, revenue passenger mile.

Example 2: quick response - local production and quick replenishment at Zara

Few industries are plagued by variability like the fashion industry, in which consumer tastes are fickle and orders are placed far in advance, typically to be produced in faroff places like East Asia. Consequently, retailers often end up with not enough of some products to meet demand (leading to missed sales opportunities) and too much of other products (requiring substantial mark-downs and lost profits). Zara's operational innovation has been one of local production, with approximately 50% of its merchandise sourced from its home country of Spain. At first glance, local production appears inefficient as wages in Spain are significantly higher than in East Asia. The local production allows for quick and frequent replenishment, however, enabling a tight integration between Zara's retail operation and their production process. As a result, Zara builds in flexibility into its operation and is able to react to unanticipated swings in demand.

Example 3: capacity pooling and chaining - Honda's platform strategy

Variability is the enemy of operations, yet the risks associated with variability decrease as we aggregate many independent sources of variability. For example, the financial risk of fire for an individual home owner is large, yet an insurance company with millions of fire policies faces relatively lower risk. Aggregating variability across independent sources is the idea behind capacity pooling. Consider an automotive company that operates multiple manufacturing plants and produces different models. A given car model can only be produced in exactly one plant. If demand increases relative to the forecast, that plant is unlikely to have sufficient capacity to fulfill it. Conversely, if demand decreases, the plant is likely to have excess capacity. The company can mitigate some of the demand-supply mismatch by pooling its capacity. Specifically, if every model could be made at every plant, high demand from one model can be served with spare capacity due to low demand from another, leading to better plant utilization and more sales. Such capacity pooling, however, would require the plants to be perfectly flexible - requiring substantial investments in production tools and worker skills. An interesting alternative to such perfect flexibility is the concept of partial flexibility, also referred to as chaining. The idea of chaining is that every car can be made in two plants and that the vehicle-to-plant assignment creates a chain that connects as many vehicles and plants as possible. Such partial flexibility can be shown to result in almost the same benefits of full flexibility, yet at dramatically lower costs [6].

Applying operations management to critical care

ICUs are faced with nearly the same throughput and capacity problems as the companies in our examples. The vast majority of critical care costs are fixed, resulting in substantial revenue increases with each additional patient [7]. ICUs also frequently operate at or near capacity, with subsequently large waiting times for admission [8]. Simply expanding capacity is not feasible due to space limitations within hospitals, workforce shortages, and government regulations [9]. Neither is expanding capacity necessarily desirable. As the above examples teach us, in the face of variable demand, expanding capacity can ultimately result in higher fixed costs, excess capacity, and long-term inefficiencies.

The science of operations management is specifically designed to solve these problems. ICU throughput is at heart a complex service problem - patients are just customers arriving at random times and with varying needs. Each takes a different amount of service time. The overall goal is to maximize quality while minimizing waste. In the ICU, quality comes in the form of low mortality and waste comes in the form of wait times (that is, admission delays), excess activity times (that is, long lengths of stay), and the need for rework (that is, the effort required to care for ICU-acquired complications and ICU readmissions).). Operations management not only can help tradeoff capacity and efficiency under our current process, but can also help us shift the frontier through continuous process improvement.

The first step is to understand the current process. What is the ICU utilization, and how much does it vary? What are the sources of ICU demand, and how much of that demand is random versus predictable? What is the average ICU length of stay (service time) and how does it differ between different patient types? How much of the current activity is true production versus waste in the form of ICU readmissions or discharge delays?

The next step is to apply queuing theory to mathematically formulate the current process and determine the point on the utilization curve that will maximize responsiveness and productivity. Increasing capacity might be necessary to achieve optimal throughput, or might only result in excess resources. Sometimes these results can be surprising. For example, an empiric analysis of ICU readmissions in the cardiac ICU at the University of Pennsylvania Hospital found that an aggressive early discharge policy resulted in an increase in overall capacity, even accounting for the increase in readmissions [10].

The final step is the search for ways to improve the current processes to increase throughput. Taking a lesson from Toyota, standardizing care through protocols might lead to decreased waste in the form of hospital-acquired infections or excess ventilator-days [11]. Splitting the single surgical ICU into two subspecialty ICUs (one for trauma and one for cardiac surgery) might introduce economies of scope, by which the specialty ICUs can perform their services more efficiently. This situation would be analogous to Southwest Airlines, which increased efficiency in part by limiting the scope of their services. To prevent adverse effects from boarding and to retain some of the gains from capacity pooling, each ICU could be cross-trained to care for the other's least sick patients - a form of chaining. Another approach might be to search for ways to minimize the effects of variable demand. For instance, if trauma cases tend to occur on the weekends, rescheduling elective cardiac cases from Friday to Monday could create capacity when it is most needed.

Conclusion

Operations management optimizes business processes. From traditional manufacturing to distribution and services, the principles and insights from operations management have been used successfully to help firms better manage their businesses. Determining the appropriate level of capacity is often challenging, particularly when dealing with variability from multiple sources. Operations management provides us with the tools to determine the optimal level of capacity and to manage the tradeoff s inherent in demand-supply mismatches.

Operations management, however, is not just about optimizing a given process or capacity allocation decision - it is also about improving process through innovation. The three examples discussed above offer a glimpse into the kinds of process innovations used by highly successful firms, but there are many more such innovations being used by firms both large and small [12]. Perhaps the greatest role operations management can play in the ICU is in teaching us how to apply these innovations to hospital medicine, thereby improving both the quality and efficiency of critical care.

Abbreviations

ICU: intensive care unit.

Competing interests

CT receives book royalty payments from McGraw-Hill Publishers. DKC and JMK declare that they have no competing interests.

Note

This article is part of a series on Healthcare Delivery, edited by Dr Andre Amaral and Dr Gordon Rubenfeld.