Nanostructure-enhanced laser tweezers for efficient trapping and alignment of particles

Abstract

We propose and demonstrate a purely optical approach to trap and align particles using the interaction of polarized light with periodic nanostructures to generate enhanced trapping force. With a weakly focused laser beam, we observed efficient trapping and transportation of polystyrene beads with sizes ranging from 10 μm down to 190 nm as well as cancer cell nuclei. In addition, alignment of non-spherical dielectric particles to a 1-D periodic nanostructure was achieved with low laser intensity without attachment to birefringent crystals. Bacterial cells were trapped and aligned with incident optical intensity as low as 17 μW/μm².

1. Introduction

Non-invasive optical manipulation of particles has emerged as a powerful and versatile tool for biological study and nanotechnology. In particular, trapping, alignment and rotation of cells, cell nuclei and sub-micron particles enables unique functionality for various applications such as tissue engineering [1,2], cancer research [3] and nanofabrication [4]. Since the inception of optical tweezers [5], researchers have been exploring new ways to increase their performance and functionality [6] while reducing the required optical intensity to achieve sufficient trapping force. Decreased optical intensity is essential for biological applications where intense optical radiation may be a concern [7–10]. Direct conversion from optical energy to mechanical energy has low efficiency, which is the underlying reason for high optical intensity requirement of optical tweezers. The challenge becomes more severe as the particle size decreases to sub-micron regime due to its small volume and therefore low optically induced dielectrophoretic force. The requirement on optical intensity can be reduced by combining conventional dielectrophoresis with optically induced conductivity change [11]. On the other hand, being able to achieve this goal through pure optical means can preserve the full configurability of optical tweezers with less system complexity, and impose no constraint on the conductivity of the sample solution. The primary approach along this direction entails optical near-field enhancement through interaction with plasmonic nanostructures to increase the local intensity and gradient of the field [12]. This has been implemented using patterned metal nanostructures [13–15], dimer nanoantennas [16], metal nanorods [17] under direct Gaussian beam illumination, through total internal reflection configurations, or involving the trapped dielectric particles in changing transmission resonance of metal nanoapertures [18]. While such methods have shown impressive results in increasing trapping force, trapping is limited to specific plasmonic “hot spots”, thus limiting their ability to simply holding particles in predetermined positions patterned onto a surface. This diminishes the functionality of conventional optical tweezers, where particles can be translated in any direction to arbitrary positions. The limitation can be alleviated using the self-assembled plasmonic platform approach [19]; however, generation of heat and the resulting convective flow is unavoidable in plasmonic effect. This phenomenon may be utilized for concentration and patterning of sub-micron particles and DNAs [20], but compromises the capability of single particle manipulation.

In addition to increasing the force of an optical trap, significant research efforts have been made to increase the functionality of optical tweezers. One area that has been of particular interest is rotation and alignment of non-spherical particles. The alignment of particles is of special interest to applications such as tissue engineering, cell surgery, and nanofabrication. In conventional optical traps non-spherical particles tend to align their long axis to the direction of laser beam propagation, thus limiting the ability of aligning the particles in the plane of the substrate. Several methods have been used to circumvent this phenomenon. Using exquisite optical setups, a pair of closely separated optical traps can be generated by a spatial light modulator to hold different part of the particle [21], and a spiral interference pattern can be generated by combining a Laguerre-Gaussian beam with a plane wave with controllable optical path length difference to rotate non-spherical particles [22]. Utilizing optical torque birefringent particles can be rotated or spun by controlling polarization of the incident beam [23]. However, in the primary applications of optical trapping, namely micro/nano-particle assembly and biological particles manipulation, there are limited number of samples with intrinsic birefringence. The need for modifying and attaching biological samples to birefringent particles would involve perturbation to the biological specimens and increase sample preparation time, which is undesirable for biological studies that require high throughput. The rotation of regular dielectric particles can be achieved using polarization control of a Gaussian beam in optical tweezers [24], but with extremely high optical intensities.

In this paper, we propose enhanced optical manipulation utilizing the interaction of a polarized laser beam with 1-D periodic nanostructures. The approach uses a simple optical configuration as shown in Fig. 1(a) . We demonstrate trapping of sub-micron particles with low intensity without being confined to specific hot spots. Minimum trapping intensity for static trapping and trap efficiency for dynamic trapping (to trap and move particles simultaneously) were characterized for particles with a wide range of sizes. In addition, we show that alignment of non-spherical dielectric particles and cells can be achieved by controlling the polarization of the incident beam with low intensity. This approach can be expanded to a 2-D hexagonal periodic structure to achieve fully controlled rotation using the configuration of a 3-phase optical rotor. Through finite-difference time domain (FDTD) simulations, we propose that the enhanced optical field near the nanostructure surface contributes to the enhanced trapping force, especially for sub-micron particles; and optical diffraction by the periodic structures results in orientation control, an effect more pronounced for micron-size non-spherical particles.

Fig. 1.

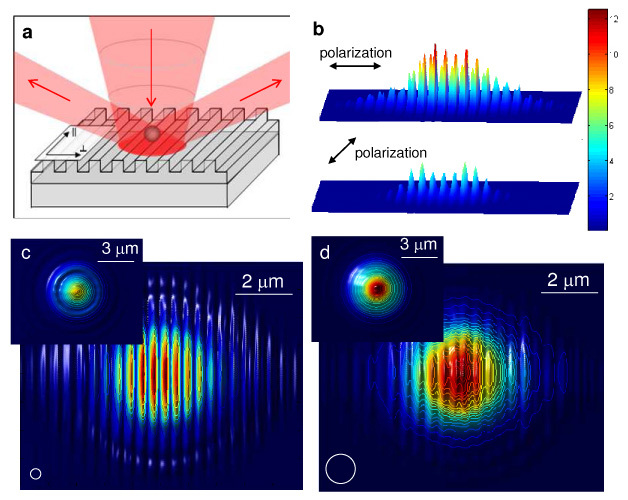
(a) Schematic drawing of the enhanced optical trapping utilizing 1-D periodic nanostructures. The incident beam is diffracted by the periodic nanostructure at far field. (b) The intensity distribution of light with two orthogonal polarizations at the surface of an aluminum grating with a 417 nm period obtained using FDTD simulations. The distribution is normalized to the intensity on a flat aluminum surface. (c) and (d) Trapping potential for particles directly above the grating surface versus location of the particle for (c) a 350 nm polystyrene bead and (d) a 1 μm polystyrene bead. The white circles illustrate the sizes of the particles. Insets show the trapping potential above a flat aluminum surface for the same particle size as comparisons. The values are normalized for each particle size. For all FDTD simulation figures the field of view is 10 × 8 μm².

2. Theoretical analysis

The effect of the periodic nanostructure on optical trapping force was investigated by first determining the intensity distribution after the incident light is scattered off the nanostructure. When coupled with appropriate material models, FDTD solvers can provide accurate representations of a wide range of optical behaviors. We calculated the intensity distribution in the volume surrounding the Gaussian beam spot incident on the surface of an aluminum grating with a period of 417 nm, same as that used in our experiments. A dispersive Lorentz-Drude model was used in conjunction with FDTD to accurately recreate the dielectric effects of aluminum, and it was verified that plasmonic effect was minimal for the wavelength used in the experiments. Once the intensity distribution is obtained, the potential energy of the optical trap for a particle versus location can be approximated by convolving the volume of the particle over the intensity distribution [25]:

$$U_{grad}\left(x,y,z\right)=\frac{n_2^2-n_1^2}{16\pi }{\displaystyle \underset{v}{\int }{\left|\stackrel{\rightharpoonup }{E}\left(x,y,z\right)\right|}^2}dv,$$

where U_grad is the gradient trapping potential, v is the volume of the particle, n ₁ and n ₂ are the indices of refraction of the surrounding medium and the particle, respectively. This approximation was used in place of the more rigorous Maxwell Stress Tensor method¹² to estimate the trapping force enhancement because the large computational area and fine mesh size required for the FDTD simulation as a result of trapping small particles with a loosely focused spot. Once the potential is found, the trapping force can be determined by calculating the gradient of the potential as follows,

$${\stackrel{\rightharpoonup }{F}}_{grad}\left(x,y,z\right)=\nabla U_{grad}\left(x,y,z\right).$$

Figure 1(b) shows the intensity distribution at the surface of the nanostructure, illustrating enhanced optical field when the incident light is polarized perpendicular to the grating rules. The trapping potentials for different particle sizes versus location of the particle are shown in Fig. 1(c) and 1(d), with the insets showing the corresponding trapping potential on a flat aluminum surface. From the potential energy, the force can be found by taking the gradient of the trapping potential. Using this approach, the trapping force enhancement over a flat aluminum surface for 1 μm-size particles was found to be 1.85, while for smaller 350 nm particles the enhancement was found to be 10.7.

3. Static, dynamic trapping and trap asymmetry

A 633-nm HeNe laser with full output power of 35 mW was used as the light source for trapping and rotation. The laser beam was coupled into the optical path of a Zeiss Axioimager fluorescence microscope using a beam splitter. 50x, 20x, or 10x objective lens (N.A. = 0.55, 0.22, and 0.25, respectively) of the microscope was used for focusing the laser beam, producing observed spot diameters of approximately 3, 8 and 18 μm, respectively. The intensity of the laser beam was controlled using a neutral density attenuator, and the laser polarization was controlled using a rotating half-wave plate. The incident intensity of the optical beam reported in this paper was obtained by measuring the optical power after the microscope objective lens, divided by the laser beam spot size which can be estimated from the CCD camera images. The substrate used for the current experiment was a holographic (sinusoidal profile) diffraction grating with a period of 417 nm and groove depth of 150 nm. The grating surface was aluminum. Alternatively, high refractive index dielectric materials can be used to make the periodic structure. Test particles were suspended in water maintained above the grating surface using a glass coverslip and spacers.

Trapping forces were characterized in two ways. First trapped polystyrene beads of sizes with diameters from 190 nm to 10 μm were dragged through solution at varying speeds by moving the microscope stage relative to the laser spot. The laser intensity was then adjusted to find the minimum intensity at which the trap could hold the bead. The maximum velocity increases linearly with the laser intensity [20]. From the velocity, trapping force was estimated using Stoke’s Drag Equation, $F_{drag}=-6\pi \eta r{v}_{flow},$ where η is the viscosity of the surrounding medium, in this case water, r is the particle radius, and v_flow is the velocity of the fluid relative to the particle. Faxen’s Law is taken into consideration to account for the particle proximity to the substrate. This measurement yielded trap efficiency in units of force per peak optical intensity. The result is shown as the square data points (blue curve) in Fig. 2(a) . Because the exact height of the particle above the surface is not known the range of possible variation in force due to surface interactions is represented in the error bars (in addition to variation from multiple experiments). On the average, the trap efficiency is about 20 times higher than what’s reported using metal nanodots optical tweezers [13]. The asymmetry in the optical trap as a result of light polarization is demonstrated by the inset polar plot for trap efficiency. A 3.87 um polystyrene bead was transported perpendicular and parallel to the rules of the grating. The solid line (large asymmetry) is obtained with incident light polarized perpendicular to the grating rules, and the dash line (small asymmetry) is obtained with incident light polarized parallel to the grating rules. Trapping was also characterized by finding the minimum intensity at which the trap could overcome Brownian motion to hold a particle steadily. The result for various particle sizes is shown as the diamond data points (red curve) in Fig. 2(a). For larger particles (> 3 um) the Brownian motion was not noticeable. Figure 2(b)-(d) demonstrates trapping of a 590 nm-diameter fluorescent particle. The red circle indicates the position of the laser spot as the laser light was too dim to be seen. At first the particle is trapped within the spot at higher power, as the power is lowered the Brownian motion of the particle overcomes the trapping force, allowing the particle to escape. The minimum incident intensity to maintain static trapping was found to be 34 μW/μm² for the 590-nm particle. Compared to our previous work on sub-micron particle trapping using plasmonic structures [20] where single-particle trapping was not possible due to convective flow, heating effect due to potential absorption of the aluminum coating in the current platform is minimal and trapping of single 190-nm particle can be achieved.

Fig. 2.

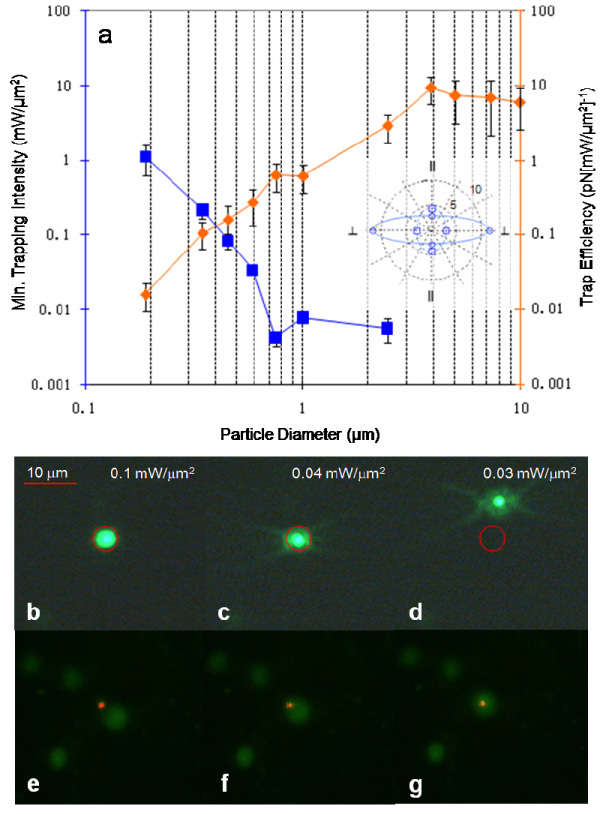
(a) Trap efficiency and minimum trapping intensity measured for polystyrene beads of various sizes with beam polarization perpendicular to grating lines. Inset shows trap asymmetry in trapping efficiency for translating a 3.87 um polystyrene bead perpendicular and parallel to the rules of the grating. The solid line (large asymmetry) is obtained with incident light polarized perpendicular to the grating, and the dash line (small asymmetry) is obtained with incident light polarized parallel to the grating. The unit is in (pN[mW/μm²]⁻¹). (b)-(d) Trapping demonstration of a fluorescent 590 nm polystyrene bead. The red circle indicates the position of the laser spot as the laser light was too dim to be seen. At first the particle is trapped within the spot at higher power, as the power is lowered the Brownian motion of the particle overcomes the trapping force, allowing the particle to escape. (e)-(g) Trapping demonstration of a fluorescent ovarian cancer cell nucleus. The minimum intensity required to initiate trapping was 16 μW/μm² obtained using a 20x objective lens.

As study of individual cancer cell nuclei may reveal informative data for cancer research [26], and holding the nuclei non-invasively with high reconfigurability is desirable to facilitating diagnostic applications, we performed trapping experiments for ovarian cancer cell nuclei using the nanostructure-enhanced laser tweezers. The nuclei were isolated and surface treated with bovine serum albumin to prevent clumping. Figure 2(e)-(g) show the snapshots of trapping a fluorescent ovarian cancer cell nucleus. The nuclei had a diameter of approximately 3 μm. The minimum incident intensity required to initiate trapping was characterized to be 16 μW/μm².

In addition to low intensity, two distinct trapping phenomena were observed. First for sub-micron particles the measured trapping efficiency (Fig. 2(a)) has a maximum at 750-nm particle diameter. Second, at larger particle sizes noticeable polarization dependence was observed. In the polarization state that produced the maximum diffracted field, perpendicular to the grating rules, the trap was found to be much stiffer when the particle was translated along the distribution of the diffracted modes. When the particle started outside the beam spot, it was repelled if approaching the trap across the grating rules, while attracted if approaching along the grating rules (Fig. 3 and Media 1 ^{(967.8KB, MOV)} ). This suggests scattering force dominates for this phenomenon. The same effects were not observed with polarization parallel to the grating rules, where the diffracted field was much weaker. The observations imply that the trap asymmetry and corresponding enhancement was enabled by diffraction from the grating, which is a far-field effect and therefore more significant for larger particles.

Fig. 3.

Snapshots of trap asymmetry experiment ( Media 1 ^{(967.8KB, MOV)} ). When the spot approaches an oblong polystyrene bead from the direction along the axis of the diffracted mode (horizontal), the bead is repelled from the laser spot and up away from the surface ((a)-(d)). When the beam approaches from the direction perpendicular to the axis of the diffracted mode, the bead is trapped normally ((e)-(g)). The time interval between shots is approximately 0.5 seconds. The grating rules are oriented vertically. The optical beam polarization is perpendicular to grating rules. The images were recorded under an objective lens with 50x magnification.

4. Alignment

Utilizing the polarization dependence, alignment was demonstrated for oblong 6.8 μm polystyrene beads (Fig. 4(a)-(f) and Media 2 ^{(3.7MB, MOV)} ) and ellipsoidal Listeria cells with a long axis of ~2 μm and a short axis of less than 1 μm (Fig. 5 ). The laser beam was polarized perpendicular to the grating rules. The 6.8 μm oblong beads could be aligned to the laser polarization with incident intensity as low as 9.2 μW/μm², which to our knowledge is over four orders of magnitude lower than previously reported for polarization-defined rotation of dielectric, non-birefringent particles using optical tweezers [24]. The rotation speed during the process of alignment versus optical intensity (Fig. 4(g)) was characterized with the long axis of the oblong beads initially close to 45° off the grating rules. The bead was trapped by approaching it with the laser spot quickly. If the bead was approached slowly, it would be pulled into the laser spot from a large distance away, giving it an initial angular momentum which might make the bead appear to align more quickly than it would otherwise. The trapping and rotation process was video-recorded and the rotation speed was determined by measuring the time duration for the bead to rotate from 45° to a steady position perpendicular to the grating in the video. If the initial position of the bead was greater than 45°, the time duration was determined by starting to count video frames when the bead reached the 45° position. The average speed over 45 degrees of rotation, was then calculated, and near 35 degree/second can be achieved with sufficient intensity. The measurement was repeated five times for each laser intensity tested, and the average and standard deviation was determined. The large uncertainty at high rotation speed was due to the variance in the beads’ initial orientation, which affects the optical torque and initial speed of rotation significantly. Figure 5 shows alignment characterization of the Listeria cells versus optical intensity using a 50x objective lens. When using a 20x objective lens, the minimum incident intensity for alignment could be reduced to 17 μW/μm², comparable to the local intensities reported for trapping and aligning E. Coli in patterned optical antennas (10-100 μW/μm²)¹⁶.

Fig. 4.

(a)-(c) Alignment of an oblong polystyrene particle on an aluminum grating under the illumination of a laser beam polarized perpendicular to the grating rules. The laser beam was polarized horizontally and focused with a 50x objective lens ( Media 2 ^{(3.7MB, MOV)} ). (d)-(f) The oblong polystyrene particle was aligned with its long axis perpendicular to the grating rules after being illuminated by the polarized laser beam. The focusing of the laser beam and image-taking was through a 10x objective lens. (g) Characterization of rotation speed during alignment versus optical intensity. Rotation speed approaching 35 degree/sec can be achieved with sufficient laser intensity.

Fig. 5.

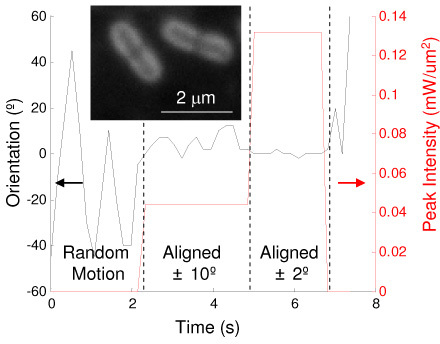
Characterization of Listeria cell (inset) alignment. The orientation angle of the Listeria cell was recorded as the laser intensity was adjusted. As laser power increases the cells are more stiffly aligned perpendicular to the grating lines. This measurement was performed using a 50x objective lens. The cell could be aligned to within ± 10° when the laser intensity exceeds 40 μW/μm².

5. Conclusion

In summary, we have demonstrated that enhanced optical trapping can be achieved utilizing the interaction between polarized light and periodic nanostructures. Particles as small as 190 nm can be trapped with laser intensity ≤1 mW/μm². In addition, oblong-shaped particles can be aligned with specific orientation of the nanostructures with low intensities. FDTD simulations of the optical near field and far field above the nanostructure reveal the origins for the observed results. Although the current experiments were conducted using 633-nm wavelength, the principle of the nanostructure-enhanced laser tweezers can be readily applied to other wavelengths that are more bio-compatible by revising the design of the periodic nanostructures. The advantages of low power and high functionality of this approach are still the same, which is highly desirable for biological studies. This approach can be extended to using 2-D periodic nanostructures for full rotation control.