Dimension Reduction and Dynamics of a Spiking Neural Network Model for Decision Making under Neuromodulation

Abstract

Previous models of neuromodulation in cortical circuits have used either physiologically based networks of spiking neurons or simplified gain adjustments in low-dimensional connectionist models. Here we reduce a high-dimensional spiking neuronal network model, first to a four-population mean-field model and then to a two-population model. This provides a realistic implementation of neuromodulation in low-dimensional decision-making models, speeds up simulations by three orders of magnitude, and allows bifurcation and phase-plane analyses of the reduced models that illuminate neuromodulatory mechanisms. As modulation of excitation-inhibition varies, the network can move from unaroused states, through optimal performance to impulsive states, and eventually lose inhibition-driven winner-take-all behavior: all are clear outcomes of the bifurcation structure. We illustrate the value of reduced models by a study of the speed-accuracy tradeoff in decision making. The ability of such models to recreate neuromodulatory dynamics of the spiking network will accelerate the pace of future experiments linking behavioral data to cellular neurophysiology.

1. Introduction

Neuromodulation plays an important role in cognitive processes such as decision making [17], but there is currently no direct connection between cellular-level effects of neuromodulators and low-dimensional models of decision dynamics. This paper investigates how neuromodulation at the synaptic level influences performance on a two-alternative, forced-choice (2AFC) decision task. Such tasks are often modeled in cognitive psychology by leaky, competing accumulators [46], each equipped with a decision variable representing the activity of a neural population selective for one of the two stimuli. Choices are signaled when the first of these variables crosses a fixed threshold. In this context, neuromodulation is typically introduced at an abstract level by changing the slope and/or bias point in the functions that characterize how the decision variables respond to stimulus inputs [39, 45, 24, 41, 42].

Such high-level models take the form of stochastic ordinary differential equations (ODEs). These are attractive not only for their analytical and computational tractability but also because, under suitable conditions, their behavior can be approximated by yet simpler one-dimensional Ornstein–Uhlenbeck (OU) and drift-diffusion (DD) processes [25, 8, 18]. As described in [26, 8], DD processes with constant drift rate are optimal in the sense that they render a decision of guaranteed accuracy in the minimum possible time, allowing one to test human and animal behavior against a normative theory, and, specifically, to compute a speed-accuracy tradeoff that optimizes performance [8].

In [19] we began a larger scale computational study of norepinephrine (NE) modulation on decision making. It is known that NE can change cellular excitability and synaptic efficacy, thus altering performance in behavioral tasks [7, 5, 9, 38]. Adapting a spiking neuronal network model from [47], we examined the effects of tonic and phasic NE release when glutamatergic and GABA-ergic synapses are both simultaneously and separately modulated. The biophysical detail in this 2000-neuron model allows comparison with both behavioral and physiological experiments [48, 6], but it contains 9200 ODEs, rendering it computationally expensive and analytically intractable. In order to better understand the underlying mechanisms and to enable faster simulation studies, a low-dimensional reduction that preserves key physiological details is desirable.

Drawing on the studies of [19], here we perform a reduction that includes neuromodulation of synaptic conductances. Spiking networks have previously been reduced to four- and two-population mean-field models for a fixed set of synaptic gains [49]. Here, we show that these models cannot capture extended neuromodulatory effects. In contrast, the models developed in this paper are designed to reproduce behavioral changes over a wide range of synaptic gains. Careful matching of reward rates and analyses of bifurcation diagrams play central roles in our analyses. The extended mean-field version of a working-memory model [13, 15] can capture the effects of neuromodulation and find attractors and bifurcation structures, but it is computationally intensive due to self-consistency calculations. It is therefore difficult to simulate behavior in order to estimate subject reaction times, accuracies, and reward rates under different gain conditions. The present reduced models overcome this problem, speeding up simulations over the spiking model by O(10³) for the four-population model and by 3600 for the two-population model, and facilitating bifurcation and nullcline analyses. Moreover, while slices of behavior can be studied and stable states can be determined in the full spiking model, the reduced models allow complete bifurcation studies with computationally determined basins of attraction.

In section 2 we extend the studies of [19] to better map the behavioral effects of different synaptic changes in the original spiking neuronal network, examining task performance metrics and network firing rate behaviors. Section 3 covers the four-population model, describing its derivation, simulated behavioral results, and bifurcation structures. In section 4 we perform the final reduction to a two-population model and compare its behavior to that of the four-population and full spiking models. Bifurcation diagrams for the reduced models illuminate various phenomena of the spiking model, which its high-dimensionality renders opaque. The transition from unarousal, through good performance, to impulsive behavior can be understood from bifurcation diagrams, noise levels, and basins of attraction. The reduced neuromodulation models are then used to implement a speed-accuracy tradeoff, described in section 5, which in principle links behavioral and neurophysiological experiments. The paper closes with a discussion in section 6. Technical details of the reduction process are relegated to appendices.

2. Neuromodulation in a spiking network model

In this section we extend the computational study of [19], which was motivated by perceptual choice experiments in which subjects are under pressure to respond correctly to as many trials as possible, under a free-response paradigm, in a session of fixed duration. The simplest choices are binary, and such tasks are widely studied. In a visual instantiation, a coherent subset of random dots moves in one of two target directions, which must be correctly signaled to gain a reward. Task difficulty is adjusted by the stimulus strength E ∈ [0, 1], E = 0 indicating complete randomness and E = 1 indicating 100% coherence [10, 11, 40].

Direct recordings in monkeys suggest that the lateral intraparietal area (LIP), among others, integrates motion evidence from the middle temporal area (MT) of visual cortex [28, 29, 40, 31], and that its firing rates reach a threshold just prior to response [37]. We apply a similar criterion in the spiking model, thus determining decision times (DT) from stimulus onset to threshold crossing, for each trial. The response-to-stimulus interval (RSI) imposed by the experimenter is also important in defining performance; it will be studied in section 5. Including nondecision latencies (NDL), such as signal processing and motor preparation, the reward rate is defined as

$$\mathit{RR}=\frac{\langle \mathit{Acc}\rangle }{\langle \mathit{DT}+\mathit{NDL}+\mathit{RSI}\rangle }:$$ (1)

this is the performance measure used below. In (1) 〈·〉 denote averages over trials and the accuracy 〈Acc〉 is the fraction of rewarded trials in the session. If a threshold is crossed before stimulus onset, the trial is defined as an impulsive choice or false alarm, and if no threshold is crossed before 2000 ms, a no-choice trial is declared. No reward is given in either case.

2.1. The model structure

The spiking network of [47, 49, 19] was derived from earlier studies [13] and specifically tuned to represent the MT-LIP system. It contains 2000 leaky integrate-and-fire neurons divided into four groups: two stimulus-selective populations of N₁ = N₂ = 240 pyramidal cells, a nonselective population of N₃ = 1120 pyramidal cells, and a population of N_I = 400 inhibitory interneurons. The state variables are the (subthreshold) transmembrane voltages V_j(t) (mV) of each cell j, the network’s internal gating variables S_AMPA,j(t), S_NMDA,j(t), and S_GABA,j(t), and gating variables S_AMPA,ext,j(t) external to the local circuit, which include noisy inputs from MT neurons as well as other brain areas, that enter all 2000 cells. These S_type,j’s describe integrated presynaptic activities which are summed and then multiplied by connection weights and synaptic conductances to yield an effective conductance in units of nS: hence only N_I S_GABA,j’s are required for the interneurons, and N_E glutamatergic synaptic variables for the pyramidal cells. Connection weights ω_j,k among the cells depend on the identity of pre- and postsynaptic populations and are supposed to have formed in a Hebbian context, with connections within each selective population enhanced and connections to other excitatory populations suppressed [2, 3].

The ODEs describing this leaky integrate-and-fire neuronal model take the form

$$C_j\frac{d{V}_j}{\mathit{dt}}=-g_L(V_j-V_L)+I_{\mathit{syn},j}(t),$$ (2)

$$\frac{d{S}_{\mathit{type},j}}{\mathit{dt}}=-\frac{S_{\mathit{type},j}}{T_{\mathit{type}}}+\sum _l\delta (t-t_j^l),$$ (3)

where type = AMPA or GABA, T_type is the time constant for that synapse type, and the summation of delta functions in (3) is over spikes in the presynaptic neuron. Here j ∈ [1, 2000] identifies presynaptic cells with j ∈ [1, 1600] for pyramidal cells and j ∈ [1601, 2000] for interneurons, with different cell types tracking their appropriate synaptic variables.

The slower NMDA synapses require two ODEs for each j ∈ [0, 1600] with separate time constants describing the rise and fall of S_NMDA,j:

$$\frac{d{S}_{\mathit{NMDA},j}(t)}{\mathit{dt}}=-\frac{S_{\mathit{NMDA},j}(t)}{{\tau }_{\mathit{NMDA},\mathit{decay}}}+\alpha x_j(t)(1-S_{\mathit{NMDA},j}(t)),$$ (4)

$$\frac{d{x}_j(t)}{\mathit{dt}}=-\frac{x_j(t)}{{\tau }_{\mathit{NMDA},\mathit{rise}}}+\sum _l\delta (t-t_j^l).$$ (5)

When V_j(t) crosses a threshold V_thresh at time $t_j^l$ the cell emits a delta function $\delta (t-t_j^l)$, after which V_j is instantaneously reset and held at V_reset for an absolute refractory period τ_ref.

Spikes from cells external to the local network, with a combined presynaptic firing rate f_ext = 2.4 kHz due to a 3 Hz background firing rate of approximately 800 external presynaptic connections, as described in [47, 49], and from upstream sensory neurons, are assumed to be filtered by AMPA receptors, and their spike times $t_j^l$, which would normally be taken as independently generated Poisson processes, are approximated by drawing from independent Gaussian distributions with mean and variance

$${\mu }_{S,\mathit{AMPA},\mathit{ext},j}=0.001f_{\mathit{ext}}{\tau }_{\mathit{AMPA}},$$ (6)

$${\sigma }_{S,\mathit{AMPA},\mathit{ext},j}=\sqrt{0.5{\mu }_{S,\mathit{AMPA},\mathit{ext},j}},$$ (7)

derived from the asymptotic values of the conductances. The factor 0.001 in (6) is due to the conversion of τ from ms to s. Thus, the external conductances S_AMPA,ext,j(t) are calculated as

$$d{S}_{\mathit{AMPA},\mathit{ext},j}(t)=-(S_{\mathit{AMPA},\mathit{ext},j}-{\mu }_{S,\mathit{AMPA},\mathit{ext},j})\frac{\mathit{dt}}{{\tau }_{\mathit{AMPA}}}+{\sigma }_{S,\mathit{AMPA},\mathit{ext},j}\sqrt{\frac{2\mathit{dt}}{{\tau }_{\mathit{AMPA}}}}N(0,1),$$ (8)

where N(0, 1) is a standard normal distribution. This is the source of variability and noise in the simulation.

The synaptic currents in (2) are given by

$$\begin{array}{ccc}\hfill I_{\mathit{syn},k}(t)& =& I_{\mathit{AMPA},\mathit{ext},k}(t)+I_{\mathit{AMPA},\mathit{rec},k}(t)+I_{\mathit{NMDA},\mathit{rec},k}(t)+I_{\mathit{GABA},\mathit{rec},k}(t),\hfill \\ \hfill I_{\mathit{AMPA},\mathit{ext},k}(t)& =& -g_{\mathit{AMPA},\mathit{ext},k}(V_k-V_E)S_{\mathit{AMPA},\mathit{ext},k}(t),\hfill \\ \hfill I_{\mathit{AMPA},\mathit{rec},k}(t)& =& -g_{\mathit{AMPA},\mathit{rec},k}(V_k-V_E)\sum _{j=1}^{N_E}{w}_{j,k}{S}_{\mathit{AMPA},j}(t),\hfill \\ \hfill I_{\mathit{NMDA},\mathit{rec},k}(t)& =& -\frac{g_{\mathit{NMDA},\mathit{rec},k}(V_k-V_E)}{(1+[M{g}^{2+}]\exp (-0.062V_k)/3.57)}\sum _{j=1}^{N_E}{w}_{j,k}{S}_{\mathit{NMDA},j}(t),\hfill \\ \hfill I_{\mathit{GABA},\mathit{rec},k}(t)& =& -g_{\mathit{GABA},\mathit{rec},k}(V_k-V_I)\sum _{j=1}^{N_I}{S}_{\mathit{GABA},j}(t).\hfill \end{array}$$ (9)

Here the subscript rec (henceforth omitted) indicates recurrent connections within the network, V_E and V_I are the glutamatergic and GABA-ergic synaptic reversal potentials, g_type,k are synaptic conductances, and g_L in (2) denotes the leak conductance. For each synapse type there are two conductance values: g_type,p for postsynaptic pyramidal neurons and g_type,I for postsynaptic interneurons. Stimuli are included by adding terms of the form μ₀(1 ± E) to f_ext in (6) defining μ_S,AMPA,ext,k for the selective cells, where μ₀ is a background input and E ∈ [−1, 1] is the coherence defined above. These will be used as bifurcation parameters in section 3.5. All parameter values for the model are listed in Appendix A.

Equations (2)-(9) define a 9200-dimensional dynamical system. Specifically, k ranges from 1 to 2000 for voltages V_k and external inputs S_AMPA,ext,k, but j ranges only from 1 to N_E = 1600 for the excitatory variables S_AMPA,j, S_NMDA,j, and x_j, and for S_GABA,j.

Neuromodulation can be modeled by changing the leak g_L and synaptic conductances g_type,k. In [19], we showed that modulating g_L has similar effects to g_type,k, and we shall not vary g_L here. Experiments have yet to distinguish any differential effects of NE on NMDA and AMPA (glutamatergic) synapses, so we introduce two parameters, γ_E which scales g_NMDA and g_AMPA equally, and γ_I which scales g_GABA. These are allowed to vary separately, since there is insufficient physiological data to determine them from NE concentrations [NE]. In [19] both tonic and phasic (dynamic) NE release were modeled (cf. [45, 43]), but here we consider only tonic NE levels. When a mapping from [NE] to (γ_E, γ_I) is determined experimentally, it can be implemented in our model. Our approach may also be generalized to include other neuromodulators which affect the same synapse types.

2.2. Model performance in conductance space

In [19] we showed that a ratio of GABA-ergic to glutamatergic synaptic modulation of approximately 2:1 is optimal for robustness in that reward rates remain at high levels over the widest range of γ_I, but only one-dimensional slices of the neuromodulation plane were examined. In Figure 1 we extend those results over the region (γ_E, γ_I) ∈ [0, 3] × [0, 3], plotting values of the performance measures that enter (1).

Figure 1.

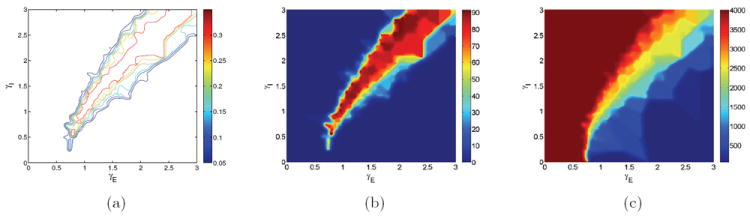
Contour maps of network performance over the glutamatergic (γ_E) and GABA-ergic (γ_I) gain modulation plane. (a) Reward rate RR: ridge of higher rewards has slope ≈ 2 near γ_E = γ_I = 1.0 that moderates to ≈ 1 at higher gains. (b) Fraction of rewarded trials 〈Acc〉: note steeper drop above the ridge, where good performance yields to no-choice trials, and shallower drop below, where impulsive trials begin. (c) Mean decision time 〈DT〉: inhibition dominates at upper left causing no-choices (aborted after 2000 ms, red shades); excitation dominates at lower right causing fast impulsive trials (blue shades).

Figure 1(a) shows that no trials are rewarded for γ_E < 0.65, because low excitation cannot overcome leak conductance, even without inhibition. For γ_E > 0.65 good performance exists between the no-choice region on the left and the impulsive region on the right, with reward rates gradually dropping along a line of slope γ_I/γ_E = 1. A line of slope 1 can remain in the good region far to the right but quickly encounters no-choices to the left. This failure mode is reversed for steeper slopes as no-choices appear for high γ_E, and impulsive choices as γ_E drops below 1 (cf. the 3:1 ratio case [19]), and a slope γ_I : γ_E = 2 keeps performance above the impulsive regime longest before reaching γ_E = 0.65.

Accuracy (Figure 1(b)) has a similar profile to reward rate, both falling more steeply toward no-choice trials at the upper left than to impulsive ones at lower right (note fast decision times in Figure 1(c)). The optimal reward rate ridge grows wider at higher gains, curving over from a high initial slope to approach a slope of 1. We wish to preserve these key features in our low-dimensional reductions, especially those of Figure 1(a), but, in addition to gross behavioral measures, we also seek to understand the network dynamics that underlie this behavior.

Supplementing Figure 1, Figure 2 delineates regions in the neuromodulation plane in which distinct system behaviors are observed. We describe these moving from top left to bottom right. In the region labeled “below threshold,” inhibition dominates excitation, and, even in the presence of stimulus and noise, a unique stable steady state exists in which the firing rates of both selective populations remain below the decision threshold (here 20 Hz): see the top row of Figure 2(b). Prefiguring the bifurcation analyses in section 3.5, we refer to this as a low-low attractor. As noted above, a certain degree of excitation, primarily from external inputs, is required to overcome leak and allow response. Interneuronal capacitances also differ from those of pyramidal cells, allowing them to spike at lower external currents. Hence as recurrent inhibition γ_I rises, it takes more excitation γ_E to escape this regime, which extends rightward at higher γ_I.

Figure 2.

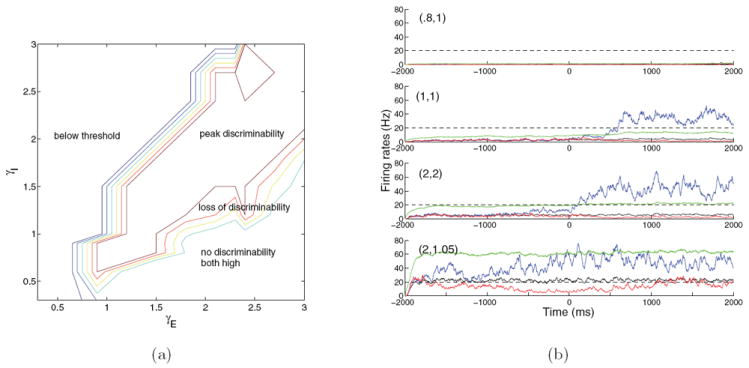
(a) Behavior of the spiking model over an expanded neuromodulation plane visualized through a plot of the relative separation between poststimulus firing rates of the two selective populations. In the below threshold region both selective populations remain subthreshold. In the peak discriminability region neural activities of the selective populations split, with one population crossing threshold and suppressing the other. Moving right and downward, impulsivity rises as excitation increases and inhibition drops, and eventually both populations approach high firing rates and pooled inhibition is insufficient to suppress any excitatory population, leading to loss of discriminability. (b) Firing rate traces illustrating different outcomes: subthreshold activity ((0.8,1), below threshold), optimal splitting ((1,1), peak discriminability), impulsive but still splitting ((2,2), upper-right peak discriminability) behaviors, and partial failure of pooled inhibition ((2,1.05), loss of discriminability). In the no discriminability, both high region all excitatory firing rates are approximately equal and very high (not shown in (b)). Traces show populations 1 (blue), 2 (red), 3 (black), and I (green); dashed lines indicate decision thresholds; stimulus onset is at time zero; (γ_E, γ_I) values are given at top left.

In the peak discriminability region, with stimulus present, the network acquires two additional high-low attractors in which one selective pyramidal population fires above threshold and the other selective and the nonselective populations are suppressed. There are two separate subregions of interest, the first of which includes the high reward rate ridge of Figure 1(a); here both selective populations remain near the low-low attractor with noise present and stimulus off, and both initially ramp up after stimulus onset until one suppresses the other and crosses threshold to approach a high-low attractor: see the second row of Figure 2(b). Moving to the lower right, the basin of attraction of the low-low stimulus-off state shrinks, and the second subregion begins, where more impulsive choices occur due to noise-assisted threshold crossing in the absence of stimulus. Eventually the low-low attractor’s basin shrinks enough that noise rapidly perturbs solutions to one of the high-low attractors: see the third row of Figure 2(b).

Throughout the peak discriminability region firing rates split, endowing one selective population with high activity and the other selective and the nonselective populations with low activity in comparison to the winner, and leaving interneurons with sufficient activity to mediate the pooled inhibition. The winning population’s firing rates remain below 80 Hz, and the nonselective population never wins, even in the impulsive subregion, because its relative recurrent weight factor ω_j,k = 1 is lower than ω₊ = 1.7 within each selective population. This region ends with loss of stability of the low-low state in the absence of stimulus, so that every trial becomes impulsive.

The loss of discriminability region marks a transition from splitting to race model behavior [8], in which all three pyramidal populations exhibit increasing firing rates in the presence of stimuli, although one selective population still wins: see the bottom row of Figure 2(b). Moving downward, firing rates of the superthreshold attractors approach 70 Hz at the boundary of the no discriminability, both high, region. Entering this region, pooled inhibition fails to suppress the losing selective population and all pyramidal populations exceed threshold, approaching their maxima at the inverse absolute refractory period 1/τ_ref = 500 Hz (not shown). Interneuronal firing rates are also high, but pooled inhibition is too weak to suppress any pyramidal population.

In section 3.5 we will investigate the network stability underlying the above behavior by computing bifurcation diagrams for a reduced model.

3. The four-population reduced models

We now derive a set of four-population models, modifying the mean-field procedure of [49] to incorporate neuromodulation. This yields 11-dimensional systems of stochastic ODEs in which populations become homogeneous units described by average firing rates ν_j(t), j = 1, 2, 3, and ν_I(t) (four variables), the inhibitory population carries one population-averaged synaptic variable S_GABA(t), and each excitatory population has two such variables S_AMPA,j(t) and S_NMDA,j(t) (six in all). The synaptic variables will be determined by firing rates and firing rates by net input currents to each population. We start by calculating these currents.

3.1. Derivation of input currents

Although the synaptic conductances and currents depend on time-varying postsynaptic membrane potentials, we simplify the self-consistency calculations of [13, 35] by employing a fixed average voltage V̄ = (V_reset+V_thresh)/2 to estimate synaptic currents that enter each of the four cell populations as follows:

$$J_{\mathit{type},k}=-g_{\mathit{type},k}(\overline{V}-V_{\mathit{type}})/1000$$ (10)

(multiplication of g_type,k in (nS) and (V̄ − V_type) in (mV) requires division by 1000 to convert J_type,k to nA, the unit of choice for currents). These effective currents to populations replace the currents into individual cells in (9). Different J_type,k’s are used for pyramidal populations (j = 1, 2, 3, also written J_type,p) and interneurons (J_type,I), because g_type,p ≠ g_type,I. Since (V̄ − V_GABA < 0) the inhibitory currents are negative, as expected. We include in J_NMDA,k the factor [1 + (1/3.57) exp(− 0.062V̄)]⁻¹ ≈ 0.12 to incorporate the effects of Mg²⁺ block (cf. (9)). Neuromodulation is now accomplished by γ_E and γ_I scaling the J_type,k’s which contain the g_type,k’s that were previously scaled in section 2.2.

Due to all-to-all connectivity, input currents are calculated by summing the presynaptic contributions from each population multiplied by the number of cells in that population:

$$I_{\mathit{syn},k}(t)=I_{\mathit{NMDA},k}+I_{\mathit{AMPA},k}+I_{\mathit{GABA},k}+I_{\mathit{AMPA},\mathit{ext},k}+I_{\mathit{stim},k},$$ (11)

$$I_{\mathit{AMPA},k}(t)=\sum _{j=1}^3{N}_j{J}_{\mathit{AMPA},k}{\omega }_{j,k}{S}_{\mathit{AMPA},j}(t),$$ (12)

$$I_{\mathit{NMDA},k}(t)=\sum _{j=1}^3{N}_j{J}_{\mathit{NMDA},k}{\omega }_{j,k}{S}_{\mathit{NMDA},j}(t),$$ (13)

$$I_{\mathit{GABA},I}(t)=N_I{J}_{\mathit{GABA},k}{S}_{\mathit{GABA},I}(t).$$ (14)

Here ω_j,k is the weight from population j to population k, being ω₊ for recurrent connections within a selective population, ω₋ from one selective population to another excitatory population, and ω_j,k = 1 otherwise. N_j is the number of excitatory cells in population j and N_I the number of interneurons. External inputs I_AMPA,ext,k are given by

$$I_{\mathit{AMPA},\mathit{ext},k}=J_{\mathit{AMPA},\mathit{ext},k}\frac{T_{\mathit{AMPA}}}{1000}{N}_{\mathit{ext}}{\nu }_{\mathit{ext}}+I_{\mathit{noise},k},$$ (15)

where N_ext is the number of connections per cell from presynaptic neurons external to the network (here 800), ν_ext is their average firing rate (3 Hz), and conversion between time constants (ms) and firing rates (Hz) requires division by 1000. I_noise,k is calculated below in section 3.3 and Appendix B. Finally, I_stim,k = J_AMPA,ext,p μ₀ (1 ± E) for the selective populations when stimuli are present.

Following [13, 49], we account for the rise in S_NMDA,j due to presynaptic spikes by including a term F(ψ(ν_j)) = ψ_j/[T_NMDA(1 − ψ_j)], where ψ_j is the steady state of S_NMDA,j. For a Poisson spike train, this is well approximated by

$${\psi }_j=\langle S_{\mathit{NMDA},j}\rangle =\frac{0.641{\nu }_j{T}_{\mathit{NMDA}}}{1000+0.641{\nu }_j{T}_{\mathit{NMDA}}}$$ (16)

[49], which yields F (ψ (ν_j)) ≡ 0.641ν_j/1000.

Equipped with these definitions and the currents (11)-(15), we can now state the reduced ODEs. The synaptic variables are determined by

$$\frac{d{S}_{\mathit{NMDA},j}}{\mathit{dt}}=-\frac{S_{\mathit{NMDA},j}}{T_{\mathit{NMDA}}}+0.641(1-S_{\mathit{NMDA},j})\frac{{\nu }_j}{1000},$$ (17)

$$\frac{d{S}_{\mathit{AMPA},j}}{\mathit{dt}}=-\frac{S_{\mathit{AMPA},j}}{T_{\mathit{AMPA}}}+\frac{{\nu }_j}{1000},$$ (18)

$$\frac{d{S}_{\mathit{GABA},I}}{\mathit{dt}}=-\frac{S_{\mathit{GABA},I}}{T_{\mathit{GABA}}}+\frac{{\nu }_I}{1000},$$ (19)

and the firing rates obey

$$\frac{d{\nu }_j}{\mathit{dt}}=\frac{-({\nu }_j-{\varphi }_j(I_{\mathit{syn},j}))}{T_{\mathit{AMPA}}}.$$ (20)

Here j = 1, 2, 3, I, and the input-output functions or f-I (firing rate-current) curves ϕ_j(I_syn,j) model the relationships between input currents and quasi–steady-state firing rates for each population, which all four ν_j’s approach with time constant T_AMPA = 2 ms [12]. We next describe several different f-I curves, distinguishing pyramidal cells and interneurons in each case.

3.2. Single neuron input-output functions

We develop a variety of simple analytic expressions for the relationships between input currents and firing rates by following both a semianalytical derivation and an empirical study that better matches the spiking network behavior. For a leaky integrate-and-fire model [14] such as (2), the expected average interspike interval for solutions to travel from reset voltage V_reset to threshold V_thresh may be calculated analytically, given a mean input current I_syn with white noise fluctuations [36, 4, 35]. The expected firing rate is the reciprocal of this interval plus the absolute refractory period τ_ref:

$${\varphi }_{\mathit{LIF}}(I_{\mathit{syn}})={\left[{\tau }_{\mathit{ref}}+{\tau }_m\sqrt{\pi }{\mathit{\int }}_{\frac{V_{\mathit{reset}}-V_{\mathit{ss}}}{{\sigma }_V}}^{\frac{V_{\mathit{thresh}}-V_{\mathit{ss}}}{{\sigma }_V}}{e}^{x^2}[1+\mathrm{erf}(x)]\mathit{dx}\right]}^{-1},$$ (21)

where V_ss = V_L + I_syn/g_L and σ_V is the standard deviation in the membrane potential due to the current fluctuations. Equation (21) is plotted in Figure 3(a) as the black curve labeled Amit–Tsodyks.

Figure 3.

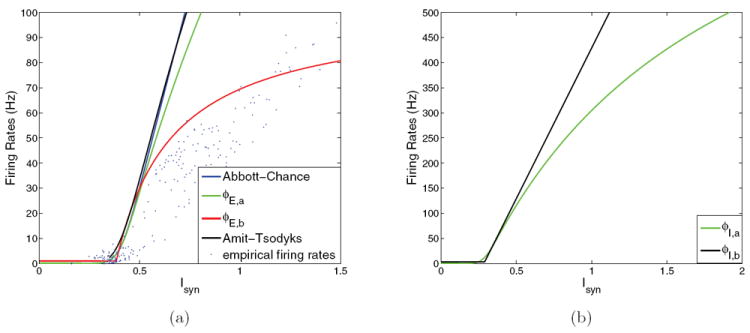
Input-output functions used in reduced models. (a) Pyramidal cell f-I curves: ϕ_LIF ((21), black) and ϕ_AC ((22), blue, as used in [49]); note that curves almost coincide; ϕ_E,a ((23), green) and the empirical ϕ_E,a ((24), red), compared with results from spiking model (blue dots). The empirical results shown (blue dots) were obtained by simulation of the full spiking network under different (γ_E, γ_I) conditions and averaging population firing rates over a 500 ms window once firing rates approached equilibrium. The average firing rates were then input into (11)-(14) to calculate the effective input currents I_syn. (b) Inhibitory cell f-I curves: ϕ_I,a (green, also given by (23); note saturation at 1/τ_ref) and ϕ_I,b ((25), black). Parameter values are given in Appendix A.

At low firing rates ϕ_LIF (I_syn) approaches the reciprocal of the integral in (21) alone and can be approximated by a simpler expression [1], except at asymptotically low input currents, where the denominator changes sign:

$${\varphi }_{\mathit{AC}}(I_{\mathit{syn}})\approx \frac{c_{p/I}(I_{\mathit{syn}}-I_{\mathit{thresh},p/I})}{1-\exp [-g_{p/I}(c_{p/I}(I_{\mathit{syn}}-I_{\mathit{thresh},p/I}))]}.$$ (22)

This is plotted as the blue curve labeled Abbott–Chance. Here c_p/I is the asymptotic slope, I_thresh,p/I is the threshold for input current, and g_p/I is the noise factor that creates nonzero spontaneous activity; values for these parameters are listed in Appendix A. Equation (22) can be improved to account for higher firing rates by including τ_ref, as follows:

$$\begin{array}{l}{\varphi }_{E,a}(I_{\mathit{syn}})\approx {\left[{\tau }_{\mathit{ref}}+\frac{1-\exp [-g_{p/I}(c_{p/I}(I_{\mathit{syn}}-I_{\mathit{thresh},p/I}))]}{c_{p/I}(I_{\mathit{syn}}-I_{\mathit{thresh},p/I})}\right]}^{-1}\\ =\frac{c_{p/I}(I_{\mathit{syn}}-I_{\mathit{thresh},p/I})}{1-\exp [-g_{p/I}(c_{p/I}(I_{\mathit{syn}}-I_{\mathit{thresh},p/I}))]+{\tau }_{\mathit{ref}}{c}_{p/I}(I_{\mathit{syn}}-I_{\mathit{thresh},p/I})}.\end{array}$$ (23)

Figures 3(a) and 3(b) show all these f-I curves for both pyramidal cells and interneurons, with the function ϕ_E,a of (23) in green. With additional modifications to effective synaptic currents J_type,k, they can reasonably approximate the region of good performance in the neuromodulation plane, but steady-state firing rates are too high because ϕ_AC(I_syn) from (22) exceeds the limit 1/τ_ref = 500 Hz in the upper-right part of the high reward rate region (left part of the peak discriminability region in Figure 2), and ϕ_E,a only reduces firing rates of the winning selective population in this region to 200 Hz. In addition, with constant synaptic coupling these modifications can capture only a region near (γ_E, γ_I) = (1, 1). The full region [0, 3] × [0, 3] of Figure 1 was reproduced only after rescaling the effective synaptic currents J_type derived from the spiking model (by just under 33% for glutamatergic currents).

To lower the excessive asymptotic firing rates while retaining currents originally derived from the spiking model, we develop an empirical f-I curve for the pyramidal populations. The full spiking model was simulated under different (γ_E, γ_I) conditions, and the firing rates for each population were averaged over a 500 ms window once the system approached equilibrium. The firing rates of the four populations in the spiking model were then used to compute effective currents to each population using the reduced model currents (11)-(14) calculated above. Comparing these currents to the population firing rates which generated them in the spiking model produces the following function:

$${\varphi }_{E,b}(I_{\mathit{syn},p})={\varphi }_{p,0}+\frac{c_p(I_{\mathit{syn},p}-I_{\mathit{thresh},p})}{1-\exp [-g_p(c_p(I_{\mathit{syn},p}-I_{\mathit{thresh},p}))]+c_p(I_{\mathit{syn},p}-I_{\mathit{thresh},p})/{\varphi }_{p,\mathit{max}}},$$ (24)

shown in red in Figure 3(a), compared with empirical results from the spiking model (blue dots: the scatter is due to the fact that firing rates were only averaged over 500 ms windows). While (24) approximates the relationship between the simulated firing rates and the reduced model input currents I_syn which correspond to the simulated average population firing rates, the function (24) is constrained to have the same initial slope as (23).

For the 2AFC application it is most important to reproduce firing rates up to the decision threshold, i.e., ϕ(I_syn,p) ≤ 20 Hz. Several features of ϕ_E,b accomplish this. First, the spontaneous firing activity ϕ_p,0 is set to 1 Hz instead of 0. Second, I_thresh,p is reduced from 0.403 nA to 0.384 nA to start the linear rise at a lower input current. In addition, c_p is increased from 310 Hz/nA to 352 Hz/nA to produce a steeper initial slope. Noting that the parameter g_p/I in (22)-(23) sets the sharpness of the transition from zero firing rate to the rising portion, we set g_p = 1 for ϕ_E,b to create a sharper threshold. Finally, ϕ_E,b saturates at ϕ_p,0 + ϕ_p,max = 101 Hz as I_syn → ∞; cf. the red curve of Figure 3(a). This not only matches ϕ_E,a of (23) in the relevant region below 20 Hz, but as shown in Figure 4(b), it also fits the spiking network neuromodulation data well, with all parameters within 6% of the values derived from that model. The function ϕ_E,b allows us to capture global neuromodulatory behavior while retaining the synaptic couplings derived in section 3.1.

Figure 4.

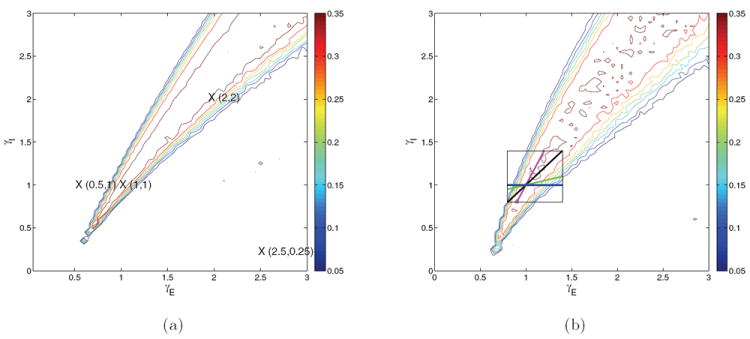
Contour maps of reward rate over the glutamatergic-GABA-ergic (γ_E, γ_I) gain modulation plane for the four-population models with f-I curves ϕ_E,a(I_syn,j) (a), and ϕ_E,b(I_syn,p) and ϕ_I,b(I_syn,I) (b). Peak synaptic currents are modified as described in text. Crosses identify gain pairs for which bifurcation diagrams are shown in Figures 5-6. Compare with spiking model results in Figure 1(a). The box with traversing lines in (b) illustrates (γ_E, γ_I) paths used to study speed-accuracy tradeoff in section 5.

The f-I curve for the interneuronal population must rise sufficiently steeply for inhibition to produce splitting behavior and correctly reproduce the no discriminability region of Figure 2. A piecewise-linear function ϕ_I,b(I_syn,I) with a spontaneous firing rate of 3 Hz, slope of 600 Hz/nA, and cutoff at I_thresh,i = 0.29 nA achieves this; see Figure 3(b) (black):

$${\varphi }_{I,b}(I_{\mathit{syn},I})=3+600\theta (I_{\mathit{syn},I}-I_{\mathit{thresh},I}),$$ (25)

in which θ is a Heaviside function. The four-population models differ in their use of different f-I curves.

Finally, the two-population model of section 4 is simplified by replacing the trivially linear f-I curve for the nonselective population of [49] by a piecewise-linear function with the same current threshold and initial slope as the selective populations, which will continue to use ϕ_E,b:

$${\varphi }_{\mathit{TL},3}(I_{\mathit{syn},3})=1+c_p\theta (I_{\mathit{syn},3}-I_{\mathit{thresh},p}),$$ (26)

but this is not necessary in the four-population models, in which all three pyramidal populations share identical f-I curves.

3.3. Noise currents in the reduced models

In typical spiking models each cell receives independent Poisson spike trains filtered through external or recurrent AMPA receptors, but in the present reduced models (as in that of [49]), additive Gaussian noise is superimposed on the external input current to each population. In Appendix B we derive an explicit description of these inputs by converting a Poisson spike train of mean frequency f to fluctuations in a single synaptic variable S about its average value f τ, where τ is the synaptic decay time constant. (See (43): the derivation is done for the distribution of fluctuations in the quantity gS, but the standard deviation is found to scale linearly with g, so it may be factored out as described in Appendix B.) The distribution of interspike fluctuations is not normal (see Figure 16(b)) but has zero mean and variance

$$\mathrm{Var}(\mathrm{\Delta }S)=\frac{\mathit{f\; \tau }}{\mathit{f\; \tau }+2}.$$ (27)

Figure 16.

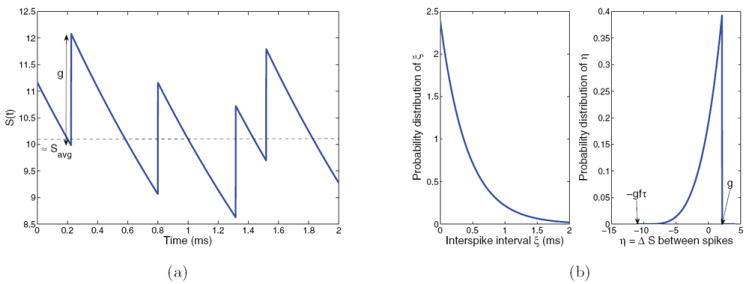
(a) Each incoming spike, with interspike intervals exponentially distributed with average 1/f, raises S(t) by g, after which it decays with time constant τ. (b) Probability distributions of ξ (left) and η (right); note flipped distribution. Simulation in (a) and distributions in (b) are both taken from I_AMPA,ext for spiking neuron model with g = 2.1, τ = T_AMPA = 2 ms, and f = 2400 Hz.

We then appeal to the Central Limit Theorem to argue that the summed effect of single spikes in single neurons (of N total) on the population-averaged synaptic variable is approximately Gaussian with zero mean and variance

$$\frac{\mathrm{Var}(\eta )}{N^2}=\frac{\mathit{f\; \tau }}{N^2(\mathit{f\; \tau }+2)}.$$ (28)

We can now calculate I_noise,k for inclusion in (15), which expresses I_AMPA,ext,k as the sum of a constant average current and I_noise,k (of mean zero). The fluctuations in S are multiplied by J_AMPA,ext,k to get the fluctuations in I_noise,k, and this relationship is maintained for varying gains since the standard deviation of fluctuations in gS scales linearly with g (see Appendix B). This is a population average of external inputs in the full model (cf. (8)). Summarizing, each I_noise,k is a sample path of the OU process

$$d{I}_{\mathit{noise},k}=-I_{\mathit{noise},k}\frac{\mathit{dt}}{T_{\mathit{AMPA}}}+J_{\mathit{AMPA},\mathit{ext},k}\sqrt{\frac{f^2\tau }{N(\mathit{f\; \tau }+2)}}\mathit{dW}.$$ (29)

3.4. Neuromodulation in the reduced models

Equipped with the f-I curves and Gaussian noise approximation described above, we can now implement neuromodulation in the four-population model by scaling all glutamatergic synaptic currents by γ_E and all GABA-ergic currents by γ_I. The model of [49] was fitted for a single point (γ_E, γ_I) = (1, 1) in the neuromodulation plane by changing peak synaptic currents and weights from those of the spiking network as follows: J_GABA,p = 1.2J_GABA,I instead of the full model’s 1.3J_GABA,I and ω₊ = 1.8 instead of the full model’s 1.7. Here we wish to obtain a good fit over a broad range of (γ_E, γ_I). Computing reward rates over [0, 3] × [0, 3] as in Figure 1, we found that this model is overdominated by excitation: the ridge of optimal performance analogous to that in Figure 1(a) rises too steeply in the (γ_E, γ_I) plane. Moreover, as noted in section 3.2, population firing rates are too high in the upper part of this ridge (results not shown).

We next consider the model with f-I curve ϕ_E,a(I_syn,j) that saturates at 1/τ_ref and with Gaussian noise and synaptic currents derived above (results not shown). The slope of the ridge is reduced but is still too high. In addition, the behavior at (γ_E, γ_I) = (1, 1) is characterized by no-choice trials. This may be corrected by setting J_GABA,p = 1.393J_GABA,I to adjust the slope and scaling glutamatergic currents by a factor in the range [1.3, 1.33]. (This adjustment is perhaps required by our assumption of uniform V̄ = −52.5 mV (cf. (10)), which most strongly affects GABA currents, since V_E,GABA = −70 mV and V_E,AMPA = V_E,NMDA = 0 mV.) This shifts the good performance region to include (1, 1), resulting in the reward rate contours of Figure 4(a), which compare reasonably well with those of Figure 1(a). Steady-state population firing rates can exceed those of the spiking network by 100%, but these are less critical for our purposes, since the 2AFC protocol focuses on trajectories up to the 20 Hz threshold and the model performs well in this region.

The match in reward rate contours can be further improved by using the function ϕ_E,b(I_syn,p) of (24) for the three pyramidal populations and the piecewise-linear function ϕ_I,b(I_syn,I) of (25) for the interneurons, as shown in Figure 4(b). For this final model, external AMPA, recurrent AMPA and NMDA currents, and J_GABA,I are exactly as derived from the spiking network, and J_GABA,p = 1.367 J_GABA,I is increased by slightly over 5% compared with the spiking network value of 1.3 J_GABA,I. These modified f-I curves properly situate the region of good behavior, moreover, and this model captures the concave curvature of the high reward rate ridge. Moreover, it allows simulation of 500 trials over 900 gain conditions in the same time as 500 trials of the spiking model for a single gain condition: this is a speed-up of O(10³).

3.5. Bifurcation analyses

To better understand the behaviors seen in Figures 1 and 2, we now study bifurcations of the four-population models as the average stimulus current μ₀ and coherence E vary. Computations are done without noise, using the software XPPAUT [20], and to reveal the system’s full structure we explore μ₀ values well beyond the physiologically realistic range, including “negative stimuli” (μ₀ < 0). Figures 5-8 show branches of equilibria for characteristic points on the neuromodulation plane in terms of the synaptic variables S_NMDA,1 and S_NMDA,2, written here and henceforth as S₁ and S₂ for brevity.

Figure 5.

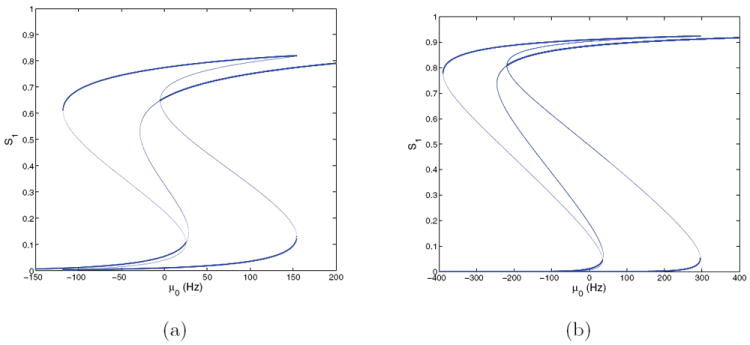
Bifurcation diagrams for the four-population model with f-I curves ϕ_E,a(I_syn,j) for E = 0 at (γ_E, γ_I) = (1, 1) (a) and (2, 2) (b); cf. Figure 4(a). Stable branches shown bold; branches for S₂ are identical due to symmetry.

Figure 8.

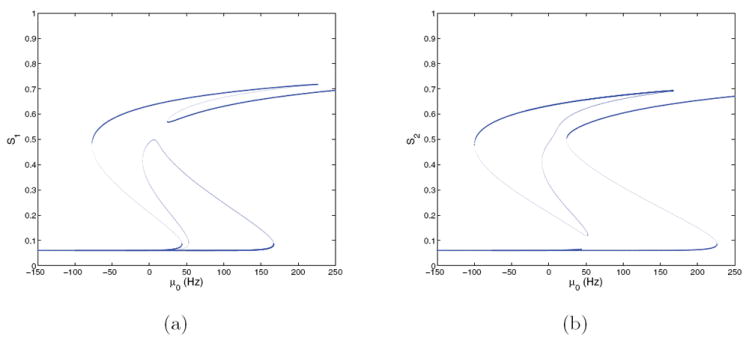
Bifurcation diagrams for the four-population model with f-I curves ϕ_E,b(I_syn,p) and ϕ_I (I_syn,I) and E = 0.128 at (γ_E, γ_I) = (1, 1); cf. Figure 4(b). (a) S₁ versus μ₀; (b) S₂ versus μ₀. Stable branches are shown in bold.

We start with the f-I curve ϕ_E,a of Figure 4(a), with rescaled glutamatergic currents as described in section 3.4, and at first set E = 0, so that the vectorfield of (17)-(20) is reflection-symmetric about the S_type,1 = S_type,2 and ν₁ = ν₂ hyperplanes. Figure 5(a) shows branches of fixed points at (γ_E, γ_I) = (1, 1) in the lower left of the peak discriminability region in Figure 2. For μ₀ = 0 the system is tristable: a state with the activities of both selective populations low coexists with a symmetric pair of “memory” attractors [47, 49] corresponding to choices, each with one population high and the other suppressed to zero. The low-low state loses stability in a subcritical pitchfork bifurcation at μ₀ ≈ 25, passes through two saddle-node bifurcations, and restabilizes as a high-high state at μ₀ ≈ −5, while the stable high-low states survive until they vanish in saddle-nodes at μ₀ ≈ 154. The low-low state persists for all μ₀ < 0, and the high-low states vanish in saddle-nodes at μ ≈ −118, leaving the low-low state as the sole attractor. Cycling μ₀ therefore allows memories of choices to be set and cleared in successive trials (e.g., by a strong inhibitory input).

The bifurcation diagram for (γ_E, γ_I) = (2, 2) is similar to that for (1, 1), but the two pitchforks move to μ₀ = 35 (low) and μ₀ = −219 (high): see Figure 5(b). This implies that both the low-low and high-high states coexist with the symmetric pair of high-low states over the range μ₀ ∈ (−219, 35), and that all four are stable (in this range there are nine fixed points).

These results help explain the network dynamics responsible for the behavior mapped in Figure 1. Prior to the start of a trial, μ₀ = 0 and the state remains near the low-low attractor, if it exists. In both panels of Figure 5 the pitchfork indicating loss of stability of this attractor lies in the range 20–35 Hz, so that, when μ₀ jumps to 40 Hz at stimulus onset, the system state diverges toward a choice attractor. In [49], the third high-high attractor does not appear until much larger μ₀, creating a pure decision dynamic in which the high-low attractors are the only stable states available. Due to the changes in synaptic currents made to match the region of good performance in the present model, this high-high state is also stable for all μ₀ ∈ (0, 40) Hz, but its basin of attraction does not include the physiologically relevant region in which both populations lie below threshold at stimulus onset, so the decision dynamics and effective tristability remain intact. This is illustrated by phase portraits of the two-population system in section 4.2.3.

The bifurcation diagrams also explain false alarm rates seen in the behavioral simulations. At μ = 0 noise can take the place of stimulus by carrying the state outside the low-low attractor’s basin. After crossing its boundary, the state moves toward a decision attractor, causing more impulsive choices. This is representative of the upper range of good performance in the peak discriminability region of Figure 2.

The diagrams of Figure 5 may seem confusing, because in the right panel, for (γ_E, γ_I) = (2, 2), the loss of stability occurs at a higher value of μ₀ than in the left panel, but the system exhibits more impulsive trials for (γ_E, γ_I) = (2, 2) than for (1, 1). This occurs due to the linear scaling of noise with γ_E, which doubles its magnitude at (2, 2).

For (γ_E, γ_I) = (0.5, 1) and (2.5, 0.25), in the blue and red regions of Figure 2, the system has unique monotonic branches of fixed points at low and high S_j, respectively (not shown here). In the latter case μ₀ and E have little influence and both S_j’s remain near 1, because both firing rates lie in the saturated part of the f-I curve where changes in input have little effect relative to the overall strong excitation within the network. No decisions are made in the blue region because there are no choice attractors, and splitting does not occur in the no discriminability region because there is a single high-high attractor.

We now turn to an asymmetric case. Figures 6(a) and 6(b) show fixed point branches for S₁ and S₂ at (γ_E, γ_I) = (1, 1) and E = 0.128 for comparison with Figure 5. The symmetric branch is now perturbed and the pitchforks become saddle-node bifurcations at μ₀ ≈ 20 and μ₀ ≈ 28, thus forcing decisions for μ₀ > 20 as solutions approach one of the choice attractors. The asymmetry due to nonzero coherence favors the state with larger S₁ (choice 1 correct) over that with larger S₂ when noise is present, since the former has a larger basin of attraction. These memory states persist for μ₀ ∈ (−105, 183) and μ₀ ∈ (−136, 133), respectively, terminating in saddle-node bifurcations much as in Figure 5. For μ₀ > 296 a unique high-high stable state exists, analogous to the one in Figure 5(a). We also computed bifurcation diagrams for (γ_E, γ_I) = (2, 2) and (0.5, 1), as for the E = 0 symmetric case above. At (2, 2) the result was generally similar to Figure 6, with some reconnections among branches typical of codimension 2 bifurcations [27]; a single monotonic branch with S₁ > S₂ was evident at (0.5, 1).

Figure 6.

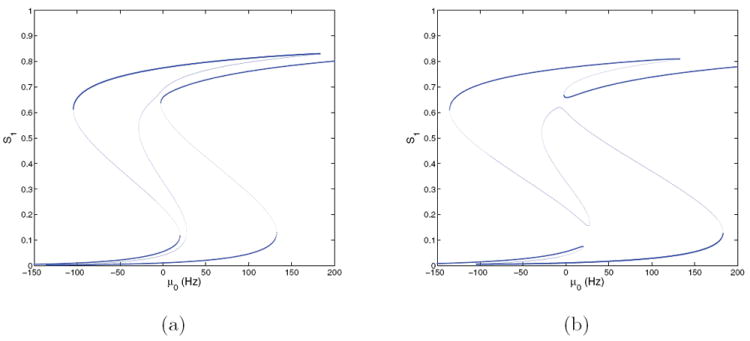
Bifurcation diagrams for the four-population model with f-I curves ϕ_E,a(I_syn,j) and E = 0.128 at (γ_E, γ_I) = (1, 1); cf. Figure 4(a). (a) S₁ versus μ₀; (b) S₂ versus μ₀. Stable branches are shown in bold.

We now consider the second four-population model that uses ϕ_E,b of (24) for pyramidal cells and the threshold-linear f-I curve (25) for interneurons, again focusing on behavior in the peak discriminability region of Figure 2(a). This model recreates the neuromodulation plane even better than that with ϕ_E,a (Figure 4(b)), and the bifurcation diagrams, shown in Figures 7 and 8, remain similar to those of Figures 5 and 6.

Figure 7.

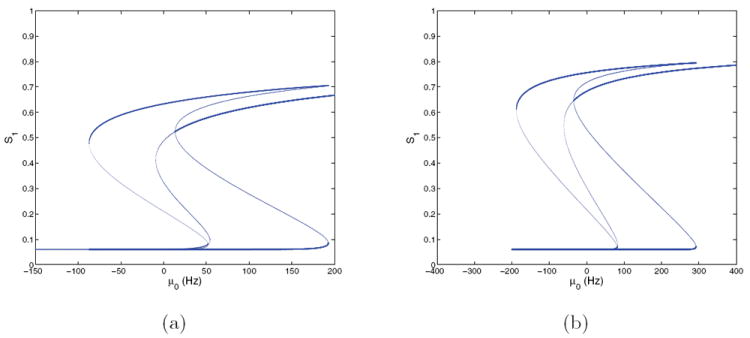
Bifurcation diagrams for the four-population model with f-I curves ϕ_E,b(I_syn,p) and ϕ_I (I_syn,I) and E = 0 at (γ_E, γ_I) = (1, 1) (a) and (γ_E, γ_I) = (2, 2) (b); cf. Figure 4(b). Stable branches are shown in bold; branches for S₂ are identical due to symmetry.

We again start with symmetric cases. Comparing Figures 7(a) and 5(a), we see that the branch structures at (γ_E, γ_I) = (1, 1) are similar but that the higher S_j values, and hence steady-state firing rates, are substantially reduced. This is as expected, since ϕ_E,b saturates at a lower value than ϕ_E,a (cf. Figure 3(a)). At (γ_E, γ_I) = (2, 2) (Figure 7(b)) the high-low states extend over a wider range in μ₀ and have higher firing rates, but the branches are much like those for ϕ_E,a shown in Figure 5(b). For (γ_E, γ_I) = (0.5, 1) and (2.5, 0.25) this system also has unique fixed point branches (not shown here), as in the ϕ_E,a case.

Figure 8 shows an asymmetric case at (γ_E, γ_I) = (1, 1) with E = 0.128. Fixed point branches are again similar to those of the analogous ϕ_E,a case (Figure 6), but the saddle-node in which the low-low state loses stability now occurs at μ₀ ≈ 44, higher than the 40 Hz value used in spiking model simulations. The high-high state appears in a saddle-node at μ₀ ≈ 20, so that, as for the E = 0 cases of Figure 7, the low-low, high-high, and two high-low states are all stable over a short range of μ₀. Although the low-low state loses stability above the stimulus-on condition μ₀ = 40, decisions still occur because the noise suffices to perturb states across the low-low basin boundary.

Figure 9 shows reaction time (RT) distributions for the asymmetric (E = 0.128) condition for both four-population models at (γ_E, γ_I) = (1, 1) and (2, 2). The reaction times measured in behavioral experiments are sums of decision times DT and nondecision latencies (NDL = 250 ms; cf. (1)). The standard gain cases on the left both produce typical RT distributions with longer tails to the right, while the high-gain conditions shown at right have tighter, faster RT distributions. The lower-right panel (ϕ_E,b, (γ_E, γ_I) = (2, 2)) also has a long tail of impulsive trials at the left, corresponding to the low-stimulus long exponential distribution noted in [32]. In this condition, firing rates of the selective populations tend to start nearer threshold and therefore to cross it sooner and with much less variance following stimulus onset. There are more impulsive choices than for (γ_E, γ_I) = (1, 1), and there is no long tail to the right. Changes in the RT distributions along with the corresponding changes in accuracy can implement a speed-accuracy tradeoff, as described in section 5.

Figure 9.

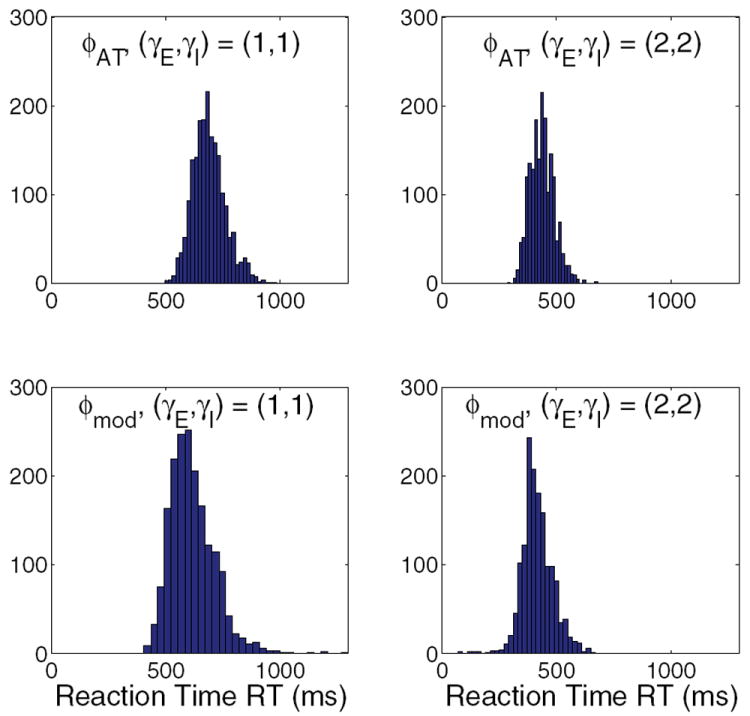
Reaction time distributions for the four-population models with ϕ_E,a (top) and ϕ_E,b (bottom) and for (γ_E, γ_I) = (1, 1) (left) and (2, 2) (right); E = 0.128 in all cases.

4. The two-population reduced model

The bifurcation studies of section 3.5 show that the four-population, 11-dimensional system (17)-(20) preserves key behaviors of the spiking model, but it is still too complex for full analytical study. Moreover, we wish to relate the original spiking network to one- and two-dimensional OU and leaky accumulator models [46, 8]. We therefore perform a further reduction to a two-population model, closely following the methods of [49], but relaxing assumptions made in that work in order to accommodate the wider range of synaptic currents due to NE modulation. This requires retaining two additional dynamic equations, and our model is therefore four- instead of two-dimensional as in [49]. The two-population model runs faster than the four-population models by a factor of four and allows analysis in a lower-dimensional space.

4.1. Two-population model structure

Reduction to two populations is based on separation of time scales [30, 27]. The synaptic time constants for AMPA and GABA are fast (T_AMPA = 2 ms; T_GABA = 5 ms), while that for NMDA decay is relatively slow (T_NMDA = 100 ms). S_AMPA,j and S_GABA,j therefore converge rapidly to quasi-steady states that closely track the population firing rates in (18)-(19) so that S_type,j ≈ ν_jT_type/1000. This eliminates three ODEs for the excitatory populations and one for the inhibitory population, giving a seven-dimensional system.

We next recognize that firing rates also rapidly approach the values set by the f-I curves in (20) since they too are dominated by T_AMPA. We may therefore set ν_j(t) ≈ ϕ_j(I_syn,j(t)) for the nonselective and interneuron populations and remove two firing rate ODEs. Now only three ODEs describing NMDA dynamics in the excitatory populations remain, along with the firing rate ODEs for populations 1 and 2. Finally, when stimuli are on, the nonselective population j = 3 typically exhibits a lower and much less variable firing rate than the selective populations so that S_NMDA,3 can be replaced by its steady-state value and its ODE may also be removed, leaving four ODEs for S_NMDA,1, S_NMDA,2, ν₁, and ν₂:

$$\frac{d{S}_1}{\mathit{dt}}=-\frac{S_1}{T_{\mathit{NMDA}}}+0.641(1-S_1)\frac{{\nu }_1}{1000},$$ (30)

$$\frac{d{S}_2}{\mathit{dt}}=-\frac{S_2}{T_{\mathit{NMDA}}}+0.641(1-S_2)\frac{{\nu }_2}{1000},$$ (31)

$$\frac{d{\nu }_1}{\mathit{dt}}=-\frac{{\nu }_1-{\varphi }_{E,b}(I_{\mathit{syn},1})}{T_{\mathit{pop}2}},$$ (32)

$$\frac{d{\nu }_2}{\mathit{dt}}=-\frac{{\nu }_2-{\varphi }_{E,b}(I_{\mathit{syn},2})}{T_{\mathit{pop}2}}$$ (33)

(here, as in section 3.5, we drop the subscript NMDA in S_j). However, input currents, which also include contributions due to nonselective and inhibitory neurons that no longer enter the dynamical equations, must be approximated in a self-consistent manner. Specifically, (30)-(33) are complicated by the fact that I_syn,j contains terms which depend on S_j and ϕ_E,b(I_syn,j), so that its vectorfield is defined recursively. Ideally, we seek linear relationships of the form

$$I_{\mathit{syn},1}={\alpha }_1{S}_1+{\alpha }_2{S}_2+{\beta }_1{\nu }_1+{\beta }_2{\nu }_2+I_{\mathit{const},1},$$ (34)

$$I_{\mathit{syn},2}={\alpha }_2{S}_1+{\alpha }_1{S}_2+{\beta }_2{\nu }_1+{\beta }_1{\nu }_2+I_{\mathit{const},2},$$ (35)

as in [49], where the parameter pairs α_j, β_j reflect the 1 ↔ 2 symmetry of the network. Accounting for all the components of the currents in (34)-(35) is difficult. The firing rates for the selective populations cannot be directly replaced by their steady states ν_j = ϕ_E,b(I_syn,j) to yield a two-dimensional model, as in [49], since the nonlinearity of ϕ_E,b(I_syn,j) makes the equations infinitely recursive. To close the system, (32)-(33) are therefore retained to track the firing rates as they approach their steady states. The calculations are summarized below and detailed in Appendix C. Given the other approximations, the rate of approach of ν_j to its quasi-steady state ϕ(I_syn,j) also must be changed from T_AMPA to T_pop2, as noted below in section 4.2.1.

4.1.1. Separation and derivation of synaptic currents

The derivation begins with the current equations (11)-(15) for the four-population model, which include synaptic variables for populations 3 and I that do not appear explicitly in (30)-(33). To account for these we break (11) into currents for each synapse type and population, expressing them as linear functions of S_j, ν_j, and constants, and gather like terms to form (34)-(35). In this section we calculate the coefficients of the input current to population 1 I_syn,1; those for population 2 follow by interchanging subscripts 1 ↔ 2 and replacing (1 + E) by (1 − E). From (11)-(15) we have

$$\begin{array}{lll}{I}_{\mathit{syn},1}& =& I_{\mathit{NMDA},1,1}+I_{\mathit{NMDA},2,1}+I_{\mathit{NMDA},3,1}+I_{\mathit{AMPA},1,1}+I_{\mathit{AMPA},2,1}\\ & +& I_{\mathit{AMPA},3,1}+I_{\mathit{GABA},I,1}+I_{\mathit{AMPA},\mathit{ext},1}+I_{\mathit{stim},1}+I_{\mathit{noise},1},\end{array}$$ (36)

where I_type,j,k denotes the current from population j to population k due to the given synapse,

$$\begin{array}{lll}{I}_{\mathit{NMDA},1,1}& =& S_1{N}_1{\omega }_{+}{J}_{\mathit{NMDA},p};I_{\mathit{NMDA},2,1}=S_2{N}_2{\omega }_{-}{J}_{\mathit{NMDA},p};\\ I_{\mathit{NMDA},3,1}& =& {\psi }_3{N}_3{\omega }_{-}{J}_{\mathit{NMDA},p};I_{\mathit{AMPA},1,1}={\nu }_1\frac{T_{\mathit{AMPA}}}{1000}{N}_1{\omega }_{+}{J}_{\mathit{AMPA},p};\\ I_{\mathit{AMPA},2,1}& =& {\nu }_2\frac{T_{\mathit{AMPA}}}{1000}{N}_2{\omega }_{-}{J}_{\mathit{AMPA},p};I_{\mathit{AMPA},3,1}={\varphi }_3\frac{T_{\mathit{AMPA}}}{1000}{N}_3{\omega }_{-}{J}_{\mathit{AMPA},p};\\ I_{\mathit{GABA},I,1}& =& {\varphi }_I\frac{T_{\mathit{GABA}}}{1000}{N}_I{J}_{\mathit{GABA},p};I_{\mathit{AMPA},\mathit{ext},1}=N_{\mathit{ext}}{\varphi }_{\mathit{ext}}\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},p,\mathit{ext}};\\ I_{\mathit{stim},1}& =& J_{\mathit{AMPA},\mathit{ext},p}{\mu }_0(1+E)\frac{T_{\mathit{AMPA}}}{1000},\end{array}$$ (37)

and I_noise,1 is determined by (29) of section 3.3. As in the four-population model of section 3, the parameters J_type,k denote peak synaptic currents, and they retain the same values. The factor ψ₃ in I_NMDA,3,1 is the steady-state value of S₃ from (16), but with ν₃ replaced by ϕ₃:

$${\psi }_3=\frac{0.641{\varphi }_3{T}_{\mathit{NMDA}}}{1000+0.641{\varphi }_3{T}_{\mathit{NMDA}}}.$$ (38)

Finally, ϕ₃ and ϕ_I are the steady-state firing rates of the rapidly equilibrating populations 3 and I, which are calculated as described below and in Appendix C.

4.1.2. Self-consistency of populations 3 and I

The currents of (37) are problematic in that they contain the quantities ϕ₃, ψ₃(ϕ₃), and ϕ_I, which do not appear explicitly in (34)-(35). These quantities must be expressed in terms of S₁, S₂, ν₁, ν₂, and constant currents I_const,j. The calculation employs the piecewise-linear f-I functions of (25) and (26), and one must determine regions of the parameter space in which the input currents exceed threshold, so that these functions are purely linear.

The main idea is to show that the firing rate ϕ₃ of population 3 can be approximated at a constant value ϕ_3,0 throughout the region of good performance. Self-consistency between populations 3 and I is then relatively easy to establish, and the coefficients α_j and β_j and constant currents I_const,j in (34)-(35) can be computed. This calculation is carried out in several stages, as detailed in Appendix C.

In Appendix C.1 we linearize ψ₃(ϕ₃) about an appropriate baseline value ϕ_3,0 and calculate consistent baseline firing rates ${\varphi }_3^{\ast }$ and ${\varphi }_I^{\ast }$ for populations 3 and I. In Appendices C.2–C.3 we consider the effects of S_j and ν_j on all four populations and calculate expressions for α_j and β_j, assuming pure linearity. We then check, in Appendix C.4, if the input currents do in fact remain above threshold throughout the relevant part of the (γ_E, γ_I)-neuromodulation plane. We find that the current due to the nonselective cells (population 3) does not satisfy this condition. We then use the self-consistency results again to show that the relationship between the currents of populations 3 and I implies that ϕ₃ can be held constant at ${\varphi }_3^{\ast }$. This necessitates resolving for ${\varphi }_I^{\ast }$ and recomputing some components of the coefficients α_j and β_j, which is done in Appendix C.5. The resulting values for the constant coefficients in (34)-(35) are as follows (cf. (79)-(85) and (91)):

$$\begin{array}{lll}{\alpha }_1& =& N_j{\omega }_{+}{J}_{\mathit{NMDA},p}+N_I{J}_{\mathit{GABA},p}\left(\frac{T_{\mathit{GABA}}}{1000}\right)\frac{c_I{N}_1{J}_{\mathit{NMDA},I}}{{\mathrm{\Gamma }}_I},\\ {\alpha }_2& =& N_j{\omega }_{-}{J}_{\mathit{NMDA},p}+N_I{J}_{\mathit{GABA},p}\left(\frac{T_{\mathit{GABA}}}{1000}\right)\frac{c_I{N}_1{J}_{\mathit{NMDA},I}}{{\mathrm{\Gamma }}_I},\\ {\beta }_1& =& N_j{\omega }_{+}{J}_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000}+N_I{J}_{\mathit{GABA},p}\left(\frac{T_{\mathit{GABA}}}{1000}\right)\frac{c_I{N}_1{J}_{\mathit{AMPA},I}\frac{T_{\mathit{AMPA}}}{1000}}{{\mathrm{\Gamma }}_I},\\ {\beta }_2& =& N_j{\omega }_{-}{J}_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000}+N_I{J}_{\mathit{GABA},p}\left(\frac{T_{\mathit{GABA}}}{1000}\right)\frac{c_I{N}_1{J}_{\mathit{AMPA},I}\frac{T_{\mathit{AMPA}}}{1000}}{{\mathrm{\Gamma }}_I},\end{array}$$ (39)

with ${\mathrm{\Gamma }}_I=1-c_I{N}_I{J}_{\mathit{GABA},I}\frac{T_{\mathit{GABA}}}{1000}$. The constant currents are (cf. (85))

$$\begin{array}{ccc}\hfill I_{\mathit{const},j}& =& I_{\mathit{AMPA},\mathit{ext},j}+I_{\mathit{stim},j}+I_{\mathit{Noise},j}+I_{\mathit{NMDA},3,j}^{\ast }+I_{\mathit{AMPA},3,j}^{\ast }+I_{\mathit{GABA},I,j}^{\ast },\hfill \\ \hfill I_{\mathit{AMPA},\mathit{ext},j}& =& N_{\mathit{ext}}{\varphi }_{\mathit{ext}}\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},\mathit{ext},p},\hfill \\ \hfill I_{\mathit{stim},1}& =& J_{\mathit{AMPA},\mathit{ext},p}{\mu }_0(1+E/100)\frac{T_{\mathit{AMPA}}}{1000},\hfill \\ \hfill I_{\mathit{stim},2}& =& J_{\mathit{AMPA},\mathit{ext},p}{\mu }_0(1-E/100)\frac{T_{\mathit{AMPA}}}{1000},\hfill \\ \hfill I_{\mathit{NMDA},3,j}^{\ast }& =& N_3{\omega }_{-}{J}_{\mathit{NMDA},p}(K_{\mathit{NMDA}}({\varphi }_3^{\ast }-{\varphi }_{3,0})+\psi ({\varphi }_{3,0})),\hfill \\ \hfill I_{\mathit{AMPA},3,j}^{\ast }& =& N_3{\omega }_{-}{J}_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000}{\varphi }_3^{\ast },\hfill \\ \hfill I_{\mathit{GABA},3,I}^{\ast }& =& N_I{J}_{\mathit{GABA},p}\frac{T_{\mathit{GABA}}}{1000}{\varphi }_I^{\ast }.\hfill \end{array}$$ (40)

The noise currents are the same as those derived in section 3.3. The baseline firing rates are ${\varphi }_3^{\ast }={\varphi }_{3,0}=1\mathrm{Hz}$, and ${\varphi }_I^{\ast }$ is calculated in section C.5 as

$${\varphi }_I^{\ast }=\frac{{\varphi }_{I,0}+c_I(I_{\mathit{AMPA},\mathit{ext},I}+I_{\mathit{NMDA},3,I}+I_{\mathit{AMPA},3,I}-I_{\mathit{thresh},I})}{{\mathrm{\Gamma }}_I}.$$ (41)

Finally, recall that the gains γ_E and γ_I enter the glutamatergic- and GABA-ergic currents as multiplicative factors in J_NMDA,p/I, J_AMPA,p/I, and J_GABA,p/I, respectively.

4.2. Two-population neuromodulation results

We now explore the effects of neuromodulation on the two-population model, ending with a bifurcation analysis under various gain conditions to compare with the spiking network and four-population models.

4.2.1. Simulation studies

We numerically integrate the system defined in (30)-(33), with currents as in (34)-(35), using a timestep Δt = 0.2 ms. The system behaves poorly with T_pop2 = T_AMPA in (32)-(33), because inhibition due to the interneurons changes with each timestep and Δt ≪ T_AMPA = 2 ms. Recurrent excitation due to AMPA currents depending on ν_j therefore takes longer to reach quasi-equilibrium, while the inhibitory current increases immediately. This affects the quasi-equilibrium values for ν_j, and the system is incorrectly dominated by inhibition. If we instead set T_pop2 = Δt, the solution remains numerically stable without overshoot, and the neuromodulation results of Figure 10 closely match those for the corresponding four-population model. In this condition, the model is effectively two-dimensional.

Figure 10.

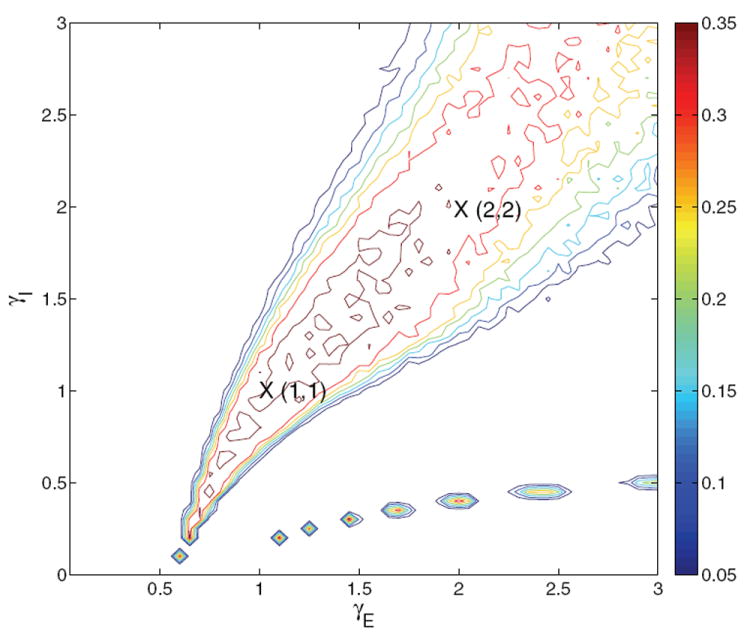
Contour map of reward rate over the glutamatergic-GABA-ergic (γ_E, γ_I) gain modulation plane for the two-population model with f-I curve ϕ_E,b for selective populations and ϕ₃ = const over part of the region and linearly varying over the rest, as described in text. Remaining parameters are as in the four-population model with ϕ_E,b, and original derived currents are retained. Crosses identify gain pairs for which bifurcation diagrams are shown in Figures 11-12. Compare with Figures 1(a) and 4(b). The chain of islands in the lower right is due to the determinant Γ, defined in Appendix C.2, passing through 0 as explained in Appendix C.4.

Simulating the system as described above, we explore the neuromodulation plane using the same parameters as the four-population model with the f-I curve ϕ_E,b of (24), obtaining the results shown in Figure 10. The location and curvature of the high reward rate ridge compare well with both Figures 1(a) and 4(b): that this match with the spiking network results is achieved with the same parameters for the two- and four-population models is a particularly good feature of ϕ_E,b. We henceforth consider only ϕ_E,b. We have already noted that ϕ_E,a gives unrealistically high firing rates in the four-population model; used in the two-population model it fails catastrophically at high gains (results not shown).

4.2.2. Bifurcation analysis

Figures 11-12 show bifurcation diagrams for (γ_E, γ_I) = (1, 1) and (2, 2) for both symmetric (E = 0) and asymmetric (E = 0.128) cases, done by determining the coefficients in the current equations from α_j’s and β_j’s appropriate to these specific locations in the modulation plane. (Note that the change in timescale for T_pop2 is irrelevant in determining fixed points of the noise-free system.) Fixed point branches are very similar to those of the corresponding four-population models (Figures 5-8): all bifurcations are of the same types, and occur within μ₀ = 1 – 2 Hz of their locations in that system. Interpretation of system behaviors and dynamics is therefore the same as in section 3.5, and we find that the two-population reduction successfully captures behavior over a substantial part of the neuromodulation plane.

Figure 11.

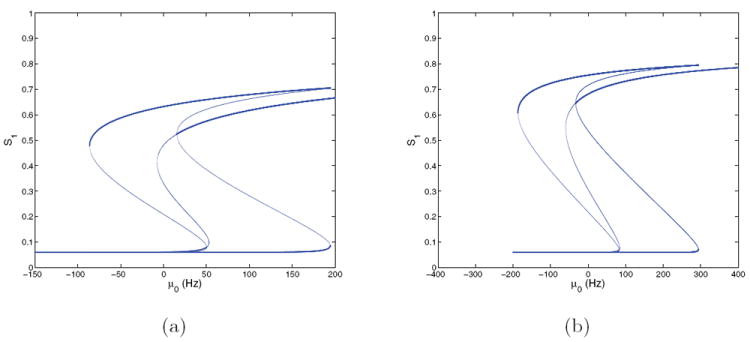
Bifurcation diagrams for the two-population model at E = 0 and (γ_E, γ_I) = (1, 1) (a) and (2, 2) (b); cf. Figure 10. Stable branches are shown in bold; all branches for S₂ are identical due to symmetry. Compare with the four-population case of Figures 5 and 7.

Figure 12.

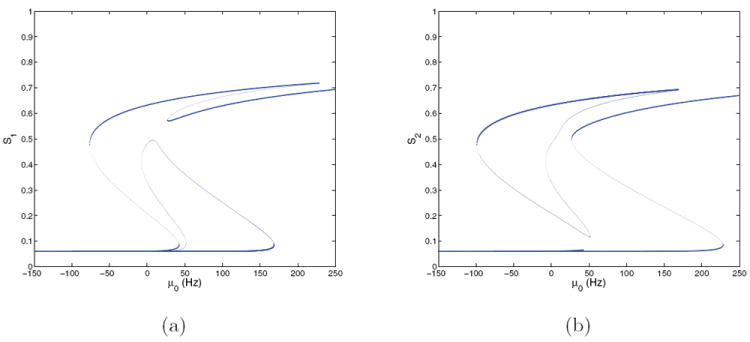
Bifurcation diagrams for the two-population model with E = 0.128 at (γ_E, γ_I) = (1, 1); cf. Figure 10. (a) S₁ versus μ₀; (b) S₂ versus μ₀. Stable branches are shown in bold.

4.2.3. Two-dimensional projections

Since the dynamics of the firing rates (ν₁, ν₂) are much faster than the NMDA synaptic variables (S₁, S₂), the two-population system can be studied through its dynamics projected onto the (S₁, S₂)-plane. Nullclines for S₁ and S₂ can be determined by fixing S₁ and S₂, allowing the firing rates ν₁ and ν₂ to rapidly equilibrate, and finding conditions for which dS₁/dt = 0 and dS₂/dt = 0 in (30)-(31). Figure 13 shows these nullclines, the fixed points with their stability types, and sample noisy trajectories of the four-dimensional flow projected on the (S₁, S₂)-plane. The two components of each nullcline—a line parallel to an axis and an approximate parabola—derive from the threshold in the f-I curve ϕ_E,b: the latter result from substitution of (34)-(35) into (30)-(33), and the lines correspond to states with synaptic currents that remain below threshold. Note that, for sufficiently large g_p, ν_j = ϕ_E,b(I_syn,j) ≈ ϕ_p,0 for I_syn,j < I_thresh,p, so that (30)-(31) become linear. Above threshold ϕ_E,b rises monotonically, behaving qualitatively like a threshold-linear function and producing the parabola-like curves when ν_j = ϕ_E,b(I_syn,j) is solved for ν_j in terms of S_j and substituted into (30)-(31).

Figure 13.

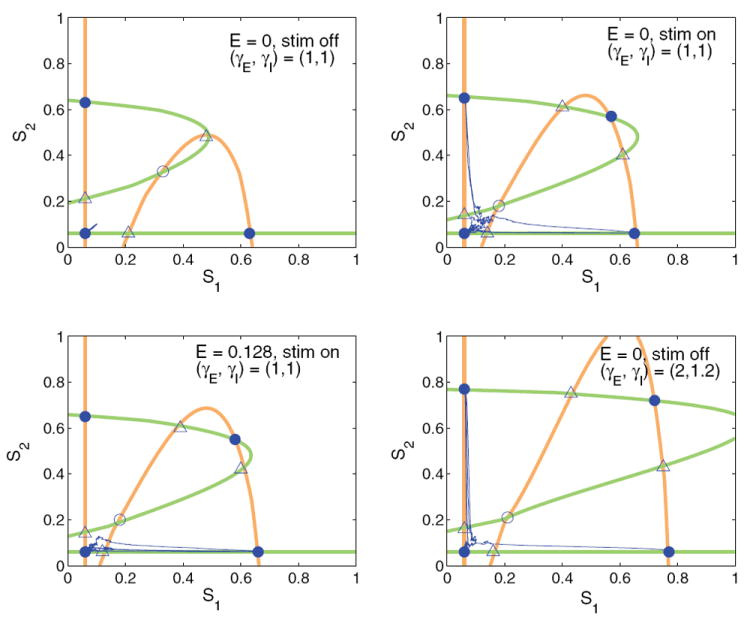
Dynamics of two-population model projected onto the (S₁, S₂)-plane, with nullclines for S₁ shown in orange and nullclines for S₂ shown in green. Stable points are shown as filled circles, saddles with one-dimensional stable manifolds as open triangles, and saddles with two-dimensional stable manifolds as open circles. From top left clockwise, nullclines, fixed points, and sample trial paths are shown without stimulus at (γ_E, γ_I) = (1, 1), with stimulus and E = 0 (symmetric) at (γ_E, γ_I) = (1, 1), without stimulus at (γ_E, γ_I) = (2, 1.2), and with stimulus for E = 0.128 at (γ_E, γ_I) = (1, 1).

We consider the standard gains (γ_E, γ_I) = (1, 1) without stimulus (top left), with symmetric stimuli (top right), and with asymmetric stimuli with E = 0.128 (lower left). Without stimulus, all trials remain near the low-low fixed point, even in the presence of noise, and both choice attractors persist, representing memory states. With stimulus (top right and bottom left), the low saddles and unstable fixed point approach the low-low stable fixed point, decreasing its basin of attraction and allowing more noisy trials to escape. Although the low-low attractor persists in this model due to the form of the modified f-I curve, it has only a small basin of attraction and the choice attractors dominate the dynamics, as in [49]. The nullclines in the lower-left panel illustrate the effects of asymmetric stimuli, and it is also clear that the high-high state does not significantly influence the dynamics.

Impulsive trials occur without stimulus for (γ_E, γ_I) = (2, 1.2), as in the lower right panel. The two low saddles and the unstable fixed point again lie near the low-low attractor, decreasing its basin of attraction, and since noise is twice as large as before, essentially all trials are impulsive. Similar phase-plane structures for two-dimensional neural systems appear in [21].

5. A speed-accuracy tradeoff via neuromodulation

The model of neuromodulation developed in [19] and reduced to lower dimensions above can implement a speed-accuracy tradeoff to optimize performance in 2AFC decision tasks. Reward rates can be maximized by appropriately balancing speed with accuracy [44], and subjects can modulate this balance in response to specific task instructions [33]. Changing task conditions such as stimulus strength or RSI can change the speed-accuracy tradeoff that maximizes the reward rate (see (1)), e.g., decreasing RSI shifts optima toward faster, less accurate performance. The models for speed-accuracy tradeoff in [39, 45, 24, 41, 42] modulate the gain of an input-output relationship or the drift rate of a DD model, and others [44, 8] implement threshold modulation, although these strategies are interchangeable in some models and both can simulate behavior very well. From a basic physiological perspective, however, identical motor responses should correspond to a similar level of firing in motor cortex, and thus threshold modulation may not be plausible.

Tonic (steady) locus coeruleus (LC) activity is known to affect cognitive performance via NE levels [5]. Experiments in a target-detection task found an inverse relationship between interstimulus interval and tonic LC firing rate [34], the latter changing from 3 to 5 Hz as the stimulus presentation frequency increased from 0.6/s to 1.0/s. Motivated by this, here we examine the ability of tonic NE levels, as represented in the four-population model of section 3 with f-I curve ϕ_E,b, to implement a physiologically derived speed-accuracy tradeoff. Such an investigation with a spiking model would be prohibitively time-consuming, and here the reduced model demonstrates its usefulness.

Simulations were done for gains lying along four line segments in a box of side length 0.6 around the point (γ_E, γ_I) = (1, 1) in the neuromodulation plane (see Figure 4(b)), and locations that maximize reward rate were determined for RSIs in a given range. Figures 14 and 15 show the results. Each curve in the upper-left panel of Figure 14 plots the reward rate at the optimal gain location (along its segment) for the RSIs specified along the horizontal axis. Continuing clockwise in Figure 14, we show the optimal γ_E’s, 〈RT〉’s, and accuracies for the same range of RSIs.

Figure 14.

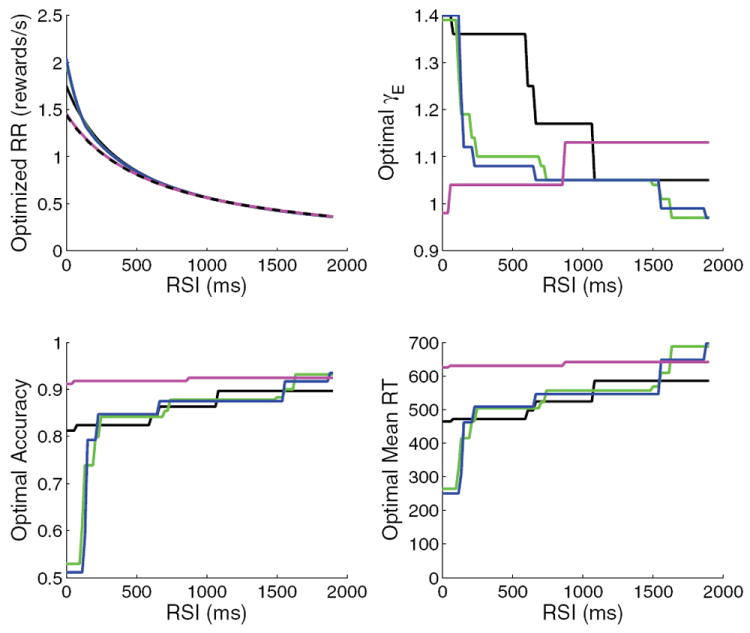
Results for linear slices through neuromodulation plane, for fixed gains (dotted black), 2Δγ_E = Δγ_I (magenta), Δγ_E = Δγ_I (black), Δγ_E = 4Δγ_I (green), and glutamatergic modulation γ_I = const (blue). The four panels (clockwise from top left) show the reward rate at the optimal gain, the optimal γ_E, the mean RT at optimal γ_E, and the accuracy at optimal γ_E. The jumps seen in the plots of optimal gain, RT, and accuracy are due to the small but not negligible random fluctuations in performance for the simulated sets of trials. An above average set may then optimize performance over a range of RSI before the solution jumps toward its expected value. Performance fluctuations are small enough with 20000 trials in each set, however, that the reward rates vary smoothly.

Figure 15.

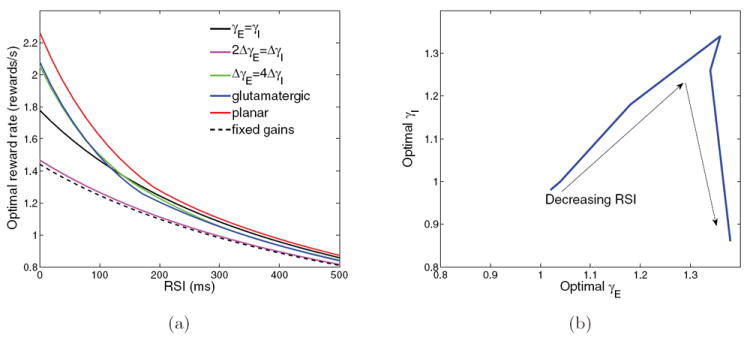
(a) Optimal reward rates as a function of RSI for each set of combinations of (γ_E, γ_I) shown in Figure 4(b). (b) Optimal gain path in neuromodulation plane; arrows denote decreasing RSIs.

The results for fixed gains at (γ_E, γ_I) = (1, 1) without neuromodulation are shown in dashed black at the bottom of the reward rate plot. Not surprisingly, this produces the worst overall performance, although decreasing RSI does increase reward rate (see (1)). The most robust case of [19], Δγ_I = 2 Δγ_E (magenta curve), does only marginally better, showing that robustness and the ability of neuromodulation to adapt performance under changing conditions are inversely related. Moreover, optimal γ’s (and therefore optimal LC firing rates) decrease with decreasing RSI for this gain modulation ratio (Figure 14, top right), opposite to what is seen experimentally. The other ratios, including those exhibiting the best performance, match the experimental results of [34].

Performances for γ_E = γ_I (solid black) and Δγ_E = 4 Δγ_I (green) successively improve on both the previous cases. The blue curve (overlapping the green) shows the result for glutamatergic modulation alone, with γ_I ≡ 1. Both excitation-dominated slices (blue and green curves) reach the fast impulsive regime at low RSIs and can therefore achieve the sharp upturn in reward rate that more robust ratios cannot. Finally, when neuromodulation conditions are allowed to vary over the entire region γ_E, γ_I ∈ [0.8, 1.4], further small improvements are obtained over the best “linear slice” results (red curve in Figure 15(a)). The optimal path through the (γ_E, γ_I)-neuromodulation plane which produces the red reward rate curve as RSI changes is shown in Figure 15(b). It rises with slope less than 1 over most of the range before plunging toward (γ_E, γ_I) = (1.4, 0.8) as RSIs fall below 300 ms. This sharply negative slope may not occur physiologically due to NE, but other cognitive mechanisms such as a switch to automatic responding can achieve similar effects (cf. the right-hand end of the optimal performance curve in [8]).

The ability of NE modulation in the present models to implement a speed-accuracy tradeoff as seen in experiments [34] suggests new experiments relating tonic LC firing rate to changes in RSI, with more RSI values tested than the two of [34]. With a linear mapping from tonic LC to NE levels [6], and assuming a linear mapping from NE to synaptic gains, our models could be fit to this data. This would inform the mapping from LC to synaptic gains, and factoring out the tonic LC to NE part would produce estimates of NE effects on synaptic gains in the full spiking model.

The optimal speed-accuracy tradeoff strategy in these models corresponds to a neuromodulation ratio with the highest slope that preserves robustness but still achieves fast, impulsive performance before the phasic response is disrupted [5]. For the limited gain range explored here, the slice Δγ_E = 4 Δγ_I (green line in Figure 4) achieves this. The more GABA-ergic modulation, the more stable the system to changes in NE concentration, and adding modulation of GABA-ergic synapses does not prevent optimal performance as long as the ratio is dominated by excitation. These results may differ in multilayer decision models [42], but that case is not examined here.

The actual path of NE effects through the neuromodulation plane may vary across brain regions, possibly due to different distributions of NE receptors. For instance, effects of NE have been found to be similar but with different frequencies of occurrence in thalamus and whisker barrel cortex of rats [16]. Effects of NE may also depend on phasic LC and the time course of NE concentration changes. Extending our models to different tasks and brain regions may require modifying basic model parameters such as the relative synaptic strength ω₊. These parameters can be fit to behavioral data under fixed task conditions, and task conditions can then be varied with these parameters fixed and changes in performance determined in terms of γ_E and γ_I.

6. Discussion

This study of physiologically realistic models of neuromodulation builds on the spiking neuronal network simulations of [19], extending from linear slices to the two-dimensional neuromodulation plane mapped in section 2.2. Many different system behaviors are observed in the spiking model, but it is difficult to understand underlying mechanisms in such a high-dimensional setting. The low-dimensional models developed in sections 3–4 facilitate this investigation: their bifurcation diagrams, in particular, are helpful in interpreting the results of Figure 2 in terms of population dynamics of cells correlated with the two choices. In the region where the full model exhibits failure of pooled inhibition, only a high-high attractor exists without stable states to which either selective population could be suppressed. In the below threshold region only low-low stable states exist and decision thresholds are never reached. In the peak discriminability region, stimulus-induced loss of stability of the low-low state can force decisions. Impulsive choices can also occur due to noise perturbing the state across a basin boundary toward a choice attractor, and higher noise levels at high excitatory gains make such jumps more likely. At still higher gains, the low-low state is unstable in the absence of stimuli, and all trials are impulsive. However, firing rates of the selective populations continue to split until the high-low choice attractors disappear in the no discriminability region.

Unlike earlier models that were tuned to fit reaction time distributions for a fixed set of synaptic gains [49], the present low-dimensional models were developed to match the global neuromodulation results of Figures 1-2. Such models cannot accurately describe all aspects of neural systems, but they do allow the study of specific behaviors in analytically tractable settings. Indeed, knowledge of the underlying neurophysiology is currently insufficient to formulate detailed models, as in the present case of NE modulation. Low-dimensional models should then be judged by their ability to increase the understanding of basic system phenomena and to suggest further experiments. In this regard our two- and four-population models are ready to incorporate physiological mappings from LC activity via NE concentration to synaptic gains, once such mappings are experimentally determined.

The main purpose of these models is to link physiological effects of NE and other neuromodulators to behaviors in decision-making tasks, as illustrated in section 5. Different locations in the neuromodulation plane correspond to different levels of subject performance. High-dimensional, cellular-level models obviously permit better representations of neurophysiology, but they are difficult to parameterize and computationally intensive. As demonstrated in [47, 19], such models can include the cellular and synaptic detail needed to relate neuromodulator effects to behavioral outcomes, but many trials must be simulated to amass reliable data and fit multiple experimental conditions, which demands extensive computational resources.

In contrast, one-dimensional DD and OU models and two-dimensional leaky accumulators, with appropriate parameterization, can describe behavioral aspects of two-alternative decisions remarkably well [46, 25, 26, 8, 18]. They are not only fast and simple to simulate, but they admit analytical investigation. Our reduction from 9200 to 11 and finally 4 variables provides a bridge across this dimensional divide that promises to better relate neuromodulation at the cellular scale to bifurcation of attractors and low-dimensional models in cognitive psychology. For the computational cost of simulating 500 trials in a single gain condition in the spiking model, it is possible to simulate 500 four-population or 2000 two-population trials over a grid of 900 gain conditions. This enables studies such as that of section 5, which are not computationally feasible in the spiking model. Moreover, as more neurophysiological data become available, the low-dimensional models can be improved.

In summary, this set of physiologically inspired models provides a bridge from neuromodulation at the single-cell level to decision-making behavior and thereby allows improvements in knowledge in each area to increase understanding in the other. The spiking model of neuromodulation provides a map from neurophysiology to behavior, but many of the neurophysiological details have yet to be experimentally determined, especially for NE dynamics under phasic LC activity. Model simulations raise important questions and suggest new experiments, as described here and in [19], but there is a limit to how far the spiking model can be taken at this time. In contrast, the reduced models are computationally efficient enough to allow data-fitting in LC-recording experiments with varying RSIs, creating a map from behavior back to neurophysiology.

Appendices: Proofs and mathematical details

Appendix A. Parameter values for spiking and reduced models

Task parameters

E = 0.128, μ₀ = 40 Hz, threshold = 20 Hz.

Leaky integrate-and-fire model neuron parameters

V_thresh = −50 mV, V_reset = −55 mV, V_L = −70 mV, g_L,p = 25 nS, g_L,I = 20 nS, C_p = 0.5 nF, C_I = 0.2 nF, τ_m,p = 20 ms, τ_m,I = 10 ms, τ_ref,p = 2 ms, τ_ref,I = 1 ms.

Synaptic time constants

T_AMPA = 2ms, T_NMDA = 100 ms, T_NMDA,rise = 2ms, T_GABA = 5 ms.

Peak synaptic conductances for spiking neuronal network

g_AMPA,ext,p = 2.1 nS, g_AMPA,ext,I = 1.65 nS, g_AMPA,p = 0.05 nS, g_AMPA,I = 0.04 nS, g_NMDA,p = 0.165 nS, g_NMDA,I = 0.13 nS, g_GABA,p = 1.0 * 1.3 nS, g_GABA,I = 1.0 nS.

Other parameters for spiking neuronal network

V_E,AMPA = 0 mV, V_E,NMDA = 0 mV, V_E,GABA = −70 mV, ω₊ = 1.7, ω₋ = 0.877, [Mg²⁺] = 1 mM, f_ext = 2.4 kHz. μ_S,AMPA,ext,j and σ_S,AMPA,ext,j are computed as in (6)-(7).

Derived synaptic currents for four-population model

J_AMPA,ext,p = 0.11025 nA, J_AMPA,ext,I = 0.08505 nA, J_AMPA,p = 0.002625 nA, J_AMPA,I = 0.0021, J_NMDA,p = 0.0010487, J_NMDA,I = 0.0008262, J_GABA,p = −0.0175 * 1.3, J_GABA,I = −0.0175.

Parameters for f-I curve ϕ_E,a

c_p = 310 Hz/nA, I_thresh,p = 0.403 nA, g_p = 0.16; c_I = 615 Hz/nA, I_thresh,I = 0.289 nA, g_I = 0.087.

Parameters for f-I curve ϕ_E,b

ϕ_p,max = 100 Hz, ϕ_p,₀ = 1 Hz, g_p = 1, c_p = 352 Hz/nA, I_thresh,p = 0.384 nA; ϕ_I,0 = 3 Hz, I_thresh,I = 0.29 nA, c_I = 600 Hz/nA.

Appendix B. Gaussian noise derivation for the reduced models

In order to calculate the effect of neuromodulation on the noise current, we include the synaptic conductance g_AMPA,ext,k in the synaptic variables S_AMPA,ext,k for this derivation. We first consider a simple case of periodic spike inputs. The values of S_NMDA, S_AMPA, S_AMPA,ext, and S_GABA for each population are averages of the S_type,k values for each neuron in the population. For a single cell with an input of frequency f, this approaches a periodic oscillation. Each spike increases S_type,k by the peak synaptic conductance g; it then decays exponentially with synaptic time constant τ, so periodicity is achieved when the decay between input spikes equals g. Letting S_peak denote the value immediately after the spike input, we therefore require

$$S_{\mathit{peak}}\exp (-1/\mathit{f\; \tau })=S_{\mathit{peak}}-g\mathrm{or}{S}_{\mathit{peak}}=\frac{g}{1-\exp (-1/\mathit{f\; \tau })}.$$ (42)

The average is computed by integrating over the interspike interval:

$$S_{\mathit{avg}}=f{\mathit{\int }}_0^{1/f}{S}_{\mathit{peak}}{e}^{-t/\tau }\mathit{dt}=\mathit{f\; \tau \; g}.$$ (43)

For a Poisson spike train of mean frequency f interspike intervals ξ are exponentially distributed with density

$$f{e}^{-\mathit{f\xi }}\mathit{d\xi },$$ (44)

so that the jumps in S_type,k are also exponentially distributed; see Figure 16(a). If S > g f τ, it decays faster than at its average value, and if S < g f τ, the decay is slower, and the average is stable. To get the true diffusive noise for use in (29), we consider fluctuations from the average. Setting S_peak ≈ S_avg + g, we compute the change in S from immediately before one input spike to immediately before the next as

$$\eta =g-(\mathit{g\; f\; \tau }+g)(1-e^{-\xi /\tau }).$$ (45)

These fluctuations can be positive or negative, depending upon the interspike interval.

Solving (45) for ξ in terms of η and differentiating, we obtain

$$\xi =-\tau \log \left(1-\frac{g-\eta }{\mathit{g\; f\; \tau }+g}\right)\mathrm{and}\mathit{d\xi }=\frac{-\mathit{\tau \; d\eta }}{(1-\frac{g-\eta }{\mathit{g\; f\; \tau }+g})(\mathit{g\; f\; \tau }+g)},$$ (46)

and substituting (45) into (44) yields the distribution for the fluctuations in η:

$$\frac{\mathit{f\; \tau }}{\mathit{g\; f\; \tau }+g}{\left(\frac{\mathit{g\; f\; \tau }+\eta }{\mathit{g\; f\; \tau }+g}\right)}^{\mathit{f\; \tau }-1}\mathit{d\eta }.$$ (47)

Here η varies from g to −g f τ as ξ varies in (0,∞); see Figure 16(b). Reversing the limits of integration so that η varies from −g f τ to g adds the extra negative sign which makes (47) a proper nonnegative probability distribution. At the end of this appendix we check that this distribution has zero mean and show that its variance is

$$\mathrm{Var}(\eta )=\frac{f{g}^2\tau }{\mathit{f\; \tau }+2}.$$ (48)

Hence, as noted in section 3.3, the standard deviation varies linearly with g, and g may be factored out in (27)-(29). The fluctuations in current input to neuron j in the spiking neuronal model are equal to Δ(gS)(V_j − V_E) (cf. (9)), and once g is factored out of Δ(gS) it is multiplied by (V_j − V_E). Once fluctuations are averaged over a population, this product must use the population average voltage V̄, and Δ(S) is multiplied by g_AMPA,ext,k(V̄ − V_E) = J_AMPA,ext,k (cf. (10)) as seen in (29).

The Central Limit Theorem [22] implies that the distribution of a sum of n independent, identically distributed random variables, with mean a and variance b, converges to a normal distribution with mean na and variance nb as n → ∞. We now appeal to this to argue that the Poisson spike trains entering individual cells in the spiking model can be replaced by additive Gaussian noise in the averaged synaptic variable ODEs (17)-(19) of the population model.

For a single cell with input frequency f = 2.4 kHz and timesteps Δt = 0.1 ms (appropriate for numerical integration of (17)-(19)), n = f Δt = 0.24 is small, and so the argument does not apply. However, the variables S_type,j/I in (17)-(19) are obtained by averaging over populations of N_j and N_I cells. The result of n fluctuations drawn from the zero-mean distribution of Figure 16(b) (right) entering each cell has variance n Var(η), so that, summing over N cells, the population average $S=\frac{{\sum }_i{S}_i}{N}$ changes by a random quantity with zero mean and variance nVar(η)/N². Since n = N f Δt, the Gaussian approximation is much better justified, and we may model the effect of a single fluctuation on the population-averaged synaptic variable as a zero mean Gaussian with variance

$$\frac{n\mathrm{Var}(\eta )}{n{N}^2}=\frac{\mathrm{Var}(\eta )}{N^2}.$$ (49)

For large N this is small, so that S_avg for a single cell will be close to g f τ, justifying our assumption prior to (45).

We now consider changes S(t + s) − S(s) due to fluctuations from time s to s + t (t ≥ 0). These have expected value 0 since all increments have expected value zero, and since ≈ N f t incoming spikes occur in (s, s + t), the variance of their summed effect is

$$\mathrm{Var}(S(t+s)-S(s))=\frac{N\mathit{f\; t}\mathrm{Var}(\eta )}{N^2}=\frac{\mathit{f\; t}\mathrm{Var}(\eta )}{N}\stackrel{\mathrm{def}}{=}{\sigma }^{2}t.$$ (50)

From the previous paragraph, this summed noise is normally distributed, so it satisfies the requirements of a Wiener process [23]. We may therefore model the noise current I by a stochastic differential equation with additive Gaussian noise, as in (29).

Finally we check that the mean and variance of the distribution (47) are as stated above. The mean is given by

$$\mu (\eta )={{\mathit{\int }}_{-\mathit{g\; f\; \tau }}^g\frac{\mathit{f\; \tau }}{g+\mathit{g\; f\; \tau }}\left(\frac{\mathit{g\; f\; \tau }+\eta }{\mathit{g\; f\; \tau }+g}\right)}^{\mathit{f\; \tau }-1}\mathit{\eta \; d\eta },$$ (51)

which may be integrated by parts to give

$${\left[\eta {\left(\frac{\mathit{g\; f\; \tau }+\eta }{\mathit{g\; f\; \tau }+g}\right)}^{\mathit{f\; \tau }}\right]}_{-\mathit{g\; f\; \tau }}^g-{{\mathit{\int }}_{-\mathit{g\; f\; \tau }}^g\left(\frac{\mathit{g\; f\; \tau }+\eta }{\mathit{g\; f\; \tau }+g}\right)}^{\mathit{f\; \tau }}\mathit{d\eta }=g-{\left[{\left(\frac{\mathit{g\; f\; \tau }+\eta }{\mathit{g\; f\; \tau }+g}\right)}^{\mathit{f\; \tau }+1}\frac{\mathit{g\; f\; \tau }+g}{\mathit{f\; \tau }+1}\right]}_{-\mathit{g\; f\; \tau }}^g=0.$$ (52)

The expression for variance,

$${{\mathit{\int }}_{-\mathit{g\; f\; \tau }}^g\frac{\mathit{f\; \tau }}{g+\mathit{g\; f\; \tau }}\left(\frac{\mathit{g\; f\; \tau }+\eta }{\mathit{g\; f\; \tau }+g}\right)}^{\mathit{f\; \tau }-1}{\eta }^2\mathit{d\eta },$$ (53)

is integrated by parts twice, first to yield

$$\mathrm{Var}(\eta )=g^2-\frac{2}{{(\mathit{g\; f\; \tau }+g)}^{\mathit{f\; \tau }}}{\mathit{\int }}_{-\mathit{g\; f\; \tau }}^g\eta {(\mathit{g\; f\; \tau }+\eta )}^{\mathit{f\; \tau }}\mathit{d\eta },$$

and then finally

$$\begin{array}{l}\mathrm{Var}(\eta )=g^2-\frac{2}{{(\mathit{g\; f\; \tau }+g)}^{\mathit{f\; \tau }}}{\left[\eta \frac{{(\mathit{g\; f\; \tau }+\eta )}^{\mathit{f\; \tau }+1}}{\mathit{f\; \tau }+1}\right]}_{-\mathit{g\; f\; \tau }}^g-\frac{1}{\mathit{f\; \tau }+1}{\mathit{\int }}_{-\mathit{g\; f\; \tau }}^g{(\mathit{g\; f\; \tau }+\eta )}^{\mathit{f\; \tau }+1}\mathit{d\eta }\\ =g^2-2g^2+\frac{2{(\mathit{g\; f\; \tau }+g)}^{\mathit{f\; \tau }+2}}{(\mathit{f\; \tau }+1)(\mathit{f\; \tau }+2){(\mathit{g\; f\; \tau }+g)}^{\mathit{f\; \tau }}}=\frac{f{g}^2\tau }{\mathit{f\; \tau }+2}.\end{array}$$ (54)

Appendix C. Details of the two-population derivation

In Appendices C.1–C.5 we provide details of the self-consistency calculations, sketched in section 4.1.2, that close the ODEs (34)-(35).

C.1. Self-consistency calculation for populations 3 and I

The firing rates of populations 3 and I must be expressed as functions of S_j, ν_j, and constant input currents. This is done by separating the inputs to these populations, calculating the output corresponding to each input, and summing them. For such a linear superposition to work, the f-I curves must also be linear (or piecewise-linear with fluctuations confined to a single linear piece). We use the form

$${\varphi }_j(I_{\mathit{syn},j})={\varphi }_{j,0}+c_j\theta (I_{\mathit{syn},j}-I_{\mathit{thresh},j}),j=3,I,$$ (55)

where ϕ_j,0 is the minimum firing rate for I_syn,j < I_thresh,j and I_thresh,j is the threshold current for population j.

To match the f-I curve ϕ_E,b in the critical region below the decision threshold (20 Hz), we set I_thresh,p = 0.384 nA for pyramidal cells and I_thresh,I = 0.29 nA for interneurons (see black curves in Figures 3(a) and 3(b)). We approximate ψ₃(ϕ₃) by linearizing (38) about a value ϕ_3,0:

$${\psi }_3({\varphi }_3)\approx {\psi }_3^{\ast }+K_{\mathit{KMDA}}{\varphi }_3,$$ (56)

where

$${\psi }_3^{\ast }=-K_{\mathit{NMDA}}{\varphi }_{3,0}+{\psi }_3({\varphi }_{3,0})\mathrm{and}{K}_{\mathit{NMDA}}=\frac{0.641T_{\mathit{NMDA}}}{{(1000+0.641T_{\mathit{NMDA}}{\varphi }_{3,0})}^2}.$$ (57)

(Here we use ϕ_3,0 = 1 Hz as for ϕ_E,b in the four-population model, but the derivation is general.) If I_syn,3 > I_thresh,p, then ϕ₃ and the approximation (56) both vary linearly with changes in I_syn,3, and the same is true for ϕ_I, so if both input currents are above their respective thresholds, increments in current and firing rate are related by

$$\mathrm{\Delta }{\varphi }_3=c_3\mathrm{\Delta }{I}_{\mathit{syn},3}\mathrm{and}\mathrm{\Delta }{\varphi }_I=c_I\mathrm{\Delta }{I}_{\mathit{syn},I}.$$ (58)

To begin to separate ϕ₃ and ϕ_I, we ignore inputs from populations 1 and 2 and focus on the external currents to populations 3 and I and recurrent connections in populations 3 and I. For I_syn,j > I_thresh,j, the step function θ disappears and (55) simplifies to

$${\varphi }_j(I_{\mathit{syn},j})={\varphi }_{j,0}+c_j(I_{\mathit{syn},j}-I_{\mathit{thresh},j}),j=3,I.$$ (59)

Define ${\varphi }_3^{\ast }$ and ${\varphi }_I^{\ast }$ as the solutions to this linear system. If ${\varphi }_3^{\ast }>{\varphi }_{3,0}$ and ${\varphi }_I^{\ast }>{\varphi }_{I,0}$, then the system is in the purely linear range and (58) applies. If either condition fails, ϕ₃ and ϕ_I must be treated otherwise, as described in sections C.4–C.5.

We solve for the baseline firing rates ${\varphi }_3^{\ast }$ and ${\varphi }_I^{\ast }$ from (55), using the components of the currents I_syn,3 and I_syn,I, except for the inputs from populations 1 and 2:

$${\varphi }_3^{\ast }={\varphi }_{3,0}+c_3(I_{\mathit{AMPA},\mathit{ext},3}+I_{\mathit{NMDA},3,3}+I_{\mathit{AMPA},3,3}+I_{\mathit{GABA},I,3}-I_{\mathit{thresh},p}),$$ (60)

$${\varphi }_I^{\ast }={\varphi }_{I,0}+c_I(I_{\mathit{AMPA},\mathit{ext},I}+I_{\mathit{NMDA},3,I}+I_{\mathit{AMPA},3,I}+I_{\mathit{GABA},I,I}-I_{\mathit{thresh},I}),$$ (61)

in which

$$\begin{array}{l}{I}_{\mathit{NMDA},3,3}=N_3{J}_{\mathit{NMDA},p}{\psi }_3({\varphi }_3^{\ast });I_{\mathit{NMDA},3,I}=N_3{J}_{\mathit{NMDA},I}{\psi }_3({\varphi }_3^{\ast });\\ I_{\mathit{AMPA},3,3}=N_3{J}_{\mathit{AMPA},P}\frac{T_{\mathit{AMPA}}}{1000}{\varphi }_3^{\ast };I_{\mathit{AMPA},3,I}=N_3{J}_{\mathit{AMPA},I}\frac{T_{\mathit{AMPA}}}{1000}{\varphi }_3^{\ast };\\ I_{\mathit{GABA},I,3}=N_I{J}_{\mathit{GABA},p}\frac{T_{\mathit{GABA}}}{1000}{\varphi }_I^{\ast };I_{\mathit{GABA},I,I}=N_I{J}_{\mathit{GABA},I}\frac{T_{\mathit{GABA}}}{1000}{\varphi }_I^{\ast },\\ I_{\mathit{AMPA},\mathit{ext},3}=N_{\mathit{ext}}{\varphi }_{\mathit{ext}}\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},\mathit{ext},p,}\\ I_{\mathit{AMPA},\mathit{ext},I}=N_{\mathit{ext}}{\varphi }_{\mathit{ext}}\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},\mathit{ext},I.}\end{array}$$ (62)

Substituting the expressions (62) into (60)-(61), using (56), and collecting terms yields a linear system of the form

$$a_1{\varphi }_3^{\ast }+b_1{\varphi }_I^{\ast }+d_1=0,$$ (63)

$$a_2{\varphi }_3^{\ast }+b_2{\varphi }_I^{\ast }+d_2=0,$$ (64)

where

$$\begin{array}{lll}{a}_1& =& c_3{N}_3\left(J_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000}+J_{\mathit{NMDA},p}{K}_{\mathit{NMDA}}\right)-1,\\ b_1& =& c_3{N}_I{J}_{\mathit{GABA},p}\frac{T_{\mathit{GABA}}}{1000},\\ d_1& =& {\varphi }_{3,0}+c_3[I_{\mathit{AMPA},\mathit{ext},3}+N_3{J}_{\mathit{NMDA},p}(-K_{\mathit{NMDA}}{\varphi }_{3,0}+{\psi }_{3,0})-I_{\mathit{thresh},p}],\\ a_2& =& c_I{N}_3\left(J_{\mathit{AMPA},I}\frac{T_{\mathit{AMPA}}}{1000}+J_{\mathit{NMDA},I}{K}_{\mathit{NMDA}}\right),\\ b_2& =& c_I{N}_I{J}_{\mathit{GABA},I}\frac{T_{\mathit{GABA}}}{1000}-1,\\ d_2& =& {\varphi }_{I,0}+c_I[I_{\mathit{AMPA},\mathit{ext},I}+N_3{J}_{\mathit{NMDA},I}(-K_{\mathit{NMDA}}{\varphi }_{3,0}+{\psi }_{3,0})-I_{\mathit{thresh},i}].\end{array}$$ (65)

Equations (63)-(64) have the solution

$${\varphi }_3^{\ast }=\frac{-d_1{b}_2+d_2{b}_1}{\mathrm{\Gamma }},{\varphi }_I^{\ast }=\frac{d_1{a}_2-d_2{a}_1}{\mathrm{\Gamma }},$$ (66)

where Γ = a₁b₂ − a₂b₁. If (58) holds, the effects of S_j and ν_j can be calculated separately and then summed. The base currents to populations 1 and 2 due to ${\varphi }_3^{\ast }$ and ${\varphi }_I^{\ast }$ are then constant and can be calculated as

$$I_{\mathit{NMDA},3,j}^{\ast }=N_3{\omega }_{-}{J}_{\mathit{NMDA},p}(K_{\mathit{NMDA}}({\varphi }_3^{\ast }-{\varphi }_{3,0})+\psi ({\varphi }_{3,0})),$$ (67)

$$I_{\mathit{AMPA},3,j}^{\ast }=N_3{\omega }_{-}{J}_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000}{\varphi }_3^{\ast },$$ (68)

$$I_{\mathit{GABA},3,I}^{\ast }=N_I{J}_{\mathit{GABA},p}\frac{T_{\mathit{GABA}}}{1000}{\varphi }_I^{\ast }.$$ (69)

These currents (67)-(69) become the part of the constant terms of (34) due to populations 3 and I. The currents into populations 3 and I due to S_j and ν_j affect the currents from populations 3 and I to each other and back to populations 1 and 2 as calculated in the next section.

C.2. Effects of S_j and ν_j on the four populations

Each of the four state variables that remain in the ODEs (34)-(35) affects the four-population system through a similar set of currents: the current back to its own population, the current to the other selective population, the current to the nonselective population, and the current to the interneuron population. Those to populations 3 and I are especially difficult to estimate because increasing the input to each population changes the currents of populations 3 and I among themselves. To show how these currents affect the system, we first describe the effects of S₁, which influence the four populations through the following NMDA currents:

$$I_{\mathit{NMDA},1,1}=N_1{\omega }_{+}{J}_{\mathit{NMDA},p}{S}_1,I_{\mathit{NMDA},1,2}=N_1{\omega }_{-}{J}_{\mathit{NMDA},p}{S}_1;$$ (70)

$$I_{\mathit{NMDA},1,3}=N_{1}1J_{\mathit{NMDA},p}{S}_1,I_{\mathit{NMDA},1,I}=N_{1}1J_{\mathit{NMDA},I}{S}_1.$$ (71)

Since populations 1 and 2 are explicitly tracked in (30)-(33), we need only calculate the changes in ϕ₃ and ϕ_I due to S₁ and the resulting currents back to populations 1 and 2. Setting Δϕ₃(S₁) to be the change in ϕ₃ as a function of S₁ and similarly for ϕ_I, we get

$$\Delta {\varphi }_3\left(S_1\right)=c_3\Delta I_{\mathit{syn},3}\left(S_1\right)\mathrm{and}\Delta {\varphi }_I\left(S_1\right)=c_I\Delta I_{\mathit{syn},I}\left(S_1\right),$$ (72)

which imply that

$$\begin{array}{lll}\mathrm{\Delta }{\varphi }_3(S_1)& =& c_3[I_{\mathit{NMDA},1,3}+N_3\left(\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},p}+K_{\mathit{NMDA}}{J}_{\mathit{NMDA},p}\right)\mathrm{\Delta }{\varphi }_3\\ & +& N_I\frac{T_{\mathit{GABA}}}{1000}{J}_{\mathit{GABA},p}\mathrm{\Delta }{\varphi }_I],\end{array}$$ (73)

$$\begin{array}{lll}\mathrm{\Delta }{\varphi }_I(S_1)& =& c_I[I_{\mathit{NMDA},1,I}+N_3\left(\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},I}+K_{\mathit{NMDA}}{J}_{\mathit{NMDA},I}\right)\mathrm{\Delta }{\varphi }_3\\ & +& N_I\frac{T_{\mathit{GABA}}}{1000}{J}_{\mathit{GABA},I}\mathrm{\Delta }{\varphi }_I].\end{array}$$ (74)

Collecting terms, (73)-(74) have the same form as (63)-(64), with a₁, b₁, a₂, and b₂ as in (65) and

$$d_1=c_3{I}_{\mathit{NMDA},1,3},d_2=c_I{I}_{\mathit{NMDA},1,I},$$ (75)

so that the solution to (73)-(74) is

$$\mathrm{\Delta }{\varphi }_3(S_1)=\frac{-c_3{b}_2{N}_1{J}_{\mathit{NMDA},p}+c_I{b}_1{N}_1{J}_{\mathit{NMDA},I}}{\mathrm{\Gamma }}{S}_1,$$ (76)

$$\mathrm{\Delta }{\varphi }_I(S_1)=\frac{-c_3{a}_2{N}_1{J}_{\mathit{NMDA},p}-c_I{a}_1{N}_1{J}_{\mathit{NMDA},I}}{\mathrm{\Gamma }}{S}_1,$$ (77)

where Γ = a₁b₂ − a₂b₁. The effects on population 1 are now calculated as follows, starting with I_NMDA,3,1:

$$\begin{array}{ccc}\hfill I_{\mathit{NMDA},3,1}& =& I_{\mathit{NMDA},3,1}^{\ast }+\mathrm{\Delta }{I}_{\mathit{NMDA},3,1},\hfill \\ \hfill \mathrm{\Delta }{I}_{\mathit{NMDA},3,1}(S_1)& =& N_3{\omega }_{-}{J}_{\mathit{NMDA},p}{K}_{\mathit{NMDA}}\mathrm{\Delta }{\varphi }_3(S_1)\hfill \\ & =& N_3{\omega }_{-}{J}_{\mathit{NMDA},p}{K}_{\mathit{NMDA}}\frac{-c_3{b}_2{N}_1{J}_{\mathit{NMDA},p}+c_I{b}_1{N}_1{J}_{\mathit{NMDA},I}}{\mathrm{\Gamma }}{S}_1.\hfill \end{array}$$ (78)

The other currents due to S₁ are calculated similarly, yielding $I_{\mathit{AMPA},3,1}=I_{\mathit{AMPA},3,1}^{\ast }+\mathrm{\Delta }{I}_{\mathit{AMPA},3,1}$ and $I_{\mathit{GABA},I,1}=I_{\mathit{GABA},I,1}^{\ast }+\mathrm{\Delta }{I}_{\mathit{GABA},I,1}$, with

$$\begin{array}{lll}\mathrm{\Delta }{I}_{\mathit{AMPA},3,1}(S_1)& =& N_3{\omega }_{-}{J}_{\mathit{AMPA},p}\left(\frac{T_{\mathit{AMPA}}}{1000}\right)\frac{-c_3{b}_2{N}_1{J}_{\mathit{NMDA},p}+c_I{b}_1{N}_1{J}_{\mathit{NMDA},I}}{\mathrm{\Gamma }}{S}_1,\\ \mathrm{\Delta }{I}_{\mathit{GABA},I,1}(S_1)& =& N_1{J}_{\mathit{GABA},p}\frac{T_{\mathit{GABA}}}{1000}\frac{c_3{a}_2{N}_1{J}_{\mathit{NMDA},p}-c_I{a}_1{N}_1{J}_{\mathit{NMDA},I}}{\mathrm{\Gamma }}{S}_1.\end{array}$$

Due to symmetry, the currents to population 2 from populations 3 and I are identical to those to population 1 and the effect of S₂ can be determined by interchanging subscripts 1 and 2 in the above formulae. The effects of ν₁ and ν₂ collected in the β’s are similar to the effects of S_j in the α’s, but with J_NMDA,p/IS₁ replaced by $\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},p/I}{\nu }_1$.

C.3. Calculation of α_j, β_j, and I_const,j

We are now in a position to compute the coefficients α_j, β_j, and I_const,j in (34)-(35). We start by writing α₁ = α_1a + α_1b + α_1c, in which α_1a is the effect of S_i directly on itself, α_1b is the effect of S_i on itself through the change in the AMPA and NMDA currents of population 3, and α_1c is the effect of S₁ on itself through the GABA-mediation of population I.

$$\begin{array}{lll}{\alpha }_1& =& {\alpha }_{1a}+{\alpha }_{1b}+{\alpha }_{1c},\mathrm{where}{\alpha }_{1a}=\frac{I_{\mathit{NMDA},j,j}}{S_j},\\ {\alpha }_{1b}& =& \frac{\mathrm{\Delta }{I}_{\mathit{NMDA},3,j}(S_j)+\mathrm{\Delta }{I}_{\mathit{AMPA},3,j}(S_j)}{S_j},\mathrm{and}{\alpha }_{1c}=\frac{\mathrm{\Delta }{I}_{\mathit{GABA},I,j}(S_j)}{S_j},\end{array}$$ (79)

which imply

$$\begin{array}{lll}{\alpha }_{1a}& =& N_j{\omega }_{+}{J}_{\mathit{NMDA},p,}\\ {\alpha }_{1b}& =& N_3{\omega }_{-}\left(\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},p}+K_{\mathit{NMDA}}{J}_{\mathit{NMDA},p}\right)\left(\frac{c_3{b}_2{N}_j{J}_{\mathit{NMDA},p}-c_I{b}_1{N}_j{J}_{\mathit{NMDA},I}}{\mathrm{\Gamma }}\right),\\ {\alpha }_{1c}& =& N_I\frac{T_{\mathit{GABA}}}{1000}{J}_{\mathit{GABA},p}\left(\frac{c_3{b}_2{N}_j{J}_{\mathit{NMDA},p}-c_I{b}_1{N}_j{J}_{\mathit{NMDA},I}}{\mathrm{\Gamma }}\right).\end{array}$$ (80)

The coefficient α₂ is computed in the same manner:

$$\begin{array}{lll}{\alpha }_2& =& {\alpha }_{2a}+{\alpha }_{2b}+{\alpha }_{2c},\mathrm{where}{\alpha }_{2a}=\frac{I_{\mathit{NMDA},2,1}}{S_2}=N_2{\omega }_{-}{J}_{\mathit{NMDA},p},\\ {\alpha }_{2b}& =& \frac{\mathrm{\Delta }{I}_{\mathit{NMDA},3,1}\left(S_2\right)+\mathrm{\Delta }{I}_{\mathit{AMPA},3,1}\left(S_2\right)}{S_2}={\alpha }_{1b},\mathrm{and}{\alpha }_{2c}=\frac{\mathrm{\Delta }{I}_{\mathit{GABA},I,1}\left(S_2\right)}{S_2}={\alpha }_{1c}.\end{array}$$ (81)

The last two equalities hold because the currents to populations 1 and 2 from populations 3 and I are the same. We have already noted the symmetry S₁ ↔ S₂ inherent in the reduced system.

We next calculate the β_j’s, which capture the effect of the currents mediated by the AMPA synapses of populations 1 and 2 through their firing rates ν_j. These are similar to the α_j’s, but with J_NMDA,p/I replaced by J_AMPA,p/IT_AMPA/1000 where appropriate. We find

$$\begin{array}{lll}{\beta }_1& =& {\beta }_{1a}+{\beta }_{1b}+{\beta }_{1c},\mathrm{where}{\beta }_{1a}=\frac{I_{\mathit{AMPA},j,j}}{{\nu }_j},\\ {\beta }_{1b}& =& \frac{\mathrm{\Delta }{I}_{\mathit{NMDA},3,j}({\nu }_j)+\mathrm{\Delta }{I}_{\mathit{AMPA},3,j}({\nu }_j)}{{\nu }_j},\mathrm{and}{\beta }_{1c}=\frac{\mathrm{\Delta }{I}_{\mathit{GABA},I,j}({\nu }_j)}{{\nu }_j},\end{array}$$ (82)

which imply

$$\begin{array}{l}{\beta }_{1a}=N_j{\omega }_{+}{J}_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000},\\ {\beta }_{1b}=N_3{\omega }_{-}\left(\frac{T_{\mathit{AMPA}}}{1000}{J}_{\mathit{AMPA},p}+K_{\mathit{NMDA}}{J}_{\mathit{NMDA},p}\right)N_j{T}_{\mathit{AMPA}}\left(\frac{c_3{b}_2{J}_{\mathit{AMPA},p}-c_I{b}_1{J}_{\mathit{AMPA},I}}{1000\mathrm{\Gamma }}\right),\\ {\beta }_{1c}=N_I\frac{T_{\mathit{GABA}}}{1000}{J}_{\mathit{GABA},p}\left(\frac{c_3{b}_2{N}_j{J}_{\mathit{AMPA},p}{T}_{\mathit{AMPA}}-c_I{b}_1{N}_j{J}_{\mathit{AMPA},I}{T}_{\mathit{AMPA}}}{1000\mathrm{\Gamma }}\right);\end{array}$$ (83)

and

$$\begin{array}{lll}{\beta }_2& =& {\beta }_{2a}+{\beta }_{2b}+{\beta }_{2c},\mathrm{where}{\beta }_{2a}=\frac{I_{\mathit{AMPA},2,1}}{{\nu }_2}=N_j{\omega }_{-}{J}_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000},\\ {\beta }_{2b}& =& \frac{\mathrm{\Delta }{I}_{\mathit{NMDA},3,1}({\nu }_2)+\mathrm{\Delta }{I}_{\mathit{AMPA},3,1}({\nu }_2)}{{\nu }_2}={\beta }_{1b},\mathrm{and}{\beta }_{2c}=\frac{\mathrm{\Delta }{I}_{\mathit{GABA},I,1}({\nu }_2)}{{\nu }_2}={\beta }_{1c}.\end{array}$$ (84)

Finally, we enumerate the constant currents in (34)-(35):

$$\begin{array}{ccc}\hfill I_{\mathit{const},j}& =& I_{\mathit{AMPA},\mathit{ext},j}+I_{\mathit{stim},j}+I_{\mathit{Noise},j}+I_{\mathit{NMDA},3,j}^{\ast }+I_{\mathit{AMPA},3,j}^{\ast }+I_{\mathit{GABA},I,j}^{\ast },\hfill \\ \hfill I_{\mathit{AMPA},\mathit{ext},j}& =& N_{\mathit{ext}}{\varphi }_{\mathit{ext}}\frac{T_{\mathit{AMPA}}}{1000}{J}_{p,\mathit{AMPA},\mathit{ext}},\hfill \\ \hfill I_{\mathit{stim},1}& =& J_{\mathit{AMPA},\mathit{ext},p}{\mu }_0\left(1+E/100\right)\frac{T_{\mathit{AMPA}}}{1000},\hfill \\ \hfill I_{\mathit{stim},2}& =& J_{\mathit{AMPA},\mathit{ext},p}{\mu }_0\left(1-E/100\right)\frac{T_{\mathit{AMPA}}}{1000},\hfill \\ \hfill I_{\mathit{NMDA},3,j}^{\ast }& =& N_3{\omega }_{-}{J}_{\mathit{NMDA},p}(K_{\mathit{NMDA}}({\varphi }_3^{\ast }-{\varphi }_{3,0})+\psi ({\varphi }_{3,0})),\hfill \\ \hfill I_{\mathit{AMPA},3,j}^{\ast }& =& N_3{\omega }_{-}{J}_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000}{\varphi }_3^{\ast },\hfill \\ \hfill I_{\mathit{GABA},3,I}^{\ast }& =& N_I{J}_{\mathit{GABA},p}\frac{T_{\mathit{GABA}}}{1000}{\varphi }_I^{\ast }.\hfill \end{array}$$ (85)

The noise currents are the same as in the four-population model.

C.4. Validity of pure linearity conditions

Currents of the form in (34)-(35) can be calculated provided that ϕ_I and ϕ₃ each stay on a single side of the thresholds in their f-I curves. For example, provided I_syn,3 < I_thresh,p for all time (at a given location in the neuromodulation plane), regardless of inputs from populations 1 and 2, ϕ₃ remains in its constant regime and can be fixed at ϕ_3,0. If I_syn,3 > I_thresh,p for all time, regardless of inputs from populations 1 and 2, ϕ₃ remains in its purely linear regime and the approximations of sections C.1–C.3 hold. Similar conditions apply for ϕ_I, and there are then four possibilities for which the parameters of (34)-(35) can be calculated: (A) I_syn,I and I_syn,3 above threshold for all time, (B) I_syn,I above threshold and I_syn,3 below threshold for all time, (C) I_syn,I and I_syn,3 below threshold for all time, and (D) I_syn,I below threshold and I_syn,3 above threshold for all time (this turns out to be impossible in the present network structure). The derivation in sections C.1–C.3 assumes case (A), and three requirements must be met for this assumption to hold, which then implies linearity in (60)-(61):

$${\varphi }_3^{\ast }>{\varphi }_{3,0},{\varphi }_I^{\ast }>{\varphi }_{I,0},\mathrm{\Gamma }\ne 0$$ (86)

(the latter must hold if ϕ₃ and ϕ_I are to be well defined). The values for ${\varphi }_I^{\ast }$ and ${\varphi }_3^{\ast }$ are calculated in section C.1 as they vary with γ_E and γ_I scaling the effective currents J_type,k, and the left panel of Figure 17 shows the regions in the neuromodulation plane over which these inequalities are satisfied. The red curve defines the boundary to the right of which ${\varphi }_I^{\ast }$ crosses ϕ_I,0 and enters its linear regime, and ${\varphi }_3^{\ast }$ enters its linear regime below the black curve. These constraints are stricter than Γ ≠ 0, which is defined by the thick blue curve. The ${\varphi }_3^{\ast }$ condition (black curve) is the strictest constraint, and case (A) applies only below this curve. The region of validity for case (A), then, does not overlap with any part of the region of interest in which RR > 0, and the α’s and β’s derived in section C.3 do not apply in the region of good behavior of the higher-dimensional models.

Figure 17.

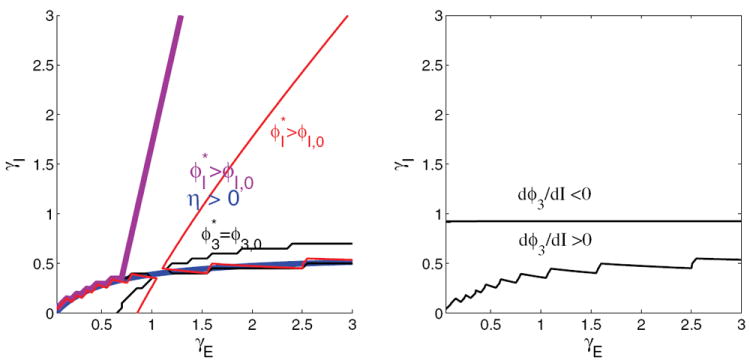
(Left panel) Two-population linearity conditions: the red curve marks the boundary of ${\mathrm{\varphi }}_{\mathrm{I}}^{\ast }>{\mathrm{\varphi }}_{\mathrm{I},\mathit{0}}$ for case (a), which fails to its upper left, the thick blue curve shows Γ = 0, and the black curve shows that I_syn,3 > I_thresh,p holds over very little of the plane. The magenta curve shows the boundary of the linear approximation for population I for case (b) parameters calculated in section C.5, which sets ϕ₃ = ϕ_3,0. Failure of this approximation to the left of the magenta curve is unimportant, since there is insufficient excitation to drive populations 1 and 2 above their base levels in this region and case (c) applies trivially. (Right panel) Signs of dϕ₃/dI (see (87)) indicating changes in ϕ₃ with input.

Above the black curve, ${\varphi }_3^{\ast }$ is fixed at ϕ_3,0 and ${\varphi }_I^{\ast }$ is recalculated as described in section C.5, and the results are examined to verify if case (B) applies. The thick magenta curve denotes the new linear regime for ${\varphi }_I^{\ast }$, which now includes the region of good performance. The α’s, β’s, and constant currents for fixed ϕ₃ can therefore be recalculated as described in section C.5. This requires I_syn,3 to remain below threshold (region above black curve) for all time in the presence of inputs from populations 1 and 2. This assumption is now tested.

Above the black curve ${\varphi }_3^{\ast }={\varphi }_{3,0}$, but if I_syn,3 were to increase above I_thresh,p due to inputs from populations 1 and 2, the assumption of constant ϕ₃ corresponding to case (B) would fail. An input to population 3 from the selective populations corresponds to an input to the interneurons in the ratio J_NMDA,p : J_NMDA,I ≈ 1.3 : 1, and we can therefore estimate their effects via the derivative

$$\frac{d{\varphi }_3}{\mathit{dI}}=\frac{d}{\mathit{dI}}\left(\frac{c_3{b}_{2}I-c_I{b}_{1}I/1.3}{\mathrm{\Gamma }}\right)=\frac{c_3{b}_2-c_I{b}_1/1.3}{\mathrm{\Gamma }};$$ (87)

cf. (76). The right panel of Figure 17 shows that dϕ₃/dI < 0 for γ_E >≈ 0.9, which covers much of the region of interest. If dϕ₃/dI < 0 and ${\varphi }_3^{\ast }={\varphi }_{3,0}$, ϕ₃ will remain at this value, regardless of the inputs from the selective populations, which have a net suppressive effect, and case (B) holds for all time. Thus, in the region above the black curve in the right panel of Figure 17 and right of the magenta curve in the left panel, which contains most of the region of good performance, case (B) applies and we may repeat the two-population model derivation with ϕ₃ = ϕ_3,0 held constant, as described in section C.5.

For the small portion of the region of good performance in which dϕ₃/dI > 0, I_syn,3 is far enough below threshold that although I_syn,3 increases with the net effect of populations 1 and 2, their limited firing rates in the green region of Figure 2 do not allow I_syn,3 to reach I_thresh,p. Applying case (B) parameters to the entire region between the magenta and black curves in the left panel has the effect of eliminating the loss of discriminability region from Figure 2 and extending “peak discriminability region” performance all the way to the boundary of the no discriminability region. This is a shortcoming of this assumption but does not critically affect the model.

Below the black curve in the left panel of Figure 17, the case (A) model parameters from section C.3 apply. To the left of the magenta curve, which is fully in the blue region, there are insufficient external inputs to any population, all firing rates remain at their minimum values (case C), and the model is trivial. Case (D) never occurs because I_syn,3 > I_thresh,p ⇒ I_syn,I > I_thresh,I, as I_thresh,p > 1.32I_thresh,I and I_syn,3 < 1.32I_syn,I due to network parameters. The lower-right transition from $\frac{d{\varphi }_3}{\mathit{dI}}>0$ to < 0 occurs as Γ = 0. This zero of the determinant Γ is responsible for the chain of erratic model behaviors seen in the lower right region of Figure 10.

C.5. Rederivation with constant ϕ₃

We now solve for ${\varphi }_I^{\ast }$, the baseline value of ϕ_I, in case (B) of section C.4 (I_syn,I > I_thresh,I and I_syn,3 < I_thresh,p). This is done by computing the firing rate given the constant inputs, including the now-constant inputs from population 3:

$${\varphi }_I^{\ast }={\varphi }_{I,0}+c_I\left(I_{\mathit{AMPA},\mathit{ext},I}+I_{\mathit{NMDA},3,I}+I_{\mathit{AMPA},3,I}+N_I{J}_{\mathit{GABA},I}\frac{T_{\mathit{GABA}}}{1000}{\varphi }_I^{\ast }-I_{\mathit{thresh},i}\right),$$ (88)

where

$$I_{\mathit{NMDA},3,I}=N_3{J}_{\mathit{NMDA},p}\psi ({\varphi }_{3,0}),I_{\mathit{AMPA},3,I}=N_3{J}_{\mathit{AMPA},p}\frac{T_{\mathit{AMPA}}}{1000}{\varphi }_{3,0},$$ (89)

and I_AMPA,ext,I is the same as in the last equation of (62). Setting ${\mathrm{\Gamma }}_I=1-c_I{N}_I{J}_{\mathit{GABA},I}\frac{T_{\mathit{GABA}}}{1000}$, we obtain

$${\varphi }_I^{\ast }=\frac{{\varphi }_{I,0}+c_I(I_{\mathit{AMPA},\mathit{ext},I}+I_{\mathit{NMDA},3,I}+I_{\mathit{AMPA},3,I}-I_{\mathit{thresh},I})}{{\mathrm{\Gamma }}_I}.$$ (90)

Here α_1a, α_2a, β_1a, and β_2a are the same as under case (A) in section C.3, (79)-(84), and since ϕ₃ is constant, α_1b = α_2b = β_1b = β_2b = 0.

The effect of population I can be calculated as follows:

$$\begin{array}{l}\mathrm{\Delta }{\varphi }_I=\frac{c_I{I}_{\mathit{syn},I}}{{\mathrm{\Gamma }}_I},\mathrm{\Delta }{I}_{\mathit{GABA},I,j}=N_I{J}_{\mathit{GABA},p}\left(\frac{T_{\mathit{GABA}}}{1000}\right)\left(\frac{c_I}{{\mathrm{\Gamma }}_I}\right)\mathrm{\Delta }{I}_{\mathit{syn},I},\\ \mathrm{and}{\alpha }_{1c}=N_I{J}_{\mathit{GABA},p}\left(\frac{T_{\mathit{GABA}}}{1000}\right)\frac{c_I{N}_1{J}_{\mathit{NMDA},I}}{{\mathrm{\Gamma }}_I},{\alpha }_{2c}={\alpha }_{1c},\\ {\beta }_{1c}=N_I{J}_{\mathit{GABA},p}\left(\frac{T_{\mathit{GABA}}}{1000}\right)\frac{c_I{N}_1{J}_{\mathit{AMPA},I}\frac{T_{\mathit{AMPA}}}{1000}}{{\mathrm{\Gamma }}_I},{\beta }_{2c}={\beta }_{1c}.\end{array}$$ (91)

The constant currents are the same as in (85) but with ${\varphi }_3^{\ast }={\varphi }_{3,0}$ and ${\varphi }_I^{\ast }$ as calculated in (90). These new parameter values then define the model for the case (B) condition.

To the left of the magenta curve in Figure 17, the firing rates trivially remain at the values ϕ₁ = ϕ₂ = ϕ₃ = ϕ_p,0 and ϕ_I = ϕ_I,0 for all time, and every trial is a no-choice trial.