Abstract
In this paper, we present a biologically detailed mathematical model of tripartite synapses, where astrocytes modulate short-term synaptic plasticity. The model consists of a pre-synaptic bouton, a post-synaptic dendritic spine-head, a synaptic cleft and a peri-synaptic astrocyte controlling Ca2 + dynamics inside the synaptic bouton. This in turn controls glutamate release dynamics in the cleft. As a consequence of this, glutamate concentration in the cleft has been modeled, in which glutamate reuptake by astrocytes has also been incorporated. Finally, dendritic spine-head dynamics has been modeled. As an application, this model clearly shows synaptic potentiation in the hippocampal region, i.e., astrocyte Ca2 + mediates synaptic plasticity, which is in conformity with the majority of the recent findings (Perea and Araque (Science 317, 1083–1086, 2007); Henneberger et al. (Nature 463, 232–236, 2010); Navarrete et al. (PLoS Biol. 10, e1001259, 2012)).
Electronic supplementary material
The online version of this article (doi:10.1007/s10867-012-9267-7) contains supplementary material, which is available to authorized users.
Keywords: Astrocyte, Calcium dynamics, Short-term potentiation, Tripartite synapse
Introduction
One of the most significant challenges in neuroscience is to identify the cellular and molecular processes that underlie learning and memory formation [4]. Cajal originally hypothesized that information storage relies on changes in strength of synaptic connections between neurons that are active [5]. Hebb supported this hypothesis and proposed that if two neurons are active at the same time, the synaptic efficiency of the appropriate synapse will be strengthened [6]. Synaptic transmission is a dynamic process. Post-synaptic responses wax and wane as pre-synaptic activity evolves. Forms of synaptic enhancement, such as facilitation, augmentation and post-tetanic potentiation, are usually attributed to effects of a residual elevation in pre-synaptic Ca2 + concentration ([Ca2 + ]), acting on one or more molecular targets that appear to be distinct from the secretory trigger responsible for fast exocytosis and phasic release of a transmitter to a single action potential [7]. It is now well established that the astrocytic mGluR detects synaptic activity and responds via activation of the calcium-induced calcium release pathway, leading to elevated Ca2 + levels. The spread of these levels within the micro-domain of one cell can coordinate the activity of disparate synapses that are associated with the same micro-domain [8]. The notion of the tripartite synapse consisting of pre-synaptic neuron, post-synaptic neuron and astrocyte has taken a firm root in experimental [1, 9, 10] as well as theoretical neuroscience [11–13]. Astrocytes play crucial roles in the control of Hebbian plasticity [14].
There is a recent report that, at least in the hippocampus, astrocyte Ca2 + signaling does not modulate short-term or long-term synaptic plasticity [15]. However, evidence of astrocytic modulation of synaptic plasticity is more abundant, including in the hippocampus [2, 16–19]. Neuronal activities can trigger Ca2 + elevation in astrocytes [14, 20] leading to a concentration increase in adjacent glial cells including astrocytes, which express a variety of receptors [10]. These activated receptors increase astrocyte [Ca2 + ] and release transmitters, including glutamate, d-serine, ATP [2, 21] etc. The released gliotransmitters feedback onto the pre-synaptic terminal either to enhance or to depress further release of a neurotransmitter [10, 22] including glutamate, which is mediated by Ca2 + concentration in the pre-synaptic terminal. It is worth noting that Ca2 + elevation is both necessary and sufficient to evoke glutamate release from astrocytes [17]. On the other hand, short-term synaptic depression is caused by depletion of the releasable vesicle pool due to recent release in response to the pre-synaptic action potentials [23]. This entire chain of Ca2 + -mediated pre-synaptic activity consisting of both short-term enhancement (STE) and short-term depression (STD) can be called short-term synaptic plasticity or simply short-term plasticity (STP).
Synaptic plasticity occurs at many time scales. Usually, long-term plasticity (LTP) happens at a time scale of 30 min or more and STP takes less than that [24]. Within the ambit of STP, STE has been more widely studied than the STD. A quantitative definition of STE has been proposed in [25]. STE has been divided into four different temporal regimes, namely fast-decaying facilitation (tens of milliseconds), slow-decaying facilitation (hundreds of milliseconds), augmentation (seconds) and post-tetanic potentiation (minutes) [25].
STP is thought to provide a biological mechanism for on-line information processing in the central nervous system [25] and therefore could be the key to the formation of working memory and intelligent behavior. A computational model of how cellular and molecular dynamics give rise to the STP in the synapses (particularly in the synapses of the hippocampus and the prefrontal cortex) can be quite useful in understanding intelligent behavior.
In this paper, we present a computational model of astrocyte-mediated synaptic potentiation in a tripartite synapse. The present model is based on experimental work of Perea and Araque [1], who used immature Wistar rats for hippocampal slice preparations. Primarily, there are just two models [12, 13] shedding light over the molecular aspects of astrocyte-mediated synaptic potentiation, where a lot of important details were omitted or were modeled hypothetically (see Table 1).
Table 1.
| Signaling processes modeled | Volman et al. [13] | Nadkarni et al. [12] | This paper |
|---|---|---|---|
| Bouton Ca2 + | No | Yes | Yes |
| Bouton IP3 | No | No | Yes |
| Synaptic vesicle / glutamate | Yes / No | Yes / No | Yes / Yes |
| Astrocytic Ca2 + | Yes | Yes | Yes |
| Astrocytic IP3 | Yes | Yes | Yes |
| Extra-synaptic vesicle / glutamate | No | No | Yes / Yes |
| Post-synaptic current / potential | Yes / No | Yes / No | Yes / Yes |
The computational model proposed here makes use of different detailed biophysical models highlighting specific aspects of astrocyte-neuron signaling. The following steps have been followed in simulation of our model. (1) Pre-synaptic action potential train has been generated using the HH model [26]. (2) Ca2 + concentration elevation in the pre-synaptic bouton incorporating fast (using single protein properties [27]) and slow (using modified Li-Rinzel model [28]) Ca2 + influx. (3) Glutamate release in the synaptic cleft as a two-step process (using Bollman et al. [36] for Ca2 + binding to a synaptic vesicle sensor and Tsodyks and Markram [29] for synaptic vesicle fusion and recycling). (4a) Glutamate modulated enhancement of astrocytic Ca2 + (using an astrocyte specific G-Chl model [30]). (4b) Glutamate mediated excitatory post-synaptic current (using Destexhe et al. [31]) and potential (using [29]). (5) Extra-synaptic glutamate elevation is also modeled as a two-step process (using a modified Bertram model [32] to fit the synaptic-like micro-vesicle (SLMV) release probability determined recently [33] and [29] for SLMV fusion and recycling). The motivations and consequences of the specific models chosen have are discussed in more detail below.
We observed an increase in average neurotransmitter release probability, Pr, after the astrocyte became active (before: 0.25; after: 0.35), which is in close conformity with the experimental observation (before: 0.24; after: 0.33) of [1]. On measuring the windowed average amplitude of the excitatory post-synaptic current (EPSC) we could observe up to a 250% increase from pre-astrocytic activities to post-astrocytic activities, which decayed with a time constant of 10 to 12 s. This signifies augmentation [24, 25].
The model
In this section, we describe the details of the mathematical model, whose computational implementation will be presented in the section that immediately follows. In order to elucidate the major neurophysiological steps in our model, we use the flow chart in Fig. 1. The mathematical formulations have been described in the subsequent subsections.
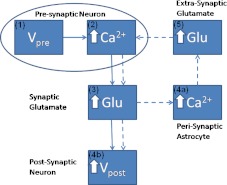
Fig. 1.
Information flow from the pre-synaptic bouton to post-synaptic dendritic spine-head, as modulated by an astrocyte. Solid line shows the astrocyte-independent pathway, while, solid-line combined with dashed line shows the astrocyte-dependent pathway. (1) AP generated at pre-synaptic axon-hillock. (2) Elevated intracellular [Ca2 + ] in the bouton. (3) Increased [Ca2 + ] leading to exocytosis of Glutamate into the synaptic cleft. (4a) Synaptic glutamate causes an increase in astrocytic [Ca2 + ]. (4b) Simultaneously synaptic glutamate can also bind with AMPA receptor causing an increase in post-synaptic membrane potential. (5) Increased astrocytic [Ca2 + ] leads to an elevated glutamate concentration in the extra-synaptic cleft, in a vesicle dependent manner. This extra-synaptic glutamate is free to bind with extra-synaptic mGluR on the pre-synaptic bouton surface. Glutamate bound to mGluR leads to an increase in Ca2 + concentration via the IP3 dependent pathway. This transient enhancement of the bouton [Ca2 + ] forms the basis of improved synaptic efficacy, through an astrocyte-dependent pathway
Pre-synaptic action potential
The action potential (AP) is generated at the axon hillock of the pre-synaptic neuron. In the cortical neurons, there may be 11 or more different types of ion channels [34]. The key features of initiation dynamics of cortical neuron APs — (i) their rapid initiation and (ii) variable onset potential—which are outside the range of behaviors described by the classical Hodgkin-Huxley (HH) theory [35]. Still, the HH paradigm has been used to generate the pre-synaptic AP in computational models [11, 13]. Since in this paper our focus is not on the detail of pre-synaptic AP generation, for the sake of simplicity here we have followed the HH model for pre-synaptic regular spike and burst generation.
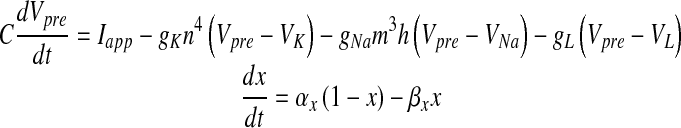 |
1 |
where Vpre is the pre-synaptic membrane potential in millivolts, Iapp is the applied current density, gK, gNa and gL are potassium, sodium and leak conductances respectively, VK, VNa and VL are potassium, sodium, and leak reversal potentials, respectively and x = m (Na + activation), h (Na + inactivation) and n (K + activation). The detail of the HH model can be found in [26]. The values of the different parameters in (1) that have been used in this paper are furnished in Table 2. αx and βx for x = m, h and n are defined as
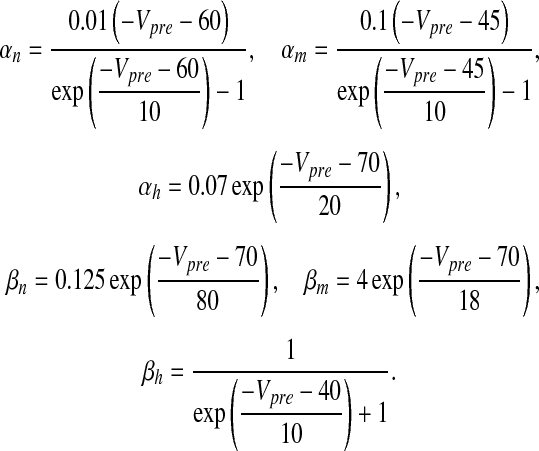 |
Table 2.
Parameter values used in the HH model (all are from Hodgkin and Huxley [26])
| Symbol | Value |
|---|---|
| gK | 36 mS cm − 2 |
| gNa | 120 mS cm − 2 |
| gL | 0.3 mS cm − 2 |
| VK | − 82 mV |
| VNa | 45 mV |
| VL | − 59.4 mV |
Bouton Ca2 + dynamics
The train of APs that has been generated in the axon hillock of the pre-synaptic neuron travels all the way down to the end of the axon without degradation and leads to an increase in cytosolic [Ca2 + ]. The increase in intracellular [Ca2 + ] can be attributed to two components:
[Ca2 + ] due to AP, denoted as cfast and
[Ca2 + ] due to intracellular stores, cslow.
Because of its rapid kinetics, [Ca2 + ] due to AP is denoted as cfast. Similarly, [Ca2 + ] due to intracellular stores is denoted as cslow. Total intracellular [Ca2 + ] denoted as ci satisfies the following simple equation
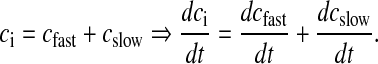 |
2 |
The sensitivity of rapid Ca2 + kinetics over neurotransmitter release is well established [36, 37]. In immature neurons, the necessary Ca2 + flux for neurotransmitter release is primarily mediated by N-type Ca2 + channels [38, 39]. Also, the contribution of P/Q-type channels is negligible as compared to N-type channels in immature cells [40]. Hence, in this article, Ca2 + influx through plasma membrane is modeled through N-type channels alone. Immature cells have been chosen following Perea and Araque [1]. The equation governing cfast consists of a simple construction-destruction type formulism and is as follows [41]
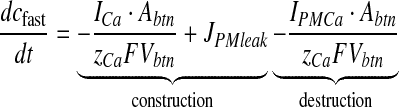 |
3 |
Here, ICa is the Ca2 + current through an N-type channel, Abtn is the surface area of the bouton, zCa is Ca2 + ion valence, F is Faraday’s constant, Vbtn is the volume of the bouton. IPMCa represents the current due to electrogenic plasma-membrane Ca2 + ATPase. This pump is known to extrude excess of Ca2 + out of the cell and it has also been shown that it regulates excitatory synaptic transmission at the CA3-CA1 pyramidal cell synapses [42]. The formulation for this pump uses the standard Michaelis-Menten (MM) type formulism [27, 43]. JPMleak is the positive leak from extracellular space into the bouton, which ensures that the MM pump does not decrease cytosolic Ca2 + to 0 [43].
The Ca2 + current through the N-type Ca2 + channel is formulated using a single protein level formulation, which is described in detail in [27], is
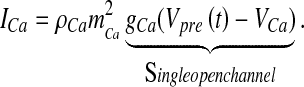 |
Here, ρCa is the N-type channel protein density, which determines the number of Ca2 + channels on the membrane of the bouton (ρCa was determined computationally so that the average neurotransmitter release probability lies in the range 0.2–0.3, when the astrocyte is not stimulated, similar to the experiments of Perea and Araque [1]), gCa is the single N-type channel conductance, VCa is the reversal potential of the Ca2 + ion determined by Nernst equation [41],
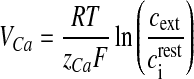 |
4 |
where R is the real gas constant, T is the absolute temperature, cext is the extracellular Ca2 + concentration and 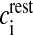 is the total intracellular [Ca2 + ] at rest. It is assumed that a single N-type channel consists of two gates. mCa denotes the opening probability in a single gate. A single N-type channel is open only when both the gates are open. Hence,
is the total intracellular [Ca2 + ] at rest. It is assumed that a single N-type channel consists of two gates. mCa denotes the opening probability in a single gate. A single N-type channel is open only when both the gates are open. Hence, 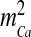 is the single-channel open probability. The time dependence of the single-channel open probability is governed by an HH-type formulation,
is the single-channel open probability. The time dependence of the single-channel open probability is governed by an HH-type formulation,
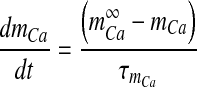 |
where 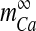 is the Boltzmann-function fitted by Ishikawa et al. [40] to the whole-cell current of an N-type channel, and mCa approaches its asymptotic value and
is the Boltzmann-function fitted by Ishikawa et al. [40] to the whole-cell current of an N-type channel, and mCa approaches its asymptotic value and 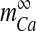 with a time constant
with a time constant 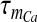 . The mathematical expression of other parameters used in (3) is as follows:
. The mathematical expression of other parameters used in (3) is as follows:
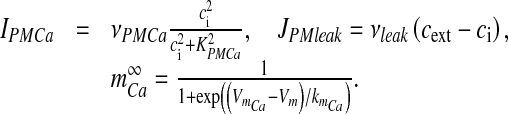 |
Here, νPMCa is the maximum PMCa current density, determined through computer simulations, so that ci is maintained at its resting concentration. All other parameter values used for simulation are listed in Table 3.
Table 3.
Parameters used for bouton Ca2 + dynamics
| Symbol | Description | Value | Reference |
|---|---|---|---|
| F | Faraday’s constant | 96487 C mole − 1 | |
| R | Real gas constant | 8.314 J / K | |
| T | Absolute temperature | 293.15 K | Temperature in Perea and Araque [1] |
| zCa | Calcium valence | 2 | |
| Abtn | Surface area of bouton | 1.24 μm2 | [77] |
| Vbtn | Volume of bouton | 0.13 μm3 | [77] |
| ρCa | N-type channel density | 3.2 μm − 2 | See text |
| gCa | N-type channel conductance | 2.3 pS | [39] |
| VCa | Reversal potential of Ca2 + ion | 125 mV | Calculated using (4) |
| νPMCa | Maximum PMCa current | 0.4 μA cm − 2 | See text |
| KPMCa | Ca2 + concentration at which νPMCa is halved | 0.1 μM | [27] |
| νleak | Maximum leak of Ca2 + | 2.66 × 10 − 6 ms − 1 | See Text |
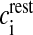 |
Resting Intracellular Ca2 + concentration | 0.1 μM | [27] |
| cext | External Ca2 + concentration | 2 mM | External [Ca2 + ] in Perea and Araque [1] |
| VmCa | Half-activation voltage of N-type Ca2 + channel | −17 mV | [40] |
| kmCa | Slope factor of N-type channel activation | 8.4 mV | [40] |
| c1 | Ratio of ER volume to volume of bouton | 0.185 | Shuai and Jung 2002 |
| ν1 | Maximum IP3 receptor flux | 30 s − 1 | See text |
| ν2 | Ca2 + leak rate constant | 0.055 s − 1 | See text |
| ν3 | SERCA maximal pump rate | 90 μM s − 1 | See text |
| k3 | SERCA dissociation constant | 0.1 μM | [86] |
| d1 | IP3 dissociation constant | 0.13 μM | Shuai and Jung 2002 |
| d2 | Inhibitory Ca2 + dissociation constant | 1.049 μM | Shuai and Jung 2002 |
| d3 | IP3 dissociation constant | 943.4 nM | Shuai and Jung 2002 |
| d5 | Activation Ca2 + dissociation constant | 82.34 nM | Shuai and Jung 2002 |
| a2 | Inhibitory Ca2 + binding constant | 0.2 μM s − 1 | Shuai and Jung 2002 |
| νg | Maximum production rate of IP3 | 0.062 μM s − 1 | [12] |
| kg | Glutamate concentration at which vg is halved | 0.78 nM | Shuai and Jung 2002 |
| τp | IP3 degradation constant | 0.14 s − 1 | [87] |
| p0 | Initial IP3 concentration | 160 nM | [87] |
The second component of bouton Ca2 + , cslow, is known to play a crucial role in STP [44]. The release of Ca2 + from the endoplasmic reticulum (ER) is mainly controlled by two types of receptors (or Ca2 + channels) i) the inositol (1,4,5)-trisphosphate receptor (IP3R) and ii) the ryanodine receptor (RyR) [45]. For the sake of simplicity, the flow is assumed to be through IP3R alone. The IP3 necessary for release of Ca2 + from the ER is produced when glutamate (agonist) binds with mGluRs (receptor) and causes, via G-protein link to phospholipase C (PLC), the cleavage of phosphatidylinositol (4,5)-bisphosphate (PIP2) to produce IP3 and diacylglycerol (DAG). We have used the conventional Li-Rinzel model (L-R model) [28] to formulate this slower Ca2 + signaling process.
There were a few modifications made to the L-R model. The L-R model assumes that, total intracellular concentration, c0, is conserved and determines the ER Ca2 + concentration, cER, using the relation
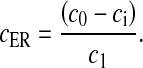 |
5 |
Such an assumption is not valid in the present model because of the presence of membrane fluxes, namely ICa and IPMCa. Also, in the L-R model intracellular IP3 concentration, [IP3], is used as a control parameter. To take care of these “inconveniences” two additional equations governing ER [Ca2 + ] and [IP3] have been incorporated into the L-R model. The [IP3] production term was made glutamate-dependent to study the effect of astrocytic Ca2 + over ci [46]. The mathematical model governing the cslow dynamics is as follows:
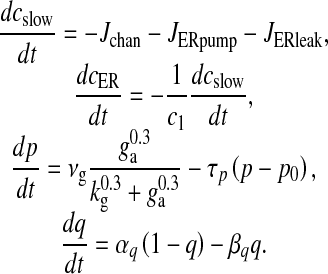 |
6 |
Here Jchan denotes Ca2 + flux from the ER to the intracellular space through IP3R, JERpump is the Ca2 + flux pumped from the intracellular space into the ER, JERleak is the leak of Ca2 + ions from the ER to intracellular space, cER is the ER Ca2 + concentration, c1 is the ratio of the ER volume to the bouton volume, p is the intracellular IP3 concentration, ga is the glutamate in the extra-synaptic cleft and q is the fraction of activated IP3R. The expressions for the fluxes are
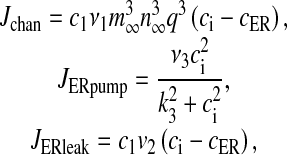 |
with 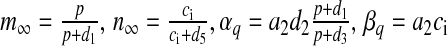 . Most of the values of v1, v2, v3 mentioned in literature are for closed-cell dynamics, which is not the case here. The values of v1, v2, v3 were fixed through extensive simulation runs so that Ca2 + homeostasis is maintained inside the cell and its organelles. Details of the parameters are listed in Table 3.
. Most of the values of v1, v2, v3 mentioned in literature are for closed-cell dynamics, which is not the case here. The values of v1, v2, v3 were fixed through extensive simulation runs so that Ca2 + homeostasis is maintained inside the cell and its organelles. Details of the parameters are listed in Table 3.
Glutamate release dynamics in the bouton
It is now widely accepted that AP waveforms lead to a transient increase in intracellular [Ca2 + ] and lead to neurotransmitter release [36, 47]. However, the study of Ca2 + sensor sensitivity becomes exceedingly challenging due to the small size of the nerve terminals [47]. It is generally assumed that Ca2 + concentration of at least 100 μM in the terminal is necessary for a “low-affinity” Ca2 + sensor to activate [12, 48]. But, recent studies performed in the giant calyx of Held terminal have revealed that intracellular Ca2 + concentration of ~10 μM is sufficient for glutamate release [36, 37]. The kinetic model governing Ca2 + binding to the Ca2 + sensor is given by the following equations [36],
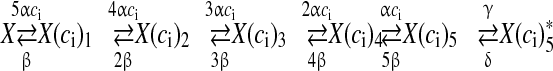 |
7 |
where alpha and β are the Ca2 + association and dissociation rate constants respectively and γ and δ are Ca2 + independent isomerization constants. X is the Ca2 + sensor (of a synaptic vesicle) with no Ca2 + bound, X(ci)1 is the Ca2 + sensor with one Ca2 + bound; likewise, X(ci)5 is the Ca2 + sensor with five Ca2 + bound; 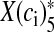 is the isomer of X(ci)5 which is ready for glutamate release. Hippocampal synapses are known as low-fidelity synapses [12]. We have assumed an active zone consisting of two docked synaptic vesicles [49, 50]. Since there are a few synaptic vesicles the number of vesicles with 5 Ca2 + ions bound cannot be determined by the average of the vesicle pool. Therefore, the fraction of docked vesicles ready to be released fr, has been determined using dynamic Monte-Carlo simulation [51] of the kinetics given by Eq. (7) and depends on the X
is the isomer of X(ci)5 which is ready for glutamate release. Hippocampal synapses are known as low-fidelity synapses [12]. We have assumed an active zone consisting of two docked synaptic vesicles [49, 50]. Since there are a few synaptic vesicles the number of vesicles with 5 Ca2 + ions bound cannot be determined by the average of the vesicle pool. Therefore, the fraction of docked vesicles ready to be released fr, has been determined using dynamic Monte-Carlo simulation [51] of the kinetics given by Eq. (7) and depends on the X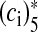 state.
state.
Apart from evoked release of docked vesicles, spontaneous release of vesicles can also occur when the pre-synaptic membrane is not depolarized. The rate of spontaneous release depends upon pre-synaptic Ca2 + concentration [36, 37, 44]. The number of vesicles ready to be released spontaneously, pr, is assumed to be a Poisson process with the following rate,
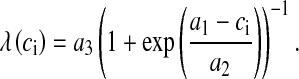 |
8 |
The formulation for the rate of spontaneous release is from Nadkarni and Jung [12]. We have to modify the parameter values (see (8)) because, as per their choice of values and system setup, the frequency of spontaneously released vesicles was as high as 19 per second (we have determined this through simulation runs of over 10000 trials). However, the experimentally determined frequency of spontaneous vesicle release in the presence of an astrocyte is in between 1 and 3 per second [52]. Thus, we determined the values of a1, a2 and a3 by simulation so that the frequency of spontaneous vesicle release is between 1 and 3 Hz. The vesicle fusion and recycling process is governed by the Tsodyks & Markram model (TMM) [29]. A slight modification has been made to the TMM to make the vesicle fusion process pr dependent. The modified TMM is as follows:
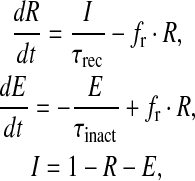 |
9 |
where R is the fraction of releasable vesicles inside the bouton, E is the fraction of effective vesicles in the synaptic cleft and I is the fraction of inactive vesicles undergoing recycling, 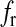 has the values (0, 0.5, 1) corresponding to the number of vesicles ready to be released (0, 1, 2), which is determined by the stochastic simulation of the kinetic model in (7) or generating a Poisson random variable with the rate given by (8). τinact and τrec are the time constants of vesicle inactivation and recovery respectively. Once a vesicle is released, whether evoked or spontaneous, the vesicle release process remains inactivated for a period of 6.34 ms [53]. The parametric values used for the simulation are listed in Table 4.
has the values (0, 0.5, 1) corresponding to the number of vesicles ready to be released (0, 1, 2), which is determined by the stochastic simulation of the kinetic model in (7) or generating a Poisson random variable with the rate given by (8). τinact and τrec are the time constants of vesicle inactivation and recovery respectively. Once a vesicle is released, whether evoked or spontaneous, the vesicle release process remains inactivated for a period of 6.34 ms [53]. The parametric values used for the simulation are listed in Table 4.
Table 4.
Parameters used for glutamate dynamics in the bouton and cleft
| Symbol | Description | Value | Reference |
|---|---|---|---|
| A | Ca2 + association rate constant | 0.3 μM ms − 1 | [36] |
| β | Ca2 + dissociation rate constant | 3 ms − 1 | [36] |
| γ | Isomerization rate constant (forward) | 30 ms − 1 | [36] |
| Δ | Isomerization rate constant (backward) | 8 ms − 1 | [36] |
| τrec | Vesicle recovery time constant | 800 ms | [29] |
| τinac | Vesicle inactivation time constant | 3 ms | [29] |
| a1 | Ca2 + concentration at which λ is halved | 50 μM | See text |
| a2 | Slope factor of spontaneous release rate λ | 5 μM | See text |
| a3 | Maximum spontaneous release rate | 0.85 ms − 1 | See text |
| nv | Number of docked vesicles | 2 | [50] |
| gv | Glutamate concentration in single vesicles | 60 mM | [54] |
| gc | Glutamate clearance rate constant | 10 ms − 1 | [31] |
Glutamate dynamics in the synaptic cleft
Various types of glutamate receptors have been detected pre-synaptically, extra-synaptically, as well as on glial cells [49], suggesting that, to study transmission of glutamatergic signals, it is essential to study how glutamate diffuses [49]. However, using Monte Carlo simulation of a central glutamatergic synapse, in particular a CA3–CA1 synapse, Franks et al. [55] showed that glutamatergic signaling is spatially independent at these synapses. The capacity of the bouton vesicle containing glutamate has been assumed to be 60 mM [49]. Since E gives the effective fraction of vesicles in the cleft, the estimated glutamate concentration in the cleft can be represented mathematically as
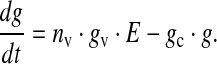 |
10 |
Here g is the glutamate concentration in the synaptic cleft, nv is the number of docked vesicles, gv is the vesicular glutamate concentration and gc is the rate of glutamate clearance i.e. re-uptake by a neuron or astrocyte [31]. Using this simple dynamics, we could achieve the estimated range of glutamate concentration 0.24–11 mM in the cleft [49, 55] and the time course of glutamate in the cleft is 2 ms [55, 56]. Although a similar equation can be used to model glutamate dynamics at other synapses, although one might have to use different parameter values. Thus, the present formulation can be considered specific to a CA3–CA1 synapse.
Astrocyte Ca2 + dynamics
Porter and McCarthy [20] showed that glutamate released from the Schaffer collaterals (SC) leads to an increase in astrocytic Ca2 + via a mGluR pathway. Recently, De Pitta et al. [30] proposed a G-ChI model for astrocytic Ca2 + oscillations mediated by the mGluR pathway while treating glutamate concentration in the synaptic cleft as a parameter. They called it G-ChI referring to the dependent variables and the glutamate concentration parameter used in their model (in their model G represented glutamate concentration in the synaptic cleft, C represented astrocytic [Ca2 + ], h represented the gating variable of IP3R and I represented the astrocytic [IP3]). We have used the G-ChI model for astrocyte Ca2 + dynamics with the exception that ‘g’ is a dynamic variable given by (10). The G-ChI model uses the conventional L-R model for astrocytic Ca2 + concentration ca with some specific terms for intracellular IP3 concentration pa. It incorporates PLC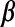 and PLC
and PLC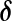 (are isoenzymes of the family of phosphoinositide-specific PLC)-dependent IP3 production. It also incorporates inositol polyphosphate 5-phosphatase (IP-5P) and IP3 3-kinase (IP3-3K)-dependent IP3 degradation (for a systematic derivation regarding the expressions, shown in (13), incorporating these effects, see De Pitta et al. [30]). It is a very detailed model based on astrocyte-specific experiments [57, 58], a model that exhibits IP3 oscillations apart from Ca2 + oscillations. However, the exact significance of IP3 oscillations is yet unknown [30]. The G-Chl model is a closed-cell model [41] i.e., without membrane fluxes. In such models, ca primarily depends upon two parameters, i) the flux from ER into cytosol and ii) the maximal pumping capacity of the Sarco-Endoplasmic Reticulum ATPase (SERCA) pump. It is known that IP3Rs are found in clusters in astrocytes [59]. However, the size of the cluster NIP3 is not known. We have assumed it to be 20 [60]. We make use of the stochastic L-R model [60]. The model can be represented as follows:
(are isoenzymes of the family of phosphoinositide-specific PLC)-dependent IP3 production. It also incorporates inositol polyphosphate 5-phosphatase (IP-5P) and IP3 3-kinase (IP3-3K)-dependent IP3 degradation (for a systematic derivation regarding the expressions, shown in (13), incorporating these effects, see De Pitta et al. [30]). It is a very detailed model based on astrocyte-specific experiments [57, 58], a model that exhibits IP3 oscillations apart from Ca2 + oscillations. However, the exact significance of IP3 oscillations is yet unknown [30]. The G-Chl model is a closed-cell model [41] i.e., without membrane fluxes. In such models, ca primarily depends upon two parameters, i) the flux from ER into cytosol and ii) the maximal pumping capacity of the Sarco-Endoplasmic Reticulum ATPase (SERCA) pump. It is known that IP3Rs are found in clusters in astrocytes [59]. However, the size of the cluster NIP3 is not known. We have assumed it to be 20 [60]. We make use of the stochastic L-R model [60]. The model can be represented as follows:
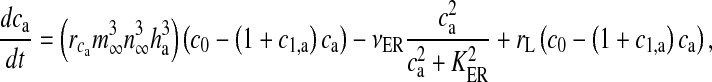 |
11 |
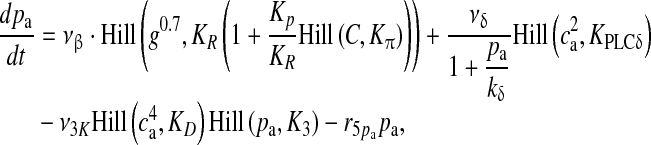 |
12 |
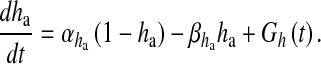 |
13 |
Here, the first term on the right-hand side of (11) represents the Ca2 + flux flowing out from the ER to the intracellular space, the second term represents the rate at which Ca2 + is removed from the intracellular space by the SERCA pump and the last term represents the leak of Ca2 + from the ER into the intracellular space. Clearly, these terms are very analogous to the terms involved in the production of cslow in (6) but with the major difference, which was mentioned earlier as well, that this model is based on a closed-cell assumption. Under such an assumption, an expression like (5) holds true and can be represented in terms of the astrocyte cell parameters as
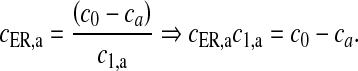 |
14 |
Equation (14) gives us the advantage to represent astrocytic Ca2 + flux terms completely in terms of cell parameters (compare (11) with (6) where a separate differential equation for 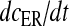 is present).
is present). 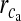 is the maximal rate of the Ca2 + flux from IP3R the cluster, and
is the maximal rate of the Ca2 + flux from IP3R the cluster, and  together represent the opening probability of the IP3R cluster. νER is the maximal rate of Ca2 + uptake into the ER and KER is the affinity of the SERCA pump for intracellular Ca2 + , and rL is the maximal rate of Ca2 + leak from the ER. The first two terms on the right-hand side of (12) incorporate agonist-dependent and agonist-independent production of IP3 and the last two terms incorporate IP3 degradation by IP3-3K and IP-5P respectively. In (13),
together represent the opening probability of the IP3R cluster. νER is the maximal rate of Ca2 + uptake into the ER and KER is the affinity of the SERCA pump for intracellular Ca2 + , and rL is the maximal rate of Ca2 + leak from the ER. The first two terms on the right-hand side of (12) incorporate agonist-dependent and agonist-independent production of IP3 and the last two terms incorporate IP3 degradation by IP3-3K and IP-5P respectively. In (13), 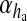 is the rate at which ha opens,
is the rate at which ha opens, 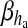 is the rate where ha closes and Gh(t) is a zero mean, uncorrelated, Gaussian white-noise term with a covariance function [60]
is the rate where ha closes and Gh(t) is a zero mean, uncorrelated, Gaussian white-noise term with a covariance function [60]
 |
Here, Δ(t) is the Dirac-delta function, t and t′ are distinct times and 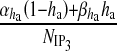 is the spectral density [61]. The present model can be classified into three categories: i) amplitude modulated (AM), ii) frequency modulated (FM) and iii) amplitude and frequency modulated (AFM) [30]. We have used AFM-encoded astrocytic Ca2 + oscillations, as coupling of IP3 metabolism with calcium-induced calcium release (CICR) does not allow pure AM encoding [30]. The mathematical expression of other parameters used in (11) and (13) are
is the spectral density [61]. The present model can be classified into three categories: i) amplitude modulated (AM), ii) frequency modulated (FM) and iii) amplitude and frequency modulated (AFM) [30]. We have used AFM-encoded astrocytic Ca2 + oscillations, as coupling of IP3 metabolism with calcium-induced calcium release (CICR) does not allow pure AM encoding [30]. The mathematical expression of other parameters used in (11) and (13) are
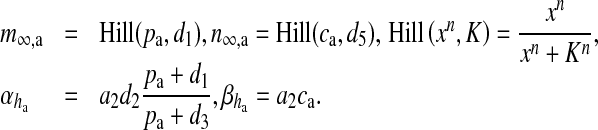 |
Hill (xn, K) is the generic Hill function [30]. Typically, the Hill function is used for reactions whose intermediate steps are unknown (or not considered) but cooperative behavior is suspected in the reaction [41]. Mathematically, it can be said that the Hill function is used for reactions whose reaction velocity curve is not hyperbolic [41]. The parametric value of all the constants are listed in Table 5.
Table 5.
Parameters used for astrocyte Ca2 + dynamics
| Symbol | Description | Value | Reference |
|---|---|---|---|
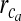 |
Maximal IP3R flux | 6 s − 1 | [30] |
| rL | Maximal rate of Ca2 + leak from ER | 0.11 s − 1 | [30] |
| c0 | Total cell free Ca2 + concentration | 2 μM | [30] |
| c1,a | Ratio of ER volume to cytosol volume | 0.185 | [30] |
| νER | Maximal rate of SERCA uptake | 0.9 μM s − 1 | [30] |
| KER | SERCA Ca2 + affinity | 0.1 μM | [30] |
| d1 | IP3 dissociation constant | 0.13 μM | [30] |
| d2 | Ca2 + inactivation dissociation constant | 1.049 μM | [30] |
| d3 | IP3 dissociation constant | 0.9434 μM | [30] |
| d5 | Ca2 + activation dissociation constant | 0.08234 μM | [30] |
| a2 | IP3R binding rate for Ca2 + inhibition | 2 s − 1 | [30] |
| N | Number of IP3Rs in a cluster | 20 | [60] |
| Glutamate-dependent IP3 production | |||
| νβ | Maximal rate of IP3 production by PLCbeta | 0.5 μM s − 1 | [30] |
| KR | Glutamate affinity of the receptor | 1.3 μM | [30] |
| Kp | Ca2 + /PKC-dependent inhibition factor | 10 μM | [30] |
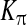 |
Ca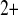 affinity of PKC affinity of PKC |
0.6 μM | [30] |
| Glutamate-independent IP3 production | |||
| νδ | Maximal rate of IP3 production by PLCδ | 0.05 μM s − 1 | [30] |
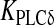 |
Ca2 + affinity of PLC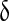
|
0.1 μM | [30] |
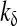 |
Inhibition constant of PLC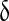 activity activity |
1.5 μM | [30] |
| IP3 degradation | |||
| r5pa | Maximal rate of degradation by IP-5P | 0.05 s − 1 | [30] |
| ν3 K | Maximal rate of degradation by IP3-3K | 2 μM s − 1 | [30] |
| KD | Ca2 + affinity of IP3-3K | 0.7 μM | [30] |
| K3 | IP3 affinity of IP3-3K | 1 μM | [30] |
Gliotransmitter release dynamics in the astrocyte
There is enough evidence that astrocytes actually release gliotransmitters in a Ca2 + -dependent manner [14, 54, 62–64]. There is again considerable evidence that the released gliotransmitters modulate synaptic plasticity via extra-synaptic NMDA receptors [21, 65–67] and extra-synaptic mGluR [1, 68] but the exact mechanism by which astrocytes release gliotransmitters is yet to be determined [69]. However, it is widely agreed upon that astrocytes release gliotransmitters in a vesicular manner similar to neurons [54, 62, 64, 70] as they possess the necessary exocytotic secretory machinery [71]. In 2000, Parpura & Haydon determined the Ca2 + dependence of glutamate release from hippocampal astrocytes and found that the Hill coefficient for glutamate release from astrocytes was 2.1–2.7, suggesting that at least two Ca2 + ions are a essential for gliotransmitter release [67]. Recently, the probability of vesicular fusion in response to mechanical stimulation and the size of the readily releasable pool of SLMVs in astrocytes has been determined by Malarkey and Parpura [33]. Based on the observation of Parpura and Haydon [67], we have assumed that the binding of three Ca2 + ions leads to a gliotransmitter release. The model governing the gliotransmitter release site activation is based on Bertram et al. [32]. Our gliotransmitter release model assumes that three Ca2 + ions must bind with three independent gates or sites (S1–S3) for a possible gliotransmitter release.
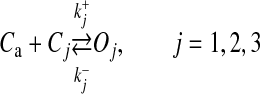 |
where Cj and Oj are the closing and opening probabilities of gate Sj, respectively, and 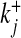 and
and 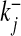 are the opening and closing rates of the gate Sj, respectively. The temporal evolution of the open gate Oj can be expressed as
are the opening and closing rates of the gate Sj, respectively. The temporal evolution of the open gate Oj can be expressed as
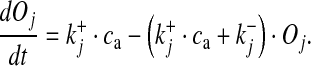 |
15 |
As the three sites are physically independent, the fraction of SLMVs ready to be released can be given as the product of the opening probabilities of the three sites
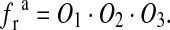 |
16 |
The dissociation constants of gates S1–S3 are 108 nM, 400 nM and 800 nM. The time constants for gate closure 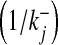 are 2.5 s, 1 s and 100 ms. The dissociation constants and time constants for S1 and S2 are the same as in Bertram et al. [32]. While the dissociation constant and time constant for gate S3 were fixed through computer simulations to fit the experimentally determined probability of fusogenic (fraction of readily releasable SLMVs in response to mechanical stimulation) SLMVs found recently by Malarkey and Parpura [33]. Once an SLMV is ready to be released, its fusion and recycling process was modeled using TMM. The governing model is as follows:
are 2.5 s, 1 s and 100 ms. The dissociation constants and time constants for S1 and S2 are the same as in Bertram et al. [32]. While the dissociation constant and time constant for gate S3 were fixed through computer simulations to fit the experimentally determined probability of fusogenic (fraction of readily releasable SLMVs in response to mechanical stimulation) SLMVs found recently by Malarkey and Parpura [33]. Once an SLMV is ready to be released, its fusion and recycling process was modeled using TMM. The governing model is as follows:
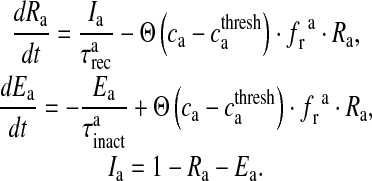 |
17 |
Here, Ra is the fraction of readily releasable SLMVs inside the astrocyte, Ea is the fraction of effective SLMVs in the extra-synaptic cleft and Ia is the fraction of inactive SLMVs undergoing endocytosis or a re-acidification. Θ is the Heaviside function and 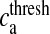 is the threshold of astrocytic [Ca2 + ] necessary for release site activation [67].
is the threshold of astrocytic [Ca2 + ] necessary for release site activation [67]. 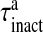 and
and 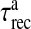 are the time constants of inactivation and recovery of SLMVs, respectively.
are the time constants of inactivation and recovery of SLMVs, respectively.
Glutamate dynamics in the extra-synaptic cleft
The glutamate concentration in the extra-synaptic cleft ga, has been modeled in a similar way to (10). This glutamate acts on extra-synaptically located mGluRs of the pre-synaptic bouton. It is used as input into the IP3 production term of (6). The SLMVs of the astrocytes are not as tightly packed as of the neurons [62]. Thus, it is assumed that each SLMV contains 20 mM of glutamate [54]. The mathematical equation governing glutamate dynamics in the extra-synaptic cleft are as follows
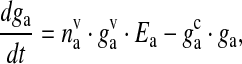 |
18 |
where ga is the glutamate concentration in the extra-synaptic cleft, 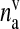 represents the readily releasable pool of SLMVs,
represents the readily releasable pool of SLMVs, 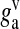 is the glutamate concentration within each SLMV and
is the glutamate concentration within each SLMV and 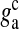 is the clearance rate of glutamate from the cleft due to diffusion and/or re-uptake by astrocytes. Parameters used in modeling glutamate dynamics in the astrocyte and in the extra-synaptic cleft are given in Table 6.
is the clearance rate of glutamate from the cleft due to diffusion and/or re-uptake by astrocytes. Parameters used in modeling glutamate dynamics in the astrocyte and in the extra-synaptic cleft are given in Table 6.
Table 6.
Parameters used for glutamate dynamics in the astrocyte and extra-synaptic cleft
| Symbol | Description | Value | Reference |
|---|---|---|---|
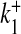 |
Ca2 + association rate for S1 | 3.75 × 10 − 3 μM − 1 ms − 1 | [32] |
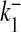 |
Ca2 + dissociation rate for S1 | 4 × 10 − 4 ms − 1 | [32] |
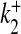 |
Ca2 + association rate for S2 | 2.5 × 10 − 3 μM − 1 ms − 1 | [32] |
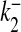 |
Ca2 + dissociation rate for S2 | 1 × 10 − 3 ms − 1 | [32] |
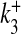 |
Ca2 + association rate for S3 | 1.25 × 10 − 2 μM − 1 ms − 1 | See text |
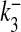 |
Ca2 + dissociation rate for S3 | 10 × 10 − 3 ms − 1 | See text |
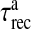 |
Vesicle recovery time constant | 800 ms | [29] |
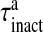 |
Vesicle inactivation time constant | 3 ms | [29] |
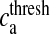 |
Astrocyte response threshold | 196.69 nM | [67] |
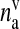 |
SLMV ready to be released | 12 | [33] |
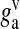 |
Glutamate concentration in one SLMV | 20 mM | [54] |
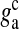 |
Glutamate clearance rate from the extra-synaptic cleft | 10 ms − 1 | [31] |
Dendritic spine-head dynamics
The dendritic spine-head is assumed to be of mushroom type. Its volume is taken to be 0.9048 μm3 (assuming a spherical spine-head of radius 0.6 μm [72]). The specific capacitance and specific resistance of the spine-head is assumed to be 1 μF / cm2 and 10000 Ω cm2, respectively. Given the dimension of the spine we can calculate its actual resistance as
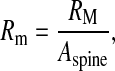 |
19 |
where RM is the specific resistance of the spine and Aspine is the area of the spine-head. NMDAR (N-methyl D-aspartate receptor) and AMPAR (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid receptor) are co-localized at most of the glutamatergic synapses, most of which are found at dendritic spines [55]. Chen and Diamond [73] showed that the post-synaptic NMDAR receives less glutamate during evoked synaptic response, suggesting that most of the post-synaptic current is contributed by AMPAR, under such conditions. Also, NMDAR is known to play a crucial role in longer forms of synaptic plasticity, long-term potentiation (LTP) and long-term depression (LTD) [74, 75]. Hence, in our model of short-term potentiation the post-synaptic density comprises of AMPAR alone. The post-synaptic potential change has been modeled using a passive membrane mechanism [29]
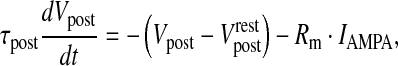 |
20 |
where τpost is the post-synaptic membrane time constant, 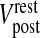 is the post-synaptic resting membrane potential and IAMPA is the AMPAR current given by the following expression [31]
is the post-synaptic resting membrane potential and IAMPA is the AMPAR current given by the following expression [31]
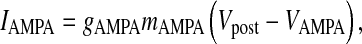 |
where gAMPA is the conductance of the AMPAR channel, VAMPA is the reversal potential of the AMPAR and mAMPA is the gating variable of AMPAR. Although there exists a more comprehensive six-state Markov model for AMPAR gating [31], in our model we have used a simple two-state model. This two-state model has been used keeping in mind that it is computationally less expensive, while retaining most of the important qualitative properties [31]. Also, it is known that detailed AMPAR mechanisms like desensitization do not play a role in STP [7]. AMPAR gating is governed by the following HH-type formulism [31]
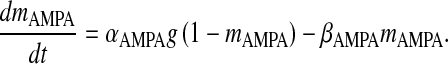 |
21 |
Here, αAMPA is the opening rate of the receptor, βAMPA is the closing rate of the receptor and g is the glutamate concentration in the cleft given by (10). The parameter values are listed in Table 7.
Table 7.
List of parameters used for post-synaptic potential generation
| Symbol | Description | Value | Reference |
|---|---|---|---|
| Rm | Actual resistance of the spine-head | 0.79 × 105 MΩ | Calculated using (19) |
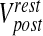 |
Post-synaptic resting membrane potential | −70 mV | |
| τpost | Post-synaptic membrane time constant | 50 ms | [29] |
| gAMPA | AMPAR conductance | 0.35 nS | [31] |
| VAMPA | AMPAR reversal potential | 0 mV | [31] |
| αAMPA | AMPAR forward rate constant | 1.1 μM s − 1 | [31] |
| βAMPA | AMPAR backward rate constant | 190 s − 1 | [31] |
Numerical implementation
All the computations have been performed using MATLAB. The model equations were discretized with a temporal precision of Δt = 0.05 ms. The canonical explicit Euler method was used to solve the system of 22 ordinary differential equations governing the model. For the numerical simulation of the noise term in (13), we have used the Box-Muller algorithm [76] to generate the noise term at each time step (Δt). All simulations were performed on a Dell precision 3500 workstation with an Intel Xeon processor with 2.8-GHz processing speed and 12-GB RAM. The time taken for the model time of 1 s (stimulation rate 5 Hz) is approximately 8.5 s. The MATLAB script written for the simulation of the model can be requested by e-mail to any of the authors.
Simulation results
The generation of post-synaptic current with and without the participation of astrocytic Ca2 + is shown in this section with extensive numerical simulations of the model equations presented above. In the latter case, output signal amplification through a processing loop consisting of feed-forward and feed-back paths, with the help of astrocytic Ca2 + signaling, is shown in Fig. 2b. Here, we have tried to answer the question, “Does the astrocyte play an active role in the modulation of synaptic plasticity?” In order to study the difference in both types of processing (see Fig. 2), first we present the results associated with astrocyte-independent processing followed by astrocyte-dependent processing.
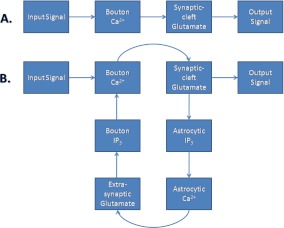
Fig. 2.
The two types of information processing simulated in this paper. a Astrocyte-independent information processing. b Astrocyte-dependent information processing. The input signal is being amplified by astrocyte-dependent feed-forward and feed-back pathways, which form a processing loop
Astrocyte-independent information processing
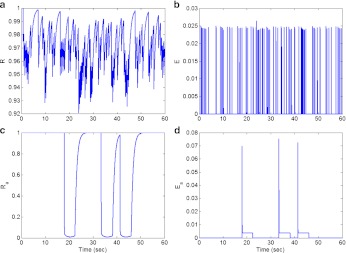
In this subsection we simulate the processing elaborated in Fig. 2a. We present results of the implementation of the models described in Subsections 2.1, 2.2, 2.4 and 2.8 (Fig. 3a, b, c, and d, respectively).
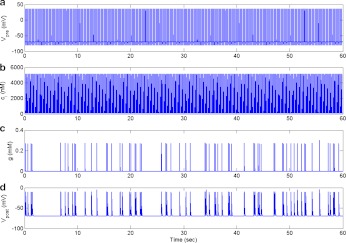
Fig. 3.
The major variables involved in astrocyte-independent information processing. aVpre (mV), 5 Hz input signal generated using the HH model, in response to a stimulus of 10 μA per cm2 of frequency 5 Hz and duration 10 ms. b Ca2 + (nM), fast Ca2 + oscillations in response to the 5 Hz input signal. c Synaptic glutamate (mM), elevated glutamate concentration in the synaptic cleft due to exocytosis of glutamate filled synaptic vesicles from the bouton. d Excitatory post-synaptic potential (EPSP) (mV), potential change in the membrane of the post-synaptic spine mediated through AMPAR channels
We used the model described in (1) to generate the input signal or pre-synaptic membrane potential. This input signal forms the basis of signal transduction and we made sure that the tripartite synapse is at rest in its absence. In response to this input signal, the N-type Ca2 + channels open and the bouton Ca2 + starts undergoing very fast oscillations (see Fig. 3b). Note that, here, there is no astrocyte present and hence there is no contribution of [Ca2 + ] from intracellular stores. We adjusted the number of Ca2 + channels on the surface of the bouton (by adjusting ρCa) so that the amplitude of Ca2 + oscillation is 5 μM, i.e., exactly half the Ca2 + sensor affinity (β/α, where β and α are given in Table 4). Doing this we could attain an average neurotransmitter release probability, in the range 0.2–0.3 (see Fig. 5), observed experimentally in the absence of an astrocytes [1]. An increased bouton [Ca2 + ] instigates the process of exocytosis and vesicles release their content (glutamate) in the synaptic cleft (see Fig. 3c). When glutamate concentration rises in the cleft, it binds with post-synaptic AMPAR, which causes this ligand-gated channel to open. Once opened, AMPAR causes a change in the post-synaptic potential (see Fig. 3d); and since this deflection is positive it is referred to as an EPSP. As described in the previous section, we also keep track of the vesicle recycling process, see (9), which is shown in Fig. 4.
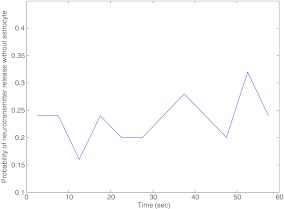
Fig. 5.
Probability of neurotransmitter release Pr, without incorporating the feedback loop due to the astrocyte, is computed as the ratio of the number of successful post-synaptic responses to the number of pre-synaptic stimuli (which was 5 Hz for the given simulation) within a time-window of length 5 seconds
Fig. 4.
Fraction of releasable and effective vesicles, in astrocyte-independent information processing, during an input signal of 5 Hz (see Fig. 3a). a The fraction of releasable vesicles i.e., vesicles ready to be fused, inside the bouton. b The fraction of effective vesicles i.e., the fraction of vesicles left in the synaptic cleft
In Fig. 4 we show the underlying process of vesicle release. In the absence of an astrocyte, it can be observed that nearly 90% of the vesicles are available for release for most of the time (see Fig. 4a). In Fig. 4b, we observe that the fraction of effective vesicles is not as dense as the input signal (see Fig. 3a) implying low probability of vesicle release. In fact, the probability of vesicle release was nearly 0.25, i.e., every fourth input signal is able to release a synaptic vesicle. We next show the Pr, i.e., neurotransmitter release probability in the absence of an astrocyte (Fig. 5). The PR has been calculated as the ratio of the number of successful post-synaptic responses to the number of pre-synaptic impulses (with a time-window of length 5 s).
Astrocyte-dependent information processing
In this subsection we show simulations associated with the biophysical model governed by (1)–(20), i.e., astrocyte-dependent information processing. In Fig. 6, we give an idea of the processes involved in the loop shown in Fig. 2b. For the simulation of the scheme, shown in Fig. 2b, we simultaneously solved (1)–(20). Of particular interest are the astrocyte-dependent feed-forward and feed-back paths which form a loop (Fig. 2b). The same input signal was used in a feed-back manner into the loop. Using such a feed-forward and feed-back pathway an input signal can be amplified as per the cognitive process requiring strengthening of synapses. Ultimately such a process may lead to enhanced synaptic efficacy.
Fig. 6.
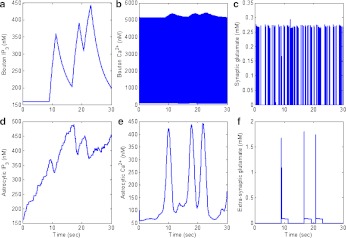
The major variables involved in astrocyte-dependent information processing. Here, the input signal is same as in Fig. 3a and is omitted. Output f is feeding back into input a. a Increased bouton IP3 concentration in response to elevated extra-synaptic glutamate concentration (see f). b Increased IP3 concentration causes the IP3R channels to open and leads to a transient enhancement in bouton [Ca2 + ], due to the influx of Ca2 + from IP3R (see Ca2 + concentration after 20 seconds). c Accumulated bouton [Ca2 + ] leads to increased transients of glutamate concentration in the synaptic cleft. d Transients of glutamate concentration set off the production of astrocytic IP3 concentration through a mGluR dependent pathway. e Elevated astrocytic IP3 concentration causes the IP3R channels to open and initiates astrocytic Ca2 + oscillations. f Astrocytic Ca2 + oscillations instigate the process of SLMV fusion, which is followed by a raised extra-synaptic glutamate concentration. This elevated extra-synaptic glutamate concentration forms the basis of bouton IP3 production shown in a
All the variables shown in Fig. 6 are inter-dependent i.e., the variation in one affects the variation in others. When the bouton is fed with an input signal, it shows its response, in the form of increased cytosolic [Ca2 + ] (see Fig. 6b). This elevated [Ca2 + ] leads to the release of glutamate into the synaptic cleft (see Fig. 6c). After being exocytosed, synaptic glutamate can have either of two fates (see Fig. 2b). It can either bind with the post-synaptic AMPAR or it can bind with the mGluRs on the surface of the astrocyte. Once this glutamate binds with mGluR, it instigates the production of astrocytic IP3 (see Fig. 6d) through a G-protein link. During this glutamate spill-over process, astrocytic IP3 concentration goes on appreciating and gradually starts oscillating (notice after the 20 s mark Fig. 6d). It can be observed from Fig. 6d and e that astrocytic Ca2 + also starts oscillating as soon as astrocytic IP3 starts oscillating. The biological significance and importance of IP3 oscillations for driving Ca2 + oscillations has not been fully understood, however [30]. This astrocytic Ca2 + is known to exocytose SLMVs filled with glutamate once it crosses its threshold value of 196.69 nM [67]. Similarly, in our model whenever astrocytic Ca2 + crosses its threshold value it can spill glutamate (contained in SLMVs) into the extra-synaptic cleft (see Fig. 6f). We have mathematically modeled this process of astrocytic glutamate release using (15)–(18). Extra-synaptic glutamate binds with extra-synaptic mGluR located on the surface of the bouton and initiates the production of bouton IP3 (see Fig. 6a) through a G-protein link. It is visible from Fig. 6f and a that bouton IP3 production starts only when the astrocyte spills glutamate into the extra-synaptic cleft, reflecting the significance of extra-synaptic glutamate in the model. This bouton IP3 is free to diffuse inside the cytosol and opens the IP3R on the intracellular stores in a Ca2 + -dependent manner. Transient accumulation of Ca2 + takes place as a result of the opening of IP3Rs on the surface of the intracellular store (e.g., see Fig. 6b at the 20 s mark). Flow of Ca2 + through these IP3Rs is a slow process and is known to play a crucial role in modulating synaptic plasticity and spontaneous vesicle release [44].
The synaptic vesicle exocytosis from the bouton and SLMV release from the astrocyte has been modeled using (7)–(9) and (15)–(17). Figure 7a and b show the fraction of releasable and effective vesicles, respectively, during the synaptic vesicle process simulated using (7)–(9). Figure 7a and b are similar to the diagrams in the Fig. 4, except for the astrocyte-dependent pathway used. The SLMV recycling process has been modeled using (17).
Fig. 7.
Fraction of releasable and effective vesicles, in astrocyte-dependent information processing, during an input AP of 5 Hz (see Fig. 3a). a Fraction of releasable vesicles inside the bouton. b Fraction of effective vesicles in the synaptic cleft, i.e., fraction of vesicles fused and residual vesicles in the synaptic cleft. c Fraction of releasable SLMVs inside the astrocyte. d Fraction of effective SLMVs in the extra-synaptic cleft, i.e., fraction of fused and residual SLMV in the extra-synaptic cleft
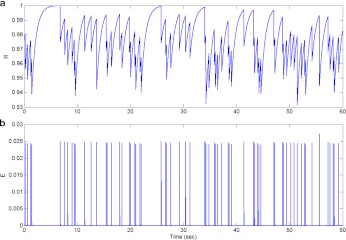
Figure 7c and d show the fraction of releasable vesicles in the astrocyte and the effective vesicles in the extra-synaptic cleft. It can be observed from Fig. 7a that nearly 92% of the releasable (docked) vesicles have been used in the astrocyte-dependent pathway. The fraction of effective vesicles in the synaptic cleft has also considerably gone up (compare with Fig. 4b), due to the transient increase in Ca2 + concentration (see Fig. 6b), which improves the synaptic vesicle release probability (see Fig. 7). In fact, the average vesicle release probability during this pathway was nearly 0.35, implying that more than one out of three spikes are able to release a synaptic vesicle. It should be pointed out that the similar amount of enhancement in the neurotransmitter release probability has been observed experimentally as well. Perea and Araque [1] reported an increased Pr after astrocyte stimulation (from 0.24 to 0.33). We next show the neurotransmitter release probability following the astrocyte-dependent pathway of information processing. A transient increase in the neurotransmitter release probability can be observed from Fig. 8 in close correlation with the astrocytic Ca2 + concentration (see Fig. 6e). The average neurotransmitter release probability under the astrocyte-dependent pathway of information processing was 0.338, compared to 0.23 for the astrocyte-independent pathway.
Fig. 8.
Probability of neurotransmitter release, after incorporating the feed-forward and feed-back loops due to the presence of an astrocyte, is computed as the ratio of the number of successful post-synaptic responses to the number of pre-synaptic stimuli (which was 5 Hz for the given simulation) within a time-window of length 5 seconds
Comparison between the two forms of information processing
In this subsection, we have undertaken a comparative study between the two forms of information processing (see Fig. 2a and b). We will discuss some of our findings, keeping in mind the recent controversy regarding whether astrocytic [Ca2 + ] contributes to synaptic plasticity or not (e.g., [2] vs. [15]).
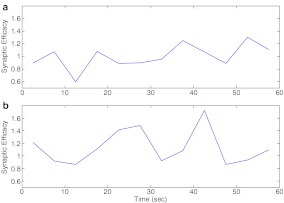
Using their experimental setup Perea and Araque [1] demonstrated an increase in synaptic efficacy at single CA3–CA1 synapses during the phase of high astrocytic [Ca2 + ] (see Figure 1F of [1]). They stimulated the pre-synaptic neuron and simultaneously increased the astrocytic [Ca2 + ] through different pathways, e.g., purinergic receptors (P2Y-R) and recorded the EPSCs. They used caged Ca2 + and UV-flash to artificially increase astrocytic [Ca2 + ]. In contrast, in our mathematical model, we allow an activity-dependent increase in astrocytic IP3 following an AP. As a measure of change in synaptic strength, i.e., synaptic efficacy, Perea and Araque [1] demonstrated an increase in mean EPSC amplitude when the astrocyte was stimulated. We measured the mean EPSC after every 5 s. In Fig. 9b, the mean EPSCs have been measured relative to the mean EPSC during the first 20 s, because it is the phase during which astrocytic [Ca2 + ] has not exceeded its threshold (see Fig. 6e). In Fig. 9a, the mean EPSCs have been measured relative to their overall mean. The impact of the astrocytic response is clearly visible when we look at Fig. 9a and b. In the astrocyte-independent information flow, there is not much deviation (± 20%) from its mean value, while in the astrocyte-dependent information flow there is a transient increase of nearly 80%. This increase is subsequent to the rise in astrocytic Ca2 + (see Fig. 6e) and has a decay time constant (the time necessary to reach 1/e of its initial magnitude [25]) of nearly 10 s. This increase in synaptic efficacy falls under short-term-enhancement, in particular augmentation, given the classification in Koch ([24], p. 311).
Fig. 9.
A Comparison of the two modes of information processing (see Fig. 2) in response to the same input signal of 5 Hz. Synaptic efficacy is calculated as the windowed-mean of post-synaptic responses including successes and failures where the window length has been taken to be 5 seconds for both figures. a Output signal using astrocyte-independent information processing. b Output signal using astrocyte-dependent information processing
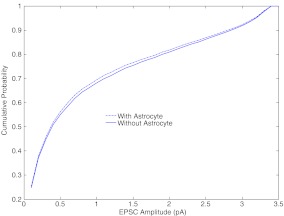
Perea and Araque [1] also demonstrated an increase in the cumulative probability of EPSC amplitude before (astrocyte-independent) and during (astrocyte-dependent) astrocyte stimulation (see Figure 1E of [1]). Similar to their experimental observations, we also observed an increase in the probability of EPSC amplitude (see Fig. 10). This implies that there are more chances of having EPSC amplitude between 0.5 and 2.5 pA when an astrocyte is present. Apart from an input signal of 5 Hz we also tested the cumulative probability for an input signal of 2 Hz and 10 Hz. We observed that the astrocyte-mediated potentiation (for an input signal of 2 Hz) of synaptic efficacy becomes more prominent as demonstrated by a significant increase in the cumulative probability of observing EPSC amplitudes between 1.5 and 4.5 pA (see Figure 1 of the Supplementary online material), similar to Fig. 10. On the other hand, the contribution of astrocyte-mediated potentiation (for an input signal of 10 Hz) of synaptic efficacy becomes less prominent or insignificant when compared with synaptic efficacy following the astrocyte-independent pathway (see Figure 2 of the Supplementary online material). The decrease in astrocyte-mediated synaptic potentiation observed with an increase in the frequency of the input signal might be due to the fact that our model has been calibrated for the experiments of Perea and Araque [1] where they applied mild pre-synaptic neuron stimulation.
Fig. 10.
Cumulative probability of EPSC amplitude in response to an input signal of 5 Hz. Astrocyte-dependent curve shifts upwards implying an increased probability of having an EPSC amplitude between 0.5 to 2.5 pA
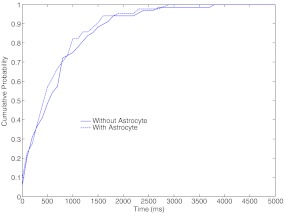
A more comprehensive way of demonstrating synaptic enhancement is to show that we have more post-synaptic spikes under astrocyte-dependent processing than astrocyte-independent processing. In Fig. 11, we show the cumulative probability distribution for the inter-arrival time of post-synaptic potentials. The cumulative probability plot tells us the probability of having a post-synaptic firing in a time-interval of length x ms (where x is an arbitrary point on the abscissa in Fig. 11). Obviously, the probability of having a post-synaptic spiking will increase as we increase the length of the time-interval (see Fig. 11 where, after 4000 ms, the cumulative probability is 1 under both forms of information processing). It is apparent from the figure that the probability of having post-synaptic spiking in short time-intervals has increased in the presence of an astrocyte (see Fig. 11).
Fig. 11.
Cumulative probability distribution of the inter-arrival time of EPSP for astrocyte-dependent and astrocyte-independent information processing. The distribution associated with the astrocyte-dependent process shifts to the left suggesting a reduced inter-arrival time due to enhanced synaptic efficacy
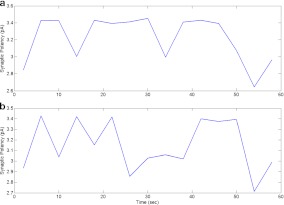
During this type of astrocyte-induced plasticity, it is known that synaptic potency remains unchanged [1]. Synaptic potency is given as a measure of mean post-synaptic response, excluding failures. We calculated the mean of each successful post-synaptic response in a time-window of 4 s. It can be observed from Fig. 12 that there is no apparent difference in synaptic potency under both forms of information processing. This observation was also confirmed statistically using a two-sample Student’s t test. Synaptic potencies were assumed to be independent normally distributed random samples. It was tested that both the samples are with equal mean and equal but unknown variances (null hypothesis), against the alternative that the means are not equal with 5% significance level. The result returned a p-value of 0.4475 indicating a failure to reject the null hypothesis.
Fig. 12.
Synaptic potency under both forms of information processing (i.e., astrocyte-independent and astrocyte-dependent). Synaptic potency is given as a measure of mean EPSC, calculated over a time-window of 4 s, excluding failures. Synaptic potency is unchanged in both cases which has also been observed in recent experiments (see Fig. 1 of [1]); a mean = −3.21 pA, std = 0.27 pA; b mean = −3.11 pA, std = 0.24 pA. The two-sample paired t-test helps establish the previous statement (p = 0.4475)
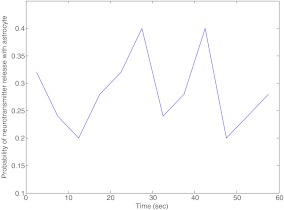
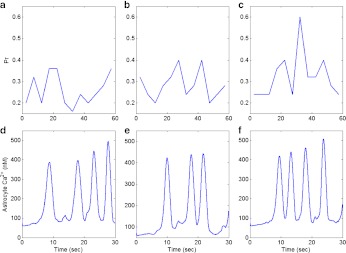
Using our simulation, we found that all these measures (like synaptic efficacy, inter-arrival time) that are used to demonstrate and establish the effect of the astrocyte-dependent pathway on synaptic plasticity depend primarily on two parameters: i) the size of readily releasable pools of SLMVs in the astrocyte and ii) the rate of IP3 production due to pre-synaptic mGluRs. The size of readily releasable pools has recently been determined using astrocyte cultures [33]. Here we show a change in the neurotransmitter release probability for a readily releasable pool ½ (see Fig. 13a) and 1½ (see Fig. 13c) in the size of the readily releasable SLMV pool determined experimentally (see Fig. 13b). Computer simulations shown in Fig. 13a–c reveal the effect of different sizes of the readily releasable pool of SLMVs. It is apparent that for a readily releasable pool of size 6 (i.e., containing 6 SLMVs) astrocytes do not contribute to enhance the pre-synaptic neurotransmitter release probability. In fact, the average neurotransmitter release probability for a readily releasable pool of size 6 was 0.25, which is similar to the average neurotransmitter release probability without an astrocyte.
Fig. 13.
Neurotransmitter release probability in response to changing the availability of a readily releasable SLMV pool inside the astrocyte. Neurotransmitter release probability is shown for pool sizes of 6 (a), 12 (b), and 18 (c). d–f Astrocytic Ca2 + concentration corresponding to the three simulations shown from a–c
Figure 13b shows the simulation of the model for the default set of parameters listed in Tables 2, 3, 4, 5, 6 and 7. It is apparent from the figure that the increase in neurotransmitter release probability is preceded by an increase in astrocytic Ca2 + concentration. In Fig. 13c we again show the neurotransmitter release probability but for an increased size of a readily releasable SLMV pool. The effect of an increased pool size is apparent from Fig. 13c. The average neurotransmitter release probability in this case was 0.35. It should be noted that the coherence between astrocytic [Ca2 + ] (see Fig. 13d–f) and neurotransmitter release probability (see Fig. 13a–c) is absent only for  (compare Fig. 13a and d), which highlights a possible biological condition under which the astrocyte does not contribute to synaptic plasticity. The average neurotransmitter release probability in the three simulations was 0.25, 0.33 and 0.35. There is no considerable difference between the experimentally determined pool size and a pool size of 18 (i.e., containing 18 SLMVs). However there was a considerable difference in the maximum extra-synaptic glutamate concentration when the latter was compared with the former (2.56 mM against 1.8 mM; data not shown). It is the negative cooperativity of mGluRs in response to extra-synaptic glutamate binding that ensures a robust response to lower concentration of glutamate and also ensures insensitivity to a higher concentration of glutamate. Thus, extra-synaptic glutamate is necessary for astrocyte-mediated synaptic potentiation, but with limited influence. A more potent contributor to astrocyte-mediated synaptic potentiation is the IP3 production rate by pre-synaptic mGluRs.
(compare Fig. 13a and d), which highlights a possible biological condition under which the astrocyte does not contribute to synaptic plasticity. The average neurotransmitter release probability in the three simulations was 0.25, 0.33 and 0.35. There is no considerable difference between the experimentally determined pool size and a pool size of 18 (i.e., containing 18 SLMVs). However there was a considerable difference in the maximum extra-synaptic glutamate concentration when the latter was compared with the former (2.56 mM against 1.8 mM; data not shown). It is the negative cooperativity of mGluRs in response to extra-synaptic glutamate binding that ensures a robust response to lower concentration of glutamate and also ensures insensitivity to a higher concentration of glutamate. Thus, extra-synaptic glutamate is necessary for astrocyte-mediated synaptic potentiation, but with limited influence. A more potent contributor to astrocyte-mediated synaptic potentiation is the IP3 production rate by pre-synaptic mGluRs.
The maximum rate of IP3 production νg by pre-synaptic mGluRs can be expressed in terms of surface density ρmGluR of mGluR; let the surface area of the bouton exposed to extra-synaptic glutamate released by the astrocyte be S, the Avogadro Number NA, the volume of the bouton Vbtn and the production rate of IP3 molecules per receptor rp. Then
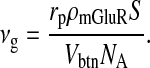 |
22 |
Nadkarni and Jung [12] estimated the maximum rate of IP3 production to be 0.062 nM ms − 1 or 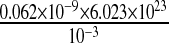 molecules/m3 ms or 0.373 × 1017 molecules/ms per unit volume by mGluRs on the surface of the astrocyte. Such an estimate of IP3 production rate is not known at the boutons of CA3 pyramidal neurons. Thus, we used the IP3 production rate by mGluRs on the pre-synaptic bouton to be the same as that determined by Nadkarni and Jung [12] i.e., 0.062 nM per ms. Hence, for an average bouton (of volume 0.13 μm3, Koester and Sakmann [77]) at the hippocampal CA3-CA1 synapse the production rate will be 0.373×1017×0.13×10 − 18 ≈ 0.0048 molecules/ms. If we assume
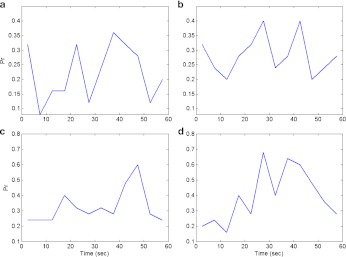
molecules/m3 ms or 0.373 × 1017 molecules/ms per unit volume by mGluRs on the surface of the astrocyte. Such an estimate of IP3 production rate is not known at the boutons of CA3 pyramidal neurons. Thus, we used the IP3 production rate by mGluRs on the pre-synaptic bouton to be the same as that determined by Nadkarni and Jung [12] i.e., 0.062 nM per ms. Hence, for an average bouton (of volume 0.13 μm3, Koester and Sakmann [77]) at the hippocampal CA3-CA1 synapse the production rate will be 0.373×1017×0.13×10 − 18 ≈ 0.0048 molecules/ms. If we assume 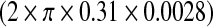 i.e. ≈ 0.0055 μm2 (0.31 μm is the radius of the bouton and 0.0028 μm is the strip of the bouton exposed to extra-synaptic glutamate) of the bouton is exposed to glutamate released into the extra-synaptic cleft by the astrocyte. Also, if we assume that receptors produce 1 IP3 molecule per ms, then the receptor density on the relevant surface of the bouton is ≈ 0.87 per μm2. This assessment is in conformity with experiments, as the receptor density at synapses is estimated to be between 200 and 2000 / μm2 [78] and the extra-synaptic receptor density is known to be 230 times less than the receptor density at the synapse [79]. The exact density of extra-synaptic mGluRs on CA3 pyramidal neurons is not known. Hence, we simulated the model for a range of possible IP3 production rates (see Fig. 14a–d). The average neurotransmitter release probability for νg = 0.05 nM ms − 1 is nearly equal to that of the astrocyte-independent pathway of information processing (Pr = 0.24 against Pr = 0.23). But as we increased the value of νg the effect of astrocyte over synaptic plasticity became more prominent. The average neurotransmitter release probabilities for νg = 0.1 nM ms − 1 and νg = 0.2 nM ms − 1 were 0.36 and 0.4 respectively. Please note that Fig. 14b is the same as Figs. 13b and 8, and is been shown for comparison purposes only. Our simulation reveals that νg is a critical parameter that can modulate the contribution of astrocyte-induced synaptic plasticity.
i.e. ≈ 0.0055 μm2 (0.31 μm is the radius of the bouton and 0.0028 μm is the strip of the bouton exposed to extra-synaptic glutamate) of the bouton is exposed to glutamate released into the extra-synaptic cleft by the astrocyte. Also, if we assume that receptors produce 1 IP3 molecule per ms, then the receptor density on the relevant surface of the bouton is ≈ 0.87 per μm2. This assessment is in conformity with experiments, as the receptor density at synapses is estimated to be between 200 and 2000 / μm2 [78] and the extra-synaptic receptor density is known to be 230 times less than the receptor density at the synapse [79]. The exact density of extra-synaptic mGluRs on CA3 pyramidal neurons is not known. Hence, we simulated the model for a range of possible IP3 production rates (see Fig. 14a–d). The average neurotransmitter release probability for νg = 0.05 nM ms − 1 is nearly equal to that of the astrocyte-independent pathway of information processing (Pr = 0.24 against Pr = 0.23). But as we increased the value of νg the effect of astrocyte over synaptic plasticity became more prominent. The average neurotransmitter release probabilities for νg = 0.1 nM ms − 1 and νg = 0.2 nM ms − 1 were 0.36 and 0.4 respectively. Please note that Fig. 14b is the same as Figs. 13b and 8, and is been shown for comparison purposes only. Our simulation reveals that νg is a critical parameter that can modulate the contribution of astrocyte-induced synaptic plasticity.
Fig. 14.
Plasticity of Neurotransmitter release probability in response to a varying rate of IP3 production by pre-synaptic group I mGluRs. Neurotransmitter release probability is shown for IP3 production rates of 0.050 μM per second (a), 0.062 μM per second (b), 0.1 μM per second (c), and 0.2 μM per second (d). Please note the change in y-axis bounds
Conclusions and future directions
There is a debate regarding the mechanism and calcium dependence of gliotransmission and the role of gliotransmission in synaptic plasticity. Together they imply that the effect of astrocytic calcium on synaptic plasticity is a controversial issue. Here we have put together a number of phenomenological and biophysical models for the processes shown in Fig. 2 to simulate the effects on synaptic strength with and without astrocytic Ca2 + . From a computational modeling point of view, this is equivalent to controlling the effect of Ca2 + in astrocytes by genetic engineering [15] and by a calcium clamp [2] in order to study the effects of astrocytic Ca2 + on synaptic plasticity. A better understanding, through a variety of approaches, of calcium dynamics, signaling and gliotransmitter release is necessary for settling the aforementioned debate [80]. Here we have taken a computational approach and concluded that the astrocytic Ca2 + does contribute to synaptic augmentation at the time scale of the order of seconds, for the given mathematical framework.
Here we presented a mathematical model that studies the effect of an astrocyte on the hippocampal CA3-CA1 synaptic strength. It is found that given the pathway shown in Fig. 2b, the astrocyte plays a significant role in modulating the synaptic information transfer. It might be possible that under physiological conditions neurons exhibit the two types of information processing: i) astrocyte-independent ii) astrocyte-dependent. A recent study performed by Di Castro et al. [81] confirms that astrocytes are activated under physiological stimulation of neighboring synapses. It is suggested that neurons process information usually in an astrocyte-independent manner unless there is a need to modify synaptic efficacy according to various plasticity events taking place in the hippocampus [3, 22, 82].
Using our computational model, we identified two important parameters (readily releasable pool size of SLMVs and maximum rate of IP3 production), which affect astrocyte-mediated synaptic potentiation at a single CA3-CA1 synapse. Our simulations reveal a possible biological condition under which astrocyte Ca2 + oscillations do not contribute to synaptic potentiation (see Fig. 13a). It was found that the maximum rate of IP3 production (νg) was a more potent modulator (of the two parameters) of astrocyte-mediated synaptic potentiation. Using (22) and performing simple algebraic calculations we could predict the mGluR density on the relevant surface of the CA3 pyramidal neuron bouton, which is experimentally unknown at the CA3-CA1 synapse but is in agreement with experiments from other synapses [78, 79].
It should be pointed out that it is not possible to conclude that the an astrocyte induces a particular type of synaptic plasticity (e.g., augmentation) using only a temporal model, like the one proposed here, as synaptic plasticity depends on several spatial constraints. As a future direction, it is proposed to develop a spatio-temporal model to study the effects of spatial constraints, like release sites, Ca2 + sources etc., on modulation of synaptic activity. It is also known that a single hippocampal astrocyte in the CA1 region ensheaths around thousands of synapses [83]. Thus, it is possible for a single astrocyte to modulate signal processing at thousands of synapses simultaneously. It has also been shown experimentally that astrocytes help to synchronize firings of neurons in the CA1 region [66]. Hence, it is worth studying the effects of astrocytes over networks of neurons. Porto-Pazos et al. [84] recently performed a study where they highlighted the importance of artificial astrocytes in modulating an artificial neural network.
The present mathematical model is quite adaptable and can be easily extended to study longer and other forms of synaptic plasticity [85]. Another advantage of this model is that it can be extended to astrocytic micro-domains, where it is difficult to experimentally manipulate calcium fluctuations. Simply increasing intracellular calcium is not sufficient for gliotransmitter release, as evident from conflicting results [2, 15, 69]. If calcium is required for transmitter release, then it may need to occur in specific micro-domains [69], which has been overlooked and needs examination using similar computational modeling approaches among others.
Electronic Supplementary Material
Acknowledgements
The work has been supported by the Department of Science and Technology, Government of India, grant no. SR/CSI/08/2009. Helpful suggestions from Vladimir Parpura are thankfully acknowledged.
Contributor Information
Shivendra G. Tewari, Email: shivendra.tewari@gmail.com
Kaushik Kumar Majumdar, Email: kmajumdar@isibang.ac.in.
References
- 1.Perea G, Araque A.Astrocytes potentiate transmitter release at single hippocampal synapses Science 20073171083–1086.2007Sci...317.1083P 10.1126/science.1144640 [DOI] [PubMed] [Google Scholar]
- 2.Henneberger C, Papouin T, Oliet SHR, Rusakov SA.Long-term potentiation depends on release of D-serine from astrocytes Nature 2010463232–236.2010Natur.463..232H 10.1038/nature08673 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Navarrete M, Perea G, Sevilla DF, Gomez-Gonzalo M, Nunez A, Martin ED, Araque A. Astrocytes mediate in vivo cholinergic-induced synaptic plasticity. PLoS Biol. 2012;10:1001259. doi: 10.1371/journal.pbio.1001259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lynch MA. Long-term potentiation and memory. Physiol. Rev. 2004;84:87–135. doi: 10.1152/physrev.00014.2003. [DOI] [PubMed] [Google Scholar]
- 5.Ramón y Cajal S. Histologie du Système Nerveux de l’Homme et des Vertébrés. Paris: Maloine; 1911. [Google Scholar]
- 6.Hebb DO. The Organization of Behavior. New York: Wiley; 1949. [Google Scholar]
- 7.Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu. Rev. Physiol. 2002;64:355–405. doi: 10.1146/annurev.physiol.64.092501.114547. [DOI] [PubMed] [Google Scholar]
- 8.Perea G, Araque A. Communication between astrocytes and neurons: a complex language. J Physiol.-Paris. 2002;96:199–207. doi: 10.1016/S0928-4257(02)00007-4. [DOI] [PubMed] [Google Scholar]
- 9.Araque A, Parpura V, Sanzgiri RP, Haydon PG. Tripartite synapses: glia, the unacknowledged partner. Trends Neurosci. 1999;22:208–215. doi: 10.1016/S0166-2236(98)01349-6. [DOI] [PubMed] [Google Scholar]
- 10.Newman EA. New roles for astrocytes: regulation of synaptic transmission. Trends Neurosci. 2003;26(10):536–542. doi: 10.1016/S0166-2236(03)00237-6. [DOI] [PubMed] [Google Scholar]
- 11.Nadkarni S, Jung P.Spontaneous oscillations in dressed neurons: a mechanism for epilepsy? Phys. Rev. Lett. 200391262681012003PhRvL..91z8101N 10.1103/PhysRevLett.91.268101 [DOI] [PubMed] [Google Scholar]
- 12.Nadkarni S, Jung P, Levine H.Astrocytes optimize the synaptic transmission of information PLoS Comput. Biol. 2008451–11.2407493 10.1371/journal.pcbi.1000088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Volman V, Ben-Jacob E, Levine H.The astrocyte as a gatekeeper of synaptic information transfer Neural Comput. 200719303–326.22783911121.92018 10.1162/neco.2007.19.2.303 [DOI] [PubMed] [Google Scholar]
- 14.Fellin T. Communication between neurons and astrocytes: relevance to modulation of synaptic and network activity. J. Neurochem. 2009;108:533–544. doi: 10.1111/j.1471-4159.2008.05830.x. [DOI] [PubMed] [Google Scholar]
- 15.Agulhon C, Fiacco TA, McCarthy KD.Hippocampal short- and long-term plasticity are not modulated by astrocyte Ca2 + signaling Science 20103271250–1254.2010Sci...327.1250A 10.1126/science.1184821 [DOI] [PubMed] [Google Scholar]
- 16.Andersson EH. Astrocytes impose postburst depression of release probability at hippocampal glutamate synapses. J. Neurosci. 2010;30(16):5776–5780. doi: 10.1523/JNEUROSCI.3957-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Haydon PG. Glia: listening and talking to the synapse. Nature Rev. Neurosci. 2001;2:185–193. doi: 10.1038/35058528. [DOI] [PubMed] [Google Scholar]
- 18.Vernadakis A. Glia-neuron intercommunications and synaptic plasticity. Prog. Neurobiol. 1996;49:185–214. doi: 10.1016/S0301-0082(96)00012-3. [DOI] [PubMed] [Google Scholar]
- 19.Yang Y, Ge W, Chen Y, Zhang Z, Shen W, Wu C, Poo M, Duan S.Contribution of astrocytes to hippocampal long-term potentiation through release of D-serine Proc. Natl. Acad. Sci. USA 20031002515194–15199.2003PNAS..10015194Y 10.1073/pnas.2431073100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Porter JT, McCarthy KD. Hippocampal astrocytes in situ respond to glutamate released from synaptic terminals. J. Neurosci. 1996;16:5073–5081. doi: 10.1523/JNEUROSCI.16-16-05073.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Parpura V, Basarsky TA, Liu F, Jeftinija K, Jeftinija S, Haydon PG.Glutamate mediated astrocyte-neuron signaling Nature 1994369744–747.1994Natur.369..744P 10.1038/369744a0 [DOI] [PubMed] [Google Scholar]
- 22.Navarrete M, Araque A. Endocannabinoids potentiate synaptic transmission through stimulation of astrocytes. Neuron. 2010;68:113–126. doi: 10.1016/j.neuron.2010.08.043. [DOI] [PubMed] [Google Scholar]
- 23.Wu L, Borst JGG. The reduced release probability of releasable vesicles during recovery from short-term synaptic depression. Neuron. 1999;23(4):821–832. doi: 10.1016/S0896-6273(01)80039-8. [DOI] [PubMed] [Google Scholar]
- 24.Koch C. Biophysics of Computation: Information Processing in Single Neurons. New York: Oxford University Press; 1999. [Google Scholar]
- 25.Fisher SA, Fischer TM, Carew TJ. Multiple overlapping processes underlying short-term synaptic enhancement. Trends Neurosci. 1997;20:170–177. doi: 10.1016/S0166-2236(96)01001-6. [DOI] [PubMed] [Google Scholar]
- 26.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Erler F, Meyer-Hermann M, Soff G. A quantitative model for pre-synaptic free Ca2 + dynamics during different stimulation protocols. Neurocomputing. 2004;61:169–191. doi: 10.1016/j.neucom.2003.11.002. [DOI] [Google Scholar]
- 28.Li Y-X, Rinzel J. Equations for IP3 receptor mediated Ca2 + oscillations derived from a detailed kinetic model: A Hodgkin-Huxley like formulism. J. Theor. Biol. 1994;166:461–473. doi: 10.1006/jtbi.1994.1041. [DOI] [PubMed] [Google Scholar]
- 29.Tsodyks M, Markram H.The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability Proc. Natl. Acad. Sci. USA 199794719–723.1997PNAS...94..719T 10.1073/pnas.94.2.719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pittà M, Goldberg M, Volman V, Berry H, Ben-Jacob E. Glutamate regulation of calcium and IP3 oscillating and pulsating dynamics in astrocytes. J. Biol. Phys. 2009;35:383–411. doi: 10.1007/s10867-009-9155-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Destexhe A, Mainen ZF, Sejnowski TJ. Kinetic models of synaptic transmission. In: Koch C, Segev I, editors. Methods in Neuronal Modeling. Cambridge: MIT Press; 1998. pp. 1–25. [Google Scholar]
- 32.Bertram R, Sherman A, Stanley EF. Single-domain/bound calcium hypothesis of transmitter release and facilitation. J. Neurophysiol. 1996;75:1919–1931. doi: 10.1152/jn.1996.75.5.1919. [DOI] [PubMed] [Google Scholar]
- 33.Malarkey EB, Parpura V. Temporal characteristics of vesicular fusion in astrocytes: Examination of synaptobrevin 2-laden vesicles at single vesicle resolution. J. Physiol. 2011;589:4271–4300. doi: 10.1113/jphysiol.2011.210435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lytton WW, Sejnowski TJ. Simulations of cortical pyramidal neurons synchronized by inhibitory interneurons. J. Neurophysiol. 1991;66:1059–1079. doi: 10.1152/jn.1991.66.3.1059. [DOI] [PubMed] [Google Scholar]
- 35.Naundorf B, Wolf F, Volgushev M.Unique features of action potential initiation in cortical neurons Nature 20064401060–1063.2006Natur.440.1060N 10.1038/nature04610 [DOI] [PubMed] [Google Scholar]
- 36.Bollmann JH, Sakmann B, Borst JGG.Calcium sensitivity of glutamate release in a calyx-type terminal Science 2000289953–957.2000Sci...289..953B 10.1126/science.289.5481.953 [DOI] [PubMed] [Google Scholar]
- 37.Schneggenburger R, Neher E.Intracellular calcium dependence of transmitter release rates at a fast central synapse Nature 2000406889–893.2000Natur.406..889S 10.1038/35022702 [DOI] [PubMed] [Google Scholar]
- 38.Mazzanti M, Haydon PG. Astrocytes selectively enhance n-type calcium current in hippocampal neurons. Glia. 2003;41:128–136. doi: 10.1002/glia.10135. [DOI] [PubMed] [Google Scholar]
- 39.Weber AM, Wong FK, Tufford AR, Schlichter LC, Matveev V, Stanley EF. N-type Ca2 + channels carry the largest current: implications for nanodomains and transmitter release. Nat. Neurosci. 2010;13:1348–1350. doi: 10.1038/nn.2657. [DOI] [PubMed] [Google Scholar]
- 40.Ishikawa T, Kaneko M, Shin H-P, Takahashi T. Pre-synaptic N-type and P/Q-type Ca2 + channels mediating synaptic transmission at the calyx of Held of mice. J. Physiol. 2005;568:199–209. doi: 10.1113/jphysiol.2005.089912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Keener J, Sneyd J. Mathematical Physiology. New York: Springer–Verlag; 1998. [Google Scholar]
- 42.Jensen TP, Filoteo AG, Knopfel T, Empson RM. Pre-synaptic plasma membrane Ca2 + ATPase isoform 2a regulates excitatory synaptic transmission in rat hippocampal CA3. J. Physiol. 2007;579:85–99. doi: 10.1113/jphysiol.2006.123901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Blackwell, K.T.: Modeling calcium concentration and biochemical reactions. In: Bower, J.M., Beeman, D. (eds.) Special Issue on Realistic Neural Modeling - Wam-Bamm ’05 Tutorials. Brains, Minds and Media, vol. 1, bmm224. (urn:nbn:de:0009-3-2245) (2005)
- 44.Emptage NJ, Reid CA, Fine A. Calcium stores in hippocampal synaptic boutons mediate short-term plasticity, store-operated Ca2 + entry, and spontaneous transmitter release. Neuron. 2001;29:197–208. doi: 10.1016/S0896-6273(01)00190-8. [DOI] [PubMed] [Google Scholar]
- 45.Sneyd J, Falcke M. Models of the inositol trisphosphate receptor. Prog. Biophys. Mol. Bio. 2005;89:207–245. doi: 10.1016/j.pbiomolbio.2004.11.001. [DOI] [PubMed] [Google Scholar]
- 46.Nadkarni S, Jung P.Modeling synaptic transmission of the tripartite synapse Phys. Biol. 200741–9.2007PhBio...4....1N 10.1088/1478-3975/4/1/001 [DOI] [PubMed] [Google Scholar]
- 47.Wang L-Y, Fedchyshyn MJ, Yang Y-M.Action potential evoked transmitter release in central synapses: insights from the developing calyx of Held Mol. Brain. 200921–11.1165.31004 10.1186/1756-6606-2-36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Neher E. Vesicle pools and Ca2 + micro-domains: new tools for understanding their roles in neurotransmitter release. Neuron. 1998;20:389–399. doi: 10.1016/S0896-6273(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 49.Danbolt NC. Glutamate uptake. Prog. Neurobiol. 2001;65:1–105. doi: 10.1016/S0301-0082(00)00067-8. [DOI] [PubMed] [Google Scholar]
- 50.Nikonenko AG, Skibo GG. Age-related changes in synaptic vesicle pools of axo-dendritic synapses on hippocampal Ca2 + pyramidal neurons in mice. Neurophysiology. 2006;38:407–411. [Google Scholar]
- 51.Fall C, Marland E, Wagner J, Tyson J. Computational Cell Biology. New York: Springer-Verlag; 2002. [Google Scholar]
- 52.Kang J, Jiang L, Goldman SA, Nedergaard M. Astrocyte-mediated potentiation of inhibitory synaptic transmission. Nat. Neuro. 1998;1:683–692. doi: 10.1038/3684. [DOI] [PubMed] [Google Scholar]
- 53.Dobrunz LE, Huang EP, Stevens CF.Very short-term plasticity in hippocampal synapses Proc. Natl. Acad. Sci. USA 19979414843–14847.1997PNAS...9414843D 10.1073/pnas.94.26.14843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Montana V, Malarkey EB, Verderio C, Matteoli M, Parpura V. Vesicular transmitter release from astrocytes. Glia. 2006;54:700–715. doi: 10.1002/glia.20367. [DOI] [PubMed] [Google Scholar]
- 55.Franks KM, Bartol TM, Sejnowski TJ.A Monte Carlo model reveals independent signaling at central glutamatergic synapses Biophys. J. 2002832333–2348.2002BpJ....83.2333F 10.1016/S0006-3495(02)75248-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Clements JD. Transmitter timecourse in the synaptic cleft: its role in synaptic function. Trends Neurosci. 1996;19:163–171. doi: 10.1016/S0166-2236(96)10024-2. [DOI] [PubMed] [Google Scholar]
- 57.Höfer T, Venance L, Giaume C. Control and plasticity of intercellular calcium waves in astrocytes: a modeling approach. J. Neurosci. 2002;22:4850–4859. doi: 10.1523/JNEUROSCI.22-12-04850.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Suzuki Y, Moriyoshi E, Tsuchiya D, Jingami H. Negative cooperativity of glutamate binding in the dimeric metabotropic glutamate receptor subtype I. J. Biol. Chem. 2004;279:35526–35534. doi: 10.1074/jbc.M404831200. [DOI] [PubMed] [Google Scholar]
- 59.Holtzclaw LA, Pandhit S, Bare DJ, Mignery GA, Russell JT. Astrocytes in adult rat brain express type 2 inositol 1,4,5-trisphosphate receptors. Glia. 2002;39:69–84. doi: 10.1002/glia.10085. [DOI] [PubMed] [Google Scholar]
- 60.Shuai J-W, Jung P.Stochastic properties of Ca2 + release of inositol 1,4,5-Triphosphate receptor clusters Biophys. J. 20028387–97.2002BpJ....83...87S 10.1016/S0006-3495(02)75151-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Coffey WT, Kalmykov YP, Waldron JT. The Langevin Equation: With Applications to Stochastic Problems in Physics, Chemistry and Electrical Engineering. 2. Singapore: World Scientific Publishing; 2005. [Google Scholar]
- 62.Bezzi P, Gundersen V, Galbate JL, Seifert G, Steinhauser C, Pilati E, Volterra A. Astrocytes contain a vesicular compartment that is competent for regulated exocytosis of glutamate. Nat. Neurosci. 2004;7:613–620. doi: 10.1038/nn1246. [DOI] [PubMed] [Google Scholar]
- 63.Bowser DN, Khakh BS.Two forms of single-vesicle astrocyte exocytosis imaged with total internal reflection fluorescence microscopy Proc. Natl. Acad. Sci. USA 20071044212–4217.2007PNAS..104.4212B 10.1073/pnas.0607625104 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Marchaland J, Cali C, Voglmaier SM, Li H, Regazzi R, Edwards RH, Bezzi P. Fast subplasma membrane Ca2 + transients control exo-endocytosis of synaptic-like microvesicles in astrocytes. J. Neurosci. 2008;28:9122–9132. doi: 10.1523/JNEUROSCI.0040-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bergersen LH, Gundersen V. Morphological evidence for vesicular glutamate release from astrocytes. Neuroscience. 2009;158:260–265. doi: 10.1016/j.neuroscience.2008.03.074. [DOI] [PubMed] [Google Scholar]
- 66.Carmignoto G, Fellin T. Glutamate release from astrocytes as a non-synaptic mechanism for neuronal synchronization in the hippocampus. J. Physiol. 2006;99:98–102. doi: 10.1016/j.jphysparis.2005.12.008. [DOI] [PubMed] [Google Scholar]
- 67.Parpura V, Haydon PG.Physiological astrocytic calcium levels stimulate glutamate release to modulate adjacent neurons Proc. Natl. Acad. Sci. USA 2000978629–8634.2000PNAS...97.8629P 10.1073/pnas.97.15.8629 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Fiacco TA, McCarthy KD. Intracellular astrocyte calcium waves in situ increase the frequency of spontaneous AMPA receptor currents in CA1 pyramidal neurons. J. Neurosci. 2004;24:722–732. doi: 10.1523/JNEUROSCI.2859-03.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Wenker I. An active role for astrocytes in synaptic plasticity? J. Neurophysiol. 2010;104:1216–1218. doi: 10.1152/jn.00429.2010. [DOI] [PubMed] [Google Scholar]
- 70.Verkhratsky, V., Butt, V.: Glial Neurobiology: A Textbook. John Wiley & Sons Ltd (2007)
- 71.Parpura V, Zorec R. Gliotransmission: Exocytotic release from astrocytes. Brain Res. Rev. 2010;63:83–92. doi: 10.1016/j.brainresrev.2009.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Dumitriu D, Hao J, Hara Y, Kaufmann J, Janssen WGM, Lou W, Rapp PR, Morrison JH. Selective changes in thin spine density and morphology in monkey prefrontal cortex correlate with aging-related cognitive impairment. J. Neurosci. 2010;30:7507–7515. doi: 10.1523/JNEUROSCI.6410-09.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Chen S, Diamond JS. Synaptically released glutamate activates extrasynaptic NMDA receptors on cells in the ganglion cell layer of rat retina. J. Neurosci. 2002;22:2165–2173. doi: 10.1523/JNEUROSCI.22-06-02165.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Bliss TVP, Collingridge GL.A synaptic model of memory: long-term potentiation in the hippocampus Nature 199336131–39.1993Natur.361...31B 10.1038/361031a0 [DOI] [PubMed] [Google Scholar]
- 75.Malenka RC, Bear MF. LTP and LTD: an embarrassment of riches. Neuron. 2004;44:5–21. doi: 10.1016/j.neuron.2004.09.012. [DOI] [PubMed] [Google Scholar]
- 76.Fox RF.Stochastic versions of the Hodgkin–Huxley equations Biophys. J. 1997722068–2074.1997BpJ....72.2068F 10.1016/S0006-3495(97)78850-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Koester HJ, Sakmann B. Calcium dynamics associated with action potentials in single nerve terminals of pyramidal cells in layer 2/3 of the young rat neocortex. J. Physiol. 2000;529:625–646. doi: 10.1111/j.1469-7793.2000.00625.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Holmes WR.Modeling the effect of glutamate diffusion and uptake on NMDA and non-NMDA receptor saturation Biophys. J. 1995691734–1747.1995BpJ....69.1734H 10.1016/S0006-3495(95)80043-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Nusser Z, Roberts ZDB, Baude A, Richards JG, Somogyi P. Relative densities of synaptic and extrasynaptic GABAA receptors on cerebellar granule cells as determined by a quantitative immunogold method. J. Neurosci. 1995;15:2948–2960. doi: 10.1523/JNEUROSCI.15-04-02948.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Ben Achour S, Pont-Lezica L, Bechade C, Pascual O. Is astrocyte calcium signaling relevant for synaptic plasticity? Neuron Glia Biol. 2010;6(3):147–155. doi: 10.1017/S1740925X10000207. [DOI] [PubMed] [Google Scholar]
- 81.Castro MA, Chuquet J, Liaudet N, Bhaukaurally K, Santello M, Bouvier D, Tiret P, Volterra A. Local Ca2 + detection and modulation of synaptic release by astrocytes. Nat. Neurosci. 2011;14:1276–1284. doi: 10.1038/nn.2929. [DOI] [PubMed] [Google Scholar]
- 82.Panatier A, Vallee J, Haber M, Murai KK, Lacaille J-C, Robitaille R. Astrocytes are endogenous regulators of basal transmission at central synapses. Cell. 2011;146:785–798. doi: 10.1016/j.cell.2011.07.022. [DOI] [PubMed] [Google Scholar]
- 83.Schipke, C.G., Peters, O.: Glial influence on synaptic transmission. In: Malenka, R.C. (ed.) Intercellular Communication in the Nervous System, pp. 112–120. Elsevier (2009)
- 84.Porto-Pazos AB, Veiguela N, Mesejo P, Navarrete M, Alvarellos A, Ibanez O, Pazos A, Araque A. Artificial astrocytes improve neural network performance. PLoS ONE. 2012;6:19109. doi: 10.1371/journal.pone.0019109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Tewari S, Majumdar K.A mathematical model for astrocyte mediated LTP at single hippocampal synapses J. Comput. Neurosci. 2012. 06067703 [DOI] [PubMed] [Google Scholar]
- 86.Jafri MS, Keizer J.On the roles of Ca2 + diffusion, Ca2 + buffers, and the endoplasmic reticulum in IP3-induced Ca2 + waves Biophys. J. 1995692139–2153.1995BpJ....69.2139J 10.1016/S0006-3495(95)80088-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Wang SS-H, Alousi AA, Thompson SH. The lifetime of inositol 1,4,5-triphosphate in single cells. J. Gen. Physiol. 1995;105:149–171. doi: 10.1085/jgp.105.1.149. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.