Label-Free Imaging of Membrane Potential Using Membrane Electromotility

Abstract

Electrical activity may cause observable changes in a cell's structure in the absence of exogenous reporter molecules. In this work, we report a low-coherence interferometric microscopy technique that can detect an optical signal correlated with the membrane potential changes in individual mammalian cells without exogenous labels. By measuring milliradian-scale phase shifts in the transmitted light, we can detect changes in the cells' membrane potential. We find that the observed optical signals are due to membrane electromotility, which causes the cells to deform in response to the membrane potential changes. We demonstrate wide-field imaging of the propagation of electrical stimuli in gap-junction-coupled cell networks. Membrane electromotility-induced cell deformation may be useful as a reporter of electrical activity.

Introduction

The electrical activity of a cell can modify an optical wave probing the cell in its amplitude, phase, and polarization through endogenous mechanisms (1). This fast intrinsic optical signal (FIOS) can be used as a reporter of changes in the membrane potential, potentially enabling label-free imaging with the advantage of simple sample preparation, low phototoxicity, and no photobleaching (2). Furthermore, knowledge about the biophysical mechanisms by which the probe light is altered by a cell's electrical activity may aid in the design of voltage-sensing probes, such as second-harmonic-generation probes (3,4).

Label-free imaging of an individual cell's electrical activity has been performed most successfully in invertebrate cells. Investigators have observed changes in the membrane potential of unstained Aplysia neurons with high signal/noise ratio and subcellular resolution using dark-field microscopy and angle-resolved light scattering (5). Optical devices based on interferometry (6), polarimetry (7,8), and light scattering (5,8) have also been used to observe optical signatures of electrical activity from various invertebrate preparations in vitro and in situ. However, to the best of our knowledge, the FIOS from single mammalian cells has never been detected. In mammalian samples, optical signals have been obtained only from aggregations of cells or nerve terminals. For example, light-scattering signals from mouse nerve terminals (9,10), rat brainstem (11), rat cortex (12,13), and cat hippocampus tissue (14) have been correlated with electrical stimulation. Also, several groups have reported (with some controversy (15–17)) the use of near-infrared spectroscopy to detect fast changes in light scattering in correlation with the brain activity of human subjects (18–20). Mammalian cells are smaller, optically transparent, and scatter significantly less light compared with invertebrate nerves and neurons, which explains in part why mammalian single-cell FIOS has been elusive up to now. Moreover, further advancements in detection techniques have been limited mainly due to the lack of information about the structural basis of the optical signals. Various nonoptical or contact methods have been used to investigate the mechanical deformation that accompanies the action potentials in squid giant axon, nerve fibers, and nerve terminals (21–25). In particular, Kim et al. (21) showed that the light-scattering signal from a spiking nerve terminal has characteristics similar to the thickness change measured by high-bandwidth dynamic atomic force microscopy, and hence demonstrated a close relation between the intrinsic optical signals and structural changes. However, most existing FIOS techniques rely on assumptions about the refractive index and shape of cells to test models of a cell's structural changes against experimental data, such as light scattering or optical retardation (5,26). For mammalian cells, which are more complex in shape, it is difficult to produce an accurate model for each cell. In fact, a microscopy-based approach that directly measures the shape of cell would be more suitable.

In this report, we present an approach that successfully detects intrinsic optical signatures associated with changes in the membrane potential from single, nonneuronal mammalian cells. The key instrument that enables us to observe FIOS of single mammalian cells is a low-noise quantitative phase microscope, low-coherence diffraction phase microscope (LCDPM), which combines optical interferometry with microscopy (27). Previous studies used optical interferometry to detect FIOS from invertebrate samples (6,28). In those studies, changes in the optical phase of light reflected from a sample's surface provided a highly sensitive measure of changes in height resulting from the cell's electrical activity. In contrast, LCDPM measures the light that is transmitted through the sample at the image plane (Fig. S1 in the Supporting Material). Our imaging-based approach makes it possible to observe the spatial organization of the optical signals from single cells, and to interpret the signal without having to rely on questionable assumptions about the cell's shape and refractive index.

LCDPM measures the retardation of the optical phase of the light that traverses a monolayer of cells using light interferometry. When an incident plane wave passes through the sample, the wave front is delayed by an amount proportional to the cell's thickness and relative refractive index. To measure the phase retardation, φ, a planar reference field is used to interfere with the light field that has traversed the sample. LCDPM employs a unique design in which the sample field and the reference field traverse the same optical components (Fig. S4) (29). This is achieved by creating the reference field from the sample field itself. First, the sample field is split into two closely directed beams with the use of a diffractive beam splitter. Then one beam is focused through a pinhole to render it into a Gaussian wave. This reference beam is recombined with the other beam that carries the sample information, creating the interference pattern on the camera. Because of the common path design, the optical path-length difference between the sample and the reference field can be smaller than the coherence length of a low-coherence light source, enabling low-coherence interferometry. The use of a low-coherence light source is advantageous because it reduces the speckle noise that often plagues laser interference microscopes (30,31).

Fig. 1 A shows the map of optical phase retardation in the light passing through a HEK 293 cell measured by LCDPM. The optical phase retardation is proportional to the integral of the refractive index along the axis of light propagation, which approximately represents the height of the cell (see Supporting Material). The change of optical phase carries information about membrane-potential-dependent changes of the cell. We observe a voltage-dependent optical phase signal that involves the deformation of the cytoskeleton but is not caused by cell swelling. We find that the signal is likely caused by isovolumetric cell deformation through membrane electromotility, a direct coupling between the membrane potential and membrane tension. The anticorrelation and complexity of the spatial structure of the optical signals explain why it has been difficult to detect FIOS with low-spatial-resolution techniques. Our technique can readily be used to observe a large number of cells simultaneously, as we demonstrate by wide-field imaging of a gap-junction-coupled network of cells.

Figure 1.

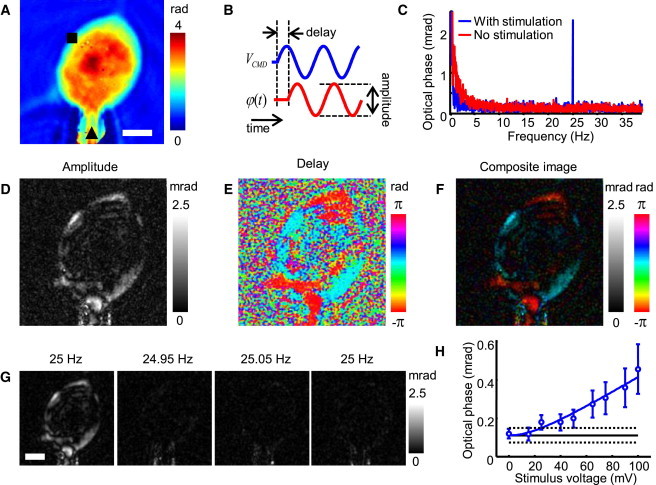
Oscillating membrane potential induces an oscillation in the optical phase of the probing light at the same frequency. (Color online) (A) Quantitative phase map of a HEK 293 cell. The patch-clamping pipette is marked with a black triangle. Color bar indicates phase in radians. Scale bar = 10 μm. (B) Diagram defining the time delay and amplitude of the optical phase modulation φ(t) to the electrical stimulation V_CMD. (C) Quantitative spectrum of the phase fluctuations from the area marked by a black square in panel A with (blue) and without (red) electrical stimulation at 25 Hz. (D) 2D map of the amplitude of the frequency component of the optical phase fluctuations at the stimulation frequency (25 Hz). (E) Delay of the signals in panel D relative to the electrical stimulation V_CMD. (F) Composite image of the amplitude (D) and delay (E) of the optical phase fluctuations. (G) 2D amplitude map of various frequency components of the optical phase fluctuations: at the stimulation frequency (25 Hz) and at frequencies just below (24.95 Hz) and above (25.05 Hz) the stimulation frequency while the cell is electrically stimulated at 25 Hz, and at 25 Hz while the electrical stimulation is not applied. (D–G) Grayscale color bars indicate the amplitude of the fluctuation in mrad. Hue color bars show the delay of the fluctuation relative to the electrical stimulation in radians. (H) Optical phase signal versus the amplitude of the electrical stimulus. The y axis is the amplitude of the optical phase signals averaged over a 4.7 μm² area. Open circles: experimental data. Error bars drawn at one standard deviation above and below the mean. The solid line in blue is a fit from the model (see text). The solid line in black is the measured background noise level, with the 2-σ range marked by the dotted black lines.

Materials and Methods

Quantitative phase microscopy

Each quantitative phase image was calculated from a single interferogram by means of a spatial phase modulation algorithm as described previously (29). Images were typically acquired at a frame rate of 500 frames/s for 10 s. Intensity images were first acquired and stored in the computer, and then processed into quantitative phase images. The quantitative phase images were Fourier transformed from the time domain to the frequency domain to select the relevant frequency component. The optical resolution was 0.89 μm and the total magnification was 178×. The light source had a center wavelength of 800 nm with 40 nm bandwidth. Details about the microscope are provided in the Supporting Material.

Cell culture and electrophysiology

HEK 293 cells were cultured in Dulbecco's modified Eagle's medium supplemented with 5% fetal bovine serum and 1% penicillin/streptomycin. Cells were plated on a poly-L-lysine-coated coverglass 1 day in advance. The optical and electrophysiology experiments were performed in recording medium consisting of (in mM) NaCl 167, KCl 5.6, HEPES 11, CaCl₂ 0.6, and MgCl₂ 0.6. The pipette solution for the whole-cell patch clamping consisted of (in mM) KCl 145, EGTA 10, and HEPES 5 (32). Patch pipettes had a bath resistance of ∼4 MΩ. The sine wave voltage stimulus had a 200 mV peak-to-peak amplitude in addition to a −60 mV holding potential, unless otherwise noted. The electrical coupling between gap-junction-coupled cells was measured in double patch-clamping experiments in which two cells were simultaneously whole-cell patch clamped, or one cell was whole-cell patch clamped with two electrode pipettes simultaneously. One patch pipette was voltage clamped to deliver the bipolar voltage pulse, and the other pipette was current clamped to measure the propagation of the pulse. Cells were not electrically coupled right after plating, because gap junctions were lost during the process of cell trypsinization. The coupling strength of adjacent cell pairs increased with the incubation time and reached a maximum in ∼36 h.

Cytochalasin D treatment

To apply cytochalasin D (CD), we first diluted a CD-DMSO mixture with culture medium and then added it to the cell culture. The final concentration of CD was 0.01 mg/mL (20 μmol), and the final concentration of DMSO was 0.4 μL/mL. Cells were incubated at 37° for 30 min in the CD-containing media before measurements were obtained. Control cells were maintained in the normal culture media. Both experiments with CD-treated cells and experiments with control cells were performed in the normal recording media, which does not contain CD.

Results

Optical correlates of the membrane-potential changes

We observed changes in optical phase retardation while the membrane potential of the cell was driven with a 100 mV peak amplitude sine wave through whole-cell patch clamping. We found that the potential-dependent phase changes were ∼3 orders of magnitude smaller than the cell's optical phase retardation. To separate these small changes in phase from background phase fluctuation noise, we drove the membrane potential at a single frequency f (Fig. 1 B). Fig. 1 C shows the frequency spectrum of the optical phase retardation acquired at the area marked by the black square in Fig. 1 A. The sharp peak at the stimulation frequency corresponds to the electrically induced optical phase modulations, which are much larger than the instrumental noise (white noise) and are well separated from the low-frequency spontaneous fluctuation of the cell. The absolute value $\left|\phi \right|\left(f\right)$ and the complex argument $\angle \phi \left(f\right)$ of the peak at the stimulation frequency correspond to the amplitude and the time lag of the electrically induced optical phase modulation as shown in Fig. 1 B. Therefore, the optical phase modulation at the stimulation frequency will be called the optical phase signal throughout this work. The amplitudes measured from the cell in Fig. 1 A are displayed in Fig. 1 D, and the associated time lags are shown in Fig. 1 E. The two quantities are shown together in the composite image of Fig. 1 F, which indicates the amplitude of the optical phase signal by brightness and the amount of time delay by hue.

To verify that the observed fluctuations of optical phase retardations are actually induced by the electrical stimulation of the cell, we displayed images at frequencies 0.05 Hz below and 0.05 Hz above the frequency of the stimulating electric field, and we also recorded an image at the same frequency with the stimulating field turned off. In each case, as shown in Fig. 1 G, the signal disappeared. Also, the amplitude of the optical phase signal increased with the amplitude of the stimulus (Fig. 1 H). Because the background noise is constant with frequency in the relevant frequency range and has a random time lag, the optical phase signal that would otherwise be proportional to the stimulus amplitude is expressed by $\left|\phi \right|\left(f\right)=\sqrt{a\times V_{CMD}^2+n^2}$, where n is the average noise, V_CMD is the amplitude of the electrical stimulation, and a is the fitting coefficient. The observed data are well fitted by this model.

Mechanism of electrical-to-optical coupling in the cell

How does electrical stimulation of a cell generate changes in optical phase such as those shown in Fig. 1? Three consequences of cellular electrical activity have been proposed as the origin of FIOS. First, the cell swells because water transport accompanies the transmembrane ion current (21). Second, the physical state of the plasma membrane is altered by the transmembrane electric field: the thickness of the cell membrane changes through the electrostriction effect (33) and the membrane birefringence changes through the interaction with membrane dipole structures (5). Third, the cell deforms in a potential-dependent manner due to direct coupling between membrane potential and membrane tension. This effect is called membrane electromotility (MEM) (32). Each of these biophysical phenomena changes the refractive index or the thickness of the cell in a different way, as illustrated in Fig. 2 A, and can be detected using LCDPM. In the case of cell swelling, both the refractive index and the thickness of the cell change. The second model predicts optical and physical changes confined to the plasma membrane. The optical phase signal associated with MEM would be solely due to the shape change and not from the refractive index change.

Figure 2.

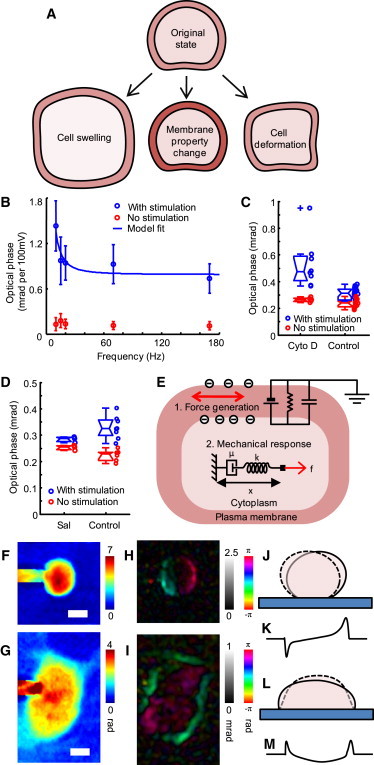
Mechanism of electrical-to-optical coupling. (Color online) (A) Changes in the membrane potential may give rise to changes in the cytoplasm refractive index, membrane refractive index, membrane thickness, or cell shape. All of these changes can be detected by changes in the optical phase of light transmitted through the cell. (B) The amplitude of the optical phase signal depends on the frequency of the electrical stimulus. Circles and error bars are the average and the standard deviation of the amplitude of optical phase fluctuations in the presence (blue) and absence (red) of electrical stimulus. The solid line is the fit from the model (shown in Fig. 2E; see text for details). (C) CD, an actin polymerization inhibitor, magnifies the amplitude of the optical phase signals. Blue circles are the amplitude of optical phase signals driven by 15–25 Hz electrical stimulation, averaged over the entire area of each cell. Red circles are the optical phase fluctuation in the absence of the stimulation. The difference between the two groups is statistically significant (p < 10⁻⁴). N = 5 for CD-treated cells, and N = 10 control cells. (D) Effect of salicylate ions. Blue circles are the amplitude of optical phase signals averaged over the cell area when the cell is electrically stimulated (30–40 Hz), and red circles are the same measurement in the absence of stimulus. The number of cells is N = 3 for the salicylate condition (Sal) and N = 6 for the control. (E) Membrane electromotility couples the membrane potential with membrane tension, and the membrane tension then mechanically deforms the cytoskeleton. Optical phase signals reflect the change of cell morphology. (F and G) Quantitative phase images of patch-clamped HEK 293 cells with different degrees of attachment to the substrate. Scale bars = 5 μm. (H and I) Optical phase signals induced by the electrical stimulations (both 87 Hz). From the spatial distribution of the optical phase signals, we can infer the morphological changes. (J and L) Simple models of cell deformation can explain the amplitude and direction of the optical phase signals in H and I. Schematic side views of a loosely attached cell (J) and a cell attached to its substrate (L). The cells deform between the solid and dashed outlines. (K and M) The height difference of the alternating shapes results in optical phase signals such as those in H and I.

To test the above models, we performed three experiments that characterize the optical phase signals. First, we studied how the optical phase signals depend on the frequency of the electrical stimulation. We obtained data by electrically stimulating a cell with sine waves of various frequencies and the same amplitude. Because the cell membrane resistance, cell membrane capacitance, and series resistance of the patch-clamp pipette act together as a low-pass filter (see Supporting Material for discussion, and Fig. S6 a), the membrane potential is not the same as the potential applied to the patch-clamping electrode (34). Therefore, before taking optical data, we determined each cell's circuit parameters and used them to calculate the membrane potential from the pipette potential. Fig. 2 B shows the optical phase signal amplitude per 100 mV of membrane potential modulation versus frequency. Note that the amplitude of the optical phase signals at high frequencies stays nearly constant or tends to decrease very slowly with frequency. This behavior is different from the swelling model in which the volume change due to swelling is equal to the integral of the water influx during each duty cycle, and hence should have amplitude inversely proportional to frequency.

To test whether the cytoskeleton is involved in generating the observed changes in phase, we compared the size of the optical phase signals from cells treated with CD with that of signals from untreated cells. CD softens the cell by inhibiting polymerization of the actin, the major component of the cytoskeleton (35). If mechanical deformation of the cell body is involved, as in the case of membrane electromotility, the optical phase signals should be larger for softened cells than for unsoftened ones. Fig. 2 C shows that this is indeed the case. The voltage-induced optical phase signals averaged over the area of each cell for CD-treated cells (N = 5) are ∼50% larger than those of the control cells (N = 10). This strong effect of cytoskeleton mechanics on the optical phase signals leads us to conclude that a pure membrane model does not account for most of the observed signals.

The membrane electromotility model, on the other hand, is consistent with the above observations. In the MEM model, the membrane potential generates membrane tension that deforms the cytoplasm and changes the shape of the cell. The membrane tension of MEM responds extremely rapidly (<150 μs response time) to the applied voltage (36), which is consistent with the nearly constant optical phase signals at high frequencies (Fig. 2 B). Also, the mechanical deformation of a cell in response to a given MEM-induced membrane tension will be larger for mechanically softer cells, as in Fig. 2 C. As another test of the MEM model, we added salicylate to the external solution. This small, negatively charged molecule can partition into the lipid bilayer, and a low concentration (4 mM) of salicylate in the external solution can alter the density of surface charge on a cell membrane and reduce the membrane electromotility (32). Fig. 2 D shows that when salicylate ions are added, the optical phase signal diminishes, just as predicted by the MEM model.

Cell deformation caused by MEM

Fig. 2 E illustrates how MEM induces a voltage-dependent shape change in a cell. A change in the membrane potential alters the density of adsorbed ions on the plasma membrane: their mutual electrostatic repulsion gives rise to voltage-dependent membrane tension, and this change in tension induces changes in the shape of the cell (32). How much and how fast a cell will deform in response to a given magnitude of change in the membrane tension depends on the mechanical properties of the cytoplasm. The behavior of a cell that elastically deforms to sudden forces but is viscous in slow deformation is described by the Maxwell model of a spring (k) and a dashpot (η) in series (37). In the frequency domain, the mechanical response x to a force F applied with an angular frequency ω is given by $x=\left(k^{-1}-i{\omega }^{-1}{\eta }^{-1}\right)\times F$. In this model, the response rapidly decreases at low frequencies and slowly converges to a constant at high frequencies, in agreement with our observations, as shown in Fig. 2 B. In applying this model to the experimental data of Fig. 2 D, we assumed that the driving force F is proportional to the membrane potential, and that the optical phase signal is linearly proportional to the response x. By fitting the data points to the Maxwell model, we find the characteristic frequency $f_c=k/\eta$ to be ∼80 Hz, which is ∼10 times larger than the characteristic frequency of mechanical behavior of adherent cells (37). This result suggests that the nanoscale motion induced by membrane electromotility may involve a different set of structural molecules from those responsible for the micron-scale displacements observed in conventional cell microrheology experiments.

Mechanical deformation provides a straightforward explanation for the observed variations of phase signals over the area of the image. Fig. 2, H and I, show that a cell exhibits domains in which time delays of the optical phase signals have similar values. Also, when a cell has a domain with a given time delay, it will have at least one other domain in which the time delay is ∼180° out of phase. This indicates that these domains are moving synchronously in opposite directions; that is, when one part of a cell becomes thicker, the other part gets thinner and vice versa. The arrangements of these domains in Fig. 2, H and I, are best explained by the cell deformations shown in Fig. 2, J and L, which change the optical phase retardations as shown in Fig. 2, K and M. This observation is consistent with the requirement that cell volume be unchanged during the MEM-induced deformation. A consequence of this anticorrelation is that the size of the optical signal does not increase when the size of the sampling area is increased. When averaged over the area of a single cell, the optical signals from the opposite domains cancel each other out. It is likely that similar anisotropy of the cell's changes accounts for the fact that higher spatial resolution increased the detectability of the FIOS in tissue studies (38).

Imaging electrical activity with optical phase signals

As noted above, FIOS imaging allows label-free measurements of cellular electrical phenomena. To demonstrate this, we observed the propagation of an electrical stimulus over the gap junctions of HEK 293 cells. A gap junction is a membrane structure that provides channels between two cells, through which they can exchange ions and metabolites (39). We used double patch clamping to confirm that our HEK 293 cells were strongly gap-junction coupled (Fig. 3 C).

Figure 3.

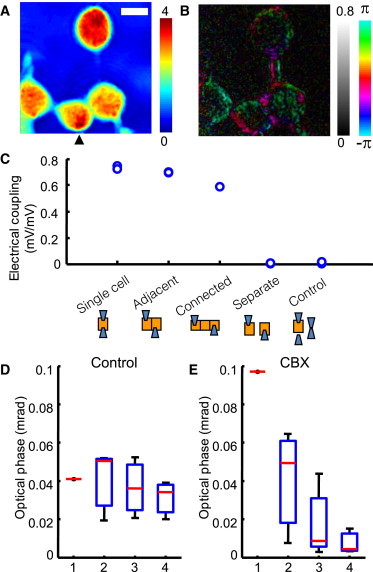
Wide-field imaging of electrical activities. (Color online) (A) Quantitative phase image of HEK 293 cells 36 h after plating. The cell marked by the black triangle is directly stimulated through a patch pipette. Color bar in radians, scale bar = 10 μm. (B) The optical phase signal shows that the electrical stimulus has propagated to neighboring cells. Grayscale bar in mrad, color bar in radians. (C) Double patch-clamping measurement of the gap junction coupling in HEK 293 cells. A voltage-clamped cell was electrically stimulated with a 10 mV bipolar pulse and the pulse size in the other cell is observed for pairs with different degrees of separation. Electrical coupling strength is defined by the ratio of the two pulse sizes. (D and E) The size of the optical phase signal decreases as a function of the distance from the electrical stimulation. Cell 1 is directly stimulated through a patch pipette. The rest of the x axis indicates the neighboring cells grouped in order of closeness to the patch-clamped cell. The y axis is the mean amplitude of the optical phase signal averaged over each cell area. (D) The amplitudes of the optical phase signals are similar regardless of the distance from the patch pipette, indicating a very small gap-junction resistance. (E) The same cells with 100 μmol/L gap junction blocker CBX. The optical phase signal amplitude decays rapidly with distance, as would be expected from increased gap-junction resistance. Number of cells in groups 2, 3, and 4: N = 4, 5, and 3, respectively.

In the experiment, one cell was stimulated by patch clamping while quantitative phase images were acquired from the entire area, including the neighboring cells. Fig. 3 A shows the quantitative phase image of a low-density culture of HEK 293 cells with well-developed gap-junction coupling. The cell marked by the arrowhead was electrically stimulated by a sine wave of 42 Hz frequency and 100 mV half-amplitude while quantitative phase images of the entire field of view were acquired for 10 s at 500 frames/s. The optical phase signals in Fig. 3 B appear on both the stimulated cell and the neighboring cells, revealing that the electrical stimulus has propagated. Note that the optical phase signals clearly reveal a fine structure connecting two of the cells (see Supporting Material for further discussion). The variations in the cells' substrate adhesion and cytoskeleton organization are the likely causes of the variations in optical signals within a cell and among different cells.

To confirm that our optical phase signals truly indicate the electrical activity of a cellular network, we added the gap-junction blocker carbenoxolone (CBX) to a HEK 293 culture (40). In this experiment, we obtained optical phase signals from a confluent cell monolayer including 13 cells, where cell 1 was directly stimulated by whole-cell patch clamping. The neighboring cells were labeled according to their proximity to cell 1 (i.e., group 2 cells are direct neighbors of cell 1, group 3 cells are direct neighbors of group 2 cells, and so on). We acquired optical phase signals from cells in the usual bath solution while cell 1 was electrically stimulated. Then we replaced the bath solution with a solution containing 100 μM CBX, and acquired optical phase signals as described above. Fig. 3, D and E, show the distribution of the amplitude of the optical phase signals averaged over each cell in the normal and CBX solutions. The marked difference between these two distributions confirms that the optical phase signals in the remote cells are induced by potential modulations propagated through gap-junction channels (see Supporting Material for discussion, and Fig. S6, b and c).

Discussion

In this work, we combined an optical apparatus with data processing to develop an approach that allows us to detect the intrinsic optical signals from single mammalian cells. In contrast to previous approaches, our technique allows cells to be observed with microscopic resolution. Spatial averaging, which is often employed in other techniques to increase sensitivity, would result in canceling out positive and negative signals. On a similar note, a previous FIOS study on amphibian retina also showed that higher spatial resolution improved the signal detection (38). We think that the high-resolution approach can be combined with various other techniques, such as light scattering (11–14) and optical coherence tomography (41), to enable the detection of FIOS signals in single mammalian cells. In a subsequent study, we were able to demonstrate that an instrument based on optical coherence microscopy could be used to detect membrane electromotility FIOS in HEK 293 cells, as will be reported in a follow-up article (T. Yamauchi, S. Oh, D. Fu, W. Choi, R. R. Dasari, and Z. Yaqoob, unpublished). Further development of a detection methodology based on reflected light will make FIOS useful for a broader range of applications in tissue preparations and in vivo.

We detected FIOS in the frequency domain and studied its dynamic property from the frequency response. From our observations, we deduced that the majority of the observed FIOS is caused by deformation of the cell body as the result of membrane electromotility. The frequency dependence, effects of CD and salicylate, and spatial distribution of the optical phase signals are well explained by our model. Because membrane electromotility is an intrinsic property of the lipid bilayer (32), which is common to all cells, the phenomenon described here should be found in all cell types, including spiking neurons. However, this does not exclude the existence of other types of FIOS mechanisms in neurons. In invertebrate neurons and mammalian nerve terminals, ion flux across ion channels or osmotic imbalance associated with the action potential can cause net water transport across the cell membrane (21,43). This causes cell swelling that can be detected by light scattering, birefringence signals, and high-bandwidth dynamic atomic force microscopy (1,8,21). Although we initially expected to observe the swelling effect in HEK 293 cells, we found that this was not the case (Fig. 2 B). The absence of a swelling effect in HEK 293 cell indicates the role of neuron-specific ion transporters in cell swelling. Moreover, our finding that there exists a mechanism other than swelling is not unprecedented. In a study using squid giant axons, Cohen et al. (44) observed that electrostriction causes the dominant part of the forward light-scattering signal from action potentials. Both electrostriction and swelling effects were shown to exist in squid giant axons, but the relative magnitude of the optical signals depended on the window of the scattering angles and the time window of the observation. Similarly, membrane electromotility and swelling would be distinguishable by different temporal characteristics because the membrane electromotility is potential-dependent and swelling is dependent on the time integral of current.

The approach presented here, which combines frequency domain analysis and transmission quantitative phase microscopy, can be applied to detect the intrinsic optical signals from spiking neurons. From the reciprocity of temporal and frequency domains, the dynamical property of the intrinsic optical signal can be inferred from the spectral response of repeated action potential spikes. Because the bandwidth from 0.2 to 5 kHz captures the characteristics of the action potential in extracellular recordings (45), and this frequency window is accessible for the frequency domain analysis, LCDPM will be able to observe the optical signal of the action potentials from mammalian neurons. Detection of a single action potential spike is more challenging and will require a different strategy to increase the signal/noise ratio. We suggest that a possible solution to this problem would be to use the band-pass filtering and spike-detection technique employed for extracellular recording of neuronal action potentials (46).

FIOS is an interesting biophysics phenomenon that is based on the interaction of chemical, mechanical, and electrical forces at the plasma membrane. Despite various careful studies on invertebrate FIOS (1,5,8), little is understood about its biophysical mechanism in vertebrate systems. We anticipate that the approach presented here will provide a useful tool for further investigating FIOS biophysics, i.e., the mechanical and optical consequences of a cell's electrical activity.