Force-Dependent Detachment of Kinesin-2 Biases Track Switching at Cytoskeletal Filament Intersections

Abstract

Intracellular trafficking of organelles often involves cytoskeletal track switching. Organelles such as melanosomes are transported by multiple motors including kinesin-2, dynein, and myosin-V, which drive switching between microtubules and actin filaments during dispersion and aggregation. Here, we used optical trapping to determine the unitary and ensemble forces of kinesin-2, and to reconstitute cargo switching at cytoskeletal intersections in a minimal system with kinesin-2 and myosin-V motors bound to beads. Single kinesin-2 motors exerted forces up to ∼5 pN, similar to kinesin-1. However, kinesin-2 motors were more likely to detach at submaximal forces, and the duration of force maintenance was short as compared to kinesin-1. In multimotor assays, force increased with kinesin-2 density but was not affected by the presence of myosin-V. In crossed filament assays, switching frequencies of motor-bound beads were dependent on the starting track. At equal average forces, beads tended to switch from microtubules onto overlying actin filaments consistent with the relatively faster detachment of kinesin-2 at near-maximal forces. Thus, in addition to relative force, switching probability at filament intersections is determined by the dynamics of motor-filament interaction, such as the quick detachment of kinesin-2 under load. This may enable fine-tuning of filament switching in the cell.

Introduction

Cells require molecular motors to properly position organelles within the cytoplasm (1). These cargos must often travel along both microtubule (MT) and actin filament (AF) networks to reach their destinations (2). For example, during endocytosis, endosomes are initially associated with the actin cytoskeleton near the cell cortex; endosomes switch to MTs to facilitate rapid movement toward the cell center. Although this track switching appears essential for normal cellular function, the mechanisms regulating switching in the cell are poorly understood (2).

One well-studied model for cytoskeletal track switching in the cell comes from Xenopus melanophores. Upon stimulation, melanosomes disperse throughout the cell by switching from the MT to the AF network (3). During aggregation, melanosomes switch from AFs to MTs, leading to rapid accumulation near the cell center. For these melanosomes, plus- and minus-end directed movements along the MTs are driven by kinesin-2 and cytoplasmic dynein, respectively, whereas actin-dependent movement is driven by myosin-V (4–6).

The kinesin-2 family consists of two subfamilies, heterotrimeric and homodimeric kinesin-2. In metazoans, heterotrimeric kinesin-2 has a role transporting vesicular cargo within the cytoplasm. Xenopus heterotrimeric kinesin-2 consists of two different motor-containing polypeptide chains, Xklp3A and Xklp3B, homologs of mammalian KIF3A and KIF3B, respectively, and a third subunit, KAP1, which mediates cargo binding (7). Dynein is the major minus end-directed MT motor in the cell (1), whereas myosin-V moves processively toward the barbed ends of AFs (8).

Transport of melanosomes by these motors may be regulated by the number of motors associated with cargos under each condition, by the activation state of the cargo-associated motors, or by changes to cytoskeletal tracks. Melanosomes purified from either dispersed or aggregated melanophores maintain regulated motility on MTs in vitro (4), consistent with cargo-mediated rather than track-directed regulation. Although the number of cargo-associated motors could potentially be modulated in the cell, studies have shown that the number of motors bound to the surface of the melanosome may remain constant (9). Instead, there appears to be a change in the proportion of motors that are actively engaged, with 1–3 dyneins driving minus end-directed movement and 1–2 kinesin-2 motors driving melanosomes in the plus-end direction (10).

In vitro biophysical experiments have examined changes in motility dependent on the number of engaged motors. For example, Mallik et al. (11) found a substantial increase in run length (usually >4 μm) and robustness of motion as the number of dynein motors bound to beads was increased (11). Similar experiments with kinesin-1-coated beads found that cargo travel distance increased when the number of actively engaged motors was increased (12). For both dynein and kinesin-1, stall force scales in a quantized fashion with the number of actively engaged motors (11,12).

In experiments with more complex geometries involving MT-MT intersections, Ross et al. (13) found that the variation of outcome with motor number differed significantly for cargos with kinesin-1 or dynein. As motor densities were increased from single molecule to multimotor conditions, there was no change in kinesin-driven movement through intersections. In contrast, dynein-bound beads became tethered at intersections at high motor densities. Together, these in vitro results suggest that modulating the number of actively engaged motors is likely to be a critical regulatory target in vivo.

Most biophysical studies performed to date have focused on a single motor type. However, given the accumulating evidence that the activities of multiple motors must be coordinated to effectively move cargos within the cytoplasm, recent work is focusing on determining how motors function as ensembles. Furthermore, these assays have begun to incorporate cell-like complexity into in vitro systems to understand how multimotor assemblies may behave when confronted with passive obstacles, such as track-associated proteins, or active ones, such as opposing motors on the same or different filaments (2). One strategy is to build in vivo-like complexity into in vitro assays by testing the collective properties of multiple motor types or by developing filament geometries that more closely resemble the cytoskeletal architecture within the cell (11–13). For example, cytoskeletal switching of cargos can be modeled in vitro (13–15). Using a simplified in vitro model, we have found that the switching of artificial cargos between MT and AF tracks can be tuned by changing the number of engaged myosin-V and dynein motors (15).

In this work, we determined the force exerted by full-length recombinant heterodimeric kinesin-2 from Xenopus. We found that stall force scaled with the increased density of kinesin-2 motors bound to beads, but was not affected by the presence of myosin-V motors bound to the same beads. We then used beads with both kinesin-2 and myosin-V motors attached to investigate cargo switching at cytoskeletal intersections. We modeled the outcomes initially using a simple tug-of-war model, but found that other motor properties, such as the force-dependent detachment of kinesin-2, also contribute to the likelihood of filament switching. Thus, in the cell, switching between cytoskeletal tracks can be tuned via the dynamic properties of a low number of engaged MT- and AF-based motors.

Materials and Methods

See Supporting Material for detailed information on protein preparation and statistical modeling.

In vitro filament switching assays

Flow chambers (∼10 μL volume) were assembled to make two perpendicular crossed flow paths with MTs and AFs bound to the coverslips via biotin-streptavidin linkers as described (15); see Supporting Material for details. MTs were flowed into the chamber in the y-direction and AFs were flowed into the chamber in the x-direction. MTs are termed underpasses and AFs termed overpasses because the MTs are closer to the glass. Motor-bound beads were captured with an optical trap and positioned onto either MTs or AFs near intersections. Image sequences were collected and analyzed as described in the Supporting Material.

For multimotor experiments, anti-GFP-bound beads were blocked, sonicated, and mixed at a concentration of 3 pM with kinesin-2 (relative concentration of 1, see Fig. 2, which corresponds to 214 nM dimer during incubation) and/or myosin V (relative concentration of 1, see Fig. 2, which corresponds to 21 nM dimer concentration during incubation). Western blots indicated that ∼14% of the loading motor concentrations bound to beads for each motor type. For force measurements at single molecule dilutions, assuming a 14% loading efficiency, the total kinesin-2 complement for single motor experiments was ∼10 motors per bead. At a loading concentration of 0.93 nM kinesin-2 dimer, ≤0.5 of the beads bound to MTs. Thus, by Poisson statistics, the probability that a bead has two or more motors bound to a MT is <0.14 (16).

Figure 2.

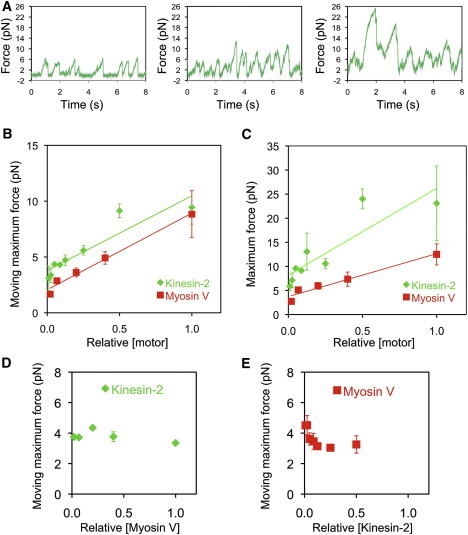
Kinesin-2 force scales with motor number and is not modified by myosin-V motors bound to the same bead. (A) Representative force traces for beads incubated with increasing concentration of kinesin-2 and a constant concentration of myosin-V. (B and C) Moving-maximum forces are shown in B and maximum forces are shown in C for beads with both kinesin-2 and myosin-V bound. Shown in green are force data from beads incubated with increasing concentrations of kinesin-2 motors, with myosin-V concentration held constant. Shown in red are force data from beads incubated with increasing concentrations of myosin-V, with kinesin-2 concentration held constant. Relative [motor] was normalized to the highest motor/bead ratio examined, corresponding to 7.3 × 10⁴ motors incubated per bead for kinesin-2 and 7.0 × 10³ motors incubated per bead for myosin-V (see Materials and Methods for more details). Each data point represents the average moving-maximum force produced per bead in a median filtered (window = 201) force trace; n = 1–7 beads for kinesin-2 data points and 1–7 beads for myosin-V data points. (D) Moving-maximum forces for kinesin-2 (at fixed loading) are plotted versus the relative loading concentration of myosin-V; normalized to 1 for a loading concentration of 7.0 × 10³ motors incubated per bead for myosin-V. (E) Moving-maximum forces for myosin-V (at fixed loading) are plotted versus the relative loading concentration of kinesin-2; normalized to 7.3 × 10⁴ motors incubated per bead for kinesin-2. Moving-maximum and maximum force measurements are plotted as mean ± SEM.

Force measurements

The plateau force for a single motor was measured when the force trace was observed to plateau, followed by a snapback (detachment and a fast return to baseline; see Fig. S1 in the Supporting Material for a graphical representation). For kinesin-1 and kinesin-2, the force plateau was required to last ≥70 ms, and this time interval could not include more than one consecutive step in the same direction. The 70 ms minimum stall time was chosen to include prolonged stalls, and exclude brief premature detachments that occurred before the motor stalled; as similar results were determined with a value of 100 ms, the conclusions do not depend on the particular value chosen for this threshold. Stall events for myosin-V were easily identified so no threshold on the stall plateau time was necessary. Events were included that were preceded by a >36 nm displacement in the force trace away from the baseline as a result of motor stepping and followed by a snapback >36 nm. To obtain pre-drop forces, force traces were median filtered (window = 11 time points, i.e., 0.0055 s); subsequently, instantaneous velocity (between time points i − 1 and i + 1) was calculated and smoothed using a Savitsky-Golay filter (full width = 3 time points, i.e., 0.0015 s; degree = 2). Velocity peaks exceeding a threshold of 20 μm/s toward baseline were selected, and for each peak, the pre-drop force was measured. Pre-drop forces ≤1 pN were excluded from further analysis. To obtain moving-maximum forces, force traces recorded at 2 kHz, were passed through a median filter (window = 201 time points, i.e., 0.1005 s) followed by a second filter, which selected the sample with the greatest force within successive 1 s windows moved in 100 ms increments. Moving-maximum forces ≤1 pN were excluded. Maximum force is defined as the maximum force observed within a force record (see Fig. S1 for a graphical representation of these definitions).

Results

Force measurements on individual kinesin-2 and kinesin-1 motors

Although the biophysical properties of kinesin-1 have been well studied (reviewed in (17)), less is known about the properties of heterodimeric kinesin-2. Thus, we first measured the unitary stall force of purified recombinant Xenopus heterodimeric kinesin-2, composed of full-length Xklp3A and Xklp3B subunits fused to a C-terminal GFP. For comparison, we also measured forces generated by kinesin-1 motors in parallel single molecule assays. When a motor-bound bead is held within the optical trap, the motor experiences increasing force with every step and eventually detaches from its track and snaps back into the center of the trap (Fig. 1, A and B). Events were considered plateaus if the force was sustained for ≥70 ms (Fig. S1). Fitting a Gaussian curve to a histogram of these measurements allowed us to estimate a unitary plateau force of 5.0 ± 0.9 pN (peak ± SD of the fitted Gaussian curve) for kinesin-2 (Fig. 1, A, B, and E). The plateau force of kinesin-1 (K560-GFP) under the same conditions was 5.3 ± 1.2 pN (peak ± SD of the fitted Gaussian curve) (Fig. 1, C, D, and E), in agreement with literature values of 5–7 pN (16,18). These values are not highly sensitive to the minimum time threshold for defining a plateau; for instance, force for plateaus lasting ≥100 ms averaged 4.8 ± 0.2 pN (mean ± SE, n = 28) for kinesin-2 and 5.2 ± 0.1 pN (mean ± SE, n = 236) for kinesin-1.

Figure 1.

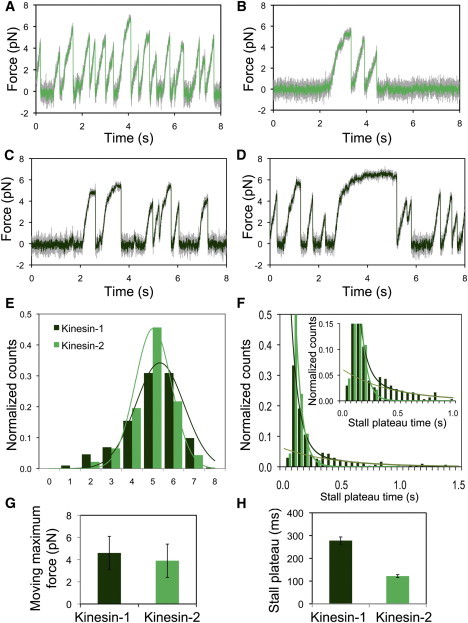
Kinesin-2 has a similar unitary stall plateau force to kinesin-1 but detaches faster from the MT. (A) Typical force trace, unfiltered (gray) and median filtered (light green) for kinesin-2. (B) Force trace illustrating an event with the longest observed plateau for kinesin-2; unfiltered (gray) and median filtered (light green) data are shown. (C) Typical force trace, unfiltered (gray) and median filtered (dark green) for kinesin-1. (D) Force event with the longest plateau time observed for kinesin-1; unfiltered (gray) and median filtered (dark green) data are shown. (E) Frequency distribution of plateau force events observed for kinesin-1 (dark green; n = 304 events) and kinesin-2 (light green; n = 46 events); curves represent Gaussian fits to the data. (F) Frequency distribution of plateau times for kinesin-1 (dark green) and kinesin-2 (light green). Kinesin-1 data were fit by a double exponential (dark curve) having time constants 66 ± 7 ms and 431 ± 130 ms (medium green curve); kinesin-2 data were fit by a single exponential decay with time constant 54 ± 4 ms. In both cases the first two bins were excluded from the fitting. Plateaus were excluded for dwells <70 ms. (G) Mean moving maximum force for kinesins-1 and -2. (H) Mean duration of plateaus for kinesins-1 and -2.

Although the observed plateau force values for kinesin-2 and kinesin-1 are similar, we observed that kinesin-2 detached more quickly under load than kinesin-1. Often, both kinesins would initiate runs that failed to reach a plateau before detachment; the percentages of runs that resulted in plateaus for kinesin-2 and kinesin-1 were 19% and 62%, respectively. The average plateau durations for kinesin-2 and kinesin-1 were 122 ± 6 and 278 ± 16 ms (means ± SE, P < 0.0001), respectively (Fig. 1 H). Histograms of plateau durations for kinesin-2 (≥70 ms) were well described by a single exponential component with a time constant of 54 ± 4 ms; no plateaus were observed to last longer than 300 ms. In contrast, stall plateau durations for kinesin-1 were often longer (29% of plateaus were >300 ms) and were better fit by two exponential components with time constants of 66 ± 7 ms and 431 ± 130 ms. The average force for kinesin-1 plateaus lasting >300 ms was 5.8 ± 0.1 pN (mean ± SE, n = 88), whereas the average force for plateaus lasting <300 ms was 4.7 ± 0.1 pN (n = 216).

Averaging all force values just before detachment regardless of stalling behavior, a measurement we term the pre-drop force (see Methods and Fig. S1 for details), gives values of 4.1 ± 1.2 pN (mean ± SD) for kinesin-2 and 4.4 ± 1.4 pN (mean ± SD) for kinesin-1. Selecting the greatest force within successive 1 s windows moved in 100 ms increments, a measurement we term the moving-maximum force (Fig. S1), gives values of 3.9 ± 1.5 pN (mean ± SD) for kinesin-2 and 4.6 ± 1.5 pN (mean ± SD) for kinesin-1 (Fig. 1 G). Both methods of analysis (pre-drop force and moving-maximum force) are estimates of the peak force exerted by the motor during attachment. The moving-maximum force method in particular is useful for analyzing multi-motor force traces (see below), as it allows us to estimate the average force exerted by a team of motors. In contrast, the maximum force observed, when divided by the unitary stall force, provides an estimate of the maximum number of motors of each type able to engage at each condition tested.

Together, these observations indicate that force exerted by single kinesin-2 motors is similar to that of kinesin-1, but there are potentially important differences in motor dynamics. Kinesin-2 is a less processive motor than kinesin-1, is more likely to detach without reaching a stall plateau, and exhibits stall plateaus of shorter duration. This increased probability of detachment under load for kinesin-2 relative to kinesin-1 is consistent with previous data indicating that kinesin-2 has shorter single molecule run lengths than kinesin-1 (19) and with recent measurements on the stepping dynamics of heterotrimeric kinesin-2 (J. Andreasson and S. M. Block, Stanford University, personal communication, 2011). The different force values we observed for short and long kinesin-1 plateaus may suggest detachment from two different states for this motor (20).

Force measurements on multiple kinesin-2 and myosin-V motors

Next, we simultaneously bound multiple kinesin-2 and myosin-V motors to polystyrene beads, using an anti-GFP antibody, and measured the forces these motors exert on their respective tracks in a static optical trap. The average moving-maximum force for kinesin-2 increased with kinesin-2 loading concentration at a fixed myosin-V loading concentration (Fig. 2, A and B). The y-intercept of a linear fit to these data, 3.8 pN, serves as another estimate of the moving-maximum force for a single kinesin-2 motor, in good agreement with the value of 3.9 pN determined from the single motor assays described previously. Plotting the moving-maximum force versus the maximum force for kinesin-2 at each motor density yields an approximately linear relationship (R² = 0.96).

The moving-maximum force for myosin-V also increased with myosin-V loading concentration at constant kinesin-2 concentration (Fig. 2 B). The y-intercept of a fitted line, 2.1 pN, once again agrees with the moving-maximum force measured for single myosin-V motors, 1.9 pN, that we determined previously (15). A plot of the moving-maximum force versus the maximum force for myosin-V can be fit by a line (R² = 0.94) with a slope similar to our previously determined measurements for myosin-V in the absence of kinesin-2 (15).

The maximum force, defined as the largest force produced during a recording (Fig. S1), increased with loading concentration for both motor families, ranging from 6 to 23 pN for kinesin-2 and 3 to 13 pN for myosin-V under the conditions of our experiments (Fig. 2 C). Dividing the maximum force by the motor's unitary plateau force (5 pN for kinesin-2 and 2 pN for myosin-V) provides an estimate of the maximum number of simultaneously engaged motors at each motor density tested. According to this ratio, the maximum number of engaged motors ranged from 1 to 5 for kinesin-2 and 1 to 7 for myosin-V in our assays. The slope of these curves is an indication of the average proportion of motors engaged with the filament, a parameter we term the engagement ratio. In our previous work on myosin V and dynein, we found that these motors have different engagement ratios (15) and the different slopes apparent in Fig. 2 C indicate that kinesin-2 and myosin V also differ in their engagement ratios. In agreement with previous findings for cytoplasmic dynein and myosin-V, we find for kinesin-2 that force increases linearly with motor number. Although kinesin-1 and myosin-V were previously shown to enhance each other's processivity in unloaded motility assays (21), we find that the binding of increasing numbers of kinesin-2 motors to myosin-V-bound beads does not enhance the force produced along an AF but, rather, induced a small decrease (Fig. 2 E). Adding myosin-V motors to kinesin-2-bound beads did not affect the force generated by kinesin-2 along the MT (Fig. 2 D).

Competition between kinesin-2 and myosin-V at cytoskeletal intersections

In the cell, cargo-bound motors mediate switching between cytoskeletal tracks. To model these crossings in vitro, we assembled perpendicular arrays of MTs and AFs on the surface of a flow chamber (Fig. 3 A). MTs were bound closer to the glass, and thus are termed underpasses, whereas AFs formed overpasses at filament intersections. We measured filament switching with anti-GFP-conjugated polystyrene beads bound to both kinesin-2 and myosin-V at different loading concentrations. Beads were optically trapped in solution and released on either MTs or AFs near filament intersections. An encounter was tallied as a pass, switch, or stop at the intersections if the bead exited on the starting filament, exited on the perpendicular filament, or remained at the intersection longer than 3 min, respectively. Importantly, at each loading concentration, we used the optical trap to determine the forces exerted by the motor-bound beads on either MTs or actin filaments, and then calculated the ratio of the moving-maximum force for myosin-V to the moving-maximum force for kinesin-2 (Fig. 3 B). We also determined the maximum forces exerted by either myosin-V or kinesin-2 motors at each motor density tested; switching frequencies are plotted as a function of the ratio of maximum forces in Fig. 3 C.

Figure 3.

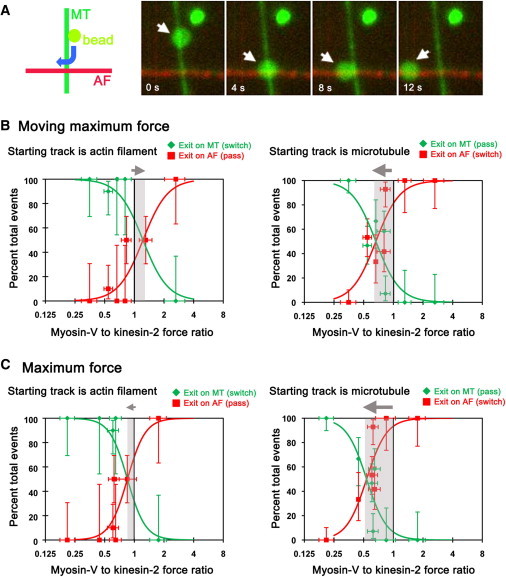
Outcomes at cytoskeletal intersections vary with the ratio of applied forces. (A) Cytoskeletal microtubule (MT)-actin filament (AF) intersections were reconstituted in vitro, as shown in the schematic on the left. GFP-labeled kinesin-2 and myosin-V motors were bound to fluorescent beads and positioned near an intersection on either a MT or AF using an optical trap. Once freed from the trap, beads move toward the intersection and may either pass through or switch to the orthogonal filament, as shown in the time series in the panels on the right, taken from Movie S1 in the Supporting Material. (B) Outcomes when a bead enters an intersection from an AF (left panel) or from a MT (right panel, as a function of the myosin-V: kinesin-2 moving-maximum force ratio. The curves (red and green) were fit to the data, to guide the eye, using the equation, y = 100/(1 + e^-(x-b)/c), where parameters b and c define the position and steepness of the curve. (C) Outcomes when a bead enters an intersection from an AF (left panel) or from a MT (right panel, as a function of the ratios of maximum forces for myosin-V and kinesin-2-bound beads. As in B, the curves (red and green) were fit to the data, to guide the eye, using the equation, y = 100/(1 + e^-(x-b)/c). In B and C, outcome at intersections for beads near force balance (force ratio = 1) is dependent on the starting track. Myosin-V has a better chance of winning at a given force ratio if the starting track is a MT rather than an AF. The relative shift in transition force ratio is indicated by the gray shading. Vertical error bars represent 68% confidence intervals calculated from binomial distributions. Horizontal error bars represent 68% confidence intervals of the force ratios. Number of outcomes at each force ratio ranged from 3 to 10 when the starting track was an AF (plots on left) and 6 to 17 when the starting filament was a MT.

We find that the percentage of beads that enter an intersection along a MT but exit along an AF increases with an increasing myosin-V: kinesin-2 force ratio (Fig. 3, B and C). We define the transition force ratio as the myosin-V to kinesin-2 force ratio at which the likelihood for exiting the intersection on the AF is equal to that for exiting on the MT. When a bead starts on a MT, the transition force ratio is 0.7. This means the bound kinesin-2 motors need to collectively exert ∼1.5 times as much force as the bound myosin-V motors to have an equal chance of exiting the intersection along their cognate track (Fig. 3 B, right panel). Alternatively, when the beads are released on an AF and allowed to proceed toward the intersection (Fig. 3 B, left panel), kinesin-2 motors exert ∼0.8 times as much force as myosin-V motors to have an equivalent chance of exiting the intersection along their cognate track (intersection of red and green curves in Fig. 3 B). At myosin-V: kinesin-2 force ratios between 0.6 and 1.3, the lower likelihood for a bead to exit on the MT when it started on a MT, relative to starting on an AF, is statistically significant (p = 0.003 – 0.05) by Fisher's test of contingencies. If we instead examine the switching probability as a function of the ratio of myosin-V: kinesin-2 maximum peak forces exerted by the motor teams during attachment, we also find that the transition force ratio is distinct for beads entering an intersection on either an AF or MT (Fig. 3 C).

These results can be compared to previous observations from an assay pairing myosin-V with dynein (15). For beads with bound myosin-V and dynein, switching probability was found to be relatively independent of whether the bead entered the intersection on either a MT or actin filament. Furthermore, we noted previously that dynein and myosin-V-bound beads at the transition force ratio often stopped at intersections — ∼40% of such beads starting on MTs did not exit the intersection on either filament, but instead remained stably tethered at the junction. This type of tethering was much rarer for beads with the kinesin-2/myosin-V motor pair. The percentage of beads that paused at intersections was <13% over the range of loading densities examined; pausing was not observed (0/35 observations) at the transition force ratio.

To further compare motor pairs, we performed a more limited set of experiments with beads with myosin-V and kinesin-1 motors bound. We found that when entering an intersection on a MT, these beads showed equal probabilities of switching and passing at a transition force ratio (maximum myosin-V force/maximum kinesin-1 force) near 0.5. Thus, similar to our observations for kinesin-2, even when the team of kinesin-1 motors is capable of exerting more force than myosin-V motors, the cargo often switches from the MT to the actin filament. Beads with bound kinesin-1 and myosin-V motors also did not exhibit prolonged pauses at intersections. Together, these observations suggest that although the balance of forces exerted on a bead at a cytoskeletal intersection is a critical driver of switching frequency, the mechanochemical dynamics of the motors also contribute to the outcome.

Modeling outcomes at intersections

We previously applied a probabilistic model based on stochastic motor engagement to describe the tug-of-war that occurs between myosin-V and dynein motors at cytoskeletal intersections (15). The model assumes that for each motor group, the number of actively engaged motors, n, out of a maximum number of motors available for generation of force, N, from each motor group follows a binomial distribution dependent on the engagement ratio, p, the probability that an individual motor is engaged. The motor group producing greater force at the intersection pulls the bead onto its respective track. Engagement probabilities based on the respective stall plateau forces and numbers of modeled motors on each bead satisfactorily described the observed switching and stalling of myosin-V/dynein beads at intersections. For myosin-V and dynein, we found that outcomes were largely independent of the starting track (15).

In contrast, in experiments with beads with bound kinesin-2 and myosin-V motors, we found that the starting filament has a much larger effect on the outcome at cytoskeletal intersections. An equal probability of exiting on the AF or MT (at the transition force ratio) was observed at a ∼twofold higher myosin-V: kinesin-2 (moving maximum) force ratio when the bead entered the intersection moving on an AF rather than from a MT (Fig. 3 B). This shift is also seen when the outcome data are plotted as a function of the ratios of maximum force (Fig. 3 C), again suggesting that kinesin-2 does not effectively compete with myosin-V when the starting track is a MT. Two possible explanations may account for this difference. First, the geometrical organization of the two bead-bound motors may affect their association/dissociation kinetics at intersections. Second, the kinetic properties of the motors may make switching from kinesin-2 to myosin-V more favorable than switching from myosin-V to kinesin-2, resulting in the shift in the transition force ratio away from 1 that is seen in Fig. 3.

To investigate these possibilities, we applied models of increasing complexity to the cytoskeletal intersections. Beginning with the binomial model previously used to describe dynein and myosin-V mediated track switching, we considered that single kinesin-2 motors bound to beads usually detach before reaching a stall plateau at 5.0 pN (Fig. 1, and see Materials and Methods as well as Fig. S1 for term definitions). The observed pre-drop and moving-maximum force values are 4.1 and 3.9 pN, respectively. Thus, the average force produced by multiple kinesin-2 motors is better estimated using the moving maximum force than the plateau force. In contrast, for myosin-V, the stall (1.8 pN), pre-drop (1.9 pN), and moving-maximum (1.9 pN) force values are very similar (15).

In the binomial model, the relationship between the association and dissociation rates is described via the engagement ratio, p, which is the ratio of the binding rate to the sum of the binding and unbinding rates. The engagement ratio for kinesin may be influenced by the intersection geometry. When switching from a MT to an AF, the actin may function as an obstacle in the path of the kinesin motors. However, when the bead enters an intersection moving on an AF, kinesin does not have to cross the AF. In support of this idea, kinesin-1 has been shown to preferentially dissociate when encountering an obstruction, whereas dynein is less sensitive to obstacles along the MT (22). Kinesin-2 may show a similar enhanced likelihood of detachment upon encountering an obstacle, such as the intersecting AF. Using this simple model, we found that reducing the engagement ratio for kinesin-2 from 0.7 in the case of switching from AF-MT to 0.56 for the case of switching from MT-AF reproduces the shift in the transition from exiting along the AF or MT (Fig. 4 A).

Figure 4.

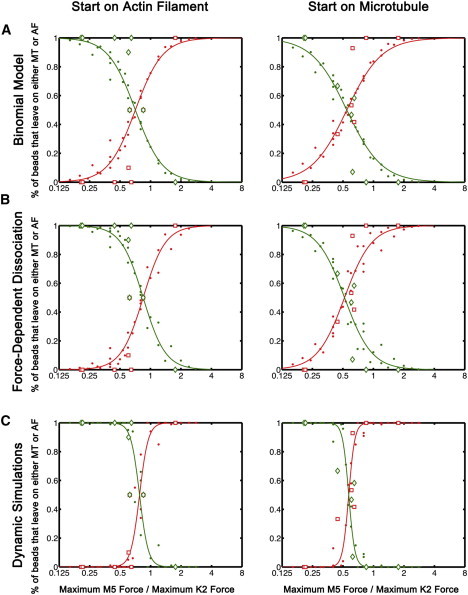
Models of filament switching driven by kinesin-2 and myosin-V. (A) The binomial model describes the switching data well assuming that the engagement ratio for kinesin-2 is 0.7 when starting on an AF and 0.56 when starting on a MT. (B) Similarly, the model including force-dependent dissociation describes the switching behavior assuming the association rate of kinesin-2 depends on the starting filament. (C) Dynamic simulations show that the dependence on the starting filament may be due to the dissociation kinetics of the motors. The dissociation rate of kinesin-2 is more dependent on force than myosin-V. Thus, switching from kinesin-2 to myosin-V is faster than switching from myosin-V to kinesin-2. Parameter values for all model results are given in Table S1.

To account for force-dependent dissociation kinetics, we adapted the steady-state model of Müller et al. (23) to cytoskeletal intersections. In this model, the detachment rate rises exponentially with resisting load on a motor with a characteristic scaling factor, F_d, termed the detachment force (Eq. S2 in the Supporting Material). Although detachment rate for kinesin is not necessarily such a simple function of force ((24); J. Andreasson and S. M. Block, Stanford University, personal communication, 2011), this model expresses, to a first order, the qualitative difference among the motor types according to which the ratio of F_d/F_plateau is lower for kinesin-2 than for myosin V or kinesin-1 (see below). Varying the parameters of this model indicates that the detachment force and binding rate determine the force transition ratio, while the slope of the transition is affected by the binding rate and the number of motors (Fig. S4). We applied this concept to the data for beads with bound kinesin-2 and myosin-V at AF-MT intersections, using parameters based on our own observations or on values from the literature, as described in the Supporting Material. Similar to the effect of the engagement ratio in the binomial model, this model reproduced the dependence of the transition force ratio on starting conditions (AF or MT) when the binding rate for kinesin-2 was changed from 5 to 2.5 s⁻¹ (Fig. 4 B). Note that the inclusion of the force-dependent dissociation rate leads to steeper transitions in the switching probabilities that better describe the data than the binomial model discussed previously.

These steady-state models suggest that switching probabilities at cytoskeletal intersections may be affected by the geometry of filament intersections through modulation of motor binding rates. Alternatively, the dependence of the switching probabilities on the starting filament may be due to differences in the kinetics of the two motor types (i.e., switching from kinesin-2 to myosin-V may be dynamically more favorable than switching from myosin-V to kinesin-2). To examine the role of transient kinetics, we used Monte Carlo calculations (see Methods, Fig. S3). F_d was set to 40% of F_plateau for kinesin-2 and 50% of F_plateau for myosin-V implying that kinesin-2 dissociates more quickly when under load, consistent with our observations. Switching from MT to AF (involving kinesin-2 detachment) is thus faster than switching from myosin-V to kinesin-2 (AF → MT). The model describes the shift in the transition force ratio observed in the experiments (Fig. 4 C) by including transient association/dissociation kinetics.

The model results suggest that switching behavior may be influenced through decreased motor binding rates in response to crossed filaments. However, outcomes can be described entirely by considering the dynamic force-dependent dissociation kinetics of the motors, without the need to change motor parameters based on the starting filament. These results suggest that the dynamic motor binding/unbinding kinetics determine behavior at cytoskeletal intersections.

Discussion

The intracellular transport of organelles is often driven by multiple motor types, including plus- and minus-end directed MT motors as well as myosins moving along AFs. The well-characterized motility of melanosomes is driven by dynein, kinesin-2, and myosin-V motors (4–6). We previously described the characteristics of bead cargos bound to dynein and myosin-V at AF-MT intersections and found that a simple mechanical tug-of-war could explain many of the observations. Here, we performed similar experiments on beads with myosin-V and heterodimeric kinesin-2 bound, to determine whether a similar tug-of-war also applies to this combination.

At filament intersections, we found that the probability that kinesin-2 can overcome a group of myosin-V motors to pull their shared cargo onto a MT depends on the ratio of forces that the two types of motors exert. The forces are, in turn, functions of the motor densities on the beads. However, unlike beads with dynein and myosin-V bound, where the probability of switching filaments is independent of the entry filament to the intersection, outcomes with kinesin-2-myosin-V beads are dependent on the identity of the starting track. If the starting filament is actin, the transition force ratio is close to 1. However, if the starting filament is a MT, the transition force ratio is biased toward a lower myosin-V/kinesin-2 force ratio.

Force dynamics of kinesin-2

In a single molecule optical trap assay, we found that kinesin-2 and kinesin-1 have similar plateau force values, 5–5.3 pN, but the kinesin-2 stall plateau time is shorter (Fig. 2). Under our assay conditions, single kinesin-2 molecules often detached during the rise of force before a plateau was reached, which was corroborated by force measurements on multiple kinesin-2 motors (Fig. 2 B). Average peak force and maximum peak force increased with increasing kinesin-2 motor density, as was found previously for myosin-V and dynein (15).

At negligible load, it has been shown that the run length of mammalian kinesin-2 is ∼4-fold shorter than that of kinesin-1 due to differences in neck linkers leading to differences in internal strain (19). The velocity of kinesin-2 was measured to be ∼1.6-fold slower than that of kinesin-1 (19). Given the relation that a motor's unbinding rate is equal to its velocity divided by its run length, these differences correspond to a 2.5-fold faster unbinding rate for kinesin-2 during a run compared to kinesin-1. Furthermore, under high load, kinesin-2 has a shorter stall plateau time than kinesin-1 (Fig. 1, F and H), again indicating a higher unbinding rate. The load dependence of run length at intermediate loads has been modeled as an exponential function (Eq. S2), assuming it follows from Kramer's theory (25). The run length of Caenorhabditis elegans heterotrimeric kinesin-2 has been reported to decrease from 243 to 80 nm when the load was increased from 2 to 4 pN (26), suggesting that the scale factor for load dependence of detachment rate (F_d in Eq. S2) is ∼2 pN. The stiffness of the optical trap in our force experiments is ∼0.05 pN/nm leading to the requirement of 100 nm of displacement for the kinesins to reach the 5 pN plateau. These values are consistent with detachment before reaching plateau in many traces. Kinesin-1 probably has a higher value for F_d and/or lower detachment rate, so that it reached plateau more often. F_d = 3 pN has been used to model kinesin-1 detachment (23,27).

Clemen et al. (28) found myosin-V's run length of ∼300 nm in an optical trap assay is essentially independent of force between 5 pN of forward (assisting) to 1.5 pN of backward load (28). This run length is somewhat less than that measured by tracking single fluorescently labeled myosin-V molecules at zero load (29), possibly due to components of trap forces perpendicular to the AF. Force independent run lengths are consistent with our previous data (15) and others (28,30) that myosin-V more often reaches its stall plateau at 2 pN.

Force production by motor ensembles

Vesicular cargos in cells are thought to engage several motors of each type during transport (2,31). Thus, the filament intersection experiments here were carried out with beads loaded with kinesin-2 and myosin-V concentrations that resulted in multiple motors geometrically positioned to interact with their filaments. The average and peak forces, given by our moving-maximum and maximum force measurements, increased with increasing kinesin-2 and myosin-V loading concentrations (Fig. 2, B and C). As mentioned, the relationship between moving maximum force and loading concentration extrapolates to an ordinate intercept (∼2 pN) near the stall force for myosin-V, but less than the plateau force for kinesin-2, because of the relatively rapid detachment under load of the kinesin-2. Taking the maximum force divided by the unitary plateau force as an estimate of the number of motors available bind to the filaments, the beads used for filament crossing trials were driven by 1–5 kinesin-2 motors and 1–7 myosin-V motors.

Modeling cytoskeletal intersections in vitro

As expected from a tug-of-war model, when either myosin-V or kinesin-2 was in excess on the beads to generate a much higher force, beads maintained their track or switched onto the track cognate to the dominant motor. Interestingly, we found that the team of myosin-V motors had to exert less force, compared to the team of kinesin-2 motors, to switch the cargo from a MT to an AF than to remain on an AF. Note that in both cases, the AF was placed over the MT. This characteristic was represented in the data as a shift of the transition force ratio to the right when the bead was started on the AF as opposed to the MT (Fig. 3).

This shift could be modeled by lowering either the engagement ratio or the binding rate of kinesin-2 at intersections when the cargo started on the MT. Physically, the AF may act as a barrier when kinesin-2 is translocating along the MT leading to motor dissociation. Alternatively, the lower detachment force of kinesin-2 relative to its plateau force compared to myosin-V (Table S1) may cause kinesin-2 to detach at intersections more easily than myosin-V at densities where their forces are comparable, and thus lead to a shift in the transition force ratio. A detailed comparison with kinesin-1, which has a slower detachment under load, might distinguish between these possibilities. Although we chose to focus in these studies on a physiologically relevant set of motors: kinesin-2, dynein, and myosin-V, which together drive melanosome motility (3), we performed initial studies with kinesin-1 and found that this motor also showed an enhanced probability of detachment from the MT upon encountering an AF at maximum force ratios below 1 (H. W. Schroeder, E. L. Holzbaur, and Y. E. Goldman, unpublished observations). This suggests that both kinesin-1 and kinesin-2 share an enhanced likelihood of detachment when encountering an obstacle along the MT track.

Dependence of outcomes at cytoskeletal intersections on the starting filament was less apparent in assays with dynein and myosin-V. The differing mechanochemical properties of dynein and kinesin-2 suggest possible explanations. First, our earlier studies examining the effects of passive obstacles, such as the MT-associated protein tau (22) or a crossing MT (13), suggest that single kinesin-1 molecules are more susceptible to detachment upon encountering an obstacle than dynein. Thus, dynein's engagement ratio or binding rate appears to be less sensitive than those of kinesin to the geometry of the intersection (Fig. S2, Table S1). Second, the mechanochemical properties of dynein and kinesin-2 may lead to differences in dissociation kinetics when they operate collectively. The unitary plateau force of dynein (1.1 pN) is less than kinesin-2 (5 pN), implying that more dynein molecules than kinesin-2 are needed to exert similar forces. Thus, under similar loads the force is distributed among a larger team of dynein motors than kinesin-2 motors, and the detachment of one motor increases the load on the remaining engaged motors less markedly. In addition, the ratio of the detachment force to the plateau force for dynein as modeled is 0.68 compared to 0.4 for kinesin-2, suggesting that the dissociation of kinesin-2 is more sensitive to load than that for dynein. Thus, at equal total force, the larger number of motors in a dynein team and the higher detachment force (relative to plateau) cause the dissociation kinetics for a group of dynein motors to be less sensitive to force than a (smaller) group of kinesin-2. Accordingly, simulations of intersection switching for cargo transported by dynein and myosin-V show little dependence on the starting filament, in agreement with experimental observations (15).

Another striking difference relates to stalling at intersections. Kinesin-2/myosin-V beads (as well as kinesin-1/myosin-V beads) rarely stopped at intersections or failed to leave on either the AF or MT. In contrast, when the forces produced by dynein and myosin-V were approximately equal, the motor-bound beads often stopped at AF/MT intersections and remained there for several minutes (∼40% of trials). These differences in the activities of kinesin-2 versus dynein when paired with myosin-V mirror those found when kinesin-1-coated beads or dynein-coated beads were allowed to encounter MT-MT intersections. When starting from a MT underpass, kinesin-1 coated beads seldom passed over a crossing MT, preferring to switch at high loading density and dissociate at low density, whereas dynein-coated beads remained tethered at MT-MT intersections (13).

Conclusions: organelle transport driven by kinesin-2, dynein, and myosin-V

Together with our previous studies (15), we are beginning to understand how kinesin-2 and dynein function when engaged in a tug-of-war with myosin-V. The hypothesis that MT motors and AF motors may compete to pull their shared cargo onto their respective tracks has received support from studies on mouse melanocytes, neurons, macrophages, and Xenopus melanophores (9,32–34). Heterotrimeric kinesin-2, cytoplasmic dynein, and myosin-V are known to be the relevant motors that actively spread melanosomes in Xenopus melanophores throughout the cytoplasm (dispersion) or congregate them near the cell center (aggregation) (9). Our in vitro data now show that switching of a cargo can be regulated to enable myosin-V to win in a tug-of-war with either kinesin-2 or dynein, or to lose to either MT motor simply by changing the maximum number of motors of each motor family available for engagement, 1–5 kinesin-2s, 1–4 dyneins, and 1–7 myosin-Vs. Furthermore, this cargo switching can be finely tuned to permit a wide range of switching probabilities due to the stochastic nature of motor attachment and detachment as illustrated by several steady-state and dynamic models in which the numbers of actively engaged motors are modulated by loading concentrations and attachment and detachment dynamics. Interestingly, the dissociation kinetics of kinesin-2 favor switching from MTs to AFs, consistent with transport during dispersion where kinesin-2 initially drives the peripherally directed transport of melanosomes along MTs, which is followed by the switching of these organelles to AFs. In contrast, the dissociation kinetics of dynein teams are less sensitive to force, consistent with the role of dynein in driving a switch in the association of melanosomes from AF to MTs during aggregation.