Abstract
Understanding how physical signals guide biological processes requires qualitative and quantitative knowledge of the mechanical forces generated and sensed by cells in a physiologically realistic three-dimensional (3D) context. Here, we used computational modeling and engineered epithelial tissues of precise geometry to define the experimental parameters that are required to measure directly the mechanical stress profile of 3D tissues embedded within native type I collagen. We found that to calculate the stresses accurately in these settings, we had to account for mechanical heterogeneities within the matrix, which we visualized and quantified using confocal reflectance and atomic force microscopy. Using this technique, we were able to obtain traction forces at the epithelium-matrix interface, and to resolve and quantify patterns of mechanical stress throughout the surrounding matrix. We discovered that whereas single cells generate tension by contracting and pulling on the matrix, the contraction of multicellular tissues can also push against the matrix, causing emergent compression. Furthermore, tissue geometry defines the spatial distribution of mechanical stress across the epithelium, which communicates mechanically over distances spanning hundreds of micrometers. Spatially resolved mechanical maps can provide insight into the types and magnitudes of physical parameters that are sensed and interpreted by multicellular tissues during normal and pathological processes.
Introduction
Mechanical signals regulate a variety of basic cellular processes, such as survival, proliferation, differentiation, and epithelial plasticity (1–4). Mechanical forces also drive the cellular changes that sculpt tissues and organs during embryogenesis (5,6) and feed back to activate key molecular regulators of morphogenesis (7). Conversely, an abnormal mechanical environment can disrupt tissue homeostasis and potentiate the malignant transformation of epithelial tissues (8,9). Understanding the physical basis of development and disease thus requires quantitative and qualitative information about the mechanical forces that are imparted and experienced by cells and tissues in a physiologically relevant context.
Investigators have developed several techniques to measure the forces generated by cells cultured on two-dimensional (2D) substrata (10). In one such technique, traction force microscopy (TFM), individual cells (10) or multicellular sheets (11–13) are cultured on synthetic hydrogels with tunable mechanical properties. Movement or contraction of the cells causes the substratum to deform, and the resulting displacements are converted into traction forces via the inverse Boussinesq formulation. One can circumvent the mathematical complexity of TFM by using microfabricated arrays of elastomeric pillars and calculating the spatially resolved cellular forces by measuring the deflection of the individual pillars (14–16). These techniques have revealed that cells exert tangential forces that are directed inward, toward the centroid of the cell. Recent studies that measured the full deformations throughout the thickness of the substratum revealed that single endothelial cells and fibroblasts can also exert forces that are normal to the planar surface on which they are cultured (17,18).
These 2D systems have furnished valuable information about the mechanical behavior of cells and have unveiled several modes of mechanotransduction (19,20). However, cells in vivo typically reside in a three-dimensional (3D) microenvironment, and the overwhelming majority of developmental, physiological, and pathological processes are inherently 3D. In an effort to assess cellular mechanics in a more physiological 3D context, Legant et al. (21) developed a method to measure the traction forces imparted by single cells fully encapsulated within a synthetic hydrogel of polyethylene glycol. Cells in these 3D matrices exerted inward-directed, tangential forces near long membrane protrusions, and small inward-directed normal forces near the cell body. The traction behavior of single cells in synthetic 3D environments was surprisingly analogous to the behavior of those on 2D surfaces. However, in contrast to the 2D case (18), no outward-directed normal forces were detected, even though the 2D and 3D studies used the same cell type.
Efforts in mechanobiology have thus focused on measuring the forces generated primarily by single, usually fibroblastic or cancerous, cells. However, early development and organogenesis are largely epithelial phenomena, and epithelial cells rarely function individually. Instead, these cells are connected to each other and the extracellular matrix (ECM) to form 3D polarized tissues. Even force information about individual, metastatic cancer cells is only partially useful for defining the physical basis of cancer if it is not considered within the mechanical context of the primary tumor or untransformed tissue. Indeed, metastasis often proceeds through the collective migration of an interconnected group of cells (22,23). It is unlikely that the mechanical stress generated by cellular collectives is simply the sum of the stresses generated by their constituent cells. The interconnectivity and altered topology of cells within 3D multicellular tissues likely cause emergent mechanical behavior. Quantitative methods to measure forces generated at the 3D tissue level are therefore needed.
Here, we took advantage of the uniform nature of microfabricated tissues to uncover the experimental parameters required to calculate mechanical forces exerted by 3D epithelial tissues. We measured the mechanical stresses exerted by 3D engineered epithelia of arbitrary geometry surrounded by a matrix of native type I collagen. The use of collagen matrices recapitulated physiologically relevant tissue-mediated changes in the local material properties, which significantly affected the magnitude of stress experienced by the tissues. Traction forces at the epithelial surface and patterns of normal and shear stresses throughout the surrounding matrix were quantified and found to be dictated by the geometry of the epithelium. Although cells within the tissues were contracting and thus generating tension, contraction by the tissue could exert compressive forces when the tissues were engineered into certain physiologically relevant shapes.
Materials and Methods
Cell culture and reagents
Functionally normal EpH4 mouse mammary epithelial cells were cultured in 1:1 Dulbecco's modified Eagle's medium:F12 supplemented with 2% fetal bovine serum (Atlanta Biologicals, Norcross, GA), 5 μg/ml insulin, and 50 μg/ml gentamicin (Sigma, St. Louis, MO).
Microfabricated tissues
3D epithelial tissues were constructed as described previously (24). Briefly, neutralized liquid type I collagen (4 mg/ml; Koken, Tokyo, Japan) was gelled at 37°C around stamps of poly(dimethylsiloxane) (Sylgard 184; Ellsworth Adhesives, Germantown, WI) to generate micrometer-scale cavities of defined size and geometry. A concentrated suspension of mammary epithelial cells was allowed to settle within the cavities, and a second layer of collagen was placed on top of the gel. The two layers were fully mechanically integrated (see Fig. S1 in the Supporting Material). The cells were initially randomly dispersed within the cavities. Subsequently, individual cells formed junctions with each other and the surrounding collagen, secreted a basement membrane, and organized into a 3D epithelial tissue within 24 h (25) (Fig. S2).
Calculation of stress within epithelial tissues
Measurement of matrix displacements
To visualize tissue-induced matrix deformations, we dispersed 1-μm-diameter fluorescent polystyrene beads (Invitrogen, Grand Island, NY) in the neutralized collagen solution at high density (∼4 × 108 beads/ml). We collected confocal stacks of 120 images (spaced 1 μm apart) before and after relaxing the tissues with 0.05% Triton X-100 in phosphate-buffered saline using a Hamamatsu ECCD camera attached to a Nikon Ti-U inverted microscope customized with a spinning disk (BioVision Technologies, Exton, PA). After the tissues were lysed, the retraction of the collagen gel was virtually instantaneous. We extracted the 3D and in-plane bead displacements using the Autoregressive Motion tracking routine in Imaris (Bitplane, South Windsor, CT). We then calculated the tissue-induced strains within the collagen gel from the full 3D displacement field using the displacement gradient matrix
| (1) |
where i = 1,2,3; ε is the strain tensor; ui is the displacement in direction i; and xi are rectangular spatial coordinates. The calculated strain values never exceeded 7%.
To quantify the experimental noise of displacement measurement, we monitored the positions of fluorescent markers in cell-free collagen gels. Averaging the displacement maps of 30 samples led to a nearly fivefold increase in the signal/noise ratio, expressed as the ratio between the maximum cell-induced displacement and maximum recorded noise.
Mechanical properties, constitutive model of collagen gels, and calculation of stress
We determined the material properties of the collagen gels via bulk rheometry using the cone-and-plate setup on a Physica MCR 501 rheometer (Anton Paar, Ashland, VA). The chamber was held at 37°C and 100% humidity by means of a Peltier plate and humidity chamber. Oscillatory strains ranging between 0.01% and the maximum cell-induced strains of 7% were imposed. The stress-strain relationship that was recorded remained linear throughout the strain regime (Fig. S3). Accordingly, Hooke's law for isotropic materials was used to describe the constitutive behavior of the collagen gels during tissue-induced deformation:
| (2) |
| (3) |
| (4) |
where δij is the Kronecker delta, T is the Cauchy stress tensor, μ and λ are the Lamé parameters, E is the Young's modulus, and ν = 0.2 is the Poisson ratio (26). The fully determined strain field allowed us to calculate the Cauchy stress directly (using Eqs. 2–4), in a forward fashion (18,27), thus circumventing the need to make assumptions about the stress state and geometry, and invoke ill-posed inverse formulations (10,28–30).
Epithelial tissue surface reconstruction, mesh generation, and calculation of surface tractions
We visualized cell membranes within the engineered epithelial tissues using Vybrant DiO dye (Invitrogen) and collected confocal stacks of 30 images (spaced 2 μm apart in the z-direction) of the tissues. Epithelial surfaces were rendered with the use of Imaris and reconstructed with AutoDesk Inventor Professional. The components and magnitude of the surface traction vector were calculated from the Cauchy stress tensor as follows:
| (5) |
| (6) |
where ti, i = 1,2,3 are the components of the stress vector; nj, j = 1,2,3, are the components of the unit normal vector at a point on the epithelial surface; Tji are the components of the Cauchy stress tensor, and is the magnitude of the traction vector. To simplify solving Eq. 5 over a complex 3D geometry, we used the finite element method (FEM). Specifically, the reconstructed 3D surface was imported into the Comsol Multiphysics 3.5a modeling environment and enclosed within a second computational domain of cylindrical geometry (2 mm in height and diameter), representing the collagen gel. A quadratic tetrahedral finite element mesh of the epithelial surface and the surrounding gel was subsequently generated.
Validation of the model for collagen
To validate our assumptions of homogeneity and isotropy, we took advantage of the fact that the strain and stress state and the internal deformation field of an elastic solid are uniquely determined by a set of displacement boundary conditions and knowledge about the solid's material properties and constitutive behavior. We thus used the experimentally measured displacements of the gel at the boundary of the epithelial tissue to simulate the corresponding internal displacements within an ideally elastic, homogeneous, and isotropic medium. The simulated displacements were then compared with the experimentally measured internal displacements. More specifically, we first substituted Eq. 1 into Eq. 2 to obtain the stress in terms of displacement gradients, and then substituted the result into the equilibrium form of the equation of motion (Eq. 7) to obtain three second-order partial differential equations for the three displacement components (Eq. 8):
| (7) |
| (8) |
The boundary conditions were as follows: three experimentally measured displacement components at the epithelium-matrix interface and three zero-displacement components at the outer boundaries of the collagen gels (zero displacement far away from the tissue). Given the complex 3D geometry of the tissue-matrix boundary, we solved Eq. 8 using FEM.
Results
Mapping of mechanical stress within 3D epithelial tissues
To compare the mechanical behavior of epithelial tissues with that of individual cells, we first examined the contractile activity of single mammary epithelial cells grown on top of or embedded within collagen gels. We monitored the contractility of the cells and the resulting matrix deformation by tracking fluorescent beads embedded within the gel. Single epithelial cells plated on top of collagen induced sharp displacement gradients, with maximum displacements occurring near large membrane protrusions (Fig. 1 A). When fully embedded in collagen, however, the cells induced negligible displacements, with magnitudes under the threshold of experimental noise (Fig. 1 B).
Figure 1.
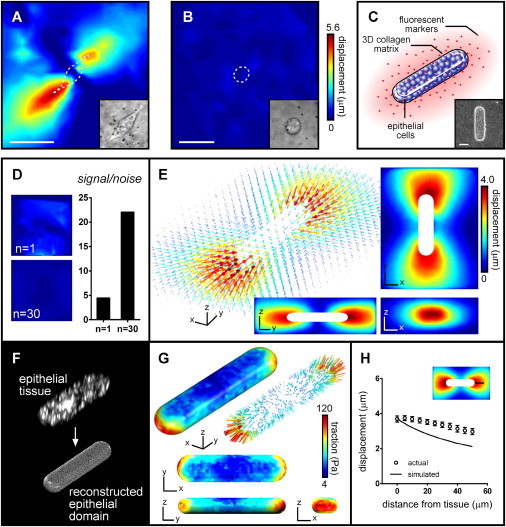
Matrix deformation and mechanical stress within 3D epithelial tissues. (A) Substratum deformation induced by a single epithelial cell plated on top of collagen gel. (B) Matrix deformation induced by a single epithelial cell fully embedded within collagen gel. (C) Diagram showing components of microfabricated tissues (multicellular epithelial duct is surrounded by type I collagen embedded with fluorescent beads). (D) Signal/noise ratio in one sample and average signal/noise ratio of 30 samples. (E) Average 3D matrix deformation induced by 34 epithelial tissues. (F) Epithelial surface reconstruction from a confocal stack of tissue stained for cell membranes and finite element mesh generation. (G) Average 3D traction forces over an epithelial surface of n = 34 tissues. (H) Validation of constitutive model and assumption of homogeneity for collagen gel. Scale bars: 50 μm.
To elucidate the mechanical behavior of epithelia, we constructed multicellular mammary tissues using a microfabrication approach (24) (Fig. 1 C). Arrays of duct-shaped cavities were formed in collagen gels by replica micromolding and subsequently filled with mammary epithelial cells. When covered with a second layer of collagen, the cells within each cavity of the array self-organized into a polarized epithelial tissue and assembled a basement membrane against the collagen gel (Fig. 1 C) (25). Because each tissue was identical in size and geometry, we were able to average the displacement data collected over multiple samples and thereby enhance the signal/noise ratio (Fig. 1 D). The epithelial tissues induced significant displacement of the beads (Fig. 1 E, n = 34). The displacements were larger than those around individual cells embedded within collagen, and formed a gradient that spanned all three dimensions of the tissue. However, in contrast to the cell-level gradients that arose from single cells on top of the gel, the displacements changed negligibly over the length of individual cells within the tissue. These data suggest that epithelial tissues contract as a continuum and hence exhibit an emergent mechanical behavior that differs starkly from the individual behavior of their constituent cells in a 2D or 3D environment.
We estimated the mesh size of the collagen from scanning electron micrographs of the gel cross sections and measurements of the Darcy permeability (Supporting Material and Fig. S4). The average pore size (<450 nm) estimated by both methods was significantly smaller than the beads (1 μm), the average distance between the beads (17 ± 4 μm), and the smallest dimension of the force-applying epithelial tissues (50 μm). Accordingly, we modeled the collagen gel as a continuous medium (31). We determined the bulk material properties of the collagen matrix via rheometry and ascertained its constitutive behavior by examining the stress-strain relation under experimentally relevant magnitudes and rates of deformation. We found that the stress-strain relation remained linear within the experimentally relevant deformation regime (strains up to 7%); that is, the material properties of the gels did not depend on the magnitude of applied strain (Fig. S3 A). Furthermore, the Young's modulus of the gels did not exhibit a strain rate dependence (Fig. S3 B). Accordingly, we modeled the collagen as a linearly elastic and isotropic solid. We calculated strains throughout the collagen gel from the 3D displacement field using the displacement gradient matrix (Eq. 1), and calculated the Cauchy stress tensor throughout the gel directly from the strains using Hooke's law for isotropic materials (Eqs. 2–4). Traction forces at the epithelium-matrix interface were subsequently calculated (Eqs. 5 and 6, and Fig. 1 F). The magnitude of the traction vectors across the surface of the epithelium was nonuniform, with the maximum traction observed at the short ends of cylindrical tissues (Fig. 1 G).
To test the validity of our constitutive model, we ascribed experimental displacements measured near the tissue as boundary conditions of a homogeneous, isotropic computational domain and simulated displacements away from the boundary into the domain (Eq. 8). The simulated displacements were compared with those measured experimentally throughout the collagen gel (Fig. 1 H). We found that the displacements measured experimentally propagated farther than those calculated from the model, suggesting that additional information is needed to calculate tissue-generated forces accurately. There are three possible explanations for this discrepancy: error in the material properties of collagen measured by bulk rheometry, an inadequate constitutive model for collagen, or local variations in the mechanics of the gel. We tested the contributions of these potential sources of error computationally. Varying the bulk mechanical properties of the computational domain to account for possible inaccuracies in the rheometric analysis did not change the simulated displacement profile (Fig. S5 A). Similarly, using a viscoelastic constitutive model to describe the computational domain did not affect the profile of the simulated displacements (Fig. S5 B). Therefore, we set out to test whether mechanical heterogeneities or anisotropies within the collagen gel were responsible for the discrepancy.
Epithelial tissues cause mechanical heterogeneities in the surrounding matrix
Cells remodel the ECM during development and disease (32). Epithelial cells in vivo synthesize and deposit several ECM proteins, thereby altering the local ECM density and possibly also its mechanical properties (33). Conversely, epithelial tissues express enzymes (e.g., matrix metalloproteinases) that can locally degrade the ECM (34–36). In addition, individual normal and cancer cells have been shown to align and compact the surrounding 3D collagen matrix in a contractility-dependent fashion (37–44). Cell-induced remodeling can give rise to local differences in the material properties of the ECM, rendering it mechanically heterogeneous or anisotropic (41,45). In such a case, the assumption of a homogeneous isotropic ECM would likely introduce inaccuracies into the solution of the inverse problem.
To determine whether multicellular epithelial tissues also remodel their surrounding ECM, we visualized the structure of the collagen gel adjacent to the engineered tissues using confocal reflection microscopy (46–48). Imaging of cell-free gels revealed a spatially homogeneous distribution of collagen fibrils, indicating that the microfabrication process alone did not introduce heterogeneities into the structure or density of the collagen (Fig. 2, A and B). However, we found consistently higher signal intensities in the matrix near the epithelial tissues, suggesting a cell-mediated local increase in collagen density (Fig. 2, C–F). These changes may be attributed to strain-induced matrix compaction, alignment, or de novo synthesis, as discussed above.
Figure 2.
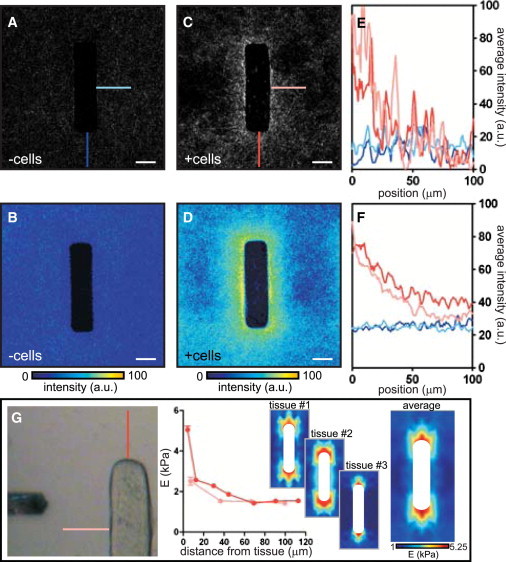
Visualization and quantification of tissue-induced mechanical heterogeneities within the matrix. (A) Confocal reflection image of collagen gel around single cell-free molded cavity. (B) Average collagen intensity around 20 cell-free cavities. (C) Confocal reflection image of collagen gel around single epithelial tissue. (D) Average collagen intensity around 20 epithelial tissues. (E) Quantification of collagen intensity in A and C. (F) Quantification of collagen intensity in B and D. (G) The elasticity of the collagen surrounding the tissue was probed by AFM. Shown is a representative plot of the collagen gel stiffness away from the side and the end of the tissue. Stiffness maps of the matrix surrounding the epithelium were generated for three separate tissues and averaged. Scale bars: 50 μm.
To test whether the heterogeneities in the density of collagen were accompanied by heterogeneities in its mechanical properties, we used atomic force microscopy (AFM) to measure the microscale elasticity of the ECM surrounding the epithelium. We probed the gel at various locations around the tissue and generated a stiffness map of the region (Fig. 2 G). This approach revealed striking mechanical variations. The stiffness of the collagen increased near the epithelium; however, whereas a relatively shallow stiffness gradient (spanning 1 kPa) was detected near the side of the epithelial tissue, a sharp gradient (spanning ∼4 kPa) was present near the ends (Fig. 2 G). Curiously, the stiffness profile of the gel did not fully correlate with the map of collagen density generated by confocal reflection microscopy. Nonetheless, the stiffness map was similar in profile to that of the bead displacements (Fig. 1 G), leading us to speculate that the increase in stiffness near the end of the tissues results from local changes in the matrix. Of note, the stiffness of the matrix measured far away from the tissue by AFM was in excellent agreement with the values obtained by bulk rheometry (∼1 kPa).
Cell-induced matrix heterogeneities significantly affect the mechanical profile of epithelial tissues
To test the effect of variations in stiffness on the calculation of force, we simulated deformation of a gel that incorporated the mechanical heterogeneities measured by AFM (Fig. 3, A–C). The resulting displacements (Fig. 3 C) were compared with those measured experimentally (Fig. 3 A) and those simulated to occur within a mechanically homogeneous gel (Fig. 3 B). We found that accounting for mechanical variations dramatically reduced the discrepancy between the simulated and measured displacements (Fig. 3, D–F), which strongly suggests that assuming homogeneous mechanical properties is not appropriate to capture the mechanical behavior of collagen in this context. Accordingly, we incorporated the stiffness variations of the gel, as measured by AFM, and recalculated the mechanical stress throughout the midsection of the epithelial tissue (Fig. 3 G). Accounting for mechanical variations did not have a discernible effect on the pattern but significantly altered the magnitude of the traction calculated, in that the average traction at the ends of the epithelium nearly doubled (Fig. 3, G and H).
Figure 3.
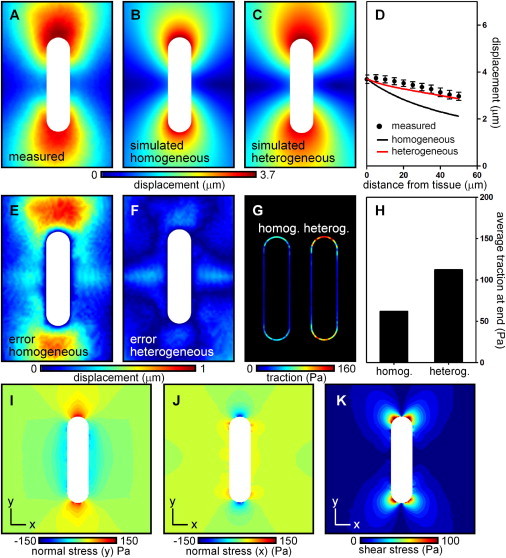
Epithelial tissue-generated forces give rise to gradients in interfacial traction and patterns of stress within the surrounding matrix. (A) Experimentally measured tissue-induced matrix displacements throughout a midsection of the tissue. (B) Matrix deformations recovered assuming a homogeneous material. (C) Matrix deformations recovered within a heterogeneous material. Mechanical variations were ascribed from experimental AFM data. (D) Matrix displacements in A–C along a line away from the end of the tissue. (E and F) Discrepancy between experimental deformation and deformation simulated in a (E) homogeneous or (F) heterogeneous matrix. (G) Traction at the epithelial surface assuming a mechanically homogeneous or heterogeneous matrix. (H) Average traction at the end of the tissue assuming a homogeneous or heterogeneous matrix. (I) Normal stress in the y-direction throughout the matrix. (J) Normal stress in the x-direction throughout the matrix. (K) Shear stress throughout the matrix.
We also used this approach to calculate the components of the stress tensor throughout the gel surrounding the epithelium (Fig. 3, I–K). These were consistent with the tractions calculated at the epithelial surface. High positive (tensile) stresses were observed in the direction locally normal to the epithelial surface, whereas negative (compressive) stresses accumulated in the direction tangential to the surface at each location (Fig. 3, I and J). The magnitude of the tensile stresses was significantly higher in the matrix regions surrounding the short ends of the epithelium. Striking patterns of shear stresses were also notable at these regions (Fig. 3 K). Hence, there appeared to exist a consistent relationship between types and magnitudes of mechanical stress on the one hand, and geometrical features within the tissue on the other.
Epithelial tissue geometry dictates the spatial distribution of mechanical stress
In vivo, epithelial tissues form into a variety of geometries to achieve their physiological functions. To examine how the geometric boundary conditions of a tissue affect the resulting mechanical behavior, we engineered epithelial tissues that contained distinct geometrical features (Fig. 4 A). The tissue-mediated increase in collagen density near the epithelium appeared to be independent of the boundary conditions and local geometry (Fig. 4 B), which, by contrast, profoundly affected the extent of deformation of the adjacent matrix and the distribution of forces across the tissue. Large matrix deformations occurred along the long axes of the tissue, near acute angles, and near regions of high curvature (Fig. 4 C). Large traction forces were observed at angular regions of the epithelium, with acute angles pulling on the matrix with higher inward force than did obtuse angles (Fig. 4 D). The mechanical stresses that arose within the ECM also depended on the tissue geometry. Tensile stresses arose in the direction locally normal to the epithelial surface, whereas compressive stresses accumulated in the locally tangential direction (Fig. 4, E and F). Tensile stresses were larger in the matrix adjacent to acute epithelial angles than near obtuse epithelial angles (Fig. 4, E and F).
Figure 4.
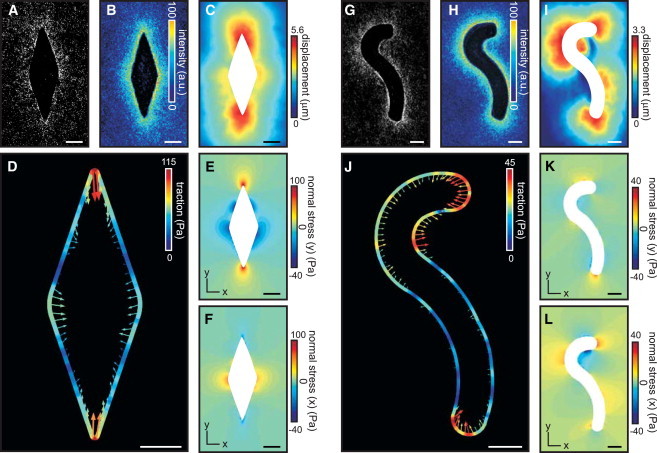
Mechanical profile of epithelial tissues depends on their geometry. (A) Epithelial tissue containing obtuse and acute angles. (B) Average intensity of collagen surrounding tissue in A (n = 20). (C) Matrix displacement induced by tissue in A. (D) Traction force over the boundary of epithelial tissue in A. (E and F) Normal stress in the (E) y-direction and (F) x-direction throughout matrix surrounding the tissue in A. (G) Epithelial tissue containing regions of varying convex and concave curvature. (H) Average intensity of collagen surrounding tissue in G (n = 20). (I) Matrix displacement induced by tissue in G. (J) Traction force over the boundary of epithelial tissue in G. (K and L) Normal stress in the (K) y-direction and (L) x-direction throughout matrix surrounding tissue in G. Scale bars: 50 μm.
We observed unexpected geometry-dependent mechanical behavior in curved duct-like tissues (Fig. 4, G–I). Although regions of high curvature consistently generated higher traction forces (Fig. 4 J), the forces were not directed inward everywhere along the boundary. In particular, the forces generated at regions of concave curvature were directed outward, suggesting that in these regions the matrix is pushed by the epithelium (Fig. 4 J). Of note, we did not observe cell proliferation localized to the regions experiencing compressive forces (Fig. S6, A and B), which suggests that the pushing is not active, i.e., it is not a product of expansive growth, as previously observed in the case of growing tumor spheroids (21,49). Furthermore, blocking myosin motor activity, which is classically associated with the generation of tension, abolished both the tensile forces at the convex regions and the compressive forces at the concave regions of the tissue (Fig. S6, C and D). This observation indicates that the existence of the compressive forces is directly dependent on the generation of tensile forces, and that the former likely serve to maintain mechanical equilibrium within the multicellular structure. This compressive mechanical behavior of the engineered tissues is reflected by the distribution of stresses within the surrounding matrix: whereas compressive stresses typically arose in the direction locally tangential to the epithelial boundary, compressive stresses near concave boundaries accumulated in both the locally normal and tangential directions (Fig. 4, K and L). This phenomenon further highlights the emergent mechanical behavior of multicellular epithelial tissues: whereas individual epithelial cells can only pull on the surrounding 3D matrix (21), the collective contraction of epithelial tissues can give rise to regions where the tissue effectively pushes against the matrix.
Mechanical interaction between adjacent epithelial tissues
It has been established that the communication of biochemical and mechanical signals between cells guides the development and homeostasis of epithelial tissues and organs (50). Communication between and within tissues is mediated by the transmission of molecular signals, which can act at varying length scales. In addition, long-range communication can be generated through mechanical cues (51). Theoretical models describing the propagation of cell-generated strain through the ECM predicted that cells can communicate and interact elastically to form aligned strings (52). The predictions of this model have since been confirmed by several experimental findings. For example, it was shown that endothelial cells plated on compliant substrata can sense each other by detecting strains generated by neighboring cells and channeled through the matrix (53). These mechanical interactions were shown to direct the migration of individual cells and promote the establishment of cell-cell contacts. Similarly, individual fibroblasts and human mesenchymal stem cells in 3D fibrin matrices can communicate position and orientation via the long-range transmission of mechanical signals (45).
To test whether a homologous form of force-mediated mechanical communication occurs at the level of the epithelial tissue, we varied the distance between epithelial tissues and measured their corresponding mechanical profiles. We used microfabrication to position the tissues relative to each other such that one end of the tissue (hereafter referred to as the distal end) was always far away from neighboring tissues, whereas the proximal ends of adjacent tissues were separated by 400, 200, 100, or 50 μm (Fig. 5). At a separation of 400 μm, there was virtually no difference between the matrix deformations or traction forces calculated at the distal and proximal ends (Fig. 5, A–C), suggesting that the tissue was mechanically unaware of the neighboring epithelium. Reducing the distance between the tissues to 200 μm resulted in a significant decrease in the matrix deformation at the proximal end and a moderate decrease in the corresponding traction forces (Fig. 5, D–F). The differences in both matrix deformation and traction between the distal and proximal ends increased further as the tissues were positioned 100 μm or 50 μm apart (Fig. 5, G–L). These results indicate that the mechanics of epithelial tissues is not fully determined by their constituent cells, the multicellular geometry, and the material properties of the matrix immediately surrounding the tissue. The final mechanical landscape of the tissue is also affected by its broader mechanical environment—in this case, forces generated by neighboring epithelia. The extent and length scale of this mechanical interaction likely depend on multiple factors, including the elasticity of the matrix and the contractile activity of the participating tissues.
Figure 5.
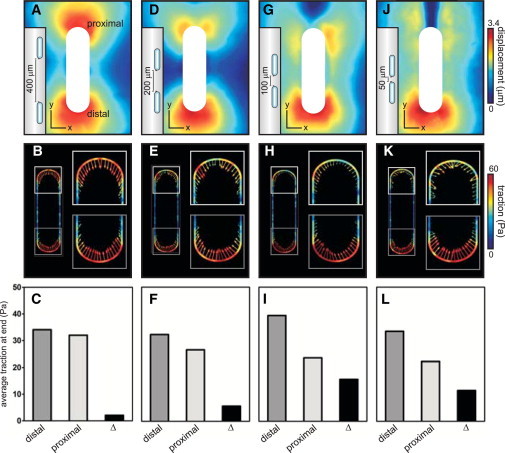
Mechanical communication between adjacent epithelial tissues. (A, D, G, and J) Matrix deformation around tissues spaced 400, 200, 100, and 50 μm apart. (B, E, H, and K) Surface traction of tissues in A, D, G, and J. (C, F, I, and L) Comparison of average surface traction at the proximal and distal ends of tissues in B, E, H, and K.
Discussion
Recent advances have enabled the measurement of 3D forces exerted by cells attached to 2D substrata (18) and fully embedded within synthetic hydrogels (21). Although such measurements have dramatically improved our knowledge about how cells interact with their physical microenvironment, we are still far from understanding how these interactions are governed in a native, physiological context (54). In particular, synthetic matrices fail to recapitulate the physical complexity of the native ECM, which is heterogeneous, viscoelastic, and nonlinear and often changes dynamically over timescales relevant to biological processes. Further, measuring forces generated by single cells leaves the contribution of intercellular forces, which serve to both maintain the integrity of epithelial tissues and regulate their morphogenesis (55,56), a major unknown (54). Although recent investigations of forces within multicellular monolayers plated on synthetic gels have significantly improved our understanding of collective mechanical behavior (11–13), the concepts have not been explored in more physiological 3D ECM. Here, we combined 3D microfabrication approaches with TFM, confocal reflection microscopy, and AFM to examine the mechanics of epithelial tissues within native ECM comprised of collagen type I. Our data reveal the existence of unexpected mechanical behaviors in multicellular tissues, and uncover several parameters that should be considered in future endeavors to map native tissues mechanically.
The microfabrication approaches allowed us to engineer epithelial tissues with architecture reminiscent of those of numerous ductal structures within the body. By embedding the epithelium within type I collagen, a major component of the native ECM, we made a step forward in capturing the complexity of the physiological environment around these multicellular tissues. In particular, we were able to recapitulate physiologically realistic ECM remodeling (32,33,40), in which the epithelial tissue introduced mechanical heterogeneities into the surrounding matrix that are absent in models using bioinert synthetic hydrogels. Mechanical interactions between individual cancer cells and 3D collagen matrix were previously quantified (31); however, possible nonuniformities and strain-stiffening effects were neglected. Here, we visualized tissue-induced nonuniformities within the collagenous ECM and demonstrated that they cause mechanical heterogeneities by measuring the local mechanical properties of the collagen gel directly. Our data strongly suggest that to accurately calculate mechanical stress in these settings, one must account for these mechanical variations, and that this parameter should be considered in attempts to quantify mechanical stress in native tissues. Our microfabrication approach also permitted us to examine the strains around several tissues of identical geometry and average these strains across the tissues during the calculation of stress, reducing the noise in the calculation. This averaging also decreased the resolution of our calculations as compared with conventional 2D TFM. Here, we focus on differences in traction stresses across large regions of the epithelial tissue, rather than attempt to pinpoint them to specific subcellular force-inducing structures such as focal adhesions, the existence of which in 3D tissues is still controversial (57). In the absence of information about the matrix heterogeneities, our data show that one can still infer qualitative information about the spatial distribution of mechanical stresses by focusing on the spatial distributions of the strains.
It must be emphasized that although our engineered tissues represent a step forward compared with cells cultured on top of or within synthetic hydrogels, they are still a simplified model of the highly complex native microenvironment. For instance, mammary ducts in vivo are embedded within a complex stroma that in addition to collagen type I contains collagen type III, proteoglycans, hyaluronic acid, fibronectin, and tenascins (58,59). Accordingly, more involved constitutive models may be required to capture the compositional heterogeneities of the microenvironment in vivo. Furthermore, deformations of the native ECM owing to morphogenesis occur slowly (0.5 mm/day during mammary development (60)), suggesting the possibility of a role for viscoelastic effects.
Whereas previous investigators measured the cell-matrix forces that arise due to the contraction of single cells, we calculated those exerted by multicellular epithelial tissues and thus were able to define their intrinsic mechanical tone. Although our study does not decouple the separate contributions of cell-cell and cell-matrix forces, it reports the overall mechanical profile of the tissue, which is sculpted by both forces and displays a number of emergent characteristics that are not observed in single cells. Indeed, the very ability of the tissues to exert a force sufficient to deform the surrounding matrix seems to be dependent on the existence of intercellular forces, because no deformation of the matrix around single epithelial cells was detected. A notable difference between the mechanics of our 3D multicellular tissues and that of single fibroblastic cells in 3D is that the latter exert large inward-directed shear forces and small inward-directed normal forces (21), whereas large, inward-directed normal forces were observed at the ends of the duct-like tissues. Moreover, we discovered that the collective contraction of the interconnected cells can give rise to emergent outward-directed normal (compressive) forces, which are absent when a single cell interacts with 3D matrix (21). Surprisingly little attention has been given to the relative effects of endogenous tensile (pulling) and compressive (pushing) forces, which may have distinct or even opposing effects. Emergent mechanical effects linked to interaction within cellular collectives were previously shown in the case of osteoblasts embedded in 3D collagen gels (41). In particular, although individual osteoblasts pulled on the surrounding matrix in a spatially random manner, the gel experienced an anisotropic bulk contraction wherein one direction of the gel was compacted more than the other by an order of magnitude. Interestingly, the anisotropic contraction occurred at cell densities above a critical threshold, underscoring the cooperative nature of the phenomenon.
The microfabrication and 3D force measurement methods presented here allow us to directly measure the mechanical stresses generated by 3D epithelial tissues, define the parameters that govern epithelial force generation, and subsequently fabricate tissues with precisely tuned mechanical profiles. Tissue geometries can be designed to control both the magnitude and type of stress (tensile, compressive, and shear) at a given location. Such controlled application of force can help elucidate how cells and tissues sense and respond to quantitative and qualitative variations in force. We propose that simultaneous imaging of cells, beads, and ECM provides a promising platform to explore the long-term spatiotemporal variations in the mechanical landscape of morphogenetic epithelial tissues.
Acknowledgments
We thank Cliff Brangwynne and Joe Tien for helpful discussions, Lynn Loo for cleanroom access, Robert Prud'homme for rheometer use, Eric Wieschaus for scanning electron microscope use, and Reba Samanta for technical assistance.
This work was supported in part by the National Institutes of Health (GM083997, HL110335, and CA128660), Susan G. Komen for the Cure, the David and Lucile Packard Foundation, and the Alfred P. Sloan Foundation. C.M.N. holds a Career Award at the Scientific Interface from the Burroughs Wellcome Fund. N.G. was supported in part by a Wallace Memorial Honorific Fellowship.
Supporting Material
References
- 1.Gomez E.W., Chen Q.K., Nelson C.M. Tissue geometry patterns epithelial-mesenchymal transition via intercellular mechanotransduction. J. Cell. Biochem. 2010;110:44–51. doi: 10.1002/jcb.22545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.McBeath R., Pirone D.M., Chen C.S. Cell shape, cytoskeletal tension, and RhoA regulate stem cell lineage commitment. Dev. Cell. 2004;6:483–495. doi: 10.1016/s1534-5807(04)00075-9. [DOI] [PubMed] [Google Scholar]
- 3.Nelson C.M., Jean R.P., Chen C.S. Emergent patterns of growth controlled by multicellular form and mechanics. Proc. Natl. Acad. Sci. USA. 2005;102:11594–11599. doi: 10.1073/pnas.0502575102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Engler A.J., Sen S., Discher D.E. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 5.Martin A.C., Kaschube M., Wieschaus E.F. Pulsed contractions of an actin-myosin network drive apical constriction. Nature. 2009;457:495–499. doi: 10.1038/nature07522. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rauzi M., Verant P., Lenne P.F. Nature and anisotropy of cortical forces orienting Drosophila tissue morphogenesis. Nat. Cell Biol. 2008;10:1401–1410. doi: 10.1038/ncb1798. [DOI] [PubMed] [Google Scholar]
- 7.Farge E. Mechanical induction of Twist in the Drosophila foregut/stomodeal primordium. Curr. Biol. 2003;13:1365–1377. doi: 10.1016/s0960-9822(03)00576-1. [DOI] [PubMed] [Google Scholar]
- 8.Levental K.R., Yu H., Weaver V.M. Matrix crosslinking forces tumor progression by enhancing integrin signaling. Cell. 2009;139:891–906. doi: 10.1016/j.cell.2009.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Paszek M.J., Zahir N., Weaver V.M. Tensional homeostasis and the malignant phenotype. Cancer Cell. 2005;8:241–254. doi: 10.1016/j.ccr.2005.08.010. [DOI] [PubMed] [Google Scholar]
- 10.Dembo M., Wang Y.L. Stresses at the cell-to-substrate interface during locomotion of fibroblasts. Biophys. J. 1999;76:2307–2316. doi: 10.1016/S0006-3495(99)77386-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Angelini T.E., Hannezo E., Weitz D.A. Cell migration driven by cooperative substrate deformation patterns. Phys. Rev. Lett. 2010;104:168104. doi: 10.1103/PhysRevLett.104.168104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tambe D.T., Hardin C.C., Trepat X. Collective cell guidance by cooperative intercellular forces. Nat. Mater. 2011;10:469–475. doi: 10.1038/nmat3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Trepat X., Wasserman M.R., Fredberg J.J. Physical forces during collective cell migration. Nat. Phys. 2009;5:426–430. [Google Scholar]
- 14.Tan J.L., Tien J., Chen C.S. Cells lying on a bed of microneedles: an approach to isolate mechanical force. Proc. Natl. Acad. Sci. USA. 2003;100:1484–1489. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.du Roure O., Saez A., Ladoux B. Force mapping in epithelial cell migration. Proc. Natl. Acad. Sci. USA. 2005;102:2390–2395. doi: 10.1073/pnas.0408482102. (Erratum in Proc. Natl. Acad. Sci. USA. 2005 102:14122) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Ghassemi S., Meacci G., Hone J. Cells test substrate rigidity by local contractions on submicrometer pillars. Proc. Natl. Acad. Sci. USA. 2012;109:5328–5333. doi: 10.1073/pnas.1119886109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hur S.S., Zhao Y., Chien S. Live cells exert 3-dimensional traction forces on their substrata. Cell Mol. Bioeng. 2009;2:425–436. doi: 10.1007/s12195-009-0082-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Maskarinec S.A., Franck C., Ravichandran G. Quantifying cellular traction forces in three dimensions. Proc. Natl. Acad. Sci. USA. 2009;106:22108–22113. doi: 10.1073/pnas.0904565106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Chen C.S., Mrksich M., Ingber D.E. Geometric control of cell life and death. Science. 1997;276:1425–1428. doi: 10.1126/science.276.5317.1425. [DOI] [PubMed] [Google Scholar]
- 20.Schwartz M.A. Integrins and extracellular matrix in mechanotransduction. Cold Spring Harb. Perspect. Biol. 2010;2:a005066. doi: 10.1101/cshperspect.a005066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Legant W.R., Miller J.S., Chen C.S. Measurement of mechanical tractions exerted by cells in three-dimensional matrices. Nat. Methods. 2010;7:969–971. doi: 10.1038/nmeth.1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Friedl P., Gilmour D. Collective cell migration in morphogenesis, regeneration and cancer. Nat. Rev. Mol. Cell Biol. 2009;10:445–457. doi: 10.1038/nrm2720. [DOI] [PubMed] [Google Scholar]
- 23.Khalil A.A., Friedl P. Determinants of leader cells in collective cell migration. Integr. Biol. (Camb.) 2010;2:568–574. doi: 10.1039/c0ib00052c. [DOI] [PubMed] [Google Scholar]
- 24.Nelson C.M., Inman J.L., Bissell M.J. Three-dimensional lithographically defined organotypic tissue arrays for quantitative analysis of morphogenesis and neoplastic progression. Nat. Protoc. 2008;3:674–678. doi: 10.1038/nprot.2008.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nelson C.M., Vanduijn M.M., Bissell M.J. Tissue geometry determines sites of mammary branching morphogenesis in organotypic cultures. Science. 2006;314:298–300. doi: 10.1126/science.1131000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Barocas V.H., Moon A.G., Tranquillo R.T. The fibroblast-populated collagen microsphere assay of cell traction force—Part 2: Measurement of the cell traction parameter. J. Biomech. Eng. 1995;117:161–170. doi: 10.1115/1.2795998. [DOI] [PubMed] [Google Scholar]
- 27.Franck C., Maskarinec S.A., Ravichandran G. Three-dimensional traction force microscopy: a new tool for quantifying cell-matrix interactions. PLoS ONE. 2011;6:e17833. doi: 10.1371/journal.pone.0017833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Butler J.P., Tolić-Nųrrelykke I.M., Fredberg J.J. Traction fields, moments, and strain energy that cells exert on their surroundings. Am. J. Physiol. Cell Physiol. 2002;282:C595–C605. doi: 10.1152/ajpcell.00270.2001. [DOI] [PubMed] [Google Scholar]
- 29.Sabass B., Gardel M.L., Schwarz U.S. High resolution traction force microscopy based on experimental and computational advances. Biophys. J. 2008;94:207–220. doi: 10.1529/biophysj.107.113670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Schwarz U.S., Balaban N.Q., Safran S.A. Calculation of forces at focal adhesions from elastic substrate data: the effect of localized force and the need for regularization. Biophys. J. 2002;83:1380–1394. doi: 10.1016/S0006-3495(02)73909-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Koch T.M., Münster S., Fabry B. 3D Traction forces in cancer cell invasion. PLoS ONE. 2012;7:e33476. doi: 10.1371/journal.pone.0033476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Gjorevski N., Nelson C.M. Bidirectional extracellular matrix signaling during tissue morphogenesis. Cytokine Growth Factor Rev. 2009;20:459–465. doi: 10.1016/j.cytogfr.2009.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Daniel C.W., Robinson S., Silberstein G.B. The role of TGF-beta in patterning and growth of the mammary ductal tree. J. Mammary Gland Biol. Neoplasia. 1996;1:331–341. doi: 10.1007/BF02017389. [DOI] [PubMed] [Google Scholar]
- 34.Mori H., Gjorevski N., Nelson C.M. Self-organization of engineered epithelial tubules by differential cellular motility. Proc. Natl. Acad. Sci. USA. 2009;106:14890–14895. doi: 10.1073/pnas.0901269106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sternlicht M.D., Sunnarborg S.W., Werb Z. Mammary ductal morphogenesis requires paracrine activation of stromal EGFR via ADAM17-dependent shedding of epithelial amphiregulin. Development. 2005;132:3923–3933. doi: 10.1242/dev.01966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Wiseman B.S., Sternlicht M.D., Werb Z. Site-specific inductive and inhibitory activities of MMP-2 and MMP-3 orchestrate mammary gland branching morphogenesis. J. Cell Biol. 2003;162:1123–1133. doi: 10.1083/jcb.200302090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kraning-Rush C.M., Carey S.P., Reinhart-King C.A. The role of the cytoskeleton in cellular force generation in 2D and 3D environments. Phys. Biol. 2011;8:015009. doi: 10.1088/1478-3975/8/1/015009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pang Y., Ucuzian A.A., Greisler H.P. The temporal and spatial dynamics of microscale collagen scaffold remodeling by smooth muscle cells. Biomaterials. 2009;30:2023–2031. doi: 10.1016/j.biomaterials.2008.12.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Pang Y., Wang X., Greisler H.P. Dynamic quantitative visualization of single cell alignment and migration and matrix remodeling in 3-D collagen hydrogels under mechanical force. Biomaterials. 2011;32:3776–3783. doi: 10.1016/j.biomaterials.2011.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Provenzano P.P., Inman D.R., Keely P.J. Contact guidance mediated three-dimensional cell migration is regulated by Rho/ROCK-dependent matrix reorganization. Biophys. J. 2008;95:5374–5384. doi: 10.1529/biophysj.108.133116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Fernandez P., Bausch A.R. The compaction of gels by cells: a case of collective mechanical activity. Integr. Biol. (Camb.) 2009;1:252–259. doi: 10.1039/b822897c. [DOI] [PubMed] [Google Scholar]
- 42.Bloom R.J., George J.P., Wirtz D. Mapping local matrix remodeling induced by a migrating tumor cell using three-dimensional multiple-particle tracking. Biophys. J. 2008;95:4077–4088. doi: 10.1529/biophysj.108.132738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Stevenson M.D., Sieminski A.L., Gooch K.J. Pericellular conditions regulate extent of cell-mediated compaction of collagen gels. Biophys. J. 2010;99:19–28. doi: 10.1016/j.bpj.2010.03.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Ulrich T.A., Jain A., Kumar S. Probing cellular mechanobiology in three-dimensional culture with collagen-agarose matrices. Biomaterials. 2010;31:1875–1884. doi: 10.1016/j.biomaterials.2009.10.047. [DOI] [PubMed] [Google Scholar]
- 45.Winer J.P., Oake S., Janmey P.A. Non-linear elasticity of extracellular matrices enables contractile cells to communicate local position and orientation. PLoS ONE. 2009;4:e6382. doi: 10.1371/journal.pone.0006382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Brightman A.O., Rajwa B.P., Voytik-Harbin S.L. Time-lapse confocal reflection microscopy of collagen fibrillogenesis and extracellular matrix assembly in vitro. Biopolymers. 2000;54:222–234. doi: 10.1002/1097-0282(200009)54:3<222::AID-BIP80>3.0.CO;2-K. [DOI] [PubMed] [Google Scholar]
- 47.Friedl P., Maaser K., Zänker K.S. Migration of highly aggressive MV3 melanoma cells in 3-dimensional collagen lattices results in local matrix reorganization and shedding of alpha2 and beta1 integrins and CD44. Cancer Res. 1997;57:2061–2070. [PubMed] [Google Scholar]
- 48.Pang Y., Wang X., Greisler H.P. Local delivery of a collagen-binding FGF-1 chimera to smooth muscle cells in collagen scaffolds for vascular tissue engineering. Biomaterials. 2010;31:878–885. doi: 10.1016/j.biomaterials.2009.10.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gordon V.D., Valentine M.T., Deisboeck T.S. Measuring the mechanical stress induced by an expanding multicellular tumor system: a case study. Exp. Cell Res. 2003;289:58–66. doi: 10.1016/s0014-4827(03)00256-8. [DOI] [PubMed] [Google Scholar]
- 50.Gjorevski N., Nelson C.M. Integrated morphodynamic signalling of the mammary gland. Nat. Rev. Mol. Cell Biol. 2011;12:581–593. doi: 10.1038/nrm3168. [DOI] [PubMed] [Google Scholar]
- 51.Nelson C.M. Geometric control of tissue morphogenesis. Biochim. Biophys. Acta. 2009;1793:903–910. doi: 10.1016/j.bbamcr.2008.12.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bischofs I.B., Schwarz U.S. Cell organization in soft media due to active mechanosensing. Proc. Natl. Acad. Sci. USA. 2003;100:9274–9279. doi: 10.1073/pnas.1233544100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Reinhart-King C.A., Dembo M., Hammer D.A. Cell-cell mechanical communication through compliant substrates. Biophys. J. 2008;95:6044–6051. doi: 10.1529/biophysj.107.127662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Trepat X., Fabry B., Fredberg J.J. Pulling it together in three dimensions. Nat. Methods. 2010;7:963–965. doi: 10.1038/nmeth1210-963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Caussinus E., Colombelli J., Affolter M. Tip-cell migration controls stalk-cell intercalation during Drosophila tracheal tube elongation. Curr. Biol. 2008;18:1727–1734. doi: 10.1016/j.cub.2008.10.062. [DOI] [PubMed] [Google Scholar]
- 56.Rauzi M., Lenne P.F., Lecuit T. Planar polarized actomyosin contractile flows control epithelial junction remodelling. Nature. 2010;468:1110–1114. doi: 10.1038/nature09566. [DOI] [PubMed] [Google Scholar]
- 57.Cukierman E., Pankov R., Yamada K.M. Taking cell-matrix adhesions to the third dimension. Science. 2001;294:1708–1712. doi: 10.1126/science.1064829. [DOI] [PubMed] [Google Scholar]
- 58.Muschler J., Streuli C.H. Cell-matrix interactions in mammary gland development and breast cancer. Cold Spring Harb. Perspect. Biol. 2010;2:a003202. doi: 10.1101/cshperspect.a003202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Schedin P., Mitrenga T., Kaeck M. Mammary ECM composition and function are altered by reproductive state. Mol. Carcinog. 2004;41:207–220. doi: 10.1002/mc.20058. [DOI] [PubMed] [Google Scholar]
- 60.Hinck L., Silberstein G.B. Key stages in mammary gland development: the mammary end bud as a motile organ. Breast Cancer Res. 2005;7:245–251. doi: 10.1186/bcr1331. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


