Computational Optogenetics: A Novel Continuum Framework for the Photoelectrochemistry of Living Systems

Abstract

Electrical stimulation is currently the gold standard treatment for heart rhythm disorders. However, electrical pacing is associated with technical limitations and unavoidable potential complications. Recent developments now enable the stimulation of mammalian cells with light using a novel technology known as optogenetics. The optical stimulation of genetically engineered cells has significantly changed our understanding of electrically excitable tissues, paving the way towards controlling heart rhythm disorders by means of photostimulation. Controlling these disorders, in turn, restores coordinated force generation to avoid sudden cardiac death. Here, we report a novel continuum framework for the photoelectrochemistry of living systems that allows us to decipher the mechanisms by which this technology regulates the electrical and mechanical function of the heart. Using a modular multiscale approach, we introduce a non-selective cation channel, channelrhodopsin-2, into a conventional cardiac muscle cell model via an additional photocurrent governed by a light-sensitive gating variable. Upon optical stimulation, this channel opens and allows sodium ions to enter the cell, inducing electrical activation. In side-by-side comparisons with conventional heart muscle cells, we show that photostimulation directly increases the sodium concentration, which indirectly decreases the potassium concentration in the cell, while all other characteristics of the cell remain virtually unchanged. We integrate our model cells into a continuum model for excitable tissue using a nonlinear parabolic second order partial differential equation, which we discretize in time using finite differences and in space using finite elements. To illustrate the potential of this computational model, we virtually inject our photosensitive cells into different locations of a human heart, and explore its activation sequences upon photostimulation. Our computational optogenetics tool box allows us to virtually probe landscapes of process parameters, and to identify optimal photostimulation sequences with the goal to pace human hearts with light and, ultimately, to restore mechanical function.

1. Motivation

The human heart propels over 7000 liters of blood through the body daily, beating more than 40 million times a year. It is a remarkably efficient, durable, and reliable mechanical pump, precisely regulated by spatially and temporally varying electrical and chemical fields. Disturbed conduction and uncoordinated electrical signals can induce abnormal heart rhythms, which may critically reduce mechanical function [11, 42]. A delicate balance between the electrical and chemical gradients across the cell membrane governs the electrophysiological activity of excitable cardiac cells. To maintain these gradients, the cell membrane is selectively permeable with respect to different ions at different points in time [4]. In a cardiac muscle cell, for example, the potential difference across the cell membrane is approximately −80 mV at rest, meaning the cell is negatively charged. It can be excited by an external electrical stimulus that pushes its transmembrane potential beyond a critical threshold value. This triggers the influx of sodium ions, generating a rapid depolarization, and the transmembrane potential increases to +20 mV. Over time, the coordinated interplay between sodium, potassium, and calcium ions brings the transmembrane potential smoothly back to its resting state [25]. Since the late 1950s, permanent cardiac pacemakers have been used successfully to correct rhythm disorders and restore smoothly propagating waves of electrical excitation [13]. Pacemakers deliver electrical stimuli via implanted pacing leads that are in contact with the heart muscle. Although permanent pacemaker implantation is a standard procedure today, pacing lead placement continues to be a subject of great controversy [30]. Choosing the optimal pacing site is becoming more challenging [36], in particular in view of novel stimulation strategies such as single chamber, dual chamber, and biventricular pacing. A potential complication of lead placement is cardiac perforation, which can have severe clinical consequences including pericardial effusion, cardiac tamponade, pneumothorax, and death [28]. However, to date, there is no conceptual alternative to electrical pacing that avoids direct contact stimulus delivery [26].

For more than 40 years, biologists have studied microorganisms that produce proteins to directly regulate the flow of charged ions across their plasma membrane in response to light [35]. The first identified protein of this kind was the light-gated ion pump bacteriorhodopsin, transporting positively charged hydrogen ions across the cell membrane [35]. While bacteriorhodopsin naturally acts as an on-switch for electrically active cells, the second reported light-gated ion pump, halorhodopsin, transports negatively charged chloride ions, thereby acting as an off-switch [29]. Despite intense research [45], the first reported light-gated ionic channel, channelrhodopsin, was only identified ten years ago [31], but has since then revolutionized neuroscience. Channelrhodopsin consists of seven transmembrane proteins embedded in the lipid bilayer [12] and absorbs blue light through its interaction with retinal, see Figure 1. Since the early nineties, we have known that phototaxis and photophobic responses in the green alga Chlamydomonas reinhardtii are mediated by rhodopsins with a microbial-type all-trans retinal chromosphore [19]. The photochemical isomerization of this all-trans retinal to 13-cis retinal is illustrated in Figure 2. It occurs at peak absorption wavelengths of 470 nm, opening channelrhodopsin non-specifically to sodium, potassium, and calcium cations in response to blue light. In the dark, the covalently bound retinal spontaneously relaxes to all-trans, providing closure of the channel and regeneration of the chromophore. In 2005, channelrhodopsin was first introduced genetically using engineered viruses [5], a technique that is now widely known as optogenetics [10]. Since then, optical tools to control the electrical activity of nerve cells have rapidly evolved [40], and are now gaining widespread use in neuronal research and medicine [21]. While initial applications of optogenetics have been restricted exclusively to the neuronal system, optogenetic tools have now advanced to a level of maturity where they can confidently be applied to other cells and organs. Natural first candidates are stem cells, electrically active glial cells, muscle cells, and cardiac cells [2, 24]. Since light can be delivered at a distance, optical pacing has the potential to become a more precise and less invasive alternative to existing electrical pacing strategies [1].

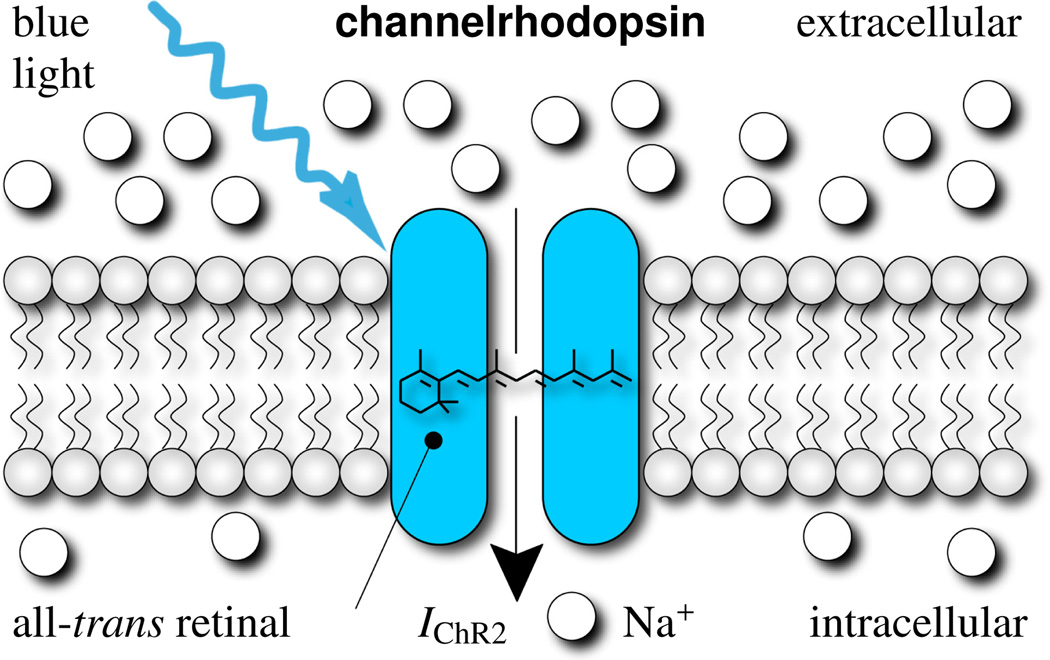
Figure 1.

Channelrhodopsin-2 is a light-gated cation channel native to the green alga Chlamydomonas reinhardtii. It consists of seven transmembrane proteins and absorbs blue light through its interaction with retinal. Photoisomerization of retinal opens the channel to sodium ions, which have a higher concentration outside than inside the cell. To make our cells responsive to light, and allow sodium concentrations to equilibrate, we induce channelrhodopsin into a conventional cardiac muscle cell model.

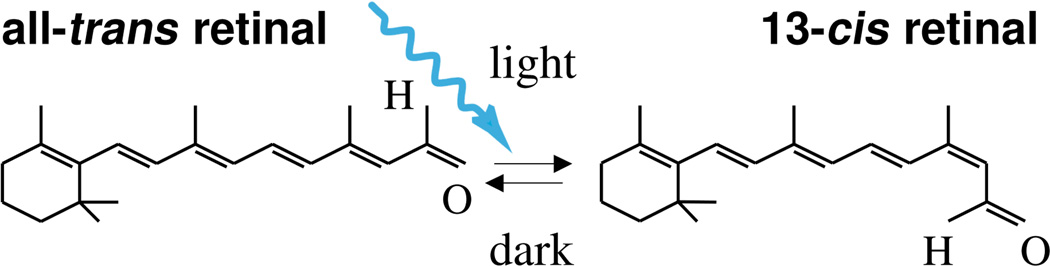
Figure 2.

Channelrhodopsin-2 is activated by photoisomerization of all-trans retinal to 13-cis retinal at wavelengths of 470 nm. After photoisomerization, the covalently bound retinal spontaneously relaxes to all-trans in the dark, providing closure of the ion channel and regeneration of the chromophore.

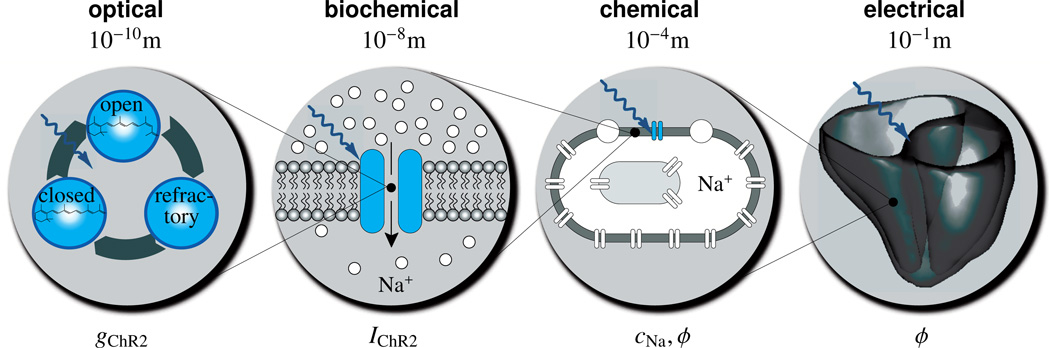
The objective of this manuscript is to establish a novel continuum model for the photoelectrochemistry of living systems that will allow us to virtually explore the potential of optogenetic pacing. The rationale for creating such a model is that it will enable patient-specific predictions of ion channel dynamics, ionic concentrations, and action potential profiles across the heart, which are outside the reach of experimental measurements in humans. Figure 3 illustrates the underlying approach in which the different physical fields interact across the different scales: On the molecular level, optical stimulation opens the cation channel channelrhodopsin initiating a photocurrent. On the subcellular level, this photocurrent increases the chemical concentration of sodium ions inside the cell. On the cellular level, concentration changes evoke changes in the electrical potential and excite the cell. On the tissue level, changes in the electrical potential propagates across the system in the form of smooth excitation waves.

Figure 3.

Multiscale model for the photoelectrochemistry of living systems. Optical stimulation opens the cation channel channelrhodopsin g_ChR2. This initiates a photocurrent I_ChR2 increasing the chemical concentration of sodium ions c_Na inside the cell. Concentration changes evoke changes in the electrical potential ϕ, which propagates across the tissue system in the form of smooth excitation waves.

In Section 2, we summarize the mathematical model for the channelrhodopsin photocycle and illustrate how channelrhodopsin can be introduced into a conventional cardiac cell model via an additional photocurrent governed by a light-sensitive gating variable. We characterize this additional photocurrent in Section 3, and demonstrate its impact on the intracellular ion concentrations in Section 4, and on the transmembrane potential in Section 5. In a side-by-side comparison with conventional cardiac muscle cells, we perform virtual case studies to demonstrate the features of genetically engineered light-sensitive cells in terms of gating variables, ionic currents, ion concentrations, and transmembrane potentials. Since our baseline model for conventional cardiac cells is well-characterized and fairly standard, we summarize its equations in the Appendix. We proceed by embedding these single cells into a novel continuum framework for photoelectrochemistry to simulate the spatial and temporal variation of electrical and chemical fields across the human heart. We briefly summarize the finite element discretization of the governing equations in Section 6. In Section 7, we virtually inject our light-sensitive cells into different locations of a human heart and explore its response to photostimulation. In Section 8, we conclude by discussing computational optogenetics and the potential of turning light into force in the context of pacing hearts with light.

2. Mathematical model of channelrhodopsin photocycle

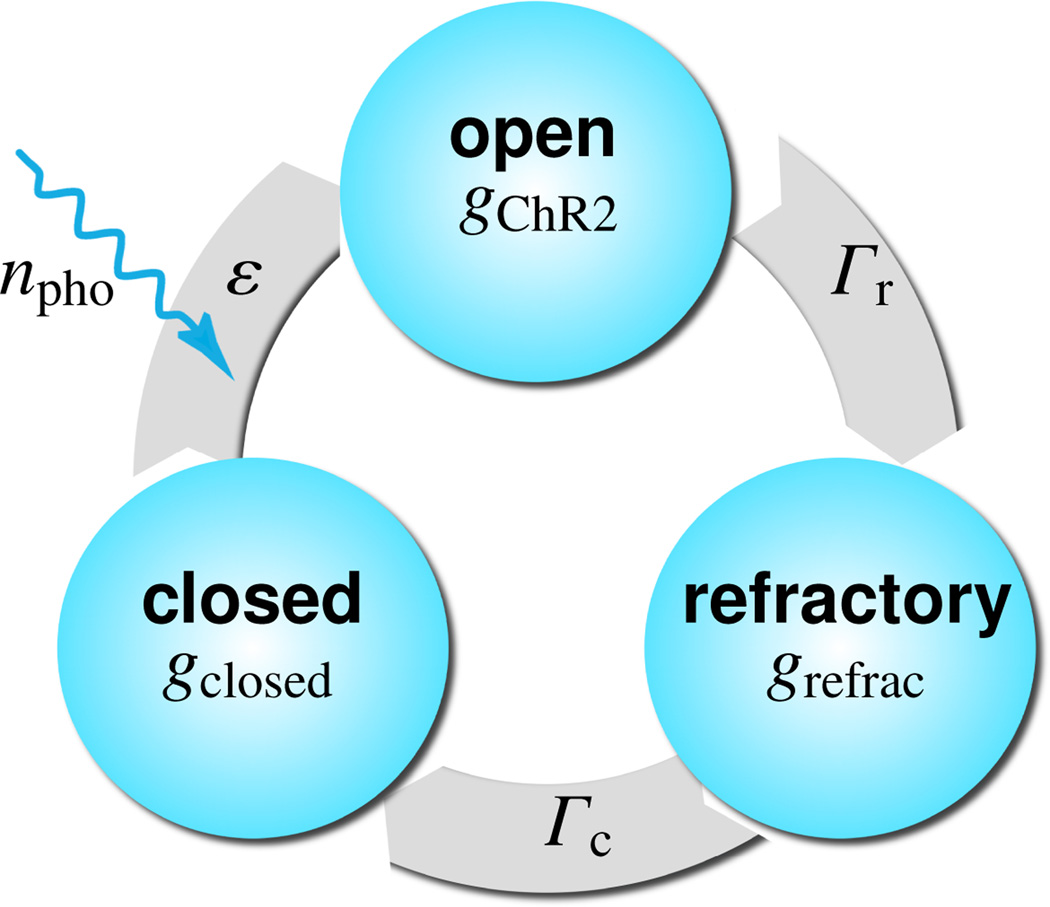
To model the light sensitivity of channelrhodopsin, we adopt the kinetics of a three-state photocycle model [20, 34], which consists of a closed, photosensitive, excitable state g_closed, an open state g_ChR2, and a closed, desensitized, absolutely refractory state g_refrac [32], as illustrated in Figure 4. Upon photo absorption, molecules which are in the closed state g_closed undergo a fast transition into the open state g_ChR2. After being open for some time, molecules spontaneously transition into the absolutely refractory state g_refrac, where the ion channels are closed, but the molecules are not yet ready to photoswitch again. After the refractory period, the molecules finally return to the closed state g_closed, ready to undergo a new photocycle when exposed to light [33]. Figure 4 suggests the following first order model for the channelrhodopsin photocycle,

$$\begin{array}{cccc}{ġ}_{\text{ChR}2}=\hfill & \hfill \epsilon n_{\text{pho}}\hfill & g_{\text{closed}}-{\Gamma }_{\mathrm{r}}\hfill & g_{\text{ChR}2}\hfill \\ {ġ}_{\text{refrac}}=\hfill & \hfill {\Gamma }_{\mathrm{r}}\hfill & g_{\text{ChR}2}-{\Gamma }_{\mathrm{c}}\hfill & g_{\text{refrac}}\hfill \\ {ġ}_{\text{closed}}=\hfill & \hfill {\Gamma }_{\mathrm{c}}\hfill & g_{\text{refrac}}-\epsilon n_{\text{pho}}\hfill & g_{\text{closed}}\hfill \end{array}$$ (1)

where Γ_r and Γ_c are the rates of recovery and full closure, ε is the quantum efficiency of the channelrhodopsin system, and n_pho is the number of photons hitting the cell per second. Here, we choose Γ_r = 0.06129, Γ_c = 0.00422, and εn_pho = 0.018. Herein, g_ChR2, g_refrac, and g_closed define the fraction of molecules in the open, refractory, and closed states. Initially, all molecules are in the closed state, i.e., g_closed = 1, g_ChR2 = 0, and g_refrac = 0. Since all three fractions sum up to one, i.e., g_ChR2 + g_refrac + g_closed = 1, the photocycle system (1) can be characterized through two independent variables [22], e.g., the fraction of molecules in the open and in the refractory states.

$$\begin{array}{cccc}{ġ}_{\text{ChR}2}=\hfill & \hfill \epsilon n_{\text{pho}}-[\epsilon n_{\text{pho}}+{\Gamma }_{\mathrm{r}}]& g_{\text{ChR}2}-\epsilon n_{\text{pho}}\hfill & g_{\text{refrac}}\hfill \\ {ġ}_{\text{refrac}}=\hfill & \hfill {\Gamma }_{\mathrm{r}}& g_{\text{ChR}2}-{\Gamma }_{\mathrm{c}}\hfill & g_{\text{refrac}}\hfill \end{array}$$ (2)

Figure 4.

Three-state model for the channelrhodopsin photocycle. Upon photo absorption, molecules in the closed state g_closed undergo a fast transition into the open state g_ChR2. The molecules spontaneously turn into the refractory state g_refrac where the ion channels are closed, but the molecules are not yet ready to photoswitch again. After the refractory period, the molecules return to the closed state g_closed, ready to undergo a new photocycle when subjected to light [32, 33].

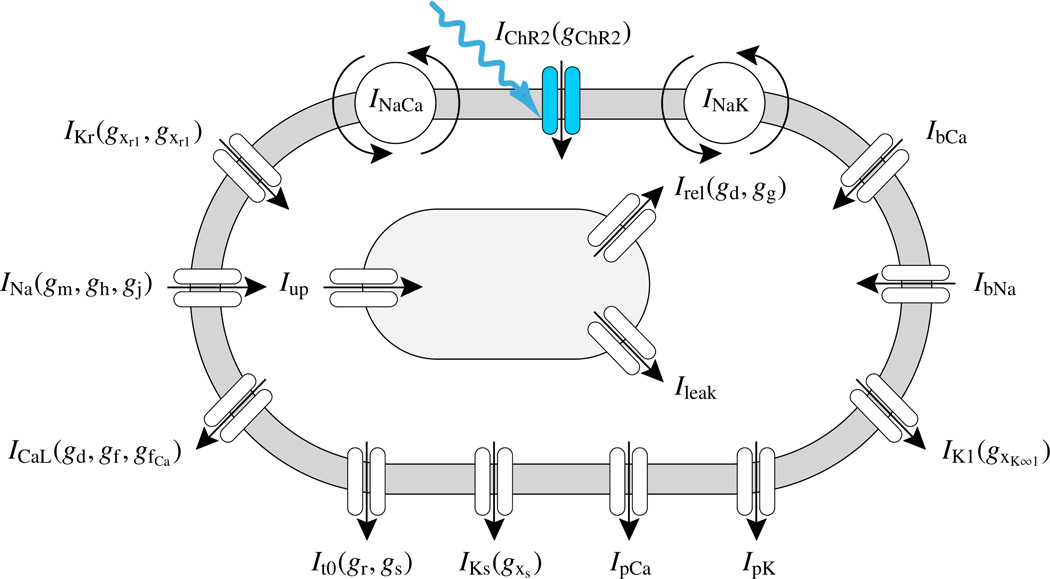
We identify the state g_ChR2 as the channelrhodopsin gating variable and integrate it into a well-characterized ventricular cell model [43, 47] characterized through a total of n_gate = 14 gating variables as illustrated in Figure 5.

$$g_{\text{gate}}=[g_{\mathrm{m}},g_{\mathrm{h}},g_{\mathrm{j}},g_{\text{ChR}2},g_{\text{xr}1},g_{\text{xr}2},g_{\text{xs}},g_{\mathrm{r}},g_{\mathrm{s}},g_{\mathrm{d}},g_{\mathrm{f}},g_{\mathrm{K}1\mathrm{\infty }},g_{\text{fCa}},g_{\mathrm{g}}],$$ (3)

Figure 5.

Genetically engineered light sensitive cardiac cell. The electrophysiology of the cell is characterized in terms of n_ion = 4 ion concentrations, the intracellular sodium, potassium, and calcium concentrations and the calcium concentration in the sarcoplastic reticulum. Ion concentrations are controlled through n_crt = 16 ionic currents, where we have enhanced the conventional cell model [43, 47] with the channelrhodopsin photocurrent I_ChR2, here shown in blue [1]. The channels are governed by n_gate = 14 gating variables, where we have added the channelrhodopsin gating variable g_ChR2 to characterize the cell’s response to photostimulation.

In particular, these are the sodium activation gate g_m, the fast and slow sodium inactivation gates g_h and g_j, the channelrhodopsin activation gate g_ChR2, the rapid delayed rectifier activation and inactivation gates g_xr1 and g_xr2, the slow delayed rectifier activation gate g_xs, the transient potassium activation and inactivation gates g_r and g_s, the long-lasting L-type calcium channel activation and inactivation gates g_d, g_f, and g_fCa, and the calcium release activation gate g_g. The gating variables are parameterized in terms of the transmembrane potential ϕ, the ionic concentrations c_ion, and the gating variables g_gate themselves. Their evolution is governed by classic Hodgkin-Huxley type equations,

$${ġ}_{\text{gate}}=\frac{1}{{\tau }_{\text{gate}}(\varphi )}[g_{\text{gate}}^{\mathrm{\infty }}(\varphi ,c_{\text{ion}})-g_{\text{gate}}]$$ (4)

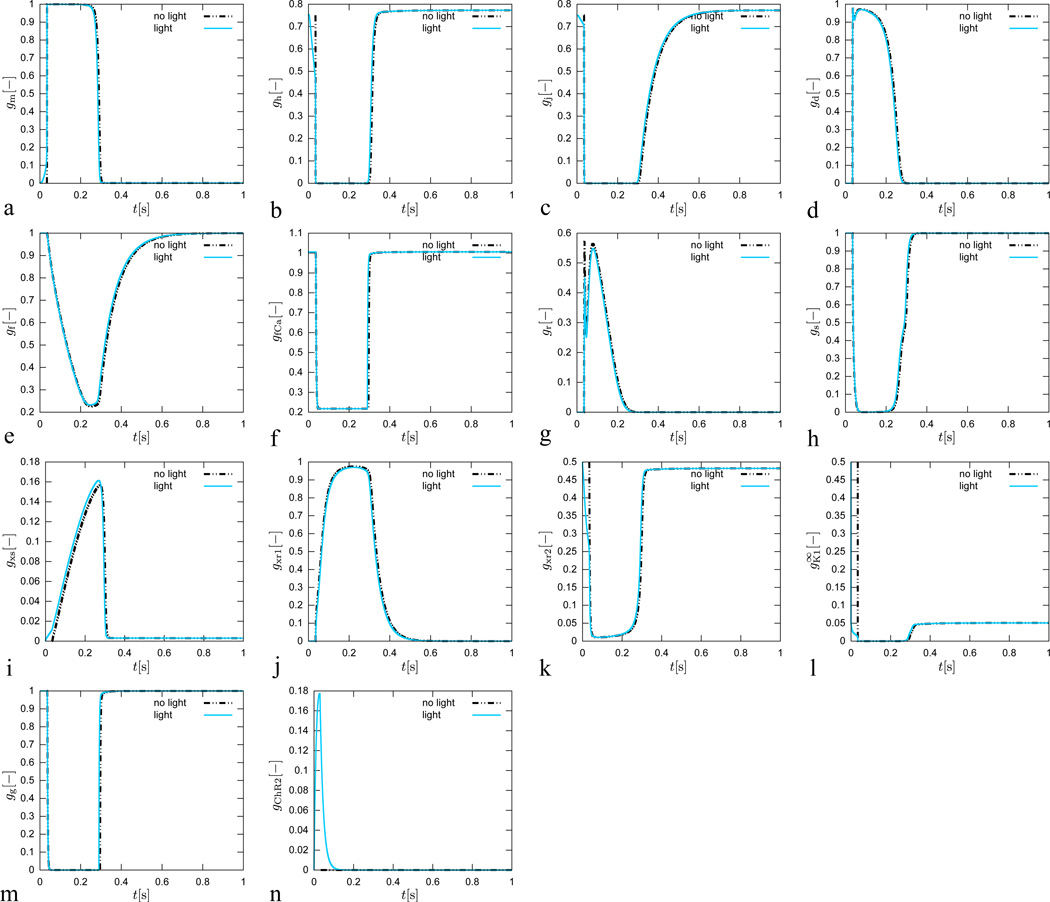
each characterized through a steady state value $g_{\text{gate}}^{\mathrm{\infty }}$ and a time constant τ_gate for reaching this steady state [47]. Both are usually exponential functions of the transmembrane potential ϕ, see Appendix for details. Figure 6 illustrates the temporal evolution of all n_gate = 14 gating variables for the conventional cell, electrically stimulated for 1 ms, dashed black lines, and for the genetically engineered cell, light stimulated for 30 ms, solid blue lines. Overall, the gating variables of the conventional cell and the genetically engineered cell display a similar behavior. The g_ChR2 gate is, of course, only active for the photosensitive cell.

Figure 6.

Genetically engineered light sensitive cardiac cell stimulated conventionally with an electric field, dashed lines, and optically with light, solid lines. Temporal evolution of sodium activation gate g_m, fast sodium inactivation gate g_h, slow sodium inactivation gate g_j, L-type calcium activation gate g_d, L-type calcium inactivation gate g_f, intracellular calcium dependent calcium inactivation gate g_fCa transient outward activation gate g_r, transient outward inactivation gate g_s, slow delayed rectifier gate g_xs, rapid delayed rectifier activation gate g_xr1, rapid delayed rectifier inactivation gate g_xr2, inward recrification factor $g_{\mathrm{K}1}^{\mathrm{\infty }}$, calcium-dependent inactivation gate g_g, and channelrhodospin activation gate g_ChR2. The gating dynamics for the electrically stimulated cell have been delayed by 34 ms for the purposes of comparison against the optically stimulated cell.

3. Mathematical model of ionic currents

The channelrhodopsin gating variable g_ChR2 introduced in the previous section governs the channelrhodopsin photocurrent I_ChR2, for which we make the following ansatz.

$$I_{\text{ChR}2}=C_{\text{ChR}2}{g}_{\text{ChR}2}[\varphi -{\varphi }_{\text{ChR}2}]$$ (5)

This implies that in our current model, the effects of conduction C_ChR2 and photostimulation g_ChR2 on the photocurrent I_ChR2 are separable. This assumption is sufficient to accurately capture most phenomena reported in the literature [1, 22]. Some more advanced four state models suggest the use of rate variables with dependence on light intensity to finetune of the photocurrent [34]. However, because of the lack of experimental data, it is currently unclear whether these electrical potential effects are truly significant. In our model, the channelrhodopsin conductance

$$C_{\text{ChR}2}=\frac{1}{g_{\text{ChR}2}^{\mathrm{\infty }}[{\varphi }_{\text{clamp}}-{\varphi }_{\text{ChR}2}]}{I}_{\text{ChR}2}^{\mathrm{\infty }}$$ (6)

is expressed in terms of a quadratic polynomial, which we have identified to $I_{\text{ChR}2}^{\mathrm{\infty }}/[{\varphi }_{\text{clamp}}-{\varphi }_{\text{ChR}2}]=0.000266{\varphi }^2-0.003658\varphi +0.498819$ using a least squares fit. With a plateau value $g_{\text{ChR}2}^{\mathrm{\infty }}$ according to [33]

$$g_{\text{ChR}2}^{\mathrm{\infty }}=\frac{\epsilon n_{\text{pho }}{\Gamma }_{\mathrm{c}}}{\epsilon n_{\text{pho }}[{\Gamma }_{\mathrm{r}}+{\Gamma }_{\mathrm{c}}]+{\Gamma }_{\mathrm{r}}{\Gamma }_{\mathrm{c}}}$$ (7)

i.e., in our case $g_{\text{ChR}2}^{\mathrm{\infty }}=0.05283$, the conductance becomes C_ChR2 = [0.05ϕ² − 0.0692ϕ + 9.442]. Moreover, ϕ_ChR2 is the reversal potential of channelrhodopsin,

$${\varphi }_{\text{ChR}2}={\varphi }_{\text{Na}}-{\tilde{\varphi }}_{\text{Na}}$$ (8)

which we approximate as the difference of the concentration-dependent reversal potential for sodium ϕ_Na and the experimental reversal potential ϕ̃_Na.

$${\varphi }_{\text{Na}}=\frac{\mathit{\text{RT}}}{\mathit{\text{zF}}}\text{ log }\left(\frac{c_{\text{Na}}^{\mathrm{e}}}{c_{\text{Na}}^{\mathrm{i}}}\right)\text{ and }{\tilde{\varphi }}_{\text{Na}}=\frac{\mathit{\text{RT}}}{\mathit{\text{zF}}}\text{ log }\left(\frac{{\tilde{c}}_{\text{Na}}^{\mathrm{e}}}{{\tilde{c}}_{\text{Na}}^{\mathrm{i}}}\right)+{\tilde{\varphi }}_{\text{Na},0}$$ (9)

Here, we choose $c_{\text{Na}}^{\mathrm{e}}=153\text{ mM}$ [22] and $c_{\text{Na}}^{\mathrm{i}}=11.6\text{ mM}$, calibrated to match the experimental reversal potential of channelrhodopsin, and ${\mathrm{c̃}}_{\text{Na}}^{\mathrm{e}}=140\text{ mM},{\mathrm{c̃}}_{\text{Na}}^{\mathrm{i}}=11.6\text{ mM}$, and ϕ̃_Na,0 = 1.79 mV. Accordingly, ${\varphi }_{\text{ChR}2}=[\mathit{\text{RT}}]/[\mathit{\text{zF}}][\text{log}(c_{\text{Na}}^{\mathrm{e}}/c_{\text{Na}}^{\mathrm{i}})-\text{log}({\mathrm{c̃}}_{\text{Na}}^{\mathrm{e}}/{\mathrm{c̃}}_{\text{Na}}^{\mathrm{i}})+{\tilde{\varphi }}_{\text{Na},0}]$. In contrast to our previous approach, where we have photostimulated an atrial nodal cell [1], we now integrate the channelrhodopsin photocurrent I_ChR2 into our conventional ventricular cell model [43, 47], defined through a total of n_crt = 16 ionic currents, see Figure 5.

$$I_{\text{crt}}=[I_{\text{Na}},I_{\text{bNa}},I_{\text{NaK}},I_{\text{NaCa}},I_{\text{ChR}2},I_{\mathrm{K}1},I_{\text{Kr}},I_{\text{Ks}},I_{\text{pK}},I_{\mathrm{t}0},I_{\text{CaL}},I_{\text{bCa}},I_{\text{pCa}},I_{\text{leak}},I_{\text{up}},I_{\text{rel}}].$$ (10)

Mathematically speaking, these currents are functions of the transmembrane potential ϕ, the individual gating variables g_gate, and the ion concentrations c_ion.

$$I_{\text{crt}}=I_{\text{crt}}(\varphi ,g_{\text{gate}},c_{\text{ion}})$$ (11)

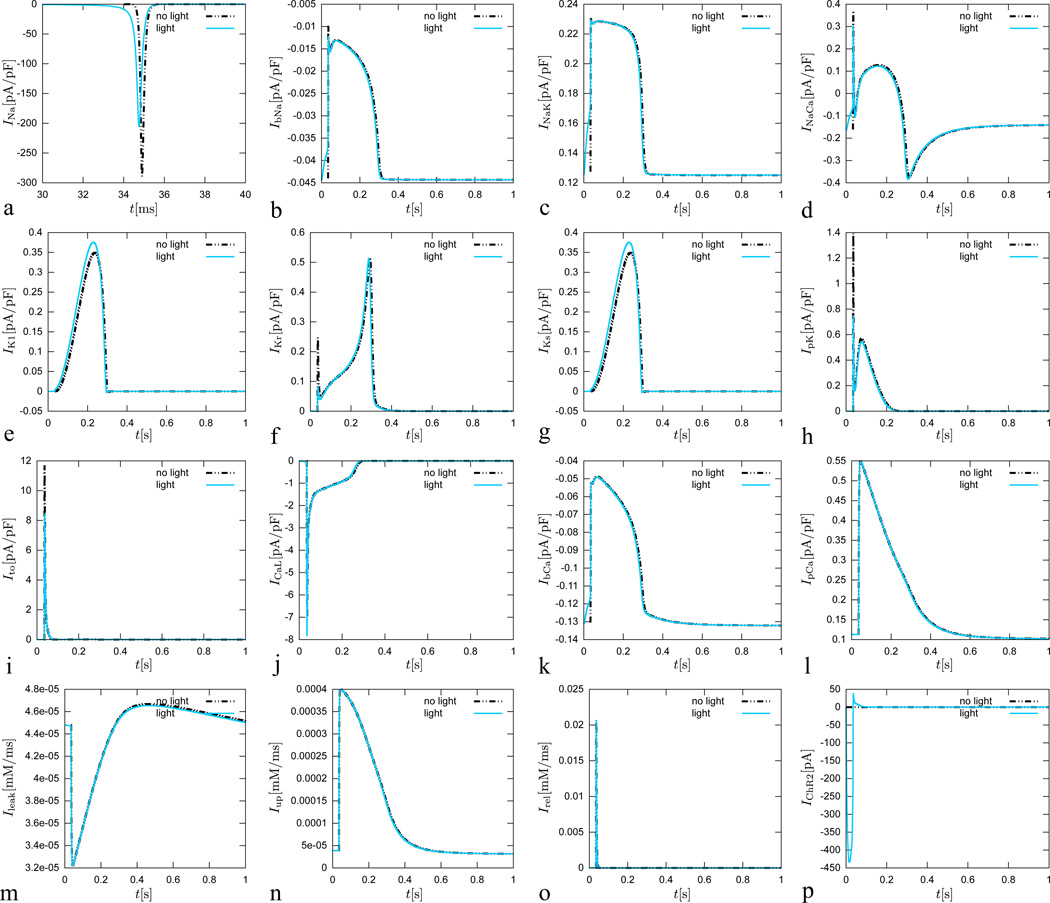
In particular, these are the fast sodium current I_Na, the background sodium current I_bNa, the sodium potassium pump current I_NaK, the sodium calcium exchanger current I_NaCa, the channelrhodopsin photocurrent I_ChR2 the inward rectifier current I_K1, the rapid delayed rectifier current I_Kr, the slow delayed rectifier current I_Ks, the plateau potassium current I_pK, the transient outward current I_t0, the L-type calcium current I_CaL, the background calcium current I_bCa, the plateau calcium current I_pCa, the leakage current I_leak, and sarcoplastic reticulum uptake and release currents I_up and I_rel, see Appendix for details. Figure 7 illustrates the temporal evolution of all n_crt = 16 currents for the conventional cell, electrically stimulated for 1 ms, dashed black lines, and for the genetically engineered cell, light stimulated for 30 ms, solid blue lines. Except for the fast sodium current I_Na, the currents of the conventional cell and the genetically engineered cell display a relatively similar behavior. Overshoots in the potassium related currents are less pronounced for the photosensitive cell. The channelrhodopsin photocurrent I_ChR2 is, of course, only active for the photosensitive cell.

Figure 7.

Genetically engineered light sensitive cardiac cell stimulated conventionally with an electric field, dashed lines, and optically with light, solid lines. Temporal evolution of fast sodium current I_Na, background sodium current I_bNa, sodium potassium pump current I_NaK, sodium calcium exchanger current I_NaCa, inward rectifier current I_K1, rapid delayed rectifier current I_Kr, slow delayed rectifier current I_Ks, plateau potassium current I_pK, transient outward current I_t0, L-type calcium current I_CaL, background calcium current I_bCa, plateau calcium current I_pCa, leakage current I_leak, sarcoplastic reticulum uptake current I_up, sarcoplastic reticulum release current I_rel, and channelrhodopsin current I_ChR2. The current dynamics for the electrically stimulated cell have been delayed by 34 ms for the purposes of comparison against the optically stimulated cell.

4. Mathematical model of ionic concentrations

From a chemical point of view, light induces a channelrhodopsin photocurrent I_ChR2, which directly impacts the intracellular sodium concentration c_Na,

$${ċ}_{\text{Na}}=-\frac{1}{\mathit{\text{FV}}}[I_{\text{Na}}+I_{\text{bNa}}+3I_{\text{NaCa}}+3I_{\text{NaK}}+I_{\text{ChR}2}]$$ (12)

where V is the cytosolic volume and F is the Faraday constant. The sodium concentration will directly, and indirectly through the resulting changes in the transmembrane potential ϕ, affect all other ionic concentrations in the cell. The biochemistry of our cell model is characterized through n_ion = 4 ion concentrations,

$$c_{\text{ion}}=[c_{\text{Na}},c_{\mathrm{K}},c_{\text{Ca}},c_{\text{Ca}}^{\text{sr}}]$$ (13)

where c_Na, c_K, and c_Ca are the intracellular sodium, potassium, and calcium concentrations, and $c_{\text{Ca}}^{\text{sr}}$ is the calcium concentration in the sarcoplastic reticulum. The concentrations obey evolution equations of the following format,

$${ċ}_{\text{ion}}=f_{\text{ion}}(\varphi ,g_{\text{gate}},c_{\text{ion}})$$ (14)

which are parameterized in terms of the transmembrane potential ϕ, the gating variables g_gate, and the ion concentrations c_ion themselves, see Appendix for details. Figure 8 illustrates the temporal evolution of all n_gate = 14 gating variables for the conventional cell, electrically stimulated for 1 ms, dashed black lines, and for the genetically engineered cell, light stimulated for 30 ms, solid blue lines. While the calcium concentrations inside the cell c_Ca and in the sarcoplastic reticulum $c_{\text{Ca}}^{\text{sr}}$ remain unaffected by photostimulation, the intracellular sodium concentration c_Na increases with light. Through the sodium potassium pump current I_NaK, this has a direct impact on the intracellular potassium concentration c_K, which decreases upon photostimulation.

Figure 8.

Genetically engineered light sensitive cardiac cell stimulated conventionally with an electric field, dashed lines, and optically with light, solid lines. Temporal evolution of intracellular sodium c_Na, potassium c_K, calcium c_Ca concentrations, and calcium concentration $c_{\text{Ca}}^{\text{sr}}$ in the sarcomplastic reticulum. The chemical concentration dynamics for the electrically stimulated cell have been delayed by 34 ms for the purposes of comparison against the optically stimulated cell.

5. Mathematical model of action potential propagation

From an electrical point of view, light induces a channelrhodopsin current I_ChR2, which directly impacts the sodium concentration c_Na, and thus, the action potential propagation ϕ in the heart. Unlike the local ion concentrations for single cells, however, the action potential ϕ is a global field variable [15]. It propagates from cell to cell via gap junction channels [24]. We can characterize its spatio-temporal evolution through a nonlinear parabolic second order partial differential equation

$$\mathrm{\varphi ̇}=f^{\varphi }(\varphi ,g_{\text{gate}},c_{\text{ion}})+\text{div }\mathit{q}(\varphi )$$ (15)

driven by a nonlinear local source term f^ϕ at the single cell level, and by a linear global flux term, div q, the divergence of the propagation vector q at the organ level. We identify the local source term

$$f^{\varphi }=\frac{1}{C}[I_{\text{Na}}+I_{\text{bNa}}+I_{\text{NaK}}+I_{\text{NaCa}}+I_{\text{ChR}2}+I_{\mathrm{K}1}+I_{\text{Kr}}+I_{\text{Ks}}+I_{\text{pK}}+I_{\mathrm{t}0}+I_{\text{CaL}}+I_{\text{bCa}}+I_{\text{pCa}}]$$ (16)

as the negative sum of all transmembrane currents scaled by the cell membrane capacitance per unit surface area C. To account for the nonlocal nature of propagating excitation waves in the heart, we introduce the propagation vector

$$\mathit{q}=\mathit{D}·\mathbf{\nabla }\varphi$$ (17)

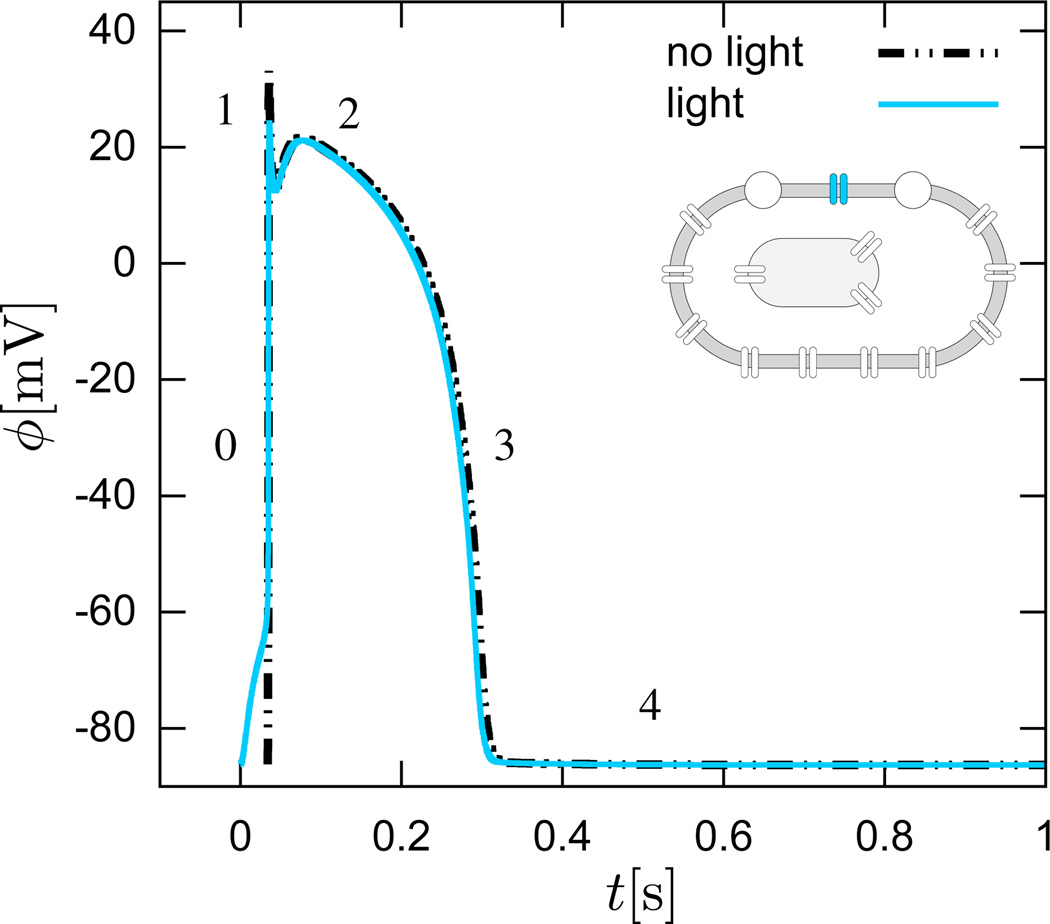
through the second order diffusion tensor D scaling the gradient of the action potential field ∇ϕ. Figure 9 illustrates the five phases of the action potential ϕ for the conventional cell, electrically stimulated for 1 ms, dashed black lines, and for the genetically engineered cell, light stimulated for 30 ms, solid blue lines. We can clearly see the impact of photostimulation, which requires the entire stimulation period of 30 ms to push the cell beyond its excitation threshold. For visualization purposes, we have shifted the transmembrane potential of the electrical stimulation, dashed lines, by 34 ms, which agrees qualitatively with the time delay of 19.7±3.4 ms reported in the literature [6]. Beyond the stimulation threshold, both cells display an almost identical electrical response with the characteristic rapid upstroke, early, partial repolarization, plateau, final repolarization, and rest phases. Again, this agrees nicely with experimental findings [6].

Figure 9.

Genetically engineered light sensitive cardiac cell stimulated conventionally with an electric field, dashed lines, and optically with light, solid lines. Temporal evolution of transmembrane potential ϕ. The characteristic action potential consists of five phases. Phase 0: The rapid upstroke is generated through an influx of positively charged sodium ions. Phase 1: Early, partial repolarization is initiated through the efflux of positively charged potassium ions. Phase 2: During the plateau, the net influx of positively charged calcium ions is balanced by the efflux of positively charged potassium ions. Phase 3: Final repolarization begins when the efflux of potassium ions exceeds the influx of calcium ions. Phase 4: Throughout the interval between end of repolarization and the beginning of the next cycle the cell is at rest. The transmembrane potential for the electrically stimulated cell has been delayed by 34 ms for the purposes of comparison against the optically stimulated cell. This delay agrees nicely with the time delay of activation of 19.7±3.4 ms reported in the literature [6].

6. Computational model of light-activated cells

To solve the spatio-temporal problem of electrochemical coupling (4), (14), and (15) for the gating variables g_gate, the intracellular ion concentrations c_ion, and the transmembrane potential ϕ, we apply a finite difference scheme in time and a finite element scheme in space. Due to the global nature of the membrane potential introduced through the diffusion term div q(ϕ), we suggest a 𝒞⁰-continuous finite element interpolation for the membrane potential ϕ, while a 𝒞⁻¹-continuous interpolation is sufficient for the sets of gating variables g_gate and ion concentrations c_ion [15, 17]. Accordingly, we introduce the membrane potential as global degree of freedom at each finite element node, and the gating variables and ion concentrations locally on the integration point level [47]. We solve the resulting staggered system with an incremental iterative Newton-Raphson solution procedure based on the consistent linearization of the discrete excitation problem [7, 9, 16].

6.1. Chemical problem - Local discretization on the integration point level

We typically initialize the chemical state variables at t₀ with their resting state values. Our goal is to determine the chemical state variables, i.e., the n_gate = 14 gating variables g_gate and the n_ion = 4 ion concentrations c_ion of the current time step t for a given action potential ϕ at t, and known chemical state variables from the previous time step tⁿ. For the temporal discretization, we partition the time interval of interest 𝒯 into n_stp subintervals [tⁿ, tⁿ⁺¹] as $𝒯={\displaystyle {\cup }_{n=0}^{n_{\text{stp}-1}}}[t^n,t^{n+1}]$ and apply a standard backward Euler time integration scheme in combination with a finite difference approximation of the first order time derivatives ġ_gateϕ and ċ_ion.

$${ġ}_{\text{gate}}=[g_{\text{gate}}-g_{\text{gate}}^n]/\mathrm{\Delta }t\text{ and }{ċ}_{\text{ion}}=[c_{\text{ion}}-c_{\text{ion}}^n]/\mathrm{\Delta }t$$ (18)

Here and from now on, we omit the index (◦)ⁿ⁺¹ for the sake of clarity, and introduce the common abbreviation Δt ≔ t − tⁿ > 0 for the current time increment. This allows us to transform the linear set of gating equations (4) into a set of update equations for the gating variables g_gate at the current time step t.

$$g_{\text{gate}}=g_{\text{gate}}^n+\frac{1}{{\tau }_{\text{gate}}(\varphi )}[g_{\text{gate}}^{\mathrm{\infty }}(\varphi )-g_{\text{gate}}]\mathrm{\Delta }t$$ (19)

The gating variables define the n_crt = 16 ionic currents I_crt(ϕ, g_gate, c_ion), which alter the n_ion = 4 intracellular ion concentrations c_ion. With the help of the finite difference approximation (18), we reformulate the nonlinear set of concentration equations (14) in the following residual format.

$${\mathrm{𝖱}}_{\text{ion}}^c=c_{\text{ion}}-c_{\text{ion}}^n-f_{\text{ion}}^c(\varphi ,g_{\text{gate}},c_{\text{ion}})\mathrm{\Delta }t\doteq 0$$ (20)

To obtain the n_ion × n_ion iteration matrix ${\mathrm{𝖪}}_{\text{ion ion}}^c$ for the local Newton iteration on the integration point level, we linearize the discrete algorithmic residual.

$${\mathrm{𝖪}}_{\text{ion}}^c={\mathrm{d}}_{c_{\text{ion}}}{\mathrm{𝖱}}_{\text{ion}}^c=1-{\mathrm{d}}_{c_{\text{ion}}}{f}_{\text{ion}}^c$$ (21)

At the end of each Newton iteration, we update the set of ion concentrations $c_{\text{ion}}\leftarrow c_{\text{ion}}-{[{\mathrm{𝖪}}_{\text{ion}}^c]}^{-1}{\mathrm{𝖱}}_{\text{ion}}^c$, the set of gating variables $g_{\text{gate}}\leftarrow g_{\text{gate}}+[g_{\text{gate}}^{\mathrm{\infty }}(\varphi )-g_{\text{gate}}]\mathrm{\Delta }t/\mathrm{\tau }$ and the set of ionic currents I_crt ← I_crt(ϕ, g_gate, c_ion), and continue to iterate locally until we achieve convergence. This local inner loop can be understood as a modern implicit version of the iterative update procedure of the original Rush-Larsen algorithm [39].

6.2. Electrical problem - Global discretization on the node point level

To evaluate the action potential ϕ on the node point level, we transform the electrical problem (15) into its residual format

$${\mathrm{𝖱}}^{\varphi }=\mathrm{\varphi ̇}-\text{div}(\mathit{q})-f^{\varphi }\doteq 0$$ (22)

in the domain of interest ℬ. We complement this initial boundary value problem with the corresponding Dirichlet and Neumann boundary conditions ϕ = ϕ̄ on ∂ℬ_ϕ and q · n = q̄ on ∂ℬ_q, typically using homogeneous Neumann boundary conditions q · n = 0 on the entire boundary ∂ℬ. As initial conditions, ϕ₀(x) = ϕ(x, t₀) in ℬ, we simply set the transmembrane potential to its resting state. We obtain the weak form of the electrical residual (22) through the integration over the domain ℬ, the standard integration by parts, and the inclusion of the Neumann boundary conditions. For the spatial discretization, we discretize the domain of interest ℬ with n_el finite elements ℬ^e as $ℬ={\displaystyle {\cup }_{e=1}^{n_{\mathrm{e}1}}}{ℬ}^e$ and apply the standard isoparametric concept to interpolate the trial functions ϕ and the test functions δϕ.

$$\begin{array}{cc}\delta \varphi ={\displaystyle {\sum }_{i=1}^{n_{\text{en}}}}{N}^i\delta {\varphi }_i\hfill & \varphi ={\displaystyle {\sum }_{j=1}^{n_{\text{en}}}}{N}^j{\varphi }_j\hfill \end{array}$$ (23)

Here, N are the standard shape functions on the element level and i, j = 1, …, n_en are the n_en element nodes. For the temporal discretization, we suggest a finite difference approximation of the first order time derivative ϕ̇,

$$\mathrm{\varphi ̇}=[\varphi -{\varphi }^n]/\mathrm{\Delta }t$$ (24)

in combination with a standard backward Euler time integration scheme. Using the discretizations in space (23) and time (24), we can introduce the discrete algorithmic residual ${\mathrm{𝖱}}_I^{\varphi }$.

$${\mathrm{𝖱}}_I^{\varphi }={𝗔}_{e=1}^{n_{\text{el}}}{\displaystyle {\int }_{{ℬ}^e}}{N}^i\frac{\varphi -{\varphi }^n}{\mathrm{\Delta }t}+\mathbf{\nabla }{N}^i·\mathit{q}\mathrm{d}V-{\displaystyle {\int }_{\partial {ℬ}_q^e}}{N}^i\mathrm{q̄}\mathrm{d}A-{\displaystyle {\int }_{{ℬ}^e}}{N}^i{f}^{\varphi }\mathrm{d}V\doteq 0$$ (25)

The operator 𝗔 symbolizes the assembly of all element contributions at the element nodes i = 1, …, n_en to the overall residual at the global node points I = 1, …, n_nd. To solve the discrete system of nonlinear equations (25), we suggest an incremental iterative Newton Raphson solution technique based on the consistent linearization of the residual, which introduces the global iteration matrix ${\mathrm{𝖪}}_{\mathit{\text{IJ}}}^{\varphi }$.

$${\mathrm{𝖪}}_{\mathit{\text{IJ}}}^{\varphi }={\mathrm{d}}_{{\varphi }_J}{\mathrm{𝖱}}_I^{\varphi }={𝗔}_{e=1}^{n_{\text{el}}}{\displaystyle {\int }_{{ℬ}^e}}{N}^i\frac{1}{\mathrm{\Delta }t}{N}^j+\mathbf{\nabla }{N}^i·\mathit{D}·\mathbf{\nabla }{N}^j-N^i{\mathrm{d}}_{\varphi }{f}^{\varphi }{N}^j\mathrm{d}V$$ (26)

For each incremental iteration, we update the global vector of unknowns ${\varphi }_I\leftarrow {\varphi }_I-{\displaystyle {\sum }_{J=1}^{n_{\text{nd}}}}{\mathrm{𝖪}}_{\mathit{\text{IJ}}}^{\varphi -1}{\mathrm{𝖱}}_J^{\varphi }$ at all I = 1, …, n_nd global nodes. At convergence of the local Newton iteration, i.e., at chemical equilibrium, we can evaluate the source term f^ϕ(ϕ, g_gate, c_ion) for the electrical problem (25), and its linearization d_ϕ f^ϕ(ϕ, g_gate, c_ion) for the global Newton iteration (26). The use of a fully monolithic implicit solution algorithm allows us to apply an adaptive time stepping procedure, for which the time step size is automatically adjusted in response to the number of Newton iterations towards global equilibrium [47]. In principle, the above equations for ${\mathrm{𝖱}}_I^{\varphi }\text{ and }{\mathrm{𝖪}}_{\mathit{\text{IJ}}}^{\varphi }$ are generically portable and can interface with any commercially available finite element package. Here, we embed the proposed algorithm in the general multipurpose nonlinear finite element program FEAP [41].

7. Computational model of a human heart

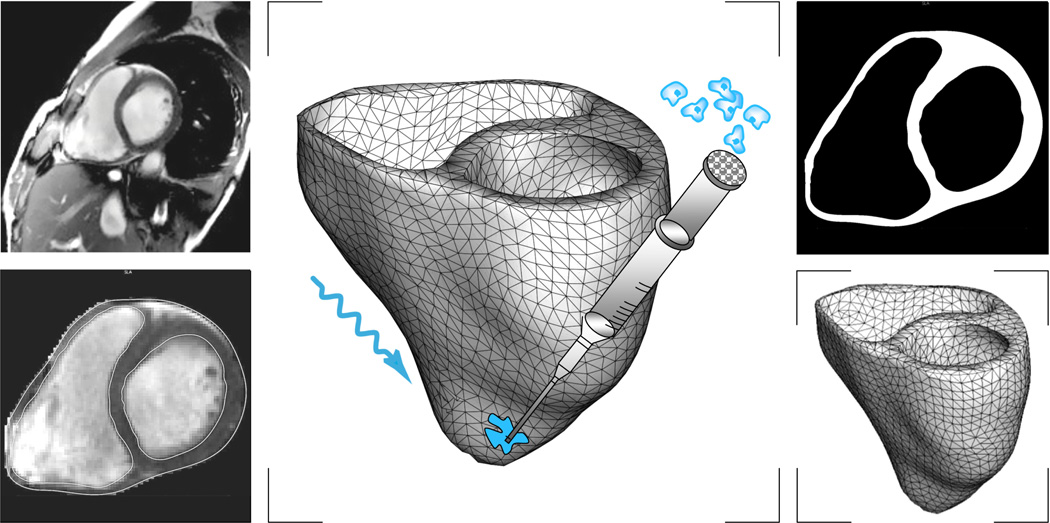
To illustrate the features of the proposed algorithm, we model the photostimulation of a human heart stimulated at three different pacing sites. We create a patient-specific heart model from magnetic resonance images taken at different depths along the heart’s long axis, see Figure 10. On these two-dimensional slices, we use semi-automated image processing tools to section the regions of the cardiac muscle. From the raw and noisy grayscale images, we create monochrome images with sharply defined boundaries using thresholding and binary masking. From the resulting black and white slices, we generate three preliminary triangular surface meshes, one for the outer surface and one for the inner surface of each ventricle. Finally, we convert the surface meshes into a tetrahedral volume mesh consisting of 3,129 nodes and 11,347 tetrahedral elements [27], see Figure 10.

Figure 10.

Virtual injection of genetically engineered light sensitive cardiac cells into a human heart. Magnetic resonance imaging generates a sequence of two-dimensional images at different depths (top, left). We segment cardiac muscle tissue semi-manually using standard image processing techniques (bottom, left). Thresholding and binary masking convert the raw grayscale images to monochrome images with sharply defined boundaries (top, right). From these slices, we create a preliminary triangular surface mesh and converted it into the final tetrahedral volume mesh consisting of 3,129 nodes and 11,347 tetrahedral elements (bottom, right). Last, we virtually inject photosensitive cells into different regions of the heart and stimulated with light (middle).

We virtually inject our genetically engineered, light sensitive cardiac cells into different regions of the heart [30], and model all other cells as conventional cardiac muscle cells [43, 47]. The former group of cells possesses the additional channelrhodopsin current I_ChR2, while the latter does not. Following the literature, we model cell injection by modifying the material properties of the myocardial wall at the injection sites [46]. Here, these regions span a volume of approximately 0.02cm³, which is roughly the size of the 0.6×0.3×0.1cm³ large atrioventricular node in humans, corresponding to approximately 10⁷ cells [23]. To initiate electrical activation, we photostimulate the light sensitive cells for a period of 30 ms with blue light, then turn off the light, and record the action potential propagation across the heart.

7.1. Atrioventricular node pacing through photostimulation

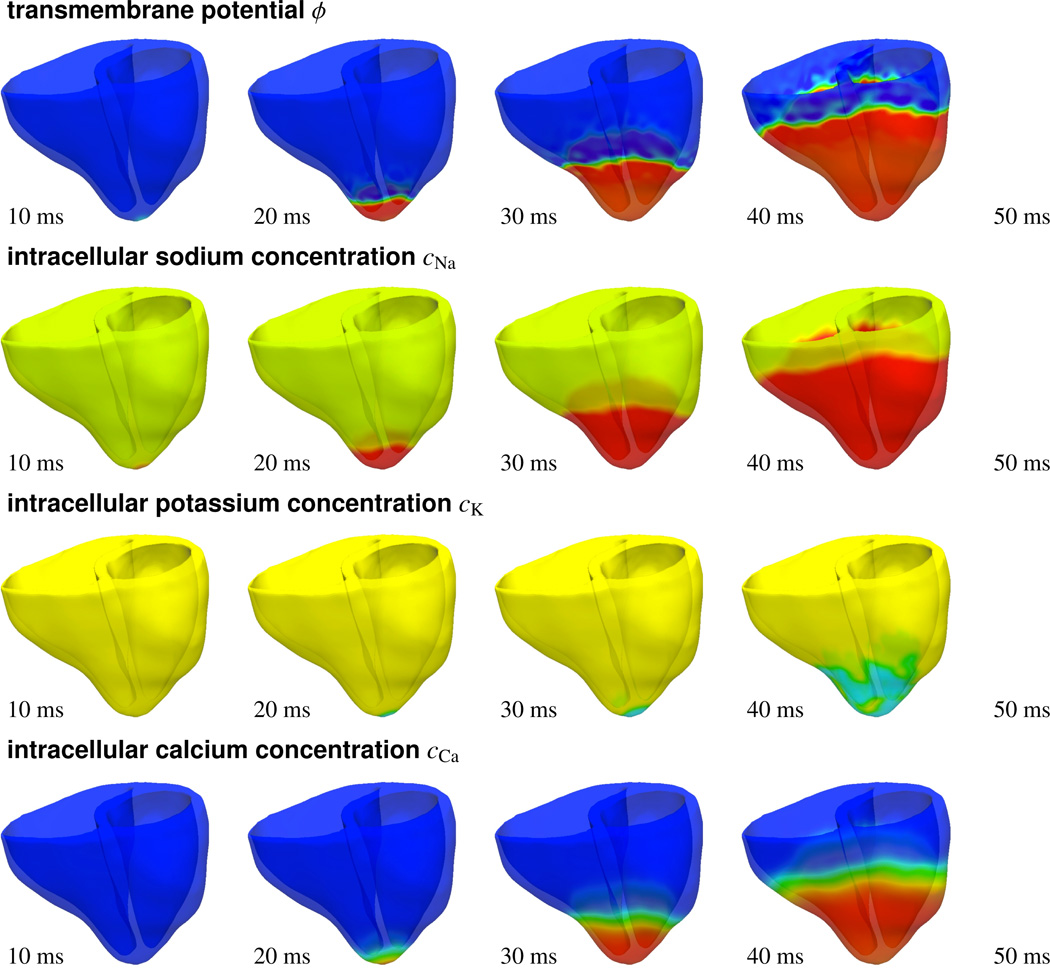
Figure 11 illustrates the activation profile in response to atrioventricular node pacing through photostimulation. To reproduce the native activation sequence of the human heart, we virtually inject photosensitive cells into the basal septal region, the location of the atrioventricular node, and pace them with blue light. A depolarization wave forms in the region of the atrioventricular node, travels down the septum, and activates the left and right ventricles. When comparing the temporal evolution of the transmembrane potential ϕ, top row, with the different ion concentrations c_Na, c_K, and c_Ca, lower rows, we observe that the sodium concentration changes first, with a sharp front, followed by changes in the potassium and calcium concentrations, with smoother fronts. These observations are in agreement with the temporal evolution of the local ion concentrations illustrated in Figure 8. After approximately 50 ms, the entire heart is depolarized. The transmembrane potential ϕ has changed from approximately −80 mV to +20 mV.

Figure 11.

Photostimulation of a human heart. Spatio-temporal evolution of transmembrane potential ϕ, intracellular sodium c_Na, potassium c_K, and calcium c_Ca concentrations for atrioventricular node paced heart. Photosensitive cells are virtually injected into the basal region of the septum, while all other regions are modeled as conventional cardiac muscle cells. A depolarization wave forms at the atrioventricular node, travels down the septum, and activates the left and right ventricles.

7.2. Apical pacing through photostimulation

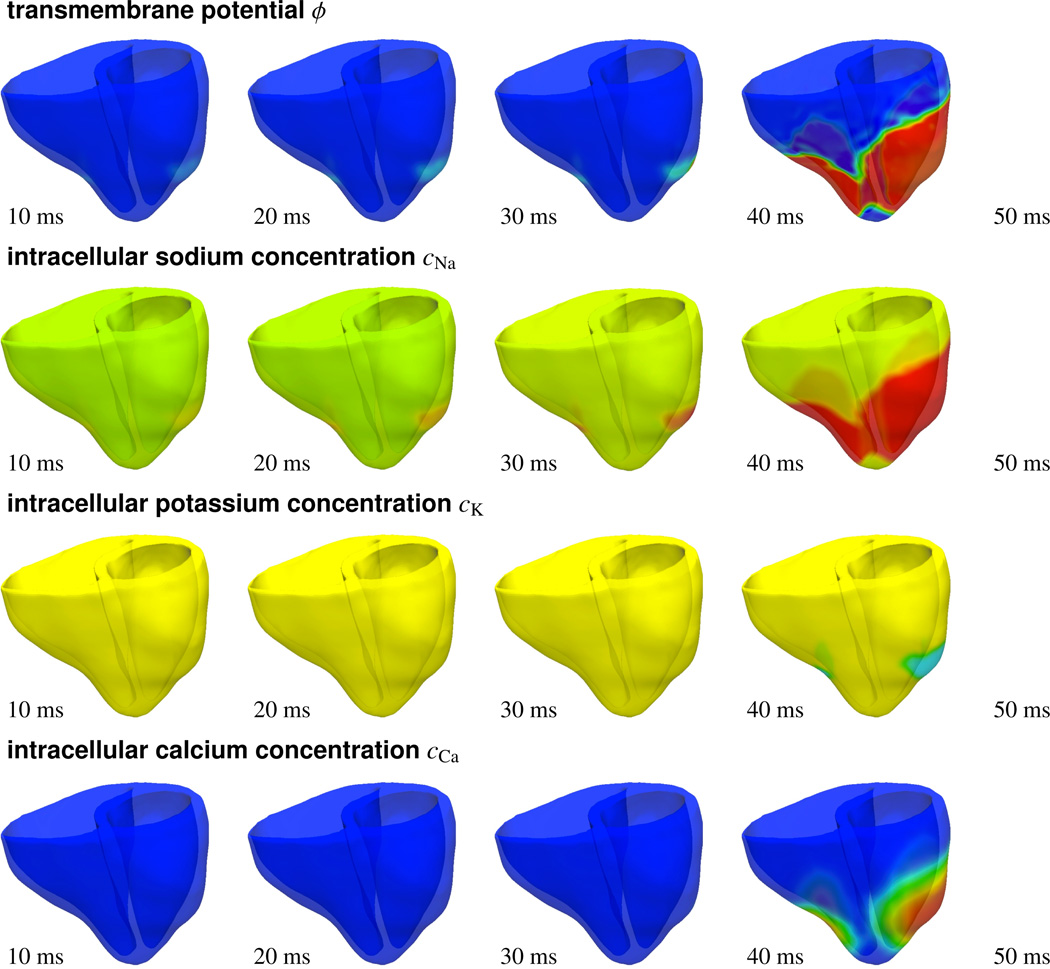
Figure 12 shows the response of the heart to apical pacing through photostimulation. The right ventricular apex has traditionally been the most prominent pacing site, providing a stable lead position associated with few complications. To predict the activation sequence in response to apical pacing, we virtually inject photosensitive cells into the apex, stimulate them with light for 30 ms, turn off the light, and monitor the electrical and chemical fields. As the transmembrane potential profile indicates, a depolarization wave forms at the apex, travels up towards the base, and activates the septum and both ventricles simultaneously. Again, we observe the rapid increase in the intracellular sodium concentration c_Na causing the heart to depolarize. The transmembrane potential changes from −80 mV to +20 mV within the first 50 ms of the cycle, until the heart is completely depolarized. The intracellular calcium concentration c_Ca follows smoothly, while the intracellular potassium concentration c_K changes only in the later stages.

Figure 12.

Photostimulation of a human heart. Spatio-temporal evolution of transmembrane potential ϕ, intracellular sodium c_Na, potassium c_K, and calcium c_Ca concentrations for apically paced heart. Photosensitive cells are virtually injected into the apex, while all other regions are modeled as conventional cardiac muscle cells. A depolarization wave forms at the apex, travels up, and activates the septum and both ventricles simultaneously.

7.3. Biventricular pacing through photostimulation

Figure 13 displays the activation of the heart, photostimulated through bi-ventricular pacing. Biventricular pacing is a common pacing strategy in patients with heart failure for which both ventricles do not contract synchronously. To simulate biventricular pacing, we virtually inject photosensitive cells into the lateral walls of the left and right ventricles and pace both locations simultaneously. In response to photostimulation, two depolarization waves form, one at each pacing site. The waves travel along the ventricles to finally activate the apex and the septum. Again, during depolarization, the transmembrane potential profile ϕ closely follows the intracellular sodium concentration c_Na, which triggers the rapid upstroke of the action potential, while the intracellular calcium concentration c_Ca follows slightly later with a smoother propagation front.

Figure 13.

Photostimulation of a human heart. Spatio-temporal evolution of transmembrane potential ϕ, intracellular sodium c_Na, potassium c_K, and calcium c_Ca concentrations for bi-vnetricularly paced heart. Photosensitive cells are virtually injected into the lateral walls of the left and right ventricles, while all other regions are modeled as conventional cardiac muscle cells. Two depolarization waves form in the lateral left and right ventricular walls to travel along the ventricles and activate the apex and the septum.

8. Discussion

8.1. Comparison with the literature

Within the past decade, optogenetics has become a tremendously active field of research [10], however, little is known about its impact on cardiac cells, neither in isolation, nor in the cardiac system. Since the channelrhodopsin photocycle itself is relatively well established from intense studies of the neuronal system [33, 34], we simply adopt the kinetics of a well-characterized three-state photocycle model [20, 32]. Creating a cellular model system that expresses Channelrhodopsin-2 allows us to validate its photocurrent using whole cell patch-clamp [24] or multielectrode array recordings [6]. Using both techniques, we have recently demonstrated that our cell model is capable of reliably reproducing experimentally measured photostimulation amplitudes, pulse widths, and frequencies from single cell recordings [1]. In this manuscript, for the first time, we quantify the impact of photostimulation in side-by-side comparisons between conventional cells, electrically stimulated for 1 ms, and genetically engineered cells, optically stimulated for 30 ms, see Figures 6 – 9. The gating variables in Figures 6 can be understood as internal variables, which cannot be measured experimentally. The ionic currents in Figure 7 can be extracted experimentally from a series of voltage and current clamp recordings using drugs to selectively block the activity of different combinations of channels. Although theoretically possible, for optogenetically engineered cells, typically only the channelrhodopsin photocurrent is measured experimentally. Its indirect impact on all other currents, however, has not be characterized systematically to date. The ion concentrations in Figure 8 could potentially be measured experimentally, however, for optogenetically engineered cells, this has not been done to date. Unfortunately, only three groups worldwide have reported the use of optogenetics to manipulate the cardiac system, one in zebrafish [2], one in transgenic mice [6], and one in stem cell derived cardiomyocytes [1]. The last study by our own group is the only one that has demonstrated the potential of optogenetics in human heart cells. This underlines the importance of computational models, which provide easy access to ion channel dynamics and ionic concentrations, both in healthy and diseased conditions.

The transmembrane potential in Figure 9 could potentially be extracted from patch clamp or microelectrode array recordings. Here, for the selected light intensity, we find 30 ms to be the minimum light exposure time to evoke a standard action potential. For photostimulation just slightly above this threshold, we identify the time delay between electrical stimulation and photostimulation to be 34 ms, which agrees nicely with the values of 19.7±3.4 ms reported in the literature [6]. Although not explicitly reported here, in agreement with the literature, we observe a decrease in activation delay for increased light intensities [6]. Beyond the stimulation threshold, however, electrically and optically activated cells display an almost identical electrophysiology with the characteristic rapid upstroke, early, partial repolarization, a pronounced plateau, a final repolarization, and a return to the resting phase, see Figures 9. Again, this agrees nicely with experimental findings, which report that channelrhodopsin expression in murine embryonic stem cells is not associated with additional leak currents, or changes in the resting membrane potential, membrane resistance, and action potential duration [6].

A first qualitative study in zebrafish has demonstrated that optogenetic tools can, in principle, be used to control the cardiac system in vivo [2]. In that study, optical perturbation of genetically engineered pacemaker cells was entirely reversible. This agrees nicely with our optically stimulated transmembrane potential returning smoothly to its resting state, see Figure 9. The study also showed that only few genetically engineered cells are needed to deliver a sufficient optical stimulus in zebrafish hearts [2]. In our human heart, we virtually inject approximately 10⁷ cells covering a volume of 0.02 cm³, which is roughly the size of the atrioventricular node in humans, see Figure 10. In agreement with an in vivo study in transgenic mice [6], we observe that smaller cell volumes require either increased light intensities or longer stimulation times. Similar to the reported activation delays of 12.2±3.7 ms and 9.3±2.2 ms upon atrial and ventricular photostimulation in mice [6], we observe an activation delay of 19.5 ms when comparing our light activated heart in Figure 11 with previous simulations of native activation sequences [27, 42] and electrical pacing [47].

Overall, because of the inherent frequency mismatch in rodents and humans, the complete in vivo validation of our model remains challenging, and can only be addressed satisfactorily by means of large animal models. This is, however, a generic limitation of the clinical translational character of cardiac optogenetics in general. Large animal models would also allow us to quantify the impact of optogenetical stimulation on cardiac function in vivo. In a previous study, we have demonstrated how light can be turned into force using optogenetic tools in vitro [1]. A related study by another group reported light-induced mechanical strains of up to 4.5% [24]. We are currently integrating our continuum model for the photoelectrochemistry of living systems into a model for excitation-contraction coupling [16]. This will allow us to characterize the mechanically-mediated ionic response of strain-gated ion channels [38, 44], and, vice versa, the calcium-mediated mechanical response of the heart [8, 37], and its impact on muscle contraction and cardiac function [14, 18].

8.2. Conclusion

At an unprecedented temporal and spatial precision, optogenetic tools enable us to manipulate electrically active cells with light. This study documents our first attempts to model genetically engineered light-sensitive heart muscle cells, with the ultimate goal to control the cardiac system by mean of photostimulation. In contrast to electrical pacemakers, light delivery is minimally invasive, genetically targeted, and temporally precise. Most importantly, light can be delivered at a distance. Unlike pacing leads for electrical stimulation, which are known to have a high perforation risk, the light source for optical stimulation does not need to be in direct contact with the moving heart muscle. Light pacing might therefore be an attractive remote, less invasive, and more durable alternative to conventional electrical pacing. Unlike traditional electrical stimulation, optogenetic stimulation allows us to precisely control the selective permeability of the plasma membrane, its conductivity with respect to different ions, its sensitivity to light of different wavelengths, and the spatio-temporal evolution of different opening and closing profiles. Given this incredible freedom, there is a pressing need to establish economic strategies to optimize the matrix of input variables. Predictive continuum models for photoelectrochemistry allow us to virtually probe landscapes of process parameters and identify optimal photostimulation sequences in various different tissues and organs. Discretized with finite element tools, they enable the combination of virtually any cell type on virtually any geometry. Our time-adaptive algorithm is highly efficient, conceptually modular, and easily portable to any commercial nonlinear finite element platfrom. While the photoelectrochemical behavior of living tissue is almost impossible to characterize in vivo, and little is known about the spatio-temporal distribution of sodium, potassium, and calcium ions, computational tools like ours allow us to predict action potential profiles and ionic concentrations across the heart in silico within the order of minutes. We believe that computational optogenetics will be widely applicable to predict the response of other genetically engineered, electrically-active cells and, ultimately, support the design of novel therapies for various types of neuronal, musculoskeletal, pancreatic, and cardiac disorders such as depression, schizophrenia, cerebral palsy, paralysis, diabetes, pain syndromes, and cardiac arrhythmias.

Appendix

Our cardiac cell model is based on a well-characterized and frequently used ventricular cell model [43, 47], enhanced by the channelrhodopsin photocurrent I_Chr and its corresponding gating variable g_ChR2. We characterize the cell through n_ion = 4 ion concentrations,

$$c_{\text{ion}}=[c_{\text{Na}},c_{\mathrm{K}},c_{\text{Ca}},c_{\text{Ca}}^{\text{sr}}]$$ (27)

where c_Na, c_K, and c_Ca are the intracellular sodium, potassium, and calcium concentrations, and $c_{\text{Ca}}^{\text{sr}}$ is the calcium concentration in the sarcoplastic reticulum. Changes in these concentrations are brought about by an in- and outflux of ions which we describe through a total of n_crt = 16 ionic currents.

$$I_{\text{crt}}=[I_{\text{Na}},I_{\text{bNa}},I_{\text{NaK}},I_{\text{NaCa}},I_{\text{ChR}2},I_{\mathrm{K}1},I_{\text{Kr}},I_{\text{Ks}},I_{\text{pK}},I_{\mathrm{t}0},I_{\text{CaL}},I_{\text{bCa}},I_{\text{pCa}},I_{\text{leak}},I_{\text{up}},I_{\text{rel}}].$$ (28)

These are the fast sodium current I_Na, the background sodium current I_bNa, the sodium potassium pump current I_NaK, the sodium calcium exchanger current I_NaCa, the channelrhodopsin photocurrent I_ChR2 the inward rectifier current I_K1, the rapid delayed rectifier current I_Kr, the slow delayed rectifier current I_Ks, the plateau potassium current I_pK, the transient outward current I_t0, the L-type calcium current I_CaL, the background calcium current I_bCa, the plateau calcium current I_pCa, the leakage current I_leak, and sarcoplastic reticulum uptake and release currents I_up and I_rel. The activation and inactivation of these currents is governed by the transmembrane potential ϕ, and by n_gate = 14 gating variables.

$$g_{\text{gate}}=[g_{\mathrm{m}},g_{\mathrm{h}},g_{\mathrm{j}},g_{\text{ChR}2},g_{\text{xr}1},g_{\text{xr}2},g_{\text{xs}},g_{\mathrm{r}},g_{\mathrm{s}},g_{\mathrm{d}},g_{\mathrm{f}},g_{\mathrm{K}1\mathrm{\infty }},g_{\text{fCa}},g_{\mathrm{g}}],$$ (29)

In particular, these are the sodium activation gate g_m, the fast and slow sodium inactivation gates g_h and g_j, the channelrhodopsin activation gate g_ChR2, the rapid delayed rectifier activation and inactivation gates g_xr1 and g_xr2, the slow delayed rectifier activation gate g_xs, the transient potassium activation and inactivation gates g_r and g_s, the long-lasting L-type calcium channel activation and inactivation gates g_d, g_f, and g_fCa, and the calcium release activation gate g_g. We will now specify the mathematic model for the concentrations c_ion, currents I_crt, and gating variables g_gate. In Table 1, we summarize all model parameters, their physical interpretations, and their parameter values [43, 47].

Table 1.

Parameters of the proposed human cardiac muscle cell model. Symbols, physical interpretations, and parameter values.

R	universal gas constant	8.3143 J K−1 mol−1
T	temperature	310K
V	cytoplasmic volume	16404 µm3
F	Faraday constant	96.4867 C/mmol
C	membrane capacitance	185 pF
Vsr	volume of sarcoplastic reticulum	1094 µm3
cNa0	extracellular sodium concentration	140 mM
cK0	extracellular potassium concentration	5.4 mM
cCa0	extracellular calcium concentration	2 mM
$I_{\text{NaK}}^{\text{max}}$	maximum sodium potassium pump current	1.362 pA/pF
$I_{\text{NaCa}}^{\text{max}}$	maximum sodium calcium exchanger current	1000 pA/pF
$I_{\text{leak}}^{\text{max}}$	maximum leakage current	0.08 s−1
$I_{\text{up}}^{\text{max}}$	maximum sarcoplastic reticulum calcium uptake current	0.425 mM/s
$I_{\text{rel}}^{\text{max}}$	maximum sarcoplastic reticulum calcium release current	8.232 mM/s
$C_{\text{Na}}^{\text{max}}$	maximum fast sodium conductance	14.838 nS/pF
$C_{\text{bNa}}^{\text{max}}$	maximum background sodium conductance	0.00029 nS/pF
$C_{\mathrm{K}1}^{\text{max}}$	maximum inward rectifier conductance	5.405 nS/pF
$C_{\text{Kr}}^{\text{max}}$	maximum rapid delayed rectifier conductance	0.0096 nS/pF
$C_{\text{Ks},\text{epi}}^{\text{max}}$	maximum slow delayed rectifier conductance for epicardial cells	0.245 nS/pF
$C_{\text{Ks},\text{endo}}^{\text{max}}$	maximum slow delayed rectifier conductance for endocardial cells	0.245 nS/pF
$C_{\text{Ks},\mathrm{M}}^{\text{max}}$	maximum slow delayed rectifier conductance for M cells	0.062 nS/pF
$C_{\text{pK}}^{\text{max}}$	maximum potassium pump conductance	0.0146 nS/pF
$C_{\mathrm{t}0,\text{epi}}^{\text{max}}$	maximum transient outward conductance for epicardial cells	0.294 nS/pF
$C_{\mathrm{t}0,\text{endo}}^{\text{max}}$	maximum transient outward conductance for endocardial cells	0.073 nS/pF
$C_{\mathrm{t}0,\mathrm{M}}^{\text{max}}$	maximum transient outward conductance for M cells	0.294 nS/pF
$C_{\text{CaL}}^{\text{max}}$	maximum calcium conductance	0.175 mm3/[µFs]
$C_{\text{bCa}}^{\text{max}}$	maximum background calcium conductance	0.000592 nS/pF
$C_{\text{pCa}}^{\text{max}}$	maximum plateau calcium conductance	0.825 nS/pF
cNaCa	half saturation sodium calcium exchanger concentration	87.50 mM
cCaNa	half saturation calcium sodium exchanger concentration	1.38 mM
cNaK	half saturation sodium potassium pump concentration	40.00 mM
cKNa	half saturation potassium sodium pump concentration	1.00 mM
cpCa	half saturation plateau calcium concentration	0.0005 mM
cup	half saturation sarcoplastic reticulum calcium uptake	0.00025 mM
crel	half saturation sarcoplastic reticulum calcium release	0.25 mM
cbuf	half saturation calcium buffer concentration	0.001 mM
ctot	total calcium buffer concentration	0.15 mM
$c_{\text{buf}}^{\text{sr}}$	half saturation sarcoplastic reticulum calcium buffer concentration	0.3 mM
$c_{\text{tot}}^{\text{sr}}$	total sarcoplastic reticulum calcium buffer concentration	10 mM
$k_{\text{NaCa}}^{\text{sat}}$	sodium calcium saturation factor	0.1
pKNa	sodium permeability factor	0.03
γrel	weighting factor	2.0
γNaCa	pump current enhancing factor	2.5
γ	sodium calcium factor	0.35

8.3. Sodium concentration, currents, and gating variables

Sodium plays a crucial role in generating the fast upstroke in the initial phase of the action potential. At rest, both electrical forces and chemical gradients pull extracellular sodium ions into the cell. The influx of sodium ions is small, however, since at rest, the membrane is relatively impermeable to sodium. An external stimulus above a critical threshold value, here generated through either photostimulation or through active neighboring cells, opens the fast sodium channels to initiate a rapid inflow of sodium ions associated with the rapid depolarization of the cell membrane. The transmembrane potential increases drastically by more than 100 mV in less than 2 ms, see Figure 9. At the end of the upstroke, the cell membrane is positively charged, and the fast sodium channels return to their closed state. The sodium concentration

$${ċ}_{\text{Na}}=-\frac{C}{\mathit{\text{VF}}}[I_{\text{Na}}+I_{\text{bNa}}+3I_{\text{NaK}}+3I_{\text{NaCa}}+I_{\text{ChR}2}]$$ (30)

changes in response to the fast sodium current I_Na, the background sodium current I_bNa, the sodium potassium pump current I_NaK, and the sodium calcium exchanger current I_NaCa, scaled by the membrane capacitance per unit surface area C = 185 pF, the cytoplasmic volume V = 16404 µm³, and the Faraday constant F = 96.4867 C/mmol. The scaling factor three indicates that both the sodium potassium pump and the sodium calcium exchanger operate at a three-to-two ratio. The sodium related currents are defined as follows,

$$\begin{array}{cc}{I}_{\text{Na}}\hfill & =C_{\text{Na}}^{\text{max}}{g}_{\mathrm{m}}^3{g}_{\mathrm{h}}{g}_{\mathrm{j}}[\varphi -{\varphi }_{\text{Na}}]\hfill \\ I_{\text{bNa}}\hfill & =C_{\text{bNa}}^{\text{max}}[\varphi -{\varphi }_{\text{Na}}]\hfill \\ I_{\text{NaK}}\hfill & =I_{\text{NaK}}^{\text{max}}[c_{\mathrm{K}0}{c}_{\text{Na}}]{[[c_{\text{Na}}+c_{\text{NaK}}][c_{\mathrm{K}0}+c_{\text{KNa}}][1+0.1245e^{-0.1\varphi F/\mathit{\text{RT}}}+0.0353e^{-\varphi F/\mathit{\text{RT}}}]]}^{-1}\hfill \\ I_{\text{NaCa}}\hfill & =I_{\text{NaCa}}^{\text{max}}[e^{\gamma \varphi F/\mathit{\text{RT}}}{c}_{\text{Na}}^3{c}_{\text{Ca}0}-e^{(\gamma -1)\varphi F/\mathit{\text{RT}}}{c}_{\text{Na}0}^3{c}_{\text{Ca}}{\gamma }_{\text{NaCa}}]{[[c_{\text{NaCa}}^3+c_{\text{Na}0}^3][c_{\text{CaNa}}+c_{\text{Ca}0}][1+k_{\text{NaCa}}^{\text{sat}}{e}^{(\gamma -1)\varphi F/\mathit{\text{RT}}}]]}^{-1}\hfill \\ I_{\text{ChR}2}\hfill & =C_{\text{ChR}2}{g}_{\text{ChR}2}[\varphi -{\varphi }_{\text{ChR}2}]\hfill \end{array}$$ (31)

where the scaling factors are the maximum fast sodium conductance $C_{\text{Na}}^{\text{max}}=14.838\text{ nS}/\text{pF}$, the maximum background sodium conductance $C_{\text{bNa}}^{\text{max}}=0.00029\text{ nS}/\text{pF}$, the maximum sodium potassium pump current $I_{\text{NaK}}^{\text{max}}=1.362\text{ pA}/\text{pF}$, and the maximum sodium calcium exchanger current $I_{\text{NaCa}}^{\text{max}}=1000\text{ pA}/\text{pF}$. The key player in generating the rapid upstroke is the fast sodium current I_Na. It follows a well-characterized three-gate formulation of Beeler-Reuter type [3] in terms of the sodium activation gate g_m, the fast sodium inactivation gate g_h, and the slow sodium inactivation gate g_j. Classical Hodgkin-Huxley type equations, ${ġ}_{\text{gate}}=[g_{\text{gate}}^{\mathrm{\infty }}-g_{\text{gate}}]/{\tau }_{\text{gate}}$, define their evolution in terms of the steady state value $g_{\text{gate}}^{\mathrm{\infty }}$ and the time constant associated with reaching the steady state τ_gate. For the sodium activation gate, ${ġ}_{\mathrm{m}}=[g_{\mathrm{m}}^{\mathrm{\infty }}-g_{\mathrm{m}}]/{\tau }_{\mathrm{m}}$, which initiates the rapid upstroke, they take the following explicit representations.

$$\begin{array}{cc}{g}_{\mathrm{m}}^{\mathrm{\infty }}\hfill & ={[1+e^{(-56.86-\varphi )/9.03}]}^{-2}\hfill \\ {\tau }_{\mathrm{m}}\hfill & =0.1{[1+e^{(-60-\varphi )/5}]}^{-1}[{[1+e^{(\varphi +35)/5}]}^{-1}+{[1+e^{(\varphi -50)/200}]}^{-1}]\hfill \end{array}$$ (32)

The kinetics of inactivation are exponential. For the fast sodium inactivation gate, ${ġ}_{\mathrm{h}}=[g_{\mathrm{h}}^{\mathrm{\infty }}-g_{\mathrm{h}}]/{\tau }_{\mathrm{h}}$, which initiates a fast inactivation of the sodium channel almost instantaneously after the rapid upstroke, we express the steady state value and the corresponding time constant as follows.

$$\begin{array}{cc}{g}_{\mathrm{h}}^{\mathrm{\infty }}\hfill & ={[1+e^{(\varphi +71.55)/7.43}]}^{-2}\hfill \\ {\tau }_{\mathrm{h}}\hfill & =\{\begin{array}{ccc}0.1688[1+e^{-(\varphi +10.66)/11.1}]\hfill & \text{if}\hfill & \varphi \ge -40\hfill \\ {[0.057e^{-(\varphi +80)/6.8}+2.7e^{0.079\varphi }+3.1·{10}^5{e}^{0.3485\varphi }]}^{-1}\hfill & \text{if}\hfill & \varphi <-40\hfill \end{array}\hfill \end{array}$$ (33)

For the slow sodium inactivation gate, ${ġ}_{\mathrm{j}}=[g_{\mathrm{j}}^{\mathrm{\infty }}-g_{\mathrm{j}}]/{\tau }_{\mathrm{j}}$, which gradually inactivates the fast sodium channel over a time span of 100 to 200 ms, we express these constants in the following form.

$$\begin{array}{cc}{g}_{\mathrm{j}}^{\mathrm{\infty }}\hfill & ={[1+e^{(\varphi +71.55)/7.43}]}^{-2}\hfill \\ {\tau }_{\mathrm{j}}\hfill & ={[{\alpha }_{\mathrm{j}}+{\beta }_{\mathrm{j}}]}^{-1}\hfill \\ {\alpha }_{\mathrm{j}}\hfill & =\{\begin{array}{ccc}0\hfill & \text{if}\hfill & \varphi \ge -40\hfill \\ [-2.5428·{10}^4{e}^{0.2444\varphi }-6.948·{10}^{-6}{e}^{-0.04391\varphi }][\varphi +37.78]{[1+e^{0.311(\varphi +79.23)}]}^{-1}\hfill & \text{if}\hfill & \varphi <-40\hfill \end{array}\hfill \\ {\beta }_{\mathrm{j}}\hfill & =\{\begin{array}{ccc}0.6e^{0.057\varphi }{[1+e^{-0.1(\varphi +32)}]}^{-1}\hfill & \text{if}\hfill & \varphi \ge -40\hfill \\ 0.02424e^{-0.01052\varphi }{[1+e^{-0.1378(\varphi +40.14)}]}^{-1}\hfill & \text{if}\hfill & \varphi <-40\hfill \end{array}\hfill \end{array}$$ (34)

The sodium potassium pump I_NaK, a metabolic pump that continuously expels sodium ions from the cell interior and pumps in potassium ions, is reponsible to remove the sodium ions, which had entered the cell rapidly during the fast upstroke. The sodium calcium exchanger I_NaCa also affects the intracellular sodium concentration through the expulsion of intracellular calcium ions. The additional parameters that characterize the sodium potassium pump current I_NaK and for the sodium calcium exchanger current I_NaCa are the extracellular sodium, potassium, and calcium concentrations c_Na0 = 140 mM, c_K0 = 5.4 mM, and c_Ca0 = 2 mM, the half saturation constants c_CaNa = 1.38 mM, c_NaCa = 87.5 mM, c_KNa = 1 mM, c_NaK = 40 mM, the sodium calcium saturation factor $k_{\text{NaCa}}^{\text{sat}}=0.1$, the outward sodium calcium pump current enhancing factor γ_NaCa = 2.5, and the voltage dependent sodium calcium parameter γ = 0.35.

8.4. Potassium concentration, currents, and gating variables

Potassium plays an important role in maintaining the appropriate action potential profile in all four phases after the rapid upstroke. Unlike for sodium, the electrical force that pulls potassium ions inward is slightly weaker than the chemical force of diffusion pulling potassium ions outward. Accordingly, potassium tends to leave the resting cell. At the end of the rapid upstroke, before the beginning of the plateau, we can observe an early, brief period of limited repolarization governed by the voltage-activated transient outward current I_t0. During the following plateau phase, we observe an influx of calcium ions which is balanced by the efflux of an equal amount of positively charged potassium ions, mainly regulated by the rapid and slow delayed rectifier currents I_Kr and I_Ks. The final repolarization phase is almost exclusive caused to potassium ions leaving the cell such that the membrane potential can return to its resting state, see Figure 9. In summary, four major currents control the evolution of the potassium concentration,

$${ċ}_{\mathrm{K}}=-\frac{C}{\mathit{\text{VF}}}[I_{\mathrm{K}1}+I_{\text{Kr}}+I_{\text{Ks}}-2I_{\text{NaK}}+I_{\text{pK}}+I_{\mathrm{t}0}]$$ (35)

the inward rectifier current I_K1, the rapid delayed rectifier current I_Kr, the slow delayed rectifier current I_Ks, and the transient outward current I_t0. The sodium potassium pump current I_NaK and the plateau potassium current I_pK play a minor role. The six potassium related currents scale by the membrane capacitance per unit surface area C = 185 pF, by the cytoplasmic volume V = 16404 µm³, and by the Faraday constant F = 96.4867 C/mmol. We adopt their following definitions,

$$\begin{array}{cc}{I}_{\mathrm{K}1}\hfill & =C_{\mathrm{K}1}^{\text{max}}{g}_{\mathrm{K}1}^{\mathrm{\infty }}{[c_{\mathrm{K}0}/5.4]}^{1/2}[\varphi -{\varphi }_{\mathrm{K}}]\hfill \\ I_{\text{Kr}}\hfill & =C_{\text{Kr}}^{\text{max}}{g}_{\text{xr}1}{g}_{\text{xr}2}{[c_{\mathrm{K}0}/5.4]}^{1/2}[\varphi -{\varphi }_{\mathrm{K}}]\hfill \\ I_{\text{Ks}}\hfill & =C_{\text{Ks}}^{\text{max}}{g}_{\text{xs}}^2[\varphi -{\varphi }_{\text{Ks}}]\hfill \\ I_{\text{NaK}}\hfill & =I_{\text{NaK}}^{\text{max}}[c_{\mathrm{K}0}{c}_{\text{Na}}]{[[c_{\text{Na}}+c_{\text{NaK}}][c_{\mathrm{K}0}+c_{\text{KNa}}][1+0.1245e^{-0.1\varphi F/\mathit{\text{RT}}}+0.0353e^{-\varphi F/\mathit{\text{RT}}}]]}^{-1}\hfill \\ I_{\text{pK}}\hfill & =C_{\text{pK}}^{\text{max}}{[1+e^{[25-\varphi ]/5.98}]}^{-1}[\varphi -{\varphi }_{\mathrm{K}}]\hfill \\ I_{\mathrm{t}0}\hfill & =C_{\mathrm{t}0}^{\text{max}}{g}_{\mathrm{r}}{g}_{\mathrm{s}}[\varphi -{\varphi }_{\mathrm{K}}]\hfill \end{array}$$ (36)

where the individual scaling factors are the maximum inward rectifier conductance $C_{\mathrm{K}1}^{\text{max}}=5.405\text{ nS}/\text{pF}$, the maximum rapid delayed rectifier conductance $C_{\text{Kr}}^{\text{max}}=0.096\text{ nS}/\text{pF}$, the maximum slow delayed rectifier conductance for epicardial and endocardial cells $C_{\text{Ks},\text{epi}}^{\text{max}}=C_{\text{Ks},\text{endo}}^{\text{max}}=0.245\text{ nS}/\text{pF}$ and for M cells $C_{\text{Ks},\mathrm{M}}^{\text{max}}=0.062\text{ nS}/\text{pF}$, the maximum sodium potassium pump current $I_{\text{NaK}}^{\text{max}}=1.362\text{ PA}/\text{pF}$, the maximum potassium pump conductance $C_{\text{pK}}^{\text{max}}=0.0146\text{ nS}/\text{pF}$, and the maximum transient outward conductance for epicardial and M cells $C_{\mathrm{t}0,\text{epi}}^{\text{max}}=C_{\mathrm{t}0,\mathrm{M}}^{\text{max}}=0.0294\text{ nS}/\text{pF}$ and for endocardial cells $C_{\mathrm{t}0,\text{endo}}^{\text{max}}=0.073\text{ nS}/\text{pF}$. The maximum inward rectifier current I_K1, which is most active during the later phases of the action potential, depends explicitly on the extracellular potassium concentration c_K0 = 5.4 mM. It scales with the time-independent inward recrification factor $g_{\mathrm{K}1}^{\mathrm{\infty }}$ parameterized in terms of the potential equilibrium potential ϕ_K.

$$\begin{array}{ccc}{g}_{\mathrm{K}1}^{\mathrm{\infty }}={\alpha }_{\mathrm{K}1}{[{\alpha }_{\mathrm{K}1}+{\beta }_{\mathrm{K}1}]}^{-1}\hfill & \text{with}\hfill & \begin{array}{c}{\alpha }_{\mathrm{K}1}=0.1{[1+e^{0.06(\varphi -{\varphi }_{\mathrm{K}}-200)}]}^{-1}\hfill \\ {\beta }_{\mathrm{K}1}=[3e^{0.0002(\varphi -{\varphi }_{\mathrm{K}}+100)}+e^{0.1(\varphi -{\varphi }_{\mathrm{K}}-10)}]{[1+e^{-0.5(\varphi -{\varphi }_{\mathrm{K}})}]}^{-1}\hfill \end{array}\hfill \end{array}$$ (37)

A balanced influx of calcium ions and efflux of potassium ions governs the action potential plateau. In particular, the rapid and slow delayed rectifier current I_Kr and I_Ks govern the potassium efflux. The channel for the rapid delayed rectifier current I_Kr is gated by an activation gate ${ġ}_{\mathrm{x}1}=[g_{\mathrm{x}1}^{\mathrm{\infty }}-g_{\mathrm{x}1}]/{\tau }_{\mathrm{x}1}$ with the steady state value and time constant given as

$$\begin{array}{cc}{g}_{\text{xr}1}^{\mathrm{\infty }}\hfill & ={[1+e^{(-26-\varphi )/7}]}^{-1}\hfill \\ {\tau }_{\text{xr}1}\hfill & =2700{[1+e^{(-45-\varphi )/10}]}^{-1}{[1+e^{(\varphi +30)/11.5}]}^{-1},\hfill \end{array}$$ (38)

and by an inactivation gate ${ġ}_{\mathrm{x}2}=[g_{\mathrm{x}2}^{\mathrm{\infty }}-g_{\mathrm{x}2}]/{\tau }_{\mathrm{x}2}$, with the following steady state value and time constant.

$$\begin{array}{cc}{g}_{\text{xr}2}^{\mathrm{\infty }}\hfill & ={[1+e^{(\varphi +88)/24}]}^{-1}\hfill \\ {\tau }_{\text{xr}2}\hfill & =3.36{[1+e^{(-60-\varphi )/20}]}^{-1}{[1+e^{(\varphi -60)/20}]}^{-1}.\hfill \end{array}$$ (39)

The channel for the slow delayed rectifier current I_Ks is a function of the reversal potential ϕ_Ks = RT/F log ([c_K0 + p_KNa c_Na0][c_K + p_KNa c_Na]⁻¹) parameterized in terms of its permeability to sodium ions p_KNa = 0.03. It is gated by an activation gate ${ġ}_{\text{xs}}=[g_{\text{xs}}^{\mathrm{\infty }}-g_{\text{xs}}]/{\tau }_{\text{xs}}$ in terms of the following parameterization.

$$\begin{array}{cc}{g}_{\text{xs}}^{\mathrm{\infty }}\hfill & ={[1+e^{(-5-\varphi )/14}]}^{-1}\hfill \\ {\tau }_{\text{xs}}\hfill & =1100{[1+e^{(-10-\varphi )/6}]}^{-1/2}{[1+e^{(\varphi -60)/20}]}^{-1}\hfill \end{array}$$ (40)

The transient potassium outward current I_t0 is responsible for the transition between the rapid upstroke and the plateau phase, where it generates an early short period of limited repolarization. It is gated by a voltage-dependent activation gate g_r with ${ġ}_{\mathrm{r}}=[g_{\mathrm{r}}^{\mathrm{\infty }}-g_{\mathrm{r}}]/{\tau }_{\mathrm{r}}$ defined through the following steady state value and time constant,

$$\begin{array}{cc}{g}_{\mathrm{r}}^{\infty }\hfill & ={[1+e^{(20-\varphi )/6}]}^{-1}\hfill \\ {\tau }_{\mathrm{r}}\hfill & =9.5e^{-{(\varphi +40)}^2/1800}+0.8\hfill \end{array}$$ (41)

and by the voltage-dependent inactivation gate g_s with ${ġ}_{\mathrm{s}}=[g_{\mathrm{s}}^{\mathrm{\infty }}-g_{\mathrm{s}}]/{\tau }_{\mathrm{s}}$ with the steady state value and time constant given as follows.

$$\begin{array}{cc}\begin{array}{cc}{g}_{\mathrm{s}}^{\infty }\hfill & =[1+e^{(\varphi +20)/5}]\hfill \\ {\tau }_{\mathrm{s}}\hfill & =85e^{-{(\varphi +45)}^2/320}+5[1+e^{(\varphi -20)/5}]+3\hfill \end{array}\}\text{ epicardium}\hfill & \begin{array}{cc}{g}_{\mathrm{s}}^{\infty }\hfill & =[1+e^{(\varphi +28)/5}]\hfill \\ {\tau }_{\mathrm{s}}\hfill & =1000e^{-{(\varphi +67)}^2/1000}+8\hfill \end{array}\}\hfill \end{array}\text{ endocardium}$$ (42)

This voltage dependent potassium inactivation gate displays a significantly different behavior for epicardial and endocardial cells and is therefore characterized differently in different regions of the heart. Similar to the previous subsection, we have introduced the extracellular sodium and potassium concentrations c_Na0 = 140 mM and c_K0 = 5.4 mM, and the half saturation constants c_KNa = 1 mM and c_NaK = 40 mM.

8.5. Calcium concentration, currents, and gating variables

Calcium is the key player to translate electrical excitation into mechanical contraction. During the plateau of the action potential, calcium ions enter the cell through calcium channels that typically activate and inactivate smoothly and more slowly than the fast sodium channels. The influx of positively charged calcium ions through the L-type calcium channel I_CaL is balanced by an efflux of positively charged potassium ions. The letter L indicates the long lasting nature of the inward calcium current. Overall, the intracellular calcium concentration evolves in response to seven currents,

$${ċ}_{\text{Ca}}={\gamma }_{\text{Ca }}[-\frac{C}{2\mathit{\text{VF}}}[I_{\text{CaL}}+I_{\text{bCa}}+I_{\text{pCa}}-2I_{\text{NaCa}}]+I_{\text{leak}}-I_{\text{up}}+I_{\text{rel}}]$$ (43)

the L-type calcium current I_CaL, the background calcium current I_bCa, the plateau calcium current I_pCa, and the sodium calcium pump current I_NaCa, weighted by the membrane capacitance per unit surface area C = 185 pF, the cytoplasmic volume V = 16404 µm³, and the Faraday constant F = 96.4867 C/mmol. In addition, the leakage current I_leak, the sarcoplastic reticulum uptake current I_up, and the sarcoplastic reticulum release current I_rel affect the intracellular calcium concentration through a calcium exchange with the sarcoplastic reticulum. We adopt the following definitions for the individual calcium related currents,

$$\begin{array}{cc}{I}_{\text{CaL}}\hfill & =C_{\text{CaL}}^{\text{max}}{g}_{\mathrm{d}}{g}_{\mathrm{f}}{g}_{\text{fCa}}[4\varphi F^2]/[\mathit{\text{RT}}][c_{\text{Ca}}{e}^{2\varphi F/[\mathit{\text{RT}}]}-0.341c_{\text{Ca}0}]{[e^{2\varphi F/[\mathit{\text{RT}}]}-1]}^{-1}\hfill \\ I_{\text{bCa}}\hfill & =C_{\text{bCa}}^{\text{max}}[\varphi -{\varphi }_{\text{Ca}}]\hfill \\ I_{\text{pCa}}\hfill & =C_{\text{pCa}}^{\text{max}}{c}_{\text{Ca}}{[c_{\text{pCa}}+c_{\text{Ca}}]}^{-1}\hfill \\ I_{\text{NaCa}}\hfill & =I_{\text{NaCa}}^{\text{max}}[e^{\gamma \varphi F/\mathit{\text{RT}}}{c}_{\text{Na}}^3{c}_{\text{Ca}0}-e^{(\gamma -1)\varphi F/\mathit{\text{RT}}}{c}_{\text{Na}0}^3{c}_{\text{Ca}}{\gamma }_{\text{NaCa}}]{[[c_{\text{NaCa}}^3+c_{\text{Na}0}^3][c_{\text{NaCa}}+c_{\text{Ca}0}][1+k_{\text{NaCa}}^{\text{sat}}{e}^{(\gamma -1)\varphi F/\mathit{\text{RT}}}]]}^{-1}\hfill \\ I_{\text{leak}}\hfill & =I_{\text{leak}}^{\text{max}}[c_{\text{Ca}}^{\text{sr}}-c_{\text{Ca}}]\hfill \\ I_{\text{up}}\hfill & =I_{\text{up}}^{\text{max}}{[1+c_{\text{up}}^2/c_{\text{Ca}}^2]}^{-1}\hfill \\ I_{\text{rel}}\hfill & =I_{\text{rel}}^{\text{max}}{g}_{\mathrm{d}}{g}_{\mathrm{g}}[1+{\gamma }_{\text{rel}}{c}_{\text{Ca}}^{\text{sr }2}{[c_{\text{rel}}^2+c_{\text{Ca}}^{\text{sr }2}]}^{-1}]\hfill \end{array}$$ (44)

where the individual scaling factors are the maximum calcium conductance $C_{\text{CaL}}^{\text{max}}=0.175{\text{mm}}^3\mu {\mathrm{F}}^{-1}{\mathrm{s}}^{-1}$, the maximum background calcium conductance $C_{\text{bCa}}^{\text{max}}=0.000592\text{ nS}/\text{pF}$, the maximum plateau calcium conductance $C_{\text{pCa}}^{\text{max}}=0.825\text{ nS}/\text{pF}$, the maximum sodium calcium pump current $I_{\text{NaCa}}^{\text{max}}=1000\text{ pA}/\text{pF}$, the maximum leakage current $I_{\text{leak}}^{\text{max}}=0.08{\mathrm{s}}^{-1}$, the maximum sarcoplastic reticulum calcium uptake current $I_{\text{up}}^{\text{max}}=0.000425\text{ mM}/\text{ms}$, and the maximum sarcoplastic reticulum calcium release current $I_{\text{rel}}^{\text{max}}=8.232\text{ mM}/\mathrm{s}$. The major calcium channel, the long-lasting L-type calcium channel I_CaL, opens and closes in response to the voltage-dependent activation gate ${ġ}_{\mathrm{d}}=[g_{\mathrm{d}}^{\mathrm{\infty }}-g_{\mathrm{d}}]/{\tau }_{\mathrm{g}}$ characterized through the following steady state value and time constant

$$\begin{array}{cc}{g}_{\mathrm{d}}^{\infty }\hfill & ={[1+e^{(-5-\varphi )/7.5}]}^{-1}\hfill \\ {\tau }_{\mathrm{d}}\hfill & =[1.4{[1+e^{(-35-\varphi )/13}]}^{-1}+0.25][1.4[1+e^{(\varphi +5)/5}]]+[1+e^{(50-\varphi )/20}],\hfill \end{array}$$ (45)

in response to the voltage-dependent inactivate gate ${ġ}_{\mathrm{f}}=[g_{\mathrm{f}}^{\mathrm{\infty }}-g_{\mathrm{f}}]/{\tau }_{\mathrm{f}}$ characterized through

$$\begin{array}{cc}{g}_{\mathrm{f}}^{\infty }\hfill & ={[1+e^{(\varphi +20)/7}]}^{-1}\hfill \\ {\tau }_{\mathrm{f}}\hfill & =1125e^{-{(\varphi +27)}^2/240}+165{[1+e^{(25-\varphi )/10}]}^{-1}+80,\hfill \end{array}$$ (46)

and in response to the intracellular calcium dependent inactivation gate ${ġ}_{\text{fCa}}=[g_{\text{fCa}}^{\mathrm{\infty }}-g_{\text{fCa}}]/{\tau }_{\text{fCa}}$ characterized through

$$\begin{array}{cc}{g}_{\text{fCa}}^{\infty }\hfill & =0.685[{[1+{(c_{\text{Ca}}/0.000325)}^8]}^{-1}+0.1{[1+e^{(c_{\text{Ca}}-0.0005)/0.0001}]}^{-1}+0.2{[1+e^{(c_{\text{Ca}}-0.00075)/0.0008)}]}^{-1}+0.23]\hfill \\ {\tau }_{\text{fca}}\hfill & =\{\begin{array}{cc}\infty \hfill & \text{if }{g}_{\text{fCa}}^{\infty }>g_{\text{fca }}\text{and }\varphi \ge -60\text{mV}\hfill \\ 2\text{ ms}\hfill & \text{otherwise}.\hfill \end{array}\hfill \end{array}$$ (47)

Accordingly, the steady state response $g_{\text{fCa}}^{\infty }$ has a switchlike shape when going from no inactivation to considerable but incomplete inactivation, depending mildly on the calcium concentration c_Ca for suprathreshold concentrations. Last, the calcium-induced calcium release current I_rel is characterized through the activation gate g_d, the same gate that is also activating the L-type calcium channel of I_CaL, and through the calcium-dependent inactivation gate ${ġ}_{\mathrm{g}}=[g_{\mathrm{g}}^{\mathrm{\infty }}-g_{\mathrm{g}}]/{\tau }_{\mathrm{g}}$ characterized through the following steady state value and time constant.

$$\begin{array}{cc}{g}_{\mathrm{g}}^{\infty }\hfill & =\{\begin{array}{cc}{[1+c_{\text{Ca}}^6/{0.00035}^6]}^{-1}\hfill & \text{if }{c}_{\text{Ca}}\le 0.00035\hfill \\ {[1+c_{\text{Ca}}^{16}/{0.00035}^{16}]}^{-1}\hfill & \text{otherwise}\hfill \end{array}\hfill \\ {\tau }_{\mathrm{g}}\hfill & =\{\begin{array}{cc}\infty \hfill & \text{if }{g}_{\mathrm{g}}^{\infty }>g_{\mathrm{g}}\text{ and }\varphi \ge -60\text{mV}\hfill \\ 2\text{ ms}\hfill & \text{otherwise}\hfill \end{array}\hfill \end{array}$$ (48)

The remaining parameters governing the response of the plateau calcium current I_pCa, the calcium uptake current I_up, and the sarcoplastic reticulum calcium release current I_rel are the half saturation constants for the plateau calcium concentration c_pCa = 0.0005 mM, for the sarcoplastic reticulum calcium uptake c_up = 0.00025 mM, and for the sarcoplastic reticulum calcium release c_rel = 0.25 mM, respectively. The parameter γ_NaCa = 2.5 enhances the outward nature of the sodium calcium pump current I_NaCa. The additional parameter γ_rel = 2 weighs the relative influence of the sarcoplastic reticulum calcium concentration on sarcoplastic reticulum calcium release I_rel. Finally, we represent the total intracellular calcium concentration $c_{\text{Ca}}^{\text{tot}}=c_{\text{Ca}}+c_{\text{Ca}}^{\text{buf}}$ in the cytoplasm as the sum of the free intracellular calcium concentration c_Ca and the buffered calcium concentration $c_{\text{Ca}}^{\text{buf}}=[c_{\text{Ca}}{c}_{\text{Cabuf}}^{\text{tot}}]{[c_{\text{Ca}}-c_{\text{Cabuf}}]}^{-1}$. Accordingly, we scale the definition of the free intracellular calcium concentration in equation (43) with the parameter γ_Ca = [1 + [c_tot c_buf][c_Ca + c_buf]⁻²]⁻¹, where c_tot = 0.15 mM and c_buf = 0.001 mM are the total and half saturation cytoplasmic calcium buffer concentrations.

8.6. Sarcoplastic reticulum calcium concentration, currents, and gating variables

The specification of the sarcoplastic reticulum calcium concentration

$${ċ}_{\text{Ca}}^{\text{sr}}={\gamma }_{\text{Ca}}^{\text{sr}}\frac{V}{V^{\text{sr}}}[-I_{\text{leak}}+I_{\text{up}}-I_{\text{rel}}]$$ (49)

is now relatively straightforward since it mimics the corresponding loss of intracellular calcium scaled by the ratio between the volume of the cytoplasm V = 16404 µm³ and the volume of the sarcoplastic reticulum V^sr = 1094 µm³. The leakage current I_leak, the sarcoplastic reticulum uptake current I_up, and the sarcoplastic reticulum release current I_rel are defined as before.

$$\begin{array}{cc}{I}_{\text{leak}}\hfill & =I_{\text{leak}}^{\text{max}}[c_{\text{Ca}}^{\text{sr}}-c_{\text{Ca}}]\hfill \\ I_{\text{up}}\hfill & =I_{\text{up}}^{\text{max}}{[1+c_{\text{up}}^2/c_{\text{Ca}}^2]}^{-1}\hfill \\ I_{\text{rel}}\hfill & =I_{\text{rel}}^{\text{max}}{g}_{\mathrm{d}}{g}_{\mathrm{g}}[1+{\gamma }_{\text{rel}}{c}_{\text{Ca}}^{\text{sr }2}{[c_{\text{rel}}^2+c_{\text{Ca}}^{\text{sr }2}]}^{-1}]\hfill \end{array}$$ (50)

We have already introduced the maximum leakage current $I_{\text{leak}}^{\text{max}}=0.08{\mathrm{s}}^{-1}$, the maximum sarcoplastic reticulum calcium uptake current $I_{\text{up}}^{\text{max}}=0.000425\text{ mM}/\text{ms}$, and the maximum sarcoplastic reticulum calcium release current $I_{\text{rel}}^{\text{max}}=8.232\text{ mM}/\mathrm{s}$, the half saturation constants for the calcium uptake c_up = 0.00025 mM, and for the calcium release c_rel = 0.25 mM, and the weighting coefficient γ_rel = 2 in the previous subsection. Finally, we introduce the total calcium concentration in the sarcoplastic reticulum $c_{\text{Ca}}^{\text{sr tot}}=c_{\text{Ca}}^{\text{sr}}+c_{\text{Ca}}^{\text{sr buf}}$ as the sum of the free sarcoplastic reticulum calcium concentration $c_{\text{Ca}}^{\text{sr}}$ and the buffered sarcoplastic reticulum calcium concentration $c_{\text{Ca}}^{\text{sr buf}}=[c_{\text{Ca}}^{\text{sr}}{c}_{\text{tot}}^{\text{sr}}]{[c_{\text{Ca}}^{\text{sr}}-c_{\text{buf}}^{\text{sr}}]}^{-1}$. Accordingly, we scale the free sarcoplastic reticulum calcium concentration in equation (49) by the parameter ${\gamma }_{\text{Ca}}^{\text{sr}}={[1+[c_{\text{tot}}^{\text{sr}}{c}_{\text{buf}}^{\text{sr}}]{[c_{\text{Ca}}^{\text{sr}}+c_{\text{buf}}^{\text{sr}}]}^{-2}]}^{-1}$, where $c_{\text{tot}}^{\text{sr}}=10\text{ mM and }{c}_{\text{buf}}^{\text{sr}}=0.3\text{ mM}$ are the total and half saturation sarcoplastic reticulum calcium buffer concentrations.