Fast range-corrected proton dose approximation method using prior dose distribution

Abstract

For robust plan optimization and evaluation purposes, one needs a computationally efficient way to calculate dose distributions and dose-volume histograms (DVHs) under various changes in the variables associated with beam delivery and images. In this study, we report an approximate method for rapid calculation of dose when setup errors and anatomical changes occur during proton therapy. This fast dose approximation method calculates new dose distributions under various circumstances based on the prior knowledge of dose distribution from a reference setting. In order to validate the method, we calculated and compared the dose distributions from our approximation method to the dose distributions calculated from a clinically commissioned treatment planning system (TPS) which was used as the ground truth. The overall accuracy of the proposed method was tested against varying degrees of setup error and anatomical deformation for selected patient cases. The setup error was simulated by rigid shifts of the patient; while the anatomical deformation was introduced using weekly acquired repeat CT data sets. We evaluated the agreement between the dose approximation method and full dose recalculation using a 3D gamma index and the root-mean-square (RMS) and maximum deviation of the cumulative dose volume histograms (cDVHs). The average passing rate of 3D gamma analysis under 3% dose and 3mm distance-to-agreement criteria were 96% and 89% for setup errors and severe anatomy changes, respectively. The average of RMS and maximum deviation of the cDVHs under the setup error was 0.5% and 1.5%, respectively for all structures considered. Similarly, the average of RMS and maximum deviations under the weekly anatomical change were 0.6% and 2.7%, respectively. Our results show that the fast dose approximation method was able to account for the density variation of the patient due to the setup and anatomical changes with acceptable accuracy while significantly improving the computation time.

1. Introduction

Understanding and inclusion of various effects of uncertainties on a planned dose distribution are vital part of the robust treatment plan optimization and evaluation process. By robust we mean the ability of the planned dose distribution to retain its target coverage and dose to limit to organs at risk. The treatment planning dose distribution is only a snapshot of the dose based on the assumed setting at the time of calculation and is therefore subject to variations under different conditions, including patient setup and anatomical changes. This is particularly true for proton therapy because proton beam ranges depend heavily on the tissue density along its path. Any changes that can influence the given water equivalent path length (WEPL) of the proton beam can potentially result indifferences between the delivered and planned dose distributions.

Uncertainties in setup and range error can cause differences between the value of WEPL from the treatment plan and actual WEPL at the time of beam delivery (Lomax, 2008b, a; Frank et al., 2010; Barker Jr et al., 2004). Also, both intra- and inter-fractional anatomical changes have been shown to cause significant changes in the planned dose distribution (Hui et al., 2008; Yoon et al., 2008; O'Daniel et al., 2007). For example, respiratory motion can cause lung and thoracic tissues and the tumor to move during treatment such that the WEPL along the beam’s path can change in any given breathing cycle (Zhang et al., 2008). In addition, trends through the weeks of treatments can further change the dose distributions compared to the original treatment plan, such as patient weight loss and tumor volume change in response to radiation (Trofimov et al., 2011a). For conventional photon therapy such as 3-dimentional conformal radiotherapy or intensity-modulated radiotherapy (IMRT), geometrically expanded volumes such as the planning target volume (PTV) or planning organ-at-risk volume (PRV) are routinely used for robust treatment planning and evaluation (ICRU Report 50, 62, 83). A photon treatment plan that is designed to deliver sufficient dose to the PTV can be thought of as a robust plan as long as clinical target volume (CTV) resides within the PTV volume. In terms of treatment evaluation, dose coverage to PTV and PRV can be thought of as the worst case scenario for the CTV and organ-at-risk (OAR) volumes, respectively. However, this is based on the assumption that the dose distribution is static and that the calculated dose distribution under the nominal (reference) setting will not change significantly with respect to the changes in patient surface contour, tissue density, and organ motion. In this situation, the photon dose distribution does not need to be re-calculated because it is independent of patient’s anatomy. This so called static dose distribution assumption holds true for conventional photon therapy to a certain extend (Cho et al., 2002). However, numerous authors have discussed the fallacy of using the static dose distribution assumption in proton therapy primarily due to the fact that proton ranges are sensitive to the change in tissue density or WEPL (Engelsman and Kooy, 2005; Moyers et al., 2001).

Ideally, in order to gauge the robustness of a given proton treatment plan under various situations, multiple dose calculations are required in order to simulate different possible changes. Recently, researchers have developed methods which incorporate multiple dose distributions under different setup and range errors to derive dose volume histograms (DVHs) or its derivatives in order to evaluate treatment robustness (Albertini et al., 2011; Lomax et al., 2004; Trofimov et al., 2011b). Similarly, researchers have shown that multiple dose distributions can be incorporated into treatment planning for robust plan optimization (Inaniwa et al., 2011; Unkelbach et al., 2009; Pflugfelder et al., 2008; Unkelbach et al., 2007). However, due to the computational cost of calculating proton dose distributions under various circumstances, the clinical feasibility of robust evaluation and optimization are difficult to implement. For example, if we wish to simulate setup errors of up to 8mm at 2mm intervals isocentrically, this would require a total of 729 dose calculations. At our institution, for a typical lung plan, this would require well over 15 hours of computation time. One approach to minimizing the number of these calculations is to only calculate a subset of these variations or the dose at the extreme boundaries of the setup or range errors in a worst-case scenario dose distribution (Lomax et al., 2004). However, this method of analysis does not give a physically realizable dose distribution and may overestimate the impact of these uncertainties on the proton plan. Therefore, robust optimization and verification can potentially benefit from a fast dose calculation method in order to include more information.

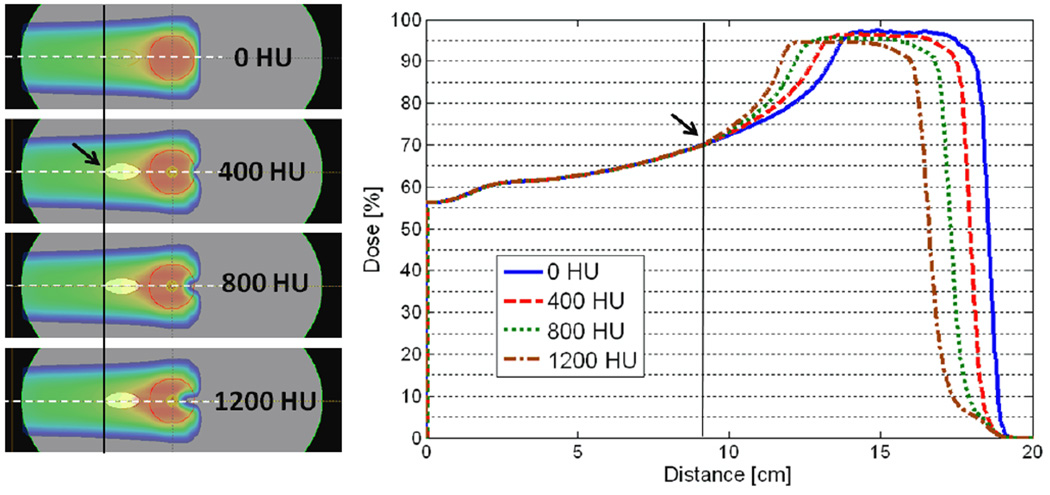
In this study, we describe a fast range-corrected dose approximation method based on a composite version of the methods described by Unkelbach et al. (2009). The major difference in method compared to theirs is that we use the dose distribution from the nominal setting to ‘predict’ the new dose under a small perturbation in WEPL without requiring the detailed knowledge of the individual dose contributions from pre-calculated virtual pencil beams. This is motivated by the heuristic observation that perturbation of the WEPL along the beam path pulls the dose profile proximally or distally from the nominal setting without significantly changing its overall shape. The new dose distribution can be created by simply shifting the dose profile based on an “iso-WEPL” along the beam direction. Figure 1 illustrates an example of dose profile variation after a single insertion of a high-density object in the beam path. This equivalent-WEPL based dose correction strategy reduces both computational time and computer memory requirements and extends its applicability to include anatomical deformations. We will benchmark the fast range-corrected dose approximation method against the full dose calculation using a commercial treatment planning system that is based on the 3D pencil beam convolution method (Schaffner et al., 1999; Hong et al., 1996). Furthermore, we will assess the ability of the dose approximation method to estimate DVH curves.

Figure 1.

An oval shaped heterogeneity was inserted in the beam path to simulate anatomical changes. The density of the object varied from 0 HU to 1200 HU in increments of 400 HU. The line dose profiles beyond the start location of heterogeneity (indicated by the arrow) are pulled proximally towards the source as the density of the hetergeneity increases according to the effective change in the WEPL while the rest of the profile proximal to the heterogeneity remains approximately the same.

2. Methods and Materials

In principle, the dose to a point can be calculated by summing up all contributions of doses from individual beamlets. In this study, we will not pursue the dose calculation of each individual beamlet; rather, we make the assumption that the scattered dose from small changes in the patient’s anatomy will remain constant and the dose effect is only caused by the change in the cumulative WEPL at each voxel along the beam path. Taking advantage of the full dose calculation at the nominal position, we can derive the new dose distribution by shifting dose along the beam path based on the equivalent WEPL from the original plan. One can think of this as a mapping process where a previously known dose distribution is re-organized to give a new dose distribution. This requires that a single full dose calculation is performed using the planning CT images under the nominal setting.

In this study, we used the clinically commissioned proton treatment planning system (Eclipse™, Varian Medical Systems, Inc., Palo Alto, CA, USA). This dose distribution is referred as the nominal dose distribution (D) while the dose under the testing situation is referred as realized dose distribution (d). D will be used as a template when we approximate d under the influence of both setup error and anatomical change. For convenience, we used a beam’s eye view (BEV) coordinate and the z-axis as the depth along the beam’s axis. A point dose at an arbitrary coordinate of (x, y, z), with (0,0,0) being defined at the isocenter, under nominal setting can be written as D_x,y,z. The realized dose to that point can be written as a function of the patient shift error (Δx, Δy, Δz) and change in physical depth (z′), giving d_x,y,z(Δx, Δy, Δz, z′). It should be noted that that z′ is a fundamentally different quantity than Δz: Δz is the magnitude of patient setup error in physical space whereas z′ is the location in depth under nominal setting which corresponds to the same WEPL for the depth at z under the realized or testing setting.

For the case of the static dose distribution (i.e. for photon beam), we can immediately approximate the realized dose to a point as follows:

$$d_{x,y,z}(\mathrm{\Delta }x,\mathrm{\Delta }y,\mathrm{\Delta }z)=D_{x+\mathrm{\Delta }x,y+\mathrm{\Delta }y,z+\mathrm{\Delta }z}$$ (1)

In this formulation, one can see that for static dose distribution, the realized dose can be approximated by simply moving the entire dose cloud to align with the patient anatomy in its new position. To account for the variant dose distribution, we assume that the perturbation in WEPL moves point doses in physical space according to their WEPL values in the original plan.

2.1 Approximation under setup error

If setup error occurs, there will be a change in WEPL due to the misaligned tissue density along the plane that is perpendicular to the beam’s axis. This will lead to a difference in WEPL between the line segments tracing different locations in space. Therefore, in order to approximate the realized dose at a point, we need to account for the difference in WEPL between the line segments tracing different locations in space by

$$d_{x,y,z}(\mathrm{\Delta }x,\mathrm{\Delta }y,z\prime )=D_{x+\mathrm{\Delta }x,y+\mathrm{\Delta }y,z\prime }\times INV(z,z\prime ),$$ (2)

where z′ is given by the following line integral relation

$${\displaystyle {\int }_s^{z}rsp(x,y,z)dz={\displaystyle {\int }_s^{z\prime }rsp(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y,z)dz.}}$$ (3)

The function rsp(x, y, z) is the relative stopping power ratio from the given CT data and s is the effective source position. Simply put, equation (2) approximates the realized point dose by shifting the ray line geometrically (in the BEV coordinate) while adjusting the longitudinal dose profile given by that shifted ray line according to the effective change WEPL from equation (3). In equation (2), $INV(z,z\prime )={\left(\frac{z\prime +VSAD}{z+VSAD}\right)}^2$ is the inverse square factor to compensate for the loss in protons in a divergent beam with the effective source-to-axis distance (VSAD). Here, the effect of a patient shift along the direction of the beam axis (Δz) is ignored (except for the inverse square factor) because it is equivalent to adding an air gap between the source to the patient body surface which adds a negligible change in WEPL.

In general, z′ can only be determined by solving (3) iteratively, making it the most time consuming step for this method. The computational time can be decreased by saving the line integral values at different depth with the corresponding D values in computer memory and referencing them as a look up table for later uses.

2.2 Approximation under anatomical change

For anatomical deformation without considering the setup error (assuming the images have been registered together), we can approximate the realized dose as

$$d_{x,y,z}(z\prime )=D_{x,y,z\prime }\times INV(z,z\prime ),$$ (4)

where z′ is given by the limit of the following integrals

$${\displaystyle {\int }_s^{z}rsp(x,y,z)dz={\displaystyle {\int }_s^{z\prime }rs{p}^{New}(x,y,z)dz.}}$$ (5)

In this case, the realized dose will be a function of the effective change in WEPL caused by the anatomical deformation which can be tracked using the new images (i.e. daily or weekly CT images), which gives the function rsp^New. For the above formula, the location of the line being integrated is identical since no setup error is assumed but rsp^New (x,y,z) is used on the right side of the equation (4) to account for the anatomical deformation given by the new images. Finally, the approximation method under setup error and anatomical deformation can be combined to give a general formulation

$$d_{x,y,z}(\mathrm{\Delta }x,\mathrm{\Delta }y,z\prime )=D_{x+\mathrm{\Delta }x,y+\mathrm{\Delta }y,z\prime }\times INV(z,z\prime ),$$ (6)

where again, z′ is given by the limit of the following integrals

$${\displaystyle {\int }_s^{z}rsp(x,y,z)dz={\displaystyle {\int }_s^{z\prime }rs{p}^{New}(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y,z)dz.}}$$ (5)

This range corrected dose approximation method can be summarized as a simple dose mapping algorithm which maps previously calculated dose distributions onto a new one based on the following steps:

• Step 1.Calculate the WEPL to a point along the beam path under the nominal setting.

• Step 2.Translate beam’s isocenter according to the setup error or introduce new CT images.

• Step 3.Calculate WEPL along the corresponding line segment and locate the physical point along the depth which has the same WEPL as calculated in Step 1.

• Step 4.Correct for inverse square factor based on the original physical location found in Step 3.

• Step 5.Repeat steps 1–4 for all points in the image.

2.3 Validation for patient cases

In order to validate our dose approximation method, we compared the dose distributions calculated using a static dose approximation, our proposed range-corrected dose approximation, and a full 3D pencil beam convolution method from our clinical treatment planning system (TPS). All dose calculations were performed using a dose grid resolution of 2 × 2 × 2.5 mm³. First, a lung cancer patient was selected. The patient received 4-dimensional computed tomography (4DCT) scans for treatment planning and weekly over the course of treatment with a 1mm pixel size and 2.5mm slice thickness over the first 6 weeks (denoted week0 to week6) of treatments. To simplify intra-fractional dose calculation, we used the average image from the 4DCT data sets for each week. Treatment plan under nominal setting and all consequent dose calculations were done on these averaged CT data sets following the clinical protocol used at our institution (Kang et al., 2007). The PTV was generated by a uniform expansion of the CTV with 5mm margins. This margin size was deliberately chosen to push the limit of the plan’s robustness to CTV coverage when we simulate setup errors up to 8mm. All the volumes of interest were contoured by a physician on the planning CT and were deformed to weekly CT data sets using an in-house developed deformable image registration software (Wang et al., 2005b; Wang et al., 2005a). The nominal dose was calculated using the planning CT data set with no assumed setup error via the spot scanning beam delivery method with single-field optimization (Smith et al., 2009). The setup error was simulated by shifting the planning CT images along the Anterior-Posterior direction ±8mm in 2mm intervals. At each interval, doses were calculated using all three different methods: static dose approximation, our proposed range-corrected dose approximation, and a full recalculation with the TPS. For the weekly CT data sets, doses were calculated using all three different methods after manual alignment of beam’s isocenter based on the bony anatomy to separate the effect of setup error.

Similarly, we validated the proposed method on a prostate and a head & neck (HN) patient case with inter-fractional anatomic changes to show the applicability of the proposed method to these sites as well. The prostate case was chosen due to a change in the femur position on the day of treatment. The HN case was chosen because of a substantial change in the nasal air cavity in the beam path on week 6 of treatment, which was partially due to a head rotation and tissue/fluid variation in the nasal cavity. We used a 270° beam angle for the prostate case, and a 0° beam angle for the HN case.

The overall accuracy of both approximation methods were quantified through the use of a 3D gamma analysis tool developed in-house (Wendling et al., 2007). Our gamma analysis was performed using a common 3% dose-difference and 3mm distance-to-distance agreement criteria. In order to quantify the accuracy of the cDVHs derived using the range-corrected method, cDVHs were subtracted from the corresponding cDVHs derived using full dose calculation (The difference is denoted as ΔcDVH).

3. Results

3.1 Dose distribution comparison and 3D gamma analysis

For all cases, the amount of dose variations gradually increased as setup error increased from 0mm to 8mm in both directions (perpendicular to the beam line). For the lung case, the amount of dose variation was gradually increased from week0 to week6 while both prostate and HN cases showed no obvious increment in dose variation over the weeks. Table 1 shows % volume change of the tumor in the entire breathing cycle (i.e. integrated gross tumor volume and clinical target volume (IGTV and ICTV), and GTV-50 and CTV-50, the volumes for the exhale phase of the breathing cycle) for the lung patient over the course of treatment. The largest variation of the planned dose distribution amongst all of the simulations was observed when we recalculated dose using the 6^th treatment week’s CT images for both lung and HN cases and the 1^st week CT images for the prostate case.

Table 1.

The measured volume change of the target volumes of interest observed in the weekly CT images for the lung case. The structures were contoured on the planning CT and deformed to the weekly CT images using in-house deformable image registration software. For the selected patient case, a reduction of 41% of the gross tumor volume (GTV-T50 and IGTV) and 21% of the clinical target volume (CTV-T50 and ICTV) was observed.

	Volume [cc] (% Volume Change)
Site (Week)	GTV-T50	CTV-T50	IGTV	ICTV
Lung (week0)	128 (0%)	323 (0%)	148 (0%)	331 (0%)
Lung (week1)	110 (−14%)	300 (−7%)	126 (−15%)	307 (−7%)
Lung (week2)	96 (−25%)	277 (−14%)	110 (−25%)	286 (−14%)
Lung (week3)	90 (−30%)	275 (−15%)	104 (−29%)	282 (−15%)
Lung (week4)	82 (−36%)	264 (−18%)	96 (−35%)	272 (−18%)
Lung (week5)	77 (−40%)	257 (−20%)	90 (−39%)	264 (−20%)
Lung (week6)	76 (−41%)	254 (−21%)	88 (−40%)	262 (−21%)

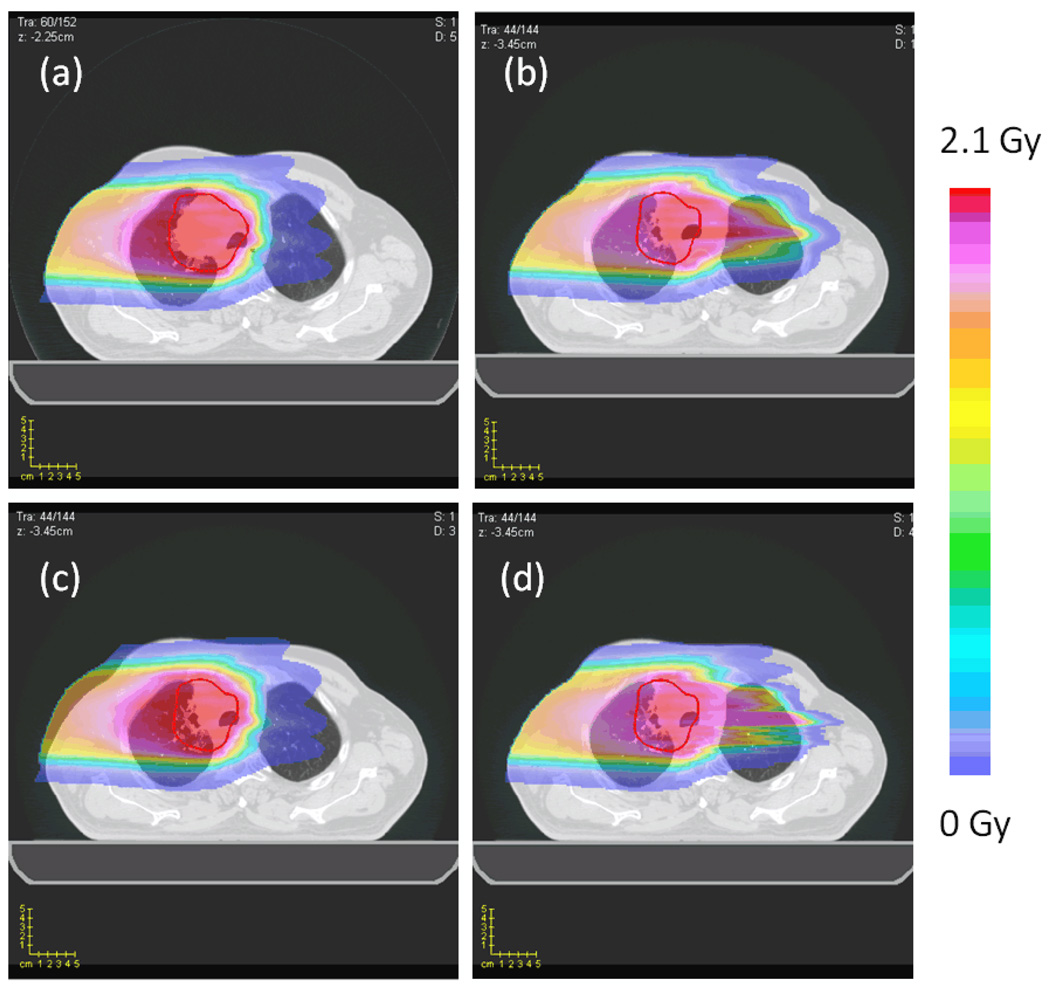
Visually noticeable change in dose distribution was observed when setup errors and anatomical deformations were introduced. Figure 2 (a) and (b) compares planned dose distribution and the realized dose distribution using full dose calculation. It shows, as a result of weight loss and tumor shrinkage, the proton beam penetrating deeper in to the patient, delivering a significant dose to the contralateral lung. The original spatial dose distribution given by the static approximation (Figure 2 (c)) fails to adjust for such a change and thereby significantly underestimates the dose to contralateral lung. However, the realized dose distribution computed using the range-corrected method (Figure 2 (d)) is able to estimate the change in depth penetration of the proton beam with a reasonable accuracy.

Figure 2.

The dose distributions for the lung case. (a) The full dose (TPS) calculation on the lung planning CT (planned dose distribution). (b) The full dose (TPS) calculation on the lung week6 CT (realized dose distribution). (c) The static dose approximation on the lung week6 CT. (d) The range corrected dose approximation on the lung week6 CT.

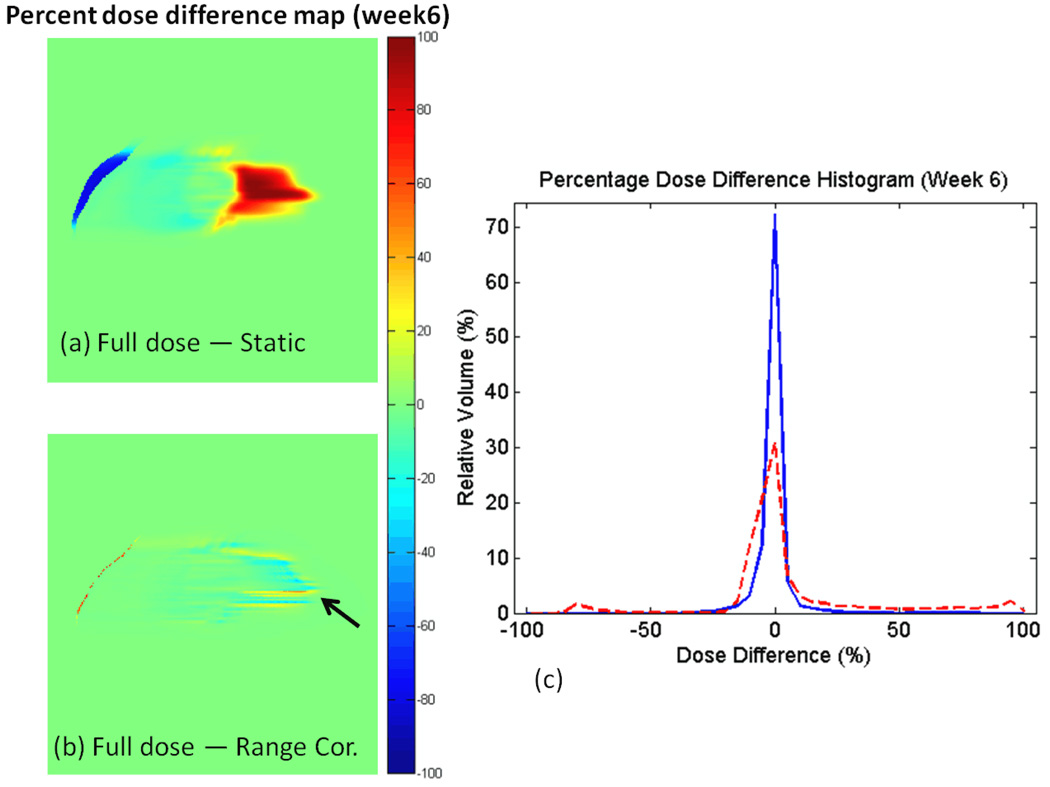
Figure 3 shows percentage dose difference maps of the dose distributions between the full dose recalculation and the static dose approximation, and the full dose and the range corrected dose approximation. Note that an over estimation near the patient skin surface and an under estimation in the contralateral lung region was apparent from the static dose approximation method while a significant improvement was observed when using the range-corrected approximation method.

Figure 3.

The percent dose difference map on the lung week6 CT between dose distribution using full calculation and dose distribution using (a) static dose approximation, (b) range corrected approximation, and (c) the percentage dose difference histograms for the two difference maps. Red dashed line in the histogram is derived from (a) while blue solid line is derived from (b).

The result of the gamma analysis is presented in Table 2. The lowest passing rate was observed at the limit of our simulation ranges (8mm setup errors and lung 6th week). Under the chosen criteria (3% dose and 3mm distance), the range-corrected method achieved a 93% passing rate for an 8mm setup error while the static dose approximation method achieved only an 81% passing rate. For the weekly CT simulation, the range-corrected method achieved an 86% passing rate for the 6^th week CT while the static dose approximation method achieved only 36% passing rate.

Table 2.

The result of the 3D gamma analysis on both the ranged-corrected approximation and static dose approximation with respect to the full dose (TPS) calculation under setup error and weekly CT simulations. A passing criterion of 3% dose difference and 3mm distance-to-distance agreement was used. For the sake of simplicity, for both prostate and HN cases, only the worst passing rate observed during weekly simulation is shown (week1 for prostate and week6 for HN).

	3D Gamma (% Passing)			3D Gamma (% Passing)
Lung AP Setup error (mm)	(3%, 3mm) Range Corrected	(3%, 3mm) Static	Site (Week)	(3%, 3mm) Range Corrected	(3%, 3mm) Static
−8	94%	81%	Lung (0)	100%	100%
−6	95%	87%	Lung (1)	89%	75%
−4	97%	93%	Lung (2)	89%	74%
−2	98%	98%	Lung (3)	91%	66%
0	100%	100%	Lung (4)	89%	54%
2	98%	998%	Lung (5)	86%	43%
4	96%	93%	Lung (6)	86%	36%
6	95%	88%	Prostate (1)	89%	83%
8	93%	83%	HN (6)	84%	70%

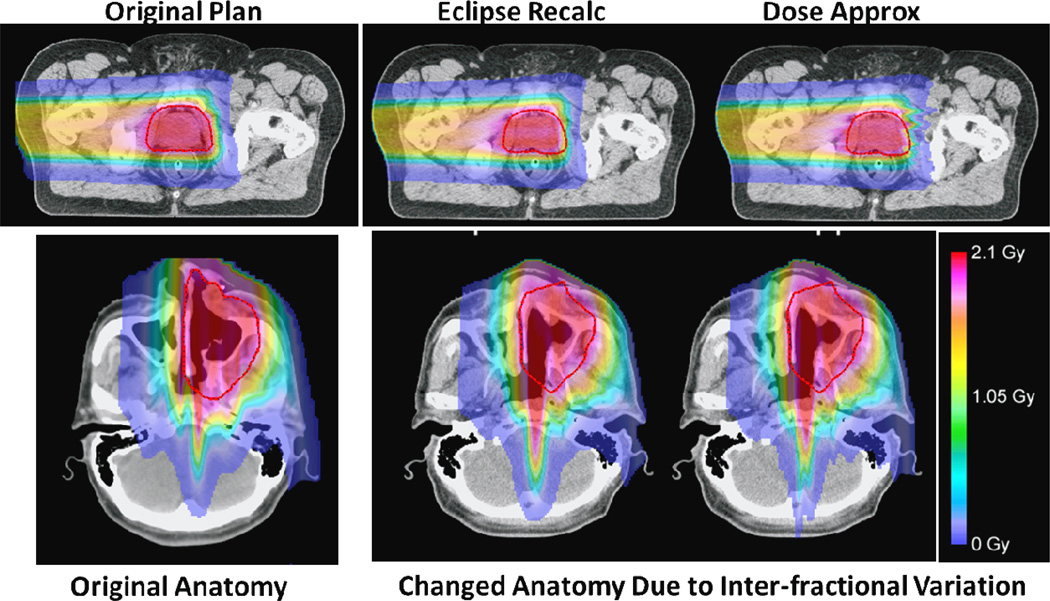
The worst passing rate found for the 3D gamma analysis of the prostate case was 89% and 83% for the range corrected and the static approximation methods, respectively. Similarly, the worst passing rate found for the HN case showed 84% and 70% passing rates for range corrected approximation and static approximation methods, respectively. Figure 4 shows the comparison graphically. The original plan calculated for the anatomy in the treatment planning CT image is shown in the left panel for each case; the dose distributions in the changed anatomy (due to inter-fractional variations) are calculated by the commercial TPS (Eclipse; middle column) and the dose approximation method (right panel), respectively. It can be seen that the range-corrected dose approximation method did a reasonable job overall. Most differences are seen in regions with sharp change in WEPL. In these regions, more accurate modeling of lateral scatter appears to be important.

Figure 4.

A comparison of the dose calculation results in the presence of inter-fraction anatomical changes. The original plan and original anatomy for a prostate case (top row) and a HN case (bottom row) are shown to the left column. The dose distributions for the changed anatomy calculated by the commercial treatment planning system (Eclipse, Varian Medical Systems) are shown in the middle column, and the dose distributions calculated by the range-corrected dose approximate method are shown to the right, respectively.

3.2 DVHs comparisons

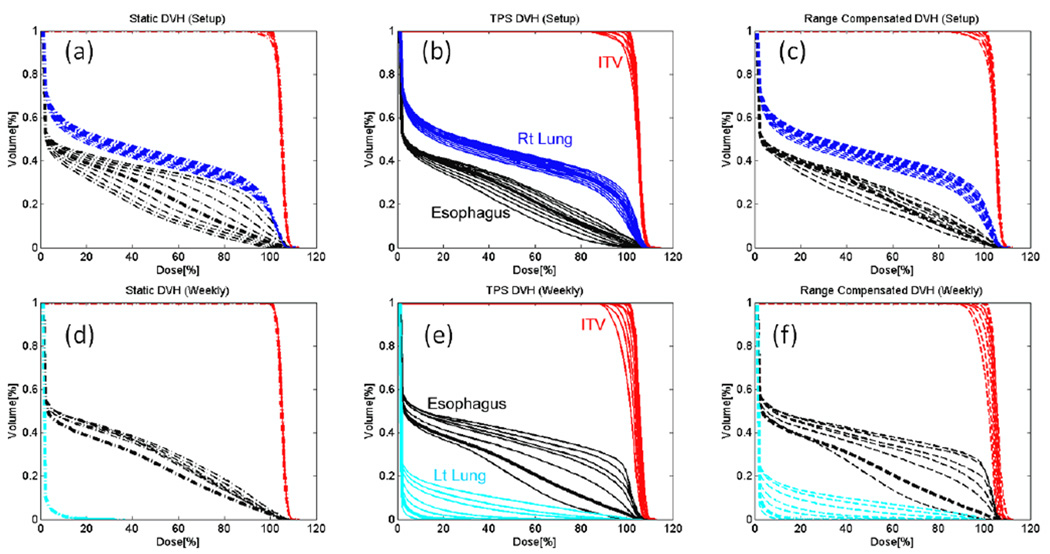
The change in the planned dose distribution due to both setup and anatomical deformation resulted in variation of cDVHs derived from realized dose distributions. Figure 5 compares the DVH-bands (the area enclosed by the envelope of the cDVHs) of various structures using full dose calculation and different dose approximation methods. The overall shape of the DVH-bands derived using range-corrected method closely resembled the DVH-bands derived using the full dose calculation while the DVH-bands derived using static method mostly under estimated the thickness of the bands for the CTV and other structures (except for the esophagus under setup error simulation). In the case of weekly simulation, the static dose approximation completely failed to account for the decrease in dose to the target volume and increase in dose to the left lung and esophagus. Table 3 lists the RMS and the maximum difference from the ΔcDVH. Overall, the RMS deviation and maximum difference were larger for the CTV and esophagus than for other structures due to their small volume size and their position near the high dose gradient. For the lung case, the largest of the RMS deviation found were within 2% for both the setup and weekly simulation. The largest of the maximum differences were found to be within 4% and 8% for setup and weekly simulation, respectively. The average of the maximum differences over all simulations was found to be 1.5% and 2.6% for setup and weekly simulation, respectively for the lung case.

Figure 5.

The cDVHs of the CTV (red), involved lung (dark blue), contralateral lung (light blue), and esophagus (black) derived from realized dose distributions under various setup error (top row) and weekly imaging (bottom row) using static approximation (a, d), full dose calculation (b, e), and range-corrected approximation methods (c, f). The thicker lines indicate original DVHs derived from the planned dose distribution.

Table 3.

The root mean square (RMS) deviations between the cumulative DVHs derived using a full dose (TPS) calculation and range-corrected dose approximation method under various simulations. The first two tables are from setup error (in the anterior-posterior direction) and weekly simulations of lung patient. For the sake of simplicity, for both prostate and HN cases, only the worst passing rate observed during weekly simulation is shown (week1 for prostate and week6 for HN)

	CTV		Lung_R		Esophagus		Lung_L		Cord
Lung Setup error (mm)	Δ cDVH (%vol)		Δ cDVH (%vol)		Δ cDVH (%vol)		Δ cDVH (%vol)		Δ cDVH (%vol)
	RMS (%)	Max (%)	RMS (%)	Max (%)	RMS (%)	Max (%)	RMS (%)	Max (%)	RMS (%)	Max (%)
−8	0.4	1.9	0.3	0.6	1.9	3.4	0.4	1.4	1.1	2.5
−6	0.3	1.5	0.3	0.6	1.5	2.3	0.5	1.2	0.9	2.2
−4	0.4	2.2	0.3	0.6	1.1	2.0	0.4	0.9	0.8	1.8
−2	0.4	2.1	0.2	0.7	0.9	1.6	0.3	0.6	0.5	1.3
0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
2	0.6	3.3	0.2	1.0	0.4	0.8	0.3	0.6	0.2	0.5
4	0.7	3.5	0.3	1.4	1.4	2.5	0.4	1.0	0.3	0.4
6	0.6	3.7	0.3	1.6	2.0	3.3	0.5	1.2	0.3	0.6
8	0.7	4.0	0.4	1.6	1.8	3.1	0.6	1.5	0.3	0.7
	CTV		Lung_R		Esophagus		Lung_L		Cord
Site (Week)	Δ cDVH (%vol)		Δ cDVH (%vol)		Δ cDVH (%vol)		Δ cDVH (%vol)		Δ cDVH (%vol)
	RMS (%)	Max (%)	RMS (%)	Max (%)	RMS (%)	Max (%)	RMS (%)	Max (%)	RMS (%)	Max (%)
Lung (0)	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0	0.0
Lung (1)	0.5	2.8	0.2	1.2	1.0	2.3	0.4	1.0	1.0	1.6
Lung (2)	1.0	6.1	0.4	1.3	1.6	3.3	0.5	0.7	0.2	0.5
Lung (3)	1.0	6.8	0.6	0.9	0.8	3.0	0.4	0.6	0.3	0.7
Lung (4)	1.0	6.0	0.4	0.6	1.4	5.7	0.4	0.8	0.1	0.3
Lung (5)	1.0	6.6	0.6	1.2	1.9	7.6	0.9	1.4	0.3	0.7
Lung (6)	1.4	5.0	0.6	1.0	1.2	5.9	0.8	1.4	0.4	0.8
	STV		Bladder		Rectum		Ant Rectal Wall		Femoral Heads
Prostate (1)	1.1	7.2	1.0	1.7	0.6	0.9	0.7	1.8	0.2	0.5
	CTV1		Brain stem		L Optic Nerve		R Optic Nerve		L Parotid
HN (6)	0.8	4.8	1.6	6.4	1.6	4.2	2.9	6.2	3.8	7.9

The range-corrected dose approximation method was implemented using MATLAB (MathWorks Inc., Natick, MA) on a computer with an Intel(R) Core™2 Duo CPU of 3.00 GHz clock speed and 3GB of RAM. The typical calculation is less than one second for each beam, which is approximately 50 times faster than the full dose calculation method using the commercial TPS.

4. Discussion

The main purpose of the range-corrected dose approximation method is to compute proton dose under various circumstances for evaluating a given treatment plan’s robustness, and for potential incorporation into robust optimization techniques. Because such tasks may require hundreds of dose calculations, accuracy of the computed dose may be sacrificed over the computational efficiency. It can be understood that the approximated dose may not reflect the accuracy requirement for the final dose calculation in a clinical plan. Nevertheless, the approximated dose can be used for gauging a plan’s sensitivity to setup and range error, for intermediate dose calculations during plan optimization, or for on-line assessment of major dosimetric impacts. For this reason, it may be sufficient for such important applications.

Our choice to use the 3D gamma analysis was to demonstrate that the approximated dose distribution is spatially comparable to the full dose calculation. The overall accuracy in terms of percentage passing rate presented in Table 2 depends heavily on the choice of passing criteria. In this work, we selected a 3% dose difference and 3mm distance-to-agreement criteria and found that the average passing rate was 93% and 89% for setup errors and anatomical changes, respectively. The question of what criteria to be used and what the minimum passing rate should be considered acceptable would depend on the nature of applications. In this study, we used CT slice spacing of 2.5mm. When performing ray-tracing in co-planar beam directions, the aliasing effect could affect the accuracy of dose mapping using our method. This is especially true when using a 3-mm distance-to-agreement criterion which is very close to the CT resolution (2.5 mm) in the slice thickness direction. In the future, we could resample between adjacent CT slices to minimize the aliasing effect.

Aside from the actual dose distribution itself, we also measured the accuracy of cDVHs derived using the approximated dose. This is highly relevant to the application of the proposed method since when evaluating the robustness of a plan or the dose on the day of treatment, it is necessary to summarize the multiple 3D dose distributions into statistical information such as DVH-bands. Previously, Cho et al. (2004) discussed the clinical recommendations on accuracy of DVH curves. Based on the assumption that the point dose accuracy of 2–4% is clinically tolerable, the RMS of the difference in relative dose between two cDVH should be less than 1–2%. This RMS criterion measures overall accuracy of the cDVH curve and permits certain dose bins to deviate more than the 2%, while still being clinically acceptable. From our experience, this can happen if the OAR is small or is situated near the beam penumbra and high dose gradient. For the proposed method, Table 3 shows that RMS deviation is well within 2% for all simulations except for the right-optic nerve and left parotid from H&N case.

It should be noted that the lung case chosen in this study was a challenging case for dose calculation. The lateral beam arrangement also maximized the dosimetric effect of anatomical changes. We selected this case to test if our dose approximation method can do well in the presence of significant anatomical changes. We also challenged the proposed method using a prostate and a HN case. Both cases had a relatively large change in patient’s anatomy that would affect the proton beam delivery for these sites. The results were similar to the ones found for the lung case (See Table 2 and Table 3).

In our current implementation, we only used a single CPU for dose calculation, which already can achieve the calculation speed of around one second. Further reduction of computation time can be realized because the proposed method allows for parallel calculation of using independent beamlets or ray-tracing lines. It can be expected that the speed of computation can benefit from the implementation of multi-processor and multi-core CPU methods or even GPU based computation method because our proposed method uses a look-up table approach. Sometimes, additional speed increase is possible if we are only interested in a sub-volume of anatomy. We can selectively choose the dose calculation region of a specific organ to further speed up the DVH calculation if necessary.

One of the limitations of the proposed method is that it does not consider change in scattered dose separately from the primary dose when mapping the pre-calculated nominal dose. The errors resulting from this simplification will be more pronounced for greater displacement of setup error and near regions with a sharp gradient of tissue density change lateral to the beam direction. The pencil-beam based dose calculation algorithm used in Eclipse treatment planning system is also not ideal in modeling the lateral scatter under complex geometries or heterogeneities. A Monte Carlo based dose calculation method would produce more accurate assessment of the proposed method.

5. Conclusion

In order to expedite robust plan evaluation or optimization process, a simple and fast proton dose approximation method was introduced. The proposed method takes advantage of the pre-calculated planned dose distribution when approximating a new dose distribution by correcting the difference in proton range under setup error or anatomical deformation given by the new set of CT images. The accuracy of the range-corrected method was shown to be superior to the static dose approximation method. The main dosimetric differences between the range-corrected method and the clinically used full dose calculation method are in small regions where a shape change in the water-equivalent path length (WEPL) exists. These regions are typically narrow and near the edge of a major WEPL change for which the lateral scatter modeling becomes important. In this study the differences between these dose distributions were quantified for selected patient cases using both a 3D gamma analysis and cDVH comparison. Our results show that the static dose approximation is inadequate to approximate dose for proton beam plans while the proposed range-corrected dose approximation method can be used effectively to approximate dose under various setup errors and anatomical deformations. The proposed method could be used for robust evaluation, robust optimization, and on-line treatment assessment.