Nanoindentation by magnetic microspheres imaged by optical interferometry permits determination of the viscoelastic properties of fine local regions of each layer of the cornea. This approach provides robust biomechanical data on corneal creep behavior that scales reliably with the magnitude of applied force throughout the tissue.
Abstract
Purpose.
A novel nanoindentation technique was used to biomechanically characterize each of three main layers of the cornea by using Hertzian viscoelastic formulation of creep, the deformation resulting from sustained-force application.
Methods.
The nanoindentation method known as mechanical interferometry imaging (MII) with <1-nm displacement precision was used to observe indentation of bovine corneal epithelium, endothelium, and stroma by a spherical ferrous probe in a calibrated magnetic field. For each specimen, creep testing was performed using two different forces for 200 seconds. Measurements for single force were used to build a quantitative Hertzian model that was then used to predict creep behavior for another imposed force.
Results.
For all three layers, displacement measurements were highly repeatable and were well predicted by Hertzian models. Although short- and long-term stiffnesses of the endothelium were highest of the three layers at 339.2 and 20.2 kPa, respectively, both stromal stiffnesses were lowest at 100.4 and 3.6 kPa, respectively. Stiffnesses for the epithelium were intermediate at 264.6 and 12.2 kPa, respectively.
Conclusions.
Precise, repeatable measurements of corneal creep behavior can be conveniently obtained using MII at mechanical scale as small as one cell thickness. When interpreted in analytical context of Hertzian viscoelasticity, MII technique proved to be a powerful tool for biomechanical characterization of time-dependent biomechanics of corneal regions.
Intraocular pressure measurement assumes typical biomechanical and geometrical properties of the cornea. The biomechanical properties of the cornea are major determinants of the effects of refractive surgeries such as photorefractive keratectomy, laser in situ keratomileusis, and conductive keratoplasty. Biomechanical properties are also determinants of potential serious complications of laser ablative surgery such as ectasia. While the importance of corneal biomechanics is widely recognized, methods of biomechanical characterization remain underdeveloped. Air-puff indentation 1 –4 has been recently popularized as a noninvasive, in vivo method, but decoupling of intraocular pressure from mechanical properties of the cornea remains a quandary. Laboratory methods include uniaxial tensile testing, 5 ultrasound propagation, 6,7 atomic force microscopy, 8 and whole-globe pressurization 9 –14 for determination of corneal elasticity 7,15 –17 and hysteresis, 1,4,18 both in vivo 19,20 and in vitro. 5,16 Some of these methods, however, produce data that are only relative or in an idiosyncratic framework difficult to integrate into modern mechanical engineering analyses. Attempts to interpret, in inappropriate context, data obtained by idiosyncratic methods can lead to severely flawed conclusions. 21
Appropriate biomechanical testing techniques depend critically on tissue composition and geometry. For instance, conventional mechanical experimental techniques such as uniaxial-tensile testing divide relatively large specimens into relatively long strips that are clamped at each end and pulled until rupture. While appropriate for tendon or extraocular muscle, uniaxial-tensile testing seems inappropriate for small, radially symmetric tissues such as cornea. Indentation techniques now permit precise measurements of indentation of flat tissue specimens by rigid probes. Specimens of arbitrary shape appear locally flat if tested by indenters that are very small relative to specimen size and if displacements are small relative to specimen thickness. Modern biomechanical methods now employ micro (submillimeter)- and nano (submicrometer)-sized test indenters having displacement and force precision in the range of nanometers (nm) and pico-Newtons (pN), respectively. 22 –25 On any scale, indentation data can be interpreted in the Hertzian viscoelastic framework suitable for general mathematical characterization appropriate to approaches such as finite element analysis (FEA).
The current investigation employed nanoscale indentation with mechanical interferometry imaging (MII) to develop quantitative models of all three layers of the bovine cornea, the epithelium, endothelium, and stroma, within the framework of Hertzian contact mechanics and the viscoelastic formulation of Oyen. 26 These models, which have general validity in the mechanics of materials irrespective of microscopic and molecular composition, accurately captured the viscoelastic behavior exhibited by each corneal layer.
Methods
Interferometer
Spherical indenter probe displacement was measured using an interference microscope (NT 1100; Veeco, Plainview, NY) with green light-emitting diode illumination and a 20× objective with a 0.28 Michelson numerical aperture through transmissive media. 27 The interferometer consists of an optical microscope with a Michelson interference objective that allows for the observation of not only lateral (x and y) specimen features with typical optical resolution (1.16 μm) but also height (z) at resolution below 1 nm through tracking of optical interference fringes. 28 The Michelson interferometer consists of a beam splitter and reference mirror. Specimens were placed in air at 100% relative humidity, in a chamber covered by a rubber membrane. The interferometer imager includes a 640 × 480-pixel charge coupled device detector array that when combined with a 20× objective produces a 315 × 240-μm field of view and 500-nm spatial sampling. Positions of reflective spherical indenters were measured with respect to the sample chamber bottom and were corrected for the effect of dispersion in liquid using a group velocity at 535-nm wavelength and Ng = 1.33 band pass at 30 nm. 29
Magnetic Force Control
A cylindrical rare earth magnet 21 mm long and 7 mm in diameter was oriented vertically below the test chamber to apply magnetic force to spherical, reflective microindenters made of grade 100, type 316 stainless steel (Salem Specialty Ball, Canton, CT). To ensure uniform magnet flux across the viewing area of 300 × 300 micrometers, the magnet was positioned coaxially with the optical path. Magnet position was controlled by stepper motor with <10-μm displacement precision. Magnetic flux as a function of axial distance was measured with a miniature Hall probe. Negligible magnetic flux was recorded when the magnet was lowered to ≥4 cm below the sample. Force exerted on the spherical indenters was calibrated as a function of magnet position by interferometric measurement of indentation of the spheres into a silicone elastomer of known elastic modulus (∼10 kPa). The total force imparted at each magnet position was then calculated using the Hertz model for each spherical indenter. Indenter probes with diameter of 700, 250, and 20 to 24 micrometers were placed on the stroma, epithelial, and endothelial specimen surfaces, respectively, and displaced by desired amounts using the magnetic force established by linearly shifting the magnet. Indenter diameters were verified by interferometry to be within <1% of nominal diameter for the two larger indenter sizes. Since relative manufacturing precision for diameter was more variable for the smallest indenters, exact indenter diameter was verified by interferometry in each trial in which the smallest nominal indenter size was employed.
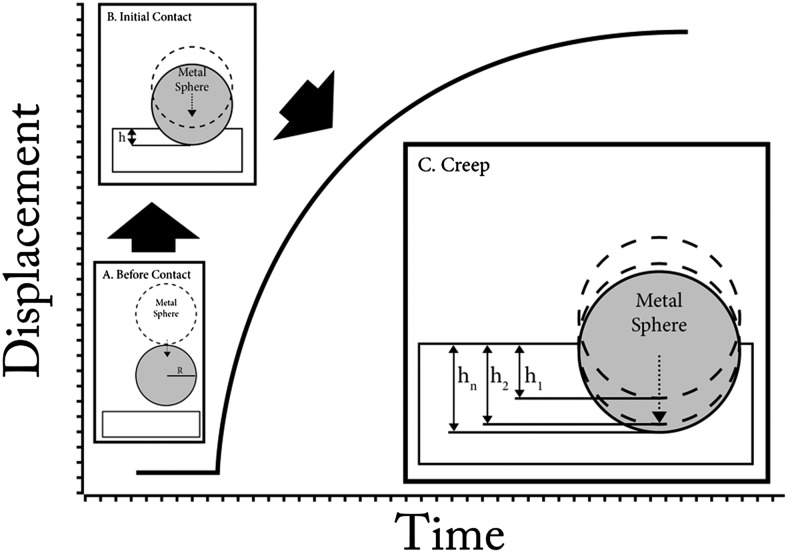
Figure 1 schematically illustrates test events. Displacement–time (h–t) data were acquired in four to five different trials at each of two different forces per specimen. Displacement during the trials did not significantly change indenter force, because indentation displacement was negligible relative to overall distance from the indenters to the magnet.
Figure 1.
Creep testing by MII. (A) Spherical magnetic probe with radius R rested on the specimen before magnetic force was imposed. (B) During ramp loading, the reflective ferrous spherical probe was displaced by constant magnetic force. (C) While magnetic force was maintained on the indenter, displacement gradually increased as measured via interferometry over a 200-second duration.
Hertzian Viscoelasticity
Viscoelastic modeling was performed based on measured creep to describe indentation by a sphere of radius R toward an asymptotic displacement over time. The present study employed the viscoelastic formulation of Oyen 26 incorporating Hertzian contact mechanics as derived in the Appendix. Briefly, creep was described by a function consisting of two exponential terms fit to the data using the Levenberg–Marquardt nonlinear least-squares method. 24 Similar to our previous microindentation study, 30 material constants C i were computed. Ideal creep testing would load the specimen instantaneously, which of course is experimentally impossible. Experimentally, loading was linearly increased as rapidly as possible as a ramp. The mathematical model incorporates a ramp correction factor (RCF) that accounts for finite loading time. Short-term (E 0) and long-term (E ∞) elastic stiffnesses were determined from the fitted viscoelastic model with computed material parameters.
Specimen Preparation
Bovine specimens were obtained fresh from a local abattoir (Manning Beef LLC, Pico Rivera, CA). Total preparation time including transportation time for specimens averaged 45 ± 15 minutes (SD). Using a suction trephine, corneal specimens 7 mm in diameter were excised. Specimen thickness ranged from 1.6 to 1.9 mm, which is normal for bovine cornea. In testing the epithelial layer, whole specimens were simply glued to the Petri dish on the endothelial side so that the probe spheres were on the upper-facing epithelium. For endothelial testing, whole specimens were glued to the Petri dish on the epithelial side so that probe spheres were on the upper-facing endothelium. For stromal testing, the epithelium layer and Bowman's membrane were removed before the remainder of the cornea was glued to the Petri dish. Approximately 400 to 450 μm of anterior stroma was then sharply excised with a scalpel, leaving a flat surface for placement of the indenter spheres. Specimens were taken from 28 different globes (9 epitheliums, 10 endotheliums, and 9 stromas).
Results
From preliminary experiments, appropriate initial ramp forces were determined for each corneal layer to obtain appropriate indenter displacement during the loading phase. Two different levels of loading forces were used for each corneal layer: 5.5 and 19.0 μN for epithelium, 632 and 1310 pN for endothelium, and 19.0 and 30.0 μN for stroma. As anticipated, higher loading force caused greater deformation of all layers. As expected for classic creep, displacement reached an asymptotic value at lower ramp force more quickly than when a high loading was imposed.
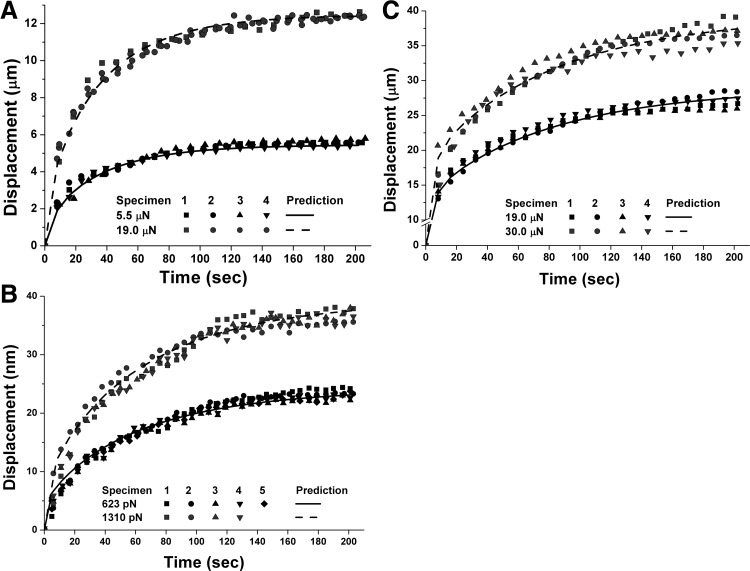
Forces during sustained indentation were highly repeatable for each imposed displacement and for all three corneal layers. Viscoelastic mechanical models based on curve-fitting parameters from one of the 9 to 10 trials for each specimen type accurately predicted behavior for both loading forces for all experiments involving the same corneal layer (Table 1). Figures 2A, 2B, and 2C compare experimental data with model predictions for all three corneal layers at two different levels of loading during a 200-second interval. Mean maximum differences between model prediction and data for the epithelium, endothelium, and stroma at lower loading forces were 8.23%, 8.24%, and 6.86%, respectively, while they were 12.93%, 11.36%, and 11.48% at higher loading.
Table 1.
Viscoelastic Parameters for Cornea
| Parameter | Epithelium | Endothelium | Stroma |
|---|---|---|---|
| C0, m2/N | 1.16E-04 | 7.11E-05 | 4.12E-04 |
| C1, m2/N | 6.02E-05 | 2.14E-05 | 1.13E-04 |
| τ1, sec | 31.76 | 60.74 | 4.17 |
| C2, m2/N | 4.98E-05 | 4.54E-05 | 2.84E-04 |
| τ2, sec | 61.76 | 95.75 | 91.32 |
| E0, kPa | 271.6 | 344.8 | 106.0 |
| E∞, kPa | 12.98 | 21.11 | 3.64 |
Computed material parameters for the cornea. See Appendix for symbol definitions and theoretical model derivation.
Figure 2.
Comparisons of predicted and observed creep in corneal epithelium (A), endothelium (B), and stroma (C). Coefficients of determination for all four trials consistently exceeded 0.94 and 0.98 for epithelial specimens, at 5.5- and 19.0-μN loading forces, respectively. Coefficients of determination exceeded 0.98 and 0.96 for endothelium at 632 and 1310 pN, respectively, and exceeded 0.98, and 0.96 for stroma at 19.0- and 30.0-μN loading, respectively.
As seen in Figure 2, two different loadings of 5.5 and 19.0 μN were imposed on epithelial surfaces. The root-mean-square error (RMSE) between four sets of data and model predictions based on fits from one experimental trial at 5.5-μN loading was small at 0.20, 0.34, 0.34, and 0.089 μm2. Coefficients of determination for all four different trials exceeded 0.94. The RMSE between the four data sets for the 19.0-μN higher loading and model predictions based on fits from one experimental trial for the 5.5-μN loading was also small at 0.35, 0.32, 0.24, and 0.27 μm2, respectively. Coefficients of determination for all four trials exceeded 0.98. For endothelium, Figure 2 shows creep responses of nine different specimens indented with loadings of 632 (five specimens) and 1310 (four specimens) pN, compared with prediction from the model based on fits from one of the trials using the lower loading. For both loadings, the RMSE between data and model predictions for all trials was <1.8 × 10−4 μm2. Coefficients of determination for fits to data exceeded 0.96 for both loadings.
Eight different stromal specimens were subjected to two different loadings of 19 and 30 μN (Fig. 2). The RMSE between experimental results and the model predictions for four different trials at the 19.0-μN loading was 0.53, 0.72, 0.78, and 0.80 μm2, respectively, while all coefficients of determination for fits to data exceeded 0.98. For four trials at higher loading of 30 μN, RMSE was 0.92, 0.70, 1.25, and 1.35 μm2, respectively, while all coefficients of determination consistently exceeded 0.96. Short- and long-term stiffnesses computed from viscoelastic models based on data from one specimen were 271.7, and 13.0 kPa, respectively, for the epithelium; 344.8 and 21.1 kPa, respectively, for endothelium; and 106.0 and 3.6 kPa, respectively, for stroma. Although the model predicted results accurately over two different loading levels, it was more accurate at lower than higher loading (Fig. 2).
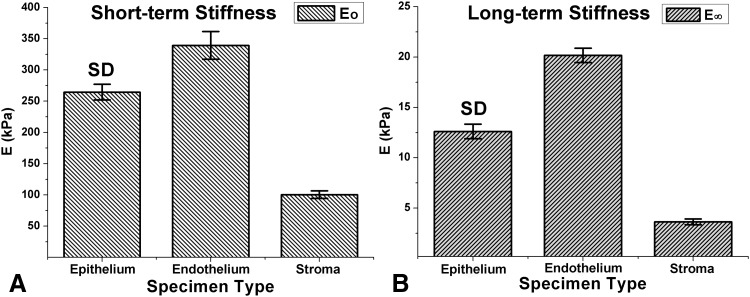
For more accurate measurements of the short- and long-term stiffnesses for all layers, a set of material creep constants was determined for each of four to six trials, and corresponding stiffnesses were determined based on each set of material creep constants. Figure 3 shows mean short- and long-term elastic stiffnesses for each corneal layer. Short- and long-term stiffnesses were highest for the endothelium at 339.2 ± 22.2 kPa (SD) (P ≥ 0.9) and 20.2 ± 0.71 kPa (P ≥ 0.8), respectively, while stroma exhibited the lowest short- and long-term stiffnesses at 100.4 ± 6.04 kPa (P ≥ 0.9) and 3.6 ± 0.29 kPa (P ≥ 0.8). Corresponding stiffnesses for epithelium were 264.6 ± 12.6 kPa (P ≥ 0.9) and 12.6 ± 0.73 kPa (P ≥ 0.9), respectively.
Figure 3.
Short-term (E 0) and long-term (E ∞) stiffness for corneal epithelium, endothelium, and stroma.
Discussion
Displacement in micro- and nanometer scales measured using MII effectively characterized creep in all three corneal layers. These data were readily incorporated in Oyen's viscoelastic formulation of Hertzian contact mechanics, which allowed not only accurate prediction of the viscoelastic behavior at various force levels, but also determination of short- and long-term stiffnesses. While derived from a single loading trial per layer, viscoelastic model predictions accounted for >94% the variance of measured creep for all loadings in all three corneal layers. These findings confirm and extend a previous report in which Hertzian viscoelastic relaxation accurately modeled larger scale indentations of various ocular tissues. 30
One notable current observation is that the thinner corneal layers have higher short- and long-term stiffnesses than stroma. Stroma, comprising the bulk of the cornea, proved most compliant of the three layers. Another interesting observation is that the stiffnesses of the endothelium, including Descemet's membrane, were the highest in the cornea. With short- and long-term stiffnesses of 339 and 22.2 kPa, the endothelium layer is threefold stiffer than stroma. Although Elsheikh et al. 9 reported that the epithelium's contribution to overall corneal stiffness is negligible, our finding shows that the intrinsic stiffness of the relatively thin epithelial layer considerably exceeded that of the thicker stroma. The stroma contributes more to overall corneal mechanical behavior than does the epithelium, because the stroma is much thicker than the epithelium, not because the stroma is intrinsically stiffer. Compressive modulus and tensile modulus can also differ because the cornea is not an isotropic material; cornea may be orthotropic or anisotropic. Hence, the discrepancy between our findings and those of Elsheikh et al. could also be due to the difference in the nature of the measured modulus.
Using atomic force microscopy, Last et al. 8 reported the mean stiffness of Descemet's membrane to range from 20 to 80 kPa, averaging 50 ± 17.8 kPa, while that of the anterior basement membrane ranged from 2 to 15 kPa and averaged 7.5 ± 4.2 kPa. Since the endothelial layer as tested in the present study included Descemet's membrane, the present finding of long-term endothelial layer stiffness of 20.2 ± 0.71 kPa falls within the range reported by Last et al.
Using holographic interferometry, Forster et al. 14 estimated whole corneal elastic modulus to be 158 kPa, which is comparable to the short-term stiffness that we calculated for stroma at 100 kPa. Considering the stiffness of the relatively thin epithelium and endothelium at 265 and 339 kPa, respectively, the current stiffness measurements are comparable to those of Forster et al. The corneal stiffness of 24.5 ± 5.7 kPa reported by Sjøntoft and Edmund is in the same order of magnitude of the long-term stiffness reported in the present study. 17 Since they calculated corneal stiffness using linear elastic theory, their reported value represents static Young's modulus, equivalent to the long-term stiffnesses reported in the current investigation. In addition, the corneal elastic coefficient reported by Edmund 16 was 24.9 ± 5.5 kPa, which is in the same order of magnitude as the current determinations.
The viscoelastic models based on creep behavior reported in the current investigation can be implemented directly to improve FEA accuracy. Although FEA investigations such as that by Pinsky and Datye 31 have provided insights into mechanical behavior of incised cornea, only stromal properties were considered. The FEA investigation by Uchio et al. 32 neglected viscous corneal properties, precluding evaluation of time-dependent behavior. By differentiating corneal layers and assigning corresponding time-dependent mechanical properties, realistic time-dependent behavior of the entire cornea can be captured in FEA.
The present report describes the equivalent viscoelastic behavior of the cornea in a manner that scales over a broad range of compressive deformations. These data were not intended to delineate which molecular processes or nanoscale phenomena underlie the apparently viscoelastic behavior, but that does not limit the utility of the results. The current findings not only provide empirical insights into the general mechanical behavior of normal whole cornea, but also can be implemented in simulation tools such as FEA to explore responses to variations in corneal thickness and geometry, or to alterations in corneal properties produced by ectasia or photic cross-linking. Accurate understanding of corneal biomechanical properties might also clarify limitations in noninvasive measurements of intraocular pressure.
Appendix
Hertzian Viscoelastic Model
The derivation of spherical indentation in an elastic medium follows Yoo et al. 30 Rearranging force P, which is a function of Poisson ratio ν, probe sphere radius R, and elastic modulus E, the governing equation can be determined as a displacement h.
Equation 1 can be written as a function of shear modulus G with incompressible assumption that Poisson ratioν = 0.5.
As suggested by Oyen, 26 this corresponds to a Boltzmann integral equation when (P/2G) is replaced by a viscoelastic integral operator for creep 33 as in equation 3.
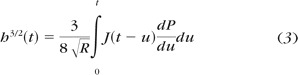 |
where J(t) is the material creep function and u is a dummy variable of integration for time. Ramp loading from 0 to maximum load at linearly increasing (ramp) rate k can be described by equations 4 and 5:
where t R is rise time to peak load.
Consistent with previous viscoelastic investigations, 24,26,30 a material creep function was employed of the form
where j = 2.
Recalling that maximum load P max = ktR, the solution for creep due to spherical indentation is given by equation 7:
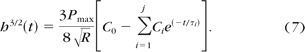 |
To account for the difference between physically realizable ramp, versus ideal step loading, a ramp correction factor (RCF) was determined, consisting of a parametric scaling of the exponential decay term that adjusted the creep function. 26,30,34
where k = 1,2.
As derived by Oyen, 24,34 the generalized creep function (equation 7) can be related to the shear creep function, allowing computation of the instantaneous E 0 and long-time E ∞ stiffnesses from material creep constants (Ci), as shown in equations 9 and 10.
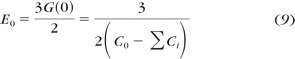 |
Footnotes
Supported by U.S. Public Health Service, National Eye Institute Grants EY08313 and EY00331, and Research to Prevent Blindness. JLD is the Leonard Apt Professor of Ophthalmology.
Disclosure: L. Yoo, None; J. Reed, None; J.K. Gimzewski, None; J.L. Demer, None
References
- 1. Luce DA. Determining in vivo biomechanical properties of the cornea with an ocular response analyzer. J Refract Cataract Surg. 2005;31:156–162 [DOI] [PubMed] [Google Scholar]
- 2. Kotecha A, Elsheikh A, Roberts CR, Zhu H, Garway-Heath DF. Corneal thickness- and age-related biomechanical properties of the cornea measured with the ocular response analyzer. Invest Ophthalmol Vis Sci. 2006;47:5337–5347 [DOI] [PubMed] [Google Scholar]
- 3. Medeiros FA, Weinreb RN. Evaluation of the influence of corneal biomechanical properties on intraocular pressure measurements using the ocular response analyzer. J Glaucoma. 2006;15:364–370 [DOI] [PubMed] [Google Scholar]
- 4. Shah S, Laiquzzaman M, Bhojwani R, Mantry S, Cunliffe I. Assessment of the biomechanical properties of the cornea with the ocular response analyzer in normal and keratoconic eyes. Invest Ophthalmol Vis Sci. 2007;48:3026–3031 [DOI] [PubMed] [Google Scholar]
- 5. Boyce BL, Jones RE, Nguyen TD, Grazier JM. Stress-controlled viscoelastic tensile response of bovine cornea. J Biomech. 2007;40:2367–2376 [DOI] [PubMed] [Google Scholar]
- 6. Hollman KW, Emelianov SY, Neiss JH, et al. Strain imaging of corneal tissue with an ultrasound elasticity microscope. Cornea. 2002;21:68–73 [DOI] [PubMed] [Google Scholar]
- 7. Wang H, Prendiville PL, McDonnell PJ, Chang WV. An ultrasonic technique for the measurement of the elastic moduli of human cornea. J Biomech. 1996;29:1633–1636 [PubMed] [Google Scholar]
- 8. Last JA, Liliensiek SJ, Nealey PF, Murphy CJ. Determining the mechanical properties of human corneal basement membranes with atomic force microscopy. J Struct Biol. 2009;167:19–24 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Elsheikh A, Alhasso D, Rama P. Assessment of the epithelium's contribution to corneal biomechanics. Exp Eye Res. 2008;86:445–451 [DOI] [PubMed] [Google Scholar]
- 10. Anderson K, El-Sheikh A, Newson T. Application of structural analysis to the mechanical behaviour of the cornea. J R Soc Interface. 2004;1:3–15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Elsheikh A, Alhasso D, Rama P. Biomechanical properties of human and porcine corneas. Exp Eye Res. 2008;86:783–790 [DOI] [PubMed] [Google Scholar]
- 12. Boyce BL, Grazier JM, Jones RE, Nguyen TD. Full-field deformation of bovine cornea under constrained inflation conditions. Biomaterials. 2008;29:3896–3904 [DOI] [PubMed] [Google Scholar]
- 13. Kasprzak H, Förster W, Von Bally G. Measurement of elastic modulus of the bovine cornea by means of holographic interferometry, Part 1: method and experiment. Optom Vis Sci. 1993;70:535–544 [DOI] [PubMed] [Google Scholar]
- 14. Förster W, Kasprzak H, Von Bally G. Measurement of elastic modulus of the central bovine cornea by means of holographic interferometry, Part II: results. Optom Vis Sci. 1994;71:27–32 [DOI] [PubMed] [Google Scholar]
- 15. Jue B, Maurice DM. The mechanical properties of the rabbit and human cornea. J Biomech. 1986;19:847–853 [DOI] [PubMed] [Google Scholar]
- 16. Edmund C. Corneal elasticity and ocular rigidity in normal and keratoconic eyes. Acta Ophthalmol. 1988;66:134–140 [DOI] [PubMed] [Google Scholar]
- 17. Sjøntoft E, Edmund C. Determination of young's modulus for the human cornea. Bull Math Biol. 1987;49:217–232 [DOI] [PubMed] [Google Scholar]
- 18. Kirwan C, O'Keefe M, Lanigan B. Corneal hysteresis and intraocular pressure measurement in children using the Reichert Ocular Response Analyzer. Am J Ophthalmol. 2006;142:990–992 [DOI] [PubMed] [Google Scholar]
- 19. Orssengo G, Pye D. Determination of the true intraocular pressure and modulus of elasticity of the human cornea. Bull Math Biol. 1999;61:551–572 [DOI] [PubMed] [Google Scholar]
- 20. Pepose JS, Feigenbaum SK, Qazi MA, Sanderson JP, Roberts CJ. Changes in corneal biomechanics and intraocular pressure following LASIK using static, dynamic, and noncontact tonometry. Am J Ophthalmol. 2007;143:39–47.e31 [DOI] [PubMed] [Google Scholar]
- 21. Shields MB. The non-contact tonometer: its value and limitations. Surv Ophthalmol. 24:211–219 [DOI] [PubMed] [Google Scholar]
- 22. Scott ON, Begley MR, Komaragiri U, Mackin TJ. Indentation of freestanding circular elastomer films using spherical indenters. Act Mater. 2004;52:4877–4885 [Google Scholar]
- 23. Bryant-Greenwood GD. The extracellular matrix of the human fetal membranes: structure and function. Oxford, UK: Royaume-Uni, Elsevier; 1998. [DOI] [PubMed] [Google Scholar]
- 24. Mattice JM, Lau AG, Oyen ML, Kent RW. Spherical indentation load-relaxation of soft biological tissues. J Mater Res. 2006;21 [Google Scholar]
- 25. Johnson KL. Contact Mechanics. Cambridge, UK: Cambridge University Press; 1987. [Google Scholar]
- 26. Oyen ML. Spherical indentation creep following ramp loading. J Mater Res. 2005;20 [Google Scholar]
- 27. Reed J, O Doherty K, Schmit J, et al. Applications of imaging interferometry. Proc SPIE Int Soc Opt Eng. 2006;6293:629301, 0277–786X [Google Scholar]
- 28. Olszak AG, Schmit J, Heaton MG. Interferometric approaches each have advantages. Laser Focus World. 2001;37:93–95 [Google Scholar]
- 29. Millard RC, Seaver G. An index of refraction algorithm for seawater over temperature, pressure, salinity, density, and wavelength. Deep Sea Res. 1990;37:1909–1926 [Google Scholar]
- 30. Yoo L, Reed J, Shin A, et al. Characterization of ocular tissues using micro-indentation and Hertzian viscoelastic models. Invest Ophthalmol Vis Sci. 2011;52:3475–3482 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Pinsky PM, Datye DV. A microstructurally-based finite element model of the incised human cornea. J Biomech. 1991;24:907–909, 911–922 [DOI] [PubMed] [Google Scholar]
- 32. Uchio E, Ohno S, Kudoh J, Aoki K, Kisielewicz LT. Simulation model of an eyeball based on finite element analysis on a supercomputer. Br J Ophthalmol. 1999;83:1106–1111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Lee EH, Radok JRM. Contact problems for viscoelastic bodies. J Appl Mech. 1960;27 [Google Scholar]
- 34. Chua W, Oyen M. Viscoelastic properties of membranes measured by spherical indentation. Cell Mol Bioeng. 2009;2:49–56 [Google Scholar]