Mental Addition in Bilinguals: An fMRI Study of Task-Related and Performance-Related Activation

Abstract

Behavioral studies show that bilinguals are slower and less accurate when performing mental calculation in their nondominant (second; L2) language than in their dominant (first; L1) language. However, little is known about the neural correlates associated with the performance differences observed between bilinguals' 2 languages during arithmetic processing. To address the cortical activation differences between languages, the current study examined task-related and performance-related brain activation during mental addition when problems were presented auditorily in participants' L1 and L2. Eleven Chinese–English bilinguals heard 2-digit addition problems that required exact or approximate calculations. Functional magnetic resonance imaging results showed that auditorily presented multidigit addition in bilinguals activates bilateral inferior parietal and inferior frontal regions in both L1 and L2. Language differences were observed in the form of greater activation for L2 exact addition in the left inferior frontal area. A negative correlation between brain activation and behavioral performance during mental addition in L2 was observed in the left inferior parietal area. Current results provide further evidence for the effects of language-specific experience on arithmetic processing in bilinguals at the cortical level.

Introduction

When bilinguals perform mental calculation in their second (L2) as opposed to their first language (L1), less accurate and slower responses have been reported in several behavioral studies (Marsh and Maki 1976; McClain and Huang 1982; Frenck-Mestre and Vaid 1993; Bernardo 2001; Campbell and Epp 2004). Many participants in these studies report “translating” mathematical problems presented in L2 to L1 to do the calculation and then translating back to L2 to provide the answer. Brain imaging studies on bilingual mental calculation would aid our understanding of mathematical processing, but as reviewed below, such studies are scarce (Venkatraman et al. 2006; Wang et al. 2007).

The study of mental calculation in bilingual people is valuable because such studies provide a unique opportunity to test theories of the role of language processing in mathematical reasoning. For example, according to the Triple Code model (Dehaene 1992; Dehaene and Cohen 1997), verbal number codes are used for storage and retrieval of simple multiplication and addition facts. On this view, mental calculation in bilinguals using auditory stimuli should directly tap language-specific representations because auditorily presented numbers can be directly connected to the verbal codes of numbers stored in memory. Moreover, auditorily presented numbers also resemble the real-life situation bilingual people encounter. Eventually, the study of number processing by bilinguals may also inform educational practices in increasingly bilingual American schools. According to the 2010 US Census, approximately 19.7% of children above age 5 speak English as a second language, a percentage that is growing in the United States (Shin and Kominski 2010).

The primary goal in the present study was to use auditory stimuli to identify the brain areas and degree of brain activation during arithmetic processing in bilinguals' L1 and L2 employing multidigit addition problems in both languages. Multidigit addition was expected to increase difficulty, and therefore to reveal brain activation differences between L1 and L2, and also to reveal brain activation differences associated with different levels of behavioral performance.

Neuroimaging Studies of Mental Addition

The majority of published studies using neuroimaging to study mental calculation employed monolingual participants and used visually presented single-digit stimuli. These studies consistently report that a network of cortical areas are activated during mathematical calculations: inferior parietal, superior parietal, and inferior frontal areas (Dehaene et al. 1999; Cowell et al. 2000; Fulbright et al. 2000; Menon, Rivera, White, Eliez, et al. 2000; Menon, Rivera, White, Glover, et al. 2000; Gruber et al. 2001; Zago et al. 2001; Dehaene et al. 2004; Kong et al. 2005; Zamarian et al. 2009). Frontoparietal activation occurs regardless of whether the arithmetic format is addition, subtraction (Burbaud et al. 1999; Chochon et al. 1999; Keller and Menon 2009), or multiplication (Fulbright et al. 2000; Jost et al. 2009). In one functional magnetic resonance imaging (fMRI) study utilizing auditory stimuli (e.g., “three plus four”), cortical activation occurred in a similar frontoparietal network but with right hemisphere dominance (Fehr et al. 2008).

Two studies have been conducted with bilingual participants, one using visual stimuli and single digits and the other using auditory multidigits. In the visual number study, bilinguals were trained on base-7 addition in one language (L1 or L2) and tested later in both languages (Venkatraman et al. 2006). Bilateral parietal and left frontal activation was found to be associated with the language-switching effect, suggesting that bilinguals recruit additional cortical areas to control access to one language as opposed to another. In the study using auditory stimuli, multidigit stimuli produced activation differences between bilinguals' 2 languages in the left precentral, postcentral, superior parietal areas, and the right medial frontal area (Wang et al. 2007). In that study, bilinguals were tested using addition and multiplication problems (e.g., “twenty-four plus twelve is thirty-six,” “eighteen times two is forty-six”), and the whole statement (including the 2 numbers for addition or multiplication, the operator of addition or multiplication, and the proposed answer) was heard before calculation started.

Examining the bilingual results and comparing the cognitive processes involved during mental calculation in L1 and L2, activation differences observed between L1 and L2 could be associated with language processes (such as encoding and translating of numbers from L2 to L1), with arithmetic processes, or with general cognitive processes (such as executive function or working memory).

In the present study, the stimuli were designed to reduce working memory load and allow us to focus on the effect of translation. To reduce working memory load, only auditory numbers were presented without the words “plus” and “equals” (e.g., “twenty-three,” “fifty-six”) and a period of more than 3 s was inserted before the proposed answer was presented to allow for calculation. Addition problems were also created to avoid potential experimental confounds, such as tie effects (Ashcraft 1992) and potential perceptual confusions in L2 listeners (Fuson 1990).

Exact versus Approximate Addition Using Multidigits

A factor not examined in previous bilingual studies is the difference between exact versus approximate calculations. The degree of language dependency differs in the 2 cases. Exact addition is argued to depend heavily on the use of language and verbal memory because it requires the retrieval of rote memorized multiplication tables and addition facts; magnitude estimation and comparison depends less on language (Ashcraft et al. 1992; Dehaene 1992; Lee and Kang 2002).

The language dependency of exact addition was demonstrated in a behavioral training study with bilingual speakers (Spelke and Tsivkin 2001). When Russian–English bilinguals were trained on 2 types of addition (i.e., exact and approximate addition), language-specific training effects on 2-digit calculations were found for exact calculations (e.g., base-6, base-8 addition, or 34 + 71 = 105 or 115) but not for approximate calculations (e.g., base-2 log, cubic root, or 34 + 71 = 110 or 80). Typically, when performance differences were observed in bilinguals in previous behavioral studies (Marsh and Maki 1976; McClain and Huang 1982; Frenck-Mestre and Vaid 1993; Bernardo 2001), exact calculation was used to test the language effect. From these studies, it appears that exact mental calculation tasks not only depend on the language used in the task but are sensitive to the language that was used when the participants originally acquired basic number terms and learned arithmetic facts.

At the cortical level, dissociation between exact and approximate addition with visually presented single digits has been reported in normal adults (Dehaene et al. 1999; Stanescu-Cosson et al. 2000) and in neuropsychological patients (Dehaene and Cohen 1997; Cohen et al. 2000; Lemer et al. 2003; Dehaene et al. 2004). Exact addition has been shown to activate the left angular gyrus and left inferior prefrontal areas, whereas approximate addition involves the intraparietal sulcus bilaterally (Dehaene et al. 1999; Stanescu-Cosson et al. 2000).

Multidigit numbers have been used in the field of education to investigate differences between exact and approximate addition (Levine 1982; Schoen et al. 1990; Hanson and Hogan 2000). When 2-digit problems are involved, exact and approximate calculations can be considered as different strategies for performing mental addition. The “exact addition” strategy relies on columnwise addition to obtain the precise sum. The “approximate addition” (estimation) strategy involves rounding both operands to the nearest multiples of 10 before adding them, one of the most frequently used strategies for computational estimation (Levine 1982; Schoen et al. 1990; Lemaire and Lecacheur 2002). In the present study, our goal was to examine brain activation patterns using both exact and approximate addition to examine these effects in bilingual people.

Performance-Related Activation

With an increasing number of bilingual students entering American schools, it is of educational interest to study individual differences in mental calculation in bilinguals. Individual differences in arithmetic performance have been noted in several behavioral studies (LeFevre et al. 1991; Lefevre and Kulak 1994). It is likely that individual differences in arithmetic performance at the behavioral level are associated with individual differences at the cortical level, but few studies to date have examined this relationship. Typically, fMRI studies examine task-related activation: Activations are averaged across subjects within a group and the observed cortical activation is associated with the cognitive components supposedly involved in that task. Performance-related activation can be used to address individual differences. Performance-related activation can be obtained by correlating cortical activation observed during a given task with individual performance levels, measured either simultaneously during the fMRI scans (Menon, Rivera, White, Eliez, et al. 2000; Rivera et al. 2005) or outside of the scanner (Grabner et al. 2007). For instance, using correlational analysis, Grabner et al. (2007) reported a positive correlation between mathematical competence measured outside of the scanner and brain activation in the left angular gyrus during a simple addition task. Increasing activation in the parietal areas, along with decreasing activation in frontal areas, is thought to be a possible neural signature of automaticity in arithmetic processes (Delazer et al. 2003; Rivera et al. 2005; Ischebeck et al. 2006). To our knowledge, no studies have used fMRI to examine performance-related individual differences in mental calculation in a bilingual population.

In summary, the goal of the current study was to advance our understanding of bilingual mental addition by using auditorily presented multidigit numbers to directly probe how language-specific codes affect mental calculation in both exact and approximate math conditions. We hypothesized that our results would support the following: 1) Activation differences between languages: Differences in cortical activation between bilinguals' L1 and L2 were expected, with activation encompassing larger areas during L2 processing when compared with L1. Based on Dehaene's model (Dehaene 1992; Dehaene and Cohen 1997), we assume translation to be the major difference between processing numbers in L2 versus L1, particularly during exact addition. Activation differences between languages might be observed in areas such as the inferior frontal areas, which have been previously reported during translation (Klein et al. 1995; Lehtonen et al. 2005). 2) Activation during exact versus approximate tasks: Task differences were expected for exact versus approximate addition in both L1 and L2. Activation differences between tasks would be expected in the inferior parietal areas, which have been previously reported (Dehaene et al. 1999; Stanescu-Cosson et al. 2000; Lemer et al. 2003). 3) Performance-related activation: Significant negative correlations between behavioral performance and cortical activation were expected in several brain areas involved in arithmetic processing, such as the inferior parietal areas.

Materials and Methods

Participants

Eleven Chinese (L1)–English (L2) bilinguals (2 males, 9 females; mean age = 26.9 years, standard deviation [SD] = ±3.91, ranging from 23 to 35) participated in this study. All participants gave written informed consent and completed a questionnaire about handedness (Oldfield 1971). All participants were right handed and none of them had a history of oral or written language impairment, neurological or psychiatric disease, nor any hearing or speech deficit.

All participants reported Mandarin Chinese as their first language (L1), the language of instruction in elementary school, the language used to acquire simple arithmetic, the preferred language for mental arithmetic, and the dominant language at the time of testing. The mean age of onset of the acquisition of English (L2) was 10.00 years of age (SD = ±3.19 years); the mean length of residence in an English-speaking environment was 2.66 years (SD = ±2.50 years). The mean percent of English use in everyday life was 44.12% (SD = ±19.34%) averaged across different contexts (e.g., at home, in school, during shopping, etc.). The mean self-rated proficiency level averaged across their listening, speaking, reading, and writing abilities was 4.23 (SD = ±1.27) (on a 7-point scale; 1 = poor and 7 = excellent).

Stimuli

Numbers were presented auditorily to resemble real-life situations in which bilingual speakers encounter difficulties processing numerical information presented in L2. For both the exact and the approximate addition conditions, the stimuli were verbal number words, which were naturally produced by one female native speaker of Mandarin Chinese and one female native speaker of American English. The Mandarin and English speakers were recorded while reading printed sentence lists. Speakers read the sentences (e.g., “one plus one equals one”) at a normal pace and intonation. All speech stimuli were recorded in a sound attenuated booth and digitized at 44.1 kHz. The digital speech files were segmented at 3 positions (i.e., first number, second number, and sum) using specifically designed software. Number words across all 3 positions had an average duration of 883.31 ms (SD = ±119.85 ms) in Mandarin Chinese and an average duration of 805.01 ms (SD = ±92.57 ms) in English. The addition problems were created by selecting sound files to represent the first number, the second number, and the sum. The 3 numbers were presented sequentially, with no intervening words (for the timing of presentation, see Procedures).

Tasks

In each of the 2 languages, 2 conditions were tested: exact addition and approximate addition (Table 1a). The first number, second number, and proposed sums were presented sequentially and participants were instructed to verify whether the proposed answer was correct or incorrect by pressing 1 of the 2 reaction buttons with their left (for correct answer) or right (for incorrect answer) thumb. Participants were instructed to use either an exact addition or an approximate addition strategy. For exact addition, participants were asked to do columnwise addition to obtain the precise sum (e.g., 23 + 38 = 61). For approximate addition, participants were asked to round both operands to the nearest multiples of 10 before adding them together (e.g., 23 + 38 20 + 40 = 60). Rounding was selected because it is the most frequently used strategy in computational estimation of multidigit problems (Lemaire et al. 2000). These 2 conditions differ only in the provided sums, one using the exact number (e.g., 61) and the other using the approximate number in multiples of 10 (e.g., 60). Participants were asked during initial interviews whether they typically translated L2 numbers into L1 and verified that they did so; during our experiment, we gave instructions to indicate that this strategy was expected. During the baseline task (number detection), participants were asked to listen to number words (e.g., “one,” “two”) and press the left and right reaction buttons alternately. This baseline task, rather than the rest baseline, allowed us to account for the auditory processing of number words and the motor responses of button pressing.

Table 1a.

Experimental paradigm used in the current study

Conditions	Examples	Response
Two-digit exact addition
Chinese	“ershi-san” + “wushi-liu” = “qishi-jiu”?	Correct or incorrect?
English	“Twenty-three” + “fifty-six” = “seventy-nine”?	Correct or incorrect?
Two-digit approximate addition
Chinese	“ershi-san” + “wushi-liu” = “bashi”?	Correct or incorrect?
English	“Twenty-three” + “fifty-six” = “eighty”?	Correct or incorrect?
Baseline (1000-Hz tone–“1” − “2”)
Chinese	“yi” − “er”	Detection and response
English	“One” − “two”	Detection and response

Note: Two addition tasks, exact addition and approximate addition, were tested in each of 2 languages (L1: Mandarin Chinese; L2: English) separately in different runs.

Problem Sets

During both the exact and the approximate addition conditions, 2-digit addition problems with sums less than 100 were used. Addition problems were created with the following constraints to avoid potential experimental confounds: 1) pairs of operands that yield different results from exact and approximate calculation strategies were excluded (e.g., 46 + 37 = 83 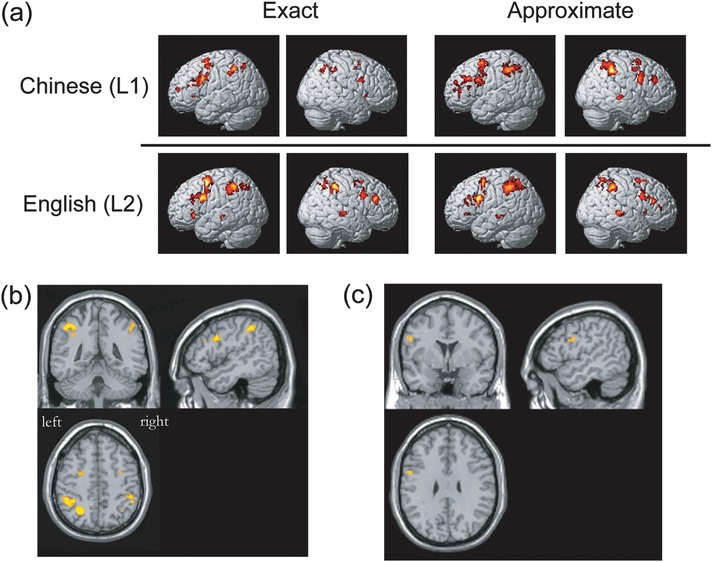80 if approximation occurs after exact addition, but 46 + 37 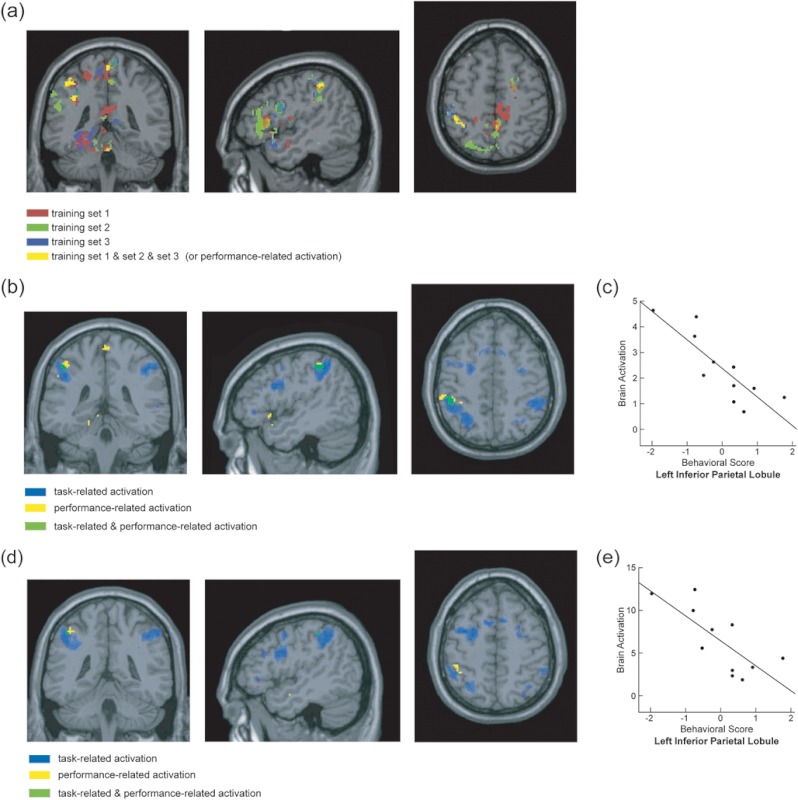50 + 40 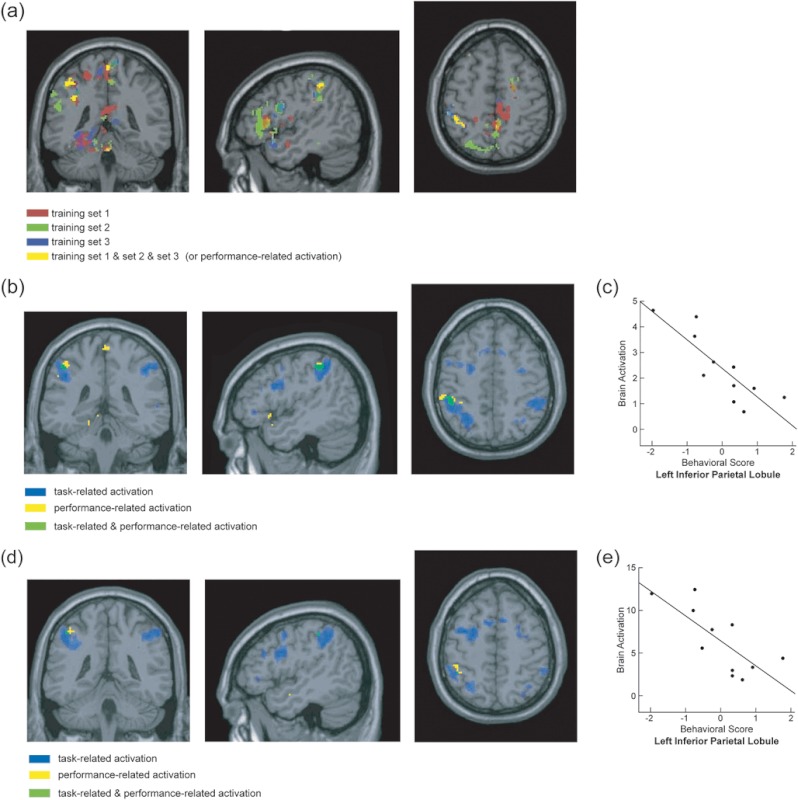90 if approximation occurs before addition); 2) “-teen” and “-ty” (e.g., nineteen, ninety) numbers were excluded to avoid potential perceptual confusion in L2 listeners and potential confusion induced by the inversed order of the ones and tens in Mandarin Chinese and English (Fuson 1990); 3) no operands had 0 or 5 in unit digits (Campbell 1994); 4) no plus-one problems were used to avoid counting rather than addition; 5) within a single addition problem, no digits were repeated in the same unit or decade position, or within a single operand, to avoid tie effects (Ashcraft 1992); and 6) no reverse order of operands were used (e.g., 26 + 62).

The probability of the true sum presented as a proposed answer was 0.5. To have a match between exact and approximate additions, false sums always had a split of ±10 or ±1 from the correct answer (e.g., 36 + 27 = 53? and 36 + 27 = 60?) in both exact and approximate addition conditions. The presentation order of the problems with correct or incorrect answers was randomized with the constraint that no more than 2 correct (or incorrect) responses occurred in a row; participants were not informed about this ordering strategy.

Procedures

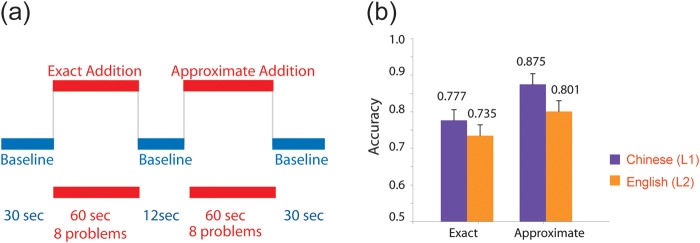
A blocked design of 6 runs was employed in the present fMRI experiment with each language tested in separate runs to avoid language-switching effects. The order of languages for each run was randomized across subjects. During each experimental run, 2 blocked conditions were tested in random order: exact addition (8 trials) and approximate addition (8 trials) (Fig. 1a). At the beginning of each run, the subjects were informed about the language to be used; in the beginning of each blocked condition, the task to be performed (exact or approximate addition) was displayed to the subjects.

Figure 1.

Experimental paradigm used in the present study and the behavioral performance. (a) Schematic diagram shows one example fMRI run. Each run contained two 60 s activation blocks, interleaved with a 12 s baseline block. There were baseline periods (30 s) at the beginning and end of each run. (b) Behavioral performance (percent accuracy) obtained during the fMRI scans in the scanner. Error bars indicate one standard error of the mean.

Each trial began with a 1000-Hz warning tone (200 ms), followed by a first number (with a stimulus onset asynchrony, SOA, of 200 ms from the warning tone), a second number (an SOA of 2250 ms from the first number), and a proposed sum (an SOA of 3150 ms from the second number). Participants were asked to respond “correct” or “incorrect” before the next trial, which was marked by a warning tone with an SOA of 1800 ms from the proposed sum. A white fixation mark + was presented at the center of the visual field throughout the experiment to avoid unnecessary eye movement. Cues regarding the hand to be used to record a correct (√) or incorrect answer (x) were continuously presented on the screen to reduce the memory load. No feedback was given to the participant regarding the correctness of the answer. Behavioral responses, including reaction times and accuracy (percent correct), were recorded inside the scanner simultaneously with the fMRI signals.

fMRI Data Acquisition

Prior to the scanning session, the experimental design was explained to subjects in their first language (Mandarin Chinese). All participants were provided with specific instructions about minimizing head motion within and across experimental runs. E-Prime software (version 1.1, Psychology Software Tools Inc., Pittsburgh, PA) was used to deliver stimuli through magnetic resonance compatible goggles and headphones. The start of stimulus presentation was synchronized with the MRI scanner initiated trigger.

The fMRI scan was performed on a 1.5-T MR scanner (version 5.8, General Electric, Waukesha, WI) at the MR Research Laboratory at the University of Washington. Twenty-one slices were acquired, oriented parallel to the AC–PC line, and using a T₂^*-weighted gradient echo, echo planar imaging pulse sequence (time echo = 52 ms, time repetition = 3 s, voxel size = 3.75 × 3.75 × 5.5 mm, field of view = 240 mm, and matrix = 64 × 64.). High-resolution (0.94 × 0.94 × 1.40 mm) anatomical images using a 3D T₁-weighted scan were also acquired from each participant at the beginning of the session.

Behavioral Data Analysis

The percent correct data collected during scanning was analyzed with 2-way repeated-measures analysis of variance (ANOVA) to examine the main effects of language (L1, L2) and task (exact, approximate addition), and their interaction at the behavioral level. The binomial test was used to examine whether the number of subjects who showed higher performance in exact than approximate addition was significantly different from 50% (chance level).

fMRI Data Analysis

All statistical analyses of the fMRI data were performed using SPM5 software (Wellcome Department of Imaging Neuroscience, London, UK). The echo planar images were first corrected for slice timing and then realigned intraindividually for head-motion correction. The realigned images were coregistered with individual anatomical images, spatially normalized to the MNI152 brain template (Montreal Neurological Institute, Montreal, Canada) and resampled to 2 × 2 × 2 mm. The functional images were spatially smoothed with a 6-mm full-width at half-maximum Gaussian kernel. The first 3 volumes of each run were excluded from the analysis. At the first level, general linear models were constructed separately for each subject with distinct regressors for each condition and run. Regressors were convolved with the canonical hemodynamic response function (HRF). The time series data were high-pass filtered at a time constant of 128 s and corrected for temporal autocorrelation with a first-order autoregressive model, AR(1). At the second level, voxelwise random effects models were used to examine task-related and performance-related activation.

To examine the overall activation pattern for each of our 4 conditions, we compared task-related activation relative with their respective baselines in the first random effects analysis. Whole-brain voxelwise analysis was performed with the following 4 contrasts: 1) Chinese Exact Addition (CE) versus Chinese Baseline (Cbaseline), 2) Chinese Approximate Addition (CA) versus Chinese Baseline, 3) English Exact Addition (EE) versus English Baseline (Ebaseline), and 4) English Approximate Addition (EA) versus English Baseline. Task-related activation was considered significant if a voxel-level uncorrected P value was less than 0.001 (t₁₀ = 4.14, z = 3.0885) and if a cluster-extent threshold of at least 10 contiguous voxels was found. In order to find common activation across the 4 addition tasks, we also performed an intersection analysis on the activation maps obtained from the above 4 task > baseline contrasts using the “and” operation.

A 2-way repeated-measures ANOVA was run to test for the LANGUAGE (i.e., English, Chinese) main effect, the TASK (Exact, Approximate addition) main effect, and the LANGUAGE × TASK interaction effect. The threshold for significant activation was set at the voxel-level uncorrected P value of 0.001 with at least 10 contiguous voxels. Because a significant interaction effect was found, differences between languages and tasks were further explored using the contrasts as described below.

To explore the activation differences between the second and first language, the following contrasts were used: 1) [EE > baseline] versus [CE > Cbaseline] and 2) [EA > Ebaseline] versus [CA > Cbaseline]. Activation was significant if a voxel-level P value was less than 0.001 (uncorrected) and if a cluster-extent threshold of at least 10 contiguous voxels was found.

The activation differences between exact and approximate addition were examined by the following contrasts: 1) CE versus CA and 2) EE versus EA. The same threshold as described above was used, a voxel-level uncorrected p-value of 0.001 with at least ten contiguous voxels.

In order to identify cortical areas that show a significant relationship between behavioral performance and the blood oxygenation level–dependent (BOLD) responses, correlations were calculated between behavioral performance (percent accuracy) and fMRI BOLD responses. To avoid the nonindependence problem in fMRI analysis (Kriegeskorte et al. 2009; Poldrack and Mumford 2009; Vul et al. 2009), 2 cross-validation approaches were used, the leave-one-run-out approach and the leave-one-subject-out approach (Kriegeskorte et al. 2009; Esterman et al. 2010).

The leave-one-run-out approach was used to test the generalization of results to independent runs of the same subjects. For iterations of this method, 1 of the 3 runs was left out of the test set (e.g., run1). All the other runs (e.g., run2 and run3) were used as the training sets. For the training set, whole-brain voxelwise correlation analysis was run using robust regression, which down-weights outliers (Wager et al. 2005). Areas that were found to consistently show significant correlation across all iterations were defined as the “performance-related activation” and used as regions of interest (ROIs). A threshold of significance that would result in large robust ROIs was chosen because different significant clusters (or ROIs) were obtained from each of the 3 training sets. Thresholding with smaller numbers of contiguous voxels (e.g., 20 and 150) resulted in small ROIs that were not stable across training sets (Supplementary Fig. 1). Thus, to obtain stable ROIs across the 3 training sets, a liberal threshold was applied, using a voxel-level uncorrected P value of 0.05 with at least 230 contiguous voxels. Because no ROIs were found for [CE > Cbaseline], [CA > Cbaseline], [EE > Ebaseline], nor [EA > Ebaseline], conditions were pooled together across tasks or across languages (i.e., [CE + CA] > Cbaseline, [EE + EA] > Ebaseline). Correspondingly, the behavioral performance scores were averaged.

ROIs were further refined by using an intersection analysis (using the “and” operation) on the significant activation obtained from performance-related and task-related analysis. This ensures that brain–behavioral correlations obtained are also specifically related to mental addition tasks, not just to performance monitoring. Correlations with performance monitoring can be obtained in any task whether language, calculation, or working memory components are required. For example, an intersection analysis was run on significant activation obtained from performance-related analysis of [EE > Ebaseline] and significant activation obtained from whole-brain voxelwise task-related analysis of [EE > Ebaseline]. Beta weights from each ROI were extracted for correlation analysis. Correlation coefficients were averaged across the 3 test sets and considered significant using a Bonferroni corrected P value threshold of 0.05.

A leave-one-subject out approach was used to ensure that the results could be generalized to independent subjects. For iterations in this method, one subject was left out. The whole-brain voxelwise correlation analysis was run on all the other subjects. In each whole-brain voxelwise correlation analysis (or performance-related analysis), a threshold of an uncorrected voxel-level P value of 0.05 with at least 230 contiguous voxels was used. Overlapping areas that were significant across all iterations were identified as the performance-related activation and used as ROIs. Then, these ROIs were further refined by using an intersection analysis (using the “and” operation) on the significant activation obtained from performance-related and task-related analysis. The resulting ROIs were used to extract beta weights from the one remaining subject for correlation analysis.

Results

Behavioral Results

A 2-way repeated-measures ANOVA showed that the main effect of language approached significance, F_1,10 = 4.487, P = 0.060. A significant main effect of task, F_1,10 = 6.417, P = 0.030, was found, with lower performance in exact addition than approximate addition. No interaction between task and language, F_1,10 = 0.219, P = 0.650, was found. Percent accuracy for each of the 4 conditions is listed in Table 1b and shown in Figure 1b.

Table 1b.

Percent accuracy, standard errors, maximum, and minimum scores for each of the 4 conditions

	Chinese (first language; L1)		English (second language; L2)
	Exact	Approximate	Exact	Approximate
Mean	0.78	0.88	0.73	0.80
Standard error	0.03	0.03	0.03	0.04
Max	0.92	1.00	0.83	0.96
Min	0.63	0.75	0.56	0.56

In L1 addition, 9 of 11 subjects (81.8%) showed higher behavioral performance in Chinese approximate addition (CA) than Chinese exact addition (CE), which is significantly different from the 50% chance level as revealed by the binomial test (P = 0.033). In L2 addition, 6 of 11 subjects (54.5%) showed higher performance in English approximate addition (EA) than in English exact addition (EE), which is not significant. In the post-fMRI questionnaire, all subjects reported translating the auditorily presented L2 numbers into L1 numbers before they started calculation.

fMRI Results

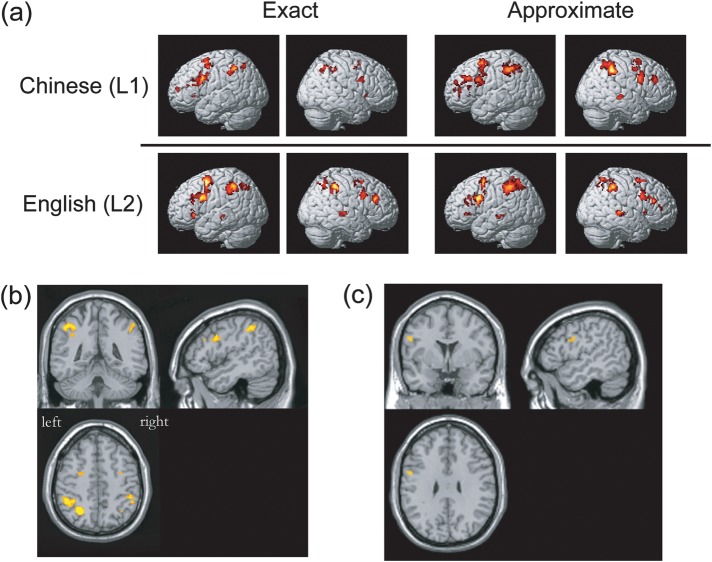
Voxelwise random effects analysis showed widespread activation in the frontoparietal network in all conditions (CE, CA, EE, and EA) relative to their baselines (Fig. 2a and Supplementary Tables 1 and 2).

Figure 2.

Task-related activation from the random effects analysis. (a) Significant task-related activation was obtained from conditions of interest versus their respective baselines (P < 0.001 uncorrected at the voxel level with at least 10 contiguous voxels). The MNI coordinates are shown in Supplementary Tables 1 and 2. (b) Intersection of significant activations across all 4 addition tasks ([CE > Cbaseline] and [CA > Cbaseline] and [EE > Ebaseline] and [EA > Ebaseline]) mentioned above (see Supplementary Table 3). (c) Activation differences between languages in exact addition, obtained by using the contrast of [EE > Ebaseline] > [CE > Cbaseline] (also see Supplementary Table 5).

For the [CE > Cbaseline] contrast, significant activation was observed bilaterally in the inferior parietal lobule (IPL), the middle frontal gyrus (MFG), the inferior frontal gyrus (IFG), and the anterior insula (AI). In the left hemisphere, significant activation was found in the supplementary motor area (SMA); in the right hemisphere, significant activation was observed in the angular gyrus (ANG) and the precentral gyrus (preCG).

The [CA > Cbaseline] contrast revealed bilateral activation in the MFG. In the left hemisphere, significant activation was found in the IPL and IFG. In the right hemisphere, significant activation involved the supramarginal gyrus (SMG), the superior frontal gyrus (SFG), SMA, the middle temporal gyrus (MTG), preCG, middle cingulate, and the insula.

For the [EE > Ebaseline] contrast, significant activation was found bilaterally in the IPL, MFG, and preCG. In the left hemisphere, the activation also involved the IFG, MTG, SMA, and AI. In the right hemisphere, significant activation involved the superior parietal lobule (SPL), SFG, and the superior temporal gyrus (STG).

The [EA > Ebaseline] contrast revealed significant activation in the following regions: bilaterally in the IPL, IFG, MFG, SFG, and preCG. In the left hemisphere, the activation was found in the MTG and AI; in the right hemisphere, the STG, SPL, and the middle cingulate.

The intersection analysis showed overlapping activation across the above 4 contrasts (task > its respective baseline) in the following regions: the IPL, SPL, IFG, MFG, and preCG in the left hemisphere and the IPL and IFG in the right hemisphere (Fig. 2b and Supplementary Table 3).

In the 2-way repeated-measures ANOVA, no voxels showed a significant main effect of LANGUAGE. A significant TASK main effect was found, with approximate addition showing greater activation than exact addition. The significant TASK main effect was found in the postcentral gyrus, middle, and posterior cingulate cortex in the left hemisphere and the postcentral gyrus, fusiform gyrus, precuneus, anterior, and middle cingulate cortex in the right hemisphere. A significant LANGUAGE × TASK interaction effect was also found in the IFG and SMG in the left hemisphere and the IFG in the right hemisphere (Supplementary Table 4 and Supplementary Fig. 2).

Activation Differences between L1 and L2

As predicted, significant activation differences were found between languages. In exact addition, significantly higher activation was found in L2 compared with L1. In the comparison of L2 versus L1 exact math, using the [EE > Ebaseline] > [CE > Cbaseline] contrast, activation in L2 was greater in the left IFG (Fig. 2c and Supplementary Table 5). This left inferior frontal activation overlapped with the activation observed in the LANGUAGE × TASK interaction effect of the ANOVA analysis. No significant L1 versus L2 activation differences were found, using the contrast [CE > Cbaseline] > [EE > Ebaseline].

Comparing L1 and L2 in the approximate addition, significant activation differences were observed for the [CA > Cbaseline] > [EA > Ebaseline] contrast in the right postcentral gyrus. No significant activation differences were found for the contrast [EA > Ebaseline] > [CA > Cbaseline].

Activation Differences between Tasks

Activation differences were found between exact and approximate addition. Unexpectedly, when comparing exact versus approximate addition in L1, no significant clusters were found to survive the chosen threshold for the contrasts of [CE > CA]. The [CA > CE] contrast showed significant activation in the MFG, IPL, postcentral gyrus, precuneus, and middle cingulate cortex in the left hemisphere and the SFG, fusiform gyrus, and SMA in the right hemisphere.

In L2, no significant activation was found for the [EE > EA] contrast. With the [EA > EE] contrast, significant activation differences were found in the MTG, anterior, and middle cingulate cortex in the left hemisphere, and the IFG, STG, and precuneus in the right hemisphere.

Performance-Related Analysis

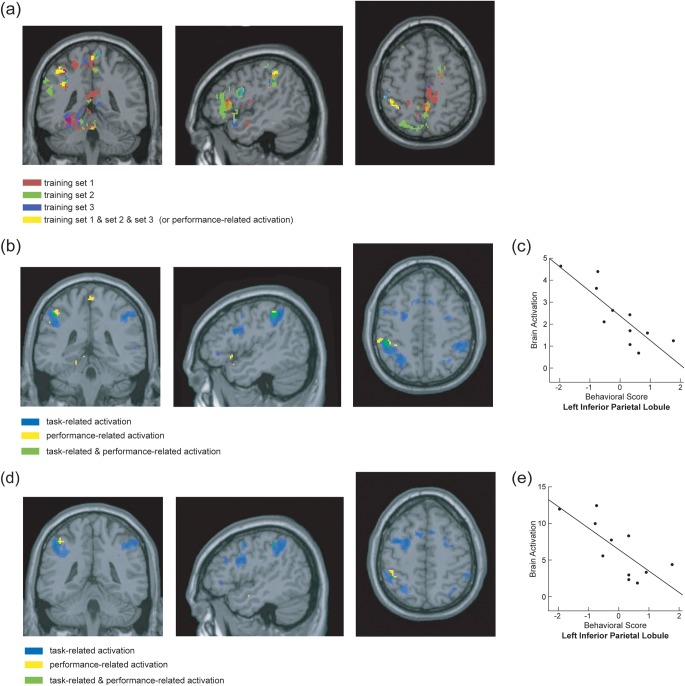
From the leave-one-run-out method, several clusters were obtained after overlapping the performance-related activation of [EE + EA] > Ebaseline from all 3 training sets, including the left IFG, SPL, IPL, precuneus, thalamus, hippocampus, and the right middle cingulum and insula. Significant performance-related activation was submitted to an intersection analysis (using the “and” operation) with task-related activation. Overlapped task-related and performance-related activation was found in 2 clusters in the left IPL (Fig. 3b and Table 2a). These clusters were used as ROIs to obtain averaged correlation coefficients from the 3 test sets. The fMRI BOLD responses obtained from the [EE + EA] > Ebaseline contrast in one of the 2 left IPL clusters showed significant negative correlations with the behavioral performance obtained during fMRI scans (i.e., average of the EE and EA percent accuracy) (for details, see Fig. 3c and Table 2a).

Figure 3.

ROIs and the brain–behavioral correlations from [EE + EA] > Ebaseline. (a) Significant correlations obtained from each of the 3 training sets from the leave-one-subject-out cross-validation approach are shown in red, green, and blue. Overlapped activation across the 3 training sets is shown in yellow. (b) Overlapped activation between the task-related and performance-related activation (obtained from the leave-one-subject-out cross-validation approach). Overlapped activation between the performance-related (yellow) and task-related (blue) is shown in green. (c) Scatter plot showing a significant negative correlation between behavioral performance and brain activation in the left IPL ROI from the leave-one-run-out cross-validation approach. Brain activation (y-axis) refers to the contrast values obtained between [EE + EA] versus their baselines with an arbitrary unit of brain activation level. Behavioral scores were obtained from the averages of scores of EE and EA. This score was averaged within a subject and adjusted to have a mean of 0 across subjects and scaled to have a unit of variance. The averaged correlation coefficient across the 3 test sets and the corresponding P values are listed in Table 2a. (d) Overlapped activation between the task-related and performance-related activation (obtained from the leave-one-subject-out approach). Overlapped activation between the performance-related (yellow) and task-related (blue) is shown in green. (e) Scatter plot showing a significant negative correlation between brain activation and behavioral performance in the left IPL from the leave-one-subject-out cross-validation approach. (also see Table 2b).

Table 2a.

Results from leave-one-run-out cross-validation approach

Leave-one-run-out	MNI coordinate			Correlation values				Correlation
	x	y	z	Run1	Run2	Run3	Number of voxels	Mean	P value
Left IPL	−46	−38	48	−0.869	−0.528	−0.670	54	−0.689	0.019
Left IPL	−38	−42	34	−0.721	−0.404	−0.617	17	−0.581	0.061

Note: Correlation coefficients r obtained from each of the test sets (i.e., run1, run2, run3) and the averaged correlation coefficient across the 3 test sets are listed.

The leave-one-subject-out method produced significant performance-related activation in the left SPL, IPL, STG, inferior temporal gyrus, precuneus, insula, and putamen and the right IFG, middle cingulum, thalamus, and insula. Significant performance-related activation overlapped with task-related activation in the left IPL (Fig. 3d and Table 2b), which is smaller than but in close proximity to the left IPL cluster found in the leave-one-run-out method. A significant negative correlation between brain activation and behavioral performance was found in this left IPL cluster (Fig. 3e).

Table 2b.

Results from leave-one-subject-out cross-validation approach

Leave-one-subject-out	MNI coordinate				Correlation
	x	y	z	Number of voxels	r	P value
Left IPL	−48	−34	48	11	−0.76	0.011

Note: Number of voxels and the MNI coordinates of ROIs are listed. The corresponding P values are also listed.

Discussion

Behavioral studies have shown poorer performance when bilinguals are tested in their less preferred language (L2) compared with their preferred language (L1). However, little is known about the neural correlates of such performance differences. The present study examined mental calculation in Chinese–English bilinguals by presenting multidigit addition problems auditorily in their L1 and L2 because current models predict that these conditions should be most relevant from a theoretical perspective.

Our results demonstrate that 1) cortical areas involved during auditory multidigit addition in bilinguals' L1 and L2 overlapped largely with areas reported in previous studies for single-digit addition. Moreover, we show that activation in the frontal and parietal areas during mental addition in bilinguals' L2 overlapped largely with activation in L1. 2) Activation differences between participants' L2 and L1 were observed in the left IFG in exact addition. 3) Activation differences between approximate versus exact tasks were found in the frontal and parietal areas. Lastly, 4) a new finding in the form of a negative correlation was observed in the left inferior parietal region in L2 addition linking higher accuracy scores in L2 addition tasks with lower activation levels in these regions. Findings from our present study provide neuroimaging evidence of the performance differences observed between bilinguals' 2 languages observed at the behavioral level and are consistent with current brain models of mental calculation.

Activation Similarities for Mental Addition across Languages, Tasks, and Input Formats

In the current study, when addition problems were presented auditorily in the subjects' L1, significant activation was observed bilaterally in the inferior parietal and the inferior frontal, extending to the precentral and middle frontal areas. Our interpretation of activation patterns is based on analyzing cognitive processes involved in the current task conditions. Multiple cognitive processes and stages are involved during mental arithmetic when problems are presented auditorily in L1. These cognitive processes include transcoding of auditory numbers into visual or abstract forms, maintaining the addition problems either in auditory or visual format, retrieving simple addition facts, performing carrying operations, and maintaining and updating intermediate results in working memory. With the blocked design used in the current study, frontoparietal activation could be associated with the arithmetic and language-related processes described above. The frontoparietal activation observed in L1 addition tasks in the current study is consistent with previous studies in which arithmetic problems were visually presented in the form of Arabic digits and tested with different operations (Burbaud et al. 1999; Chochon et al. 1999; Fulbright et al. 2000; Menon, Rivera, White, Glover, et al. 2000; Jost et al. 2009; Keller and Menon 2009). Other tasks, such as numerical magnitude comparison (Pesenti et al. 2000; Pinel et al. 2001) and nonnumerical magnitude comparison (Fias et al. 2003; Pinel et al. 2004), also activated this frontoparietal network. Considering the similarities in tasks and activated regions between these previous reports and our results, frontoparietal activation could be associated with arithmetic and numerical processes that are required in order to carry out exact and approximate addition.

During L2 addition in the present study, frontoparietal activation was also observed. This result suggests that mental addition in L1 and L2 might generally rely on similar neural substrates. Moreover, the frontoparietal network is activated irrespective of the language backgrounds of the subjects tested, including French (Dehaene et al. 1999), American English (Menon, Rivera, White, Eliez, et al. 2000; Rivera et al. 2005), German (Gruber et al. 2001), Japanese (Kazui et al. 2000), and Mandarin Chinese (Tang et al. 2006; Wang et al. 2007). Taken together with previous studies, our findings suggest that a distributed network, including the bilateral inferior parietal region and left inferior frontal gyri, is activated for numerical and arithmetic processing, irrespective of input formats (visual or auditory), language backgrounds, and whether the first or second language is used.

Activation Differences between Languages

Activation differences between languages were also observed. When exact addition problems were given auditorily, a higher level of activation in L2 compared with L1 was observed in a small cluster in the left inferior frontal area. Interpretation of such activation patterns should be taken with caution because the involvement of specific cognitive processes cannot be inferred from cortical activation (Poldrack 2006), in that activation in a single cortical region could be associated with multiple different cognitive functions. Exact addition in L2 requires additional cognitive components of processing L2 auditory verbal numbers and translating those numbers into L1. After L2 verbal numbers are translated into L1, the calculation processes are most likely to be carried out in the L1 format; that is, processes of retrieving simple addition facts, maintaining, and updating intermediate results are likely to be performed using L1 verbal codes. These results are consistent with Dehaene's Triple Code Model (Dehaene 1992; Dehaene 1995). Thus, the left inferior frontal activation observed during L2 exact addition could be associated with the extra language-related processes.

Compared with the previous work (Wang et al. 2007), only addition problems were tested in the present study and the addition problems were not presented in the format of one whole statement. In the Wang et al. study, activation differences between languages were found in the left precentral, postcentral, superior parietal, and precuneus areas and the right medial frontal area. The current study aimed to reduce the working memory load and focus on the effect of translation. Using this design, only the left inferior frontal area showed activation differences between languages.

Inferior frontal activation observed in the present study could be associated with the process of translating L2 auditory verbal numbers into L1, which occurs before calculation takes place. The postscan survey conducted with participants in the current study indicated that all participants “translated” before carrying out mental addition. Differences between exact calculation in L2 versus L1 requires the additional process of translating L2 verbal numbers into L1, and therefore, the activation differences observed between languages in the left inferior frontal area might be associated with the translation process. Neuroimaging studies have also shown that translation at the sentence level involves the left IFG along with activity in the subcortical structures and the left basal ganglia (Klein et al. 1995; Lehtonen et al. 2005). Frontal activation level has also been associated with proficiency level in L2. Chee et al. (2001) reported increased levels of activation in the left inferior frontal area in bilinguals with low L2 proficiency compared with high proficiency. In a recent study, the BOLD response in the left IFG was found to correlate negatively with proficiency level of L2 (Klein et al. 2006).

In the present study, the significant activation differences between languages found in exact addition in the left inferior frontal region (from the [EE > CE] contrast) overlapped with that found from the interaction effect LANGUAGE × TASK of ANOVA. However, no significant main effect of LANGUAGE or TASK was found in these same voxels. Therefore, the left inferior frontal area appears to be the area that shows activation patterns as predicted; that is, a significantly higher level of activation in L2 compared with L1 in exact addition but not in approximate addition.

Activation Differences between Tasks

The exact and approximate addition tasks used in the present study involve similar cognitive processes. The only difference is the carrying operation in exact addition, in contrast to the rounding up/down process in approximate addition. Exact addition, compared with approximate addition, did not show significantly higher activation levels in either L1 or L2 in any brain region. Instead, significantly higher levels of activation were observed in approximate addition, compared with exact addition, in both L1 and L2 in several brain regions, including the left inferior frontal, middle frontal, and inferior parietal regions. These results imply that the carrying operation might be associated with activation in the same regions as the other common arithmetic operations, such as retrieving simple addition facts. Despite higher performance accuracy in approximate addition, the additional operation of rounding up/down in approximate addition appeared to give subjects a higher cognitive load and require more neural resources than the carrying operation in exact addition.

Of particular interest is the higher activation levels observed in the L1 approximate than exact addition in the left inferior parietal area, whereas no significant activation differences were observed in this same area between exact versus approximate addition in L2. This activation difference observed between tasks in the left inferior parietal area in the present study could be associated with the additional rounding process required in approximate addition. Activation in the inferior parietal region is close to the intraparietal sulcus, where activation differences between approximate versus exact addition was reported in previous studies using single-digit numbers (Dehaene et al. 1999; Stanescu-Cosson et al. 2000; Lemer et al. 2003).

Performance-Related Activation

Significant correlations between behavioral performance and brain activity could reflect activation associated with the specific task at hand as well as with general performance monitoring. Activation associated with general performance monitoring would be observed whether the specific task at hand requires language, numerical, or spatial information processing. To obtain the brain regions that are directly related to the addition tasks per se rather than brain regions that are related to general performance monitoring or error-related responses, an “and” operation was performed between the results obtained from the correlation analyses and task-related analyses. Thus, from our performance-related activation analysis, we obtained brain regions that show performance-related activation specific to mental addition.

We note also that when using a block design, it is possible that error-related activation contributes to the overall fMRI activation we observed, though errors were few in our task. Two recent fMRI studies used algebraic equations and algorithms to investigate error-related activation during mathematical processing (Ravizza et al. 2008; Anderson et al. 2011). Anderson et al. (2011) found an interaction effect between accuracy (correct vs. error) and response period (before vs. after response). Comparing error versus correct problems during the calculation period, Ravizza et al. (2008) reported increased activation in the left lateral prefrontal area during the calculation period when problems were correctly solved compared with when errors were made. However, when summing activities before and after the response period, Ravizza et al. (2008) found no significant differences between error and correct trials. With a block-design analysis, the overall fMRI activation we observed in the [EE + EA] > Ebaseline contrast could be associated with error-related as well as calculation-related processes.

For L2 addition tasks ([EE + EA] > Ebaseline), significant negative correlations were observed in the left inferior parietal regions, whereas no significant correlations were obtained in L1 addition. This left inferior parietal region was found to show significant negative correlations using both the leave-one-subject-out and the leave-one-run-out cross-validation approaches. These results suggest that individuals who show a higher percent accuracy in L2 addition tasks tend also to show lower activation in the left inferior parietal regions. Because the significant activation observed in the left inferior parietal areas from performance-related analysis overlapped with the task-related activation, we speculate that the correlations observed in the parietal areas are more likely to reflect cognitive processes that are supporting mental addition in L2 rather than simply performance monitoring. Given the mental arithmetic tasks used in the current study, a negative correlation found in the inferior parietal areas could be associated with verbal language and arithmetic-related processes (Dehaene et al. 2004) that are supporting mental arithmetic in L2.

In the present study, significant negative correlations observed in the left inferior parietal area overlapped with the common activation obtained from CE, CA, EE, and EA. In the left inferior parietal area, higher behavioral performance (reflected by higher percent accuracy scores measured inside the scanner) was associated with lower activation levels. Given that the common cognitive processes across tasks (i.e., CE, CA, EE, and EA) is calculation itself, we speculate that the significant negative activation observed in the left inferior parietal area might be associated with the calculation process. Interestingly, brain activation in this inferior parietal area did not correlate significantly with behavioral measures of L1 tasks ([CE + CA] > Cbaseline). A possible explanation is that when cognitive and neural resources for arithmetic processing are taxed by L2 individual differences emerge.

The 2-digit addition problems used in the present study, which require maintaining and updating of verbal numbers in working memory, suggest that the negative correlation observed between the BOLD responses reflect more efficient use of neural and general cognitive resources in subjects with higher performance levels in L2 addition. In the domain of speech processing, electromagnetic measures also showed wider and longer activation in a nonnative compared with native language task (Zhang et al. 2005). After 12 training sessions on an L2 phonetic contrast, less extended and shorter duration of brain responses to the L2 phonetic contrast were found compared with before training (Zhang et al. 2009). Similarly, in a training study of arithmetic with adult subjects, decreased frontal activation was observed after short-term training on a set of 18 complex multiplication (2-digit times 1-digit) problems (Delazer et al. 2003). During the fMRI scans after training, less-practiced and untrained problems were found to require higher levels of left inferior frontal activation relative to trained problems. A shift of activation from the frontal to the parietal region is taken as improvement and development of automaticity in arithmetic processing based on training (Delazer et al. 2003; Ansari et al. 2005; Rivera et al. 2005). Taken together, negative correlations observed between left inferior parietal activation and behavioral performance in L2 addition in the present study might reflect additional neural resources and increased effort required for arithmetic processes in bilinguals with poorer performance when compared with bilinguals who showed better performance during mental addition tasks in the less proficient language (L2).

In conclusion, our study showed that 1) the frontoparietal regions involved during multidigit addition when problems were given auditorily produced a similar pattern of activation observed in previous studies using single-digit addition. Also, activation in the frontoparietal regions observed when problems were presented in bilinguals' less preferred language (L2) overlapped largely with areas that were involved when problems were given in the preferred language (L1). This result indicates that L2 mental calculation might rely on similar brain areas as L1. 2) Regarding activation differences between languages, higher activation levels were observed in L2 than in L1 in the left inferior frontal areas in exact addition, which might reflect an extra load on language processing during mental addition in L2, such as translation of numbers from L2 into L1. This is consistent with the Triple Code Model in that once L2 numbers are translated into L1, the retrieval and calculation processes are similar to that in L1. 3) Comparing activation differences between tasks, approximate addition in L1 showed stronger levels of activation than exact addition in the left inferior parietal region, possibly reflecting the additional process of rounding up/down. Finally, 4) our performance-related analysis showed significant negative correlations between the fMRI BOLD responses and behavioral performance in L2 in the left inferior parietal regions. Negative correlations observed in these regions might be associated with arithmetic-related processes because correlation in the left inferior parietal region overlapped with common activation across tasks. Higher behavioral performance scores were associated with lower levels of fMRI BOLD responses, suggesting that better performance in L2 addition tasks might be associated with more efficient use of cognitive and neural resources.

Supplementary Material

Supplementary material can be found at: http://www.cercor.oxfordjournals.org/

Funding

National Science Foundation Science of Learning Center grant to the University of Washington's LIFE Center (SBE-0354453 to P.K.K., Principal Investigator.