Chemical physics of protein folding

Protein molecules generally fold into precise three-dimensional shapes. While of direct interest to biochemists, the question of how folding occurs has attracted the interest of a much broader audience of scientists ranging from the traditional chemical scientists to computer scientists and physicists. Also changing over time has been the very meaning of the question of protein folding. To the descriptive scientist it may be sufficient to assert that folding occurs on a time scale no slower than protein biosynthesis, and that the information required to find the precise three-dimensional shape is contained in the one-dimensional sequence. Although exceptions to these generalizations recently have begun to emerge; in the study of prion-associated diseases (1), they have sufficient generality to allow us to treat the folding process as a black box for transcribing one-dimensional information into three-dimensional structures. It is, however, necessary to probe deeper into the mechanism if the prediction of protein structure from sequence and the design of truly novel protein-like molecules are to be achieved. These goals are of great practical significance in biology and medicine. The question of the mechanism of folding was once thought to be entirely analogous to the question of mechanism in intermediary metabolism or classical organic chemistry. In those problems the small number of participating species and the relatively specific routes by which they interconvert owing to the large scale of covalent energy barriers compared with thermal energies means that a small number of fairly discrete chemical steps can be isolated. This is the classic notion of a protein folding pathway with a series of discrete intermediates. Such discrete intermediates do occur in the late stages of protein folding, and to a great extent, the chemical kinetic details of these interconversions have been catalogued (2). However, to answer the practical questions of structure prediction and design, one must go a considerable distance beyond this phenomenology—a new viewpoint on folding is required.

This new viewpoint is that of the chemical physicists rather than the classical chemists (3). The chemical physics view brings the problem in much closer connection to the underlying forces and the underlying microscopic events. This view has required a new set of theoretical ideas, computational techniques, and major advances in experimental methodology.

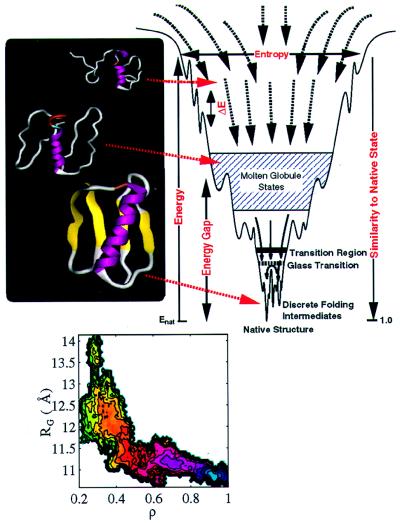
Energy landscape theory provides the theoretical framework, asserting that a full understanding of the folding process requires a global overview of the landscape. The folding landscape of a protein resembles a partially rough funnel riddled with traps where the protein can transiently reside (Fig. 1). There is no unique pathway but a multiplicity of convergent folding routes toward the native state (3–7). Although we focus on developments from our groups in this paper, several other groups have participated in developing this new view.

Figure 1.

The energy landscape for a folding protein. The major phenomonological parameters needed to capture this landscape include: the width of the funnel at small values of native similarity, indicating the entropy of denatured states; the roughness of the landscape, ΔE, which is related to the glass transition temperature, T_g; the stability of the native state relative to the collapsed but non-native (molten) globule states, the energy gap. The ribbon diagrams of the α/β protein, segment B1 of streptococcal protein G (GB1) provide structures from ensembles of unfolded, molten globule, and native conformations. The folding landscape for GB1 is projected onto two coordinates, the radius of gyration, R_g, of the folding globule, and the fraction of native contacts, ρ, which indicates how close the folding protein is to the native. The free energy change as folding occurs is shown as a contoured surface: (native) state corresponds to the blue region and the most unfavorable unfolded state is represented by the green contours.

The importance of a funnel landscape can be seen by contrasting random heteropolymeric molecules and proteins. Random heteropolymers have an underlying driving force to collapse but do not adopt well-defined three-dimensional structures because of the conflict or frustration of different interaction energies. Instead, they exist in an ensemble of dissimilar low-energy structures and move among this multitude of states, jumping over barriers between adjacent minima, giving multiexponential kinetics. Proteins, on the other hand, have a single manifold of structurally similar collapsed low-energy structures. When the slope toward the native state is dominant over the ruggedness of the landscape, folding kinetics is exponential and fast. The essence of the funnel landscape idea is competition between the tendency toward the folded state and trapping because of ruggedness. This competition is measured by the ratio between the folding temperature (T_f) and the glass temperature (T_g). Good folding sequences fold rapidly on minimally frustrated landscapes with large values of T_f/T_g (3, 5, 7).

Minimally frustrated sequences not only fold fast at relevant temperatures but are robust folders, only weakly dependent on minor variations of the folding environment or to mutations. Robustness is essential for biology. Minor variations in pH, temperature, or mutations will affect the native configuration by favoring other low-energy structures, which in a funnel-like landscape are very similar to the original one. Energy landscape theory suggests a diversity of folding scenarios that has been observed by computer simulations of minimalist models (see, for example, references in refs. 3, 8, 11, and 15–18) allowing connections to studies of real proteins (19, 20).

A deeper understanding of how the landscape relates to particular properties of a protein’s sequence or final folded topology requires detailed molecular calculations. Such calculations often use explicit atomic level models of the protein and surrounding solvent together with molecular dynamics and biased sampling methods to map the free energy landscape onto coordinates describing folding progress (21). These permit detailed atomic information about folding to be related to experimentally measurable quantities. Atomistic studies may be compared with general predictions of landscape theories.

In Fig. 1 we display the folding free energy profile for the α/β protein GB1 under conditions strongly favoring the native state (22). Folding of this protein is dominated by an initial collapse without significant formation of native interactions, followed by folding toward the native without significant change in size. This behavior contrasts with the mechanism seen for some small helical proteins that are even less frustrated (14, 23). These fold with commensurate reduction in size and gain in tertiary interactions. Thus, two apparently different mechanisms are used by proteins that differ in their final folded topology. Such behavior can be mimicked with minimalist lattice models by changing the balance of native and non-native (hydrophobic) attractive interactions (24).

Also directly connected to phenomenological models of folding is the distribution of stabilizing native interactions in the transition region of folding (20). For helical proteins (at 300 K), this is rather broad centering around 50% occupation of the native contacts. The interactions that stabilize the protein at this point in folding are distributed throughout the structure. For the α/β protein GB1, this distribution is more bimodal, with a larger number of native interactions formed with the highest and lowest probabilities compared to those that occur with 50% probability.

Simulations with detailed atomic models are extremely intensive numerically. The number and size of systems that can be studied is limited. Therefore, it is difficult for such simulations to provide a general view of folding dynamics. Here an intermediate level of model is sought giving the ability to directly simulate the folding process and broadly explore the connections between thermodynamics and kinetics (9, 18, 25–27).

Experiments also have been devised to explore the landscape. Methods such as dynamic NMR, protein engineering, laser initiated folding, and ultrafast mixing are being used (28–30). During the past 5 years it has become possible to study “burst phase kinetics,” which cannot be resolved within the dead time of conventional stopped-flow experiments. In some cases, e.g. apomyoglobin, substantial secondary structure and nativelike tertiary contacts are observed to have already formed. Such burst phases could represent kinetics with a small or negligible activation barrier. Even in the case where kinetics is limited by activation, much structure formation occurs by the subsequent downhill dynamics to the native state. These must be studied via fast folding experiments.

One experiment uses cold denaturation in supercooled water to prepare unfolded proteins (30). An infrared laser pulse then jumps the temperature by directly heating water 10–30° in 10 ns, placing the unfolded chain in an environment conducive to folding. The refolding is monitored by a series of UV pulses spaced 14 ns apart. The UV light excites tryptophan fluorescence, for which specific quenching mechanisms are introduced to serve as structural markers. Experiments on horse apomyoglobin show that the cold denatured state has some residual structure in the GH helices and loop; the N terminal A helix is largely destabilized at low temperature. The fast refolding experiment indicates that formation of the AGH core of apomyoglobin is an extremely efficient process (30). Refolding of phosphoglycerate kinase, a 415-residue two-domain enzyme, displays multiscale kinetics on a time scale from 10 to 6,000 microseconds, indicating the roughness of the free energy landscape. Experiments are beginning to build up a phase diagram of folding kinetics that can be used to test and refine theoretical models.