THE IMPACT OF PLACE AND TIME ON THE PROPORTION OF LATE-STAGE DIAGNOSIS: THE CASE OF PROSTATE CANCER IN FLORIDA, 1981–2007

Abstract

A suite of techniques is introduced for the exploratory spatial data analysis of geographical disparities in time series of health outcomes, including 3D display in a combined time and geography space, binomial kriging for noise filtering, space-time boundary analysis to detect significant differences between adjacent geographical units, and spatially-weighted cluster analysis to group units with similar temporal trends. The approach is used to explore how time series of annual county-level proportions of late-stage prostate cancer diagnosis differ across Florida. The state-average proportion of late-stage diagnosis decreased 50% since 1981. This drop started in the early 1990s when prostate-specific antigen (PSA) test became widely available and several parts of Florida underwent fast urbanization. Boundary analysis revealed geographical disparities in the impact of the screening procedure, in particular as it began available. The gap among counties is narrowing with time, except for the Big Bend region where the decline is much slower.

1. Introduction

Interpretation of cancer incidence and mortality rates in a defined population requires an understanding of multiple complex factors that likely change through time and space, and interact with the different types and scales of places where people live. These factors include the prevalence of risk factors in the population, changes in the use of medical interventions to screen and treat the disease, and changes in how data are collected and reported. Analyzing temporal trends in cancer incidence and mortality rates can provide a more comprehensive picture of the burden of the disease and generate new insights about the impact of various interventions (Potosky et al., 2001). The analysis of temporal trends outside a spatial framework is however unsatisfactory, since it has long been recognized that there is significant variation among U.S. counties and states with regard to the incidence of cancer (Cooper et al., 2001). Visualizing, analyzing and interpreting these geographical disparities should bring important information and knowledge that will benefit substantially cancer epidemiology, control and surveillance.

Despite the significant work accomplished in health data visualization and analysis this last decade, spatial and temporal data are still displayed in separate views and so one does not capitalize on the human visual processing engine to extract knowledge from the spatial interconnectedness of information over time and geography. For example, Geographic Information System (GIS) products, such as GeoDA (Anselin et al., 2006) or ESRI ArcView, show events in the single dimension of space on a map. In each case, only a thin slice of a multidimensional picture is represented. Recently Goovaerts (2010a) proposed the use of time as a third dimension to display time series of cancer mortality and incidence data. The 3D view of time series of health outcome maps makes it easier to comprehend spatiotemporal relationships because there is no disconnect between the temporal and spatial dimensions as opposed to a combination of 2D map and linked time line plots or an animation.

During the analysis of large space–time–attribute datasets, users may have difficulty perceiving, tracking and comprehending numerous visual elements that change simultaneously both in space and time, such as yearly time series for 67 counties in Florida. A common solution adopted in the spatial domain is to group or cluster geographical units with similar properties (Guo, 2008). Including additional information, such as the geographical locations of observations, in the classification creates clusters that are spatially compact and more easily interpretable. One popular approach in soil sciences is spatially weighted classification that is based on a dissimilarity matrix that accounts for distances in both the attribute and geographical spaces (Caeiro et al., 2003; Simbahan and Dobermann, 2006). This approach has however been applied mainly to stratify isopleth maps of interpolated values and it has always been used outside a temporal framework. In this paper, we introduce a dissimilarity measure to assess differences between time series of health outcomes in both the geographical and attribute spaces. To account for the instability of rates recorded in sparsely populated counties (small number problem), the dissimilarity measure is computed after noise-filtering using binomial kriging (Goovaerts, 2009b). This approach is similar to the practice of computing local Moran’s I on rates that are first noise-filtered using empirical Bayes smoothers (Anselin et al., 2006).

A natural complement to the clustering of geographical units is provided by boundary analysis since the edge of a cluster necessarily implies a boundary (Jacquez et al., 2008). Yet, boundary detection allows a finer analysis than cluster detection because only two entities are considered at a time, leading to the detection of significant changes or edges that might go undetected when neighboring rates are averaged. In recent years, substantial insights and benefits have accrued by using geographic boundary analysis to study spatial patterns of cancer health outcomes. The identification of zones of rapid change has allowed researchers to focus scientific and epidemiological inquiry on those areas where mortality and/or incidence are changing rapidly, and to then evaluate whether these transition zones tend to occur near boundaries in putative environmental exposures (Jacquez and Greiling, 2003). The application of boundary analysis to space-time health data poses however two challenges: 1) the need to account for the instability of rates recorded in sparsely populated counties, and 2) the incorporation of the time dimension in this intrinsically spatial technique. These two aspects are here tackled by the repetition across time of the geostatistical boundary analysis introduced by Goovaerts (2010b).

Prostate cancer is the most frequently diagnosed non-skin cancer and the second leading cause of male cancer-related death in the US. Prostate cancer mortality and late–stage diagnosis started declining after 1991 (Smart, 1997; Chu et al, 2002). According to some studies, this decline in mortality is due to early detection (prostate-specific antigen (PSA) screening) although screening for prostate cancer is still controversial (Farkas et al, 1998; McDougall et al, 2000; Coldman et al, 2003; Shaw et al., 2004). Other studies showed that men who are diagnosed with and treated aggressively for localized prostate cancer have higher survival rates compared to men diagnosed with advanced-stage cancer (Wong et al, 2006). Although prostate cancer-related incidence and mortality have declined recently, striking geographical and racial/ethnic differences in incidence and mortality persist in the United States. For example Jemal et al (2005) showed that non-metro counties generally had higher death rates and incidence of late-stage disease and lower prevalence of PSA screening (53%) than metro areas (58%), despite lower overall incidence rates. Their analysis was however conducted for a single time period (1995–2000) and based on State-level data.

This paper explores how the county-level proportions of prostate cancer diagnosed late among patients 65 years and older changed yearly over the period 1981–2007 in Florida. This exploratory spatial data analysis of aggregated data is a preliminary step toward the quantification of the relative contribution of contextual (neighborhood-level) and compositional (individual-level) factors through multi-level regression. The approach rely on techniques that are either new or were recently introduced in the field of health geostatistics and medical geography (Goovaerts, 2009a). Although a county-level analysis might seem rather crude and limits the interpretation of results because of potentially wide heterogeneity within a county, the present study represents a substantial improvement over most analyses of temporal trends which are usually aspatial and conducted at the National level or for a single cancer registry. In addition, county-level analysis allowed the use of a fine temporal resolution (i.e. year) which would not be possible for finer spatial resolutions because of rate instability caused by the small number problem.

2. Data and Methods

Number of cases of prostate cancer and associated stage at diagnosis recorded yearly from 1981 through 2007 for non-Hispanic white males within each county of Florida were downloaded from the Florida Cancer Data System website. Proportions of late-stage diagnosis were computed for each year and county using only cases 65 years and over to minimize the impact of disparities in age distribution across Florida and attenuate the impact of variability in health coverage since all cases are covered by Medicare. One potential problem associated with the analysis of time series of areal data is temporal changes in the definition of administrative units used to report the results. This was not the case in the present study since no county has been deleted or created in Florida since 1925. In addition, out of the 144 boundaries that exist between adjacent Florida counties, only four slightly changed between 1981 and 2007. Two of these changes consisted in a shift of the boundary over water bodies (e.g. from the east bank to the middle of a river), so without any impact on the county population.

The rates of late-stage diagnosis were processed using binomial kriging (Goovaerts, 2009b) to filter the noise caused by the small number problem. Geographical and temporal changes were visualized using three-dimensional space-time displays (Goovaerts, 2010a) of the data. A boundary analysis (Goovaerts, 2010b) was conducted to detect county boundaries where significant changes in rates of late-stage diagnosis occur. Finally, counties that have similar temporal trends of late-stage incidence rates were grouped using a hierarchical cluster analysis (Ward’s minimum-variance method in SAS) that was spatially weighted. Following Jemal et al. (2005), results were interpreted on the basis of the US Department of Agriculture Rural-Urban Continuum Codes (USDA, 2004) described in Table 1. This nine-part county codification distinguishes metropolitan (metro) counties by the population size of their metro area, and non-metropolitan (non-metro) counties by degree of urbanization and adjacency to a metro area or areas. This information was available for 1983, 1993 and 2003. For 1983 and 1993 codes 0 and 1 were combined to make these classifications comparable to the 2003’s codification. These codes were linearly interpolated over the periods 1983–1993 and 1993–2003 to explore relationships between yearly health outcomes and urbanization.

Table 1.

Definition of 2003 Rural-Urban Continuum Codes (From http://www.ers.usda.gov/data/RuralUrbanContinuumCodes/).

Code	Description
Metro counties
1	Counties in metro areas of 1 million population or more
2	Counties in metro areas of 250,000 to 1 million population
3	Counties in metro areas of fewer than 250,000 population
Non-metro counties
4	Urban population of 20,000 or more, adjacent to a metro area
5	Urban population of 20,000 or more, not adjacent to a metro area
6	Urban population of 2,500 to 19,999, adjacent to a metro area
7	Urban population of 2,500 to 19,999, not adjacent to a metro area
8	Completely rural or less than 2,500 urban population, adjacent to a metro area
9	Completely rural or less than 2,500 urban population, not adjacent to a metro area

The geostatistical filtering was conducted using the commercial software SpaceStat (BioMedware Inc, 2011), while the clustering analysis was performed using the SAS procedures DISTANCE and CLUSTER. Three-dimensional displays were created using SGeMS, the Stanford Geostatistical Modeling Software (Remy et al., 2008), 3D visualization panel and FORTRAN programs developed to format the data. Similarly, the boundary analysis was conducted using the first author’s programs.

2.1. Binomial kriging

For a given number N of geographical units v_α (i.e. counties here), denote the observed proportion or rate of late-stage diagnosis as z(v_α)=d(v_α)/n(v_α), where d(v_α) is the number of late-stage cases and n(v_α) is the total number of cases. Mapping the rates z(v_α) might lead to misleading conclusions since in sparsely populated counties the number of prostate cancer cases recorded in a single year can be too small to compute reliable estimates of late-stage diagnosis rates. Smoothing methods have been developed to improve the reliability of observed rates by borrowing information from neighboring entities. These methods range from simple deterministic techniques (Wang et al., 2008) to sophisticated full Bayesian models (Mather et al., 2006). Geostatistics provides a model-based approach with intermediate difficulty in terms of implementation and computer requirements. The noise-filtered rate for a given area v_α is estimated as a linear combination of the kernel rate z(v_α) and the rates observed in (K-1) neighboring entities v_i:

$$\widehat{r}(v_{\alpha })=\sum _{i=1}^K{\lambda }_{i}z(v_i)$$ (1)

The weights λ_i assigned to the K rates are computed by solving the following system of linear equations; known as “binomial kriging” system (Webster et al., 1994; Goovaerts, 2009b):

$$\begin{array}{l}\sum _{j=1}^K{\lambda }_j\left[\overline{C}(v_i,v_j)+{\delta }_{ij}\frac{a}{n(v_i)}\right]+\mu (v_{\alpha })=\overline{C}(v_i,v_{\alpha })\text{i}=1,\dots ,K\\ \sum _{j=1}^K{\lambda }_j=1.\end{array}$$ (2)

where δ_ij=1 if i=j and 0 otherwise, a= m*(1 − m*)− C̄(v_i, v_i), and m* is the population-weighted average of the N rates. The addition of the error variance term, a/n(v_i), for a zero distance accounts for variability arising from population size, leading to smaller weights for less reliable late-stage rates based on fewer cases. The term μ(v_α) is a Lagrange parameter that results from the minimization of the estimation variance subject to the unbiasedness constraint on the estimator.

The area-to-area covariance terms C̄(v_i, v_j) = Cov{Z(v_i),Z(v_j)} and C̄(v_i, v_α) are numerically approximated by averaging the point-support covariance C(h) computed between any two locations discretizing the areas v_i and v_j. The point-support covariance C(h), or equivalently the point-support semivariogram γ(h), cannot be estimated directly from the observed rates, since only areal data are available. Thus, only the regularized semivariogram can be estimated using the following population-weighted estimator (Goovaerts, 2005):

$$\widehat{\gamma }(\mathbf{h})=\frac{1}{2{\displaystyle \sum _{\alpha ,\beta }^{N(\mathbf{h})}}n(v_{\alpha })n(v_{\beta })}\sum _{\alpha ,\beta }^{n(\mathbf{h})}\left\{n(v_{\alpha })n(v_{\beta }){\left[z(v_{\alpha })-z(v_{\beta })\right]}^2\right\}$$ (3)

where N(h) is the number of pairs of areas (v_α, v_β) whose population-weighted centroids are separated by the vector h. The different spatial increments [z(v_α)−z(v_β)]² are weighted by the product of their respective population sizes to assign more importance to the more reliable data pairs. Derivation of a point-support semivariogram from the experimental semivariogram γ̂(h) computed from areal data is called “deconvolution”, an operation that is conducted using an iterative procedure (Goovaerts, 2008a).

2.2. Boundary analysis

The objective is to detect for every year any significant change between neighboring units which are here defined as Florida counties sharing a common border or vertex (1-st order queen adjacencies). The dissimilarity between rates measured in any two adjacent entities v_α and v_β was quantified as half their absolute difference:

$${\mathrm{\Delta }}_{\alpha \beta }=\frac{\left|z(v_{\alpha })-z(v_{\beta })\right|}{2}$$ (4)

A change is declared significant either if z(v_α) is sufficiently greater than z(v_β) or if z(v_α) is sufficiently less than z(v_β), which amounts at testing whether the statistic Δ_αβ is significantly different from zero. In order to test the null hypothesis H₀ (Δ_αβ =0), one needs to compare the observed boundary statistic to its expected distribution under H₀, which allows the computation of the probability (p-value) of obtaining a result as extreme as the test statistic by chance alone when H₀ is true.

Following an approach detailed in a previous issue of this journal (Goovaerts, 2010b), the reference distribution was obtained by conducting the boundary analysis on 999 realizations of proportions of late-stage cancer diagnosis generated by the sampling of binomial distributions (one for each county) using a set of spatially autocorrelated probabilities (p-field). Each binomial distribution is characterized by two parameters: population-weighted average of rates across the edge (i.e. the null hypothesis is that the risk does not change across the county border) and population size of each county. This so-called “neutral model of type IV” accounts for the fact that rates in adjacent counties are usually spatially correlated and less reliable for sparsely populated counties.

Since each county typically consists of multiple edges, boundary analysis greatly increases the number of tests relative to the other types of analysis (e.g. cluster detection) conducted in the health literature. In the present application, the test will be repeated for each of the J=144 edges, increasing the likelihood that some tests will turn out significant by chance alone (i.e. false positives), even if the null hypothesis of no change is true in all cases. Multiple testing corrections reduce the significance level applied to each test so that the overall false positive rate is kept to less than or equal to the user-specified significance level α. We used the false discovery rate (FDR) approach which was proven to be less restrictive and more powerful than other approaches, such as the simple Bonferroni correction (Castro and Singer, 2006). The first step is to rank all J p-values by ascending order (smallest p-value has rank 1) and apply a correction that increases as the rank r of the p-value decreases, i.e. the multiplication factor is r/J. The decision rule is however sequential and involves checking that the p-value of rank r does not exceed the adjusted significance level, starting with the largest p-value (r=J). Once this condition has been met for a given rank r′, the adjusted significance level α_FDR is set to r′α/J and applied to all tests of hypothesis.

2.3 Spatially weighted cluster analysis

The objective is to group counties v_α that display similar temporal trends in proportion of late-stage diagnosis and are close geographically. A common approach is to apply a clustering algorithm (e.g. complete linkage, kth-Nearest-Neighbor) to a matrix of dissimilarities d_αβ that quantifies the difference between any two pair of geographical units v_α and v_β. We here used the Ward’s minimum variance hierarchical method that is one of the most frequently used (Milligan, 1981) and has been shown to give the best recovery of cluster structure. This iterative algorithm aims to minimize the total within-cluster variance. It starts by identifying each observation with a single cluster, then clusters are merged so as to minimize the increase in the error sum of squares.

Dissimilarity in attribute space is generally measured by metrics such as Euclidean or Mahalanobis distance. In the present study, the following squared Euclidian distance e_αβ that accumulates over T years the differences between noise-filtered rates recorded in any two counties was computed:

$$e_{\alpha \beta }=\sum _{t=1}^T{\left[\widehat{r}(v_{\alpha };t)-\widehat{r}(v_{\beta };t)\right]}^2$$ (5)

where r̂(v_α; t) is the rate recorded for geographical unit v_α at year t after filtering using binomial kriging. Although the uncertainty attached to the kriging estimates r̂(v_α; t) is ignored in the computation of the dissimilarity metric (5), simulation studies (Goovaerts, 2008b) have demonstrated that quantity [r̂(v_α; t)− r̂(v_β; t)] provides a more accurate assessment of differences between underlying risks relative to differences computed on the basis of local empirical Bayes smoothers or even simulated values. The measure is thus accurate enough to aggregate geographical units during an exploratory phase.

To increase the spatial continuity of the clusters formed, the dissimilarity measure (5) was weighted by a function of the geographic separation between the two geographical units, as measured by the Euclidian distance h_αβ between their respective centroids. By analogy with the approach developed by Oliver and Webster (1989), the following weighting scheme was developed:

$$d_{\alpha \beta }=\frac{e_{\alpha \beta }}{e_{max}}\times \frac{\gamma \left(h_{\alpha \beta }\right)}{\mathit{Sill}}$$ (6)

where e_max is the maximum value taken by the squared Euclidian distance, and Sill is the sill of the semivariogram model γ(.) that was fitted to the population-weighted semivariogram (Eq. (3)) computed from late-stage diagnosis rates aggregated over the 27 year period. The rescaling of both the Euclidian and the variogram distances ensures that the maximum dissimilarity in both the attribute and geographical spaces is one. The new metric d_αβ tends to enhance the dissimilarity between counties that are geographically distant from one another, which increases the likelihood of joining neighboring counties. The use of kriging estimates in the metric (5) also helps creating spatially compact clusters because of the smoothing effect of kriging. In absence of any spatial correlation (pure nugget effect), the semivariogram value will be constant for any separation distance: γ(h) = Sill ∀ h, and measure d_αβ will identify the distance in the attribute space.

3. Results and Discussion

3.1 Visualization of space-time trends

Fig. 1 shows how the total number of cases and proportion of late-stage diagnosis for white males changed with time according to the patient age. For all statistics, results were averaged over Florida and 3-year time windows to increase stability. Both age categories display opposite patterns for the total number of diagnosed cases: the number of cases 65 years and older has strongly declined since the early nineties while the number of younger cases kept increasing during the same period (Fig. 1A). Therefore, the percentage of prostate cancer cases 65 years and over, which peaked at 87.6% in 1989, was only 67.5% in 2006.

Fig. 1.

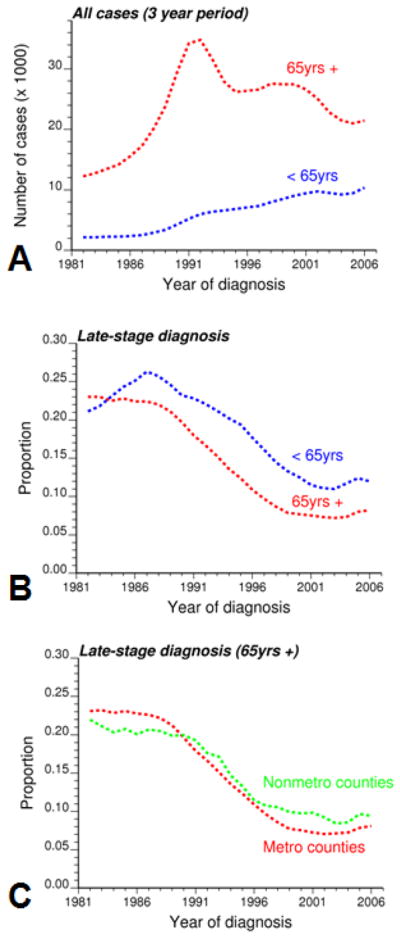
Evolution of the number of white males (total and proportion of late-stage diagnosis) diagnosed with prostate cancer annually over the period 1981–2007 for the entire state of Florida. Results, which are averaged over a 3-year window to reduce random fluctuations, are presented for cases younger or older than 65 years, as well as for metro and non-metro counties (cases older than 65 years).

Both age categories share a similar trend for the proportion of late-stage diagnosis over the period 1981–2007: substantial decline between 1990 and 2000, followed by a plateau and a slight increase in the most recent years (Fig. 1B). For example, the percentage for cases 65 years and older decreased from 22.96% in 1982 to a minimum of 7.22% in 2003 and slightly increased since then. Yet, diagnosis at younger ages tends to occur at a later stage and this age disparity has widened with time. In 1990, patients younger than 65 years were 18% more likely to be diagnosed late than older individuals (0.232/0.197=1.18). The odd ratio was 1.46 in 2006 (0.120/0.082).

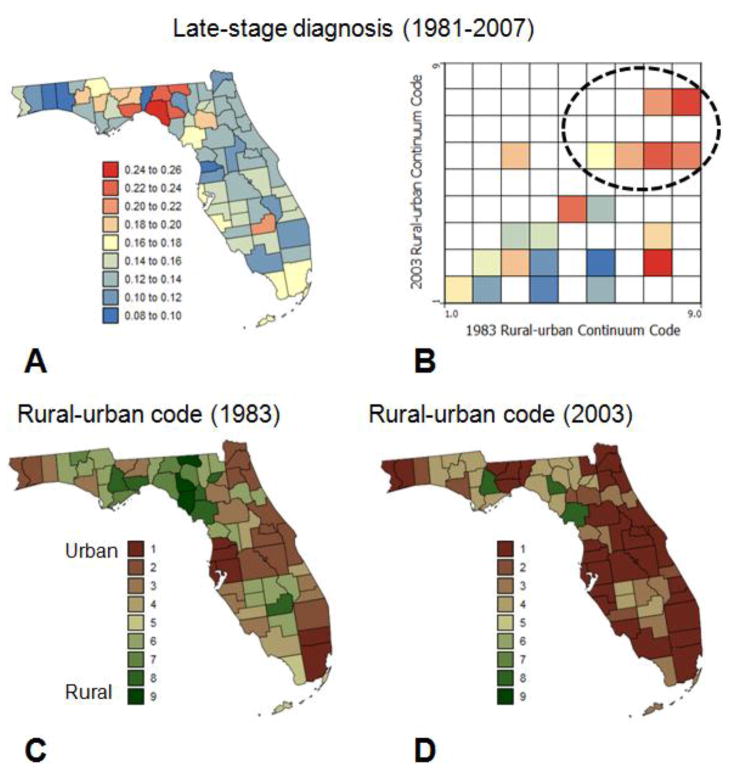
Although differences between age categories are worth studying, the focus of this paper is on patients 65 years and over. The pattern of the stadewide proportion of late-stage diagnosis encompasses significant geographical disparities among counties, as illustrated by the time-averaged map of Fig. 2A. On average over the period 1981–2007, the proportion of late-stage diagnosis was higher in the Big Bend region, as well as in Alachua County (Gainesville) and Glades County (Fig. 2A). Results for Glades County are, however, based on only 92 cases and are not very reliable. This spatial pattern reflects to a large extent the spatial distribution of county-level degree of urbanization and population density as captured by the USDA county Rural-Urban Continuum Codes (Figs. 2C&D). The association between proportion of late-stage diagnosis and residence in non-metro areas was explored using the three-way contingency table introduced in Goovaerts (2010c). The two covariates in the frequency table of Fig. 2B are the Rural-Urban Continuum Codes for 1983 and 2003. Based on these codes the 67 counties were assigned to one of the 9×9 classes and the corresponding proportion of late-stage diagnosis was computed. Many classes are empty and the degree of urbanization of most counties increased since 1983 (i.e. lower rural urban-code in 2003). The only county that showed a decrease in urbanization over that time period (i.e. non-empty class above the diagonal in the frequency table) is Bradford County. Clearly, more cases were diagnosed at later stages in non-metro counties that remained completely rural or with urban population less than 19,999 (classes 6 through 9).

Fig. 2.

Proportions of late-stage cases (white males older than 65 years) that were diagnosed over the period 1981–2007 within each county (A), and each combination of 1983 and 2003 rural-urban continuum codes (B). These rural-urban county codes are mapped in C and D.

The impact of urbanization on the proportion of late-stage diagnosis was analyzed at a finer temporal scale by grouping county-level time-series into non-metro and metro subsets based on whether their USDA Rural-Urban Continuum codes exceed 3 or not. In agreement with Jemal et al. (2004) metro areas had a smaller percentage of late-stage diagnosis than non-metro counties: 7.83% versus 9.64% in 2005 (Fig. 1C). Yet, this was not always the case and in the eighties late-stage diagnosis was more prevalent in metro areas: 23.1% versus 20.77% in 1985. Interestingly the two curves cross in the early 1990s when PSA became widely available, which might suggest that better access to health care in urbanized areas did not impact late-stage diagnosis until the introduction of the new screening procedure.

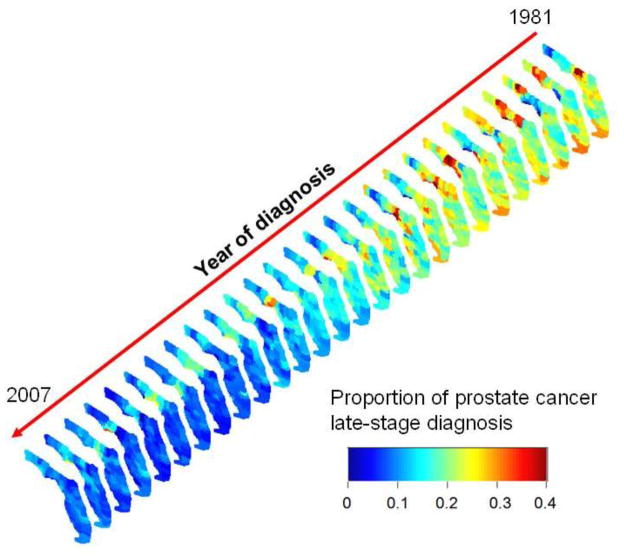
Except for the metro versus non-metro analysis of Fig. 1C, the spatial and temporal domains were visualized and studied separately so far. The three-dimensional representation of Fig. 3 allows the visualization of fluctuations at the highest resolutions in both space (county-level) and time (year). This display highlights in particular the Florida Panhandle where proportions were consistently high in the Big Bend region whereas they were much lower in the adjacent Tallahassee area. The trend is intermediate in Central and South Florida where late-stage diagnosis has been declining since the mid nineties. In Southern Florida, percentages appeared however to remain high for a longer time on the West coast relative to the East Coast.

Fig. 3.

Three-dimensional representation of yearly proportions of late-stage prostate cancer for white males 65 years and older. Rates were noise-filtered at the county level using binomial kriging. The same color scale is used for all the maps that were aligned along a time axis rotated so as to minimize slide overlaps and the resulting loss of information.

3.2 Space-time boundary analysis

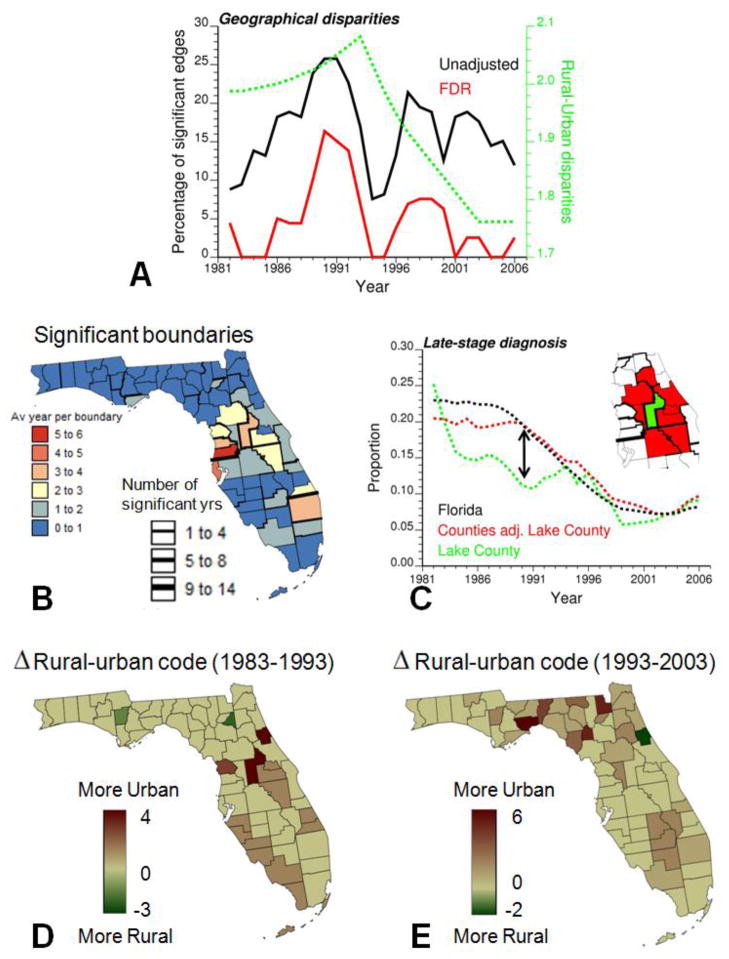
Proportions of late-stage diagnosis were first computed over a 3-year moving window to reduce random fluctuations, yielding for each county a times series spanning 1982 through 2006. Boundary analysis was then conducted on each of the 25 time periods using the absolute boundary statistic (rate difference) and the aforementioned Neutral model IV as randomization scheme. The percentage of the total number of 144 edges declared significant at α-level = 0.05 was computed every year before and after adjustment using the False Discovery Rate approach. Fig. 4A shows that the percentage of significant boundaries peaked in the early 1990s when PSA became widely available. This temporal trend, which is even more pronounced after multiple testing correction, suggests the existence of geographical disparities in the implementation and/or impact of the new screening procedure, in particular as it began available. The absolute boundary statistic was also computed on the USDA Rural-Urban Continuum codes, and interestingly the magnitude of the statistic follows a similar temporal trend with a peak in the early nineties (Fig. 4A, dashed curve). This result supports the prior hypothesis about possible interactions between urbanization and efficiency of PSA screening (Fig. 1C).

Fig. 4.

Results of the boundary analysis of proportion of late-stage diagnosis: (A) Annual percentage of boundaries that were declared significant before and after adjustment for multiple testing: this percentage peaked in the early 1990s when PSA became widely available and between-counties disparities in rural-urban continuum codes were the largest (dashed curve), (B) Location of significant boundaries: thickness of black lines is proportional to the number of years when the boundary was found significant after multiple testing correction, whereas the county color code indicates the average number of significant years per boundary for each county, (C) temporal trend of Lake County (green curve) that displayed the most significant differences with the trend of its adjacent counties (red curve) according to the space-time boundary analysis, and (D,E) maps of change in rural-urban continuum codes for Florida counties over the periods 1983–1993 and 1993–2003.

The geographical location of the most significant boundaries over the 27-year time period was derived by computing for each edge the number of years it was found significant. Boundaries that were significant at least once are depicted in black in Fig. 4B. The larger the thickness of the black segments the more years that edge tested statistically significant (up to 14 years). The background color is an index of dissimilarity between each county and its neighbours which was computed by adding up the number of significant years over all the county edges and dividing the total figure by the number of edges. The counties that differed the most frequently from their neighbours were mainly located in Central Florida, an area that underwent large urbanization in the eighties (Fig. 4D). The case of Lake County (isolated green polygon in Fig. 4C), located just North of Orlando area, is particularly striking. This county, which takes one of the largest values of the dissimilarity index, is also the county that experienced the largest drop in the urban-rural code between 1983 (code 4) and 1993 (code 1); see dark brown polygon in Fig. 4D. The time series for Lake County and the average of adjacent counties are compared in Fig. 4C. The urbanization of Lake County coincided with a decline in the proportion of late-stage diagnosis. Differences were the largest in 1989 and vanished in the nineties when the adjacent counties, in particular on the Eastern side, started getting more urban (Fig. 4E).

3.3 Spatially weighted cluster analysis

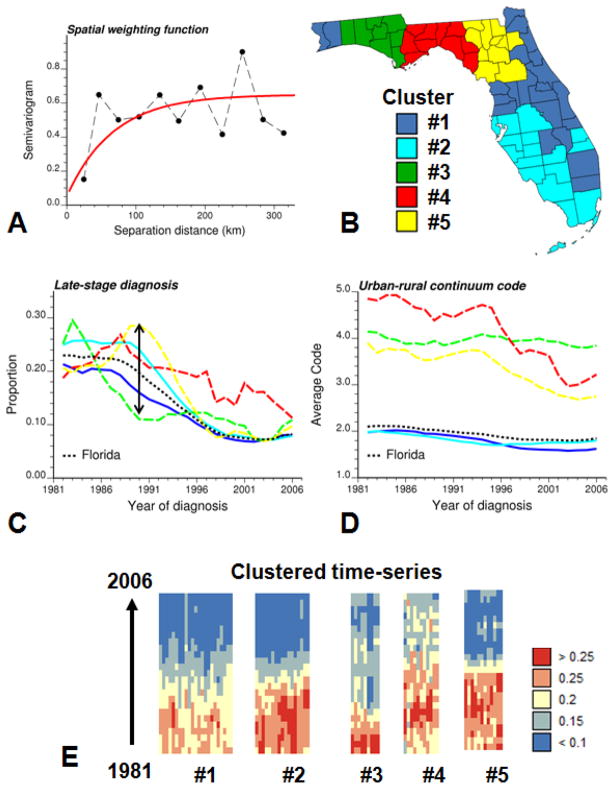
During the analysis of large space–time–attribute datasets, users may have difficulty perceiving, tracking and comprehending numerous visual elements that change simultaneously, such as the 67 time series in Fig. 3. One solution (Ward, 2004) illustrated in Fig. 5 is to reduce the data size being displayed by grouping time series into subsets (i.e. aggregation or clustering). The spatially weighted clustering algorithm described in Section 2.3 was applied to the county-level time series of noise-filtered 3-year averaged proportions of late-stage diagnosis. Fig. 5A shows the semivariogram model used as spatial weighting function f(.) in the computation of the dissimilarity measure (Equation 6). Based on the analysis of the dendrogram five groups of counties (Fig. 5B) were selected and their corresponding time series of yearly proportions of late-stage diagnosis and Rural-Urban Continuum codes are displayed in Figs. 5C–D using the same color scheme. Solid lines are used to represent the time series of the first two clusters which include 52% and 40% of the cases, respectively. Individual time series are also displayed according to their cluster allocation in Fig. 5E. Each column corresponds to a particular county and each pixel to a particular year; the color scale indicates the proportion of late-stage diagnosis.

Fig. 5.

Results of spatially weighted classification of 67 counties in Florida: population-weighted indicator semivariogram model used as weighting function in the computation of the dissimilarity measure (A), grouping of counties based on the similarity of their temporal trends in proportions of late-stage diagnosis and their geographically proximity (B), time series of proportion of late-stage diagnosis and population-weighed rural-urban code for each of the five clusters and Florida (black dashed line) (C,D), individual time series of noise-filtered rates of late-stage diagnosis displayed as horizontal strings and ordered according to their allocation to one of the five clusters (E). The same color code is used for the counties in the choropleth map B and the corresponding time series in plots C and D.

Fig. 5C reveals clear differences among regions of Florida. While some regions experienced a substantial decline coinciding with the introduction of PSA test, others (in particular the area around Tallahassee, Cluster #4 in red color) display much smaller changes and higher rates of late-stage diagnosis in this last decade. Cluster #5 (Central West Panhandle) even showed a steep increase in the proportion of late-stage diagnosis just before the introduction of PSA screening. Three of these clusters include however fewer cases and their time series, displayed using dashed lines in Fig. 5C, are less smooth than the results obtained for the first two clusters. These clusters, located in North Florida and Florida Panhandle, are mainly rural according to their Rural-Urban Continuum codes. Interestingly, the largest spread of the five time series in Fig. 5C is observed in the late eighties, just before the introduction of PSA screening.

The two most stable time series correspond to the most populated Cluster #1 (East coast) and Cluster #2 (West coast and Keys). These two time series start overlapping with the Florida State curve (black dashed curve) in the mid nineties, following the introduction of PSA screening. Until then, a smaller proportion of cases were diagnosed late in the North-east coast of Florida compared to the Western coast of Southern Florida. During this period, Cluster #1 was slightly less urban than Cluster #2 according to the rural-urban code (Fig. 5D), which confirms the positive relationship between degree of urbanization and frequency of late-stage diagnosis found in the eighties (Fig. 1C). Cluster #3, centred on Panama City, stands out from other clusters because it is the only area that has not seen a decline in percentage of late-stage diagnosis since the early nineties. Interestingly, it is also the only area with no substantial change in the Rural-Urban continuum code over that time period.

4. Conclusions

A comprehensive picture of the burden of cancer and the impact of various interventions can only be achieved through the simultaneous incorporation of the spatial and temporal dimensions in the visualization and analysis of health outcomes and putative covariates. Analysis of a single snapshot can lead one to overlook interesting trends, such as the changing relationships between degree of urbanization and county-level percentages of prostate cancer late-stage diagnosis in Florida over the period 1981–2007. Similarly, the analysis of temporal trends outside a spatial framework would lead one to ignore substantial geographical differences in the speed and nature of the decline in the percentage of late-stage diagnosis over a large State, such as Florida.

The application of spatial cluster and boundary analysis to space-time health data posed two challenges: 1) the need to account for the instability of rates recorded in sparsely populated counties, and 2) the incorporation of the time dimension in these intrinsically spatial techniques. The first aspect was addressed using geostatistical filters that account for the spatial patterns of data in the processing of rates for rare diseases (Poisson kriging) or percentages of late-stage diagnosis (binomial kriging). On the other hand, the analysis was extended to the temporal dimension using either a multivariate approach for the cluster analysis or the repetition of the boundary analysis across time using the geostatistical approach introduced by Goovaerts (2010b).

The 3D display of time series of county-level health outcomes makes it easier to comprehend spatiotemporal relationships because there is no disconnect between the temporal and spatial dimensions as opposed to a combination of 2D map and linked time line plots or an animation. Boundary analysis, used in conjunction with binomial distributions and the False Discovery rate approach, allows one to tackle the issues of unstable rates and increased risk of false positives in hypothesis testing. We also proposed a new index that summarizes for each geographical unit (county here) the results obtained over the set of edges and years. Mapping this index of dissimilarity highlighted similitude in the spatial patterns of geographical disparities in percentage of late-stage diagnosis and temporal changes along the rural-urban continuum. Spatially weighted cluster analysis allowed the study of temporal trends at spatial scales intermediate between the State level and the county or boundary level. Fig. 5 gave an original example of space time visual analytics where the map of county clusters is displayed together with individual time series, providing the user with a geographical summary of temporal trends without masking information pertaining to each county.

The case-study demonstrated that the 50% decline in the proportion of late-stage diagnosis observed in Florida between 1981 and 2007 encompasses substantial geographical disparities in the temporal patterns of changes. This drop generally started in the early 1990s when prostate-specific antigen (PSA) test became widely available and several parts of Florida underwent a fast urbanization. Geographical disparities were substantial at that time, which suggests disparities in the impact of the new screening procedure, in particular as it began available. The gap among Florida counties is narrowing with time as the percentage of late-stage diagnosis is decreasing. One outlier is the Big Bend region of Florida where the decline in percentage of late-stage diagnosis has been the slowest in the entire State. In the eighties, a smaller proportion of cases were diagnosed late in non-metro areas, a trend that has changed since then.

The present study was mainly exploratory and the interpretation of the results suffers from limitations typically associated with ecological studies. In particular, the analysis was conducted at the county level and it is well known that different geographic scales can lead to inconsistent results for health outcomes (Krieger et al., 2002; Meliker et al., 2009). However, the analysis of temporal trends at a fine resolution (e.g. year) requires some level of spatial aggregation in order to capture enough cases for a reliable estimation of percentages of late-stage diagnosis. In addition, by focusing on the population covered by Medicare one source of individual-level heterogeneity was controlled for. Individual-level data available for the same time period are currently analyzed to explore the impact of race, individual characteristics, area-level census measures of education, income, and environmental exposure on prostate cancer mortality, incidence and stage at diagnosis (Xiao et al., 2011). These data will help test hypothesis on the potential influence of urbanization and the introduction of PSA test that were formulated on the basis of results of the current exploratory county-level analysis.

Highlights.

1. The state-average proportion of prostate cancer late-stage diagnosis was halved over the 26-year time period.

2. Time trends in prostate cancer late-stage diagnosis vary greatly among Florida counties.

3. Noise in cancer rate data can be filtered using binomial kriging.

4. Geographical disparities were the most widespread when a new screening procedure was introduced in the early nineties.

5. Spatially-weighted cluster analysis creates spatially compact groups of counties with similar temporal trends.