Adjusted significance cutoffs for hypothesis tests applied with generalized additive models with bivariate smoothers

Abstract

In spatial epidemiology, generalized additive models (GAMs) can be applied with bivariate locally weighted regression smoothing terms (LOESS), smoothing over longitude and latitude, to evaluate whether there is spatial variation in disease risk across a study region. Two hypothesis testing methods applicable with GAMs with bivariate LOESS smoothes, an approximate chi-square test (ACST) and the conditional permutation test (CPT), have inflated type I error rates. Using simulated data we determined empirical adjustments to significance cutoffs for nominal type I error rates of 0.01, 0.05, and 0.10. When applied with adjusted significance cutoffs, both ACST and CPT were appropriately sized across region shapes, population densities, sample sizes, and probabilities of disease.

1. Introduction

Generalized additive models (GAM), a generalization of generalized linear models (GLM), can account for nonlinear associations between outcomes and predictors using nonparametric smoothing functions of one or more covariates. In spatial epidemiology, GAMs with a bivariate locally weighted regression smoothing term (LOESS) to smooth over longitude and latitude can be applied to evaluate whether disease status varies across geographic location (Aschengrau et al., 2008; Hoffman et al., 2010; Vieira et al., 2009; Vieira et al., 2005; Webster et al., 2006). To test this hypothesis, researchers compare models with and without the LOESS smoothing term to determine whether its inclusion substantially improves the model fit (Webster et al., 2006).

For GLMs, the difference in nested model deviance statistics has an asymptotic chi-square distribution (Casella and Berger, 2002). For GAMs, however, the asymptotic chi-square distribution is only approximate (Hastie and Tibshirani, 1990). An approximate chi-square test (ACST) based on the GLM framework exists and the test statistic, degrees of freedom, and p-value are provided in standard software packages (R, 2010; S-PLUS, 2007). ACST has been applied in recent research studies (Guisan et al., 2002; Maravelias et al., 2000), though a recent simulation study found that when applied with GAMs with a bivariate LOESS smoothing term, the type I error rate was nearly 4 times the nominal level of 0.05 (Young et al., 2011).

Webster et al. (2006) proposed a conditional permutation test (CPT) to test for associations between location and disease risk where, after selecting the span size, models with and without the smoothing term were applied to the observed data and the difference in deviance statistic was recorded. Geographic location was permuted, maintaining the link of any non-smoothed covariates and the outcome. Models were applied to permuted datasets, conditioning on the span selected for the observed data, and the differences in deviance statistics were recorded. The observed statistic was compared to the permutation distribution of difference in deviance statistics and, if the statistic fell in the upper α·100% of the permutation distribution, the null hypothesis was rejected (Webster et al., 2006). In previous research, CPT was also shown to have an inflated type I error rate when applied with a nominal significance level of 0.05 (Young et al., 2011).

In a recent power comparison, ACST and CPT, applied with adjusted significance cutoffs, were compared to other variations of permutation tests. ACST and CPT, with corrected type I error rates, performed as well or better than other appropriately sized permutation methods (Bliss et al., 2010). In a separate power comparison, the corrected CPT performed as well or better than the spatial scan statistic (Kulldorff and Nagarwalla, 1995) under simple alternative hypotheses (Young et al., 2011). For example, in a study region containing a single circular cluster with 3 times the odds of disease compared to unexposed subjects and a sample size of 1,000, ACST had 91.8% power, CPT had 92.3% power, and the scan statistic had 96.3% power (Bliss et al., 2010; Young et al., 2011). For a point source in the center of a circular study region, a linear association between risk of disease and distance from the source, and an odds ratio of 3.0, CPT had 71.4% power while the scan statistic had 58.4% power (Bliss et al., 2010). The evaluation of the corrected ACST and CPT under the null and alternative hypotheses has not considered irregular region shapes or nominal type I error rates other than 0.05.

The motivation for this research was a series of studies applying CPT to evaluate risks of low birth weight, learning disability, and breast, bladder, kidney, lung, and pancreatic cancer on Cape Cod, Massachusetts (Hoffman et al., 2010; Vieira et al., 2009; Vieira et al., 2005). The Upper Cape is irregularly shaped with jagged edges, there is a larger population living on the edge, near the ocean, than in the middle of the land mass. Additionally, the Massachusetts Military Reservation is a sparsely populated area located in the middle of Upper Cape Cod (Aschengrau et al., 2008). It may be that the deviance statistic value is affected by varied region shapes, distributions of subjects, sample sizes, and incidence of cases. As the deviance statistic is of interest for both the CPT and ACST, it is unclear whether these features will also affect the type I error rates of the tests.

ACST and CPT require significance cutoff adjustments and, while other cluster detection methods exist (e.g. spatial scan statistic (Kulldorff and Nagarwalla, 1995), kernel smoothing (Hazelton and Davies, 2009), Bonetti’s M statistic (Bonetti and Pagano, 2005), Cuzick and Edward’s T_k statistic (Cuzick and Edwards, 1990), etc), GAMs are of particular interest because of their application to generalized outcomes, the availability of regression-based inference, and the ability to control for many covariates in a single model without stratification of data. Further, the superior performance of ACST and CPT when compared to some hypothesis testing methods makes the determination of significance cutoff adjustments under a variety of scenarios an important contribution to current literature. In this study we evaluated the type I error rates of ACST and CPT when applied to four sets of synthetic data. We examined common variations in patterns of population distribution, deviations of region shape, sample size, and probability of disease. We recognize that we cannot examine the infinite number of possible scenarios; however we selected scenarios for examination in this study that commonly appear in public health research. Using simulated data we determined the implications of variations in commonly varying factors on the type I error rates of ACST and CPT. We determined appropriate significance cutoff adjustments for a range of nominal type I error rates.

2. Methods

2.1 Simulated Data

Synthetic data had a dichotomous outcome and probabilities of “disease” of 0.01, 0.05, 0.10, 0.20, and 0.50 to emulate epidemiologic cohort studies of both rare and common outcomes and case-control studies with 1 to 1 matching. Data were simulated under the global null hypothesis with no association between the outcome and geographic location. For each scenario, 1,000 datasets were simulated, using each of the following numbers of observations: 400, 1,000, 1,515 (the size of the Cape Cod Family Health Study), 1,600, 3,000, and 6,400. The sample sizes were selected to provide a range similar to the sizes of previous epidemiological studies that used GAMs as a statistical analysis technique (Aschengrau et al., 2008; Hoffman et al., 2010; Vieira et al., 2009; Vieira et al., 2005). As similar results were observed across scenarios, for simplicity, we present results for probabilities of disease 0.01, 0.10, and 0.50 and for sample sizes 400, 1,600, and 6,400. Additional results are available upon request.

2.2 Synthetic Study Regions

Circular

Observations were uniformly distributed across a circular study region with a radius of 1 unit. These data were simulated in an identical fashion to Young et al. (2011), a simulation study evaluating the test sizes of ACST and CPT for a nominal type I error rate of 0.05.

City

The longitude and latitude followed independent normal distributions with means at the origin and variances of 0.5 to form a high density center and sparser density edges. Lake: Data were uniformly distributed across the study region with the exception of a “lake”, represented by a circular area with radius 0.10, centered in the unit-square study region.

Cape Cod

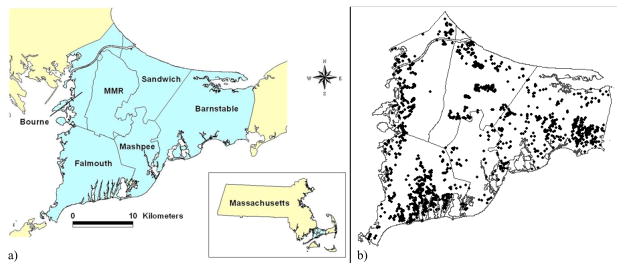
Locations of 1,515 subject residences, obtained from the Cape Cod Family Health Study where subjects lived in one of five towns on Upper Cape Cod, Massachusetts (Aschengrau et al., 2008), were used as an example data for the evaluation of the hypothesis testing methods. All subject characteristics were stripped from the data, leaving only the longitude and latitude of geographic location of residence. Disease status was randomly assigned for each simulated dataset with probabilities of 0.05, 0.10, 0.20, and 0.50. (A 1% probability of disease was excluded as models could not converge given the complexity of the Cape Cod data and the small expected number of cases.) Cape Cod has an irregular shape, a dense population near the region edges, and areas of sparse data in the center of the map (Figure 1).

Figure 1.

Map of Cape Cod, Massachusetts and distribution of geographic locations of example data on Upper Cape Cod

Figure 1a) displays a map of Upper Cape Cod, Massachusetts. Figure 1b) illustrates the distribution of geographic locations (with jigger) of observations in the example data across Upper Cape Cod.

Syntax to produce synthetic data in R (R, 2010) for the circle, city, and lake scenarios is available upon request. Data for the Cape Cod Family Health Study is not publicly available; however shape files for the region are available upon request.

2.3 Hypothesis Tests

Models were applied with bivariate LOESS smoothing terms to account for geographic location of residence. GAMs were applied with span sizes ranging between 0.05 and 0.95. Akaike Information Criterion (AIC) goodness of fit statistics were recorded and the span corresponding to the minimal model AIC was selected. Larger span sizes (near 1) correspond to smoother maps, indicative of little spatial variation in the outcome and are expected for data under the null hypothesis (Hastie and Tibshirani, 1990).

Approximate Chi-Square Test (ACST): For GLMs, the difference in nested model deviance statistics has an asymptotic chi-square distribution. That is,

$$-2(L_1-L_0)\stackrel{n\to \infty }{\sim }{\chi }_{df(L_0)-df(L_1)}^2$$

where L₁ is the deviance statistic of the model of interest, L₀ is the deviance statistic from a simplified model, nested within L₁, and df(·) are the degrees of freedom for the respective models (Casella and Berger, 2002). While the asymptotic distribution is known to be only approximate in the additive framework, the ACST assumes that the difference in deviance statistic followed an asymptotic chi-square distribution (Hastie and Tibshirani, 1990). For each dataset, GAMs were applied and the difference in deviance statistic was compared to a chi-square distribution. The statistic, degrees of freedom, and p-value were produced by standard software (R, 2010; S-PLUS, 2007).

Conditional Permutation Test (CPT): After selecting the span size, two GAM models, one with and one without the smoothing term, were applied to observed data. The difference between model deviance statistics was recorded. Geographic location was permuted, maintaining the link of case/control status and non-smoothed covariates, to generate 999 permuted datasets. GAMs were then applied to permuted data using the span size selected for the observed data. The difference in deviance statistics between the application of GAMs with smoothing terms to permuted data and the model without the smoothing term were recorded. The statistics were ranked from lowest to highest values and the p-value for the hypothesis test was the rank of the observed data when compared to the conditional permutation distribution divided by 1,000 (Webster et al., 2006).

2.4 Type I Error Rates and Significance Cutoff Adjustments

Nominal type I error rates, the desired probability of false positives, α, when evaluating hypothesis tests applied to data generated under the null hypothesis, were 0.01, 0.05, and 0.10. The goal of this study was to determine an adjusted significance cutoff, a value α^* where the probability that hypothesis test p-value is less than α^* is less than, or equal to the nominal type I error rate (P(p − value<α^*|null hypothesis true)≤α). The circular study region was used as a “training set” to empirically determine appropriate adjusted significance cutoffs. The ACST and CPT were first applied using the nominal cutoffs. The resulting type I error rates were observed and reported. Adjusted significance cutoffs were determined through an empirical systematic procedure to produce type I error estimates falling at or below the nominal levels. Procedure:

1. For the circular study region with a sample size of 1,000, type I error rates were observed using the nominal significance cutoffs.

2. We determined the maximum type I error rate inflation (observed type I error divided by nominal level) across three probabilities of disease (0.01, 0.10, and 0.50). The initial candidate value to obtain the empirical type I error rate was the nominal value divided by the inflation factor.

3. The type I error rate using the candidate cutoff value was observed. The cutoff was then adjusted by a small margin (+/− 0.001 for CPT, +/− 0.0001 for ACST due to differential precision of p-values) until the 95% confidence interval for the observed type I error rate included the nominal type I error rate for at least two of the three probabilities of diseases.

At least three candidate values were examined for each nominal significance level. Preference was given to larger values and values rounded to the nearest 0.005 for CPT and 0.0005 for ACST.

Using the adjusted significance cutoffs, ACST and CPT were applied to each of the remaining scenarios and the observed type I error rates (P(p− value<α^*|null hypothesis true)≤α) were recorded.

3. Results

3.1 Type I Error Rates for Nominal and Adjusted Significance Cutoffs

When applied to the circular study region with the nominal significance level, ACST and CPT had inflated type I error rates. Across probabilities of disease and sample sizes, ACST had type I error rates five times, three times, and over twice the respective nominal levels of 0.01, 0.05, and 0.10 (Table 1). CPT had type I error rates of twice the nominal of 0.01 and 0.05 and between 1.5 and two times the nominal significance α level of 0.10 (Table 2). Using the circular study region as a training set and the procedure described in Section 2.4, adjusted significance cutoffs were determined empirically. The adjusted significance cutoffs for ACST were 0.001, 0.0125, and 0.025 for nominal levels of 0.01, 0.05, and 0.10, respectively. For CPT, the adjusted cutoffs were 0.004, 0.025, and 0.055.

Table 1.

Approximate chi-square test applied with nominal significance levels to simulated data in circular study region

N = 400	α = 0.01 Type I Error (95%CI)	α = 0.05 Type I Error (95%CI)	α = 0.10 Type I Error (95%CI)
P(Disease)=0.01	0.034 (0.023,0.045)	0.151 (0.129,0.173)	0.269 (0.242,0.296)
P(Disease)=0.10	0.059 (0.044,0.074)	0.188 (0.164,0.212)	0.288 (0.260,0.316)
P(Disease)=0.50	0.062 (0.047,0.077)	0.179 (0.155,0.203)	0.272 (0.244,0.300)
N = 1,000	α = 0.01 Type I Error (95%CI)	α = 0.05 Type I Error (95%CI)	α = 0.10 Type I Error (95%CI)
P(Disease)=0.01	0.036 (0.024,0.048)	0.156 (0.134,0.178)	0.250 (0.223,0.277)
P(Disease)=0.10	0.048 (0.035,0.061)	0.156 (0.134,0.178)	0.256 (0.229,0.283)
P(Disease)=0.50	0.060 (0.045,0.075)	0.170 (0.147,0.193)	0.269 (0.242,0.296)
N = 1,600	α = 0.01 Type I Error (95%CI)	α = 0.05 Type I Error (95%CI)	α = 0.10 Type I Error (95%CI)
P(Disease)=0.01	0.045 (0.032,0.058)	0.181 (0.157,0.205)	0.283 (0.255,0.311)
P(Disease)=0.10	0.046 (0.033,0.059)	0.142 (0.120,0.164)	0.237 (0.211,0.263)
P(Disease)=0.50	0.047 (0.034,0.060)	0.156 (0.134,0.178)	0.235 (0.209,0.261)
N = 6,400	α = 0.01 Type I Error (95%CI)	α = 0.05 Type I Error (95%CI)	α = 0.10 Type I Error (95%CI)
P(Disease)=0.01	0.053 (0.039,0.067)	0.160 (0.137,0.183)	0.238 (0.212,0.264)
P(Disease)=0.10	0.044 (0.031,0.057)	0.147 (0.125,0.169)	0.237 (0.211,0.263)
P(Disease)=0.50	0.056 (0.042,0.070)	0.177 (0.153,0.201)	0.258 (0.231,0.285)

Table 2.

Conditional permutation test applied with nominal significance levels to simulated data in circular study region

N = 400	α = 0.01 Type I Error (95%CI)	α = 0.05 Type I Error (95%CI)	α = 0.10 Type I Error (95%CI)
P(Disease)=0.01	0.028 (0.018,0.038)	0.077 (0.06,0.094)	0.159 (0.136,0.182)
P(Disease)=0.10	0.027 (0.017,0.037)	0.1 (0.081,0.119)	0.182 (0.158,0.206)
P(Disease)=0.50	0.031 (0.02,0.042)	0.1 (0.081,0.119)	0.185 (0.161,0.209)
N = 1,000	α = 0.01 Type I Error (95%CI)	α = 0.05 Type I Error (95%CI)	α = 0.10 Type I Error (95%CI)
P(Disease)=0.01	0.023 (0.014,0.032)	0.091 (0.073,0.109)	0.156 (0.134,0.178)
P(Disease)=0.10	0.025 (0.015,0.035)	0.094 (0.076,0.112)	0.173 (0.150,0.196)
P(Disease)=0.50	0.027 (0.017,0.037)	0.109 (0.090,0.128)	0.180 (0.156,0.204)
N = 1,600	α = 0.01 Type I Error (95%CI)	α = 0.05 Type I Error (95%CI)	α = 0.10 Type I Error (95%CI)
P(Disease)=0.01	0.017 (0.009,0.025)	0.097 (0.079,0.115)	0.187 (0.163,0.211)
P(Disease)=0.10	0.021 (0.012,0.030)	0.088 (0.070,0.106)	0.147 (0.125,0.169)
P(Disease)=0.50	0.023 (0.014,0.032)	0.094 (0.076,0.112)	0.169 (0.146,0.192)
N = 6,400	α = 0.01 Type I Error (95%CI)	α = 0.05 Type I Error (95%CI)	α = 0.10 Type I Error (95%CI)
P(Disease)=0.01	0.028 (0.018,0.038)	0.098 (0.080,0.116)	0.167 (0.144,0.190)
P(Disease)=0.10	0.026 (0.016,0.036)	0.092 (0.074,0.110)	0.171 (0.148,0.194)
P(Disease)=0.50	0.032 (0.021,0.043)	0.105 (0.086,0.124)	0.194 (0.169,0.219)

The adjusted significance cutoffs corrected the ACST type I error rates across nearly all probabilities of disease, sample sizes, and study region shapes. Of the 81 combinations of parameters presented here (three nominal type I error rates, three region shapes, three probabilities of disease: 0.01, 0.10, 0.50, and three sample sizes: 400, 1,600, 6,400) 12 (14.8%) had type I error rates with 95% confidence intervals falling below the nominal value while an additional 12 (14.8%) had inflated type I error rates. Most often (17/24) this occurred for a sample size of 400, perhaps indicating less reliable results for small sample sizes; however the upper and lower confidence limits for the deflated and inflated type I error rates did not fall far from the nominal levels (Table 3). Figure 2 displays the observed type I error rates of ACST when applied to the data in the circular study region with a 0.10 probability of disease and sample sizes varying from 400 to 6,400. Observed type I error rates were consistent across sample sizes (Figure 2). Similar results were observed for other probabilities of disease and region shapes.

Table 3.

Approximate chi-square test applied with adjusted significance cutoffs

	N = 400 Type I Error (95%CI)			N = 1,600 Type I Error (95%CI)			N = 6,400 Type I Error (95%CI)
P(Disease)	α = 0.01	α = 0.05	α = 0.10	α = 0.01	α = 0.05	α = 0.10	α = 0.01	α = 0.05	α = 0.10
	α* = 0.001	α* = 0.0125	α* = 0.025	α* = 0.001	α* = 0.0125	α* = 0.025	α* = 0.001	α* = 0.0125	α* = 0.025
Circle
0.01	0.003 (<0.001,0.006)	0.044 (0.031,0.057)	0.076 (0.060,0.092)	0.004 (<0.001,0.008)	0.055 (0.041,0.069)	0.110 (0.091,0.129)	0.007 (0.002,0.012)	0.060 (0.045,0.075)	0.100 (0.081,0.119)
0.10	0.014 (0.007,0.021)	0.069 (0.053,0.085)	0.110 (0.091,0.129)	0.003 (<0.001,0.006)	0.055 (0.041,0.069)	0.083 (0.066,0.100)	0.012 (0.005,0.019)	0.051 (0.037,0.065)	0.090 (0.072,0.108)
0.50	0.015 (0.007,0.023)	0.069 (0.053,0.085)	0.116 (0.096,0.136)	0.011 (0.005,0.017)	0.056 (0.042,0.070)	0.098 (0.080,0.116)	0.014 (0.007,0.021)	0.066 (0.051,0.081)	0.106 (0.087,0.125)
City
0.01	0.002 (<0.001,0.005)	0.027 (0.017,0.037)	0.061 (0.046,0.076)	0.005 (0.001,0.009)	0.041 (0.029,0.053)	0.099 (0.080,0.118)	0.009 (0.003,0.015)	0.063 (0.048,0.078)	0.102 (0.083,0.121)
0.10	0.019 (0.011,0.027)	0.086 (0.069,0.103)	0.126 (0.105,0.147)	0.010 (0.004,0.016)	0.064 (0.049,0.079)	0.115 (0.095,0.135)	0.010 (0.004,0.016)	0.047 (0.034,0.060)	0.085 (0.068,0.102)
0.50	0.019 (0.011,0.027)	0.083 (0.066,0.100)	0.126 (0.105,0.147)	0.008 (0.002,0.014)	0.076 (0.060,0.092)	0.116 (0.096,0.136)	0.010 (0.004,0.016)	0.057 (0.043,0.071)	0.091 (0.073,0.109)
Lake
0.01	<0.001 (<0.001, <0.001)	0.023 (0.014,0.032)	0.057 (0.043,0.071)	0.008 (0.002,0.014)	0.064 (0.049,0.079)	0.101 (0.082,0.120)	0.006 (0.001,0.011)	0.066 (0.051,0.081)	0.089 (0.071,0.107)
0.10	0.014 (0.007,0.021)	0.07 (0.054,0.086)	0.119 (0.099,0.139)	0.011 (0.005,0.017)	0.054 (0.040,0.068)	0.095 (0.077,0.113)	0.014 (0.007,0.021)	0.054 (0.040,0.068)	0.083 (0.066,0.100)
0.50	0.016 (0.008,0.024)	0.078 (0.061,0.095)	0.115 (0.095,0.135)	0.003 (<0.001,0.006)	0.052 (0.038,0.066)	0.095 (0.077,0.113)	0.006 (0.001,0.011)	0.042 (0.030,0.054)	0.071 (0.055,0.087)

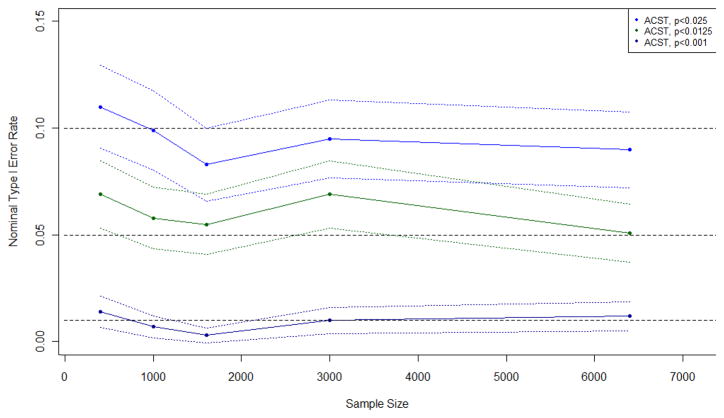
Figure 2.

Observed type I error rates and 95% confidence intervals of approximate chi-square test (ACST) when applied with an adjusted cutoff to a circular study region with a probability of disease of 0.10

Figure 2 displays the observed type I error rate and 95% confidence intervals of the approximate chi-square test when applied with an adjusted cutoff to data from the circular study region with a probability of disease of 0.10 and sample sizes ranging from 400 to 6,400. Similar plots were observed for other probabilities of disease and region shapes and are available upon request.

When applied to the irregularly shaped and non-uniformly distributed sample of 1,515 on Cape Cod, Massachusetts, the corrected ACST was appropriately sized for all significance cutoffs and probabilities of disease presented here (Table 5). Similar results were observed for other probabilities of disease with one scenario (probability of disease of 0.05, nominal type I error rate of 0.01) having slightly deflated type I error. (Results are available upon request.)

Table 5.

Corrected approximate chi-square and conditional permutation tests applied to simulated data in Cape Cod study region

	Approximate chi-square test (N = 1,515) Type I Error (95%CI)
P(Disease)	α = 0.01	α = 0.05	α = 0.10
	α* = 0. 001	α* = 0.0125	α* = 0.025
0.10	0.007 (0.002,0.012)	0.062 (0.047,0.077)	0.097 (0.079,0.115)
0.50	0.007 (0.002,0.012)	0.063 (0.048,0.078)	0.100 (0.081,0.119)
	Conditional permutation test (N=1,515) Type I Error (95%CI)
P(Disease)	α = 0.01	α = 0.05	α = 0.10
	α* = 0.004	α* = 0.025	α* = 0.055
0.10	0.010 (0.004,0.016)	0.061 (0.046,0.076)	0.106 (0.087,0.125)
0.50	0.013 (0.006,0.020)	0.060 (0.045,0.075)	0.110 (0.091,0.129)

The corrected CPT was also appropriately sized for nearly all probabilities of disease, sample sizes, and region shapes. In 9 (11.1%) of the 81 combinations of parameters presented here, CPT had a slightly inflated type I error rate, most often occurring for a sample size of 400 (6/7 occurrences). In one instance (1.2%), the observed type I error rate was deflated (Table 4). Figure 3 displays the observed type I error rates of CPT when applied to the data in the circular study region with an outcome probability of 0.10 and sample sizes varying from 400 to 6,400. Figure 3 displays nearly straight lines for the three nominal type I error rates illustrating consistent values across sample sizes. Similar results were observed for other probabilities of disease and region shapes. When applied to the Cape Cod, Massachusetts sample of 1,515, appropriate type I error rates were observed for all presented scenarios (Table 5). Similar results were observed for other probabilities of disease with one slightly inflated type I error rate observed for a probability of disease of 0.20 and a nominal type I error rate of 0.05. (Results available upon request.)

Table 4.

Conditional permutation test applied with adjusted significance cutoffs

	N = 400 Type I Error (95%CI)			N = 1,600 Type I Error (95%CI)			N = 6,400 Type I Error (95%CI)
P(Disease)	α = 0.01	α = 0.05	α = 0.10	α = 0.01	α = 0.05	α = 0.10	α = 0.01	α = 0.05	α = 0.10
	α* = 0.004	α* = 0.025	α* = 0.055	α* = 0.004	α* = 0.025	α* = 0.055	α* = 0.004	α* = 0.025	α* = 0.055
Circle
0.01	0.014 (0.007,0.021)	0.052 (0.038,0.066)	0.083 (0.066,0.100)	0.007 (0.002,0.012)	0.053 (0.039,0.067)	0.104 (0.085,0.123)	0.017 (0.009,0.025)	0.049 (0.036,0.062)	0.105 (0.086,0.124)
0.10	0.009 (0.003,0.015)	0.057 (0.043,0.071)	0.105 (0.086,0.124)	0.007 (0.002,0.012)	0.050 (0.036,0.064)	0.097 (0.079,0.115)	0.015 (0.007,0.023)	0.047 (0.034,0.060)	0.101 (0.082,0.120)
0.50	0.018 (0.010,0.026)	0.056 (0.042,0.070)	0.104 (0.085,0.123)	0.014 (0.007,0.021)	0.051 (0.037,0.065)	0.105 (0.086,0.124)	0.017 (0.009,0.025)	0.060 (0.045,0.075)	0.115 (0.095,0.135)
City
0.01	0.009 (0.003,0.015)	0.043 (0.03,0.056)	0.094 (0.076,0.112)	0.008 (0.002,0.014)	0.055 (0.041,0.069)	0.114 (0.094,0.134)	0.016 (0.008,0.024)	0.065 (0.050,0.080)	0.109 (0.090,0.128)
0.10	0.023 (0.014,0.032)	0.069 (0.053,0.085)	0.123 (0.103,0.143)	0.011 (0.005,0.017)	0.063 (0.048,0.078)	0.119 (0.099,0.139)	0.010 (0.004,0.016)	0.051 (0.037,0.065)	0.094 (0.076,0.112)
0.50	0.017 (0.009,0.025)	0.070 (0.054,0.086)	0.121 (0.101,0.141)	0.009 (0.003,0.015)	0.06 (0.045,0.075)	0.119 (0.099,0.139)	0.019 (0.011,0.027)	0.055 (0.041,0.069)	0.095 (0.077,0.113)
Lake
0.01	0.006 (0.001,0.011)	0.035 (0.024,0.046)	0.082 (0.065,0.099)	0.014 (0.007,0.021)	0.056 (0.042,0.070)	0.107 (0.088,0.126)	0.013 (0.006,0.020)	0.052 (0.038,0.066)	0.101 (0.082,0.120)
0.10	0.016 (0.008,0.024)	0.071 (0.055,0.087)	0.116 (0.096,0.136)	0.007 (0.002,0.012)	0.051 (0.037,0.065)	0.096 (0.078,0.114)	0.016 (0.008,0.024)	0.052 (0.038,0.066)	0.094 (0.076,0.112)
0.50	0.012 (0.005,0.019)	0.062 (0.047,0.077)	0.116 (0.096,0.136)	0.009 (0.003,0.015)	0.056 (0.042,0.070)	0.104 (0.085,0.123)	0.008 (0.002,0.014)	0.042 (0.030,0.054)	0.077 (0.060,0.094)

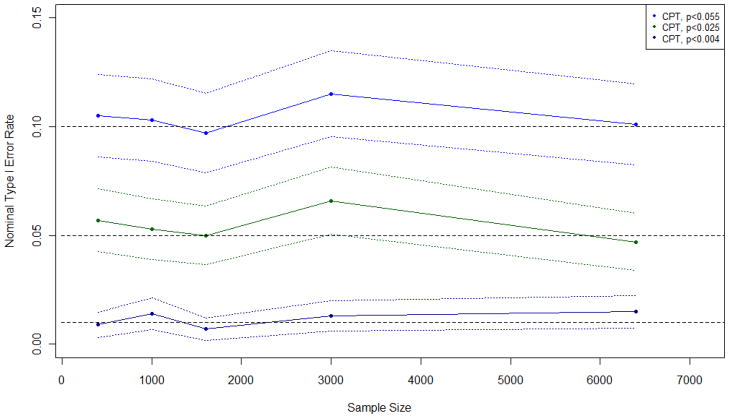
Figure 3.

Observed type I error rates and 95% confidence intervals of conditional permutation test (CPT) when applied with an adjusted cutoff to a circular study region with a probability of disease of 0.10

Figure 2 displays the observed type I error rate and 95% confidence intervals of the conditional permutation test when applied with an adjusted cutoff to data from the circular study region with a probability of disease of 0.10 and sample sizes ranging from 400 to 6,400. Similar plots were observed for other probabilities of disease and region shapes and are available upon request.

3.2 Deviance Statistics

For some probability distributions, well-known critical values can be used in place of significance cutoffs. For example, the probability of a z-statistic having an absolute value of at least 1.96 is equal to 0.05. For z-statistics, a decision rule can be based on the value of the test statistic (|z| > 1.96) or on the corresponding p-value (p< 0.05). The critical values for t-statistics vary depending on the test statistic degrees of freedom. Such critical values are not available for the difference of deviance statistic in application of CPT.

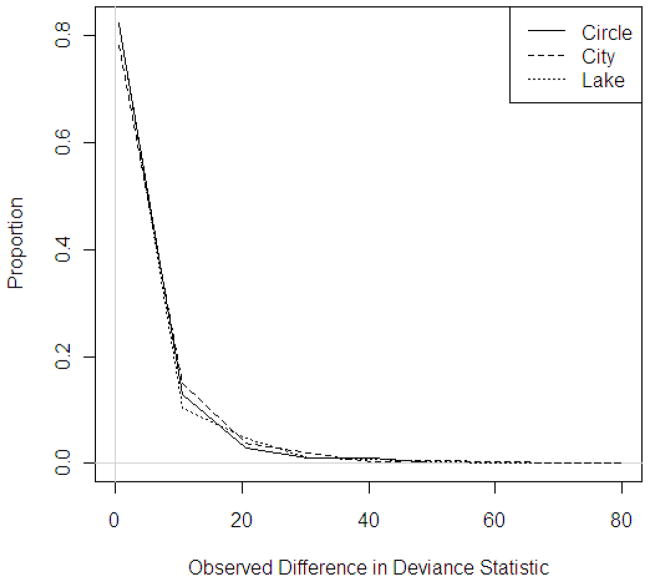
Distributions of observed differences in deviance statistics were similarly right-skewed across region shape, sample size, and probability of disease (Figures 4–6). Though not visually obvious, there is substantial variation between the tail lengths and numbers of observations falling in the right-tails of the permutation distributions. The distributions vary by region shape, population density, sample size, and probability of disease making the determination of a single critical value impossible. For a sample size of 1,600, adjusted cutoffs for a nominal α of 0.01 ranged between 16.8 and 18.9, for α of 0.05, cutoffs ranged between 12.9 and 15.0, and for α of 0.10, adjusted cutoffs ranged between 11.1 and 13.2 (Table 6).

Figure 4.

Distribution of observed deviance statistics across region shapes, N = 1,600, P(Disease) = 0.10

Figure 2 displays the distribution of observed deviance statistics across region shapes for a sample size of 1,600 and a probability of disease of 0.10. Similar trends were observed for other sample sizes and probabilities of disease and plots are available upon request.

Figure 6.

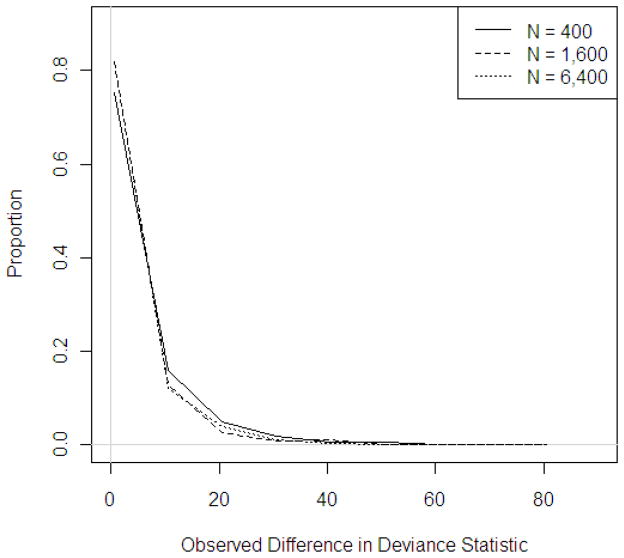
Distribution of observed deviance statistics across sample sizes, P(Disease) = 0.10, circular study region

Figure 4 displays the distribution of observed deviance statistics across sample sizes for a probability of disease of 0.10 when applied to data in the circular study region. Similar trends were observed for other probabilities of disease and region shapes and are available upon request.

Table 6.

Average critical values^† for difference in deviance statistic permutation distributions for adjusted significance cutoffs

	N = 400 Mean Difference in Deviance Statistic Cutoff (SD)			N = 1,600 Mean Difference in Deviance Statistic Cutoff (SD)			N = 6,400 Mean Difference in Deviance Statistic Cutoff (SD)
P(Disease)	α = 0.01	α = 0.05	α = 0.10	α = 0.01	α = 0.05	α = 0.10	α = 0.01	α = 0.05	α = 0.10
	α* = 0.004	α* = 0.025	α* = 0.055	α* = 0.004	α* = 0.025	α* = 0.055	α* = 0.004	α* = 0.025	α* = 0.055
Circle
0.01	14.49(3.39)	11.34(3.04)	9.73(2.86)	17.02(5.13)	13.35(4.87)	11.63(4.74)	17.23(7.08)	13.39(6.58)	11.58(6.30)
0.10	18.13(8.08)	14.24(7.54)	12.41(7.28)	16.82(6.11)	12.99(5.63)	11.21(5.36)	16.79(6.13)	12.98(5.60)	11.17(5.33)
0.50	17.98(9.82)	14.10(9.22)	12.24(8.84)	16.90(6.80)	13.08(6.23)	11.28(5.96)	17.47(7.76)	13.63(7.21)	11.79(6.90)
City
0.01	15.51(3.31)	12.05(3.04)	10.32(2.89)	17.33(4.49)	13.62(4.22)	11.86(4.05)	18.13(5.99)	14.31(5.49)	12.50(5.22)
0.10	18.85(7.24)	15.01(6.79)	13.20(6.52)	18.34(6.68)	14.46(6.17)	12.65(5.91)	17.86(5.38)	14.00(4.92)	12.18(4.68)
0.50	19.60(11.83)	15.72(11.14)	13.86(10.78)	18.81(7.82)	14.96(7.29)	13.12(7.01)	17.95(5.64)	14.14(5.14)	12.33(4.88)
Lake
0.01	14.24(3.33)	11.17(2.96)	9.61(2.74)	16.85(4.67)	13.20(4.41)	11.49(4.30)	17.41(6.66)	13.58(6.21)	11.78(5.94)
0.10	17.94(7.82)	14.09(7.39)	12.27(7.13)	17.23(6.91)	13.45(6.34)	11.65(6.07)	17.53(7.93)	13.67(7.39)	11.85(7.07)
0.50	18.23(9.45)	14.26(8.77)	12.41(8.43)	16.81(5.32)	12.94(4.82)	11.14(4.59)	17.38(7.22)	13.53(6.68)	11.72(6.39)

^†Critical value C* such that P(C*< d)=α where α is the nominal type I error rate and d is the difference in deviance statistics

4. Discussion

When applied with the nominal significance cutoffs, ACST and CPT had inflated type I error rates. Empirical adjustments were determined using a circular study region and were subsequently applied to the remaining study regions. For nominal type I error rates of 0.01, 0.05, and 0.10, adjusted significance cutoffs for ACST (0.001, 0.0125, and 0.025) and for CPT (0.004, 0.025, and 0.055) provided appropriately sized tests across study region shapes, population densities, sample sizes, and probabilities of disease. When applied to example data from Cape Cod, Massachusetts with irregular edges, dense population near the edges, and sparse population in the center, both ACST and CPT were appropriately sized. For small sample sizes, some deflated type I error rates were observed, likely due to the low number of expected events in the study region. In a few instances for moderate and large sample sizes the observed type I error rates were either inflated or deflated due to random error.

The ACST is computationally efficient, relying on an approximate asymptotic distribution and may be useful for model building strategies as standard software provides the ACST statistic, degrees of freedom, and p-value (R, 2010; S-PLUS, 2007) after only short computations. The ACST has been used extensively in research studies without type I error rate adjustments (Examples: Maravelias et al., 2000 and Guisan et al., 2002). The availability of this hypothesis test along with the inflated type I error rates when applied with nominal significance cutoffs is concerning. When applied with models including bivariate LOESS smoothing terms, a reduced significance cutoff may adjust the test to an appropriate size regardless of the region shape, sample size, or probability of disease; however notices of inflated type I error rates are not provided with standard software. In a previous study, it was shown that the type I error rate of ACST when applied with univariate smoothes was also inflated (Young et al., 2011); however determining appropriate significance cutoff adjustments for univariate or other smoothing techniques is left for future research.

Permutation tests provide desirable, albeit more computationally intensive, alternatives to ACST as they can identify geographic locations of variation in risk in addition to global hypothesis tests. Webster et al. (2006) applied point-wise permutation tests to point-wise predicted values obtained on a fine grid overlaying the study region. From this they were able to identify geographic locations of increased and decreased risk and to produce maps displaying variations in risk across the study region (Webster et al., 2006). Such methods are not available for ACST.

CPT was appropriately sized across all region shapes, sample sizes, and probabilities of disease when applied with a reduced significance cutoff. Compared to other permutation tests, it is more computationally efficient and has high power estimates, even after appropriate type I error rate adjustments (Bliss et al., 2010). Of note, these cutoff adjustments are only necessary when the observed p-value falls close to the nominal level. The CPT type I error rate when applied with other smoothing techniques has yet to be evaluated and is left for future research.

Deviance statistic distributions were visually similar across region shape, sample size, and probabilities of disease; however the right-tail lengths and proportions of observations falling in the upper tails varied between simulation parameter values. As the deviance statistic is a measure of model fit, its value is affected by the region shape, sample size, probability of disease, and selected span size (Young et al., 2011). Model complexity and covariate distributions will also likely affect the deviance statistic distributions making it impossible to determine a single critical value to be applied across all models as is available for z- and t-statistics.

ACST and CPT have been evaluated under a limited number of region shapes, population densities, sample sizes, and probabilities of disease. We examined common variations that exist in real data (such as a non-uniform population density and areas of sparse data) to determine the influence of variations of these factors on the type I error rates of ACST and CPT including the use of Upper Cape Cod as an example of an irregular study region shape with non-uniform population density. While we did not examine an exhaustive list of factors, we believe that the parameters considered were substantially varied and that the consistent results across combinations of the parameters supports the significance cutoff adjustments proposed in this research. It is possible that the significance cutoff adjustments are not adequate for all possible scenarios, including multiple cities, multiple areas of sparse data, different numbers of covariates, and other irregularities. Examination of the type I error rate under a greater variety of scenarios is left for future research; however we have developed general software for researchers to apply to any spatial data to evaluate the type I error rates of ACST and CPT. The software is available in an online appendix and future updates will be available at http://www.busrp.org/.

5. Conclusion

In practice, geographic region shape and population density are neither simple nor uniform and large sample sizes cannot be guaranteed. Cape Cod, Massachusetts provided an example study region with highly irregular boundaries, an uneven population distribution, and the highest density population near the edges. Across nominal type I error rates, disease incidences, and irregularities in region shape and population density, both ACST and CPT can be appropriately applied in spatial epidemiologic studies using adjusted significance cutoffs.

Figure 5.

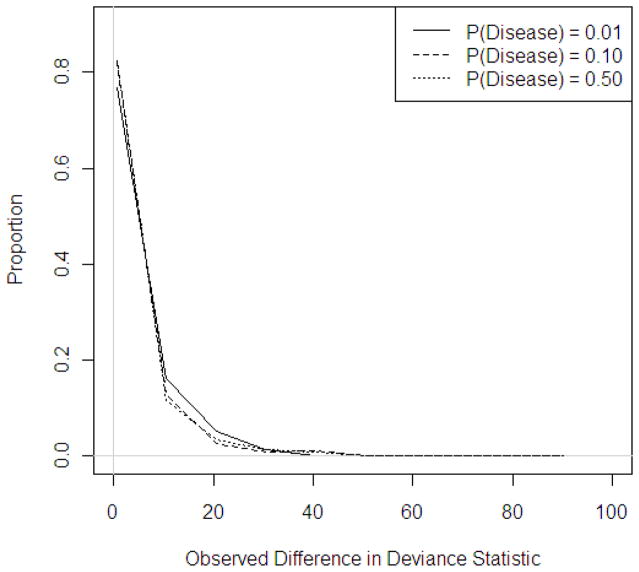
Distribution of observed deviance statistics across probabilities of disease, N = 1,600, circular study region

Figure 3 displays the distribution of observed deviance statistics across probabilities of disease for a sample size of 1,600 when applied to data in the circular study region. Similar trends were observed for other sample sizes and region shapes and plots are available upon request.

Highlights.

• The approximate chi-square test for GAMs has an inflated type I error rate

• The conditional permutation test for GAMs has an inflated type I error rate

• Significance cutoff adjustments are empirically derived for both tests

• The corrected tests had appropriate sizes across region shapes and sample sizes

Abbreviations

ACST

Approximate chi-square test

AIC

Akaike Information Criterion

CPT

Conditional permutation test, GAM, Generalized additive model

GLM

Generalized linear model

LOESS

Locally weighted regression smoothing term