String theory

Particle physicists have spent much of this century grappling with one basic question in various forms: what are the fundamental degrees of freedom needed to describe nature, and what are the laws that govern their dynamics? First molecules, then atoms, then “elementary particles” such as protons and neutrons all have been revealed to be composite objects whose constituents could be studied as more fundamental degrees of freedom. The current “standard model” of particle physics—which is nearly 25 years old, has much experimental evidence in its favor and is comprised of six quarks, six leptons, four forces, and the as yet unobserved Higgs boson—contains internal indications that it, too, may be just another step along the path toward uncovering the truly fundamental degrees of freedom. The standard model is valid to distances as small as 10⁻¹⁶ cm, and there is some evidence (such as that obtained by extrapolating the strengths of the four forces to determine the distance scale at which they might become indistinguishable) that the next level of structure will be detected only at a distance scale of roughly 10⁻³² cm, far beyond our abilities to measure in the laboratory.

The study of motion and gravity also has undergone several revisions during this century. Reconciling the Newtonian theory of motion with the experimentally observed constancy of the speed of light required the introduction of special relativity, which quite remarkably insists that space and time are intimately related, much as different faces of the same coin. Incorporating gravity into this framework required an even more drastic modification of our view of space and time: in general relativity, space time is seen as intrinsically warped, and the warping is responsible for the gravitational force. General relativity is a “classical” theory, which takes no notice of effects from quantum mechanics (whose development was another of the triumphs of theoretical and experimental physics in the early part of the century). A serious problem arises when general relativity is extrapolated to tiny distance scales (again roughly 10⁻³² cm) where quantum effects must be taken into account: the quantum-mechanical perturbation expansion of this theory has uncontrollable divergences. Lessons learned from the history of particle physics suggest that this should be a signal of new physics occurring at these tiny distance scales.

String theory offers a hope of addressing both of these issues. There is only one known way to “smear out” the gravitational interaction and hence cure the divergence problem in the quantum-mechanical expansion of general relativity: model the particles in the theory not as points, but as one-dimensional loops of “string.” In fact, every consistent such string model necessarily contains a special kind of particle—the graviton—whose long-distance interactions are described by general relativity. So in a sense, string theory predicts gravity. Moreover, some of the simplest string theories, the Calabi–Yau models, closely resemble unified (super-symmetric) versions of the standard model.

However, before recent developments our understanding of string theory was limited to situations in which small numbers of strings interact weakly. This is unsatisfactory for several reasons. First, we are undoubtedly missing important dynamical effects in such a limited study. (Analogous effects in quantum field theory such as quark confinement and spontaneous symmetry breaking are crucial ingredients in the standard model.) And second, we are really lacking the fundamental principle underlying string theory. It is quite likely that the theory will look very different once this principle is uncovered.

An exciting new frontier was opened during the past few years with the discovery of “string duality,” which predicts equivalences among various seemingly different physical systems. This discovery has its roots in the properties of super-symmetry, a novel type of symmetry that all consistent string theories possess. Briefly, super-symmetry relates properties of two basic types of particles—bosons and fermions—which cannot be related by any ordinary symmetry. There are a number of good reasons for suspecting that super-symmetry will play a role in the structure of particle physics beyond the standard model. And it turns out that super-symmetric theories are highly constrained, and certain properties of them can be identified, which can be calculated when the interactions are weak, yet cannot change when the interactions become small. That invariance under variation of the interaction strength was key to the discovery of string duality.

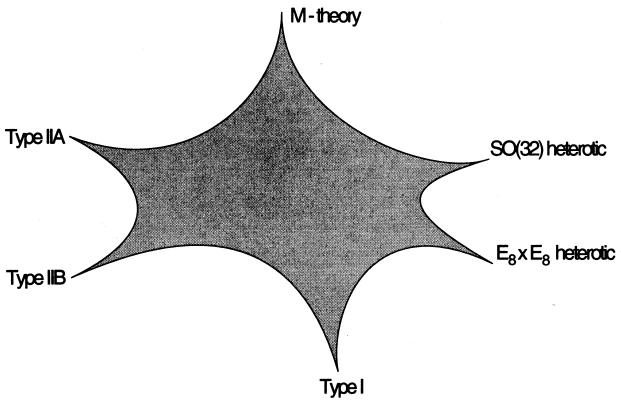
One of the important achievements of string duality has been the determination of the behavior of all of the various consistent string theories (there are five of them) when the interactions become strong. Surprisingly, they all are related to each other, and to one additional theory—not quite a string theory—known as M-theory. The duality relationships introduce additional objects into the theory known as D-branes, which may have 0, 1, 2, 3, … spatial dimensions. (This answers one natural objection to the introduction of strings in the first place: why stop at one-dimensional objects?) The relationships among these theories are illustrated in Fig. 1, which shows six limit points in a large parameter space that admit six different descriptions as a string theory or M-theory. We do not yet understand how to describe the theory when the parameters are out in the middle of this space—the sought-after fundamental principle underlying string theory should provide such a description in the future.

Figure 1.

Space of string vacua. The cusps are limits in which a weakly coupled string description is possible, except for the M-theory limit. [Reproduced with permission from Polchinski, J. (1996) Rev. Mod. Phys. 68, 1245–1258; copyright 1996 by the American Physical Society.]

A second important achievement of string duality has been yet another drastic modification of our notion of space and time. The five consistent string theories all involve 10 space-time dimensions, and M-theory needs 11 space-time dimensions. All but four of these must be curled up into a very tiny compact shape to produce a model of our world, i.e., one with only four observable space-time dimensions. This is an old idea, dating from the earliest attempts to unify gravity with the other forces, and in such models detailed properties of the elementary particles will be determined by the structure of the tiny compact space. The quandary for string theory has been that there is a very large number of such compact spaces to choose among. However, by using string duality we have learned that when nonperturbative effects are included, string theory manages to link together the models based on many such compact spaces, effectively ripping and tearing the fabric of space time yet in a perfectly smooth way using quantum effects. In technical language, the topology of the universe itself is changed. This is an exciting result, as it gives rise to renewed hope that there may be only one possible string-theoretic model of the universe, and it may be possible to eventually predict such features as particle masses and interaction strengths directly from such a theory.

Development has been rapid on many fronts since string duality was introduced. We may be seeing glimpses of the underlying principle manifested in these new results. The challenging task that lies ahead is to discover that principle, and thereby find what may well be the truly fundamental degrees of freedom in our universe.