SINA: Accurate high-throughput multiple sequence alignment of ribosomal RNA genes

Abstract

Motivation: In the analysis of homologous sequences, computation of multiple sequence alignments (MSAs) has become a bottleneck. This is especially troublesome for marker genes like the ribosomal RNA (rRNA) where already millions of sequences are publicly available and individual studies can easily produce hundreds of thousands of new sequences. Methods have been developed to cope with such numbers, but further improvements are needed to meet accuracy requirements.

Results: In this study, we present the SILVA Incremental Aligner (SINA) used to align the rRNA gene databases provided by the SILVA ribosomal RNA project. SINA uses a combination of k-mer searching and partial order alignment (POA) to maintain very high alignment accuracy while satisfying high throughput performance demands.

SINA was evaluated in comparison with the commonly used high throughput MSA programs PyNAST and mothur. The three BRAliBase III benchmark MSAs could be reproduced with 99.3, 97.6 and 96.1 accuracy. A larger benchmark MSA comprising 38 772 sequences could be reproduced with 98.9 and 99.3% accuracy using reference MSAs comprising 1000 and 5000 sequences. SINA was able to achieve higher accuracy than PyNAST and mothur in all performed benchmarks.

Availability: Alignment of up to 500 sequences using the latest SILVA SSU/LSU Ref datasets as reference MSA is offered at http://www.arb-silva.de/aligner. This page also links to Linux binaries, user manual and tutorial. SINA is made available under a personal use license.

Contact: epruesse@mpi-bremen.de

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Multiple sequence alignment (MSA) is a core building block in the analysis of biological sequence data. Phylogenetic tree reconstruction, structure prediction or hidden Markov modeling require MSA to infer residue-level homology or structural or functional identity. The ubiquitous need for MSA computation has made this field an active research topic with over 100 methods published in the past 30 years and numerous review papers discussing their relative merits and deficiencies (Kemena and Notredame, 2009; Notredame, 2007; Pei, 2008).

The dependency of the subsequent analysis methods on the results of the MSA stage and the drastic effect differing MSAs can cause (Löytynoja and Goldman, 2008; Morrison and Ellis, 1997) make alignment accuracy the primary benchmark for novel and improved methods. The task of computing the optimal alignment [as determined by the Sum-of Pairs (SP) score] was shown to be non-deterministic polynomial (NP)-complete (Wang and Jiang, 1994), and is therefore only feasible for very few sequences. For sets of sequences, comprising several thousand or more sequences, heuristic algorithms are used. The most prevalent algorithms are based on the progressive alignment (Feng and Doolittle, 1987) technique, which builds the MSA via a series of pairwise alignments of sequences and partial alignments along the branches of a guide tree.

Sequence data volumes are growing exponentially. This was already observed almost 20 years ago (Rice et al., 1993), and the effect has not diminished since (Leinonen et al., 2010). MSA has long been largely unaffected, because the numbers in which homologous gene sequences were available remained low. For many genes, however, this situation is changing. Especially frequently sequenced marker genes, such as the ribosomal RNA, are rapidly becoming available in volumes exceeding the scalability of traditional alignment techniques. In 2007, the first release of the SILVA SSU database contained over 353 366 small subunit rRNA (SSU) gene sequences (Pruesse et al., 2007). Until September 2011, that database grew more than sevenfold to contain 2 494 582 sequences. The two other large rRNA databases, greengenes (DeSantis et al., 2006a) and RDP (Cole et al., 2009), are of similar size (Amaral-Zettler et al., 2008). The large subunit rRNA (LSU), provided only by SILVA, grew only slightly slower. In 2007, the database contained 46 979 sequences. Currently, it contains almost six times as many sequences (269 498).

Although each of these databases uses a different tool to compute their alignments, the used methods share one important characteristic: rather than computing an alignment de novo, the alignment of each individual sequence is derived from a static reference MSA. The reference MSA implicitly defines a fixed set of alignment columns into which the bases comprising the query sequence are placed. By avoiding mutual comparisons between the sequences considered for inclusion in the final MSA (candidate sequences), the alignment process becomes inherently scalable. Furthermore, the MSA offered by the database provider can be easily extended by database users in the same manner in which the MSA was originally constructed. This, in turn, allows using established alignment-based methods to analyze even large-volume next generation sequencing (NGS) datasets.

The MSA provided by RDP II is computed using Infernal, which implements a model-based approach using a special form of stochastic context-free grammar (SCFG) termed covariance models (CM). These are similar to Hidden Markov Models (HMM) but are able to capture the co-variations caused by the highly conserved secondary structure of rRNAs (Nawrocki and Eddy, 2008; Nawrocki et al., 2009). The Infernal model used by RDP II is computed from a set of several hundred carefully chosen sequences, which were manually aligned to match the well-known secondary structure of the 16S rRNA. The nearest alignment space termination (NAST) method DeSantis et al. (2006b) used by greengenes uses BLAST (Altschul et al., 1990) to obtain a pairwise alignment between the candidate sequence and the best match in the reference MSA. The alignment is then used to map the candidate sequence into the reference MSA via a series of gap character reintroduction and removal operations. Improved implementations of the same principle have been published as PyNAST (Caporaso et al., 2010) and as part of mothur (Schloss et al., 2009). PyNAST uses UCLUST (Edgar, 2010) instead of BLAST, whereas mothur relies on its own implementations of a k-mer search to select the reference sequence and a Needleman–Wunsch type alignment algorithm to perform the pairwise alignment.

In this study, we describe the SILVA Incremental Aligner (SINA) which is part of the rRNA gene processing pipeline of the SILVA ribosomal databases project.

2 ALGORITHM

Our algorithm is based on the assumption that the the sequences contained in the reference MSA are more likely to have a sibling relationship with the candidate sequence than to be direct ancestors or descendants. Because each sibling will have diverged differently from the common ancestor, some parts of the candidate sequence may be resembled most closely by one of the siblings while other parts are more similar to different siblings. Instead of seeking the optimal alignment with a single, best reference sequence (as is done by NAST) or optimizing the SP score between the candidate and all of its siblings, we attempt to align each part of the candidate with the most similar counterpart found in any sibling. To prevent arbitrary alignment in hypervariable regions, we further demand that consecutive “parts” must be joined by at least one mutually aligned, identical base.

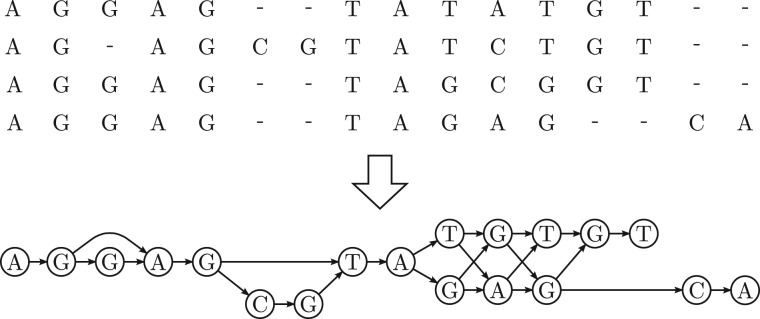
The optimal sequence of parts and the optimal alignment of the candidate with these parts can be found at the same time using dynamic programming. The algorithm used by SINA for this purpose is essentially equivalent to partial order alignment (POA) as described in Lee et al. (2002). The reference MSA is reduced to a directed acyclic graph (DAG) as shown in Figure 1. Each node of the graph represents an evolutionarily unique base. That is, all identical bases sharing a column in the reference MSA are coalesced into one node. Gaps and the order of bases are represented by the graph topology: two nodes are connected exactly if there is a sequence in which the two bases they represent occur consecutively. Thus, there is exactly one path through the graph for each combination of “parts” as defined above. By applying a Needleman–Wunsch (Needleman and Wunsch, 1970) modified to allow a DAG along one axis we obtain the least costly alignment of the candidate and the corresponding path.

Fig. 1.

The alignment of the selected reference sequences is converted from RC-MSA representation (top) to PO-MSA representation (bottom)

The time and space complexity of the alignment stage is decoupled from the size of the entire reference MSA by prefixing a sequence selection stage. This stage chooses a small set of sequences from the results of a heuristic similarity search. The DAG used as alignment template is constructed from these sequences only.

The fixed-column constraint necessary to allow concatenation of the individually aligned sequences into a joint MSA is maintained during DP alignment using a further modification of the Needleman–Wunsch algorithm.

2.1 Reference sequence selection

The sequences to be used in building the alignment template are assembled from the result of a k-mer sequence search on the reference MSA. SINA does not implement this search itself but uses a component from the ARB software package called the PT server (Ludwig et al., 2004). The PT server offers several parameters to configure the k-mer search, all of which are exposed by the SINA command line interface. These parameters are: (i) the value of k. (ii) a number of allowable mismatches at arbitrary positions within each k-mer. (iii) a range of alignment columns to which the search for shared k-mers is restricted. (iv) a fast mode which searches only for k-mers beginning with ‘A’. (v) a ‘non-relative’ mode which computes the fractional k-mer count by dividing the number of shared k-mers by the query length rather than by the minimum of the lengths of query and matched sequence.

On basis of the findings in Edgar (2004a), we apply a logarithmic transformation to obtain a measure in approximately linear relationship with fractional identity. Here, F is the fractional k-mer count, L_q is the length of the query sequence and Y is the obtained measure.

(1)

After executing the search, SINA iterates through the matches in order of descending identity and decides according to the following rules and parameters which sequences are to be kept and passed into the alignment template construction stage. (i) The first fs-min sequences are always kept. (ii) Up to fs-max sequences are kept if their similarity to the candidate is at least fs-msc. (iii) Further sequences of at least fs-full-len bases length are kept independent of their match score until the set of selected sequences contains at least fs-req-full such sequences. (iv) Further sequences are kept if they cover the start and end of the gene as determined by the alignment positions gene-start and gene-end until at least fs-cover-gene such sequences have been found. The latter two rules are designed to ensure that the outer edges of the alignment are covered even if the reference alignment contains partial sequences.

As a performance optimization, the candidate sequence is compared to all sequences in the reference set. If it is found to be contained in one of them, the candidate sequence is aligned by simply copying the matching part of the alignment of the reference sequence. An explaining remark is made in the log and the remaining alignment stages are skipped.

2.2 Construction of alignment template

We use a DAG to represent the selected set of aligned reference sequences. The nodes of this graph correspond to unique base-column combinations in the reference sequences. The nodes are linked by edges if the corresponding bases occur consecutively in any of the reference sequences (Fig. 1). Consider the aligned reference sequences as lists of base-column pairs. Then, for each such sequence, there is a path in the graph comprising an equivalent list of nodes. This type of graph is described as ‘partial order MSA’ (PO-MSA) by Lee et al. (2002). The term expresses that the structure itself only imposes a partial order on the bases comprising the alignment, whereas the traditional ‘row-column MSA’ (RC-MSA) representation imposes a total order. When storing a list of sequence identifiers with each edge, exact conversion between the two representations is possible.

Our method of constructing a PO-MSA from a RC-MSA and the data stored within the nodes differs slightly from the method described in Lee et al. (2002). We preserve the frequency of the represented base in its column to be used as a weight during the alignment process. Also, we do not construct the PO-MSA by iteratively adding sequences and merging those nodes that represent homologous bases. Instead, we use a scan-line algorithm passing horizontally through the input RC-MSA: For each sequence S_i in the RC-MSA the last created node N_i is remembered. We then pass through all alignment columns j. In each column, one node is created for each non-gap character encountered. For each sequence S_k in which the character was encountered, an edge from the last remembered node N_k is created to the new node and the new node is remembered as N_k. After all columns have been processed, duplicate edges are removed.

2.3 Dynamic programming alignment

To align a candidate sequence with an alignment template in PO-MSA format, we extend the dynamic programming recursion from the Needleman–Wunsch algorithm. Our extension is similar to that used by POA. In Needleman–Wunsch and its derivative algorithms, two sequences A and B are aligned by computing a matrix H such that the value of H_i,j is the optimal score for the alignment of the prefixes A₁… A_i and B₁… B_j of lengths i and j of the sequences A and B. The value of each cell H_i,j is defined as a function of the scores of the three prefix pairs where either one or both of the prefixes is one item shorter. Given a function S(i,j) defining the matching score for A_i and B_j and using g as the score for a gap, we have:

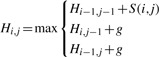(2)

This recursion is generalized to allow using a PO-MSA instead of one of the sequences by replacing the notion of ‘prefix of length i’ with ‘path leading up to node A_i’. Leaving B as a sequence, H_i,j then becomes the optimal score of the alignment of the prefix of B of length j with any path in A leading to A_i. Using A_p→A_i to denote that an edge from A_p to A_i exists, we arrive at:

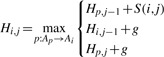(3)

2.3.1 Affine gap penalties

To support affine gap penalties of the form g_k=g_open+(k − 1)g_extend, SINA uses a further extension of this induction, modified in the same way as was shown by Gotoh for the original induction (Gotoh, 1982):

(4)

(5)

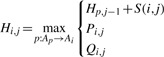(6)

2.4 Scoring

Although SINA supports the use of arbitrary substitution matrices to define S(i,j), the default is to use 2 as the score for matching bases and -1 for mismatching bases. IUPAC encoded ambiguities are treated as a match if a match is conceivable (i.e., ‘N’ matches anything).

SINA also implements two methods for weighting S(i,j) according to the variability in the reference MSA: (i) the score is multiplied with the frequency with which the base A_i occurs among the selected reference sequences in column i according to a configurable scaling factor. (ii) the score is multiplied with a per-column conservation indicator derived from a conservation profile computed within ARB (‘positional variability by parsimony (PVP)’, see Supplementary Materials). After POA sequence alignment, the total score is normalized via division by the sum of the weighted rewards for a match in each template column contributing to the alignment.

2.5 Treatment of sequence ends

SINA uses what is sometimes referred to as ‘overlap’ alignment. Although global alignment allows no unaligned sequence tails and local alignment allows both sequences to have unaligned tails, overlap alignment allows only one unaligned tail at either end. At both ends, either the candidate sequence or the template is aligned until its last base. The cost-free terminal gap is achieved by initializing H_0,j and H_i,0 with 0 and choosing the best scoring cell H_i,j where at least A_i or B_j has no successor to start the backtracking through the alignment matrix.

Three policies are provided for dealing with the unaligned sequence tails: (i) The unaligned bases may be omitted from the final alignment. (ii) The unaligned bases may be placed consecutively following the outermost aligned base. (iii) The unaligned bases may be placed at the out-most columns of the MSA.

2.6 Treatment of insertions

The alignment of the candidate with the PO-MSA yields column positions only for substitution events (matches and mismatches). Although deletions in the candidate with respect to the reference sequences pose no problem, appropriate column positions must be determined for inserted bases. If the number of alignment positions between the two bases enclosing an insertion, that is the size of the gap in the reference alignment, is larger than the insertion, the insertion is placed right-bound in this gap. SINA offers three choices for dealing with insertions that cannot be accommodated by the reference MSA: (i) The insertion may be shortened as required by erasing bases. (ii) The bases surrounding the insertion may be shifted outwards. (iii) A modified DP algorithm may be used that disallows insertions not mappable to the reference MSA.

Our base shifting algorithm is a greedy search for free alignment positions to the left and right of the insertion which we believe to be equivalent to NAST. If the gap closest to the insertion is of insufficient size, the bases between this gap and the original insertion are included in the insertion and the process repeated until the insertion can be placed.

As an alternative option, we further extended the DP alignment to observe constrained alignment space by only considering gap open and gap extension events that can be accommodated by the reference MSA. For a node A_i in the template DAG, the amount of free columns f_i to the right of it is defined as the difference between its alignment position and the lowest alignment position of its immediate successor nodes minus one. Ignoring gap extension, the induction defining H becomes:

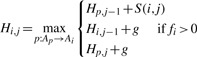(7)

Note that this is equivalent to using a cost function for gaps which assigns an infinite penalty for inserting a gap into the reference alignment. However, the Gotoh optimization for DP alignment with affine gap penalties requires the cost for extending gaps to be monotonically decreasing (Gotoh, 1982). Nonetheless, we have implemented an analogous extension, aware that the induction we use constitutes a loss of optimality where alignment space is insufficient. F_i,j is set to f_i when Q_i,j is based on a gap open event and set to F_i,j−1−1 if Q_i,j is based on a gap extension.

(8)

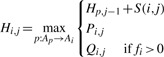(9)

3 IMPLEMENTATION

SINA has been implemented in C++ making heavy use of generic programming techniques. External components used include several BOOST libraries, the ARB database library and the ARB PT server. ARB and FASTA formats are supported for sequence input and output. Per sequence meta data can be exported via ARB database fields, FASTA headers, FASTA comments or a separate file in comma-separated value (CSV) format. The reference MSA must be in ARB format. Conversion of reference alignments from FASTA to ARB format is possible with SINA

3.1 Reverse complement detection

If instructed, SINA will execute the k-mer search multiple times using the reversed and/or complemented candidate sequence. If an orientation different to the original yields a better best scoring match, the candidate is transformed accordingly.

3.2 Sequence search and classification

We also implemented a simple search and classify stage. The search uses the alignment (as computed by SINA or by an external tool) to quickly determine fractional identities. Both an exhaustive search and a quick search considering only the best matches from a k-mer search can be performed.

Also, a least common ancestor (LCA) classification can be performed if the searched database contains taxonomy data in materialized path format. LCA classification can be relaxed to allow a percentage of outliers.

3.3 Visualization of alignment differences

Manual inspection of the alignment differences (resulting, for example, from different tools, changed parameters or modifications to the reference MSA) is supported via a differencing function. This function prints a coloured RC-MSA representation of the sections of the alignment in which the reference alignment and the alignment to be inspected differ. Columns containing only gap characters are removed from this view. The reference sequences used to construct the PO-MSA template are listed together with the new and the original alignment. If the SINA alignment stage was bypassed, the SINA search stage can be used to select suitable sequences for display in combination with the two different alignments of the candidate. Rows are consolidated such that only unique alignments remain.

3.4 Parameter tuning

The default parameter settings in SINA were tuned for the alignment of SSU rRNA gene sequences. To simplify determining correct parameters for other genes, SINA offers automated evaluation of alignment accuracy using a leave-query-out approach. In this mode, each sequence in the reference alignment is newly aligned (excluding the sequence itself from the set of selected reference sequences), the result compared to the original alignment and the average scores reported. Alignment parameters such as match and mismatch scores, gap penalties or k-mer length can then be adjusted to maximize this score.

To simulate more difficult alignment cases where the candidate sequence is distant to the closest match in the reference MSA, reference sequence selection may be constrained using a maximum identity parameter. The identity of each sequence considered during reference sequence selection with the candidate sequence is computed using their original alignments. Sequences with an identity higher than the configured threshold are discarded and not included in computing the alignment template.

4 EVALUATION OF SINA

MSA computation methods are generally validated by quantifying their ability to accurately reproduce benchmark MSAs known to be of high quality. The degree to which a tool was able to reproduce the benchmark MSA is measured by determining the fraction of exactly reproduced alignment columns [CS score (Thompson et al., 2011)] and the fraction of correctly aligned residue pairs [Q score (Edgar, 2004b), also called SP-score (Thompson et al., 1999)]. This measure was used in the evaluation of SINA. However, we expect significantly higher scores than commonly achieved by de novo methods (see Discussion).

For evaluation, we used the three MSAs provided with BRaliBase III (5S rRNA, tRNA and U5) and the manually aligned subsets of the MSAs provided by SILVA (SSU and LSU). The SILVA alignments where chosen because they are the largest manually created alignments available to us. The BRaliBase alignments were chosen to complement the SILVA alignments with test data from a source not affiliated in any way with the authors of this article. The SSU and LSU test data were generated by excluding all sequences in the SILVA databases that were themselves aligned by SINA, leaving only manually aligned sequences from the SILVA seed. This test data are equal to the published subsets of the SILVA seed alignments. The SILVA seed alignments are based on alignments published by the ARB project in 2004. During construction and maintenance of the SILVA seed, sequences were removed if they could not be aligned unambiguously and new sequences added to enhance phylogenetic coverage. All sequences in the seed (and therefore in the test data) were aligned manually by rRNA alignment experts. The alignment itself is guided strongly by the secondary and tertiary structure of the respective rRNA. The SSU and LSU test data are made available at ftp.arb-silva.de/SINA/test_data/.

We compared SINA with the NAST implementations by mothur and PyNAST. The align.seqs command from mothur (version 1.19.1) was used with default parameters. PyNAST (version 1.1, UCLUST version v1.2.exportedq, cogent version 1.5.0) was used with identity threshold below which it refuses alignment lowered to 0.0001. Minimal reference sequence length was set to 50 for SINA and PyNAST. SINA (version 1.2.8) was also configured with appropriate values for full-length sizes (5S rRNA: 120, tRNA: 80, U5: 80, SSU: 1400, LSU: 2900). The k-mer size used by SINA was lowered to eight for the tRNA and U5.

Three different benchmarks were performed, one using the four smaller MSAs and two using the large SSU MSA. The three benchmarks differ in the way the benchmark MSA is split into the set of sequences to be used as a reference MSA and the set to be used for measuring the alignment accuracy. Because all three tools expect sizable reference MSAs, the benchmark based on the four smaller MSAs follows a ‘leave-query-out’ scheme: every sequence in the benchmark MSA is aligned using all other sequences as reference MSA (benchmark 1). The SSU MSA is large enough to create reference MSAs of different size by randomly sampling sequences. Sampling was repeated 100 times, once using 1000 sequences and once using 5000 sequence. Candidate sequence sets of equal size were sampled from the remaining sequences.

The typical identity between each candidate and its best matching reference sequence remains very high, even when sampling a reference MSA of only 1000 sequences. To obtain more difficult test cases having lower rates of identity, we constrained the reference sequence selection algorithm to exclude sequences above a cut-off value (see section parameter tuning). Using 21 cut-off values between 50 and 100% at 2.5% intervals (100% being equivalent to leave-query-out benchmarking), we examined the accuracy in relation to the identity of the candidate with the reference. This benchmark was repeated for numerous sets of parameter settings and also used for parameter optimization (benchmark 2).

Lastly, we repeated benchmark 2 with an alternative alignment template implementation relying on column profiles rather than a PO-MSA for comparison. All other settings including the selection of reference sequences remained identical to the original benchmark 2.

5 RESULTS

Table 5 shows that SINA performed better than both mothur and PyNAST for all MSAs used in the leave-query-out benchmarks. Friedman rank tests using the results for each sequence as blocks showed significant P-values (2*10⁻⁵) for all pairs of tools in each data-set except PyNAST vs mothur in the U5 dataset (0.55).

Table 1.

Results from leave-query-out benchmarks

	5S rRNA	tRNA	U5	SILVA LSU
Dataset sequences	597 (%)	1113 (%)	232 (%)	1588 (%)
PyNAST	98.6	96.4	94.0	98.9
mothur	97.5	92.1	93.3	98.9
SINA	99.3	97.6	96.1	99.2

The reported percentages are the average Q scores. Only sequences aligned by all three tools where considered.

Table 2.

Results using test data sampled from the SILVA SSU dataset

	All SSU samples		<80 % Identity
Reference size	1000	5000	1000	5000
sequences	100 000	500 000	5443	8811
mean identity (%)	92.34	95.24	75.71	75.9
(PyNAST1) (%)	96.7	97.6	90	89
	(0.20)	(0.08)	(1.7)	(1.5)
mothur (%)	96.6	97.8	88	88
	(0.23)	(0.07)	(2.0)	(1.3)
SINA (%)	98.9	99.3	94	93
	(0.12)	(0.03)	(1.2)	(1.1)

The average Q scores shown were obtained by randomly sampling sequences from the SILVA SSU-based test data to create 100 reference MSAs and benchmark sets. This was repeated once with a reference MSA size of 1000 and once with a size of 5000. The SD between Q score averages from each of the 100 reference MSAs is shown in parentheses. The two columns on the right show the results when considering only difficult cases where the candidate sequences have <80% identity with all sequences in the respective reference MSA.

^a PyNAST failed to align 0.5% of the sequences.

Table 5 shows the results for the benchmarks using candidate sequences and reference MSAs sampled from the SSU dataset. We show the average Q scores from all successfully aligned sequences, although this slightly inflates the scores for PyNAST which failed to align all candidate sequences. Lowering the identity threshold below which alignment is refused by PyNAST to 0.0001 reduced the number of failed alignments. However, of the 100 000 sequences aligned using 1 k reference MSAs, PyNAST still failed to align 547. Of the 500 000 sequences aligned using 5 k reference MSAs PyNAST failed to align 2750 sequences. The average Q scores achieved by mothur for the sequences refused by PyNAST were 91.36 and 94.8%, respectively. The average Q scores achieved by SINA for these sequences were 97.45 and 98.46%.

In addition to the average Q scores, we show the SD between averages computed for each of the 100 samples. The variance between tests is much lower than the differences between tools, indicating that the reported Q score averages are sufficiently robust for comparing the tools. Pearson rank tests using the per sample averages as blocks showed P-values below 2×10⁻⁵ for all pairs of tools except PyNAST versus mothur in the 1 k reference MSA benchmarks.

The second benchmark showed marked differences in alignment accuracy for varying reference sequence set sizes. The average Q scores rises over all identity thresholds with each increase in the number of reference sequences used. Above 40 sequences, the effect tapers off (Fig. 2, Supplementary Fig. S1). The same can be observed for the average fraction of bases that were part of an insertion with respect to the template PO-MSA (Fig. S2). Configuring SINA to use a column profile as alignment template yielded lower accuracy (Fig. 3). Especially, when candidate and reference sequences share a lower fractional identity, alignment accuracy drops significantly. Increasing the reference set size beyond five had a detrimental effect.

Fig. 2.

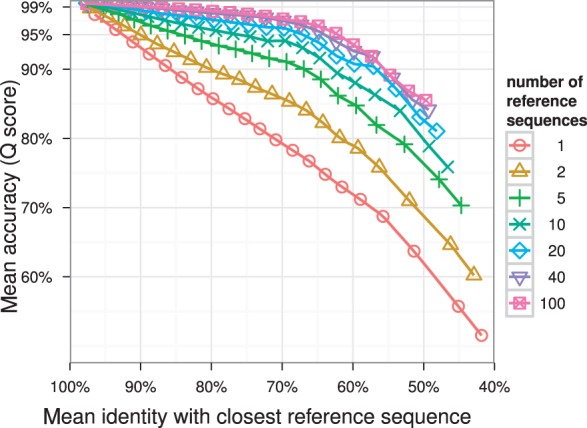
SINA alignment accuracy decreases almost linearly with the shared fractional identity of candidate and reference when using one reference sequence (red line). Using larger numbers of reference sequences markedly increases accuracy

Fig. 3.

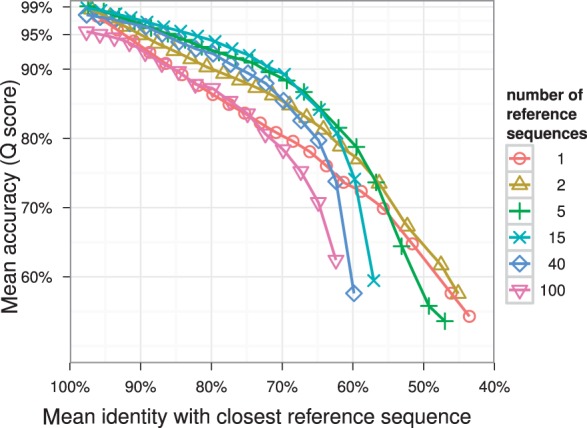
An alternative implementation which used simple column-profiles built from the selected reference sequences showed overall lower accuracy. Increasing the number of reference sequences quickly led to a degradation in accuracy

At a reference set size of 40 sequences, and match/mismatch scores of 2 and −1 (Fig. S3), a gap open penalty of 5 and a gap extension penalty of 2 was found to perform best (Fig. S4). Enforcing the inclusion of at least one sequence of at least 1400 bases in the reference set improved results at identity thresholds lower than 0.9 visibly (Fig. S5). Using the modified DP, algorithm to maintain fixed columns gave a slight improvement over using base shifting (Fig. S6). Varying the k-mer size had little impact, values between 8 and 10 were found to produce best results (Fig. S7). Using only k-mers beginning with ‘A’ resulted in a slight accuracy degradation (Fig. S8). Among the three methods for weighting match/mismatch scores per column using the base frequency in the reference set performed best by far, improving Q scores by almost 0.5% points (Fig. S9).

We did not benchmark speed and memory requirements specifically as these depend heavily on sequence length, reference MSA size and parameter settings. In the tests using reference MSAs sampled from the SSU dataset, we observed mothur to align roughly 20 sequences per second per core and SINA to align roughly 2 sequences per second per core. PyNAST was as fast as mothur in the benchmark using a reduced width alignment and matched SINA when using the full 51 000 column MSA. Tests were executed on a non-dedicated heterogeneous cluster comprising current 2, 4 and 8-way servers equipped with Intel and AMD quad core CPUs.

6 DISCUSSION

We reported the average Q scores because they are commonly used as accuracy indicator for sequence alignment. However, the values are not directly comparable to results obtained for de novo methods as these lack the benefit of a guiding reference alignment. Given a consistent reference alignment, selecting a reference sequence closely resembling the candidate sequence and transferring the alignment positions of the shared segments suffices to perfectly align those shared segments. The identity between the candidate sequences and the available reference sequences should therefore be considered as a baseline when interpreting the results. This also affects the precision with which accuracy can be measured. As can be seen in Table 5, the variance among sampled test cases was extremely low. When considering only those sequences that had an identity with the reference sequences of <80%, variance increased by an order of magnitude. We therefore believe that assessing alignment accuracy to a precision of 0.1% is permissible for the benchmarks we performed.

In interpreting the results, it may also be more informative to consider error rates, rather than the fraction of correctly aligned bases. For example, PyNAST achieves 98.55% accuracy (Q) on the BRAliBase 5S rRNA dataset, whereas SINA achieves 99.23%. This amounts to error rates of 1.45 and 0.77%, thus SINA placed only half as many bases in the wrong columns. Because sequence alignment is only one of many sources for error in sequence alignment, the permissible margin of error depends on many factors. We can, however, determine an upper bound at which it is more sensible to forgo extension of the reference MSA and instead use a homology search to map candidate sequences to results based solely on the reference MSA. In this case, the error would be equivalent to the distance between candidate and best matching reference because both error and distance are measured as a fraction of differing base positions. The average distance may therefore be used as a point of reference for the permissible error. Methods expecting a MSA as input do not commonly incorporate measures to deal with errors in the MSA. They will also make mutual comparisons between the aligned candidate sequences. Demanding that the error be at least an order of magnitude lower than the distance therefore seems prudent.

According to the SSU benchmark, the distance between candidates and references averages to 7.66% using 1000 reference sequences and 4.76% using 5000 reference sequences. The same benchmark shows error rates for the NAST-based methods of above 3.37 and 2.19%. In absolute numbers, this means that when using a 5k reference MSA, the candidates and their best matching reference sequences where on average distinguished by 71 positions (according to the original alignment). Thirty-two positions where misaligned by NAST. SINA fares much better. At 0.74% error rate ( or 11 misaligned positions), its error was only a third of that produced by PyNAST and mothur. Although the aforementioned order of magnitude difference between error and distance would demand at most seven misaligned positions, we may have reached the resolution of the benchmark.

When manually inspecting the positions comprising the error, we found that most cases were related to extensions of homo-polymers, conflicts between primary and secondary structure alignment or inconsistencies in the reference MSA. From the SILVA, rRNA gene datasets and the online SINA alignment service, both of which having been available for several years now, we were able to gather user feedback on these shortcomings. In general, users stated that the changes they made in manually refining the SINA alignment were related to the secondary structure. However, we were unable to collect sufficient problematic sequences in which secondary structure awareness would clearly improve alignment accuracy to build a dataset for benchmarking. We therefore concur with the observation made by Kemena (Kemena and Notredame, 2009) that much larger, high quality benchmark MSAs are needed, especially for improving and evaluating the accuracy of high throughput MSA methods. Although the dataset extracted from the SILVA SSU Ref database used in the evaluation of SINA is of high quality, it is merely a subset of the SILVA SSU seed. As such, it lacks a representative distribution of distances between sequences and would require further refinement and extension to become a good benchmark. Furthermore, a benchmark MSA explicitly constructed to comprise fewer columns than a correct alignment demands would be required to test the performance of alternative methods for constraining the number of columns. Because we expect that many other genes besides the RNAs will soon become available in numbers surpassing what can be feasibly aligned using de novo techniques, we also see a need for advanced interactive tools to support building and curating large MSAs to be used as benchmark or reference MSAs. Once benchmarks of sufficient resolution at high alignment accuracy levels become available, it may be interesting to investigate whether improving the POA based stage in SINA with methods used by de novo MSA tools such as Infernal, MUSCLE or MaFFT can further enhance alignment accuracy.

7 CONCLUSION

We have shown that combining a k-mer distance search with POA incremental MSA to integrate candidate sequences into an existing MSA yields highly accurate results. Using multiple reference sequences as a basis for the alignment of the candidate sequences significantly improves alignment quality. Dynamically selecting a low, fixed number of sequences from which the alignment template is constructed rather than basing the alignment on a global template built from all reference sequences allows the use of very large reference MSAs, lowering the number of bases remaining unaligned because they do not occur in the reference MSA. Furthermore, suboptimal alignment behaviour for groups of novel candidate sequences can be easily corrected by manually optimizing the alignment of one of these sequences and adding it to the reference MSA.

With SINA, we provide a versatile and flexible tool for accurate high-throughput MSA that has proven its reliability and robustness over several years of testing in the context of the SILVA project.