Magnetic Relaxometry with an Atomic Magnetometer and SQUID Sensors on Targeted Cancer Cells

Abstract

Magnetic relaxometry methods have been shown to be very sensitive in detecting cancer cells and other targeted diseases. Superconducting Quantum Interference Device (SQUID) sensors are one of the primary sensor systems used in this methodology because of their high sensitivity with demonstrated capabilities of detecting fewer than 100,000 magnetically-labeled cancer cells. The emerging technology of atomic magnetometers (AM) represents a new detection method for magnetic relaxometry with high sensitivity and without the requirement for cryogens. We report here on a study of magnetic relaxometry using both AM and SQUID sensors to detect cancer cells that are coated with superparamagnetic nanoparticles through antibody targeting. The AM studies conform closely to SQUID sensor results in the measurement of the magnetic decay characteristics following a magnetization pulse. The AM and SQUID sensor data are well described theoretically for superparamagnetic particles bound to cells and the results can be used to determine the number of cells in a cell culture or tumor. The observed fields and magnetic moments of cancer cells are linear with the number of cells over a very large range. The AM sensor demonstrates very high sensitivity for detecting magnetically labeled cells does not require cryogenic cooling and is relatively inexpensive.

1. Introduction

Magnetic relaxometry is a method of measuring the magnetic field decay of magnetic nanoparticles following a magnetizing pulse. The decay time is strongly influenced by the size of the nanoparticles [1] and if they are bound to surfaces. The size dependence follows approximately the exponential of the volume of the particle and thus the time of decay changes rapidly with particle diameter. The mechanism for decay is described by different theoretical approaches depending on whether the particles are free or hindered. These properties offer advantages in situations where magnetic sensors are used to distinguish bound vs unbound particles in a variety of applications. As the nanoparticles are typically superparamagnetic for magnetic relaxometry, relatively small magnetization fields are required to align the particles. Weak field sensors are typically used to measure the decaying field when the number of nanoparticles in the sample is relatively small.

Magnetic relaxometry has been shown to have a number of advantages in detecting and imaging biological samples using live cells and animal models [2]. Applications have been diverse and, for example, include detection of T-cells associated with transplant rejection [3], blood platelets [4], leukemia cells [5] and breast cancer [6]. The method also holds promise as an in vivo diagnostic and imaging procedure for a variety of diseases. The advantages obtained using magnetic relaxometry include high sensitivity, high contrast, and no exposure to ionizing radiation or high magnetic fields. Magnetic relaxometry is still an emerging technology with many options to improve sensitivity and imaging accuracy in biological applications.

In the method of magnetic relaxometry discussed here, magnetic nanoparticles are briefly magnetized by a small magnetic field pulse, and their decaying magnetic fields are observed following this pulse by sensitive magnetic field detectors. Properties of magnetic nanoparticles are important in the application of magnetic relaxometry and characterizing and improving their magnetic properties is an active area of investigation [7, 8]. In order for magnetic relaxometry to be used in applications involving biological samples, the particles must fall within definitive size ranges, on the order of tens of nanometers, and have high magnetic moments. These particles are classified as superparamagnetic, since they are single domain, and all of the atomic magnetic moments in the domain are aligned. When an ensemble of such particles is exposed to an external field, the particle moments collectively align to produce the observed net magnetic moment. This method separates out particles that are bound to objects, such as cells, from those that are free to rotate in a suspension liquid [9]. For unbound particles, the decay times are determined by Brownian motion and occur in microseconds. For bound particles, the decay is through a reorientation of the electron orbits of the nanoparticle core, and the time constant is determined by the Néel mechanism [10] which scales approximately as the exponential of the volume of the particle. These properties have also been extensively investigated theoretically [11, 12].

The sensitivity of the approach is determined by the net magnetic moment induced in the nanoparticle ensemble by the magnetizing pulse, the number of nanoparticles bound in the sample, and by the sensitivity of the magnetic field sensors. Weak magnetic field sensors fall into a variety of categories depending upon their sensitivity. Most notable are giant magnetoresistive (GMR) [13], vibrating sample magnetometers [14], SQUID sensors [15], and atomic magnetometers (AM) [16, 17]. The majority of magnetic relaxometry data has been obtained using SQUIDs to detect the decaying magnetic fields following the magnetizing pulse [2, 9]. These sensors typically operate at liquid helium temperature, 4 K, although high temperature SQUIDs operating at 77 K are sometimes used but are less sensitive [15]. SQUID sensors use a sensing coil that is inductively coupled to the actual SQUID loop, and these coils can be arranged in a variety of configurations. One such configuration is as an axial gradiometer, where a superconducting wire is wound as several coils, arranged along a common axis in such a manner as to measure the gradient of the magnetic field. In this arrangement, external fields from distant sources are cancelled due to their uniformity at the sensors whereas local sources produce an effective current in the loops that yield a net field to the SQUID loop. These gradiometers may be of 2^nd order to provide higher cancellation [2]. This type is used in the work reported here. The sensitivity of this configuration for local sources is determined by the baseline (the separation of the multiple canceling coils) of the gradiometer.

A new approach to magnetic field sensors for magnetic relaxometry applications is the use of an AM. In recent years, AMs operating in a low-field, high-density spin-exchange-relaxation-free regimes have achieved sensitivities rivaling SQUIDs [17, 18]. AMs have been applied to the measurement of cardiac magnetic fields from mice [19] and humans [20, 21] and to the measurement of magnetic fields from the human brain [22, 23]. Detection of magnetic nanoparticles for potential application in biomolecular labeling has also been carried out [24]. Recently, a highly miniaturized AM magnetometer with a sensitivity of 100 fT/√Hz has been used for magnetic relaxometry, comparing AM and SQUID detection of artificially immobilized nanoparticles [25].

In the results presented here, the AM application is extended to superparamagnetic nanoparticles bound to cancer cells using a system with a 15 fT/√Hz noise floor limited by the intrinsic thermal noise of the magnetic shields surrounding the AM sensor. An extensive study of various types of cancer has been carried out using SQUID sensors [2] and the AM measurements can be taken and compared to these results. The AM and SQUID data reported here demonstrate the application of these sensors for detecting relatively small numbers of cancer cells, as well as demonstrating the high contrast for detecting cells vs unbound nanoparticles.

2. Material and Methods

2.1 Magnetic Nanoparticles

The magnetic (Fe₃O₄) nanoparticles were obtained from Ocean Nanotech (Springdale, AR). These particles (SHP-28-50 lot JL229) were single core and relatively monodisperse in size, with a mean diameter of 22.5 nm and a standard deviation of 2.3 nm, very close to the theoretically predicted optimal size (24 nm) for the magnetic relaxometry method used here [11]. The particle sizes were measured from transmission electron microscopy images of ~1500 particles. The temperature dependence of the relaxometry signal from these particles was measured over a range of 0° to 40°C using the SQUID sensor system and found to be negligible. The details of characterization of similar nanoparticles have been previously described [7].

2.2 Nanoparticle and Cancer Cell Samples

Nanoparticles were prepared as either samples in solution or dried. Unbound particles were prepared by mixing 20 °l of stock nanoparticle solution, at a concentration of 10 mg [Fe]/ml, in 30 °l deionized water. The solution sample was sealed in a 5 mm thin-walled glass tube, which was then placed in the cylindrical portion of a 0.6 ml Eppendorf tube. No precipitation was observed in this solution during experiments. For the dried sample, 20 °l of the same nanoparticle solution were applied to the tip of a cotton swab and allowed to dry.

The cells used in these experiments were MCF7/Her2-18 breast cancer cells that overexpress the Her-2/neu receptor on their surface and were kindly provided by Mien-chi Hung [26]. Flow cytometry on these cells indicates a high expression of Her-2 (of order 10 million sites per cell) [6]. The Ocean nanoparticles were conjugated, using the carbodiimide coupling method to a monoclonal antibody that binds to the Her2/neu receptor on the cells. Three million cells were incubated with the Her-2 conjugated nanoparticles for 15 minutes, centrifuged at 300 g for 10 minutes, washed in phosphate buffered saline (PBS), and fixed with 4% paraformaldahyde. Figure 1 is a Transmission Electron Microscope (TEM) photo of a cancer cell showing that the nanoparticles are bound to the surface. This is also characteristic of the MCF7/Her2-18 cells. The photo shows that large numbers of the nanoparticles coat the surface with typically hundreds of thousands per cell, exceeding the number of nanoparticles that could coat a cell surface uniformly.

Fig. 1.

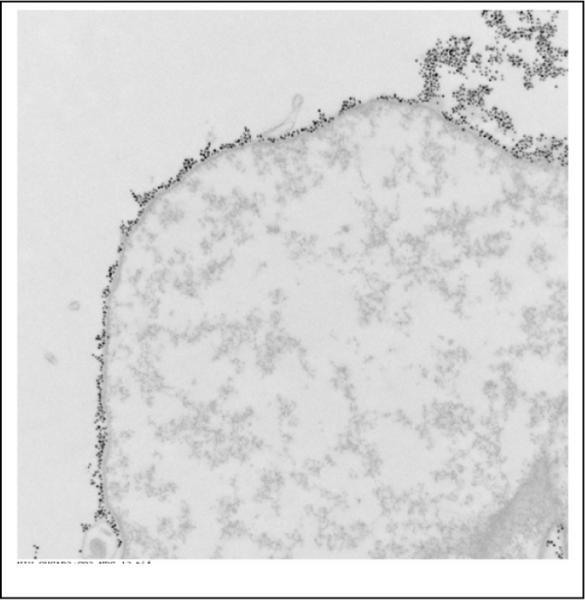
A TEM of a cancer cell showing that the nanoparticles are bound to the surface and completely cover the surface. The particles were bound to this cell with a specific antibody.

For the AM experiments the cells were then solidified in a 1% agarose gel in a 0.6 ml Eppendorf tube. The conical bottom of the tube was filled with gel so that the solidified cells were located in the cylindrical part of the tube for convenience of winding a magnetizing coil around the tube for the AM experiments.

2.3 The SQUID system for magnetic relaxometry

A seven channel SQUID sensor system (4D Neuroimaging, San Diego, CA) was used to obtain the SQUID magnetic relaxometry data. The sensor system consists of seven 2^nd-order gradiometers with a baseline of 4 cm [2, 15]. The sensors are arranged with one central sensor and six surrounding this in a circle of 2 cm radius and pitched at an angle of 10°. All of the sensors are submerged in a liquid helium dewar with the closest sample-to-sensor distance being 1.5 cm. Samples are placed under these sensors, at typical distances of 2 – 3 cm from the sensors, on a non-metallic stage capable of movements in three dimensions. The bandwidth of the system is 4 kHz, determined by a 4 kHz low-pass filter applied to each sensor channel.

A large set of Helmholtz coils is placed around the SQUID system and centered at the position of the gradiometers to minimize effects of pulsing on the pickup coils. These coils provide the magnetizing field for the magnetic nanoparticles. The SQUID system is operated without magnetic or RF shielding, and the noise floor is limited by external magnetic and RF fields to approximately 2 pT (2 × 10⁻¹² T).

Magnetic moments of samples were obtained by pulsing the Helmholtz coils with a field of 49 G for 0.75 s and measuring the decay time for 2.215 s following a 35 ms period to allow induced currents in the SQUID sensor system to dissipate. This 3 s measurement sequence was repeated 10 times and signal averaging performed to increase the signal-to-noise ratio. The data acquisition was controlled by a program written in CVI Lab Windows (National Instruments, Austin, TX) that provided timing sequences to the power supply for the Helmholtz coils and placing the SQUIDs in reset mode during pulsing. The SQUID seven channel voltage signals were digitized in a National Instrument PX18336 16 channel digitizing chassis. Pulse sequence parameters, display options, and output options were programmed into the CVI code with the final data stored as a tdms file for compression. An analysis program, also written in CVI, was used to analyze the resulting data files to extract the magnetic moments after signal averaging, correcting for flux jumps in the SQUIDs, and removing line frequency contaminants.

Magnetic moments were obtained by first fitting the decaying magnetic fields following the pulse with a logarithmic term that corrected for DC shifts in the SQUID output. Then an exponential term was used to fit the early decay data to50 ms after the end of the magnetizing pulse. The seven values obtained from this extrapolation for each channel were then used in a dipole model fitting routine to extract the magnetic moment and position of the sample. This solution of the magnetic inverse problem was accomplished using a least squares code, based on the Levenberg-Marquardt algorithm, which varied the position and magnitude of a theoretical magnetic dipole until the resulting theoretical fields matched the experimental fields with minimum error. The analysis code then displayed the parameters of the fit along with three-dimensional confidence limits on the position of the particle and standard deviation errors on the magnetic moment determination.

2.4 The AM system for magnetic relaxometry

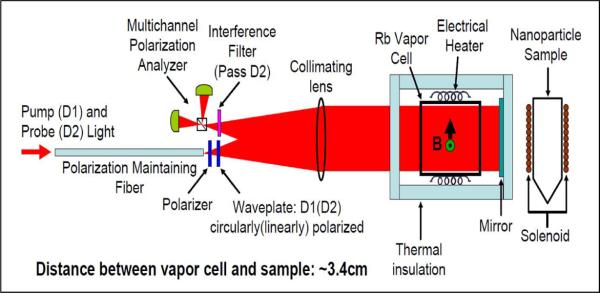
The principle of operation of the AM used in this study is based upon the interaction of atomic electron spins with an external magnetic field. Details of the design and operation of the AM are found in [23, 27], but a brief description is provided here. A schematic drawing is given in Figure 2. The electron spins of an alkali metal vapor, produced inside a heated glass vapor cell containing a small droplet of ⁸⁷Rb, are aligned via optical pumping with a circularly polarized pump beam. The aligned spins form a collective magnetic moment which responds to an external magnetic field. The orientation of the collective magnetic moment is determined by passing a linearly polarized probe beam through the vapor cell. The field-dependent Faraday rotation is measured via polarization analysis of the probe laser beam, giving a measure of the magnetic field. The analyzer output signal is a dispersive Lorentzian centered at zero magnetic field, and the linear portion is used as a field discriminator.

Fig. 2.

Schematic of the atomic magnetometer. Pump and probe light enters the magnetometer through the optical fiber, passes through polarization optics, and is collimated by the lens. The light then passes through the atomic vapor cell, the magnetically sensitive volume of the magnetometer, and the mirror reflects the light back through the cell and the lens to the polarization analyzer. The interference filter allows only probe light to enter the polarization analyzer.

The AM design is unique from more common implementations for several reasons. First, the pump and probe lasers are tuned to different strong atomic transitions in rubidium, the D1 (795 nm) and D2 (780 nm) lines, respectively. This allows both beams to share a common optical axis, which simplifies alignment and allows for compactness, as shown schematically in Figure 2. Second, the pump and probe beams are delivered to the sensor head via a polarization-maintaining single-mode optical fiber. A dichroic waveplate at the output of the fiber circularly polarizes the pump laser while maintaining linear polarization of the probe laser. The beam is collimated, passes through the vapor cell, retroreflects off a dielectric mirror, passes back through the vapor cell, and is focused on the polarization analyzer. The vapor cell is heated to ~190 °C by a 20 kHz AC electrical heater. The retroreflected beam design allows a magnetic sample to be positioned closely to the sensing volume. The magnetometer must be operated near zero magnetic field to operate in its most sensitive mode, so during measurements it is installed inside a four-layer high magnetic permeability metal shield which provides a calculated shielding factor of 10⁶. The AM has four spatially separated magnetometer channels, but only one of the four channels was used for the measurements reported here. The sensitivity of a single channel is 15 fT/Hz^1/2 over a measurement frequency range of 3–30 Hz. This noise floor is not due to the intrinsic sensitivity of the magnetometer, which is 5 fT/Hz^1/2, but due to magnetic thermal Johnson noise from the magnetic shields.

In this study, nanoparticle measurements were made by placing the Eppendorf tube containing the sample ~ 3.4 cm from the center of the vapor cell. A microporous ceramic oven and an air gap provided thermal insulation between the vapor cell and the nanoparticle samples. In addition, air cooling of the cancer cell sample was provided to maintain it near room temperature. A solenoid wrapped around the cylindrical portion of the Eppendorf tube provided a 45 G magnetizing field. The field was pulsed for one second and data were collected for the following 4 s at a rate of 2 kHz. The first 50 ms of the data are not shown in the figures below because the AM recovers from the large magnetic field pulse during this time.

3. Results

3.1 SQUID measurements

For initial measurements on the nanoparticle and cell samples, the standard magnetic relaxometry protocol used in our laboratory, as discussed above, was employed. Samples were placed under the 7-channel SQUID system and magnetized using a 49 G flat pulse of 0.75 s duration. Three types of samples were used: (1) 20 μl of bound nanoparticles obtained by drying the nanoparticles on a cotton tip, (2) 20 μl of unbound nanoparticles diluted in a PBS solution, and (3) cancer cells, incubated with antibody-conjugated nanoparticles, fixed, and potted in agarose gel. The SQUID sensor measurements were made at room temperature before and after the AM measurements, confirming that there was no significant change in the magnetic moments during the AM measurements. The relevant data for these samples is shown in Table 1. The SQUID measurements were repeated over a temperature range of 0° to 40° C using an ice bath and a non-conducting heating pad and found to have no temperature dependence. This measurement is important and often overlooked as there can be substantial temperature dependence of the relaxometry signal of some magnetic nanoparticles [7].

Table 1.

Magnetic moments and maximum magnetic fields for all cell samples used.

Sample	Contents	Distance to sensor 1	Moment (pJ/T)	Max Field (pT) (ch 1)
Bound np	20 μl	3.11 cm	8.64E+05	4.52E+03
Unbound np	20 μl	3.11cm	0.0	0
Cells	3.2E+06	2.65 cm	3.26E+05	2.55+03
Cells	1.6E+06	2.71 cm	1.75E+05	1.25E+03
Cells	4.0E+05	2.80 cm	4.58E+04	1.96E+02
Cells	1.0E+05	2.80 cm	1.27E+04	8.0E+02
Cells	2.5E+04	2.80 cm	5.41E+03	4.9E+02

The results were analyzed using the time point at 50 msec after the end of the magnetizing pulse and their magnetic moments obtained using a magnetic dipole model to represent the nanoparticle samples. For the SQUID sensor measurements, the Helmholtz coils are oriented such that the nanoparticles are magnetized parallel to the axis of the second-order gradiometers of the system. The resulting magnetic field of these magnetized samples is described by the relation:

$$\mathit{B}\left(\mathit{r}\right)=\frac{{\mu }_0}{4\pi }\frac{3r(\mu \cdot r)-\mu r^2}{r^5}$$ (1)

The magnetic moment, μ, is aligned with the displacement vector, r, for the central sensor in the SQUID array, reducing the distance dependence to $\frac{2\mu }{r^3}$. The values shown in Table 1 are obtained from all seven channels and averaged over ten runs with no-sample backgrounds subtracted. The magnetic moments shown in Table 1 are typical of this type of nanoparticle [7]. The approximate number of nanoparticles/cell for the fixed breast cancer cells can be calculated using the measured properties of the Ocean nanoparticles [7]. For these particles one mg of the particles used in Table 1 have a magnetic moment of 3.3 × 10⁶ pJ/T. Given the density of magnetite of 5.24 × 10³ kg/m³ and a nanoparticle diameter of 24 nm, the moment/nanoparticle is then 1.3 × 10⁻⁷ pJ/T giving 2.6 × 10¹² nanoparticles in the 3.2 million cell sample in Table 1 or 8.0 × 10⁵ nanoparticles/cell. This corresponds well with previously measured nanoparticle/cell measurements and substantially exceeds steric hindrance if the cell were a uniform sphere. The cell sample containing 2.5 ×10⁴ cells yields a moment of 5.4 × 10³ pJ/T which is near the detection limit of the current SQUID system, indicating a sensitivity limit of 2 × 10⁹ nanoparticles. This system is not optimized and has no electromagnetic shielding and could be improved by several orders of magnitude if properly shielded from environmental background.

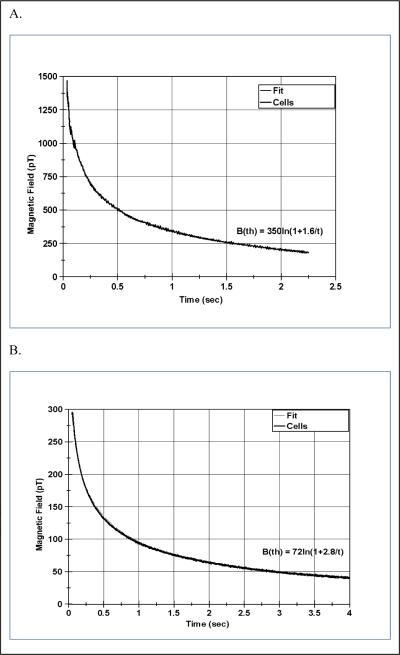
The magnetic relaxation curves for the cell sample containing 3.2 million cells are shown in Figure 3A. A theoretical fit to the decay curve is also shown in this figure and is discussed below. No signal was observed for the unbound nanoparticles in solution so no graph is shown.

Fig. 3.

Magnetic relaxometry decay curves from sample containing 3.2E+06 cancer cells labeled with magnetic nanoparticles. Figure A is the field measured by the SQUID sensor and Figure B is the field measured by the AM sensor. The fit shown by the B(th) curve from equation 2 lies on top of the data and is not discernible from the data. The difference in amplitude between the SQUID and AM data is due to differences in the detector geometry and magnetizing field strength as described in the text.

3.2 AM Measurements

After initial measurements of the sample properties by the SQUID sensors, the samples were then placed in the shielded chamber of the AM sensor and measured by magnetic relaxometry. Because of the greater sensitivity of the AM sensor and the large shielding factor of the four concentric magnetic shields, signal averaging was not performed for these measurements. The data were acquired at 2 kHz and then decimated to compare to the 1 kHz rate used for the SQUID sensor data.

The magnetizing field was applied for one second followed by a delay of 50 ms, sufficient to permit the magnetometer to recover from the pulse. The magnetic field was generated using a small solenoidal coil around the Eppendorf tube containing the samples. In all of the present measurements, a current of 1A through this coil was used to produce a field of 45 G. As shown in Figure 2, the orientation of the magnetizing coil was orthogonal to the optical axis of the AM sensor so the resulting induced magnetic moment is orthogonal to the radius from the sample through the sensor, as opposed to the geometry of the SQUID system. This results in a reduction of a factor of two in the observed fields because the radial dependence is now μ/r³. By careful measurement of the geometry of the magnetometer, the distance of the sample relative to the AM is estimated to be 3.4 cm as compared to 2.65–3.11 cm for the SQUID system dipole to sensor distance.

All of the data were passed through a 10 Hz Butterworth 2-pole filter and adjusted to zero-phase, to remove high frequency sampling noise. The resulting AM magnetic relaxation curve and theoretical fits are shown in Figure 3B where they are compared to the SQUID sensor results of Figure 3A. These curves illustrate that the AM and SQUID sensors yield very similar decay properties with respect to time, with the variation in magnitude of a factor of approximately 5 reflecting differences in the source orientation, distance to sensor, and magnetizing field.

3.3 Theoretical fitting of Magnetic relaxation data

The magnetic relaxation of superparamagnetic nanoparticle samples was first described by Néel [10] who derived a formula for the decay of polydisperse particles using a logarithmic expression of the field as a function of time after the magnetizing field is turned off. This was generalized by Chantrell [28] who derived the following formula for the magnetization or moment

$$M=a_1\ln (1+\frac{a_2}{t})$$ (2)

The value of the parameter a₁ depends upon the magnitude of the magnetic moment of the sample which in turn depends upon the number of nanoparticles in the sample and their individual magnetic moments. The value of the parameter a₂ characterizes the decay time of the sample magnetization and is affected by the bandwidth of the sensor system. In order to see if the magnetic relaxometry data acquired here is described by this theory, this equation is compared to the magnetic fields from the cell data for both the AM and SQUID sensor data. Although equation 2 gives the magnetization as a function of time, the observed magnetic fields are produced by the changing magnetization as the nanoparticles randomly reorient following the termination of the magnetizing field, and these fields follow the same time course as the magnetization described by equation 2 thus also describing the time course of the magnetic fields. The magnetization of the sample, M, is determined by fitting the SQUID sensor data with a magnetic dipole approximation. It is thus sufficient in determining that the magnetization is described by equation 2 to show that the magnetic fields follow this relation. The magnetization or moment of the sample is calculated at 50 msec after turning off the magnetizing field as determined by the functional fit to the decay curve.

The magnetic field data has been fit by this equation and the results are shown in Figures 3A and 3B with the values of the parameters given in Table 2 along with the square root of the mean-square error. The AM sensor data has a somewhat longer time constant than the SQUID sensor data for the early time periods, due to different frequency response characteristics, but the shape of the decay curves for both systems is well described by equation 2.

Table 2.

Coefficients extracted from fitting equation 2 to SQUID and AM magnetic relaxation curves.

Data set	a1 (pT)	a2 (sec)	Mean error (pT)
SQUID	350	1.6	15
AM	72	2.8	21

The relationship given by Chantrell in equation 2 describes the data extremely well and the fit tothe data shown in Figure 3 for both AM and SQUID sensors is indistinguishable from the data.

The parameter a1 in this case is directly related to the magnetic field strength, which depends on both the induced magnetic moment and the detector geometry. The observed magnitude of the magnetic fields differs between the SQUID sensors and the AM sensor by a factor of 4.86 between the SQUID sensors and the AM sensor based on the a1 parameters listed in Table 2. The parameter a1 in this case is directly related to the magnetic field strength and indirectly to the magnetic moment. In this case, the AM measurement was performed with the sensor orthogonal to the magnetization direction, resulting in a factor of 2 decrease in field strength relative to the SQUID detector orientation. The AM sensor was also further from the source (3.4 cm for the AM, 2.65 cm for the SQUID, (3.4/2.65)³ = 2.11), resulting in an expected difference in the field amplitude of a factor of 4.22 due to these known geometric factors. The remaining ~15% discrepancy between the two measurements is attributed to the difference in magnetizing fields (45 G for the AM, 49 G for the SQUID), resulting in slightly less magnetization in the AM case. The observable magnetization of nanoparticles of this type and size is generally not fully saturated at these magnetizing field strengths [7]. 3.4 Linearity of Signal with Cell Number

An important application of magnetic relaxometry with cell samples is the linearity of the measured magnetic moment with the number of cells as this makes it possible to measure the number of cells in a sample using this technique. Other methods for observing cell clusters, such as MRI, suffer from saturation effects. In Table 1 above, the results of a number of cell samples for the SQUID sensor measurements are shown. Similar measurements were made using the AM sensors, and a plot of magnetic field strengths for both SQUID and AM sensors is shown in Figure 4 over a range of cells from 3.2 million down to 25,000 cells. For this comparison, since the AM sensor measures a different magnetic field strength than the SQUID sensor due to the difference in geometries, the AM sensor data have been normalized to the SQUID sensor data average. Figure 4 demonstrates linearity with cell number over the range of 3 million cells examined here for both the SQUID and AM sensors. The relationship between magnetic field (as measured 50 msec after the magnetization pulse) and cells for the SQUID sensors, for example, is 8.0 × 10⁻⁴ pT/cell. This linear relationship also implies that the number of nanoparticles/cell is independent of the number of cells in the sample.

Fig. 4.

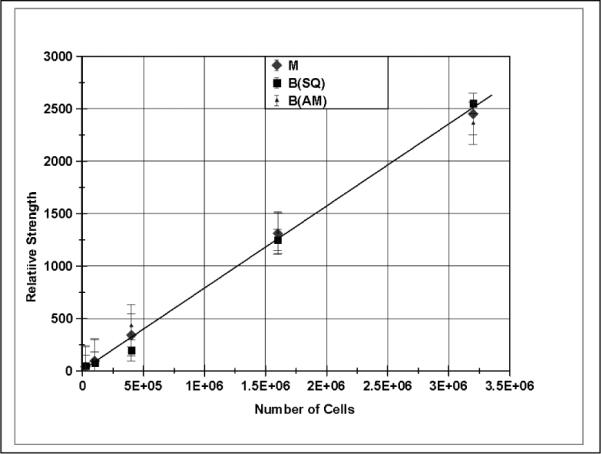
The magnitude of the magnetic field produced in magnetic relaxometry is linear with the number of cells in the sample as expressed for the four samples given in Table 1. Shown here are the relative magnetic fields from the SQUID and AM sensors and also the magnetic moment as measured by the SQUID array.

3.5 Sensitivity for Cell Detection of SQUID and AM Sensors in Magnetic Relaxometry

The present configuration of the SQUID sensors is limited in its sensitivity to approximately 2 pT due to environmental electromagnetic noise since the system is unshielded. The 25,000 cell sample shown in Table 1 is at the limit of detection for this system until further EM shielding is added. The AM sensor has much greater sensitivity due to the shielded environment it resides in and this is indicated in Figure 5 where the magnetic relaxation decay curve from the AM sensor is shown for this sample. The solid line superimposed on the data is the result of passing the data through the 10 Hz filter. The FFT of the data is shown in the insert and shows the 60 Hz line frequency being the principal contaminating noise component.

Fig. 5.

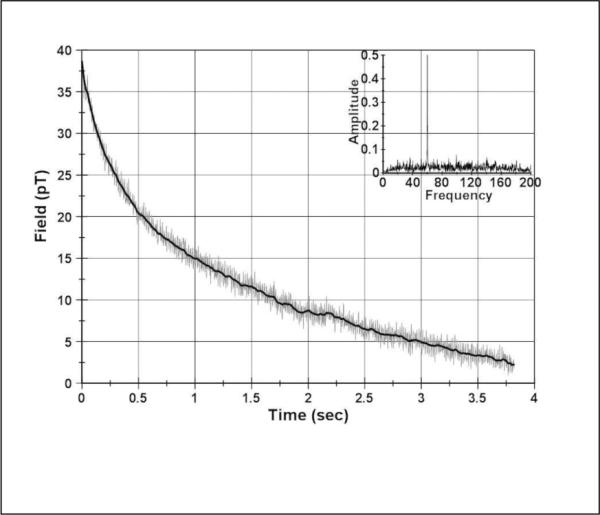
Magnetic relaxation decay curve as measured by the AM sensor for a magnetized sample of 25,000 cancer cells. The solid curve through the data is from filtering the data below 10 Hz. The insert is the FFT of the unfiltered data.

The signal-to-noise ratio of the data shown in Figure 5 is high enough that the AM sensor arrangement used for the magnetic relaxometry of these cells could detect less than ten thousand of the breast cancer cells used here. The detection limit of the current AM system is limited by an anomalous signal present on the AM after the magnetizing pulse whether or not a cell sample is present. This anomalous signal is most likely due to magnetizing pulse inducing currents into the s. It is unlikely that the anomalous signal is coming from the magnetometer since it is constructed entirely from nonmagnetic components, largely G-10 fiberglass. With a redesign of the system specifically optimized for magnetic relaxometry using techniques to minimize the undesired effects of the magnetizing pulse [29], this type of AM sensor shows significant application in detecting small numbers of cancer cells in a sample such as a fine-needle aspirate obtained in biopsies.

4.0 Discussion

The magnetic relaxometry results obtained here demonstrate that this methodology is an important addition to instruments for detecting and assessing medical samples for the presence of cancer cells that are targeted with superparamagnetic nanoparticles through the action of specific antibodies. Two sensor methods are reported here, SQUID and AM magnetic sensors, with the AM sensor representing a new method for this type of application. These results indicate that these sensors can be used to detect small numbers of cancer cells in samples extracted from tumors or body fluids. The AM sensor requires multiple layers of magnetic shielding to achieve the lowest limit of cell detection and this must be considered for in vivo applications, but this is not a limitation for measuring small in vitro samples. Arrays of AM sensors are possible and small arrays have been tested [21]. The SQUID and AM decay curves are quite similar and both the SQUID and AM sensor data fit the theoretical prediction for magnetic relaxation decay of superparamagnetic nanoparticles over the time range considered here.

The sensitivity limit of the SQUID sensor system used here for comparisons is limited to several pT because of background electromagnetic field interference, although the inherent sensitivity of the SQUID sensor is of the same order of magnitude of the AM device. However, the results presented here demonstrate that the present SQUID sensor can detect fewer than 100 thousand breast cancer cells at a distance of several cm from the sensor and represents a significant improvement over x-ray mammography that requires over 100 million cells for detection [6]. The AM sensors have the advantage that they require no cryogens for cooling and are relatively inexpensive compared to SQUID systems. This possibility extends the use of magnetic relaxometry into a regime of new applications in cancer cell detection.

Research Highlights for article MAGMA57486 (editorial ref MAGMA_MAGMA-D-11-01187)

• Magnetic relaxometry is used to study antibody targeted nanoparticles and cells

• Atomic magnetometer and SQUID sensor performance is compared

• High sensitivity of magnetic relaxometry for cancer cell detection is demonstrated

• Magnetic relaxometry decay curves from cancer cells are fit by log function