Native secondary structure formation in RNA may be a slave to tertiary folding

The discovery of catalytic activity in RNA (1) has prompted serious attempts to decipher the mechanisms of their assembly into functional native states starting from linear strands (2). The outlines of the folding mechanisms of large RNA molecules are beginning to emerge thanks to several novel experiments (3–7) and theoretical arguments (8) originally advanced in the context of protein folding. It is becoming increasingly clear that the folding kinetics of RNA is complex (3–7), involving parallel pathways (5) and kinetic traps. These complexities arise because the underlying energy landscape governing RNA folding is rugged. The most dramatic finding, common to most of the recent experimental studies (5, 6), is that the slow processes in the transition to the functionally competent state of RNA involve transitions from misfolded structures. These structures, which have many elements in common with the native state, serve as kinetic traps for the majority of the initial population of molecules (5, 8).

Implicit in all of the proposed folding mechanisms is the assumption that there are two major structural changes in RNA en route to the native state, starting from an ensemble of unfolded molecules. It is supposed that stable secondary structures form rapidly, perhaps on microsecond time scales. The subsequent assembly leading to tertiary folding takes place by bringing the secondary structural elements together. The resulting kinetics of the assembly of the secondary structural elements is complex because of inherent topological frustration (8). The evidence for the two-step process (reminiscent of framework-like models in protein folding), namely, fast secondary structure formation followed by a slower acquisition of tertiary interactions, came from the folding studies of tRNA (9). In an illuminating paper in this issue of the Proceedings, Wu and Tinoco (10) show that this commonly held picture of RNA assembly may not always be correct.

The NMR experiments of Wu and Tinoco were performed on a fragment of the Tetrahymena group I self-splicing intron, which has served as the prototypical model for examining the folding kinetics of large RNA (3–5, 7). This intron consists of two large domains (base-paired P regions), namely, P4-P6 and P1-P2/P3-P9 (11). The resolution of the crystal structure of the P4-P6 domain (12, 13) has provided considerable insight into the folding process of the intron. In the stable P4-P6 domain, which can fold independently (14), resides the three helices (P5a, P5b, and P5c) that form the three-helix junction P5abc. By rapid time-resolved mapping of the accessible surface area of RNA to hydroxyl radical generated by using x-ray, Scalvi et al. (7) concluded that the 56-nt P5abc subdomain forms very rapidly. The rest of the P4-P6 domain nucleates around this scaffold. The rapid folding of P5abc together with the earlier work showing that this subdomain can fold independently (14) make the study of the folding of P5abc important in understanding the assembly of P4-P6 and ultimately the intron itself. This “bottom-up” strategy is used by Wu and Tinoco (10).

The secondary structure of P5abc subdomain in the absence of Mg²⁺ ions, which are needed to initiate tertiary folding of group I introns (11), was determined by NMR (10). This structure is substantially different from the x-ray secondary structure. The calculated free energy of the solution structure is lower than the crystal structure. Upon adding sufficient amount of Mg²⁺ the incorrect secondary structure undergoes substantial rearrangement en route to the folded conformation in which the secondary structure coincides with the x-ray structure. Thus, under folding conditions the nucleation of the magnesium ion core that leads to the tertiary folding of the P5abc subdomain also triggers the formation of the native secondary structure. This is the central result in the paper by Wu and Tinoco (10).

The substantial rearrangements in the secondary structure in P5abc, when sufficient amount of Mg²⁺ is added to drive folding, is explained by supposing that favorable tertiary interactions compensate for the loss of free energy in the breakup of non-native secondary structure base pairs (10). It follows from this that such rearrangements are thermodynamically feasible only if N_tɛ_t > N_sɛ_s where N_s is the number of lost secondary structure base pairs, ɛ_s is an average free energy for base pair formation, N_t is the net gain in the number of favorable tertiary interactions, and ɛ_t is the associated free energy gain. For simplicity we have assumed that ɛ_t and ɛ_s do not depend on the nature tertiary or secondary interactions. The thermodynamic requirement for the structural rearrangement suggests that if N_s is large, as is the case in P5abc (10), then a very compact tertiary fold containing many favorable tertiary interactions is needed to compensate for lost secondary base-pair interactions. This is unlikely to happen when the number of nucleotides is too small. On the other hand, topological frustration would prevent substantial structural reorganization in large RNA (8). Thus, it is logical to postulate that optimal length of the sequence and the compactness of the tertiary fold are the factors that determine the order of events in RNA folding.

There are mechanistic implications of the findings by Wu and Tinoco (10) as well. This becomes particularly clear if analogies to protein folding, which seem to be emerging from theoretical models (8) and recent experiments (3–6, 15, 16) on large RNA, are made. Wu and Tinoco estimated, based on chemical shifts and line broadening, that the conversion between the unfolded (at zero Mg²⁺ concentration) and folded (at 30–40 mM Mg²⁺) triple-helix junction takes place in about 33 msec, which is not inconsistent with the inference made by Scalvi et al. (7). A theoretical estimate for this folding time, τ_F, can be made if we assume that nucleation-collapse mechanism in the presence of Mg²⁺ drives the tertiary folding of P5abc. It has already been proposed (4) that the consolidation of the magnesium ion core (five discrete Mg²⁺ bound to various regions in the P5abc subdomain) nucleates the tertiary folding of not only P5abc but of the entire P4-P6 domain. If the nucleation-collapse mechanism is operative then the tertiary folding time is estimated to be (17) τ_F ≈ τ₀N^4.2 where N is the number of nucleotides, and τ₀ (a function of viscosity, persistence length of the polyion, and effective surface tension) ≈10⁻⁹ s. For the 56-nt P5abc we find τ_F ≈ 20 msec, which is in reasonable agreement with experiments. The associated barrier to nucleation is about 10 kcal/mol. The preceding arguments and previous experiments suggest that, in all likelihood, tertiary folding of P5abc occurs by a nucleation-collapse mechanism. A major implication of this is that both thermodynamically and kinetically the folding of the isolated P5abc subdomain must exhibit two-state behavior. As far as we know this has not been established experimentally.

The anticipated nucleation-collapse mechanism in tertiary folding of P5abc invites comparisons to the folding of small proteins. Fersht and coworkers (18) have shown, by using protein engineering methods, that the 64-residue chymotrypsin inhibitor 2 (CI2) folds by a nucleation-collapse mechanism in about 15 msec under optimal folding conditions. The wealth of data on this protein suggests that in these small proteins the formation of secondary structure, collapse, and tertiary structure formation occurs almost synchronously (18). The plausible similarity in the folding mechanism between CI2 and P5abc suggests that native secondary and tertiary structures occur on very similar time scales in this subdomain.

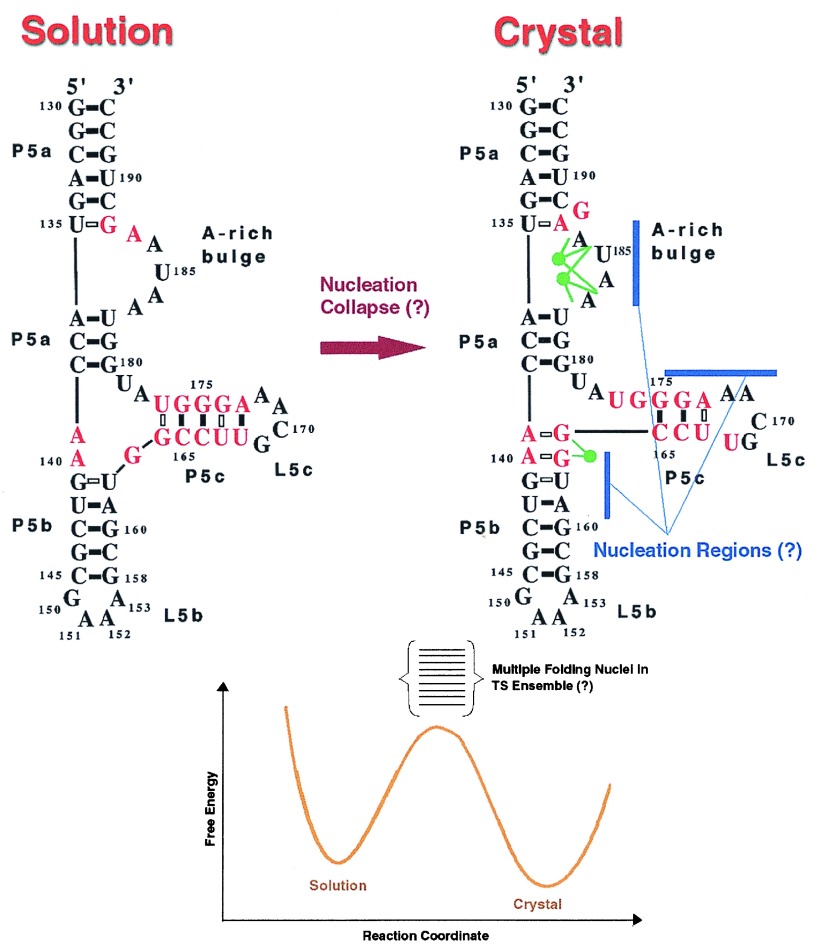
The two-state nucleation-collapse mechanism for tertiary folding of P5abc implies that the bottleneck for folding is associated with the search for the critical nucleus or a set of critical nuclei. Once the nuclei are located then with overwhelming probability the folded state would be reached extremely rapidly. In Fig. 1 the interconversion between the unfolded and folded states of the P5abc subdomain is schematically sketched. The structure(s) of the transition state(s) and their free energies then would determine the folding routes. If the structures near the bottleneck are similar then one might have a relatively unique transition state as is often the case in small molecule reactions. However, if there is diversity in the transition state structures then it is more fruitful to think in terms of transition state ensembles (19, 20). Thus, it is of vital interest to probe the degree of heterogeneity of the transition states. In protein folding, where the major driving force arises from the need to form a hydrophobic core, the characterization of transition states for two-state proteins has not provided a clear picture about the structures near the bottleneck. Although the formation of the magnesium ion core may be the logical analogue of the hydrophobic core in RNA folding (4), the transition states in RNA may be easier to decipher than in proteins. The primary reason is because of the profound differences in the nature of the driving force. Because RNA is highly charged “polyelectrolyte effects” (condensation of counterions that can drastically alter packing interactions) dominate (21). It has been suggested (22) that if the interactions stabilizing the core of the nucleus are sufficiently strong, as is be the case in electrostatically dominated folding folding of RNA, then one expects a structurally more homogeneous transition state ensemble. Because discrete binding of magnesium ions is the major driving force for tertiary folding of the P5abc subdomain we conjecture that the nucleus in this case is less dispersed than in proteins (21, 22). This does not imply that if the nucleotides to which the magnesium ions are coordinated are mutated the assembly of the subdomain would not take place at all. In fact, the recent experiments of Treiber et al. (16) show that although certain mutations destabilize the P5abc subdomain they lead to an overall enhancement of the folding of the entire intron. This suggests that there is diversity in the folding nuclei. However, because of the polyelectrolyte effect in RNA folding there may not be much structural diversity of the transition state structures. In addition, the need to form a tight fully coordinated magnesium ion core (4) and complimentarity of base-pair interactions further constrain the degree of heterogeneity of the transition state ensemble. These factors may render greater specificity to the folding nuclei in RNA than in proteins.

Figure 1.

(Upper) The structural rearrangements involved in the transition from the unfolded state to the folded conformation. The secondary structures of P5abc are adopted from ref. 10. The green circles represent the magnesium ions. For clarity of presentation only part of the magnesium ions in the core is shown. The possible nucleation regions are shown in blue. (Lower) A schematic sketch of the free energy profile and the associated ensemble of transition states is shown. The question marks indicate that the nature of the kinetic steps in the interconversion of the solution structure to the crystal structure under folding conditions are conjectural and require experimental validation. This figure was prepared by Oksana Klimov, and her assistance is greatly appreciated.

The dissection of the structures of the P5abc subdomain by using NMR by Wu and Tinoco (10) offers a unique opportunity to answer some of the questions posed in the form of illustration in Fig. 1. In particular, it would be of great interest to probe the kinetics of the wild-type and mutant P5abc subdomains cloned by Treiber et al. (16). Such RNA engineering experiments would offer us a glimpse of the transition states in tertiary folding of not only the P5abc subdomain but also of the intron itself. Cumulatively, these experiments and new class of fast folding experiments, similar to those on proteins (23), will go a long way in providing a fuller understanding of the way large RNA molecules fold. In the process, one may better appreciate the common themes used by nature to fold biomolecules.