Sex Modifies Genetic Effects on Residual Variance in Urinary Calcium Excretion in Rat (Rattus norvegicus)

Abstract

Conventional genetics assumes common variance among alleles or genetic groups. However, evidence from vertebrate and invertebrate models suggests that residual genotypic variance may itself be under partial genetic control. Such a phenomenon would have great significance: high-variability alleles might confound the detection of “classically” acting genes or scatter predicted evolutionary outcomes among unpredicted trajectories. Of the few works on this phenomenon, many implicate sex in some aspect of its control. We found that female genetic hypercalciuric stone-forming (GHS) rats (Rattus norvegicus) had higher coefficients of variation (CVs) for urinary calcium (CV = 0.14) than GHS males (CV = 0.06), and the reverse in normocalciuric Wistar–Kyoto rats (WKY) (CV_♂ = 0.14; CV_♀ = 0.09), suggesting sex-by-genotype interaction on residual variance. We therefore investigated the effect of sex on absolute-transformed residuals in urinary calcium in an F₂ GHS × WKY mapping cohort. Absolute residuals were associated with genotype at two microsatellites, D3Rat46 (RNO3, 33.9 Mb) and D4Mgh1 (RNO4, 84.8 MB) at Bonferroni thresholds across the entire cohort, and with the microsatellites D3Rat46, D9Mgh2 (RNO9, 84.4 Mb), and D12Rat25 (RNO12, 40.4 Mb) in females (P < 0.05) but not males. In GHS chromosome 1 congenic lines bred onto a WKY genomic background, we found that congenic males had significantly (P < 0.0001) higher CVs for urinary calcium (CV = 0.25) than females (CV = 0.15), supporting the hypothesis of the inheritance of sex-by-genotype interaction on this effect. Our findings suggest that genetic effects on residual variance are sex linked; heritable, sex-specific residuals might have great potential implications for evolution, adaptation, and genetic analysis.

HOMOGENEITY of variance among genotypes, strains, or genetic groups has been a major assumption of quantitative genetic analysis and evolutionary theory (see Falconer and Mackay 1996; Lynch and Walsh 1998) for nearly 100 years (Fisher 1922). However, a number of vertebrate and invertebrate model systems suggest the possibility of genetic variance in residual variability or phenotypic heterogeneity: Drosophila experiments in the 1950s found twice the variance for body size in homozygote flies compared to heterozygotes (Reeve and Robertson 1953) and increasing phenotypic variance for both low- and high-selected lines selected for abdominal bristle number (Clayton and Robertson 1957). Reaction time in attention deficit/hyperactivity disorder (ADHD) (see Castellanos et al. 2005; Russell et al. 2006) shares familial effects with intra-individual variability (IIV) in reaction time, suggesting a genetic basis for residual variation (Andreou et al. 2007; Wood et al. 2009). Genetic effects on residual variance has been observed in several systems including rodent genetic models of ADHD (Perry et al. 2010a,b), associations of genotype with thermotolerance in fish (Perry et al. 2003), and abdominal bristles in Drosophila (Mackay and Lyman 2005). The basis of this phenomenon is unknown: genetic structure in residual variance might be from the inability of homozygotes to buffer their physiology against microfluctuations in external environment (genetic homeostasis) (Lerner 1977) or from genotype/allele-specific variance functions, much as allele-specific means (termed here allelic heterogeneity; see Hill and Zhang 2004). Numerous examples of this genetic phenomenon explicitly involve sex: operant behavior in rats (Perry et al. 2010a), sex-chromosomal × autosomal interaction for thermotolerance (Perry et al. 2003), clonal lines and bristle number in Drosophila (Clayton and Robertson 1957; Mackay and Lyman 2005), and gene expression in mice (Fraser and Schadt 2010). Sex may be a common element in this effect; buffering of environmental effects on genetic systems may be a predominantly female physiological process (Fraser and Schadt 2010).

Nephrolithiasis (kidney stones) is a common condition in industrialized countries, affecting up to 12% in men and 6% of women and having a recurrence of up to 10% (Devuyst and Pirson 2007). The most common risk factor for nephrolithiasis is hypercalciuria, the excess excretion of urinary calcium (Coe et al. 2005). We have used the genetic hypercalciuric stone-forming rat (GHS), a model of this phenotype developed from Sprague–Dawley (SD) rats selected for urinary calcium excretion (Li et al. 1993; Bushinsky et al. 1995, 2002, 2006; Levy et al. 1995; Krieger et al. 1996; Tsuruoka et al. 1997; Yao et al. 1998; Frick and Bushinsky 2003), to map two quantitative trait loci (QTL) for urinary calcium excretion using F₂ intercrosses of GHS rats and normocalciuric Wistar–Kyoto (WKY) rats (Hoopes et al. 2008): HC1 (on rat chromosome (RNO) 1; (Hoopes et al. 2003), and HC2 (RNO4) (Scheinman et al. 2008), both of which were detected only in females. These genes are underlain by an array of genes associated with calcium physiology (Hoopes et al. 2006). However, further examination of Hoopes et al. (2003) revealed that female GHS rats also had a variance 40 times and a coefficient of variation (CV = σ/µ) 2.3 times that of male GHS rats and that nearly the reverse was true in male and female WKY progenitors, implicating genotype-by-sex interaction in the generation of random variation. Further, there was increasing generation-to-generation variability in urinary calcium over the selective development of the GHS line, a pattern suggestive of increasing variation in selection lines of Drosophila bred by Clayton and Robertson (1957) (see Hill and Bunger 2004; Hill and Zhang 2004). The architecture of urinary calcium and stone formation differs markedly between the sexes in mammals: males and females have different urinary calcium in rats (Hoopes et al. 2003) and humans (Coe 1988; Curhan et al. 1997), which have more stones than females (Monk and Bushinsky 2003; Alaya et al. 2010).

We hypothesized that sex would have a significant effect on genetic dispersion in calcium excretion in our rat model. Specifically, we hypothesized that: (i) such dispersion would be associated with particular microsatellite markers (individual locus model) rather than overall inbreeding coefficients (genetic homeostasis), (ii) sex would affect dispersion in calcium excretion, and (iii) the effects of QTL for individual phenotypic dispersion (PD_i) in calcium excretion would be sex linked. We tested these hypotheses using residuals and heterozygosity analysis in 236 male and female F₂ GHS × WKY rats genotyped at 176 microsatellites and annotational gene expression analysis in strain progenitors.

Materials and Methods

Husbandry and experimentation

Calcium excretion in the GHS, selectively bred from SDs over 70 generations (D. Bushinsky, University of Rochester), is eight times that of normocalciuric WKY and SD controls (Bushinsky and Favus 1988; Bushinsky et al. 2006). F₁ GHS × WKY rats were bred from GHS females and WKY males, since mean urinary calcium and molecular differentiation were greatest between these groups (Hoopes et al. 2003). Male and female F₂ rats were then bred from F₁ rats for the mapping of QTL for calcium excretion. GHS, WKY, F₁, and F₂ rats were subjected to the same protocol for the assay of urinary calcium excretion: at 8 weeks of age, each rat was placed in a separate metabolic cage (Acme Metal Products, Chicago, IL) and fed 13 g/day of a normocalciuric rat diet (0.6% calcium, 0.65% phosphorus, 0.24% magnesium, 0.40% sodium, 0.43% potassium, 2.2 IU vitamin D3/g food) for 4 days. Rats consuming <12 g food or 15 ml water on any of the 4 days were removed from the experiment. Individual 24-hr urine collections on the fourth day of the protocol were stored in 12 M hydrochloric acid and urinary calcium assayed from photometric absorbance after reaction of the total sample with arsenazo III (Michalylova and Ilkova 1971) (see Bushinsky and Favus 1988; Kim et al. 1993; Li et al. 1993; Bushinsky et al. 1995, 2002; Tsuruoka et al. 1997). We produced three cohorts of F₂ rats: March 1997, November 1998, and January 2001.

Genetic analysis

Whole-genomic DNA was extracted from frozen (−70°) liver tissue (Puregene DNA Isolation Kit, Gentra Laboratories, Minneapolis, MN). We PCR amplified 255 microsatellites on a PCT-200 (MJ Research, Waltham, MA) in the F₂ rats using run parameters from Research Genetics (now Invitrogen). Initially, microsatellites were selectively genotyped within date-cohort (∼20% of the upper and lower tails for calcium excretion); those with interesting associations with urinary calcium were selected for further genotyping. DNA fragments were separated on either 6% acrylamide sequencing gels or 4% agarose gels (see Hoopes et al. 2003).

Residuals by sex and genotype

All statistics were run in SAS (2000). We calculated the mean (µ), standard deviation (σ), variance (σ²), and coefficient of variation (CV) within each sex in the F₂ mapping cohort.

We estimated the residual deviation (r) of individual F₂ rats from their predicted phenotype as defined by the independent variables in the general linear model

$$y_{ijkm}=\mu +{\alpha }_i+{\varphi }_j+{\gamma }_k+{\phi }_{\text{s}}+{\beta }_{\text{wt}}{X}_{\text{wt}}+{\epsilon }_{ijkm},$$ (1)

where $y_{ijkm}$ was day 4 urinary calcium excretion, μ mean calcium excretion, α_i microsatellite locus, ${\varphi }_j$ rat litter, ${\gamma }_k$ rearing date of the cohort, φ_s effect of sex, ${\beta }_{\text{wt}}{X}_{\text{wt}}$ effect of rat weight, and ${\epsilon }_{ijkm}$ the residual. These independent variables are associated with urinary calcium excretion in this F₂ cohort (Hoopes et al. 2003). Residuals were absolute transformed for analysis; absolute residuals (|r|), as the absolute deviation from all independent variables, were considered to represent residual phenotypic instability (PD_i). Since litter and rearing cohort were partially confounded, we used mean phenotype for each level of each term as a quantitative variable rather than a factorial. The locus term was included in the model as a control against mean urinary excretion among genotypes at known and unknown classically acting QTL for calcium excretion (Hoopes et al. 2008). Next, to determine the effect of sex on PD_i, we used a reduced version of the above fitting no effect for sex, but modeling the effects of sex separately,

$$y_{ijkm}=\mu +{\alpha }_i+{\varphi }_j+{\gamma }_k+{\beta }_{\text{wt}}{X}_{\text{wt}}+{\epsilon }_{ijkm},$$ (2)

where $y_{ijkm}$ was day 4 urinary calcium excretion, μ mean calcium excretion, α_i microsatellite locus, ϕ_j rat litter, ${\gamma }_k$ rearing date of the cohort, ${\beta }_{\text{wt}}{X}_{\text{wt}}$ effect of rat weight, and ${\epsilon }_{ijkm}$ the residual. Only loci for which at least 66% of all individuals had been genotyped were included in either model analysis to limit false positives from small n.

We then tested for significant differences among genotypes for PD_i in model 1 and Model 2 using nonparametric Kruskal–Wallis (K-W) ranking via χ² (SAS 2000) with microsatellite locus as the independent variable to avoid bias from the altered phenotypic structure; K-W ranking was preferred to avoid complications of the distribution under linear statistics. Mean PD_i and CV and σ² for untransformed calcium excretion were estimated by genotype within each microsatellite locus; t-tests with Bonferroni correction were used to separate differences in PD_i among genotypes (SAS 2000). Mode of action (additivity, dominance, or over-/underdominance) at each putative QTL was estimated using general linear models with contrast statements in SAS (2000) based on heterozygote potence ratio (h_p = Q/L) (Griffing 1990), where L was the linear difference between the parental (GHS, WKY) genotypes (L = |µ_P1 – µ_P2|) and Q the difference of twice the mean quadratic heterozygote effect (Q = 2F₁ – L). Contrast vectors of −1 0 1 were fit for WKY, heterozygote and GHS genotypes to calculate L. Contrast vectors were +/−0.5 +/−0.5 −/+1 for positive/negative WKY allele dominance (Lynch and Walsh 1998), −/+0.5 −/+0.5 +/−1 for GHS dominance, and +/−0.5 −/+1 +/−0.5 for under-/overdominance, respectively, for WKY, heterozygote, and GHS genotypes.

P-values at or below the Bonferroni-adjusted α_0.05 threshold were considered to be significant evidence for rejection of the null hypothesis, and those at or below the sequential false discovery rate (FDR) (Verhoeven et al. 2005) as suggestive. FDR is less stringent than Bonferroni for family-wise error rate (FWER) but has less incidence of type II error (Holm 1979; Moran 2003; Verhoeven et al. 2005). In the FDR, empirical P-values (P_emp) from the m independent tests were ranked from P₁ … P_m. P_i for each locus (i – m) was then tested against the partial inequality P_i ≤ αi/m, where α = 0.05 and i was the rank of that test based on P_emp in ascending order. Where P_(i=emp) ≤ α_i/m, that null hypothesis and those with lower P_i (ranked from 1 to P_(i=emp) were rejected (Benjamini and Hochberg 1995; Benjamini et al. 2001; Verhoeven et al. 2005). The significance of all loci was also tested using permutational thresholds created from 1000 bootstrapped ${\chi }^2$ values in which phenotype had been randomized against all explanatory variables, creating a distribution of ${\chi }^2$values ranked ${\chi }_i^2\mathrm{...}{\chi }_{1000}^2$. ${\chi }^2$ values for each test on the above criteria were compared against this distribution; those higher than the fifth percentile of the distribution were considered to support the null hypothesis (Churchill and Doerge 1994) after correction for multiple testing. We tested whether sexual differences in expression at QTL for PD_i in urinary calcium were scalar (similar PD_i means genotypic means for males and females, but nonsignificant in one sex) (see Lynch and Walsh 1998), or whether crossovers in mean PD_i occurred for the same genotype in males and females. For this test, we calculated PD_i as above and used a subsequent model with a main effect for the microsatellite locus (α_i) and an interactive term for sex-by-locus interaction (α_iλ_j) for those loci with significant (Bonferroni) or suggestive (FDR) associations with PD_i in urinary calcium. FDR thresholds were calculated separately for tests using all individuals (model 1), males, and females (model 2).

General differences in PD_i by sex were tested using nonparametric ranking on absolute residuals from a model as above but without terms for sex or microsatellite locus. Sexual differences in PD_i overall were then tested using a one-way nonparametric model (SAS 2000).

Multilocus heterozygosity

We regressed multilocus heterozygosity (MLH = p(homozygous loci)) for each chromosome RNO1-X, and genome-wide MLH from loci on all chromosomes, on PD_i from a general linear model including body weight, litter, sex, and cohort date as a rough test of the role of genetic homeostasis on dispersion (“heterozygosity–trait correlation” (Hansson and Westerberg 2002) in the complete F₂ cohort. MLH-PD_i regression was also modeled separately within males and females to determine whether MLH-PD_i associations differed by sex for comparison to results from model 2, above. P-values by chromosome were Bonferroni corrected for multiple testing (Verhoeven et al. 2005).

Gene expression

We screened gene expression in kidney and duodenal tissue collected from three female GHS and three female SD rats; the latter strain was chosen to represent the unselected state of the GHS strain comparable to the GHS save for selective history. As the sites of calcium uptake and excretion (Moe and Bonny 2005), renal and duodenal tissue was sampled from GHS and SD rats immediately post-mortem. RNA analysis was carried out at the University of Rochester Functional Genomics Center (http://www.urmc.rochester.edu/fgc/index.cfm) according to Affymetrix protocols (Affymetrix 2009). RNA was extracted with Trizol (Invitrogen) and purified by column chromatography (Qiagen RNeasy kit) with DNase treatment. RNA quality was determined using an Agilent 2100 Bioanalyzer. Affymetrix kits were used to produce cleaned biotinylated complementary RNA (cRNA). cRNA was hybridized for 17 hr to Affymetrix Rat Genome 230 GeneChips (Affymetrix, Santa Clara, CA) in 300-µl cocktails at 42°. All R230A chips were washed in a GeneChip Fluidics Station 450 and subsequently scanned in a GeneChip Scanner 3000 7G. We ignored all fluorescence values below a signal of 50 fluorescence units as possibly erroneous.

To identify genes with high variance in expression, CV was calculated for each gene amplified in the R230A array panel within strain and the ratio of CV_GHS/CV_SD (= CVR) calculated to account for integral variance in gene expression using CV from the unselected SD strain. We tested for gene function enrichment by annotation for CVR at those genes with nonerroneous signal (as interpreted above) within a 20-Mb (10 Mb upstream and downstream) window around our significant and suggestive QTL. The SNP probe Affymetrix identifications of all genes within these windows were submitted to the Database for Annotation,Visualization and Integrated Discovery (DAVID v. 6.7) (Huang et al. 2009). This program groups genes by biological function and tests for significant enrichment according to functional annotation and physiological relationship to other genes on the basis of published gene annotation lists (i.e., Cicala et al. 2002). P-values from Fisher’s exact tests of enrichment proportion were Benjamini adjusted for multiple testing in DAVID to control family-wise error rate; an adjusted threshold of P_0.05 was considered significant. “Fuzzy functional annotation clustering” in DAVID was also used to identify modular gene clusters with enrichment in variance for gene expression according to annotation (Huang et al. 2009).

Results

Genetic dispersion

Variance in urinary calcium excretion:

Female F₂ rats had significantly higher PD_i than males in the F₂ cohort (χ² = 5.23, P = 0.0221, µ_♀ = 0.91 ± 0.12 mg/day, µ_♂ = 0.70 ± 0.13 mg/day). Variance and coefficients of variance were considerably higher in the F₂ rats (σ² = 1.59, CV = 0.55) than in the WKY and GHS progenitors (see Hoopes et al. 2003).

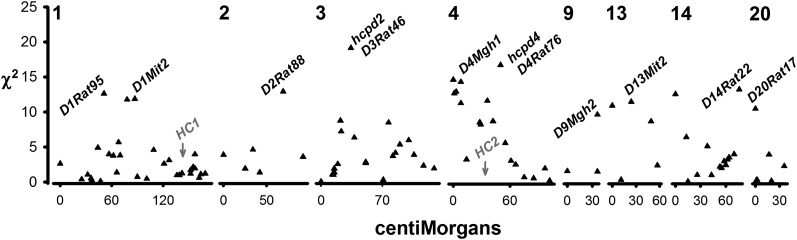
We identified significant genotypic differences (P < 0.05) in PD_i at the microsatellites D3Rat46 (RNO3, 33.9 Mb) and D4Rat76 (RNO4, 84.8 Mb) over the entire population after Bonferroni correction (Table 1 and Figure 1). We considered these to represent QTL for PD_i in urinary calcium excretion, here termed hcpd1 (linked to D3Rat46) and hcpd2 (linked to D4Rat76) (Table 1). Contrast analysis indicated that hcpd1 was underdominant (P < 0.001); σ² in untransformed urinary calcium excretion in WKY homozygotes was three times that in WKY/GHS heterozygotes and twice that of GHS homozygotes (Table 1). Hcpd2 was additive (P < 0.001); PD_i for urinary calcium excretion was significantly higher for WG heterozygotes than WW homozygotes (P < 0.01), and higher in GG homozygotes than WG heterozygotes (P < 0.05; Table 1). CVs for urinary calcium within genotypes strongly resembled results from PD_i, although hcpd2 appeared more additive at D4Rat76 (Table 1). Hcpd2 was overlapped by the very wide (∼90 Mb) 95% Bayesian CI for the conventionally acting QTL for hypercalciuria HC2 (43.4 Mb) (Hoopes et al. 2003; Scheinman et al. 2008), although physically somewhat distant from it (D4Mgh1, 17.6 Mb; hcpd2, 84.8 Mb). No other locus associated with PD_i in this study was linked to any classically acting QTL for hypercalciuria. PD_i at each locus was statistically independent of all others, with the exception of D4Mgh1 and hcpd2 (P < 0.001, Spearman rank and Pearson tests) (SAS 2000), although the mode of action at these two loci differed (overdominant vs. additive; Table 1).

Table 1 . QTL effects linked to simple sequence length polymorphisms (SSLP) for urinary calcium excretion residuals in a cohort of 236 F₂ genetic hypercalciuric stone-forming (GHS) × Wistar–Kyoto (WKY) rats at the 5% (α_0.05) and 10% (α_0.10) false discovery rate (FDR; Verhoeven et al. 2005).

Mbp (cM)			${\mu }_{WW}\pm 95\%CI$	${\mu }_{WG}\pm 95\%CI$	${\mu }_{GG}\pm 95\%CI$
Locus	Region	n	${\sigma }_{WW}^2$($C{V}_{WW}$)	${\sigma }_{WG}^2$($C{V}_{WG}$)	${\sigma }_{GG}^2$($C{V}_{GG}$)	P	r2	Ar	Pcont
D1Rat95	66.8 (51)	160	0.75 ± 0.19	0.60 ± 0.16a**	0.98 ± 0.19a**	0.0018	5.73	UD	0.0031
	1p11		1.43 (52.1)	1.03 (48.8)	2.46 (61.3)
D1Mit2	135.0 (87)	236	0.78 ± 0.18	0.70 ± 0.12a**	1.05 ± 0.17a**	0.0026	4.06	DW	0.0031
	1q31		1.17 (47.7)	1.18 (47.8)	2.79 (61.2)
D2Rat88	222.3 (69)	178	0.84 ± 0.21	1.08 ± 0.15a**	0.67 ± 0.20a**	0.0016	5.25	OD	0.0023
	2q42		1.38 (47.9)	2.69 (61.5)	1.07 (49.1)
D3Rat46	33.9 (34)	231	1.09 ± 0.18a**	0.65 ± 0.12a**	0.84 ± 0.17	<0.0001	6.03	UD	0.0007
	3q12		2.90 (63.8)	0.95 (43.8)	1.52 (53.4)
D4Mgh1	17.6 (8)	236	0.58 ± 0.16a**	0.94 ± 0.12a**	0.73 ± 0.19	0.0008	6.01	OD	0.0012
	4q12		0.75 (44.0)	2.16 (56.8)	0.96 (40.8)
D4Mit2	55.4 (36)	236	0.58 ± 0.17a*	0.82 ± 0.12	0.92 ± 0.17a*	0.0029	3.59	DG	0.0073
	4q22		0.83 (51.6)	1.61 (52.5)	2.06 (46.9)
D4Rat76	84.9 (50)	231	0.55 ± 0.17a**b***	0.79 ± 0.12a**c*	1.01 ± 0.17b***c*	0.0002	5.36	AD	0.0004
	4q24		0.89 (45.1)	1.44 (53.0)	2.24 (52.4)
D9Mgh2	84.4 (36)	197	0.86 ± 0.20	0.82 ± 0.14a**	1.09 ± 0.22a**	0.0079	2.21	DW	0.0267
	9q35		1.46 (49.8)	1.97 (61.1)	2.11 (56.0)
D13Mit2	62.1 (24)	197	0.65 ± 0.18a*	0.96 ± 0.14a*	0.99 ± 0.23	0.0032	5.21	DG	0.0024
	13q21		2.20 (44.2)	2.35 (61.1)	2.80 (56.9)
D14Rat22	102.5 (76)	236	0.78 ± 0.18	0.73 ± 0.12a*	1.04 ± 0.18a*	0.0013	3.25	DW	0.0044
	14q22		2.39 (43.7)	2.30 (54.0)	2.53 (58.7)
D20Rat17	3.4 (0)	178	0.77 ± 0.20a*	0.86 ± 0.15	1.16 ± 0.21a*	0.0052	4.99	DW	0.0022
	20q12		2.22 (49.8)	2.43 (50.9)	2.82 (67.9)

Genomic location within the chromosome is indicated in megabase pairs and in centimorgans on our F₂ GHS × WKY genomic map. Variance in untransformed urinary calcium excretion within genotypes (${\sigma }_{\text{geno}}^2$), coefficient of variation within genotypes (CV_geno), number of genotyped and phenotyped animals (n), adjusted P value (P_adj) from the ratio of the empirical P value against the 5% FDR threshold, correlational coefficient (r²) from linear statistical analysis, and variance within genotype (WW = WKY homozygote, WG = WKY/GHS heterozygote, GG = GHS homozygote) for PD_i in calcium excretion are given. Ar indicates the architecture (AD, additive; D_W, WKY dominant; D_G, GHS dominant; OD, overdominance; UD, underdominance) by SSLP locus and P_cont the significance of the contrast test associated with that architecture. All statistics were run in (SAS 2000). Means by genotype (µ) are given in milligrams per day. *, P < 0.05; **, P < 0.01; ***, P < 0.001.

^aSignificant differences among genotypes for mean PD_i.

Figure 1 .

${\chi }^2$ scores from all tests of the association of PD_i according to simple sequence length polymorphism (SSLP; microsatellite) locus position (cM). Names of microsatellite loci significantly associated with PD_i at the 5% false discovery rate are indicated. The positions of the previously identified conventionally acting quantitative trait loci for urinary calcium excretion hypercalciuria 1 (HC1) and hypercalciuria 2 (HC2) (Scheinman et al. 2008) are indicated in gray type for comparison.

Genotype at six additional microsatellite loci was associated with PD_i at the α_0.05 FDR threshold: D1Mit2, D4Mgh1, D4Mit2, D9Mgh2, D13Mit2, and D14Rat22 (Table 1 and Figure 1). Several markers linked to D4Mgh1 spanning 8 cM ≈ 14.6 Mb (Scheinman et al. 2008) were associated with PD_i at the 5% FDR; we consider our results to indicate eight loci for PD_i at the 5% FDR (Table 1). PD_i was not associated with rearing period, litter, weight, or sex at any microsatellite locus (P_avg > 0.4). At genotypes with high PD_i (i.e., GHS homozygotes at D1Mit2, WKY/GHS at D4Mgh1) variance in untransformed calcium excretion was two to three times higher than that of the other genotypes.

Sex-limited QTL for dispersion:

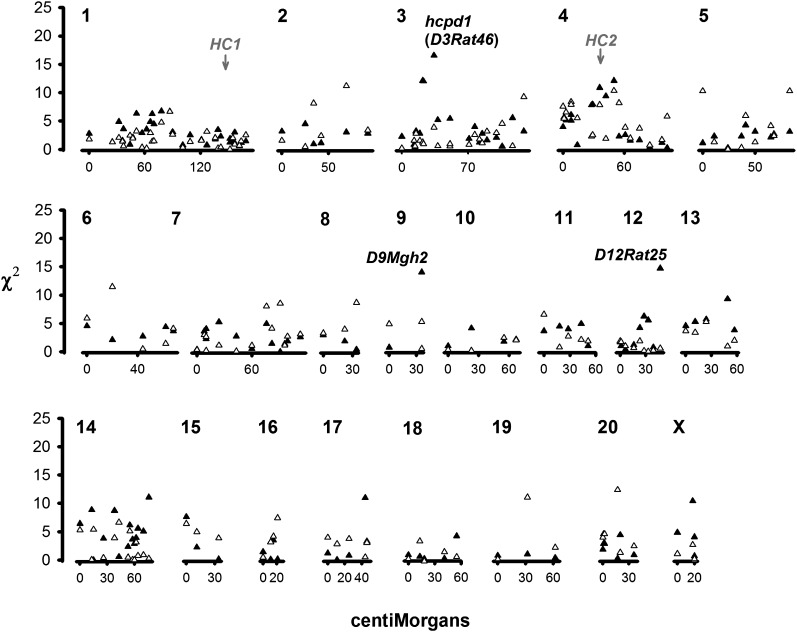
D3Rat46, which was linked to the QTL hcpd1 in the complete F₂ cohort (above), was associated with PD_i in urinary calcium excretion at the α_0.05 Bonferroni threshold (Figure 2). At this position, female WKY homozygotes had significantly higher PD_i than WKY/GHS heterozygotes after Bonferroni correction (P = 0.003; Figure 2 and Table 2). There was an a priori difference between GHS/WKY heterozygotes and WKY homozygotes in male F₂s (P = 0.0486), but this locus was not significantly associated with PD_i in males after multiple correction (P > 0.1). There was no evidence of significant interaction between D3Rat46 and the sex of the F₂ rat after Bonferroni correction (P = 0.128). Contrast tests in SAS (2000) indicated that PD_i at this locus was overdominant in females (F_{2, 125} = 8.62, P = 0.004).

Figure 2 .

χ² scores from nonparametric testing of absolute residuals (phenotypic dispersion, PD_i) for urinary calcium in male (solid triangles) and female (open triangles) female F₂ GHS × WKY rats. The location of the significant quantitative trait locus (hcpd1) and the suggestively linked markers D9Mgh2 and D12Rat25 are indicated; also indicated are the significant QTL for classical mean differences in urinary calcium HC1 and HC2 (Scheinman et al. 2008).

Table 2 . Significant and suggestive QTL for PD_i in urinary calcium excretion assayed at four microsatellites (Locus) in female F₂ GHS × WKY rats.

Locus	n	${\sigma }_{WW}^2$ (CV)	${\sigma }_{WG}^2$ (CV)	${\sigma }_{GG}^2$ (CV)	P	Sig	r2
D3Rat46 (hcpd1)	125	3.76 (66.4)	1.23 (45.8)	1.58 (53.7)	0.0002	Bonf	10.6%
D9Mgh2	105	1.15 (42.4)	2.72 (68.5)	2.61 (52.9)	0.0009	FDR	10.7%
D12Rat25	101	3.49 (64.5)	1.49 (55.0)	0.983 (45.6)	0.0007	FDR	16.9%

Results significant at the α_0.05 Bonferonni (Bonf) or FDR (Verhoeven et al. 2005) thresholds, the number of F₂ rats (n), variances (σ²), coefficients of variance (CV) for each genotype, and empirical P-value are indicated. All statistical analysis was performed in SAS (2000). Proportions of PD_i explained by microsatellite genotype (r²) were estimated using PROC VARCOMP (SAS 2000).

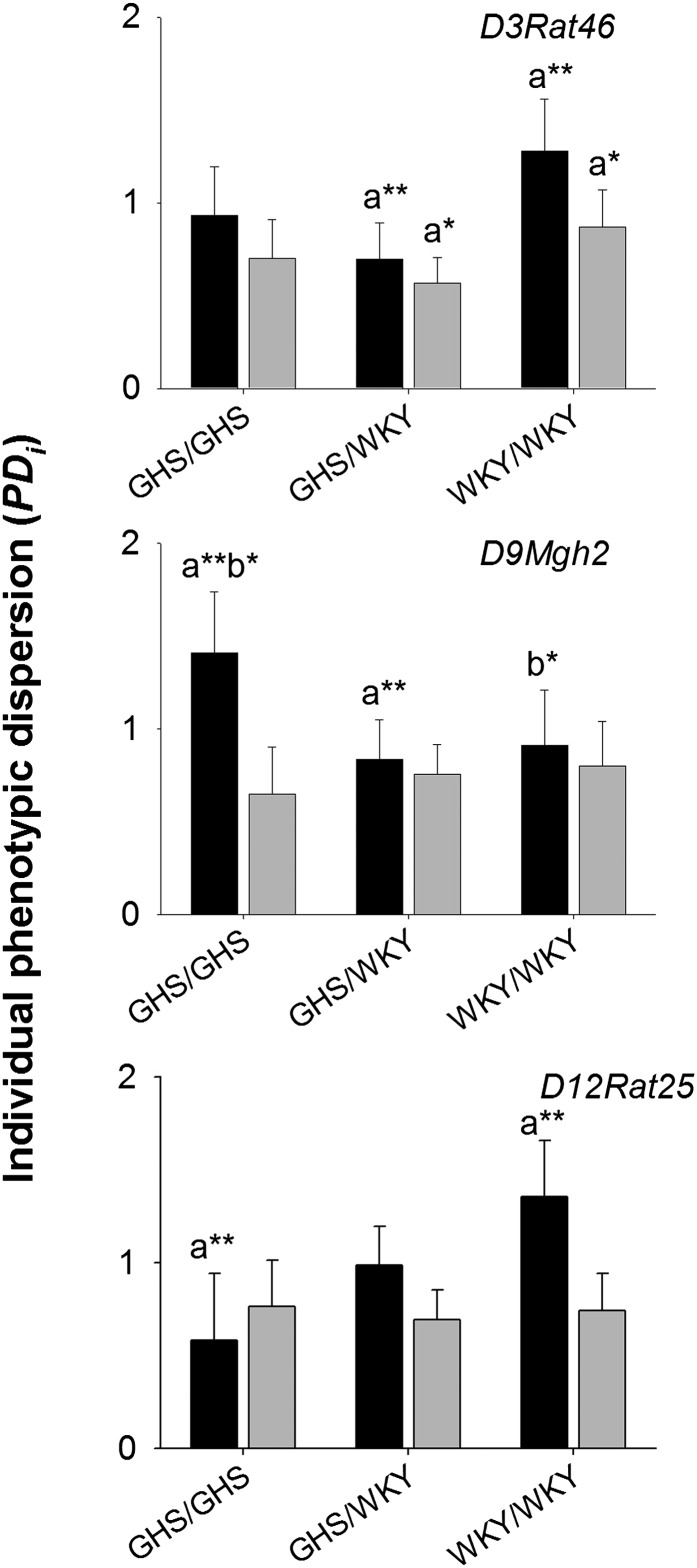
Two other loci—D9Mgh2, D12Rat25—were associated with PD_i at the FDR in female F₂ rats (P < 0.001; Figure 2 and Table 2). GHS homozygotes had significantly higher PD_i than WKY/GHS heterozygotes (P = 0.0147) and WKY homozygotes lower PD_i than GHS homozygotes in females at D9Mgh2 (P = 0.0873; Figure 3), which had negative dominance for the WKY allele (P = 0.0060). Contrast tests indicated additivity at D12Rat25 (P = 0.0018); WKY homozygotes had significantly higher PD_i than GHS homozygotes (P = 0.0054; Figure 3 and Table 2). Neither of these loci were linked to PD_i in male F₂ rats (Figure 1). There was significant statistical interaction between sex and genotype at these microsatellite loci in the F₂’s (D9Mgh2: F = 4.13, P = 0.0293; D12Rat25: F = 7.82, P = 0.0043). At D9Mgh2, female GHS homozygotes had significantly higher PD_i than male GHS homozygotes (P = 0.012), while female WKY homozygotes had significantly higher PD_i than male WKY homozygotes (P = 0.0225; see Figure 3). There was no significant sex–locus interaction for hcpd1 or hcpd2 (P > 0.3).

Figure 3 .

Mean individual phenotypic dispersion (PD_i) in urinary calcium excretion at D3Rat46 (hcpd1), D9Mgh2, and D12Rat25 in female (solid bars) and male (shaded bars) F₂ GHS × WKY intercrosses. Differences between means within sex are indicated as P < 0.05 (*), P < 0.01 (**).

Multilocus heterozygosity:

Whole-organismal multilocus heterozygosity (MLH) was not associated with residuals of calcium excretion (P > 0.8). MLH on RNO2 was marginally negatively association with residuals for calcium excretion (F = 3.16, P = 0.0766, β = -0.272 ± 0.300 |mg/day|) and MLH on RNO7 was marginally positively associated with calcium excretion residuals (F = 2.95, P = 0.0871, β = 0.251 ± 0.288 |mg/day|).

MLH was negatively associated with PD_i in females on RNO3 (β = −0.639 ± 0.508, r² = 0.0466, P = 0.0151), but positively associated with PD_i at a priori significance in males on RNO15 (β = 0.303 ± 0.267, r² = 0.0496, P = 0.0284) and 19 (β = 0.347 ± 0.276, r² = 0.0534, P = 0.0157). None of these associations passed correction for multiple testing.

Gene expression

A total of 8846 renal genes and 9038 duodenal genes had an acceptable signal-to-noise ratio (>50) in the 230A Affymetrix R230A assay. Numerous genes with high CVs in expression in these regions were associated with acetylation, spliceosome formation, RNA modification, serine/threonine physiology, immunology, and metal-ion physiology (Supporting Information, File S1 and Table S1).

Renal genes with acceptable signal within 10 Mb of PD_i QTL were enriched for acetylation (P < 0.05) and intracellular organelle lumen/organelle lumen (P < 0.05) functions by annotation (Table 3). Significant (α_0.05) clusters of genes (EASE score (E) = geometric mean –log(P)) were identified for nuclear membranes/lumena (E = 2.91), mitochondrial (E = 1.87), protein catabolism (E = 1.52), and mitochondrial transit peptides (E = 1.39) using DAVID (Huang et al. 2009).

Table 3 . Fold enrichment (fER), percentage hit rate by annotation term, and Benjamini-corrected significance (P_Benj) for renal and duodenal genes with significant (>50 fluorescence units) mean expression within 10 Mb of microsatellite loci associated with PD_i in urinary calcium.

	Kidney			Duodenum
Pathway	fER	%	PBenj	fER	%	PBenj
Intracellular organelle lumena	1.56	14.5	0.0089	1.54	12.1	0.3809
Organelle lumena	1.59	15.3	0.0098	1.54	12.6	0.4985
Membrane-enclosed lumena	1.54	15.3	0.0129	1.50	12.6	0.3379
Acetylationb	1.46	17.8	0.0374	1.63	17.3	0.0115

Fluorescence means were calculated from three female Genetic Hypercalciuric Stone-forming and three Sprague-Dawley rats. Database of origin are indicated in the footnotes.

^aSP_PIR_KEYWORDS.

^bGOTERM_CC_FAT.

Duodenal genes with acceptable signal linked to PD_i QTL were enriched for acetylation (P < 0.05) genes according to annotation (Table 3). Hit rates were relatively high for each group (∼15%). Annotational clusters identified from duodenal samples included organellar lumena (E = 2.04), ribosomal translation (E = 1.78), intracellular protein transport (E = 1.57), and those located in the endoplasmic reticulum (E = 1.46).

Sex and CV in RNO1 congenic rat lines

Because of our findings of differences in dispersion between male and female F₂ rats, we further tested for sex differences in residuals in our subcongenic RNO1 rat line (Hoopes et al. 2003). These lines are descended from a single GHS male (Hoopes et al. 2003). Congenic rats used in this analysis had been retrocrossed to WKY animals for 6–11 generations in the process of fixation of WKY genetic background, including RNO1 outside the 95% critical region for HC1 (220–239 Mbp). WKY genotype was determined during this selection using microsatellite genotyping (Hoopes et al. 2003). Four-day CVs in urinary calcium were calculated for each congenic rat. Given the higher CV for urinary calcium in WKY males, and the concentration of WKY genotype in the congenic lines via retrocross, we predicted higher CVs for male rats in the congenic lines. Congenic rats were fed a high-calcium diet (1.2% Ca, 0.65% PO₄); TD.90312.PWD; Harlan Teklad, Indianapolis) for 10 days and urinary calcium was measured daily (as above). We calculated the CV for urinary calcium for each congenic individual; male–female differences in mean CV were compared for each sex within each line and generation using nonparametric ranking and t-tests.

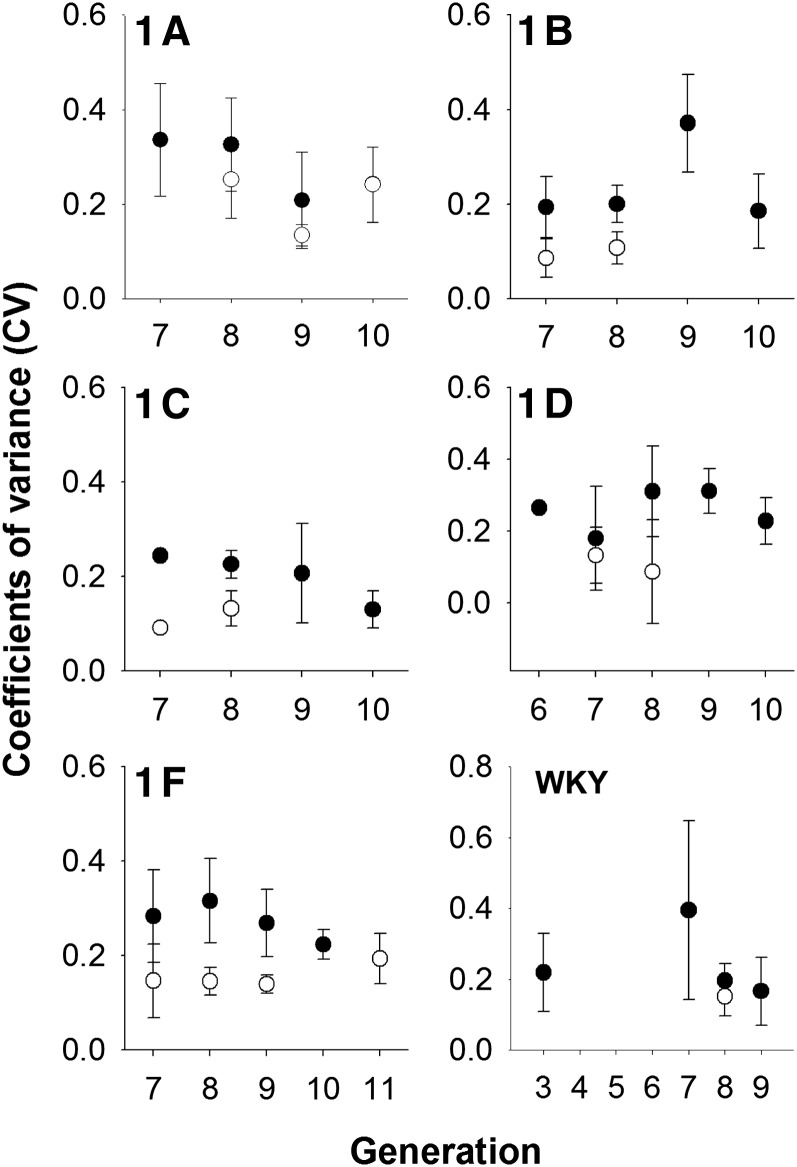
In 5 generations, 270 males and 61 female congenics were available. Males had significantly higher CV than females overall in the congenic population (F_1,322 = 30.4, P < 0.0001, µ_M = 0.246 ± 0.0225, µ_F = 0.150 ± 0.0169) in multifactorial linear modeling and in nonparametric single-factor modeling (χ² = 31.2, P < 0.0001). This effect was also detected in comparisons of CVs within subcongenic lines 1A–1F: of these lines, CV was significantly higher in males than in females in all lines (P < 0.05) except for line 1A, in which male CVs were only suggestively higher than those in females (P < 0.1) (Figure 4 and Table 4). There was no statistical difference between WKY males and females for urinary calcium excretion (P > 0.3) although urinary calcium was available only for a single generation of WKY females, and mean CVs for calcium excretion by sex in the WKYs were very similar to those in the other subcongenics, although not significantly different (µ_M = 0.238, µ_F = 0.158; Figure 4 and Table 4).

Figure 4 .

Coefficients of variation (CV) ± SE for 4-day urinary calcium excretion in male (●) and female (○) female chromosome 1 subcongenic lines 1A–1F and in WKY rats by generation.

Table 4 . Differences in CVs for urinary calcium excretion in male and female by line tested using Wilcoxon nonparametric one-way analysis.

Line	N	χ2	P	µM	µF
1A	39	2.84	0.0919	0.292 (0.0476)	0.203 (0.0761)
1B	45	7.68	0.0056	0.217 (0.0331)	0.106 (0.0853)
1C	42	5.82	0.0158	0.214 (0.0306)	0.109 (0.0708)
1D	53	11.1	0.0008	0.266 (0.0478)	0.123 (0.0911)
1F	66	8.87	0.0029	0.261 (0.0349)	0.139 (0.0629)
WKY	42	1.12	0.2905	0.238 (0.0670)	0.158 (0.140)

Mean CVs for calcium excretion in males (µ_M) and females (µ_F) (95% CI) are derived from calcium excretion across all generations within each subcongenic lines.

Discussion

Two microsatellite loci were significantly associated with absolute residual dispersion at Bonferroni-corrected significance thresholds across the entire population, which we consider evidence for QTL for residual variance in urinary calcium. The likelihood of all 11 tests significant at the 5% FDR being false positives was 9%, and 0.3% for all results significant a priori (see Moran 2003). MLH was not associated with dispersion. Allelic heterogeneity appears the most likely explanation for our findings (Hill and Bunger 2004; Hill and Zhang 2004). Our hypotheses of sex linkage on dispersion in urinary calcium are as follow: female F₂ rats had higher dispersion in urinary calcium than males (P < 0.05), and QTL for phenotypic dispersion were detected only in female F₂s (P < 0.05), while male WKY animals and male congenics in each RNO1 subcongenic line (being >1 – 0.5⁶ ≈ 98% WKY genome) had significantly higher CVs for urinary calcium than females (P < 0.001), suggesting differences in sex linkage between GHS and WKY rather than sex limitation. Sex differences in the effect of hcpd1 (D3Rat46) and hcpd2 (D4Rat76) on dispersion were scalar, but there were significant male–female differences in dispersion patterns by genotype at D9Mgh2 and D12Rat25.

Sex may be the most fundamental contrast in biology (Andersson 1994; Gabory et al. 2009); there is widespread sexual dimorphism in gene expression (Waxman and Celenza 2003; Clodfelter et al. 2006; Yang et al. 2006; Wauthier and Waxman 2008) and intersexual genetic correlation is routinely less than unity (Chippindale et al. 2001; Stewart et al. 2010; van Doorn 2009). Previous work of ours indicates sex effects on the genetic structure of residuals for operant behavior in rats (Perry et al. 2010a) and sex chromosomal–autosomal interaction for thermotolerance in rainbow trout (Perry et al. 2003). Other work suggests the effects of sex on plasticity (Fernandez-Montraveta and Moya-Larano 2007; Stillwell et al. 2010) or on phenotypic residuals over environmental gradients (Mackay and Lyman 2005); however, we found no association of dispersion with rearing group or litter (P > 0.1). Various X-chromosomal peculiarities, including pseudoautosomal recombination and mutation (Lien et al. 2000; Lercher and Hurst 2002; Filatov and Gerrard 2003; Ross et al. 2005), variable X-chromosomal deactivation (Heard and Disteche 2006; Leeb and Wutz 2010) including among lineages (Patrat et al. 2009) might explain such effects (Charlesworth et al. 1987; Evans et al. 2007). Some molecular chaperones including hsp70, hsp90, and Piwi-interacting RNA canalize variability in morphological and over environmental and genetic axes (Gibert et al. 2007; Fernandino et al. 2011; Gangaraju et al. 2011). Work in mice suggests that environmental buffers of gene expression are sex specific (Fraser and Schadt 2010). Sex might also affect dispersion via simple hormonal fluctuations over estrus. All animals were used specifically at 8 weeks of age to minimize estral effects, which may have been common to litter and/or cohort. Other work of ours also indicates significant genetic effects on CVs for urinary calcium in males alone, suggesting a genetic basis for residual variability independent of estral cycling (Perry et al. 2011).

Gene expression

Enrichment for calcium excretion genes around QTL for untransformed urinary calcium (Hoopes et al. 2003) and for acetylation, luminal, and MHC II genes around our dispersion QTL suggests a firebreak between conventional genetic effects and those on variance; interesting, both conventionally acting QTL for calcium excretion in the F₂ mapping cohort (HC1 and HC2) were detectable only in males (Scheinman et al. 2008; Perry et al. 2009). Lysine acetylation is a common (up to 90% of all Eukaryotic proteins (Glozak et al. 2005; Sadoul et al. 2008) modifier of histone and nonhistone proteins (Sadoul et al. 2008; Yang and Seto 2008) and may interact with other post-translation protein modification processes such as methylation and ubiquitination (Yang and Seto 2008). Such a ubiquitously active genetic pathway might explain the frequently encountered 10% CV in juvenile mammalian body size (see Hill and Zhang 2004). Several genes with high-expression CV linked to our dispersion loci are also known gene expression modifiers including several serine-rich protein genes, which are also involved in alternate splicing (Fu 1995). LSm5 is a member of the like-Smith protein gene family, ubiquitous in eukaryotes (Marz et al. 2008) and critically involved in spliceosome function by binding to U6 small nuclear RNA (snRNA) (Tkacz et al. 2008; Valadkhan 2010). Methylmalonic aciduria and homocystinuria type D protein (Mmadhc) is associated with methylation (Coelho et al. 2008; Radmanesh et al. 2008). Tra2a is critically involved with sexual differentiation in Drosophila (Hoshijima et al. 1991; Ryner and Baker 1991) and mammals (Tacke et al. 1998; Lieberman et al. 2001; Shiraishi et al. 2004) and promotes pre-mRNA splicing (Tacke et al. 1998).

Conclusions

Genes for residual variability might conceivably interfere with the detection, characterization, and localization of phenotype–genotype correlation by increasing type II error and reducing power due to increasing residual genetic variation. Sex-limited or sex-specific residual variance structures could create an entirely new level of analytical complexity, creating unsuspected genotypic architectures for seemingly classical phenotypes. Using our own example: hcpd2 is linked (16 cM; ∼40 Mb) to a classically acting QTL for hypercalciuria (HC2) in our study population (Perry et al. 2009). HC2 is partially sex limited to males and has an exceedingly wide 95% confidence interval (CI) (48 cM; ∼90 Mb (Scheinman et al. 2008); HC2 is also flanked by two positions associated with dispersion. HC1 was of equivalent effect but narrower CI (∼12 cM) and was not flanked by dispersion loci in our F₂ population (Perry et al. 2009). Much of the theoretical correction for such effects might revolve around sex, requiring explicit inclusion of sex-specific phenotypic or genotypic heterogeneity. The fundamental construction of this phenomenon leaves no reason to believe that it should be confined to any particular system: such a phenomenon might theoretically affect any genetic analysis, although the risk would presumably be greatest for dispersion loci in linkage or linkage disequilibrium with more typical QTL. Practically, the identification of such effects would require either identification of genetic structure in residuals or the use of multiple measurements to account for genetic residuals. Dispersion genotypes could also promote escape from local fitness peaks by creating wider trait ranges over adaptive phenotypic landscapes (see Wright 1931), crossing of fitness troughs by liberating genotype–phenotype associations or even reducing sib competition by limiting overlap in phase space (Begon et al. 2006; Brigatti et al. 2007; Leone and Estevez 2008). Such a bet-hedging strategy might be more common in r-selected organisms; for example, juvenile coral growth rates are highly variable, but recruits to coral communities have stable growth functions (Vermeij 2006). Rapid evolution in changing environments is sometimes cited as an advantage of sex (Crow 1992); in addition to the exposure of deleterious mutations to selection (Maynard Smith 1978; Kondrashov 1988; Loewe and Hill 2010; Park et al. 2010), sex might also facilitate evolution by the liberation of residual variance. These suppositions remain largely untested: little is known of the potential statistical or natural state of such systems and further work is required to establish their role. Urinary calcium itself might have fitness relevance; calcium is a critical element in numerous physiological pathways including but not limited to signal transduction, membrane potential, cofactor activity, and bone physiology in addition to its function in muscular metabolism (Boron and Boulpaep 2011). Genetic dispersion in calcium metabolism might be a system for rapid reaction to changing ionic requirements, using bone as a stable reserve against physiological outlay; our findings suggest that dispersion systems might be common in evolutionary biology, active at many levels from large to small and integrally involved in the essentials of cellular physiology.