Fine-Scale Maps of Recombination Rates and Hotspots in the Mouse Genome

Abstract

Recombination events are not uniformly distributed and often cluster in narrow regions known as recombination hotspots. Several studies using different approaches have dramatically advanced our understanding of recombination hotspot regulation. Population genetic data have been used to map and quantify hotspots in the human genome. Genetic variation in recombination rates and hotspots usage have been explored in human pedigrees, mouse intercrosses, and by sperm typing. These studies pointed to the central role of the PRDM9 gene in hotspot modulation. In this study, we used single nucleotide polymorphisms (SNPs) from whole-genome resequencing and genotyping studies of mouse inbred strains to estimate recombination rates across the mouse genome and identified 47,068 historical hotspots—an average of over 2477 per chromosome. We show by simulation that inbred mouse strains can be used to identify positions of historical hotspots. Recombination hotspots were found to be enriched for the predicted binding sequences for different alleles of the PRDM9 protein. Recombination rates were on average lower near transcription start sites (TSS). Comparing the inferred historical recombination hotspots with the recent genome-wide mapping of double-strand breaks (DSBs) in mouse sperm revealed a significant overlap, especially toward the telomeres. Our results suggest that inbred strains can be used to characterize and study the dynamics of historical recombination hotspots. They also strengthen previous findings on mouse recombination hotspots, and specifically the impact of sequence variants in Prdm9.

RECOMBINATION events are not uniformly distributed across the genome; rather they tend to occur at hotspot regions typically 1–2 kb in size (Jeffreys et al. 2001; Kelmenson et al. 2005; Myers et al. 2005; Mancera et al. 2008). The dense map of single nucleotide polymorphisms (SNPs) created by the HapMap Project enabled the high-resolution mapping of recombination rates in the human genome and led to the identification of ∼33,000 recombination hotspots with a coalescent method (Myers et al. 2005). The very large number of hotspots and the very high resolution of this mapping made it possible to pinpoint sequence motifs in these hotspots, one of which was instrumental in finding a gene, PRDM9, thought to be a critical component of the recombination mechanism (Baudat and de Massy 2007; Grey et al. 2009; Parvanov et al. 2009).

Until recently, the primary strategy for analysis of recombination hotspots in mice has been to use pedigree analysis in strain crosses (Paigen et al. 2008; Billings et al. 2010; Dumont and Payseur 2011; Dumont et al. 2011). The problem with this approach is the high cost of typing SNPs for sufficient numbers of cases in order to define recombination hotspots with power and precision. A different approach that relies on the binding of RAD51 and DMC1 proteins was recently used to map meiotic DNA double-strand breaks (DSBs) that initiate recombination (Smagulova et al. 2011). Recombination initiation sites were found to be associated with testis-specific trimethylation of lysine 4 on histone H3. There has been one study that showed that recombination rates in outbred mice are associated with patterns of linkage disequilibrium (LD) in inbred strains, but the average distance of 167 kb between SNPs was nevertheless insufficient to attempt replicating the human analysis (Shifman et al. 2006). LD blocks are considerably larger in inbred mice compared to human populations and wild mice (Laurie et al. 2007). Still, a subset of experimentally tested boundaries of LD blocks in inbred mice was shown to correspond to active recombination hotspots (Kauppi et al. 2007).

The complete sequencing of 17 inbred strains (Keane et al. 2011), in addition to the reference genome, provides a new resource for mapping hotspots. Recombination events in the laboratory strains are historical events that occurred over hundreds of generations during the genetic fixation of laboratory strains from wild Mus musculus progenitor subspecies. The 17 strains include classical inbred strains as well as four wild-derived inbred strains (Kang et al. 2010; Kirby et al. 2010). The classical inbred strains predominantly originate from M. m. domesticus, whereas the wild-derived strains derive from M. m. musculus, M. m. domesticus, or M. m. casteneus with intersubspecific introgression (Yang et al. 2011).

In the present study, we report high-resolution recombination rate estimates across the mouse genome and the identification of 47,068 hotspots using the 12 classical sequenced mouse strains. We show that recombination hotspots evolve rapidly and have different positions in mouse and human, but share certain key characteristics and distributions. In both species, hotspots tend to avoid gene promoters, but are associated with specific repeat elements, and in both species these regions are enriched for motifs associated with PRDM9 protein binding.

Materials and Methods

SNP data

We used two datasets to detect recombination hotspots. First, we obtained 64,618,703 SNPs from 17 inbred strains covering a genomic region of 2567.89 Mb from the Mouse HapMap Imputation Genotype Resource (http://mouse.cs.ucla.edu/mousehapmap/beta/index.html). The SNP data were generated as part of the Mouse Genome Project, The Wellcome Trust Sanger Institute (http://www.sanger.ac.uk/resources/mouse/genomes/). The SNPs were mapped to Build 37 (National Center for Biotechnology Information). We removed known regions of segmental duplications, which left us with 63,494,751 SNPs. We also removed from the analysis wild-derived strains that are not of M. m. domesticus origin (Yang et al. 2011). We removed two additional strains (129P2 and 129S1/SvImJ) with high correlation (r > 0.8) with another strain in the sample (129S5SvEvBrd). The resulting 12 strains used in this study were: 129S5/SvEvBrd, AKR/J, A/J, BALB/cJ, C3H/HeJ, C57BL/6NJ, CBA/J, DBA/2J, LP/J, NOD/ShiLtJ, NZO/HILtJ, and WSB/EiJ. The genetic correlation between the 12 strains is presented in Supporting Information, Figure S1.

The second dataset was of 100 classical strains genotyped with the Mouse Diversity array (Yang et al. 2011). The initial dataset included 548,769 SNPs. To reduce the relatedness between strains, we removed strains with genetic correlation to any other strain in the sample of >0.6. The final sample consisted of 60 strains with 252,547 informative SNPs.

Recombination rates calculation

The Interval program in LDhat 2.1 (Auton and McVean 2007) was used for recombination rate estimation between pairs of successive polymorphic SNPs. LDhat calculates the likelihood surface for different recombination rates for each pair of SNPs by simulating coalescent trees under a reversible jump Markov chain Monte Carlo (rjMCMC) scheme. The likelihoods between SNPs are combined to the likelihood of a region using a composite likelihood method. The recombination rates yielding the highest likelihoods are then chosen for each region. We allowed the rjMCMC in Interval to run for a million iterations using a block penalty of 20 (see Simulations section for a reasoning), a burn-in of 2,000 iterations, and sampling every 2,000 iterations.

Detection of recombination hotspots

We used sequenceLDhot (Fearnhead 2006) for the definition of high recombination regions (hotspots). The program sequenceLDhot makes use of large-scale recombination rates, (background rates), and subsequently tests smaller regions for the presence of elevated recombination rates by taking into account local SNPs and LD. To test the smaller regions for significantly higher local recombination rates, it relies on a likelihood-ratio statistic of the background rate and the local rate. Regions with significantly elevated local recombination rates are determined to be hotspots. The median of the recombination rates estimated by Interval for the 60 genotyped strains, calculated with sliding windows of 1 Mb, and a shift of 1 Kb was used as the background recombination rate. We set up sequenceLDhot to estimate local recombination rates on the basis of seven informative, local SNPs for each window (Fearnhead 2006). On the basis of simulation results, a likelihood-ratio statistic >15 was used as a cutoff value to determine significant hotspots. To detect hotspots using the 12 sequenced strains, we calculated hotspots for windows of 2 kb in size with shift of 1 kb.

For the 60 genotyped strains, which have much lower density of SNPs, we calculated hotspots on sliding windows of 18 kb in size and a shift of 10 kb.

Comparisons to other maps

To compare the recombination rates estimated by LDhat in terms of 4N_er/kb with a previously calculated genetic map by Cox et al. (2009), we normalized the resulting map from LDhat by setting the total length of the maps to be the same. Since the Cox map was calculated at a much lower SNP resolution, we made the maps comparable by smoothing recombination rates over windows of different sizes. The comparison between LDhat estimates and previously published maps for chromosome 11 (Billings et al. 2010) and chromosome 1 (Paigen et al. 2008) was performed similarly by normalizing the map from LDhat according to the length of the genetic maps of chromosome 11 or 1. Comparisons between the different estimations of recombination rates were done using Pearson correlation.

Simulations

We conducted several simulations to assess the appropriateness of parameters used in the recombination rate and hotspots estimation. To assess the optimal sample size from the newly genotyped classical strains, we subsequently calculated recombination rates for samples that had maximal correlations of 0.8, 0.6, 0.4, and 0.3. For the calculation of recombination rates, we again used the Interval program of LDhat. The block penalty in Interval, which controls the number of changes in the recombination rate of a chromosome, was set to 0, 10, or 20. For any combination of those parameters, we compared the resulting recombination rates to the map of Cox et al. (2009) and chose the set of parameters that achieved the highest correlation with it.

To assess the influence of inbreeding on the estimated recombination rate, we ran the following simulation. We used the msHOT program (Hellenthal and Stephens 2007) to generate 12 × 8 randomly mated mice. We simulated SNPs for this population on a region of 1 Mb on chromosome 1 with a total background recombination rate of 13.789 4N_er and a mutation rate of 3.8 × 10⁻⁸ (Lynch 2010). This background recombination rate is the average recombination rate for regions of 1 Mb in size on chromosome 1 as estimated by LDhat. We included 10 hotspots in the simulation that were set to be uniformly distributed in the simulated region, 1–5 kb in size: two were 1 kb, two were 2 kb, two were 3 kb, two were 4 kb, and two were 5 kb. We set the hotspots to have a 100-fold rate compared to the average recombination rate. To form a sample of 12 inbred mice, we sampled 1 mouse from each of the 12 × 8 groups of mice. We performed inbreeding by sib mating always choosing two parental strains from each of the 12 groups of 8 mice. We then calculated the recombination rates and hotspot positions for this sample. This was repeated 100 times.

Repeats enriched in hotspots

We downloaded the positions of all repeats using the RepeatMasker tool on the University of California Santa Cruz (UCSC) genome browser. For each repeat family and repeat type, we counted the number of hotspots and coldspots overlapping the repeat. We tested for significant differences between hotspot and coldspot counts using Fisher’s test.

Sequences enriched in hotspots

For each repeat background, we conducted an extensive search for all sequences of 5–12 bases and tested their enrichment using Fisher’s test and then corrected the resulting P-values for the number of motifs tested (11,184,640) using a Bonferroni correction. A separate extensive search for motifs was also conducted in nonrepeat parts of hotspots and coldspots. To this end, we masked all repeats in hotspots and coldspots using RepeatMasker. Occurrences of all motifs were then counted in hotspots and coldspots.

Prdm9 genotyping

We sought to identify the Prdm9 allele for each of the 12 inbred strains used here. The Prdm9 allele in 11 of the 17 sequenced strains (129S1/SvImJ, AKR/J, A/J, BALB/cJ, C3H/HeJ, CAST/EiJ, CBA/J, DBA/2J, NOD/ShiLtJ, PWK/PhJ, and WSB/EiJ) was reported by Parvanov et al. (2010). To determine the allele of the 6 unknown strains, we used an imputation method. We obtained genomic DNA samples for 30 inbred strains for which some were identified by Parvanov et al. (2010) and some overlapped with the original 17. None of these strains, however, were one of the unknown 6.

Sanger sequencing was used to determine the number of zinc fingers at exon 12 of Prdm9 using the primers (1) 5-ATATGGAATGGAATCATCGC-3 and (2) 5-ATTGTTGAGATGTGGTTTTATTG-3 for PCR amplification and (3) 5- ATGTGGGCAATATTTCAGTGATAA-3 for sequencing (as previously described, Parvanov et al. 2010). Primer 2 was used for reverse sequencing when forward sequencing did not yield conclusive results. PCR was performed in 32 cycles of 94° for 1 min, 57° for 30 sec, and 72° for 1 min and 30 sec. The last cycle was followed by 10 min at 72°. The reaction conditions were the following: 200 µM dNTPs, 2 mM MgCl₂, 500 pmol primers 1 and 2, and 0.45 units Qiagen HotStarTaq polymerase with 1× buffer. The PCR product was treated with shrimp alkaline phosphatase and exonuclease I for 30 min at 37°, followed by 10 min at 80°, and then sequenced using the ABI PRISM 3730xl DNA analyzer.

Using the results from the sequencing, we obtained 40 strains for which the Prdm9 alleles were known and 5 strains with an unknown Prdm9 allele. We imputed the Prdm9 alleles for the 5 strains using EMINIM (Kang et al. 2010) in the following way: We created three artificial SNPs in the Prdm9 region whose combination uniquely represented the five reported Prdm9 alleles (Parvanov et al. 2010). For strains with unknown alleles we set the three SNPs to be missing. The known alleles and SNPs in a surrounding region of 10 kb were then used to impute the missing alleles. EMINIM returned allele probabilities for each missing SNP. We considered the imputation successful if the probability of a genotype was at least 0.9 in all three SNPs. We cross-checked the imputation by using simple hierarchical clustering on SNPs surrounding Prdm9.

Enrichment of Prdm9 binding sequences

We tested the enrichment of each position weight matrix (PWM) of the Prdm9 alleles by summing the probabilities for a motif at each position in a hotspot. The final score for each hotspot was the maximum of all sums within the hotspot. We calculated these maxima for each hotspot and coldspot and compared their distributions by a paired Student’s t-test. We corrected for multiple testing for the different PWMs using a Bonferroni correction. We also calculated scores on the background of each individual repeat in hotspots and coldspots and compared the distributions with a Wilcoxon rank-sum test. Multiple testing was again accounted for by a Bonferroni correction.

Results

Sensitivity and specificity of the approach

There are potential drawbacks to the use of inbred strains for recombination analysis. The most crucial is that inbred strains have undergone substantial inbreeding, which violates coalescent assumptions of random mating. To address the possible influence of inbreeding and the violation of coalescent assumptions, we conducted a simulation. We used a genomic region with a fixed background recombination rate that included 10 hotspots of varying lengths (mean of 3 kb) but with equal hotspot intensities. We generated an inbred population similar to the population of the 12 inbred strains used in this study by simulation. We tested the ability to detect simulated hotspots in this type of population, repeating the simulation 100 times.

The general performance of hotspot detection (true positive rate vs. false positive rate) using a simulated sample of 12 inbred lines dependent on the significance threshold used in the sequenceLDhot package (Fearnhead 2006) (Figure S2). The average true positive rates were between 0.2 and 32.6%, and the average false positive rates, between 0 and 10.9%. The average size of the detected hotspots was 3.3 kb, relative to the average 3.0 kb size of the simulated hotspots. On the basis of the simulation results, we selected a threshold likelihood ratio of 15, which reduced the false positives to 0.7%, but retained a true positive rate of 8%. While our simulation does not capture the full complexity of inbred strain genomes, it does suggest that LDhat and sequenceLDhot are fairly robust to violations of neutral coalescent assumptions.

Fine-scale recombination rate

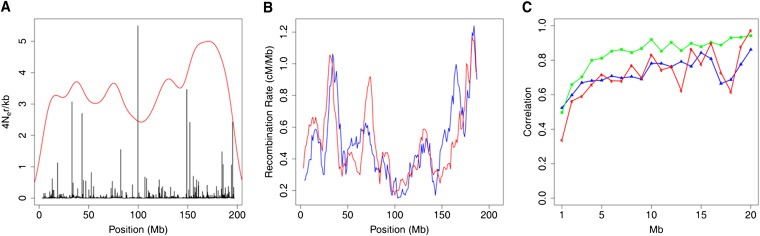
We constructed a fine-scale genome-wide recombination rate map on the basis of 252,547 SNPs that were genotyped in 60 mouse inbred strains. The average genetic correlation between the 60 strains was 0.2, with a maximum correlation of 0.6. The fine-scale recombination rates and the SNP density for each chromosome are presented in Figure S3. Recombination rates showed substantial variation between and within chromosomes (Table S1). An example of the SNP density and the recombination rates on chromosome 1 are shown in Figure 1A.

Figure 1 .

Recombination rate estimations for chromosome 1. (A) Recombination rates estimated by LDhat (black lines, unsmoothed) and SNP density (scaled to 100) across the chromosome (red line). (B) Comparison of recombination rates across chromosome 1 between the rates estimated by LDhat (red line) and a pedigree-based genetic map by Cox et al. (2009) (blue line). Both lines are recombination rates smoothed over windows of 10 Mb and shifted every 1 Mb. (C) Correlations between the recombination rates estimated from mouse crosses, Cox and Paigen (green line), between Cox and the current study (blue line), and Paigen and the current study (red line). The correlations (y-axis) are shown as a function of the window size in Mb (x-axis). The correlations were calculated with different sizes of nonoverlapping windows.

We examined the extent to which the estimated rates of recombination were comparable to crossover rates estimated from pedigree-based studies. We compared our results with a genetic map based on mouse pedigrees (Shifman et al. 2006) recently revised by Cox et al. (2009). The results are presented in Figure 1B for chromosome 1 and for the rest of the chromosomes in Figure S4. The average correlation between the two maps increased with larger window size and showed a correlation of >0.47 for windows >10 Mb (Figure S5), but with large variations among chromosomes (Figure S4). In several chromosomes, local discrepancy between the maps causes the correlation to be low. These variations in the correlations may be due to segmental duplications or large gaps between SNPs where recombination rates cannot be accurately estimated by LDhat. Alternatively, it could be real differences between historical and current recombination landscape. Nevertheless, the average correlations are equivalent to the ones that was recently observed between the DSB map and crossover maps (Smagulova et al. 2011). We also compared recombination rates to a recently published dense genetic map on chromosomes 1 and 11 (Paigen et al. 2008; (Billings et al. 2010) (Figure 1C and Figure S6 and Figure S7). There are similar high correlations between the three maps (Cox, Paigen, and LDhat estimates) for chromosome 1, as can be seen in Figure 1C.

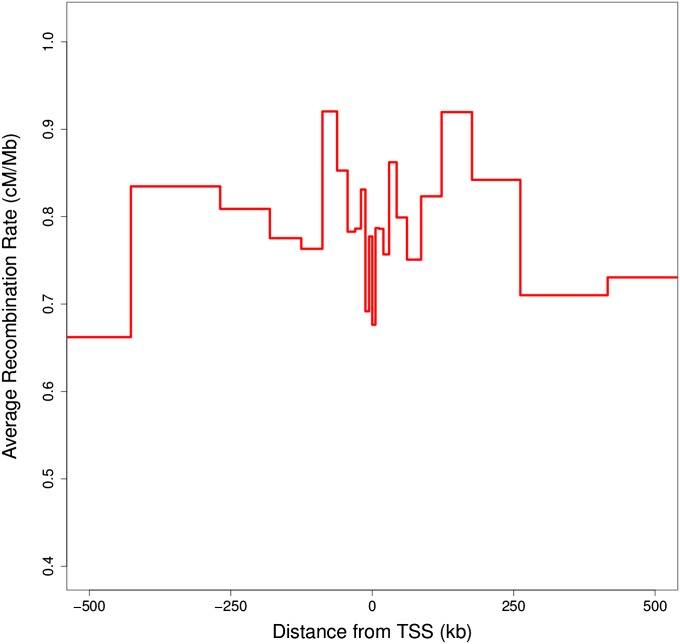
We next investigated fine-scale recombination as a function of the distance from TSS. We used midpoint positions between SNPs and determined their closest distances to a TSS. We related these distances to the recombination rates obtained from LDhat. Recombination rates were significantly lower near TSS and were the highest when they were tens or hundreds of kilobases from the closest TSS (Figure 2). A similar result has been observed in humans (Myers et al. 2005; Coop et al. 2008).

Figure 2 .

Recombination rates as a function of the distance to transcription start site (TSS). Distances are expressed in means over successive windows of 1,000,000 SNPs. Mean recombination rates as estimated by LDhat were calculated for the same windows.

Recombination hotspots

We proceeded to identify recombination hotspots using the SNP genotypes of 12 inbred strains that were fully sequenced. Recombination hotspots were tested in sliding regions of 2 kb with shifts of 1 kb using the package sequenceLDhot (Fearnhead 2006). A total of 47,068 potential hotspots were defined with significantly elevated recombination rates and a likelihood ratio >15 (Table S2). As expected, hotspots were not uniformly distributed across the genome (Figure S8). The median length of the identified hotspots was 5 kb.

We compared these sex-averaged historical hotspot locations to the list of DSB hotspots reported by Smagulova et al. (2011). We found that 27.8% of the DSB hotspots overlapped a historical recombination hotspot. We calculated the sampling distribution of this overlap by repeatedly and randomly choosing intervals on the genome of the same length as our hotspots and calculating the overlap with the DSB hotspots. The overlap proved to be highly significant (P < 0.001; none in 1000 simulations). For each of our hotspots, we also chose a matched coldspot: a region of the same size as the hotspot, but with no evidence of historical recombination. Additionally, the region was matched for SNP density, GC content, and whether the hotspot was in a gene. We also chose the coldspot to be as close to the hotspot as possible but not <5 kb from a hotspot. This was to ensure that effects of small errors in estimation of the location of hotspots would not influence coldspots. The overlap of DSB hotspots with the coldspots was 18%, significantly lower than the overlap with historical hotspots (P = 2.2 × 10⁻¹⁶). The recombination rate in females is known to be higher near the centromere, whereas in males it is higher in subtelomeric regions (Shifman et al. 2006). Since the DSB hotspots were found in male mice while the historical hotspots capture sex-averaged events, we tested the relationship between the relative distance from the telomeres and the probability for DSB hotspots to overlap an historical hotspot. Consistent with known sex differences, DSB hotspots had a higher likelihood to overlap a historical hotspot if located closer to the end of the chromosome (P = 3.65 × 10⁻⁴, Figure S9).

We next compared the positions of historical recombination hotspots between humans (Myers et al. 2005) and mice on a genome-wide scale. We determined the orthologous human positions of mouse hotspots using the UCSC LiftOver tool. We were able to find an orthologous human region for 78.8% of the mouse hotspots. Of the orthologous hotspots, 17.3% had a nonzero overlap with at least one human hotspot. The orthologs of the mouse coldspots (83%) showed approximately the same fraction of overlap with human hotspots (17.28%) as the orthologs of the mouse hotspots. That is, hotspots are not more conserved than their control regions.

Hotpot features and sequence elements

For a further characterization of hotspots, we compared the frequency of individual repeats and repeat families in hotspots relative to coldspots. We restricted the analysis to 25,825 hotspots of <5 kb in size. At the family level, only simple repeats were highly significantly enriched in hotspots (Table S3 for repeats enriched in hotspots). At the level of individual repeats, several individual repeats were enriched in hotspots. In addition to simple repeats [(GA)n, (TC)n, and (TA)n], L1Md_F2 (a LINE-1 repeat) was by far the most significantly enriched repeat in hotspots (P = 3.35 × 10⁻²⁶).

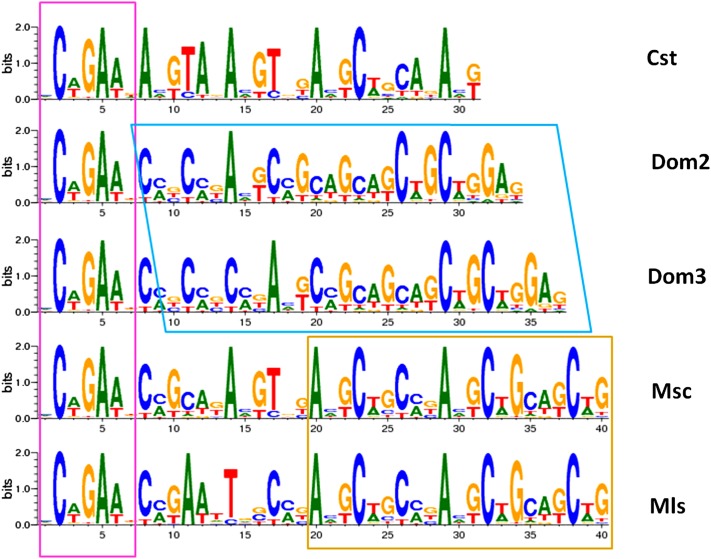
For human hotspots, a degenerate sequence motif, estimated to account for 40% of hotspots, has been reported (Myers et al. 2005). We sequenced the variable region of Prdm9 in 35 different inbred strains (Table S4), and based on the strains with known alleles, we imputed the alleles of Prdm9 for other strains that were not resolved (Figure S10). As a result, among the 12 inbred strains used for the hotspot identification, eight are Dom2 and four are Dom3. We produced a prediction for the binding sequences for each of these alleles using an available algorithm (Persikov et al. 2009; Persikov and Singh 2011). Figure 3 shows the predicted degenerate sequences for each variant of Prdm9. For each Prdm9 allele, we also obtained a PWM.

Figure 3 .

Predicted binding sequences for the five different protein alleles of the Prdm9 gene. Colored squares show sequence similarities between different alleles. Dom2 and Dom3 only differ in 3 bases in length and otherwise have the same sequence. Furthermore, Msc and Mls have a binding sequence of the same length, which only differs in a few bases. Across all alleles, the first 7 bases are common to all five groups.

To test whether recombination hotspots were associated with the predicted degenerate binding sequences of Prdm9, we compared the distributions of PWM scores in hotspots and coldspots. We found that all of the predicted sequences of Prdm9 were significantly enriched in hotspots (Dom2, 8.87 × 10⁻⁹; Dom3, 2.8×10⁻⁷; Mls, 8 × 10⁻⁸; Msc, 5.2×10⁻³; and Cst, 6.3 × 10⁻⁷). The PWM of Dom2 was the most significantly enriched matrix in hotspots, in line with the large number of inbred strains with a Dom2 allele. We also ran the same test on the background of individual repeats that were found to be enriched in hotspots. Significant enrichment was only found on the background of certain repeats: Dom2 was found enriched in L1_Mus2 (P = 0.02); Dom3 in L1Md_F2 (P = 0.02) and L1_Mus2 (P = 0.02); Mls in L1_Mus1 (P = 0.001) and L1_Mus3 (P = 0.00005); and Cst in L1_Mus1 (P = 0.002) and L1_Mus2 (P = 0.04). Finally, we performed an unbiased search for nondegenerate sequences enriched in hotspots with all possible motifs of 5–12 bases in size. This search for nondegenerate motifs was less successful. When the search was conducted on the background of repeat elements that were enriched in hotspots, no motif was significantly enriched. A similar search conducted on nonrepeat sequences revealed motifs that seemed to be unmasked simple repeats, including mainly combinations of C, CA, and CG repeats.

Discussion

We studied fine-scale recombination rates in the mouse genome on the basis of complete genome sequences available for 12 inbred mouse strains. We used a coalescent-based approach to infer the distribution of 47,068 putative ancestral recombination hotspots in the genome. We found that the historical hotspots significantly overlap with previously identified DSB hotspots and tend to avoid the promoters of genes. The historical hotspots were enriched with the predicted binding sequences of Prdm9 when studying nonrepeat sequences, but also on the background of specific repeat elements that were enriched in hotspots.

Our findings are subject to some qualifications. First, inbred strains are not a randomly mated wild population, such that some assumptions behind the method used to identify hotspots were violated. In addition, the small sample size of inbred strains used to identify hotspots reduces the power and the accuracy of this method. Our simulations show that estimates of recombination are robust, although we cannot rule out the possibility that estimates were influenced by selection, genetic drift, and mutations. Unlike other methods to study recombination, inferred recombination rates from population data represent events that occurred over many generations.

Second, we used genetic variations in classical mouse strains, which represent a complex genealogy. Consequently, recombination hotspots that have been inferred from the LD patterns are historical hotspots that may have been active in the past and are not necessarily active in the current population. Recombination rates estimated from this complex LD data are average rates across the sample’s genealogy, across males and females, and across different individuals with different recombination patterns (recombination position and intensity). Nevertheless, this computational approach has many advantages, including the high resolution and the ability to screen the entire genome.

Our results are similar to those obtained from human population genetic data. We found that recombination hotspots are ubiquitous, with an average hotspot every 42.7 kb. The detected hotspots cover ∼13% of the mouse genome. The relation between recombination rates and distance to TSS, and the tendency of lower rates near gene promoters, is strikingly similar in both species. However, we found no significant overlap (homologous synteny) in the precise locations of hotspots in mouse and human. This is not surprising since it has been established that hotspots are not conserved between chimps and humans (Winckler et al. 2005).

We compared the estimated historical recombination rates with current estimates, both at a fine scale, the level of the hotspots, and on a larger scale. At the level of the hotspot, we found an overlap between DSB hotspots (Smagulova et al. 2011) and historical hotspots. This noncomplete overlap between historical hotspots and the DSB hotspots is expected, since sex and PRDM9 alleles have been found to be associated with hotspot locations (Paigen et al. 2008; Parvanov et al. 2010). The historical hotspots are based on sex-averaged recombination rates and the DSB hotspots were found in male mice. In addition, the strains used for identifying the DSB hotspots (Hop2^−/− mice) is a hybrid between two strains (C57BL/10.S × C57BL/10.F), one with Dom2 allele and the other with a unique PRDM9 allele that was not found in any of the strains used in this study.

At a broad scale (at the resolution of megabases) we found a significant correlation between recombination rates estimated from mouse pedigrees and historical estimates of recombination. However, there are several regions that show large discrepancies. This is consistent with a recent study that reported considerable variation among closely related mouse subspecies in large-scale recombination rates (Dumont et al. 2011). Previous studies also showed that genetic background influences overall recombination rate as well as local rates (Paigen et al. 2008). Similar to the comparison between estimates of recombination from pedigrees and LD data, recombination rates estimated using different types of crosses are more correlated using larger interval size (Shifman et al. 2006; Paigen et al. 2008). This was suggested as evidence for stronger conservation at the large scale (Paigen et al. 2008). In addition to the expected differences between recombination rates estimated from mouse with different genetic background, recombination rates estimated on the basis of LD may also be influenced by gene conversion (noncrossover events), mutations, genetic drift, selection, and possible genome assembly errors.

In an attempt to find DNA motifs that underlie hotspot distributions, we studied sequences of hotspots and compared them to coldspots. Similar to findings in human hotspots, we identified an association between repeat elements and mouse recombination hotspots that may be mediated through PRDM9 binding. We identified highly significant enrichments of specific repeat elements within hotspots. Simple repeats are enriched in hotspots as a group, but this is mainly caused by enrichment of particular types of simple repeats, mainly composed of alternating G’s and A’s. GA and CT repeats were also previously found to be enriched in mouse high recombination regions and in human recombination hotspots (Myers et al. 2005; Shifman et al. 2006). The other types of repeat elements that are associated with hotspots do not belong to any particular family. Surprisingly, the most enriched repeat type is L1Md_F2, which belongs to the LINE-1 repeat family that was previously found to be underrepresented in high-recombination regions (Myers et al. 2005; Shifman et al. 2006).

Because hotspots evolve rapidly, and because this is attributed to the rapid evolution of Prdm9, we suspected that hotspots and the enriched repeat elements might contain binding motifs for the mouse PRDM9 protein. Our search included the predicted binding motif of five different Prdm9 alleles among different mouse strains. Comparing the alignment score of the predicted binding sequence of PRDM9 showed a significant enrichment of all five predicted matrices in hotspots, but especially for the most frequent Prdm9 allele—Dom2.

In conclusion, our study shows that genetic variations in mouse inbred strains can be used to study historical recombination events, albeit with some limitations. The results support the link between the rapid evolution of Prdm9 and hotspot distribution and the conservation of recombination rates at the broad range. It is still not clear what the factors are that control the rates of recombination at the broad and fine scale and what the nature of the association is between repeat elements and recombination hotspots.