Properties and Power of the Drosophila Synthetic Population Resource for the Routine Dissection of Complex Traits

Abstract

The Drosophila Synthetic Population Resource (DSPR) is a newly developed multifounder advanced intercross panel consisting of >1600 recombinant inbred lines (RILs) designed for the genetic dissection of complex traits. Here, we describe the inference of the underlying mosaic founder structure for the full set of RILs from a dense set of semicodominant restriction-site–associated DNA (RAD) markers and use simulations to explore how variation in marker density and sequencing coverage affects inference. For a given sequencing effort, marker density is more important than sequence coverage per marker in terms of the amount of genetic information we can infer. We also assessed the power of the DSPR by assigning genotypes at a hidden QTL to each RIL on the basis of the inferred founder state and simulating phenotypes for different experimental designs, different genetic architectures, different sample sizes, and QTL of varying effect sizes. We found the DSPR has both high power (e.g., 84% power to detect a 5% QTL) and high mapping resolution (e.g., ∼1.5 cM for a 5% QTL).

THE ultimate goal of modern genetics is to determine how molecular genetic variation is translated into organismal phenotypes. The vast majority of continuously varying phenotypes are influenced by many genetic variants that often interact with one another and with environmental factors (Falconer and Mackay 1996; Roff 1997; Lynch and Walsh 1998). This underlying complexity has made identifying causative genetic variants for most traits a steep challenge for which the scientific community has only had limited, albeit increasing, success (Mackay 2001; Chanock et al. 2007; Wellcome Trust Case Control Consortium 2007; Mccarthy et al. 2008; Stranger et al. 2011). As a result, there is a large discrepancy between the known heritability of most traits and the fraction of that heritability that can be explained by known causative genetic variants (Manolio et al. 2009; Stranger et al. 2011). This discrepancy has spurred the development of new mapping panels designed to address the shortcomings of existing genome-wide association studies and QTL mapping panels derived from only two parents.

The Drosophila Synthetic Population Resource (DSPR) is one such panel (King et al. 2012) similar in concept to other available linkage-based resources: the mouse Collaborative Cross (Churchill et al. 2004; Aylor et al. 2011; Philip et al. 2011), the Arabidopsis multiparent recombinant inbred line population (AMPRIL) (Huang et al. 2011), the Arabidopsis multiparent advanced generation intercross lines (MAGIC) (Kover et al. 2009), and the maize nested associated mapping population (NAM) (Yu et al. 2008; Buckler et al. 2009; Mcmullen et al. 2009; Li et al. 2011). The DSPR is a linkage-based panel that uses a synthetic population approach (Macdonald and Long 2007). To create the DSPR, two separate synthetic populations were created each from a 50-generation intercross of 8 inbred founder lines with one founder line shared between the two populations. From these two synthetic populations, >1600 recombinant inbred lines (RILs) were created via 25 generations of full-sib inbreeding. The large number of generations of recombination experienced by the DSPR produces a panel with genomic segments averaging 3 cM in size and, as a result, has the potential for much higher mapping resolution than previously available Drosophila mapping panels (King et al. 2012). In addition, a major strength of the synthetic population approach is the expectation of high power to detect genetic variants irrespective of their population frequency, provided such variants are sampled in the founder chromosomes (Macdonald and Long 2007).

Different types of mapping designs have different advantages depending on the nature of the genetic variation underlying a phenotype. Rare alleles are statistically very difficult to detect via genome-wide association in randomly ascertained panels that sample the natural genetic variation (Bansal et al. 2010). However, both empirical (Cohen et al. 2004; Ji et al. 2008; Stefansson et al. 2008; Helbig et al. 2009; Nejentsev et al. 2009; Pinto et al. 2010; reviewed in Bansal et al. 2010) and theoretical (Pritchard 2001) studies suggest rare alleles of large effect can be an important source of genetic variation underlying complex diseases. A major advantage of using a linkage-based approach founded from a small set of inbred lines is that all alleles in the panel are expected to be at a fairly high frequency. The DSPR RILs were founded by 15 founder lines and thus the lowest expected frequency of any allele in the panel is 1/15 (6.7%). For rare alleles of large effect to underlie a majority of the genetic variation in complex traits, there must be many different large-effect alleles, each individually rare. Obviously, the majority of such rare variants will not be present in linkage-based panels like the DSPR, but a subset of these rare variants will be present in a single founder contributing to the DSPR. The ability to study a random subset of the rare variants in a population is worthwhile, especially in the potential case of multiallelism where a single gene has many different individually rare alleles (reviewed in Bansal et al. 2010). The natural gene-based mapping approach of a linkage-based panel is expected to perform well in this case.

Successful mapping with any panel depends on the amount of genome information available. In the DSPR and other linkage-based panels, full genome information for all members of the panel can be inferred using hidden Markov model (HMM) techniques given the full genome sequences of all founders and dense genotyping of all RILs (Broman and Sen 2009). Given the size of the DSPR panel, >1600 RILs, the ability to genotype a dense set of SNPs and achieve the same level of information as fully resequencing all genomes of all RILs is a major advantage. Different genotyping technologies and the different types of genetic markers that result will present different challenges for inferring complete genome information. In the DSPR, genotyping was done using very cost-effective restriction-site–associated DNA (RAD) (Baird et al. 2008) markers. This method results in small clusters of tightly linked SNPs, each flanking a restriction cut site, distributed throughout the genome. The RAD method, along with other newly developed genotyping methods, such as whole-genome sequencing (WGS) (Huang et al. 2009) and multiplexed shotgun genotyping (MSG) (Andolfatto et al. 2011), combines SNP discovery and SNP genotyping into a single step and takes advantage of the high throughput of next-generation (next-gen) sequencing to genotype large numbers of SNPs in large numbers of samples. However, the resulting genotype data include the potential sequencing errors that accompany any next-gen application, and these sources of error must be considered in the model to infer full genotype data. In addition, the resulting markers although dense are “semicodominant”, meaning that the observation that a known SNP is fixed for one allele in a line in the pileup of short reads covering that SNP does not imply that that line is not a heterozygote. The line is instead a heterozygote with some probability that is a function of coverage at that SNP and the distribution of allele counts given the underlying genotypes.

Common to all such diversity reduction resequencing methods is a trade-off between the number of markers obtained and sequence coverage per marker. As sequence coverage per marker decreases, confidence that the observed allele counts accurately reflect the true genotype decreases as well. To what extent this uncertainty can be compensated for with increased marker density is not known. It is also of value to determine at what marker density and coverage we observe saturation of genetic information. This defines the optimal total sequencing effort per RIL and, in turn, defines the level of assay multiplexing that can be achieved. The multiplexing level greatly affects the total cost of the genotyping experiment, which can be nontrivial when the resource consists of thousands of RILs, which is the case for the DSPR.

In this article, we describe in detail the characteristics of the semicodominant genetic markers used in the DSPR and the development of the HMM that translates these markers into the mosaic founder structure of the RILs. In addition, we examine the factors limiting our inference of genome information and explore how varying coverage and marker density affects the inference, specifically exploring the trade-off between marker density and marker coverage when the underlying goal is to infer genotypes. Finally, we simulate phenotypes corresponding to different genetic architectures and different experimental designs to determine the mapping power and resolution of the DSPR panel.

Methods

The development of the DSPR, founder whole-genome resequencing, and RIL genotyping are all described in detail in King et al. (2012). We repeat only the most relevant points here.

Development of the DSPR

The DSPR RILs are derived from two synthetic populations, pA and pB, each created from eight founder strains, seven unique to a population (A1–A7 or B1–B7) and one common to both populations (AB8; see Figure 1 for a schematic of the experimental design). Initially, the eight founder lines were intercrossed using a round robin (e.g., A1 × A2, A2 × A3, . . . , AB8 × A1) to bring all founder genotypes together and 10 F₁ flies per genotype per sex were used to establish the next generation. Subsequently, two subpopulations for each of pA and pB were maintained in 1/2-gallon jars at a large population size and allowed to recombine freely for 50 generations. At generation 50, recombinant inbred lines were initiated using 576 pairs from each subpopulation, which underwent a minimum of 20 generations of full-sib mating. After completion of inbreeding, the RILs were maintained on a 14-day cycle (at ∼23°, 40–60% relative humidity, 24 hr light), with each RIL maintained as a pair of standard 1 × 3-in. fly vials, filled with standard cornmeal–yeast–molasses food.

Figure 1 .

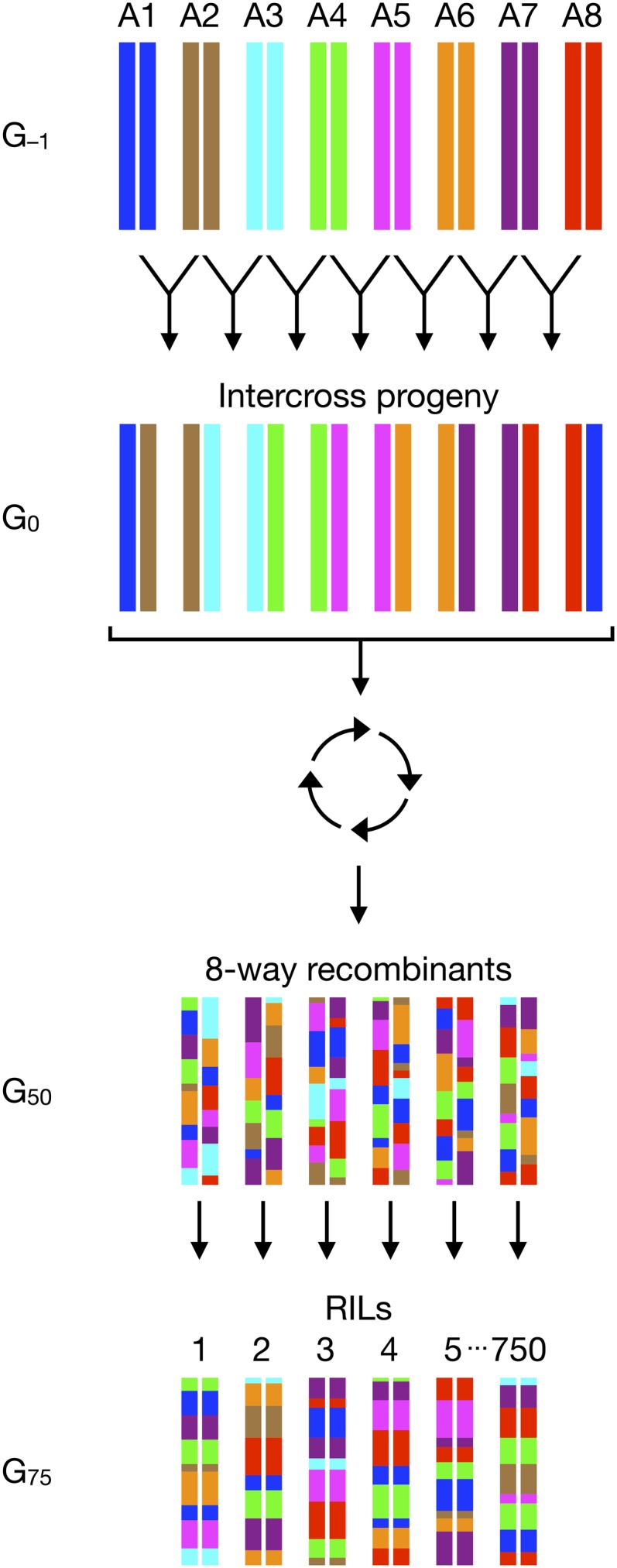
Experimental design for the creation of the DSPR panel.

Founder resequencing

We used 50 females from each founder to create DNA libraries for whole-genome resequencing. Two of our founders have a common inversion: founder A2 has In(3R)P and B5 has In(2L)t. For founder A2, we were able to identify a set of A2 individuals that are homozygous for the standard chromosome arrangement for genome sequencing. We were unable to identify a similar set of homozygous standard B5 individuals [the strain appears to have a balanced lethal on chromosome 2L, as all B5 individuals tested were heterozygous for In(2L)t]. Instead, we crossed founder B5 to AB8 and iso1 (y¹; cn¹ bw¹ sp¹) to create trans-heterozygotes for genome sequencing. The standard chromosome sequence for the B5 2L chromosome was inferred from the sequences of these two crosses. We resequenced the genomes of all 15 founders, the homozygous standard chromosome 3 arrangement of A2, and both trans-heterozygous B5 genotypes, using paired-end 54-bp Illumina to an average coverage of 50×.

We used MosaikAligner (version 1.0.1388, http://bioinformatics.bc.edu/marthlab/Mosaik, relevant switches = -hs 13 -mhp 100 -m all -a all -mm 5 -ac 40 -bw 17) to align the raw founder reads to the Drosophila melanogaster genome (release 5.1). A custom program was used to create “pileup” tables, requiring a minimum quality score of 25 for a base to contribute to the pileup and a minimum mapping quality of 30 for a read to contribute. We then used the cumulative pileup tables over all founders to identify SNPs when the following conditions were met: (1) the pileup at that site was >100, (2) the minimum count of the minor allele was ≥5, (3) a LOD test for the allele frequency being >2% at the second most common allele gave a score >3 (Bloom et al. 2009; Burke et al. 2010), and (4) a similar LOD test for an allele frequency >2% at the third most common allele gave a score <3. Conditions 3 and 4 effectively filter out errors and triallelic sites. The table of allele counts at this set of SNPs for all founders is available at http://flyrils.org/Data (Release 1).

Genotyping of the recombinant inbred lines

To genotype the set of recombinant inbred lines, we prepared 96plex RAD libraries with DNA from 12–15 females (isolated ∼9 months following completion of inbreeding) and SgrAI as the restriction enzyme. The general RAD method has been described in detail elsewhere (Baird et al. 2008). Briefly, DNA samples initially underwent a restriction enzyme digest. Our enzyme SgrAI cuts at the site CRCCGGYG. An adapter and a barcode uniquely identifying the sample were then ligated onto the sticky ends, and the sample was sheared, PCR amplified, and then sequenced using Illumina SE100 (all sequencing was done before the release of version 3 chemistry). Each plate of DNA also included one sample of iso1 DNA in a different well, which uniquely marks each plate and its orientation and effectively identifies possible sample mix-ups, cross-contamination events, and plate spins.

We processed the resulting FASTQ files (standard output files containing both the sequence data and the quality scores), using a custom Perl script that stripped the barcodes from any given lane of reads, and generated 96 new barcode-specific FASTQ files. These files were then processed using the same pipeline described above to generate pileup tables. These pileup tables were initially reduced to include only sites that scored as a SNP in the founders and had at least four reads covering the site in at least one-quarter of the RILs. We then applied several further quality-control filters to this initial set of SNPs: (1) at least 50% of RILs have nonzero coverage for the SNP; (2) the proportion of RILs that are heterozygous at that SNP is <20%; and (3) for SNPs with coverage >10 in the set of iso1 samples, heterozygosity at that SNP in the iso1 samples is <0.05. The table of allele counts for this set of SNPs is available at http://flyrils.org/Data (Release 1).

The result is a set of semicodominant markers. Across the genome, we have 100-bp reads on either side of each SgrAI cut site. Thus, at each cut site there is the potential for several closely linked SNPs. These SNPs essentially form a single, potentially highly informative marker as recombination between these SNPs is highly unlikely. Our final cleaned data set consists of 10,275 SNPs, representing 4026 SgrAI restriction cut sites.

Hidden Markov model

We implemented a HMM to infer the underlying founder ancestry at each genomic segment in each RIL (see Rabiner 1989 and Broman and Sen 2009 for tutorials on implementing HMMs), using perl. The complete code is available in Supporting Information, File S1. A HMM consists of a Markov chain of hidden (unobservable) states and a set of observed variables where each observation depends only on the underlying hidden state. In our HMM, the hidden states are the 8 homozygous founder genotypes and the 28 possible heterozygous founder genotypes and the observations are the observed allele counts at each position in each RIL. The distribution of the observed states and hidden states is parameterized by three sets of probabilities: initiation, transition, and emission probabilities. We used these three sets of probabilities in the standard forward and backward equations (Rabiner 1989; Mann 2006; Broman and Sen 2009) in our hidden Markov model to get the probabilities each marker is derived from each of the possible founder states across the genome of each RIL. These three sets of probabilities in our HMM are described in detail below.

Initiation probabilities:

The initiation probabilities give the naive probability of each possible founder state. Here we consider the 8 homozygous founder states and the 28 heterozygous founder states. Despite the theoretical expectation that following 25 generations of full-sib inbreeding virtually the entire genome should be homozygous, in reality inbreeding is much less effective at homozygosing a genome in outbred species. We speculate this is due to closely linked strongly deleterious recessive alleles in repulsion. As a result we assume that only 95% of the genome will be in a homozygous state, an assumption that seems justified on the basis of visual inspections of the data. Thus, initiation probabilities are

$$\text{Homozygous states: 0}\mathrm{.95\cdot }\left(\text{1}/8\right)$$

$$\text{Heterozygous states: 0}\mathrm{.05\cdot }\left(\text{1}/28\right).$$

Transition probabilities:

Between every set of markers, the underlying founder state transitions either to the same founder state or to a different founder ancestry state with a given probability. These are the transition probabilities. These probabilities are dependent on the probability of a recombination event occurring between two markers during the creation of the DSPR. Given the density of markers in our panel (i.e., mean distance between cut sites is physical = 29 kb, genetic = 0.069 cM and the largest distance between markers is physical = 482 kb, genetic = 1.14 cM), the recombination fraction between any pair of markers is small enough that we assume only a single recombination event took place in a given interval during the free recombinant phase of the synthetic population (i.e., any transition event that would require two recombination events to occur is given a probability of zero). For intervals approaching 1 cM in size there is a reasonably large probability that two events have occurred in that interval in the history of the population (although it is unclear how many such events can actually be sampled in the final set of RILs). Thus this assumption is clearly biologically false, and it is made to greatly simplify the representation of the transition matrices. The above being said, this assumption is unlikely to be restrictive; the HMM can easily resolve such double-recombination events via transitions in sequential intervals (since two transitions in adjacent intervals allow the HMM to move between any two states). Given our expectation of 95% homozygosity, transitions to homozygous states are given a higher probability than transitions to heterozygous states. All transition probabilities are given in Table 1, where r is the probability of a recombination event occurring in the interval.

Table 1 . Transition probabilities between any given set of markers.

Founder state at position 1	Founder state at position 2	Transition probability
ii	ii	e−r + 0.95 ⋅ (1 − e−r) ⋅ 1/8
	jj	1/8 ⋅ 0.95 ⋅ (1 − e−r)
	ij	1/7 ⋅ 0.05 ⋅ (1 − e−r)
	jk	0
ij	ij	e−r + 2 ⋅ 0.05 ⋅ (1 − e−r) ⋅ 1/14
	ii or jj	(1 − e−r) ⋅ 1/2 ⋅ 0.85
	ik or jk	(1 − e−r) ⋅ 1/14 ⋅ 0.15
	kl	0

General founder genotypes are represented by i, j, k, and l with different letters denoting different founders: e.g., ii represents a homozygous founder genotype while ij denotes a heterozygous founder genotype, with i and j representing different founders. r is the probability of a recombination event occurring in the interval and is equal to X chromosome: 33*d*(1/10) Autosomes: 25*d*(1/10), where d is the genetic distance between any pair of markers (interpolated from FlyBase).

Initially r is estimated from the map conversion available in FlyBase and scaled up to the 50 generations of recombination experienced by the DSPR. In D. melanogaster crossing over occurs only in females and the FlyBase map is in female units. Therefore the autosomes effectively experience 25 generations of recombination, and the X chromosome (which spends two-thirds of the time in females) experiences 33 generations of recombination. In a visual inspection of initial results, transitions appeared to occur too readily. For example, in a few instances either the founder state would transition to a different founder state for very short distances or the probability would dip fairly low without actually transitioning to another state on the basis of minor inconsistencies between the founder genotype and the RIL genotype (e.g., a heterozygous state in the RIL, a low-coverage “incorrect” flavor SNP). To help correct for this, we scaled r by 1/10. Thus, our value for r was

$$\text{X chromosome}:r\hspace{0.17em}=33\hspace{0.17em}\cdot \hspace{0.17em}d\hspace{0.17em}\cdot \hspace{0.17em}\left(\text{1}/10\right)$$

$$\text{Autosomes}:r=25\hspace{0.17em}\cdot \hspace{0.17em}d\hspace{0.17em}\cdot \hspace{0.17em}\left(\text{1}/10\right),$$

where d is the genetic distance between any pair of markers.

Comparing the HMM results with the scaled transition probabilities to the results using unscaled probabilities corrected this problem while maintaining similarity overall. The founder state assigned the maximal probability changed in very few cases and these were limited to fairly uncertain inferences (probabilities <0.8).

Emission probabilities:

Emission probabilities define the probability of the observed RAD pileup at a SNP given each underlying hidden state. For our data set, this observation is a paired set of minor allele and total allele counts (k, N) from our RAD sequencing at each position. Thus, the emission probability is the probability of observing (k, N) at a SNP given the underlying founder sequences. All founders are sequenced to 50× coverage and thus the probability each founder harbors the minor allele at each SNP location can be calculated accurately from the allele counts. We incorporated uncertainty into these estimates by bounding the probabilities at 0.995 and 0.005 such that the probability each founder harbors the minor allele was never exactly 1 or exactly 0 (to avoid assigning perfect certainty to our inference). Given this parameterization, we can calculate the probabilities any given SNP in any given RIL is AA, Aa, or aa conditional on the genotype of the RIL with respect to the eight founders (i.e., AA, BB, … , HH, AB, AC, … , GH). If both homozygous and heterozygous states followed a binomial distribution (as one would naively expect), we could then use the binomial distribution to calculate emission probabilities conditional on founder genotype. We observed the allele frequencies of all SNPs where coverage was >4× and the minor allele frequency was between 0.1 and 0.9. Given these SNPs had already passed through our quality filters (see above), these sites represented sites with residual heterozygosity (i.e., segregating variation). These positions did not follow a single binomial distribution with a mean of 0.5 (in contrast to the expectation for a single heterozygous individual). Therefore, to better estimate emission probabilities for regions with segregating variation we used a β-binomial distribution wherein the probability parameter from the binomial distribution is itself a β-variate (Evans et al. 2000). This distribution more accurately reflects our observed distribution for regions with segregating variation. Emission probabilities were therefore calculated as

$$p_i\cdot p_j\cdot B\left(k,n,1-\epsilon \right)\hspace{0.17em}+$$

$$p_i\cdot \left(1-p_j\right)\cdot \beta B\left(k,n,v,\omega \right)\hspace{0.17em}+$$

$$p_j\cdot \left(1-p_i\right)\cdot \beta B\left(k,n,v,\omega \right)\hspace{0.17em}+$$

$$\left(1-p_i\right)\cdot \left(1-p_j\right)\cdot B\left(k,n,0+\epsilon \right),$$

where p_i is the probability of the major allele for founder i, p_j is probability of the major allele for founder j, ε = 0.005 (sequencing error rate), B is the binomial probability density function parameterized by (k, number of minor alleles; N, total number), and βB is the β-binomial density function parameterized by (k, number of minor alleles; N, total number; ν = ω = 0.5) (Evans et al. 2000). Missing data are easily incorporated into the HMM. For any position where we have no coverage in the RIL, all emission probabilities are 1, meaning that observation is consistent with any underlying founder state. The results of this HMM are available at http://flyrils.org/Data (Release 1).

Varying marker density and coverage

For a given amount of sequencing effort (e.g., one lane on the HiSEQ2000), employing more barcodes or choosing a more frequent cutting restriction enzyme results in lower coverage per marker. So there are clear experimental trade-offs in terms of maximizing the marker density, number of RILs genotyped, and coverage per marker. To explore the effect of coverage and marker density on the performance of the HMM, we down-sampled the actual coverage or marker density in our data set. To simplify the analysis, we focused on pA and a single chromosome arm (2R) for these simulations as results are expected to generalize to the other chromosome arms and pB. To simulate lower coverage, we began with 100 randomly selected RILs with average coverage over SNPs >20× (because under the RAD approach coverage varies over DNA samples). We randomly discarded alleles at each SNP in each RIL to reach average coverage levels of 1, 2, 4, 6, 8, 10, 12, 14, 16, 18, and 20×. To do this, at each ith SNP, we obtained a new SNP coverage $\left({C^{\prime }}_i\right)$ by calculating a Poisson deviate $\left(\lambda =\left(C^{\prime }/\stackrel{-}{C}\right)\cdot C_i\right)$, where $\stackrel{-}{C}$ is the original average coverage, C′ is the new average coverage, and C_i is the original coverage at SNP i. We then randomly sampled the original set of major and minor allele counts at SNP i to obtain the new minor allele and total allele counts (k, N) at each SNP. We note that this approach does not precisely simulate randomly discarding sequencing reads to lower average coverage (because it does not model the sampling properties of pairs of SNPs located in the same 100-bp read) but is computationally less demanding because alignments are time consuming. To test the effect of marker density, we selected the 100 RILs with the largest number of markers on 2R. For each RIL we randomly selected a subset of our actual cut sites to reduce marker density to values of 1, 3, 5, 7, 9, 11, 13, and 15 cut sites per centimorgan. Reducing the number of cut sites per centimorgan mimics the effect of choosing different restriction enzymes. We then ran our HMM on these data sets.

We also compared the performance of our RAD markers to an equal number of single SNPs. At each cut site, we randomly sampled a single SNP for each cut site and then ran the HMM on this reduced data set. We randomly selected 100 RILs from pA and again focused on only 2R for this comparison.

QTL mapping of simulated phenotypes

We explored the power of the DSPR panel by performing QTL mapping on simulated phenotypes corresponding to several different possible scenarios. Briefly, we used the founder sequences and HMM probabilities to infer the genotype of each RIL and then added environmental variance to assign a phenotype. The simulations for the different scenarios are described in detail below. All simulations and necessary statistical analyses were done with R (R Development Core Team 2011). The complete code to produce the phenotypes used for mapping is available in File S1.

Direct phenotyping of the inbred RILs:

To examine the case of direct phenotyping on the inbred RILs, we considered only the population A RILs. We selected 200 randomly chosen SNPs polymorphic among the pA founders (but homozygous, having a coverage >4× within founders, and at least 1 Mb from the telomeres and centromeres) per chromosome arm for 1000 total SNPs (see methods above). Then, for each position, we used our HMM probabilities to calculate the probability each RIL harbors the major allele at that position. We then used the binomial distribution to assign either the major or the minor allele to each RIL at that position. We considered four different possible effect sizes, 1%, 2.5%, 5%, and 10% of the phenotypic variance, and randomly assigned each to 250 of our positions. We generated a set of random normal deviates $N\left(\mathrm{\mu }=0,\hspace{0.5em}\mathrm{\sigma }=\sqrt{(1-z)/z\mathrm{\cdot }{\sigma }_{\text{G}}^2}\right)$ to correspond to environmental variance for each effect size, where z is the percentage of the phenotypic variance explained by the QTL and ${\sigma }_{\text{G}}^2$ is the genetic variance at the QTL.

pA–pB cross:

Mapping in fully inbred panels of RILs carries the risk that mapped QTL may represent regions contributing to inbreeding depression. An alternative design that avoids this problem is to phenotype the F₁ individuals from matched crosses between pA and pB RILs (e.g., RA1 × RB1, RA2 × RB2, …). To simulate phenotypes for a cross between pA and pB RILs, we once again identified 1000 random positions (200 per chromosome arm) in the genome found to be a SNP in the pA and pB founders, using the same restrictions described for the inbred design. We assigned either the major or the minor allele to each RIL at that position, using the binomial distribution and our HMM probabilities. We then assigned each cross a genetic value corresponding to its genotype (0, homozygous for the minor allele; 0.5, heterozygous; 1, homozygous for the major allele) and generated environmental variance as above to correspond to effect sizes of 1%, 2.5%, 5%, and 10%. For both designs, to examine the power of a reduced panel size, we randomly sampled the phenotypes generated above to achieve sample sizes of 100, 200, 400, and 600 and the full pA panel size of 828.

Multiallelism:

Both designs described above assume genetic variation from the QTL is due to a single biallelic SNP. We also simulated two specific multiallelic genetic models. The first scenario corresponds to a multiallelic common disease, common variant model. There are four alleles, equally common (all at frequency 2/8 in the founders), having additive genotypic effects (i.e., genetic values = 1, 2, 3, 4). The second scenario corresponds to a rare multiallelic model. Once again there are four alleles; however, in this case there is one common “wild-type” allele (frequency 5/8) and there are three additional rare alleles each at a frequency of 1/8. The wild-type allele was assigned a genetic value of 1 and the genetic values for the three other alleles were pulled from normal distribution N(μ = −1, σ = 1). For these simulations, we considered only the full pA inbred RILs design (828 RILs) and scaled the environmental variance so that the QTL explained 5% of the phenotypic variance.

QTL mapping:

To perform QTL mapping on our simulated phenotypes, we converted the 36 state probabilities described above to 8 additive probabilities by assuming heterozygous states are intermediate to the two homozygous states. For the inbred RIL design, we regressed each phenotype on the 8 additive pA probabilities. For the pA–pB cross design, we regressed each phenotype on the 16 additive probabilities corresponding to the probabilities parent one was derived from each of the pA founders and the probabilities parent two was derived from each of the pB founders. We simulated all phenotypes as being measured only on females such that the genetic model for the X chromosome was the same as for the autosomes. For both designs, mapping was done only for a 10-Mb region surrounding the true location of the QTL. At each position in this region, we converted the resulting F-statistic to a LOD score (Broman and Sen 2009). It was not computationally feasible to determine the genome-wide significance threshold for each simulated phenotype separately. Instead, we determined the significance threshold for a randomly chosen phenotype for each effect size and each sample size. To do this, for each chosen phenotype, we performed a genome-wide scan on 1000 permutations of the data, determined the maximum LOD score for each scan, and calculated the quantile corresponding to a 5% genome-wide false positive rate (Churchill and Doerge 1994). Effect size and sample size did not appear to influence the significance threshold and we thus used the average significance threshold for the 20 permuted phenotypes (inbred RILs, average threshold = 6.9, min = 6.5, max = 7.3; pA–pB cross, average threshold = 10.1, min = 9.6, max = 10.9). If a LOD score in the mapped 10-Mb region exceeded the significance threshold, the QTL was deemed successfully mapped.

Location error and mapping resolution:

To calculate location error and mapping resolution, a QTL must be successfully mapped. We therefore focused only on sample sizes of ≥400 and effect sizes of ≥5%. These effect size/sample size combinations all have a power >15%, allowing a sufficient number of phenotypes to be successfully mapped to estimate location error and mapping resolution. For each combination, we generated phenotypes (separately from those described above for the power analysis) at random SNP locations in the genome until we obtained a set of at least 500 successfully mapped QTL. For each of these QTL, we calculated the location error as the distance from the peak LOD score to the true location of the QTL. We used a standard 2-LOD support interval to estimate confidence intervals (i.e., mapping resolution) on the locations of all successfully identified QTL.

Results

Marker architecture

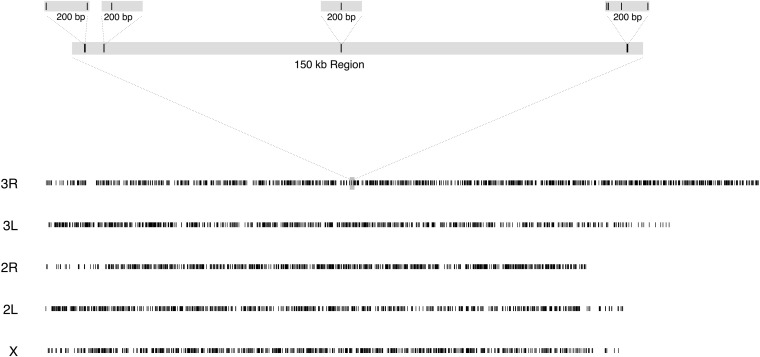
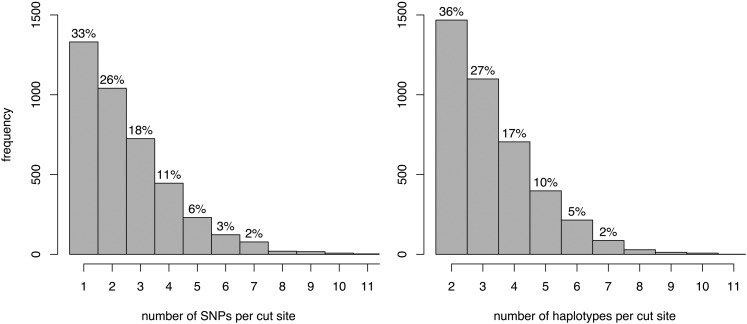
The RAD genotyping approach produced ∼100-bp reads flanking SgrAI cut sites throughout the genome for each RIL. SgrAI sites with at least one SNP had an average density of 14 cut sites per centimorgan (SD = 0.4) while the average density of SNPs per RIL was 26 SNPs per centimorgan (SD = 1.1; Figure 2). The reads were aligned to the reference genome, and pileup tables were created for each site known to be segregating in the founders. The average coverage per SNP per RIL is 63 (SD = 28). Figure S1 shows the distribution of coverage both across sites and across RILs as well as the distribution of RILs missing data at each marker. The resulting marker data for any given site in any given line consist of a minor and major allele count. We consider these markers to be semicodominant, because at modest coverage levels the observation of monoallelism does not imply an underlying homozygous genotype. The RAD method provides us with the same global set of markers in each RIL distributed fairly evenly throughout the genome. These RAD markers can contain multiple tightly linked SNPs in each 200-bp region associated with an SgrAI cut site, creating a marker that is potentially much more informative than a single SNP. Two-thirds of cut site locations are associated with multiple SNPs (range = 1–13 SNPs per cut site; Figure 3A). A slightly smaller percentage of these sites define more than two haplotypes because an additional SNP does not always translate to additional haplotypes (range = 2–11 haplotypes per cut site; Figure 3B).

Figure 2 .

Semicodominant marker architecture across the genome in the DSPR. Each solid line represents a single SNP. The shaded box on 3R represents a 150-kb region and is magnified above. Each 200-bp region is also magnified to show the individual SNPs associated with each cut site.

Figure 3 .

Histogram of the number of SNPs per each cut site (left) and the number of haplotypes defined by each cut site (right). The percentage of each number is above each bar. Percentages <1% are not displayed.

HMM performance

The hidden Markov model gives the probability of each possible founder ancestry state at each marker for each RIL. Overall, the HMM performed very well. A useful metric of performance is the proportion of uncertain positions (positions where the maximum founder genotype probability is <95%). The information theory concept of entropy (Shannon 1948) can also be used to assess the amount of missing genome information. For our data, entropy was well correlated (r = 0.95) with the proportion of uncertain sites and we report the latter here for ease of understanding. Across all positions and all RILs, only 5% of positions have an uncertain assignment.

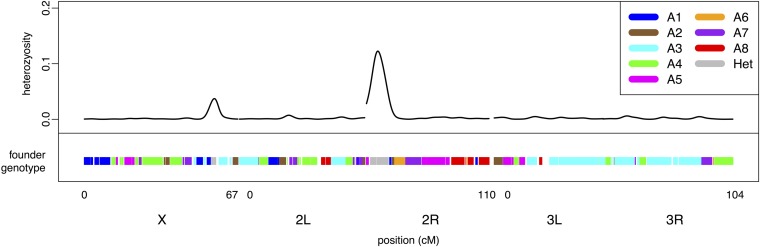
As expected for inbred lines, the vast majority of inferred states are homozygous founder genotypes; however, the HMM was able to successfully identify heterozygous states where they exist. We compared average heterozygosity at SNPs in regions where the HMM assigned a heterozygous founder state (with >95% certainty) to heterozygosity over the rest of the genome for each RIL, using a t-test. Heterozygosity is significantly higher in regions identified as a heterozygous founder state (heterozygous state mean heterozygosity = 0.09; nonheterozygous state mean heterozygosity = 0.002; t_68,900 = 141, P < 0.001). A visual comparison of heterozygosity across the genome and HMM assignment of heterozygous founder states also makes this ability apparent (Figure 4). Interestingly, we observed that the HMM assigned centromeric regions a heterozygous state more often than the rest of the genome (King et al. 2012), as was also found in the NAM mapping panel (Mcmullen et al. 2009). The SNP data used by the HMM are all derived from reads mapping uniquely to the five major euchromatic arms (with the unassembled arms included as part of the reference genome to help mask repetitive DNA); thus there is little reason to suspect the quality of SNP data on which the inference is based. Because the HMM considers the haplotypes flanking a centromere, and recombination is so suppressed across the centromere, the DSPR experimental design is capable of detecting centromeric regions that cannot be easily homozygosed. We speculate that physically large centromeric regions with residual heterozygosity could easily go undetected on the basis of resequencing of a random collection of inbred strains.

Figure 4 .

Heterozygosity at SNPs across the genome of a single RIL (top) and the inferred founder genotype state (bottom). Different colors represent the different homozygous states while gray represents any heterozygous state. White regions indicate an uncertain (probability <0.95) assignment.

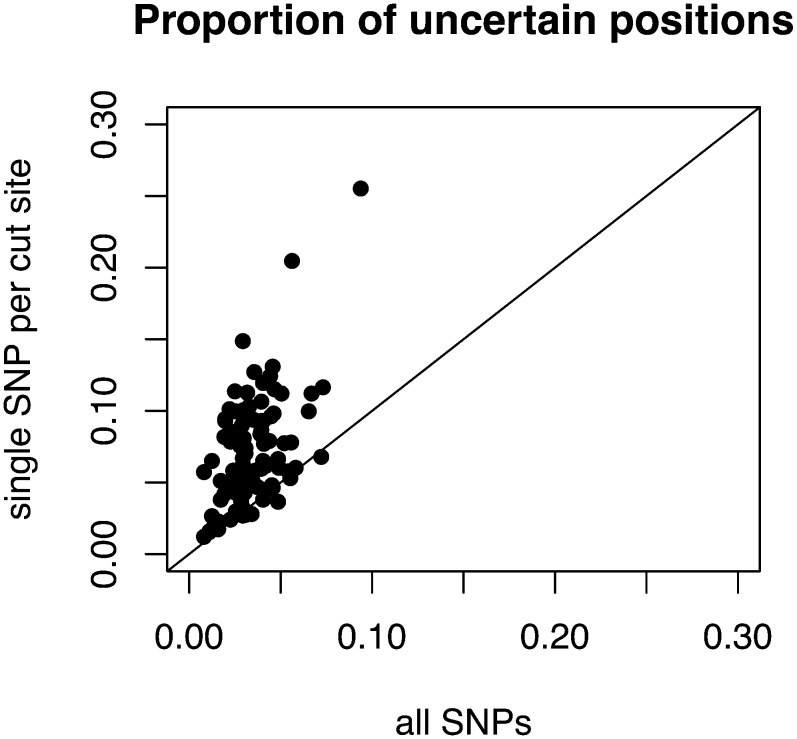
A paired t-test revealed our semicodominant markers were significantly more informative than an equivalent number of single SNP markers, resulting in an average increase in certain assignments of 3% (t₉₉ = 10.7, P < 0.001; Figure 5). This fact is not surprising given the increased number of haplotypes defined by ∼64% of semicodominant markers.

Figure 5 .

Comparison between the proportion of uncertain positions from the HMM with all SNPs (x-axis) and the HMM with a single SNP per each cut site (y-axis). Each point is an individual RIL. The line is the 1:1 line—points along the line indicate an equal amount of uncertain positions while points above the line indicate a greater proportion of uncertain positions for the set with a single SNP per cut site.

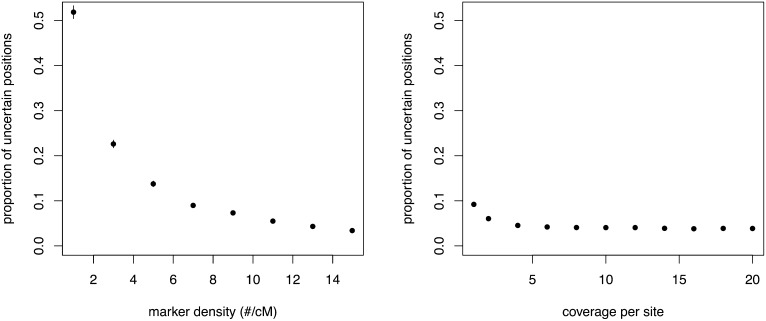
By altering marker density and coverage we were able to assess the effect of these parameters on the performance of the HMM in inferring founder ancestry. Obviously both reducing marker density and reducing coverage result in an increase in missing information; however, reducing marker density has a much larger effect than reducing coverage (Figure 6). The proportion of uncertain positions increases sharply when marker density drops below approximately five cut sites per centimorgan. Decreasing coverage has a minimal effect in comparison. In general, experimental designs using diversity reduction methods such as RAD for genotype inference should utilize enzymes that provide at least six cut sites per centimorgan. The level of plexing should keep average coverage above 4×. Generally, an increase in the number of markers will provide a greater benefit than an increase in average coverage. However, these two parameters are not independent and as coverage decreases, an increasing number of sites will have 0× coverage, effectively decreasing marker density as well.

Figure 6 .

The effect of reducing marker density (number of cut sites per centimorgan; left) and coverage per site on the proportion of uncertain positions (right). Each point is the average for 100 RILs. Error bars are ±1 standard error; when they are not visible they are smaller than the size of the point.

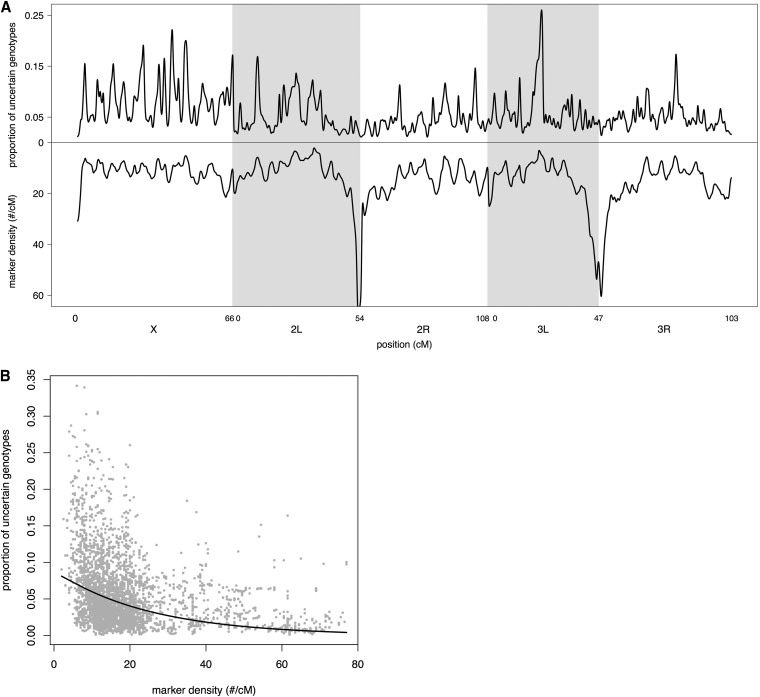
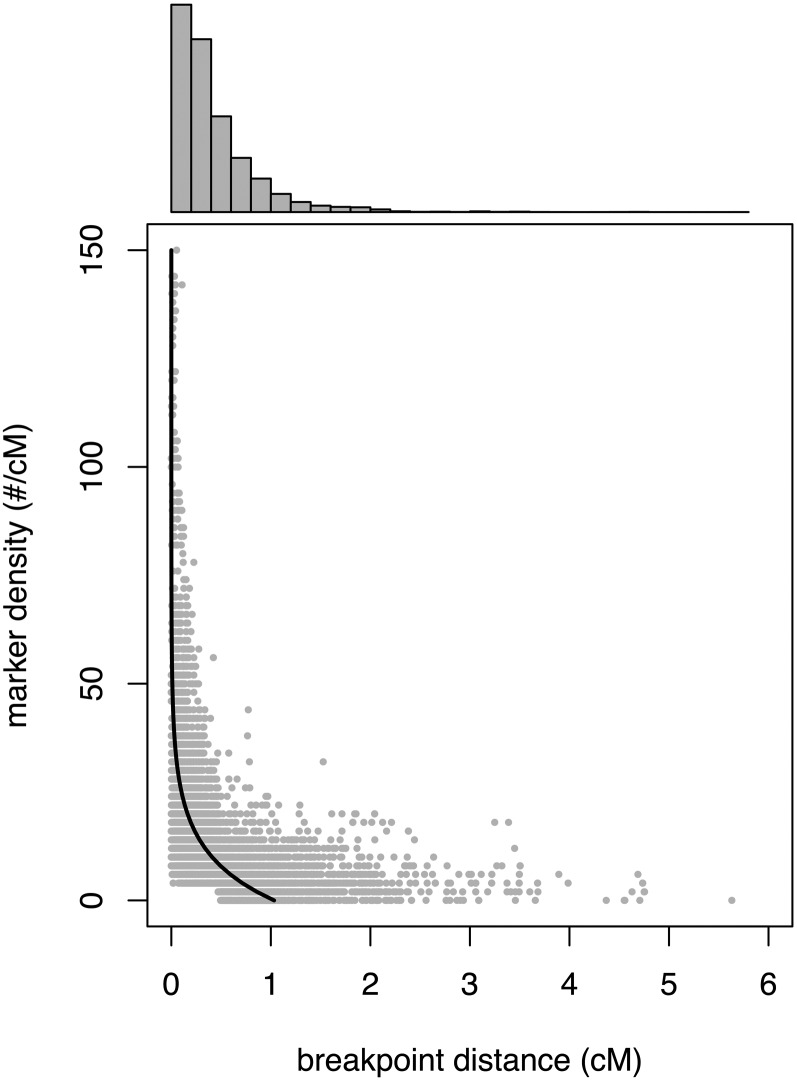
The critical importance of marker density is also apparent when we consider the effect of local marker density across the genome. There is a close, exponential relationship between the local marker density (number of cut sites in a 1-cM interval surrounding each position) and the proportion of uncertain genotypes at each position (Figure 7) with the highest proportions occurring at the lowest marker densities. A linear regression on log-transformed data revealed that local marker density explains 17% of the variation in the proportion of uncertain genotypes (t_10,111 = −46.1, R² = 0.17, P < 0.001). Another assessment of our HMM is how well we are able to resolve recombination breakpoints and this is also influenced strongly by local marker density. We inferred a breakpoint wherever the founder genotype inferred with probability >0.95 switched to a different founder genotype inferred with probability >0.95. The distance over which this switch occurred was defined as a breakpoint distance. Here, we calculated local marker density as the number cut sites per centimorgan over 5-cM intervals because recombination breakpoints can span fairly large regions. Once again, the relationship is exponential; in areas where marker density is high, breakpoint distances were always quite small while all of the largest distances occur in areas where marker density is low (Figure 8). Here, the linear regression on log-transformed data revealed that local marker density explains 44% of the variation in breakpoint distance (t_45,019 = −186.4, R² = 0.44, P < 0.001).

Figure 7 .

(A) The proportion of uncertain genotypes at each position across the genome for all RILs in the DSPR (top) and local marker density (number of cut sites per centimorgan, bottom). (B) Scatterplot of the proportion of uncertain genotypes at each position vs. local marker density (number of cut sites per centimorgan). The line is the best-fitting exponential curve.

Figure 8 .

The relationship between marker density (number of semicodominant markers per centimorgan) and breakpoint distance. The breakpoint distance is the distance over which the inferred founder genotype (with 95% certainty) switches between two different founder genotypes. The line is the best-fitting exponential curve. Above is the histogram of breakpoint distances.

QTL mapping power

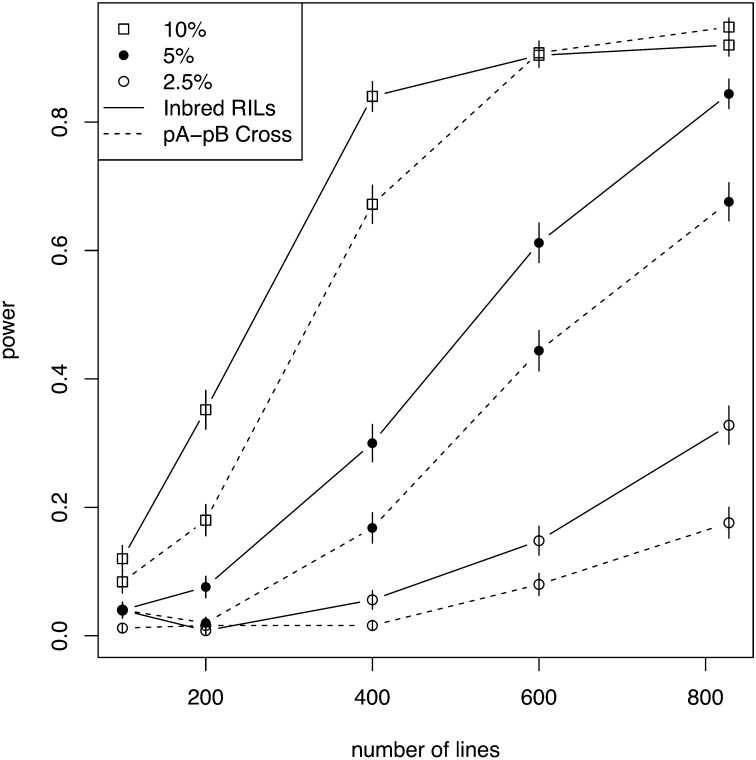
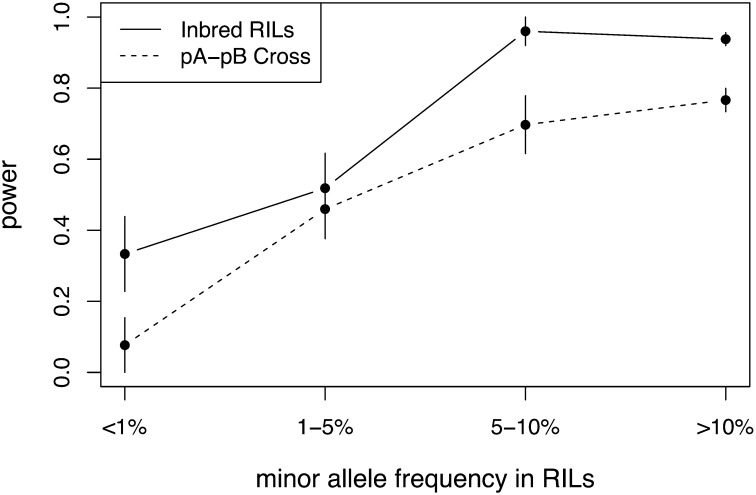
The power of the DSPR panel is high, and, as expected, the number of phenotyped RILs and the effect size of the QTL strongly influenced power in both designs (Figure 9). The full pA panel of inbred RILs has 92% power to detect a 10% QTL and 84% power to detect a 5% QTL. Power is modest to detect smaller-effect QTL with 33% power to detect a 2.5% QTL and only 5% power to detect a 1% QTL. These QTL will generally be difficult to detect for any mapping panel. In the pA–pB cross design, power is lower for the smaller-effect sizes. The panel has 95% power to detect a 10% QTL, 68% power to detect a 5% QTL, 18% power to detect a 2.5% QTL, and 2% power to detect a 1% QTL. The lower power for a given effect size in the pA–pB cross design is likely due to the increased degrees of freedom in the statistical model (i.e., 16 possible founder genotypes instead of 8 for the inbred pA RILs).

Figure 9 .

Power in the DSPR panel for a design in which inbred RILs are phenotyped directly (solid line) and matched crosses between the pA and pB RILs are phenotyped (dashed line) for different sample sizes (x-axis) and different effect sizes. Different symbols represent different effect sizes: ◻ = 10%, • = 5%, ○ = 2.5%. Power for a 1% QTL was <0.05 for all sample sizes and is not shown.

In both designs, frequency of the allele in the RIL panel affects power when the total variation associated with the QTL is held constant (at 5%). Quantitative trait loci with minor allele frequencies of <5% in the panel are much more poorly detected than QTL with minor allele frequencies of >5%. Power is largely independent of allele frequency once allele frequencies are >5% (Figure 10). Excluding low-frequency alleles (<5%), the power to detect a QTL that explains 5% of the phenotypic variance is higher in both designs, 94% in the inbred RILs and 75% in the pA–pB cross.

Figure 10 .

Power in the DSPR panel for alleles with different frequencies in the RILs. Different points correspond to different experimental designs: solid line, inbred RILs; dashed line, pA–pB cross. In both designs, the QTL explains 5% of the variation.

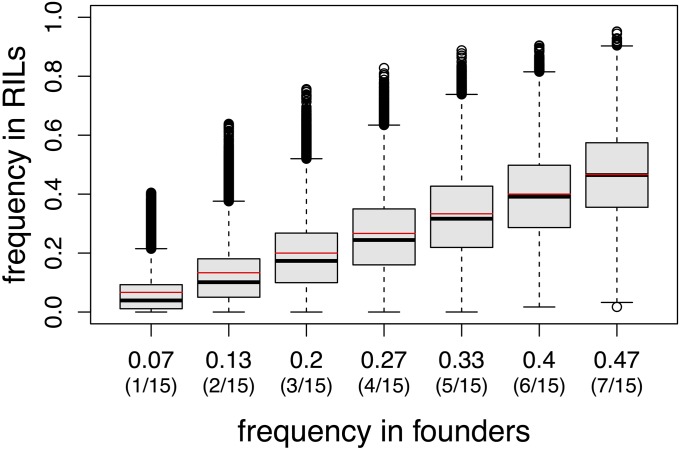
The null expectation for allele frequencies in the RIL panel is that it should equal the frequency in the founders. Figure 11 shows the frequency of the minor allele in the founders and frequency of the same allele in the full RIL panel (calculated from the inferred genotypes of the pA and pB RILs using the pA and pB HMM probabilities) for our full set of SNPs. Of these, 8.5% are at a frequency of <1% and 25% are at a frequency of <5%.

Figure 11 .

Boxplots of the minor allele frequency of 1000 randomly selected SNPs in the DSPR RILs for each of the possible starting frequencies in the 15 founders. The black center line of the box is the median frequency in the RILs derived from a given founder (bottom edge of the box is the first quartile, top edge is the third quartile, and whiskers extend to 1.5 times the interquartile range). The red line indicates the expected frequency (i.e., the frequency in the founders).

Having established the effect of sample size and effect size on power, we simulated both multiallelic scenarios for the full-panel inbred RILs design for a QTL explaining 5% of the phenotypic variance. The DSPR is equally likely to detect a QTL in the common variant scenario vs. the rare variant scenario (common design, power = 93.9%, SE = 0.75%; rare design, power = 93.5%, SE = 0.77%). Here, power is fairly equivalent to the power for the biallelic case (above) excluding low-frequency variants.

Mapping resolution and location error

Average location error was low (ranging from 0.22 to 0.84 cM) with larger sample sizes and larger effect sizes resulting in the lowest average location error (Table 2). Figure 12 shows an example of a successfully mapped 5% QTL in the full panel of pA inbred RILs with the true location marked. Using a standard 2-LOD support interval, resolution was high, ranging from 0.81 to 1.5 cM. However, the coverage of the 2-LOD support interval achieved the proper 95% confidence interval only for the highest-powered designs and declined with lower power, giving overly narrow estimates (corresponding to only a 61% confidence interval for an effect size of 5% and a sample size of 400 in the pA–pB cross). Location errors for the multiallelic scenarios were smaller than for both biallelic scenarios (inbred RILs and pA–pB cross) for an effect of the same size (5%) in the largest sample size. In addition, the confidence interval provided appropriate 95% coverage while in the inbred RIL panel coverage was 93% and in the pA–pB cross coverage was only 86% for the same effect size and sample size.

Table 2 . Location error and confidence interval distance means and standard errors (in both genetic and physical distance) for different effect sizes and sample sizes in the different designs.

			Location error		Confidence interval
Design	Effect size (%)	Sample size	Physical (kb)	Genetic (cM)	Physical (kb)	Genetic (cM)	% within C.I.
Inbred RILs
	5	400	304 (25)	0.67 (0.06)	712 (36)	1.5 (0.05)	79
	5	600	177 (14)	0.37 (0.03)	648 (31)	1.4 (0.04)	89
	5	828	164 (16)	0.34 (0.03)	590 (22)	1.3 (0.04)	93
	10	400	179 (15)	0.34 (0.02)	632 (31)	1.3 (0.04)	89
	10	600	112 (9)	0.22 (0.01)	530 (26)	1.1 (0.03)	96
	10	828	116 (13)	0.26 (0.04)	411 (20)	0.86 (0.03)	94
pA–pB cross
	5	400	389 (31)	0.84 (0.09)	480 (25)	0.93 (0.03)	61
	5	600	235 (18)	0.51 (0.04)	491 (23)	1.1 (0.03)	75
	5	828	157 (11)	0.33 (0.02)	489 (22)	1.1 (0.03)	86
	10	400	178 (14)	0.36 (0.03)	450 (19)	0.99 (0.03)	83
	10	600	139 (14)	0.29 (0.03)	430 (21)	0.89 (0.03)	88
	10	828	118 (11)	0.23 (0.02)	388 (23)	0.81 (0.02)	92
MC	5	828	130 (9)	0.27 (0.02)	596 (28)	1.2 (0.03)	95
MR	5	828	136 (10)	0.27 (0.02)	598 (26)	1.2 (0.03)	95

MC, multiallelic common design; MR, multiallelic rare design. A standard 2-LOD support interval was used for all confidence intervals.

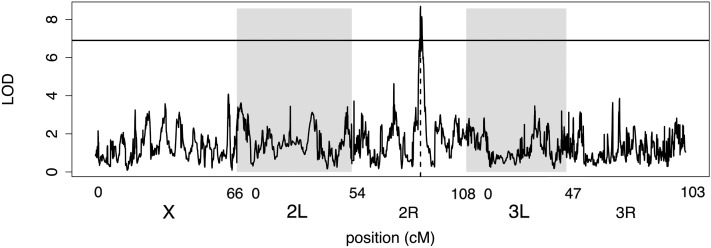
Figure 12 .

An example of a successfully mapped 5% QTL in the full panel of pA inbred RILs. The horizontal solid line is the significance threshold. The vertical dashed line shows the true location of the QTL. White and gray shading denotes the different chromosome arms.

Discussion

We describe our ability to infer complete genome information from a dense set of semicodominant markers for the DSPR panel and assess the power of the panel to map QTL under various experimental designs and genetic architectures. In developing a mapping panel for the genetic analysis of complex traits, several key issues that affect the performance of the panel must be balanced against one another.

First, the amount and quality of genome information depends on the genotyping method used. The DSPR employed RAD markers to discover and genotype the RILs. The RAD method is one preferred method when a large number of SNPs and a large number of lines need to be genotyped (Andolfatto et al. 2011). Other genotyping technologies are typically optimized either for few SNPs in a large number of samples or for a large number of SNPs in few samples (e.g., Affymetrix and other array-based methods). In most cases, the resources will not exist to employ an array-based method in a large number of samples and an investigator is likely to favor a more cost-effective technique like RAD, as we did in the case of the DSPR. We identified several important challenges when inferring genome information from the semicodominant markers that result from RAD (and will result from any genotyping method relying on short reads from next-gen sequencing). A key challenge for a genotyping method that takes advantage of next-generation sequencing is the distribution of allele counts for regions with segregating variation. We found that segregating regions did not follow a single binomial distribution and were more often biased toward one allele, as was also found by Andolfatto et al. (2011) in their use of multiplexed shotgun sequencing. Andolfatto et al. (2011) approached this issue by randomly sampling a single allele from the set of allele counts at each position. We employed a β-binomial distribution in our hidden Markov model to better approximate the distribution of allele frequencies (although other distributions could also fit the observed overdispersion) and successfully infer the state in areas of the genome with segregating variation in each RIL. By using the β-binomial, we did not need to exclude any information by sampling our allele counts and we were still able to accurately identify regions segregating variation.

Additionally, for methods such as RAD and MSG that sample a subset of the genome, the per position coverage must be balanced against marker density. We used the restriction enzyme SgrAI, which cuts approximately every 30 kb and produced 4026 semicodominant markers. A more frequent cutter would have produced more markers across the genome but at reduced coverage per site. Our results indicate that marker density is more important than high coverage at each site when using a hidden Markov model to infer genome information. This effect is largely due to the ability of the HMM to incorporate uncertainty. At low-coverage sites, the true genotype is less certain due to potential sequencing errors. The HMM relies on a binomial (or in the case of heterozygous sites the β-binomial) distribution for the emission probabilities and incorporates an error rate for both the founder genotype and the RIL genotype at each position. Thus, a low number of incorrect allele counts (incorrect low-coverage site) is not very improbable and is not likely to cause an incorrect inferred state. Thus, with enough represented sites across the genome, the HMM is able to infer the correct state even with low average coverage. It is important to note that our results apply specifically to eight-way RILs that are largely (>95%) homozygous. With more possible states, as is the case in heterozygous regions and would be the case with more than eight founders, the amount of missing genotype information for a given marker density and coverage is expected to be higher and a larger marker density may be necessary.

Our marker density in the DSPR is sufficient to infer complete genome information with a high degree of confidence. There are few uncertain sites and our simulations reducing marker density show the proportion of uncertain sites is low and fairly constant at our marker density levels (Figure 6). Our major source of uncertain assignments occurs at recombination breakpoints. We found that local marker density had a large effect on how tightly we could resolve breakpoints. Therefore, increasing marker density in the DSPR, while it would not produce large decreases in our already low proportion of uncertain sites, would increase our ability to tightly resolve recombination breakpoints. A fairly general observation is that the regions of the genome associated with the most genotyping uncertainty are those that stochastically happen to have the lowest density of RAD markers cut sites. Thus, in choosing an appropriate restriction enzyme it is more important to manage minimum local cut-site density than genome-wide average cut-site density.

The breeding design to create the mapping panel must balance mapping resolution against the allele frequency distribution in the panel. At one extreme, association studies use natural populations with alleles at their natural frequencies (e.g., the Drosophila Genetic Reference Panel). These designs rely on the natural history of recombination and thus have very high mapping resolution but many alleles will be at low frequency. At the other extreme, in a traditional QTL mapping design utilizing a two-line cross, allele frequencies will be near 50%, but resolution is rarely greater than ∼10 cM (Mackay 2001). The eight-way synthetic populations from which the DSPR RILs were created underwent 50 generations of free recombination. This allows us to localize QTL precisely and achieve high mapping resolution. However, during the free recombination phase the forces of drift and selection were able to act on the synthetic populations, altering the allele frequency distribution. The longer the maintenance phase is, the more likely alleles will be lost and/or frequencies will deviate from the null expectation, while at the same time mapping resolution will increase (Valdar et al. 2006; King et al. 2012). The DSPR has the longest maintenance/crossing phase (F₅₀) of any of the available linkage-based panels (see Introduction: AMPRIL, CC, NAM, and MAGIC). This provides lower location error and higher average resolution than has been achieved by these other panels (Kover et al. 2009; Aylor et al. 2011; Huang et al. 2011). However, the allele frequency distributions in these other panels also more closely match the allele frequency distribution in the founders (Kover et al. 2009; Mcmullen et al. 2009; Aylor et al. 2011; Huang et al. 2011).

The major problem with uneven founder representation is reduced power when allele frequencies fall below 5%. The DSPR panel is positioned between an association study and a more traditional QTL study. In this regard, some of the benefits of an association study (increased mapping resolution) are accompanied by some of the drawbacks (some low-frequency variants). One case where the presence of low-frequency alleles did not influence power was multiallelism. If many individually rare variants at the same gene underlie the majority of genetic variation in a trait and the DSPR panel contains multiple variants, our simulations show the DSPR is highly powered to detect these QTL due to the natural gene-based mapping for a linkage-based panel. In fact, both the multiallelic scenarios performed better than the biallelic case, with smaller location error (∼0.3 vs. 0.4 cM) and higher power (∼95% vs. 84%). The higher power is in part due to the fact that multiallelic sites will be less affected by changes in frequency. While in the biallelic case some alleles were found to be at very low frequencies in the DSPR panel, it is less likely that several alleles at a site are at very low frequency. Generally, an association study would have high power in the multiallelic common design but very low power in the multiallelic rare design where there are many individually rare variants. At their natural population allele frequencies, these rare alleles would be statistically very difficult for an association study to detect, while in the DSPR, the expectation is that a subset of these rare variants would be sampled in the set of 15 founders. An example of a trait with this type of genetic architecture is phenylketonuria, where there are many different individually rare mutant alleles, and afflicted individuals generally have two different mutant variants (Konecki and Lichter-Konecki 1991). Indeed, in human populations where association studies are the only mapping option, gene-based and family-based analysis approaches are beginning to be developed to try to increase power to detect rare variants (Bansal et al. 2010; Ionita-Laza and Ottman 2011).

Third, the potential pitfalls of phenotyping inbred lines must be balanced against the potential loss of power when phenotyping crosses between two RIL lines. We considered two experimental designs: (1) phenotyping the inbred pA RILs and (2) phenotyping matched crosses between the pA–pB RILs. Another potential design is to do RIL crosses within the pA or pB populations, although these designs require special analytical techniques (Tsaih et al. 2005; Zou et al. 2005). Complete homozygosity (fully inbred lines) is an unnatural state for Drosophila and most other animals. Of particular concern when phenotyping inbred lines is the potential for mapping QTL contributing to variation in inbreeding depression (Lynch and Walsh 1998). It is sometimes stated that power is expected to be greater in inbred panels because the effect due to the QTL is expected to double in a homozygous panel. However, it should be noted that the effect of the background genetic variance will also double in such a panel (Falconer and Mackay 1996), and the assumption of doubled effect sizes may not be empirically realized in the face of substantial background genetic variation (Valdar et al. 2006). We therefore considered QTL of equal effect sizes in the two designs. We found that power in the pA–pB cross was reduced compared to that in the inbred RILs design, presumably because the statistical model requires effects to be estimated for 16 probabilities (8 pA probabilities and 8 pB probabilities) instead of the 8 in the model for the pA inbred RILs.

The fact that all individuals of a given cross/RIL are genetically identical does allow multiple measures per cross to reduce environmental error, effectively increasing the effect of the QTL. Our simulations did not explicitly model any particular genetic architecture (e.g., a specific heritability, a specific number of other QTL, etc.) aside from biallelism vs. multiallelism. This allowed us to make conclusions regarding power in a general sense for any QTL that explains a given amount of the total variance. In the case of a single measurement of each RIL, in our simulations a 5% QTL would correspond to a QTL contributing 5% to the total variance of a character. However, in the case of multiple measurements per RIL or cross, environmental variance is decreased, and the total variance between genotypes quickly approaches the genetic variance. Here, our simulations are equally valid but a 5% QTL now corresponds more closely to a QTL that contributes 5% to the genetic variance of the character.

Experimental design also influenced the LOD support interval necessary to achieve a 95% confidence interval. Previous simulations have shown that different experimental designs require different support intervals to achieve a 95% confidence interval. Manichaikul et al. (2006) showed that a 1.5-LOD support interval should be used for a two-line backcross, while a 1.8-LOD support interval should be used in the case of a two-line intercross and the coverage of the support interval depends on power. In most QTL studies, a standard 2-LOD interval is often used and considered to be conservative. In our eight-way RILs, the 2-LOD interval coverage ranged from 87% to 96% for the inbred panel and from 70% to 95% for the pA–pB cross design. These results indicate that a larger LOD support interval should be used for eight-way RILs, especially for the pA–pB cross, where the average size of the confidence interval was lower than for the inbred RILs design despite similar average location error. We also observed these support intervals to be a function of the number of RILs examined and the true effect size of the QTL. Clearly, the necessary support intervals in multiway RILs corresponding to different designs warrant further investigation across a large range of conditions.

As we learn more about the underlying genetic architecture of complex traits, it is becoming clear that we need to approach the genetic dissection of these traits with diverse approaches to provide a complete picture of the underlying causative genetic variants. Here, we have described the genetic properties and power of one such approach, the DSPR panel, which straddles the design gap between an association study and a traditional two-line QTL mapping panel. Ideally, this panel will complement existing Drosophila RIL panels (e.g., Nuzhdin et al. 1997; Kopp et al. 2003), the Drosophila Population Genomics Project (http://www.dpgp.org/), and the Drosophila Genetic Reference Panel (DGRP) (Mackay et al. 2008, 2012). One potentially powerful approach would be to use the DGRP to validate the mapping results achieved in the DSPR or vice versa, because a validation experiment would not require the same stringent correction for multiple tests. Through a combined community effort, we can move toward a better understanding of the genetic basis of complex traits.