Abstract
Purpose: There is a growing need to localize prostate cancers on magnetic resonance imaging (MRI) to facilitate the use of image guided biopsy, focal therapy, and active surveillance follow up. Our goal was to develop a decision support system (DSS) for detecting and localizing peripheral zone prostate cancers by using machine learning approach to calculate a cancer probability map from multiparametric MR images (MP-MRI).
Methods: This IRB approved Health Insurance Portability and Accountability Act compliant retrospective study consisted of 31 patients (mean age and serum prostate specific antigen of 60.4 and 6.62 ng/ml, respectively) who had MP-MRI at 3 T followed by radical prostatectomy. Seven patients were excluded due to technical issues with their MP-MRI (e.g., motion artifact, failure to perform all sequences). Cancer and normal regions were identified in the peripheral zone by correlating them to whole mount histology slides of the excised prostatectomy specimens. To facilitate the correlation, tissue blocks matching the MR slices were obtained using a MR-based patient-specific mold. Segmented regions on the MP-MRI were correlated to histopathology and used as training sets for the learning system that generated the cancer probability maps. Leave-one-patient-out cross-validation on the cancer and normal regions was performed to determine the learning system's efficacy, an evolutionary strategies approach (also known as a genetic algorithm) was used to find the optimal values for a set of parameters, and finally a cancer probability map was generated.
Results: For the 24 patients that were used in the study, 225 cancer and 264 noncancerous regions were identified from the region maps. The efficacy of DSS was first determined without optimizing support vector machines (SVM) parameters, where a region having a cancer probability greater than or equal to 50% was considered as a correct classification. The nonoptimized system had an f-measure of 85% and the Kappa coefficient of 71% (Rater's agreement, where raters are DSS and ground truth histology). The efficacy of the DSS after optimizing SVM parameters using a genetic algorithm had an f-measure of 89% and a Kappa coefficient of 80%. Thus, after optimization of the DSS there was a 4% increase in the f-measure and a 9% increase in the Kappa coefficient.
Conclusions: This DSS provides a cancer probability map for peripheral zone prostate tumors based on endorectal MP-MRI. These cancer probability maps can potentially aid radiologists in accuratelylocalizing peripheral zone prostate cancers for planning targeted biopsies, focal therapy, and follow up for active surveillance.
Keywords: support vector machine, decision support system, prostate cancer localization, multiparametric MRI, multispectral MRI
INTRODUCTION
In 2011, an estimated 33 720 American men died from prostate cancer (PCa), making it the second most common cause of cancer deaths in males after lung cancer.1 Improved diagnosis, higher prevalence in an aging population, and increases in potential environmental and dietary carcinogens contribute to the high incidence of PCa. Earlier and more accurate diagnoses promise to reduce the morbidity and mortality of PCa. Advances in imaging techniques have already helped in the detection of tumors that are localized within the prostate gland.2, 3, 4, 5, 6, 7, 8, 9 Magnetic resonance imaging (MRI) is the most common modality used to image localized prostate cancer, however, interpretation can be challenging especially to readers without extensive experience. MRI is complex because it is actually composed of multiple distinct “parameters” that are derived from T2-weighted imaging (T2W), proton density imaging (PD), diffusion-weighted imaging (DWI), dynamic contrast-enhanced MRI (DCE-MRI), and three-dimensional spectroscopic imaging (3DSI). Each of these techniques has advantages and disadvantages in the detection and localization of the tumor and, thus, must be used together. For instance, T2W imaging provides the best resolution and contrast to depict the anatomy of the prostate and has a very high sensitivity to PCa, but it suffers from a low specificity. Maps of the apparent diffusion coefficient (ADC) of water that are calculated from DWI are useful in detecting PCa with higher specificity but have lower resolution than T2W imaging and are subject to magnetic susceptibility artifacts. DCE-MRI is sensitive to increased vascularity resulting from enhanced angiogenesis in the tumor but increased vascularity can also be seen in benign conditions such as prostatitis and hyperplasia.2, 10, 11 DCE-MRI can be analyzed with two compartment pharmacokinetic models that can be used to generate additional parameters on MRI such as the rate constants Ktrans and kep. The 3DSI method has high specificity, however, it has the disadvantages of having long acquisition time, fat and water interference, and very coarse anatomic resolution.3 Many studies have shown that a single MRI technique is inadequate to provide good detection and tumor localization, and the use of various MRI techniques together, the so-called “multiparametric” approach, has been reported in recent studies to improve accuracy.2, 3, 4, 5, 6, 7, 8, 9, 12, 13, 14, 15, 16
However, multiparametric imaging is inherently difficult for observers to interpret correctly and consistently. An automated decision support system (DSS) or computer-aided diagnosis that includes different algorithms to perform image segmentation, image feature extraction, and classification can provide a systematic and objective approach to fuse information from different types of MR images. Chan et al. generated statistical maps using support vector machines (SVM) and Fisher linear discriminant (FLD) analysis on calculated ADC, PD, and T2 maps from T2W and DWI images performed at 1.5 T with transrectal ultrasound guided biopsy results as a gold standard.13 Unfortunately, biopsy results can be unreliable for validation, therefore, whole mount histopathology sections are preferred. Viswanath et al. used whole mount histopathology sections to train a method of combined clustering of T2W images and DCE-MRI reduced with locally linear embedding (LLE).17 Vos et al. used T2W and parametric DCE-MRI maps at 3.0 T validated with whole mount sections for developing a CAD system based on SVM.18 Ozer et al. reported that their supervised machine learning method performed better than an unsupervised method using T2 maps from fast spin-echo MRI (FSE-MRI), pharmacokinetic maps from DCE-MRI, and ADC maps from DWI obtained at 1.5 T with whole mount histopathology as the gold standard.19 Systems using T2W and 3DSI have also been reported despite the complications from the large dimensionality difference between the two methods.20
Although whole mount histopathology is considered the gold standard, it has limitations as well. If the specimen is cut at a significantly different angle than that obtained with MRI, discordant results can be seen. The correlation of in vivo MRI and histopathology findings is improved if the histology sections are in the same orientation and location as the MRI, but achieving this is not straightforward. The prostate is a deformable gland; hence, its shape can change after removal from the body. Additionally, in order to increase SNR and resolution, prostate imaging is often performed using an endorectal coil, which compresses the gland in the anterior–posterior direction during the scan. This makes the task of correlation more difficult. Some studies have focused on coregistering MRI and histological techniques using image processing technology.21, 22 However, the assumption here is that histology sections obtained are always parallel, which is generally difficult task to achieve. Jhavar et al. developed a tissue slicer that facilitated slicing the prostate with parallel cuts, however, it does not guarantee correspondence with the MR imaging plane.23 Recently, a novel method to process the specimens with patient-specific molds (PSM) designed from the presurgical MRI scans of each patient has been used to ensure that the tissue blocks correspond to the MRI slices.24
Herein, we present a new method of DSS for detecting and localizing peripheral zone prostate cancer. The PSM method was used to process whole mount histopathology sections. Unsupervised clustering analysis was performed first on the multiparametric maps of normalized T2W (NT2W), ADC, Ktrans, kep, and T1 obtained at 3.0 T to generate region maps which were then matched to histopathology maps to train the classifiers. Genetic algorithms were used to optimize the SVM component of the system. The resulting cancer probability maps on unseen data showed high performance and potentially could be used to localize tumors and facilitate targeted biopsy and focal therapy.
METHODS
The general block diagram for the DSS that included the MP-MRI scans prior to surgery and the radical prostatectomy specimen of each patient is shown in Fig. 1. Whole mount histopathology sections which served as gold standards for the DSS were prepared from the specimens using PSMs. The system was designed to be trained on known data (MP-MRI feature sets and histopathology slices) and then to be applied to new data sets (MP-MRI only) to produce cancer probability maps. The training phase, which branches to the left in the diagram, involved segmentation of MP-MRI feature set into different regions which were matched with the PSM-processed histopathology slides and used to train and optimize the classifier model. Once the system was trained, it was applied to new MP-MRI feature sets to obtain cancer probability maps as shown on the right branch of the diagram. To accomplish these tasks, a GUI for the DSS was implemented in Java as a plug-in tool for MIPAV image processing software (http://mipav.cit.nih.gov/). It was interfaced with modules written in MATLAB programming environment and open-source software RAPIDMINER (http://rapid-i.com/) for backend algorithm computation. Subsections 2A, 2B, 2C, 2D, 2E, 2F describe these methods in more detail.
Figure 1.
Flow chart for a DSS based on a multiparametric MRI. The cancer probability map is the final outcome of the algorithm.
Patient population
Approval from the local institutional review board was granted and written consent was obtained from all patients for their images to be used for research purposes. This Health Insurance Portability and Accountability Act (HIPAA) compliant retrospective study consisted of 31 patients who were referred from the Urology department for MRI at 3.0 T and underwent robot-assisted radical prostatectomy (RARP) within 180 days after their scan. Their mean (range) age was 60.4 (48–75) yr and the mean serum prostate specific antigen (PSA) was 6.62 (0.42–35.9) ng/ml. Patients who had MRI performed without endorectal coil (anorectal surgery and colostomy, inflammatory bowel disease, severe hemorrhoids, etc.), those who exhibited significant motion during the MP-MRI scans, or did not undergo a DCE-MRI study, or where error occurred in generating the mold were excluded from the study. Seven patients were excluded.
Clinical in vivo MRI
MRI was performed on a 3.0 T system (Achieva, Philips Healthcare, Best, The Netherlands) using a 16-channel anterior cardiac SENSE array coil (Philips Healthcare, Best, the Netherlands) combined with an endorectal coil (BPX-30, Medrad, Pittsburgh, PA, USA) without prior bowel preparation. After performing a digital rectal examination, the endorectal coil was placed in the rectum using a semianesthetic gel (Lidocaine, AstraZeneca, USA) and the balloon around the coil was distended with Fluorinert (FC-770, 3M, St. Paul, MN, USA) to a volume of ∼50 ml to avoid susceptibility artifacts caused by air in the balloon.
Three-plane scout views of the prostate were obtained to confirm correct positioning of the endorectal coil. Multislice T2-weighted turbo spin-echo (TSE) images of the entire prostate were obtained in three orthogonal planes (sagittal, axial, and coronal) at a scan resolution of 0.461 × 0.598 × 3.0 mm3; field of view (FOV), 140 × 140 mm2; TR/TE, 8869/120 ms; flip angle (FA), 90°; slice thickness, 3 mm without gaps; and image reconstruction, 512 × 512. To reduce scan time, a lower refocusing pulse angle of 100° was used for the sagittal and coronal images.
An axial DWI scan was carried out using a single-shot spin-echo EPI sequence. Five b-values (b = 0, 188, 375, 563, 750 s/mm2) of diffusion-sensitive gradients were applied in data acquisitions and high b-values images (b = 563 and 750 s/mm2) were averaged twice to increase S/N. To avoid fold-over artifacts, a SENSE factor of 2 (plus oversampling factor of 2) was employed along the phase encoding (RL) direction with acquisition parameters of TR/TE of 4243/57 (ms); FOV (AP/RL/FH), 160, 180, and 60 mm; scan resolution 1.25 * 1.25 * 3.0 mm3; EPI factor, 73; partial Fourier scan factor, 0.73; and number of scan average (NSA), 4.
Finally, the DCE-MRI were acquired using T1-weighted fast field echo (T1W-FFE) dynamic scan using nonselective or thick slab excitation pulses to suppress arterial inflow artifact (FA = 8.5; TR/TE 3.65/1.75 ms; 10 × 6 mm2 slices; 4× slice oversampling; SENSE factors of 3.1 and 2 or 5 and 1 in the phase and slice directions, respectively; temporal resolution of 5.6 s; acquisition matrix 256 × 187; FOV 262 × 262 mm2) with contrast infusion (0.1 mmol/kg dose of Magnevist, rate 3.0 cc/s) after the third dynamic scan. A separate T1W-FFE scan with FA = 2 was acquired prior to the dynamic scan for use in calculating T1 maps. To compensate for rf field excitation (B1) inhomogeneity, B1 maps were acquired using a dual-TR method at a scan resolution of 4.1 × 5.95 × 6.0 mm3; FOV, 262 × 262 mm2; TR, 17 and 85 ms; TE, 2.3 ms; FA, 50°; slice thickness, 6 mm without gaps; and image reconstruction, 256 × 256.
Creating a multiparametric MRI feature set for DSS
In order to reduce interpatient variance, NT2W maps were calculated from the axial T2W intensities using the average fat signal adjacent to the prostate as reference. This task was performed by writing a plug-in tool for MIPAV software (http://mipav.cit.nih.gov/).
Quantitative ADC maps were calculated with the Philips scanner software from the axial DWI by fitting the dependence of the signal intensity in each pixel, S, on the b-value or diffusion gradient factor, b, according to the equation S = S0 × exp(–b × ADC), where S0 is the pixel value at b = 0.
For the DCE-MRI dataset, each dynamic curve was denoised using a wavelet-based technique.25 Then, the pharmacokinetic parameters were extracted using the generalized kinetic model (GKM) that required an arterial input function (AIF), as described by Murase.26, 27 An in-house algorithm was developed to derive the AIF using a semiautomated approach where the initial operator interaction was limited to extracting the AIF from one slice and was followed by automated AIF extraction method to derive AIF from all slices. An initial AIF mask was obtained by comparing percentage enhancement curve of voxels with the seed curve using two different metrics––correlation coefficient and spectral angle mapper. Any voxels that did not meet the criteria were automatically excluded from the AIF mask. Finally, the remaining voxels were averaged on a slice basis and then converted to gadolinium concentration curves, while the final AIF was obtained by averaging the concentration curve for all slices.28 For each voxel, the GKM was fitted to the measured concentration time curves, using the linear least-squared method published by Murase27 to yield the volume transfer constant, Ktrans, from blood plasma to extracellular extravascular space (EES) and the rate constant, kep, from the EES to blood plasma. Analysis was performed on a pixel-by-pixel basis using a tool developed in-house using IDL 7.1 (Interactive Data Language, ITTVIS, Boulder, CO, USA). Finally, the NT2W and ADC maps were resampled (using MATLAB functionality of imresize) to have voxel resolution equivalent to the T1 and pharmacokinetic maps (Ktrans and kep) to form the feature set for the DSS.
Correlating MRI to whole mount histopathology using PSM
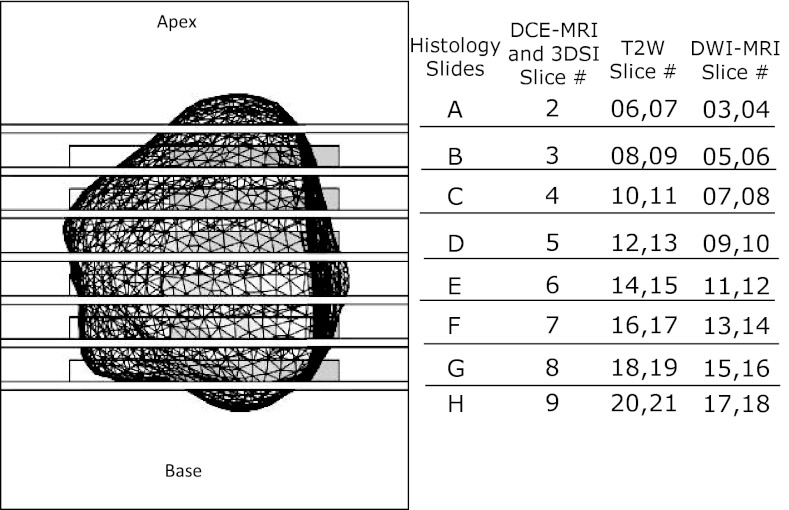
A PSM was created using a MR-based high-resolution prostate model for each patient as described previously.24 To achieve this, contour lines were manually drawn along the prostate capsule on the MR images obtained in sagittal, axial, and coronal plane using MIPAV (http://mipav.cit.nih.gov/). Instead of the binary object fusion method used in the previous work,24 these contour lines, which represent groups-of-points, were merged from all three views to create a point-clouds model of the prostate. Finally, the surface was extracted using MESHLAB (http://meshlab.sourceforge.net/) to obtain a high-resolution model of the prostate. The PSM was created in a 3D-CAD software, SolidWorks (Dassault Systèmes SolidWorks Corp., Walthan, MA, USA), by subtracting the prostate model from a predesigned box with slots to guide a knife and dividing the part into two halves, and printed on a 3D-printer. The knife slots were positioned such that each tissue block matched the location of a 6 mm thick DCE-MRI slice and two 3 mm T2W and ADC slices as shown in Fig. 2. To allow the pathologist to view the specimen during the cutting process, earlier versions included rectangular openings next to each slot. In vivo volume and surface area of the prostate were also obtained from the high-resolution prostate model in Solidworks.
Figure 2.
Top view of the patient-specific mold showing the prostate cavity (wire mesh), the slots for the knife every 6 mm, and correspondence of the locations of 5 mm histology slices to the locations of MP-MRI slices. The rectangular outlines near each slot indicate the location of optional windows that were also visible in the MRI slices shown in Figs. 3d, 3e, 3f, 4d, 4e, 4f.
The RARP specimen from each patient was painted such that the anterior was black, the right posterior was blue, the left posterior was red, and the urethra was yellow to provide correct orientation for placing the specimen in the PSM. Afterward, the specimen was fixed in formalin for 2–24 h at room temperature. The seminal vesicles were amputated before placing and cutting the specimen in the PSM.
Ex vivo imaging of specimen in PSM for validation
In order to evaluate the performance of the PSM, ex vivo MRI imaging was performed in 12 specimens within their respective PSM. TSE images were obtained using a SENSE Flex-M coil (Philips Healthcare, Best, The Netherlands) in three orthogonal planes (sagittal, axial, and coronal) at a scan resolution of 0.461 × 0.438 × 3.0 mm3, acquisition matrix, 320 × 304; TR/TE, 7000/65 ms; other parameters remained the same as the in vivo images. For comparison, the volume and surface area of the specimen were obtained by creating a high-resolution prostate model from ex vivo images using the approach for in vivo prostate volume calculation. An experienced radiologist evaluated both in vivo and ex vivo MR images, slice by slice, for visible anatomical structures such as lobes, cysts, and urethra.
Histopathology processing and analysis
The specimen was serially sectioned in the PSM from apex to base at 6-mm intervals using a 10 in. long autopsy knife (Scientific Supplies, order No. MII-5000). The resulting tissue blocks were labeled and allowed to fix in formalin for an additional 48–72 h. The formalin was removed by wax addition and graded alcohol was added to dehydrate the specimen. The alcohol was cleared by adding xylene and paraffin to the media. The histology slides were prepared after this process was repeated in reverse order. Whole mount sections were cut at 5 μm thickness and stained with hematoxylin-eosin for histopathologic evaluation by two pathologists (H.M., M.J.M.), neither of whom had knowledge of the imaging results. They assessed the sections for the presence of tumor, Gleason score, extracapsular extension, and seminal vesicle invasion and outlined the tumor foci.
DSS training and application
Prostate region segmentation
The extracted sets of MP-MRI features from the prostate gland were used as an input to an unsupervised algorithm (also known as clustering technique) that seeks to summarize and explain key features of the data. This work used the model-based expected maximization (EM) unsupervised learning algorithm29 provided in the open-source software RAPIDMINER to generate a cluster map from MP-MRI features. This approach can also be considered as generalized k-means where each cluster can be mathematically represented by a parametric distribution. EM is used widely because it has a strong statistical basis, it converges fast when given good initialization, it allows for easy memory management for high-dimensionality dataset, and it is fairly robust with noisy data. Using a MATLAB code, morphological processing based on the 3D-connectivity of pixels was applied to this cluster map to obtain a region map, where 3D-connectivity defined which pixels were connected to other pixels either by their faces or edges. A set of pixels in a cluster map that formed a connected group were combined into a region.
Training the classifier model
Machine learning-based systems such as the one presented here require training datasets with known results to create a model which are used to predict outcome of similar datasets with unknown result. The training dataset for DSS region identification was generated with the help of an expert radiologist (B.T.). This was accomplished by overlaying each region map on the T2W image, and matching them to the cancer and noncancer regions that were outlined on corresponding histology maps. The resulting average MP-MRI voxel values for NT2W, ADC, Ktrans, kep, and T1 from each matched cancer and noncancer region served as input training data for the machine learning algorithm.
We used SVMs, a statistical learning-based approach, in RAPIDMINER to create a classifier model that could be used to predict outcome of similar data.30, 31, 32 For SVM training, given a set of training data {(xi,yi)} in RD × R, where, D represents the number of attributes of input data xi and yi ∈ {–1, 1} for a two class problem (e.g., cancer and noncancer), the goal is to create a model that finds an optimal decision boundary that achieves maximum separation between these two classes. The training examples that are closest to the decision boundary are known as support vectors.
Generally, real world data are not fully linearly separable, i.e., a dataset might fall on the “wrong side” of the decision boundary. Thus, we used the SVM implementation that allowed relaxed constraint for misclassified points. In addition, real world data are usually nonlinear. Linear separation can be achieved by mapping the data to a higher dimensional space, however, it could be computationally expensive. We used SVMs “kernel trick” to enable operations to be performed in the input space rather than the potentially high-dimensional feature space.35 For this work, we used radial basis functions with a Gaussian form as the kernel function.30, 31, 32
To find the optimal values for a set of parameters for SVM algorithm we used a genetic algorithm, an evolutionary strategies approach, provided in RAPIDMINER.33 A “chromosome” encoding for an individual was performed by considering each SVM parameter that needed to be optimized as a “gene,” while the length of the chromosome depended on the number of parameters to be optimized. The evaluation of individual fitness for the selection process was based on the f-measure metric discussed in Sec. 2F.
Creating cancer probability maps
Once trained on histopathology-correlated MP-MRI data, the optimized SVM model was applied to unseen MP-MRI data to obtain cancer probability maps. Standard SVM do not output calibrated posterior probability. In order to do this, we used RAPIDMINER's implementation that converts SVM output into posterior probability using the algorithm presented by Platt.34
Decision support system validation
A leave-one-patient-out cross-validation (LOPOCV) technique which avoided training and testing on the same patient was used to assess efficacy of the DSS. The LOPOCV estimated the cancer probability in the patient “left out” of the analysis, and the procedure repeated until each patient had been tested individually. The analysis was performed separately for both nonoptimized SVM and optimized SVM. After calculating the probability of the region by the LOPOCV method, a threshold of 50% was applied to calculate accuracy, sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and Kappa coefficient of the DSS as defined in Table 1. Sensitivity is the ability of the system to find all tumors that are positive on histopathology, while PPV is the probability that a region defined as a tumor proves to be positive for tumor. Ideally, one strives to increase both sensitivity and PPV to one. For DSS, it is useful to report both sensitivity and PPV in order to evaluate the system's efficiency. However, there is a tradeoff between those quantities. For example, if a system detects everything as tumor, it would have 100% sensitivity but may have a lower PPV, and vice versa (i.e., a system can have 100% PPV if fewer tumors are detected). However, if sensitivity is low, many obvious tumors may be missed. Hence, a system's optimization and efficacy evaluation is performed using a positive agreement (commonly known as the f-measure in machine learning community35). Kappa coefficient known as Rater's agreement was calculated, where the raters are DSS and histopathology gold standards.
Table 1.
Definition terms for contingency table used in system evaluation.
| Pathology cancer | Pathology not cancer | Precision | |
|---|---|---|---|
| Predicted cancer | True positive (TP) | False positive (FP) | PPV = TP/(TP + FP)1 |
| Predicted not cancer | False negative (FN) | True negative (TN) | NPV = TN/(TN + FN)2 |
| Class recall | Sensitivity = TP/ (TP + TN) | Specificity = TN/ (FP + TN) | Accuracy = (TP + TN)/ (TP + TN + FP + FN) |
Note: F-measure (also known as positive agreement) = (2* sensitivity * PPV )/(sensitivity + PPV). Kappa coefficient = (accuracy – Pr(e))/(1 – Pr(e)), where Pr(e) is probability of random agreement; Pr(e) = [{(TP + FP) * (TP + FN) } + {(FN + TN) * (FP + TN) }]/(TS2) for total sample TS = TN + TN + TP + FP.
PPV: Positive predictive value.
NPV: Negative predictive value.
RESULTS
Quantitative and qualitative evaluation of the PSM
Volume and surface area calculations of the prostate on in vivo and ex vivo MRI for 12 patients are provided in Table 2, while the best and worst case ex vivo imaging of specimens in the mold are shown in Figs. 34, respectively. The average interval between MRI and the surgery was 2.67 months. The mean (range) relative difference in the volume was 9.09 (2.10%–25.68%) and surface area was 7.21 (2.15%–19.27%). In vivo and ex vivo images were compared on a slice by slice basis by a radiologist. For two of 12 ex vivo specimens, radiology evaluation could not be performed because it was observed that the urethral marker in the mold did not correlate well with that of the specimen. The radiologist was able to correlate the in vivo and ex vivo for various structures for the other nine patients, however, in one case it was challenging to correlate because of insufficient landmarks throughout the prostate.
Table 2.
Results from ex vivo validation of PSM.
| Volume (cc) |
Surface area sq cm |
||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case no. | Interval (month) | Age (yrs) | In vivo | Ex vivo | % Diff | In vivo | Ex vivo | % Diff | PSA |
| 1 | 5 | 60 | 36.30 | 35.10 | 3.31 | 58.02 | 56.17 | 3.20 | 8.6 |
| 2 | 4.5 | 69 | 51.75 | 39.70 | 23.28 | 72.06 | 61.34 | 14.88 | 5.5 |
| 3 | 2 | 63 | 43.89 | 39.98 | 8.91 | 65.96 | 60.80 | 7.83 | 5.8 |
| 4 | 2 | 60 | 47.35 | 45.98 | 2.90 | 69.87 | 67.81 | 2.94 | 4.0 |
| 5 | 2 | 58 | 46.94 | 43.37 | 7.61 | 68.30 | 65.51 | 4.09 | 3.9 |
| 6 | 2 | 63 | 48.07 | 46.72 | 2.80 | 67.80 | 66.34 | 2.15 | 5.7 |
| 7 | 3 | 58 | 47.80 | 35.53 | 25.68 | 68.55 | 55.34 | 19.27 | 7.7 |
| 8 | 2 | 54 | 67.46 | 58.74 | 12.93 | 85.27 | 78.40 | 8.06 | 2.4 |
| 9 | 1.5 | 59 | 40.99 | 40.13 | 2.10 | 63.03 | 60.67 | 3.74 | 35.9 |
| 10 | 1 | 58 | 74.41 | 71.50 | 3.91 | 92.31 | 88.42 | 4.21 | 8.1 |
| 11 | 2 | 58 | 43.71 | 39.49 | 9.64 | 66.45 | 60.49 | 8.96 | 1.7 |
| 12 | 5 | 65 | 43.51 | 40.89 | 6.03 | 67.13 | 62.27 | 7.23 | 3.5 |
| Mean | 2.67 | 60.55 | 49.35 | 44.76 | 9.09 | 70.40 | 65.30 | 7.21 | 7.73 |
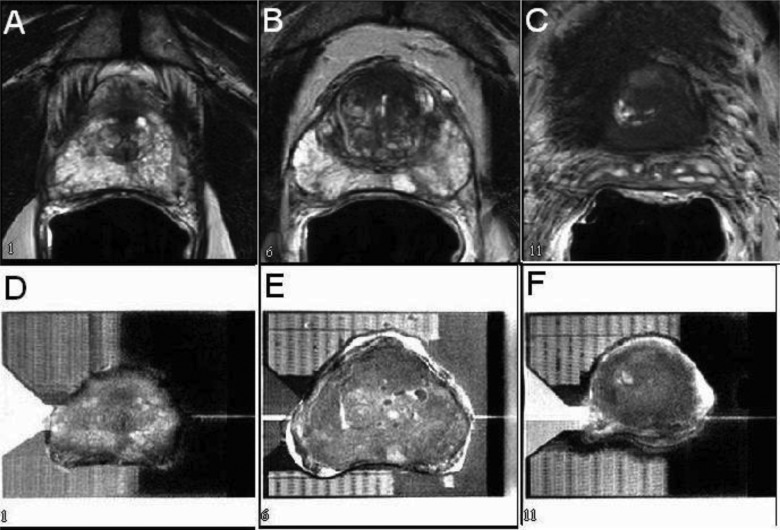
Figure 3.
Selected slices from MR images of a prostate gland in vivo (a)–(c) and ex vivo inside a mold (d)–(f) showing good correlation when tissue shrinkage was minimal.
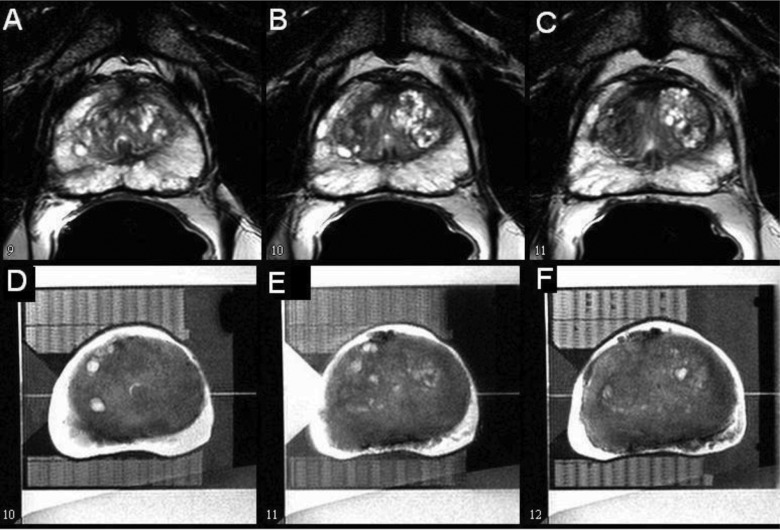
Figure 4.
Selected slices from MR images of a prostate gland acquired in vivo (a)–(c) and ex vivo inside a mold (d)–(f) showing poor correlation when tissue shrinkage was significant.
Efficacy of a decision support system
For the 24 patients included in the study, one-to-one correspondence was first established between histology and T2W slices, and then 225 cancer and 264 noncancerous regions were identified from the region maps as shown in Fig. 5. The mean value ± standard-deviation for each MP-MRI parameter in cancer regions was NT2W (0.55 ± 0.18), ADC (1.24 ± 0.27) × 10−3 mm2/s, T1 (1.65 ± 0.38) s, Ktrans (0.56 ± 0.55) min−1, and kep (1.63 ± 1.61) min−1, while for normal regions NT2W (0.78 ± 0.33), ADC (1.81 ± 0.41) × 10−3 mm2/s, T1 (1.99 ± 0.63) s, Ktrans (0.20 ± 0.17) min−1, and kep (0.82 ± 0.64) min−1. The box and whisker plot for the dataset is shown in Fig. 6. For each parametric map, the t-test of the null hypothesis that data in the cancer and noncancer regions have equal means and unknown variances was rejected with p < 0.0001, indicating that there is statistically significant difference between these regions in each individual parameters.
Figure 5.
T2-weighted image (a) and segmented region map (b) from MP-MRI images show good correspondence with histology map gold standard (c).
Figure 6.
Box and whisker plot for cancer (C) and noncancer regions (NC). Center line = median, top of box = 75th percentile, bottom of box = 25th percentile, whiskers = data within 1.5 interquartile ranges, outlier = +, shape of the notches represents statistically significant differences between two groups p < 0.0001 for all modalities.
Table 3 shows the efficacy of the DSS without optimizing SVM parameters, where a cancer probability greater than or equal to 50% was considered positive for cancer. The nonoptimized system had an f-measure of 85% (also known as positive agreement) and the Kappa Coefficient was 71% (Rater's agreement, where raters are DSS and ground truth histology). Table 4 shows the efficacy of the DSS after optimizing SVM parameters using a genetic algorithm, again using a 50% probability threshold. The optimized system had an f-measure of 89% and a Kappa coefficient of 80%. Thus, after optimization of the DSS there was a 4% increase in the f-measure and a 9% increase in the Kappa coefficient. Figure 7, shows the performance comparison of multiparametric images with individual sequences in terms of sensitivity, specificity, f-measure, and kappa statistics.
Table 3.
Results without optimized SVM parameters.
| Pathology cancer | Pathology not cancer | Precision | |
|---|---|---|---|
| Predicted cancer | 192 | 36 | 84% |
| Predicted not cancer | 33 | 228 | 87% |
| Class recall | 85% [Sensitivity] | 86% [Specificity] | 86% |
Table 4.
Results with optimized SVM parameters.
| Pathology cancer | Pathology not cancer | Precision | |
|---|---|---|---|
| Predicted cancer | 203 | 27 | 88% |
| Predicted not cancer | 22 | 237 | 92% |
| Class recall | 90% [sensitivity] | 90% [specificity] | 90% |
Figure 7.
DSS performance using individual MR sequences in comparison to different combinations of multiparametric MR images.
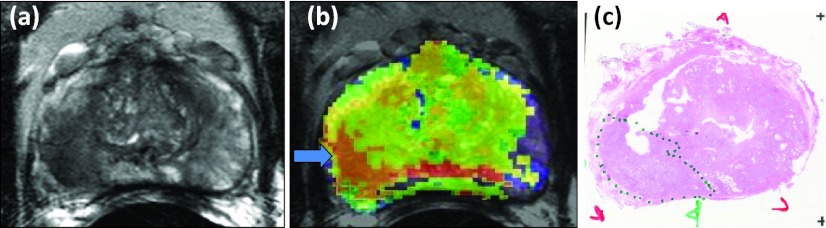
Figure 8 illustrates the application of the DSS, where MP-MRI images shown in Figs. 8a, 8b, 8c resulted in the cancer probability map shown in Fig. 8d. The region with >90% probability of cancer corresponded to the PCa region that was outlined with green ink (dotted line) by the pathologist on the histopathology slide shown in Fig. 8e.
Figure 8.
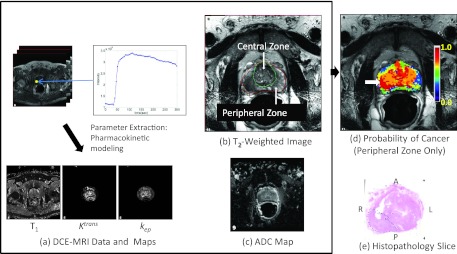
Illustration of the DSS. Multiparametric MRI images (a)–(c), resulting color coded cancer probability map (d) superimposed on T2W image with a white arrow indicating region of highest probability, and histopathology slide (e) confirming the presence of tumor (Gleason score 3 +4, dotted line) in the region with the highest probability. The anterior (A), posterior (P), left (L), and right (R) sides are labeled.
DISCUSSION
The ability to accurately localize prostate cancer with imaging is critical to the success of MRI for guiding biopsy, focal therapy, and as an alternative to biopsy during active surveillance. However, this emerging technique requires accurate detection despite a complex dataset consisting of multiple parameters. In the last decade, many studies have shown the advantages of using MP-MRI consisting of T2W, DCE MRI, DWI, and MRSI for the detection and localization of prostate cancer both at 1.5 and 3.0 T.2, 3, 4, 5, 12, 13, 16 However, the success of such studies depended on the expert opinion of experienced radiologists in interpreting MRI and the methodology used for correlating MR and histology findings. Additional MRI sequences for better cancer detection also make interpretation even more difficult and subject to inconsistency. The DSS developed by our work could help radiologists overcome these limitations.
In this work, we used a PSM to provide histologic data for the training set. The prostatectomy specimen is deformable and fixation introduces variable change in the prostate volume. The PSM not only aided in orienting the specimen but also in holding the deformable specimen in the shape of the MR image while the slots guided the knife so that the resulting tissue blocks matched the MRI slices. The quantitative evaluation of PSM substantiated the fact that the tissue blocks correlated with the in vivo MR slices when the specimen had a good fit inside the mold. However, in some cases, there was too much shrinkage and the tissue blocks obtained did not have a complete one-to-one correspondence with in vivo MR slices. In Fig. 4, for example, the in vivo and ex vivo MR images were off by one MRI slice (3 mm) because of tissue shrinkage. The effectiveness of the PSM was demonstrated in our recent paper where direct one-to-one region-based correlation of MP-MRI to histology was possible using the PSM.16 In contrast, our earlier work using the same imaging protocol required the use of a nearest neighbor approach without the PSM.3 The use of the PSM has become a standard practice in processing all prostatectomy specimens at our institution and we have now processed over 200 cases to add to our training database for future studies.
The concept of developing a computerized approach for automated diagnosis and detection of prostate cancer has been an active research area for the last decade. Similar systems have been developed to identify breast cancers on mammography. However, in the case of prostate MRI, improvements in existing sequences and the development of new imaging sequences to map new parameters mean that such techniques are under constant reevaluation. Training and evaluation of the system using manually outlined tumor regions are inefficient and subject to reader variability. The use of an unsupervised clustering method followed by morphology processing to segment the MP-MRI maps not only reduced variability but also streamlined the process. It allowed the radiologist to concentrate on matching the segmented regions to the marked histopathology slides instead of manually segmenting tumor margins in the MP-MRI maps. To account for distortions in the specimen during processing and the large discrepancy between the 3 mm and 6 mm thick MRI slices and the 5 μm thin histopathology sections, we relaxed the match criteria in terms of shape and size. We choose to use SVM for the classification instead of the popular heuristic-based approach, artificial neural network (ANN). ANN suffers from the overfitting problem due to the use of empirical risk minimization compared to theoretical SVM's structural risk minimization approach. Additionally, optimization of ANN can be challenging in the presence of multiple local minima, while solution obtained by SVM is global and unique. Finally, ANN's computational complexity depends on the input space. SVM's main limitation is with the choice of parameters for kernel function.30, 31, 32 We optimized the SVM component of the DSS using genetic algorithm, which was not used in previous studies.17, 18, 19
As expected, differences between the NT2W, ADC, and DCE parameters in cancerous compared to noncancerous regions were statistically significant (p < 0.05) as seen in Fig. 6. In addition, although not often reported, we observed a small, but statistically significant, difference between the mean T1-values of cancerous and noncancerous regions consistent with a recent publication.36 For individual sequence evaluation, the order in terms of performance was ADC > DCE > NT2W > T1 as seen in Fig. 7. ADC maps performed better than other imaging sequences, while as expected, all individual sequences had lower efficiency compared to the full combination of all sequences.
The increase in the overall efficacy of the DSS when using MP-MRI over individual parametric maps in detecting prostate cancer is in agreement with other studies. Evaluation and optimization of DSS are necessary with individual maps and different combinations because in clinical practice there are instances in which certain sequence will not be available (e.g., renal insufficiency may cause a DCE-MRI not to be performed). In such cases, probability maps can still be obtained from available MR parameters. The performance with the inclusion of additional MP-MRI maps such as metabolite ratio and amide proton transfer (APT) (Ref. 37) or other imaging modalities such as PET that are also sensitive to prostate cancer can also be evaluated. The method presented here can be used to determine the optimum combination to maximize performance and minimize scan time and cost.
There are some limitations and possible improvements to our study. Since we had very few tumors outside the peripheral zone to train the system, the current DSS focused only on the peripheral zone where the majority of PCa occurs. We also did not have enough data to distinguish between different Gleason scores, thus we cannot predict the aggressiveness of prostate cancer. The use of the PSM would allow us to acquire a large enough training data set, so that future DSS implementations could be trained to predict PCa outside the peripheral zone and to predict aggressiveness. Quantitative T2 maps were not available for our study, so we used NT2W images, which may not provide robust quantitative values across patients and different scanners and also required manual intervention in identifying a fat region. The use of quantitative T2 maps which are now practical using accelerated sequences is expected to improve DSS performance. We minimized geometric distortion in the DWI sequence by using parallel imaging (SENSE acceleration factor of 2) to increase pixel bandwidth and by using perfluorocarbon to inflate the endorectal coil, so that there was no noticeable distortion in the data set. Significant magnetic field distortion due to calcification, air in the endorectal coil balloon, fecal matter, or metallic hip implants could limit the inclusion of DWI in calculating probability maps. In such cases, coregistration of the DWI to the T2W images could be used. Additionally, initial image segmentation of MP-MRI images could be improved by optimizing the weight of each parametric MRI map and evaluating the use of other advanced clustering algorithm such as kernel k-means and support vector clustering. For system evaluation we used the leave-one-patient-out technique, which is a substitute for a prospective study, however, our future work will focus on evaluating the system in a classical prospective clinical study.
CONCLUSION
In conclusion, we developed a DSS to provide a cancer probability map for peripheral zone tumors based on 3.0 T endorectal MP-MRI of the prostate. These cancer probability maps can potentially aid radiologists in accurately localizing peripheral zone prostate cancers for planning targeted biopsies, focal therapy, and follow up for active surveillance. Some of the focal therapeutic methods that would benefit from the DSS include high intensity focused ultrasound (HIFU), focal laser ablation (FLA), cryotherapy, intensity modulated radiation therapy (IMRT), and brachytherapy where it can be used to boost therapy to the tumor while avoiding unwanted off-target effects to reduce side effects.
ACKNOWLEDGMENTS
This research was supported in part by the Intramural Research Program of the Center for Cancer Research, NCI, NIH. This project was funded in part with federal funds from the National Cancer Institute (NCI), National Institutes of Health (NIH) under Contract No. HHSN261200800001E. The content of this publication does not necessarily reflect the views or policies of the Department of Health and Human Services, nor does mention of trade names, commercial products, or organizations imply endorsement by the U.S. Government.
References
- See http://www.cancer.org/ for American Cancer Society. Last accessed December 8, 2011.
- Ocak I., Bernardo M., Metzger G., Barrett T., Pinto P., Albert P. S., and Choyke P. L., “Dynamic contrast-enhanced MRI of prostate cancer at 3 T: A study of pharmacokinetic parameters,” AJR, Am. J. Roentgenol. 189, 849 (2007). [DOI] [PubMed] [Google Scholar]
- Turkbey B., Pinto P. A., Mani H., Bernardo M., Pang Y., McKinney Y. L., Khurana K., Ravizzini G. C., Albert P. S., Merino M. J., and Choyke P. L., “Prostate cancer: Value of multiparametric MR imaging at 3 T for detection–histopathologic correlation,” Radiology 255, 89–99 (2010). 10.1148/radiol.09090475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haider M. A., van der Kwast T. H., Tanguay J., Evans A. J., Hashmi A. T., Lockwood G., and Trachtenberg J., “Combined T2-weighted and diffusion-weighted MRI for localization of prostate cancer,” AJR, Am. J. Roentgenol. 189, 323–328 (2007). 10.2214/AJR.07.2211 [DOI] [PubMed] [Google Scholar]
- Langer D. L., van der Kwast T. H., Evans A. J., Trachtenberg J., Wilson B. C., and Haider M. A., “Prostate cancer detection with multi-parametric MRI: Logistic regression analysis of quantitative T2, diffusion-weighted imaging, and dynamic contrast-enhanced MRI,” J. Magn. Reson. Imaging 30, 327–334 (2009). 10.1002/jmri.21824 [DOI] [PubMed] [Google Scholar]
- Bonekamp D., Jacobs M. A., El-Khouli R., Stoianovici D., and Macura K. J., “Advancements in MR imaging of the prostate: From diagnosis to interventions,” Radiographics 31, 677–703 (2011). 10.1148/rg.313105139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi Y. J., Kim J. K., Kim N., Kim K. W., Choi E. K., and Cho K. S., “Functional MR imaging of prostate cancer,” Radiographics 27, 63–75 (2007). 10.1148/rg.271065078 [DOI] [PubMed] [Google Scholar]
- Rogerson P. A., Sinha G., and Han D., “Recent changes in the spatial pattern of prostate cancer in the U.S,” Am. J. Prev. Med. 30, S50–S59 (2006). 10.1016/j.amepre.2005.09.006 [DOI] [PubMed] [Google Scholar]
- Kurhanewicz J., Vigneron D., Carroll P., and Coakley F., “Multiparametric magnetic resonance imaging in prostate cancer: Present and future,” Curr. Opin. Urol. 18, 71–77 (2008). 10.1097/MOU.0b013e3282f19d01 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padhani A. R., Hayes C., Landau S., and Leach M. O., “Reproducibility of quantitative dynamic MRI of normal human tissues,” NMR Biomed. 15, 143–153 (2002). 10.1002/nbm.732 [DOI] [PubMed] [Google Scholar]
- O’Connor J. P., Jackson A., Parker G. J., and Jayson G. C., “DCE-MRI biomarkers in the clinical evaluation of antiangiogenic and vascular disrupting agents,” Br. J. Cancer 96, 189–195 (2007). 10.1038/sj.bjc.6603515 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Futterer J. J., Heijmink S. W., Scheenen T. W., Veltman J., Huisman H. J., Vos P., Hulsbergen-Van de Kaa C. A., Witjes J. A., Krabbe P. F., Heerschap A., and Barentsz J. O., “Prostate cancer localization with dynamic contrast-enhanced MR imaging and proton MR spectroscopic imaging,” Radiology 241, 449–458 (2006). 10.1148/radiol.2412051866 [DOI] [PubMed] [Google Scholar]
- Chan I., W.WellsIII, Mulkern R. V., Haker S., Zhang J., Zou K. H., Maier S. E., and Tempany C. M., “Detection of prostate cancer by integration of line-scan diffusion, T2-mapping and T2-weighted magnetic resonance imaging; a multichannel statistical classifier,” Med. Phys. 30, 2390–2398 (2003). 10.1118/1.1593633 [DOI] [PubMed] [Google Scholar]
- Miao H., Fukatsu H., and Ishigaki T., “Prostate cancer detection with 3-T MRI: Comparison of diffusion-weighted and T2-weighted imaging,” Eur. J. Radiol. 61, 297–302 (2007). 10.1016/j.ejrad.2006.10.002 [DOI] [PubMed] [Google Scholar]
- Noworolski S. M., Henry R. G., Vigneron D. B., and Kurhanewicz J., “Dynamic contrast-enhanced MRI in normal and abnormal prostate tissues as defined by biopsy, MRI, and 3D MRSI,” Magn. Reson. Med. 53, 249–255 (2005). 10.1002/mrm.20374 [DOI] [PubMed] [Google Scholar]
- Turkbey B., Mani H., Shah V., Rastinehad A. R., Bernardo M., Pohida T., Pang Y., Daar D., Benjamin C., McKinney Y. L., Trivedi H., Chua C., Bratslavsky G., Shih J. H., Linehan W. M., Merino M. J., Choyke P. L., and Pinto P. A., “Multiparametric 3T prostate magnetic resonance imaging to detect cancer: Histopathological correlation using prostatectomy specimens processed in customized magnetic resonance imaging based molds,” J. Urol. 186, 1818–1824 (2011). 10.1016/j.juro.2011.07.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viswanath S., Bloch B. N., Genega E., Rofsky N., Lenkinski R., Chappelow J., Toth R., and Madabhushi A., “A comprehensive segmentation, registration, and cancer detection scheme on 3 Tesla in vivo prostate DCE-MRI,” Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention (Springer-Verlag Berlin, Heidelberg, New York, 2008), Vol. 11, pp. 662–669. [DOI] [PMC free article] [PubMed]
- Vos P. C., Hambrock T., Barenstz J. O., and Huisman H. J., “Computer-assisted analysis of peripheral zone prostate lesions using T2-weighted and dynamic contrast enhanced T1-weighted MRI,” Phys. Med. Biol. 55, 1719–1734 (2010). 10.1088/0031-9155/55/6/012 [DOI] [PubMed] [Google Scholar]
- Ozer S., Langer D. L., Liu X., Haider M. A., van der Kwast T. H., Evans A. J., Yang Y., Wernick M. N., and Yetik I. S., “Supervised and unsupervised methods for prostate cancer segmentation with multispectral MRI,” Med. Phys. 37, 1873–1883 (2010). 10.1118/1.3359459 [DOI] [PubMed] [Google Scholar]
- Tiwari P., Viswanath S., Kurhanewicz J., Sridhar A., and Madabhushi A., “Multimodal wavelet embedding representation for data combination (MaWERiC): Integrating magnetic resonance imaging and spectroscopy for prostate cancer detection,” NMR Biomed. 4, 607–619 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhan Y., Ou Y., Feldman M., Tomaszeweski J., Davatzikos C., and Shen D., “Registering histologic and MR images of prostate for image-based cancer detection,” Acad. Radiol. 14, 1367–1381 (2007). 10.1016/j.acra.2007.07.018 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiessling F., Le-Huu M., Kunert T., Thorn M., Vosseler S., Schmidt K., Hoffend J., Meinzer H. P., Fusenig N. E., and Semmler W., “Improved correlation of histological data with DCE MRI parameter maps by 3D reconstruction, reslicing and parameterization of the histological images,” Eur. Radiol. 15, 1079–1086 (2005). 10.1007/s00330-005-2701-5 [DOI] [PubMed] [Google Scholar]
- Jhavar S. G., Fisher C., Jackson A., Reinsberg S. A., Dennis N., Falconer A., Dearnaley D., Edwards S. E., Edwards S. M., Leach M. O., Cummings C., Christmas T., Thompson A., Woodhouse C., Sandhu S., Cooper C. S., and Eeles R. A., “Processing of radical prostatectomy specimens for correlation of data from histopathological, molecular biological, and radiological studies: A new whole organ technique,” J. Clin. Pathol. 58, 504–508 (2005). 10.1136/jcp.2004.021808 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shah V., Pohida T., Turkbey B., Mani H., Merino M., Pinto P. A., Choyke P., and Bernardo M., “A method for correlating in vivo prostate magnetic resonance imaging and histopathology using individualized magnetic resonance-based molds,” Rev. Sci. Instrum. 80, 104301-1–104301-6 (2009). 10.1063/1.3242697 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mallat S., “A Theory of multiresolution signal decomposition: The Wavelet representation,” IEEE Trans. Pattern Anal. Mach. Intell. 11, 674–693 (1989). 10.1109/34.192463 [DOI] [Google Scholar]
- Tofts P. S., Brix G., Buckley D. L., Evelhoch J. L., Henderson E., Knopp M. V., Larsson H. B., Lee T. Y., Mayr N. A., Parker G. J., Port R. E., Taylor J., and Weisskoff R. M., “Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusible tracer: Standardized quantities and symbols,” J. Magn. Reson. Imaging 10, 223–232 (1999). 10.1002/(SICI)1522-2586(199909)10:3%3C223::AID-JMRI2%3E3.0.CO;2-S [DOI] [PubMed] [Google Scholar]
- Murase K., “Efficient method for calculating kinetic parameters using T1-weighted dynamic contrast-enhanced magnetic resonance imaging,” Magn. Reson. Med. 51, 858–862 (2004). 10.1002/mrm.20022 [DOI] [PubMed] [Google Scholar]
- Shah V. P., Turkbey B., Pang Y., Liu W., Choyke P., and Bernardo M., paper presented at the World Molecular Imaging Congress, Kyoto, Japan, 2010, http://www.wmicmeeting.org/2010/Abstracts/forSystemUse/papers/P0754A.html. Last accessed September 5, 2011.
- Witten I. H., Frank E., and Hall M. A., Data Mining: Practical Machine Learning Tools and Techniques, The Morgan Kaufmann Series in Data Management Systems 3rd ed. (Morgan Kaufmann, Burlington, MA, 2011). [Google Scholar]
- Vapnik V., The Nature of Statistical Learning Theory (Springer-Verlag, New York, 1995). [Google Scholar]
- Burges C., “A tutorial on support vector machines for pattern recognition,” in Data Mining and Knowledge Discovery (Kluwer Academic, Boston, 1998), Vol. 2. [Google Scholar]
- Cristianini N. and Shawe-Taylor J., An Introduction to Support Vector Machines and Other Kernel-based Learning Methods (Cambridge University Press, Cambridge, England, 2000). [Google Scholar]
- Goldberg D., Genetic Algorithms in Search, Optimization and Machine Learning (Kluwer Academic, Boston, MA, 1989). [Google Scholar]
- Platt J. C., Probabilities for SV Machines, in Advances in Large Margin Classifiers (MIT, Cambridge, MA, 1999). [Google Scholar]
- Baeza-Yates R. and Ribeiro-Neto B., Modern Information Retrieval (Addison-Wesley-Longman, Harlow, 1999). [Google Scholar]
- Foltz W. D., Haider M. A., Chung P., Bayley A., Catton C., Ramanan V., Jaffray D., Wright G. A., and Menard C., “Prostate T1 quantification using a magnetization-prepared spiral technique,” J. Magn. Reson. Imaging 33, 474–481 (2011). 10.1002/jmri.22450 [DOI] [PubMed] [Google Scholar]
- Jia G., Abaza R., Williams J. D., Zynger D. L., Zhou J., Shah Z. K., Patel M., Sammet S., Wei L., Bahnson R. R., and Knopp M. V., “Amide proton transfer MR imaging of prostate cancer: A preliminary study,” J. Magn. Reson. Imaging 33, 647–654 (2011). 10.1002/jmri.22480 [DOI] [PMC free article] [PubMed] [Google Scholar]