Abstract
Purpose: To develop efficient algorithms for fast voxel-by-voxel quantification of tissue longitudinal relaxation time (T1) from variable flip angles magnetic resonance images (MRI) to reduce voxel-level noise without blurring tissue edges.
Methods: T1 estimations regularized by total variation (TV) and quadratic penalty are developed to measure T1 from fast variable flip angles MRI and to reduce voxel-level noise without decreasing the accuracy of the estimates. First, a quadratic surrogate for a log likelihood cost function of T1 estimation is derived based upon the majorization principle, and then the TV-regularized surrogate function is optimized by the fast iterative shrinkage thresholding algorithm. A fast optimization algorithm for the quadratically regularized T1 estimation is also presented. The proposed methods are evaluated by the simulated and experimental MR data.
Results: The means of the T1 values in the simulated brain data estimated by the conventional, TV-regularized, and quadratically regularized methods have less than 3% error from the true T1 in both GM and WM tissues with image noise up to 9%. The relative standard deviations (SDs) of the T1 values estimated by the conventional method are more than 12% and 15% when the images have 7% and 9% noise, respectively. In comparison, the TV-regularized and quadratically regularized methods are able to suppress the relative SDs of the estimated T1 to be less than 2% and 3%, respectively, regardless of the image noise level. However, the quadratically regularized method tends to overblur the edges compared to the TV-regularized method.
Conclusions: The spatially regularized methods improve quality of T1 estimation from multiflip angles MRI. Quantification of dynamic contrast-enhanced MRI can benefit from the high quality measurement of native T1.
Keywords: magnetic resonance imaging, variable flip angles, T1 estimation, total variation, spatial regularization, dual approach, quadratic penalty
INTRODUCTION
Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) has shown its value for diagnosis of neurological disorders,1 detection of tumors, and evaluation of tissue response to therapies.2, 3, 4 Quantification of tissue longitudinal relaxation time (T1)-weighted DCE-MRI using pharmacokinetic models requires measurement of T1 prior to contrast injection.5 Since T1 values vary in tissue and tumor and can change during and after therapy, an accurate T1 measurement is vital for characterization of perfusion parameters from DCE-MRI. Furthermore, quantitative tissue T1 could be a distinctive metric for tissue discrimination, disease detection, and therapy monitoring.6
The conventional T1 estimation is based upon either an inversion-recovery (IR) or a saturation-recovery (SR) pulse sequence. Although the methods generate accurate results, the prolonged acquisition time of these methods makes them less practical to be a part of a DCE-MRI protocol in clinical setting.7, 8, 9, 10 The approach that is widely used in a DCE-MRI study is to acquire gradient-echo images with variable flip angles (VFA) and with one or more short TRs.11, 12, 13, 14, 15, 16 The scanning time of VFA imaging can be further decreased by undersampling acquisition.17 Estimation of T1 values is usually done by nonlinear least-squares fitting (NLS) of the VFA MRI,18 but also can be done by linear least-squares fitting after transforming intensities of MRI into a linear form with T1.9, 13, 19 Several authors have shown that the VFA method can achieve accuracy of the T1 estimation similar to those by the IR and SR techniques for the image data having a high signal-noise ratio (SNR), which are usually accomplished by performing computation in a region of interest.14, 19 However, voxel-by-voxel estimated T1 values show a large amount of fluctuation due to the noise in the original images and the limited number of flip angles. This poor repeatability of the T1 estimation affects utilization of the T1 map in voxel-based DCE quantification. In order to reduce the variation in the T1 estimation, a different approach is needed. T1, as a characteristic property of the tissue, should exhibit locally spatial continuity, except at the boundary of tissue compartments. The locally spatial continuity has been successfully incorporated into the PET reconstruction,20 the B1 magnetic field correction,21 and the DCE-MRI kinetic parameter quantification.22 In addition, the pharmacokinetic modeling of DCE-MRI with spatial regularization reduces both bias and variance of derived kinetic parameters.22
Tikhonov quadratic regularization, the most commonly used spatial regularization in image applications,20, 23 has been proposed for the T1 estimation from IR MR signals,24 and improves the SNR in the resultant T1 map. However, it is well-known that the quadratic penalty tends to oversmooth image at the boundaries of tissue compartments.25 Total variation (TV), a nonquadratic regularization, can preserve edges at tissue boundary. In this study, we proposed an efficient method by incorporating the TV regularization in the T1 NLS cost function in order to reduce voxel-level noise without blurring edges or decreasing the accuracy in the estimates. First, we develop a quadratic surrogate function from a log likelihood cost function according to the majorization principle, and then extend the fast iterative shrinkage thresholding algorithm (FISTA) for the TV-regularized (TVR) least-squares fitting of T1. To the best of our knowledge, this has not been done before. We also present an efficient quadratically regularized (QR) method for T1 estimation from the VFA MR images. The proposed methods were evaluated by using synthesized, phantom, and clinical MR data.
MATERIALS AND METHODS
Nonlinear least-squares T1 estimation
Based upon the Bloch equation,26 a steady-state MR signal intensity (sk) acquired by a T1-weighted spoiled gradient-echo sequence with a flip angle (FA) of αk (k = 1, 2, …, NFA; NFA is the number of FAs) and a repetition time TR is given by
| (1) |
where s0 is the equilibrium longitudinal magnetization, and E = exp (−TR/T1). The T1 and s0 values at a pixel are conventionally estimated from measured MR signals {yk} by a NLS fitting:
| (2) |
where l T1 and uT1 are defined by the T1 range of the tissue and utilized as a constraint to avoid unrealistic solutions and improve robustness of the computation.
It has been shown that the SNR () of the T1 values relates to the SNR (s0/σ) of the images by ,27 indicating the noise in the original images is amplified into the T1 map by the ratio of T1/TR. Therefore, the voxels with large T1 values are prone to potential errors. In addition, the image noise and the limited number of flip angles can cause a solution of the NLS fitting [Eq. 2] to be trapped into a local minimum before reaching the real solution during minimization.22 Although optimally selecting image acquisition parameters can improve the T1 estimation,13, 14 the errors seem to persist. Therefore, we propose to incorporate prior knowledge of tissue T1 spatial continuity to improve T1 estimation without compromising its accuracy.
Spatially regularized T1 estimation
TV-regularized T1 estimation
TV-regularized T1 estimation is to minimize the NLS cost function incorporated with TVR which is defined as
| (3) |
| (4) |
| (5) |
where (i, j) are pixel indices in a 2D space, L is a log likelihood function, and λ is a constant that controls the relative strength of the spatial regularization.
To minimize Ψ over the two unknown parameters (T1 and s0), we use a block alternating approach, in which T1 (T1-step) and s0 (s0-step) are iteratively determined by minimizing one parameter at a time while holding the other at the previously obtained value. To minimize Ψ in the s0-step, an analytic solution of s0 is given by
| (6) |
where However, minimizing Ψ for T1 in the T1-step is a nontrivial problem, because Ψ is nonlinearly related to T1 and the TV function [Eq. 5] is not continuously differentiable. We develop a fast iterative method to minimize Ψ with respect to T1. First, we convert the log likelihood L to a quadratic surrogate function using the majorization principle. Then, we minimize the TV-regularized surrogate function using an efficient algorithm based on a gradient-based dual approach.
Quadratic surrogate
We develop a quadratic surrogate function of the log likelihood L using the majorization principle.28 The derivation is provided in the Appendix. In brief, L(T1) is approximated by ‖T1 − z‖2 for T1 near the nth iteration solution T1,n, where z = T1, n − v/(2μ) is given in the Appendix. Then, using a matrix format, the TV-based cost function [Eq. 3] at the (n + 1)th iteration becomes
| (7) |
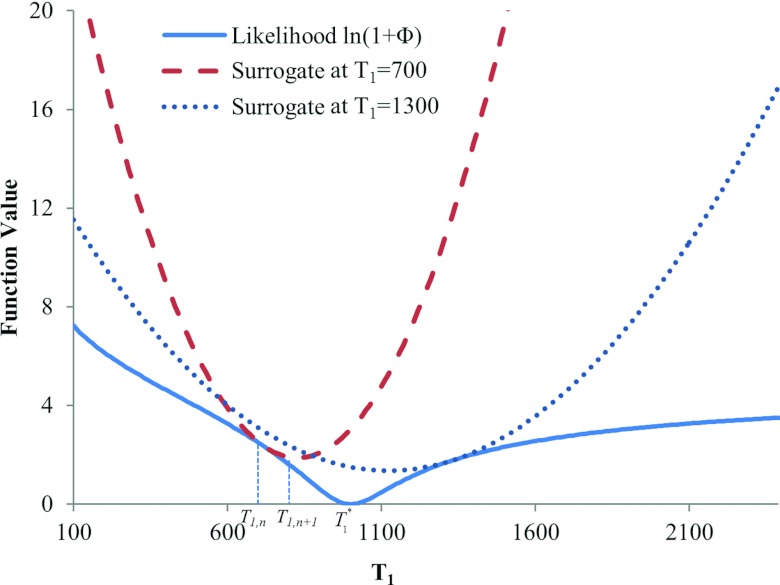
where μ is the spatially variant weighting defined in the Appendix [Eq. A3]. As demonstrated by Eq. A1 in the Appendix, the quadratic function is always greater than L except at T1,n, and so can be a surrogate of L.28 Figure 1 plots an original log likelihood function L(T1) with the true minimum at T1* = 1000 and quadratic surrogate functions at T1,n = 700 ms and T1,n = 1300 ms. At each iteration, the minimum of the surrogate function moves toward the minimum of L (T1*).
Figure 1.
Quadratic surrogates of the likelihood term of the cost function. The likelihood function has a minimum at T1 = 1000. The quadratic surrogates equate the likelihood function at T1 = 700 and 1300, but are above the likelihood curve at all other locations. The minima of the quadratic functions are converging toward the minimum of the likelihood function over iterations.
Optimization of the TV-regularized surrogate function
The surrogate function transforms the original cost function [Eq. 3] to Eq. 7 which is a typical TV-based denoising problem with a spatially variant weight μ and a spatially invariant weight λ. Minimization of Eq. 7 still is a challenging problem due to the noncontinuously differentiable TV term. Beck29 proposes to convert the TV-based minimization to a smooth dual problem and then solves the dual problem using FISTA. According to the approach, two new spatially distributed parameters (p, q) are introduced to convert the TV-based cost function equation 7 to a smooth dual function. The minimizer of the smooth dual function (p, q) is determined by iterating
| (8) |
where Pc and Γ are two projection operators,29 and t is the iteration index. The iteration started with (p, q) being 0. After convergence of iteration 8, the T1 solution at the (n + 1)th step is computed as
| (9) |
The final solutions of s0 and T1 are sought via these interleaved iterations of s0-step and T1-step.
Quadratic-regularized T1 estimation
We also develop a method to estimate T1 with the conventional quadratic regularization, namely, QR, which is to minimize
| (10) |
with , the pair index (m, n) = (1,0), (–1,0), (0,1), (0,–1) denotes the coordinate offsets of the four nearest neighbors, and β is a weighting parameter for the quadratic regularization. The minimization of Eq. 10 is also done by interleaved optimizations of s0 and T1. At the T1-step, again, the log likelihood L(T1, s0) is converted to the quadratic surrogate function. As both terms in Eq. 10 become quadratic, T1 at the (n + 1)th iteration is analytically solved as
| (11) |
where matrix μ and v are given in the Appendix. The final solutions of the QR method are obtained by iterating s0-step [Eq. 6] and T1-step [Eq. 11].
Implementation of T1 estimation algorithms
NLS T1 estimation
We implement the voxel-based NLS T1 estimation (Eq. 3 with λ = 0) by using the quadratic surrogate function, and refer it as QS-NLS method. The computation is initialized with T1 = 800 ms at each voxel and cycles through s0-step [Eq. 6] and T1-step. In T1-step, the solution at the (n + 1)th iteration is analytically determined as
| (12) |
The iteration is terminated when the T1 tolerance meets |T1, n + 1 − T1, n|/|T1, n| ⩽ 10−6 or the number of iterations n ⩾ 500.
TV-regularized T1 estimation
The TVR minimization begins with the T1 estimated by the QS-NLS method. Then s0 and T1 are sought iteratively through s0-step [Eq. 6] and T1-step [Eq. 9]. This iterative process is terminated when the relative change in T1 < 10−6 or the number of iterations n ⩾ 250. In each T1-step, the T1 [Eq. 9] is determined by (p, q) that result from iteration of Eq. 8. The iteration to obtain (p, q) terminates when the (p, q) tolerance is <10−6 or the iteration numbern ⩾ 100. Selection of λ will be described below.
Quadratic regularized T1 estimation
The QR optimization is also initialized with the T1 obtained by the QS-NLS method, and the iterative process is terminated when T1 tolerance is less than 10−6 or the number of iterations n ⩾ 250.
Selection of weighting parameters
The “hyperparameter” λ and β weigh the spatial regularization terms in the TVR and QR cost functions, respectively. Large values of the parameters can cause overweighing of the spatial regularizations, and lead to oversmoothing in the resulting T1 map; conversely, small values can result in insufficient noise reduction. To determine an appropriate weighting value of λ (or β), we estimated T1 maps of a central slice in the simulated brain MR data with various noise levels using the TVR (or QR) method and varying λ (or β) values on a regular grid. We selected the λ (or β) value that minimized the averaged difference between the true and estimated T1 in the central slice. We found that λ = 1 and β = 0.001 were appropriate for the images with noise levels less than 7%, and λ = 10 and β = 0.01 for the data with higher level noise. We applied these values to both the simulated and experimental image data for evaluation of the methods.
T1 bound constraints
For all three methods of QS-NLS, QR, and TVR, T1 bound conditions were set to be l T1 = 50 ms and uT1 = 3000 ms in the simulated and phantom experiments, and uT1 = 6000 ms for the patient data.
Simulation studies
In order to evaluate the performance of the proposed methods, we utilized the Brainweb MRI simulator to simulate VFA MRI data.30 This simulator accounts for the effects of various image acquisition parameters, including partial volume averaging, noise, and sampling in Fourier domain, and intensity inhomogeneity in the brain tissue.31 We simulated T1-weighted MRI of a normal brain phantom using a spoiled gradient-echo pulse sequence (TR / TE of 18/10 ms, matrix size of 217 × 181 × 60, resolution of 1 × 1 × 3 mm3, and flip angles of 5°, 10°, 20°, 30°, and 40°). Gaussian noise was added onto both real and imaginary components of MR signals in the Fourier domain to obtain noise levels of 1%, 3%, 5%, 7%, and 9% in the images. The QS-NLS, QR, and TVR methods were applied to the simulated data to estimate T1. Because of the high in-plane resolution, spatial regularizations in both QR and TVR methods were applied in 2D images.
In order to quantitatively evaluate the methods, relative mean and relative standard deviation (rSD) are computed as the percentages of the mean and SD of the estimated T1 to the true T1 value, respectively. For the rSD calculation, the original T1 variations in WM or GM were removed. The relative mean and SD measure the accuracy and stability of the methods, respectively. For statistical analysis in GM and WM, we excluded the voxels within a 2-pixel wide band from the boundary to remove the effect of blurring edges.
We also examined whether the spatially regularized methods can estimate a T1 map with spatial variations. We created a digital phantom that consists of the regions with (a) linear and quadratic T1 spatial variations, (b) uniform but high T1 value (1200 ms), and (c) uniform but low T1 values (200 ms). MR images of the digital phantom were simulated using the Bloch equation [Eq. 1] with five FAs (10°, 20°, 30°, 50°, and 70°) and TR 13 ms. Random Gaussian noise was added to make the MR data have a noise level of 5%.
Experimental MRI studies
We applied the methods to experimental MR data of a EuroSpin TO5 phantom from the RIDER project,3 which was designed to evaluate the accuracy and repeatability of MR T1 measurement. The phantom consisting of 18-compartments with different T1 contrasts was imaged on a 1.5 T GE scanner.3 The acquisition protocol included a 2D IR spin-echo sequence and a 3D multiple flip angles fast-spoiled gradient-echo sequence (FSPGR). The FSPGR images were acquired with seven flip angles (2°, 5°, 10°, 15°, 20°, 25°, and 30°), TR/TE = 6.4/1.2 ms, and a resolution of 0.55 × 0.55 × 5 mm3. Our methods were applied to the MRI data of five of the seven flip angles (5°, 10°, 15°, 20°, and 25°) to estimate T1. The correlation of the compartmental means of the T1 estimated from the IR and the VFA data was computed to evaluate the accuracy of the T1 quantification by the proposed methods.
The methods were also tested on the brain MRI of a patient who was enrolled in a prospective DCE-MRI study of brain radiation therapy. Multiflip angle MR data were acquired on a clinical 3 T MR scanner (Ingenia, Philips Medical Systems, Best, Netherlands) with a fast spoiled gradient-echo sequence. The image parameters were TR/TE of 30 ms/2.8 ms, matrix size of 256 × 256 × 80, resolution of 1 × 1 × 2 mm3, and flip angles of 5°, 15°, 20°, and 45°. To evaluate the proposed methods, the patient was also imaged using a SR sequence with the TR of 100, 200, 500, 1000, and 2000 ms. The SR images have the same resolution and matrix as the VFA MRI. T1 values were estimated voxel-by-voxel from the SR MRI by nonlinear least-square fitting.
RESULTS
Simulated brain
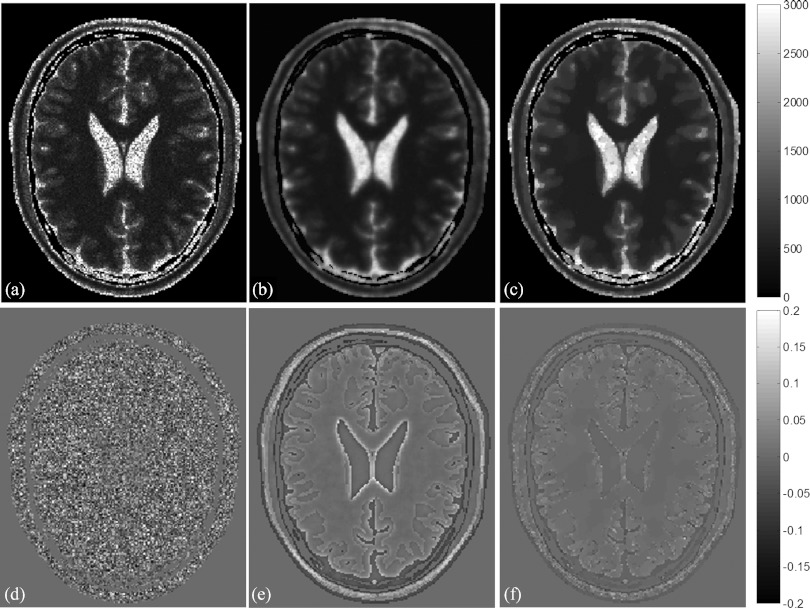
Figure 2 shows estimated T1 maps of a slice in the simulated brain with 5% of noise using the QS-NLS, QR, and TVR methods, as well as relative differences between the estimated T1 and the ground truth. There are substantial amounts of noise in the regions of GM, WM, and cerebrospinal fluid (CSF) of the T1 map and the difference map calculated by the QS-NLS method [Figs. 2a, 2d], indicating the QS-NLS method propagates or even amplifies noise from the original images onto the T1 map. In contrast, the QR and TVR methods reduce the noise in each of tissue compartments substantially [Figs. 2b, 2c, 2e, 2f]. However, the relative differences between the T1 estimated by the QR method and the true values are greater at edges of tissue compartments and in the small regions [see edge enhancement in Fig. 2e], indicating the effect of overblurring of the QR method. The TVR method preserves boundaries well while producing marked reduction of the intraregion noise in the T1 map [Figs. 2c, 2f].
Figure 2.
T1 maps (top) estimated from the simulated brain dataset with five FAs and 5% noise by the QS-NLS (a), QR (b), and TVR (c). The relative differences between the estimated T1 and the ground truth are displayed in bottom row (d)–(f). The T1 values range from 0 to 3000 ms in (a)–(c). The relative differences vary from –0.2 to 0.2 in (d)–(f).
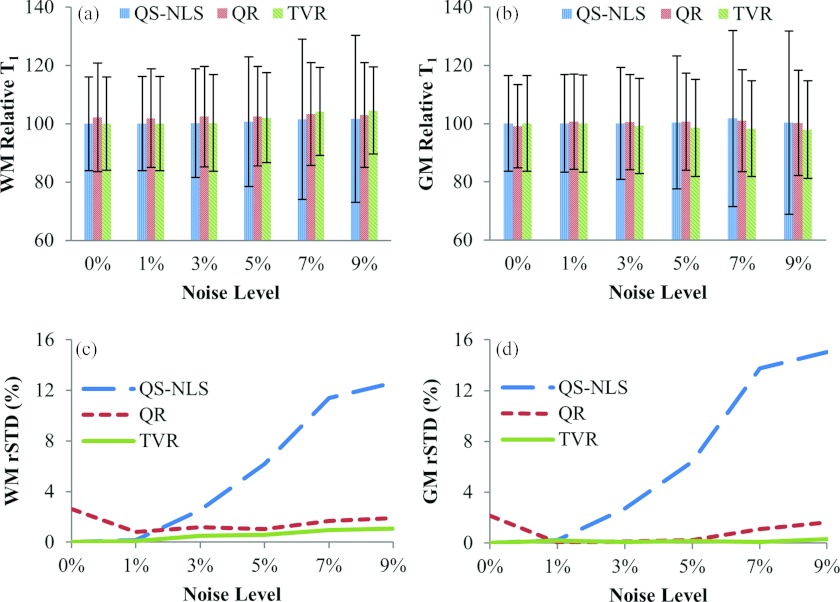
Quantitative evaluations of the performance of the methods with respect to noise on the simulated data are shown in Fig. 3. The means of the T1 estimated by all the three methods show less than 3% errors from the true T1 values in both GM and WM with image noise up to 9% [Figs. 3a, 3b]. The relative SDs of the T1 estimated by the QS-NLS method increase nonlinearly with noise in the images, reaching approximately 12% and 15% when there are 7% and 9% noise [Figs. 3c, 3d], respectively. In comparison, the TVR method is able to suppress the relative standard deviations of the T1 values to less than 2% in both WM and GM regardless of the noise level in the image. The QR method also reduces the noise-related variations in the T1 values to be less than 3%, which is slightly greater than the one obtained by the TVR method and possibly due to the edge-blurring effect of the quadratic regularization [Figs. 3c, 3d].
Figure 3.
The relative means and standard deviations of the T1 values in WM (a) and GM (b) estimated by the QS-NLS, QR, and TVR methods vs noise levels in the original images. (c) and (d) are the relative standard deviations for WM and GM with the inner-structure T1 variation (rSD at noise level 0%) removed. The three methods have a similar accuracy, but the QR and TVR methods substantially decrease the standard deviations of the estimated T1 values for noise >3%.
Simulated digital phantom with spatial variations
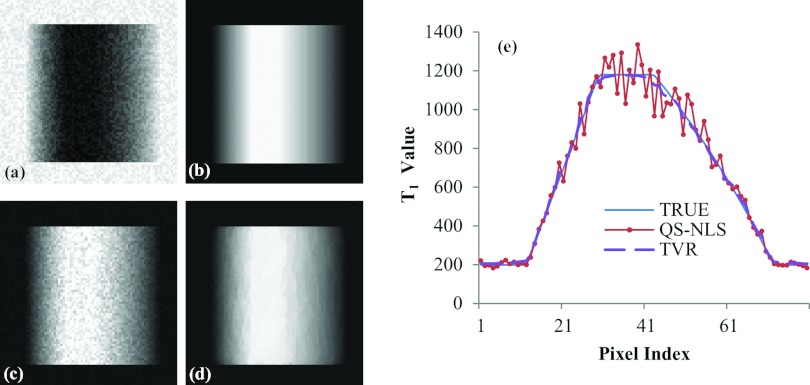
Evaluation of the performance of the spatially regularized methods on the simulated phantom with linear and quadratic spatial variations in T1 is shown in Fig. 4. As expected, the T1 map estimated by the QS-NLS method is very noisy, and the central region, where the T1 value is homogeneous and high, cannot be recognized [Figs. 4c, 4e]. The noise in the T1 map estimated by the TVR method is reduced substantially, and the T1 estimates clearly differentiate the homogeneous region from the surrounding [Fig. 4d]. Figure 4e plots profiles of the T1 values along a horizontal line of the phantom estimated by the QS-NLS and TVR methods. Compared to the true T1 values along the line, the TVR method reduces the variance in the T1 values to be 3% from 7% by the QS-NLS method.
Figure 4.
T1 maps of a simulated digital phantom with spatial variations of T1: homogeneous low T1 values at the left and right peripheries, homogeneous high T1 values at the central region, and linearly and quadratically changed T1 values from the low to high T1 values in left and right, respectively. (a) The simulated T1-weighted MRI with 5% of noise and a flip angle of 20°; (b) the T1 map without noise; (c) the T1 map estimated by the QS-NLS methods; (d) the T1 map obtained by the TVR method; and (e) central-line profiles of the T1 maps obtained by the QS-NLS and TVR methods compared to the true values.
Phantom experiments
Figure 5 shows T1 maps of the 18-compartment RIDER phantom estimated by the QS-NLS, QR, and TVR methods from the VFA MR data. Using the T1 values in each of the compartments estimated from the IR acquisition as a reference, the pixelwise relative differences between the T1 values estimated by the three VFA-based methods and the reference are shown in Figs. 5d, 5e, 5f. Again, the TVR method produces the T1 map with better noise reduction and better edge preservation compared to the QS-NLS and QR methods. It is interesting to see that the QR method causes underestimation of T1 values [enhancement in Fig. 5e] around the tube edges due to overblurring of the quadratic regularization.
Figure 5.
The T1 maps (top) of a phantom estimated from the VFA MR data using the QS-NLS (a), QR (b), and TVR methods (c), and the relative differences (bottom) of the estimated T1 between the three VFA-based methods and the IR method (d)–(f). Gray bars denote the ranges of the T1 values (top) and the relative differences (bottom).
T1 measurements of the RIDER phantom are shown in Fig. 6. There are strong linear correlations (R2 > 0.99) between the compartmental averaged T1 values estimated from the VFA MR data using the QS-NLS, QR, and TVR methods and the T1 measured from the IR MRI (a reference measure). The SDs obtained by the QS-NLS method increase with the T1 values but not by the TVR method. Overall, the TVR method reduces the SDs of the T1 values by a factor of 2–4 in most of the compartments compared to the QS-NLS method. The SDs obtained by the QR method are similar to the ones obtained by the QS-NLS method due to the edge-blurring effect of the QR method.
Figure 6.
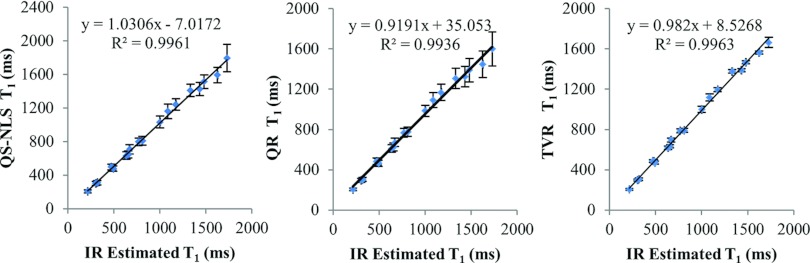
Plots of the compartmental means of the estimated T1 from the phantom MRI using the QS-NLS (left), QR(middle), and TVR methods (right) vs T1 values from the IR MRI data. The error bars are the standard deviations of the T1 values estimated from the VFA MR data in each compartment.
Human brain study
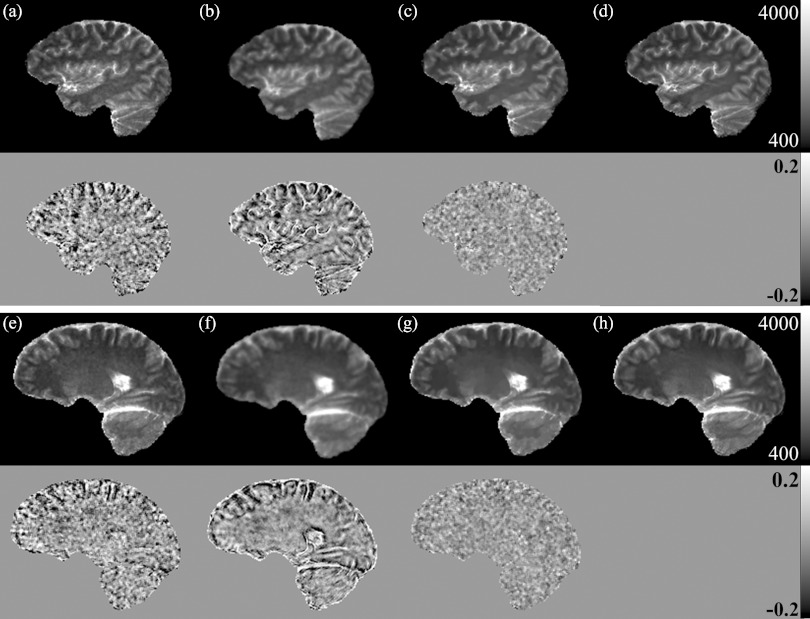
Figure 7 shows T1 maps of the human brain of a patient by using the QS-NLS, QR, and TVR methods. Compared with the T1 estimated by the SR method [Figs. 7d, 7h], the T1 maps estimated by the QS-NLS method [Figs. 7a, 7e] are presented with noise, which could compromise physiological parameters derived from DCE-MRI if used in DCE quantification. The T1 maps obtained by the QR method [Figs. 7b, 7f] show noise reduction but also edge blurring, as evidenced by enhanced edges on the relative difference maps between by the QR and SR methods. However, the TVR method [Figs. 7c, 7g] not only reduces noise but also preserves structure boundaries in the T1 maps, as shown in the relative difference maps between the TVR and SR methods.
Figure 7.
T1 maps of two brain slices (first and third rows) from a patient data by the QS-NLS (a) and (e); QR (b) and (f); TVR (c) and (g); and SR (d) and (h) methods. The relative differences of the three VFA-based T1 estimates to the SR results are shown, respectively, in the second and forth rows for the two slices.
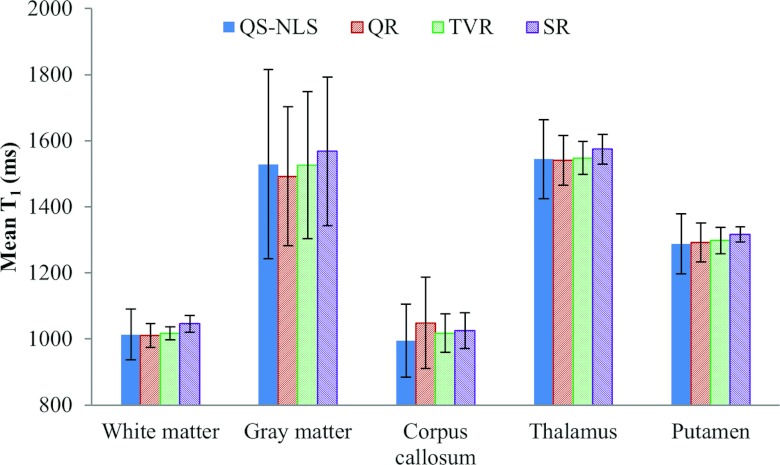
The ROIs related to five different tissue structures were manually delineated on the brain images. Compared with the T1 values obtained by the SR method, the mean T1 in the ROIs estimated by QS-NLS, QR, and TVR methods has errors less than 5% (Fig. 8). But the QS-NLS results have greater T1 variations in the ROIs compared with the spatially regularized methods. Due to edge blurring, the QR method increases the standard deviation of T1 estimates in gray matter, which is also shown in the difference maps in Fig. 7.
Figure 8.
Mean T1 in the five brain ROIs on the patient images by the QS-NLS, QR, TVR, and SR methods.
DISCUSSION
In this paper, we propose spatially regularized methods to improve T1 estimation based upon prior knowledge of T1 local continuity. We develop a theoretical framework for fast iterative optimization of the spatially regularized T1 quantification, including majorizing the log likelihood function to a quadratic surrogate function, converting the TV-based optimization to a smooth dual problem, and providing an iterative solution for T1 calculation. The TVR method substantially reduces the noise in the T1 map without image blurring or decreasing the accuracy of the estimated T1 values. Given that the quadratic surrogate only uses the T1 gradient of the MR signals, our methods can be generalized to estimate T1 values from MR data acquired with variable flip angles, variable TRs, or a combination of the two. Incorporating the T1 produced by our methods into quantification of DCE-MRI will improve the robustness of the pharmacokinetic analysis, reduce potential errors in local perfusion estimates, and possibly improve the spatial discrimination of local changes in perfusion parameters.
The basic assumption of spatial regularization is the T1 local continuity in the tissue. To reduce the noise influence on the T1 estimation, we enforce local continuity of the T1 values while permitting rapid changes of T1 at tissue boundaries. Our results show that the quadratic regularization, although reducing noise in the T1 map compared to the QS-NLS method, overblurs the boundaries at the tissue compartments. In contrast, the TVR method is able to overcome the overblurring problem present in the quadratic regularization method as well as reduce the noise in the T1 map. A gradual T1 change in a region can also be preserved by the TVR method. These two spatial regularization methods can be selected in the clinical application based upon the organ or anatomy of interest. The organs with fine tissue compartments, e.g., brain and kidney, could benefit from the TVR method. One of the potential benefits of the spatially regularized methods for the T1 estimation is voxel-by-voxel quantification of DCE-MRI using pharmacokinetic models, e.g., Toft model.32 The noise in the T1 map can propagate into the DCE quantification and reduce reproducibility of derived kinetic parameters,33 which could subsequently reduce the ability of these quantitative imaging parameters as a biomarker for assessment of tumor and normal tissue response to therapy. The spatially regularized methods have the potential to overcome this challenge.
The total variation, as an edge-preserving regularization, has been long considered for image restoration. However, the total variation has not been widely used in the medical image field due to the complexity of the method, which involves optimizing a noncontinuously differentiable TV function. The optimization becomes even more computation demanding when the likelihood function is a complicate nonlinear function, i.e., the T1 problem. A quadratic surrogate can be used to replace the nonlinear least-squares likelihood function, and therefore to simplify the optimization process. However, direct majorization of the original nonlinear least-squares cost function [Eq. 2] to a quadratic surrogate results in a slow converging process in the T1 minimization due to the large Lipschitz constant.34 Instead, we majorize a logarithm likelihood function to a quadratic surrogate that converges much more rapidly. Furthermore, we apply the gradient-based dual approach that has been theoretically proven to have a converging rate in the order magnitude of 1/t2 (t is the iteration number).29 Our experiments show that the T1 solution can converge within 100 iterations with a tolerance of 10−6.
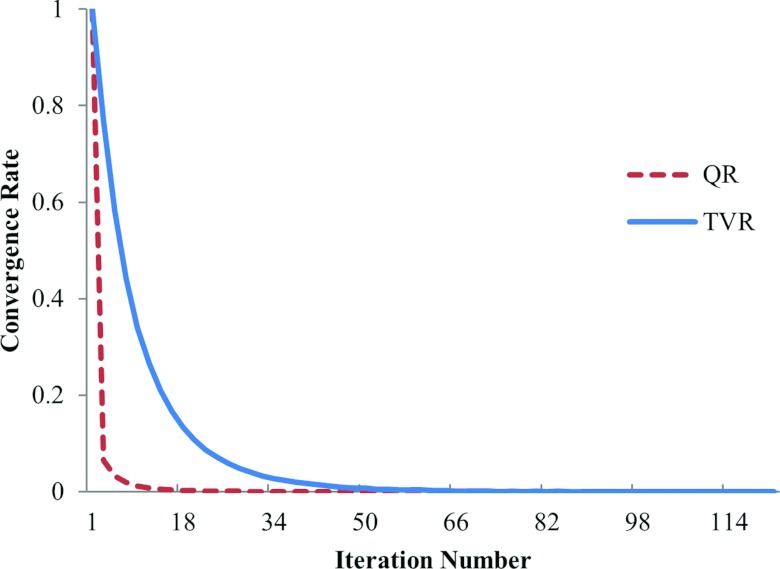
The computation of the QS-NLS method is much faster than the conventional NLS T1 estimation,18 due to that the QS-NLS method updates T1 of all pixels in an image slice simultaneously in each of the iterations, while the conventional NLS method minimizes the cost function voxel-by-voxel. For the computation of the simulated data on a Xeon 2.668 GHz machine and using MATLAB 2010b, it takes ∼6 s to compute T1 of a 256 × 256 slice by the QS-NLS method, but 8 min by the conventional NLS method (using “fminsearch” in MATLAB). Also, the differences between the T1 computed by the conventional NLS and the QS-NLS method are less than 1%, indicating there is no compromise in the accuracy of the estimated T1 using the QS-NLS method. With the spatial regularizations, both the QR and TVR minimizations are converged within 100 iterations (Fig. 9). Initialized with the T1 estimated by the QS-NLS method, the QR and TVR methods take additional 1.2 s and 15 s to compute the final T1 values of a 256 × 256 slice, respectively.
Figure 9.
Convergence of the QR and TVR methods from the simulated brain data with five FAs and 5% noise. The cost functions are normalized to the maximal value at the initial iteration. The two methods reach a tolerance of 1 × 10–6 within 100 iterations.
The TVR method preserves edges at tissue boundaries in a T1 map. However, the minimum size of an object or a lesion, which can be detected by the TVR method, has not been tested and compared to the conventional methods. Like other VFA-based methods, B1 inhomogeneity can bias the T1 estimated by the proposed methods because B1 inhomogeneity causes variation of flip angles. Approaches have been proposed to map B1 inhomogeneity.16, 35 Therefore, correcting the flip angles can be performed prior to using the proposed methods.
CONCLUSION
T1 estimation based upon variable flip angles gradient-echo MRI has been improved by applying the prior knowledge of spatial continuity. Spatial regularization, either QR or TVR, can reduce random fluctuation in the T1 estimates compared to the conventional NLS method, and thereby improve the repeatability of the pixelwise estimates. The TV regularization can preserve the sharp transitions between the tissue compartments better than the QR method.
ACKNOWLEDGMENTS
The authors would like to thank Dr. Edward Jackson for providing the RIDER phantom data. This work is supported in part by NIH P01 CA59827, RO1 CA132834, RO1 NS064973, and R21 CA126137.
APPENDIX: QUANDRATIC SURROGATE
The log likelihood L near the nth iteration solution of T1,n at pixel (i, j) can be approximated by
| (A1) |
The right-hand side of the inequality is greater than or equal to the original , and therefore, can be a surrogate for L.28 By defining , ak = tan αk, and bk = tan αk(cos αk − 1), we have fk(T1) = ak + bkdk(T1). Substituting fk(T1) into the right side of Eq. A1 and applying the first order Taylor expansion to dk(T1), Eq. 3 in matrix format at the (n + 1)th iteration of T1-step becomes
| (A2) |
where z = T1, n − v/(2μ), μ = {μi, j}, and ν = {νi, j} are matrix formats of μi, j and νi, j over the images computed as
| (A3) |
where is a gradient of dk with respect to T1 at T1, n. The quadratic surrogate function is always above L except at the point T1,n, and thus iteratively converges to the minimum of L. Now, minimization of Eq. 3 becomes a conventional TV-based denoise problem.36
References
- Armitage P. A., Farrall A. J., Carpenter T. K., Doubal F. N., and Wardlaw J. M., “Use of dynamic contrast-enhanced MRI to measure subtle blood-brain barrier abnormalities,” Magn. Reson. Imaging 29, 305–314 (2011). 10.1016/j.mri.2010.09.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strecker R., Scheffler K., Buchert M., Mross K., Drevs J., and Hennig J., “DCE-MRI in clinical trials: Data acquisition techniques and analysis methods,” Int. J. Clin. Pharmacol. Ther. 41, 603–605 (2003). [DOI] [PubMed] [Google Scholar]
- Jackson E. F., Barboriak D. P., Bidaut L. M., and Meyer C. R., “Magnetic resonance assessment of response to therapy: Tumor change measurement, truth data and error sources,” Transl. Oncol. 2, 211–215 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padhani A. R., “Dynamic contrast-enhanced MRI in clinical oncology: Current status and future directions,” J. Magn. Reson. Imaging 16, 407–422 (2002). 10.1002/jmri.10176 [DOI] [PubMed] [Google Scholar]
- Tofts P. S., “Modeling tracer kinetics in dynamic Gd-DTPA MR imaging,” J. Magn. Reson. Imaging 7, 91–101 (1997). 10.1002/jmri.1880070113 [DOI] [PubMed] [Google Scholar]
- Vymazal J., Righini A., Brooks R. A., Canesi M., Mariani C., Leonardi M., and Pezzoli G., “T1 and T2 in the brain of healthy subjects, patients with Parkinson disease, and patients with multiple system atrophy: Relation to iron content,” Radiology 211, 489–495 (1999). [DOI] [PubMed] [Google Scholar]
- Gai N. D. and Butman J. A., “Modulated repetition time look-locker (MORTLL): A method for rapid high resolution three-dimensional T1 mapping,” J. Magn. Reson. Imaging 30, 640–648 (2009). 10.1002/jmri.21842 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S. G., Hu X., and Ugurbil K., “Accurate T1 determination from inversion recovery images: Application to human brain at 4 Tesla,” Magn. Reson. Med. 31, 445–449 (1994). 10.1002/mrm.1910310414 [DOI] [PubMed] [Google Scholar]
- Kingsley P. B., “Methods of measuring spin-lattice (T1) relaxation times: An annotated bibliography,” Concepts Magn. Reson. 11, 243–276 (1999). 10.1002/(SICI)1099-0534(1999)11:4%3C243::AID-CMR5%3E3.0.CO;2-C [DOI] [Google Scholar]
- Young I. R., Hall A. S., and Bydder G. M., “The design of a multiple inversion recovery sequence for T1 measurement,” Magn. Reson. Med. 5, 99–108 (1987). 10.1002/mrm.1910050202 [DOI] [PubMed] [Google Scholar]
- Christensen K. A., Grant D. M., Schulman E. M., and Walling C., “Optimal determination of relaxation times of fourier transform nuclear magnetic resonance. Determination of spin-lattice relaxation times in chemically polarized species,” J. Phys. Chem. 78, 1971–1977 (1974). 10.1021/j100612a022 [DOI] [Google Scholar]
- Pelc N. J., “Optimization of flip angle for T1 dependent contrast in MRI,” Magn. Reson. Med. 29, 695–699 (1993). 10.1002/mrm.1910290519 [DOI] [PubMed] [Google Scholar]
- Haselhoff E. H., “Optimization of flip angle for T1 dependent contrast: A closed form solution,” Magn. Reson. Med. 38, 518–519 (1997). 10.1002/mrm.1910380321 [DOI] [PubMed] [Google Scholar]
- Wang H. Z., Riederer S. J., and Lee J. N., “Optimizing the precision in T1 relaxation estimation using limited flip angles,” Magn. Reson. Med. 5, 399–416 (1987). 10.1002/mrm.1910050502 [DOI] [PubMed] [Google Scholar]
- Fram E. K., Herfkens R. J., Johnson G. A., Glover G. H., Karis J. P., Shimakawa A., Perkins T. G., and Pelc N. J., “Rapid calculation of T1 using variable flip angle gradient refocused imaging,” Magn. Reson. Imaging 5, 201–208 (1987). 10.1016/0730-725X(87)90021-X [DOI] [PubMed] [Google Scholar]
- Cheng H.-L. M. and Wright G. A., “Rapid high-resolution T1 mapping by variable flip angles: Accurate and precise measurements in the presence of radiofrequency field inhomogeneity,” Magn. Reson. Med. 55, 566–574 (2006). 10.1002/mrm.20791 [DOI] [PubMed] [Google Scholar]
- Velikina J., Alexander A. L., and Samsonov A. A., “A novel approach for T1 relaxometry using constrained reconstruction in parametric dimension,” in Proc. of ISMRM 2010, 350 (2010).
- Chang L. C., Koay C. G., Basser P. J., and Pierpaoli C., “Linear least-squares method for unbiased estimation of T1 from SPGR signals,” Magn. Reson. Med. 60, 496–501 (2008). 10.1002/mrm.21669 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deoni S. C., Rutt B. K., and Peters T. M., “Rapid combined T1 and T2 mapping using gradient recalled acquisition in the steady state,” Magn. Reson. Med. 49, 515–526 (2003). 10.1002/mrm.10407 [DOI] [PubMed] [Google Scholar]
- Chang J. H., Anderson J. M., and Votaw J. R., “Regularized image reconstruction algorithms for positron emission tomography,” IEEE Trans. Med. Imaging 23, 1165–1175 (2004). 10.1109/TMI.2004.831224 [DOI] [PubMed] [Google Scholar]
- Funai A. K., Fessler J. A., Yeo D. T., Olafsson V. T., and Noll D. C., “Regularized field map estimation in MRI,” IEEE Trans. Med. Imaging 27, 1484–1494 (2008). 10.1109/TMI.2008.923956 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelm B. M., Menze B. H., Nix O., Zechmann C. M., and Hamprecht F. A., “Estimating kinetic parameter maps from dynamic contrast-enhanced MRI using spatial prior knowledge,” IEEE Trans. Med. Imaging 28, 1534–1547 (2009). 10.1109/TMI.2009.2019957 [DOI] [PubMed] [Google Scholar]
- Stayman J. W. and Fessler J. A., “Regularization for uniform spatial resolution properties in penalized-likelihood image reconstruction,” IEEE Trans. Med. Imaging 19, 601–615 (2000). 10.1109/42.870666 [DOI] [PubMed] [Google Scholar]
- de Pasquale F., Sebastiani G., Egger E., Guidoni L., Luciani A. M., Marzola P., Manfredi R., Pacilio M., Piermattei A., Viti V., and Barone P., “Bayesian estimation of relaxation times T(1) in MR images of irradiated Fricke-agarose gels,” Magn. Reson. Imaging 18, 721–731 (2000). 10.1016/S0730-725X(00)00149-1 [DOI] [PubMed] [Google Scholar]
- Borsic A., Graham B. M., Adler A., and Lionheart W. R., “In vivo impedance imaging with total variation regularization,” IEEE Trans. Med. Imaging 29, 44–54 (2010). 10.1109/TMI.2009.2022540 [DOI] [PubMed] [Google Scholar]
- Zur Y., Stokar S., and Bendel P., “An analysis of fast imaging sequences with steady-state transverse magnetization refocusing,” Magn. Reson. Med. 6, 175–193 (1988). 10.1002/mrm.1910060206 [DOI] [PubMed] [Google Scholar]
- Deoni S. C., Peters T. M., and Rutt B. K., “Determination of optimal angles for variable nutation proton magnetic spin-lattice, T1, and spin-spin, T2, relaxation times measurement,” Magn. Reson. Med. 51, 194–199 (2004). 10.1002/mrm.10661 [DOI] [PubMed] [Google Scholar]
- Böhning D. and Lindsay B. G., “Monotonicity of quadratic-approximation algorithms,” Ann. Inst. Stat. Math. 40, 641–663 (1988). 10.1007/BF00049423 [DOI] [Google Scholar]
- Beck A. and Teboulle M., “A fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM J. Imaging Sci. 2, 183–202 (2009). 10.1137/080716542 [DOI] [Google Scholar]
- Höhne K., Kikinis R., Kwan R., Evans A., and Pike G., “An extensible MRI simulator for post-processing evaluation,” in Visualization in Biomedical Computing (Springer, Berlin, 1996), Vol. 1131, pp. 135–140. [Google Scholar]
- Kwan R. K., Evans A. C., and Pike G. B., “MRI simulation-based evaluation of image-processing and classification methods,” IEEE Trans. Med. Imaging 18, 1085–1097 (1999). 10.1109/42.816072 [DOI] [PubMed] [Google Scholar]
- Tofts P. S., Brix G., Buckley D. L., Evelhoch J. L., Henderson E., Knopp M. V., Larsson H. B., Lee T. Y., Mayr N. A., Parker G. J., Port R. E., Taylor J., and Weisskoff R. M., “Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: Standardized quantities and symbols,” J. Magn. Reson. Imaging 10, 223–232 (1999). 10.1002/(SICI)1522-2586(199909)10:3%3C223::AID-JMRI2%3E3.0.CO;2-S [DOI] [PubMed] [Google Scholar]
- Cao Y., Li D., Shen Z., and Normolle D., “Sensitivity of quantitative metrics derived from DCE MRI and a pharmacokinetic model to image quality and acquisition parameters,” Acad. Radiol. 17, 468–478 (2010). 10.1016/j.acra.2009.10.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck A. and Teboulle M., “Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems,” IEEE Trans. Image Process. 18, 2419–2434 (2009). 10.1109/TIP.2009.2028250 [DOI] [PubMed] [Google Scholar]
- Siversson C., Chan J., Tiderius C. J., Mamisch T. C., Jellus V., Svensson J., and Kim Y. J., “Effects of B(1) inhomogeneity correction for three-dimensional variable flip angle T(1) measurements in hip dGEMRIC at 3 T and 1.5 T,” Magn. Reson. Med. 67, 1776–1781 (2012). 10.1002/mrm.23150 [DOI] [PubMed] [Google Scholar]
- Combettes P. L. and Pesquet J. C., “Image restoration subject to a total variation constraint,” IEEE Trans. Image Process. 13, 1213–1222 (2004). 10.1109/TIP.2004.832922 [DOI] [PubMed] [Google Scholar]