Abstract
The Generalized Born (GB) solvent model is widely used in molecular dynamics simulations because it can be less computationally expensive and it samples conformational changes more efficiently than explicit solvent simulations. Meanwhile, great efforts have been made in the past to improve its precision and accuracy. Previous studies have shown that reducing intrinsic GB radii of some hydrogen atoms would improve AMBER GB-HCT solvent model's accuracy on salt bridges. Here we present our finding that similar correction also shows dramatic improvement for the AMBER GB-OBC solvent model. Potential of mean force and cluster analysis for small peptide replica exchange molecular dynamics simulations suggested that new radii GB simulation with ff99SB/GB-OBC corrected salt bridge strength and achieved significantly higher geometry similarity with TIP3P simulation. Improved performance in 60 ns HIV-1 protease GB simulation further validated this approach for large systems.
Keywords: intrinsic radii, salt bridge, PMF, cluster analysis, HIV-1 protease, HIVPR
Introduction
Since it was first introduced in 1980's, the Generalized Born (GB) solvent model [1-3] has provided an alternative way to represent the solvent's electrostatic effects in atomic simulations such as Molecular Dynamics (MD) [4, 5]. Instead of giving an atomistic description of every water molecule, as in explicit solvent (EXP) simulations [6], the GB model uses a Born equation to approximate the solvent's electrostatic effects during MD simulation. This implicit treatment of solvent during simulation is attractive because 1), most of the time we focus on the solute's dynamics only, 2), exclusion of water molecules largely reduces the system size and generally can make simulations less computationally demanding and 3), the lack of viscosity during simulations results in much faster conformational sampling. There are excellent review articles published discussing this method [7-10].
In MD simulations, an energy function is used to calculate the energy of each sampled conformation. The energy calculated acts as the driving force of MD and is crucial for meaningful results. The parameter set used in such calculations is termed force field. In GB simulations, as a tradeoff of faster sampling, any force field defect would show up much sooner and be amplified. Also, because of the solvent approximation, any weaknesses in the GB parameter set would also render the simulation erroneous.
Over the past two decades, development of simulation methods has provided several generations of force fields and GB solvent models [10-12]. Many studies have focused on assessing and comparing accuracy of different force fields or solvent models [13-16]. Unfortunately, a “gold standard”, or a consensus force field/solvent model combination that provides a correct balance of protein secondary structures is still elusive, and simulation results are likely to continue depending on chosen force fields and solvent models in the near future. Under the circumstances specific optimization for each combination may be necessary, at times with cancellation of errors in the solvent model with those in the solute model. Here we will present our work on improving simulations with ff99SB [17] and GB-OBC [18] in AMBER [19]. The former is a modified version of ff99 force field [20] which improved backbone dihedral term in ff99 through reparameterization of ff94 force field [21], and the latter is an AMBER generalized born solvent model shown [22] to outperform GB-HCT [23] and GB-NECK [24].
Although regarded as one of the best performing force fields and applied to many MD simulations [25, 26], ff99SB was recently shown to marginally destabilize helical structures in some systems [27]. In contrast, the GB model widely used with ff99SB, GB-OBC, was shown to slightly over stabilize helical structures and, more importantly, to produce significantly erroneous salt bridge strength and geometry [28-30]. Coupled optimization on both force field and solvent model for CHARMM [31] parameters has been explored by Chen et al. previously [32]. However, our intent was not to change backbone parameters; instead, we aimed to improve the ability of GB to reproduce salt bridge strength and geometry from explicit solvent calculations performed with the same backbone conformations.
In order to improve salt bridge strength and geometry, an intrinsic radii correction is of great interest due to the simplicity of implementation. In GB model, a molecule is described by a set of atomic spheres with associated intrinsic Born radii. Since intrinsic radii define the dielectric boundary between solute and solvent, they are the foundation of GB calculation and they influence solute-solvent interactions such as H-bonds and salt bridges. However, definitions of GB intrinsic radii are empirical because the atomic spheres only approximate the molecular surface used in more accurate solvent models. Hydrogen atoms are harder to describe in GB due to the sensitivity of their electron density to the varying electronegativity of neighboring atoms [33]. Therefore, optimizing intrinsic radii parameters for theoretical study was pursued by various groups and indeed it was shown to improve GB simulations with CHARMM force fields [34], OPLS force fields [35], and more importantly to us, AMBER force fields. Geney et al. have shown previously [33] that reducing intrinsic radii of hydrogen atoms linked to charged nitrogen would improve AMBER GB simulations using ff99SB/GB-HCT and modified Bondi radii set [36]. Due to the close relationship between force field/solvent model chosen here and in Geney's study, we evaluated similar modification in our GB simulations with ff99SB/GB-OBC, although the radii sets we used are not identical.
We first applied radii modification to a small model peptide (Ace-Arg-Ala-Ala-Glu-NH2). Okur et al. have shown previously [29] that, in GB replica exchange molecular dynamics (REMD [37]) simulation (with ff99SB/GB-OBC) this peptide has too strong salt bridge strength compared to explicit solvent (EXP) REMD simulation. In addition, the most populated salt bridge geometry found in GB REMD differs from EXP REMD. In order to elucidate whether radii choice plays a role here, we carried out several GB REMD simulations using the same input as Okur's except that various Hn radii were applied (Hn: Hε and 4 Hη on Arg side chain), and then compared to their EXP REMD simulation. Our results showed that reducing Hn radii could improve both the strength and the geometry of Arg-Glu salt bridge in GB simulations.
Besides experimental observables and EXP simulations, Poisson-Boltzmann (PB) implicit solvent method [38] has been used as a standard for GB optimizations as well [39, 40]. It models solvent's electrostatic effects by solving the Poisson equation numerically, which is accurate but slow, while most GB methods achieve speedup by seeking instead analytical and even pairwise approximations [18, 24]. Nevertheless, both PB and GB methods rely on the choice of intrinsic radii. Therefore it would be important to evaluate the salt bridge strength in PB simulations with the same intrinsic radii set. Instead of carrying out PB REMD, which is very time consuming to get converged data, we simplified the GB and PB comparison by only looking at energetically preferred salt bridge distances in each method, given a set of structures. Energy was calculated for structures sampled in small peptide EXP REMD with GB or PB method using either original or smaller Hn radii. Energy differences between salt bridge interactions at various distances were compared. This energy profile approach has been shown previously to be useful in qualitative screening [17, 41]. Our results predicted that the PB method would also produce inaccurate salt bridge strength compared to EXP when using original Hn radii, which suggests caution in using PB as a reference for evaluating GB quality.
After validating the effectiveness of radii modification in small peptide, we also evaluated the same modification in a larger macromolecular system: HIV-1 protease (HIVPR, figure 1). HIVPR plays an important role in HIV virus maturation and is a common drug target for AIDS treatment. Lengthy, stable HIVPR GB simulations are desirable because adequate flap sampling of HIVPR would reveal further statistical information about the equilibrium populations among different flap conformations, flap opening mechanisms, and even ligand binding process [42] in the future (which is almost impractical for EXP simulations). Previously, using EXP simulation, our lab reproduced EPR spin label distance and gave structural interpretation of experimental data [43]. These comparisons could be more readily obtained if quantitative GB simulations were possible.
Figure 1.
HIVPR. Two monomers are colored in cyan and yellow. Protease's flap, elbow, cantilever and termini region are labeled with black text. There are four salt bridge pairs involving Arg near elbow region (two on each monomer). These salt bridges as well as catalytic site residues are shown in ball representation. The figure was generated using a crystal structure (PDB ID 1HVR).
In spite of our previous qualitatively correct simulations of HIVPR [42, 44], there are two main problems that obstruct lengthy, converged GB simulations (with ff99SB/GB-OBC, figure S1). First, the interleaved beta sheet formed by the four terminal strands tends to convert to helical structures, thus weakening the dimer interface and rendering simulations unstable. Second, the two beta-hairpin flaps sample wide open structures that are qualitatively comparable to those from EXP, but occurring too often in GB and sometimes leading to distorted flap conformations. The incorrect helicity at the terminal β-sheet is attributable to GB-OBC's backbone helical propensity [28]; since the present focus is on salt bridges, we applied restraints to maintain termini backbone structure (see Methods for details). The reason for the difference in opening was unclear. There are two salt bridges involving Arg on each flap elbow region (figure 1), which have been proposed to have allosteric coupling to flap opening [44]. We therefore hypothesized that incorrect treatment of these electrostatic interactions may be the source of changes in the opening behavior. We modified all Hn radii in HIVPR to investigate this hypothesis and to determine whether more accurate dynamics of large proteins such as drug targets could be obtained with a simple GB model.
Methods
Small peptide REMD
We simulated a small peptide Arg-Ala-Ala-Glu capable of forming a salt bridge, with its N termini acetylated and C termini amidated. GB REMD simulation with this peptide was shown previously to give inaccurate salt bridge strength and geometry compared to EXP REMD [29].
Small peptide EXP REMD
EXP REMD reported by Okur et al. [29] and an additional run they did subsequently were used here directly. Their simulation details are as follows: the AMBER simulation package [19] version 9 and ff99SB force field [17] were used. The peptide was solvated in a 16 Å octahedral TIP3P water box using 2 286 TIP3P [6] water molecules. Minimization/equilibration was done at 300 K for 65 ps, with reducing harmonic positional restraints on solute atoms. Then 46 replicas with temperatures ranging from 296 K to 584 K were used, which gave a uniform exchange acceptance ratio of ∼ 25%. A time step of 2 fs was used. Exchange between neighboring temperatures were attempted every 1 ps, and each replica had 30 000 exchange attempts (30ns per replica). All bonds involving hydrogen atoms were constrained in length using SHAKE [45], with geometry tolerance of 10-7. Long range electrostatic interactions were calculated with PME [46-49]. 7 Å cutoff for vdW interactions was applied. REMD was run in NVT ensemble with Berendsen temperature control [50]. Backbone conformation was restrained to that in the representative structure of unrestrained TIP3P REMD with harmonic positional restraints (1 kcal/mol·Å2). Same REMD procedure was repeated with a different starting velocity seed to give an independent REMD run for convergence check. The first 5 ns of both simulations were discarded to remove initial-structure bias, resulting in 50 ns combined trajectory for each temperature. The last 36 ns of the combined 300 K temperature trajectory was used for PMF plot and cluster analysis, and all 50 ns combined 300 K temperature trajectory was used for lowest energy plot (see below).
Small peptide GB REMD
We performed GB REMD simulations with the sander module of the AMBER simulation package [19] version 10 using the ff99SB force field [17]. The GB-OBC [18] implicit solvent model (igb=5 in AMBER) was used here in combination with mbondi2 [18, 36, 39] intrinsic radii. 3 sets of GB REMD simulations were carried out, which only differ in Hn (Hε and 4 Hη on Arg side chain) radii parameters: Hn were set to 1.3 Å (standard mbondi2), 1.2 Å and 1.1 Å, respectively. For each set, 6 replicas were chosen covering temperatures from 300 K to 636 K, no non-bonded cutoff was used. All other parameters were the same as described above for the EXP REMD. 3 sets were run for 44 ns, 50 ns, 50 ns, respectively. The last 36 ns of 300 K temperature's trajectory from each set was used for PMF plot and cluster analysis.
HIVPR MD
The simulation starting structure was prepared by deleting the inhibitor from protein-inhibitor complex (PDBID: 1HVR [51]) and introducing inactive mutation D25N at catalytic site using tleap tool in AMBER. The D25N mutant is widely used in X-ray and NMR studies because it retains native-like fold and binds to nature substrate without initiating cleavage event [52, 53]. The tleap tool was also used to add hydrogen atoms, evaluate crystal structure (bond lengths, torsion angles, atom clashes, etc.), and add TIP3P water for EXP MD (8 Å octahedron TIP3P [6] water box, resulting in 7 219 water molecules). For all HIVPR MD, AMBER simulation package [19] version 10 and ff99SB force field [17] were used, and equilibration was performed before every MD or REMD simulation (750 ps for EXP equilibration and 125 ps for GB equilibration). Following minimization, the system was heated gradually from 100 K to the desired temperature. Positional restraints were added first on heavy atoms then on backbone atoms only (with restraint force constant decreasing from 100 to 0.1kcal/mol·Å2).
HIVPR EXP MD
400 ns unrestrained MD simulation was performed at 2 fs time step. All bonds involving hydrogen atoms were constrained in length using SHAKE [45] with geometry tolerance of 10-5. PME [46-49] was used for long range electrostatic interactions. 8 Å cutoff was applied to vdW interactions. Berendsen temperature and pressure control [50] were applied to maintain the system at 325 K and 1 atm. Full length of MD simulation was used for PMF plots and RMSD comparison.
HIVPR GB MD
GB-OBC [18] implicit solvent model (igb=5 in AMBER) was used here in combination with mbondi2 [18, 36, 39] intrinsic radii. Two 60ns HIVPR GB simulations were carried out, which only differ in Hn radii settings: radii of Hn were set to 1.3 Å (standard mbondi2) and 1.1 Å, respectively. Simulations were in 1 fs time step. All bonds involving hydrogen atoms were constrained in length using SHAKE with geometry tolerance of 10-6. No cutoff for long range electrostatic/vdW interactions was applied. 25 Å distance cutoff was applied to pair interactions involved in effective radii calculation. Forces related to effective radii calculation, along with each pair interaction whose distance was greater than 15 Å, were evaluated every 4 steps. Langevin temperature control for 325 K with collision frequency of 1 ps-1 was used. Harmonic distance restraints were applied to the terminal portion of the dimer interface (figure S2) to prevent flexible termini region from forming helical structure, which is possibly attributable to GB-OBC's helical propensity [28]: Atom pairs Asp29_Cγ to Arg87_Hη21, Asp29_Cγ to Arg87_Hε, Arg87_Hη11 to Leu5′_O, Arg87_Hη12 to Trp6′_O were restrained (Leu5′ denotes Leu5 on the other monomer). Asp Cγ was chosen to account for carboxyl rotamers. For each atom pair, a distance cutoff was chosen near its average distance measured from EXP simulation (4 Å for pairs involving Asp Cγ, 3 Å for the rest). An atom pair was only restrained when pair distance went beyond the cutoff, with restraint force constant at 10 kcal/mol·Å2. Different initial velocity seeds were used to unsynchronize Langevin dynamics [54].
Analysis
Ptraj tool in AMBER package was used for all distance and RMSD measurements.
Potential of mean force (PMF)
We studied salt bridge pairs Arg-Glu (in small peptide and HIVPR) and Arg-Asp (in HIVPR). Considering rotamers of charged groups, Cγ atom from Asp, Cδ from Glu and Cζ from Arg were chosen for salt bridge description as done previously [29]. Populations of distances extracted from 300 K temperature trajectories were converted to PMFs directly. Error bars in each set were obtained by comparing PMF generated using the first and second half of data.
Cluster analysis
To further compare salt bridge geometry in small peptide REMD, cluster analysis was performed on 300 K temperature trajectories with Moil-View [55] using following heavy atoms as the similarity criterion: Arg_Cδ, Arg_Nε, Arg_Nη1, Arg_Nη2, Arg_Cζ, Glu_Cδ, Glu_Oε1, Glu_Oε2. Every 2nd structure from TIP3P and 3 GB trajectories (18000 each, 72000 in total) were combined; the resulting set of structures was subjected to clustering. Clusters were then formed with bottom-up approach using 1.3 Å similarity cutoff: each structure was initially assigned to a distinct cluster, followed by calculation of averaged root mean square deviation (RMSD) between all cluster pairs, then cluster pair with the smallest RMSD was merged until the most similar cluster pair exceeded the similarity cutoff. In the end, percentage of population for each simulation's structures in each cluster was calculated and plotted for comparison.
RMSD
HIVPR flap RMSDs were calculated for individual trajectories using ptraj. Fitting and RMSD calculation were both performed using the Cα atoms of residues 46-55 in both monomers (46-55 and 46′-55′). Reference structures were the closed structure (PDB ID 1HVR [51]) and the semiopen structure (1HHP [56]).
Lowest energy profile
The combined 300 K trajectory of small peptide EXP MD (50 ns, 50 000 structures) was used and 4 sets of energy calculation were performed: two GB calculations which only differ in Hn intrinsic radii (1.1 or 1.3 Å), two PB calculations which only differ in Hn intrinsic radii (1.1 or 1.3 Å). Both GB and PB calculations used mbondi2 intrinsic radii for atoms other than Hn. GB calculations used AMBER package version 10, GB-OBC solvent model, and no non-bonded cutoff. Internal energies, electrostatic and vdW energies were calculated as well as polar solvation energies. Then their sum (potential energy) was extracted from GB outputs. PB calculations were performed using DelPhi [57] with 0.25 Å grid spacing. Internal and external dielectric constants were set to 1 and 78.5, respectively, to be consistent with AMBER calculation. Since DelPhi only calculates polar solvation energies, potential energies for PB were calculated by replacing polar solvation energies in GB calculation results with DelPhi's. After potential energy calculation, structures were grouped according to the salt bridge distance (bin size 1 Å). The average potential energy of 20 structures with lowest energies in each bin was plotted against the salt bridge distance to get so called “lowest energy profile” [17]. Each curve's minimum was zeroed for easier comparison. Error bars in each set were obtained by comparing PMF generated using the first and second half of data.
All molecular structures in this article were generated using VMD [58]. All data graphs in this article were generated using matplotlib [59].
Results and Discussion
Comparison in small peptide REMD
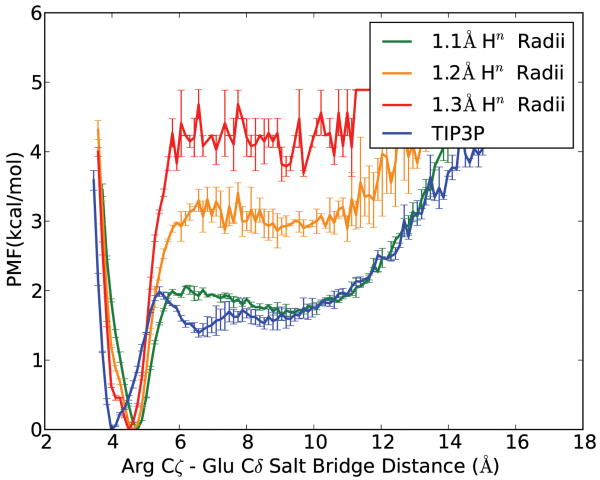
GB REMD simulations with different Hn intrinsic radii were performed on the Ace-Arg-Ala-Ala-Glu-NH2 peptide, and results were compared with EXP REMD simulations. Figure 2 illustrates their PMF profiles, which were calculated directly from populations in 300K REMD trajectories. Taking TIP3P data as the reference, GB MD using standard Hn radii in mbondi2, which is 1.3 Å, overstabilized the salt bridge by as much as 2.3 kcal/mol, whereas 1.2 Å radii decreased the energy gap to 1.2 kcal/mol. Further reducing the Hn radii to 1.1 Å precisely reproduced TIP3P data's energy barrier as well as curve shape, except for the solvent separated minimum (near 6Å in TIP3P curve), which is caused by structured water molecules and is difficult to model in implicit solvent unless time-consuming calculation of solvent accessible surface is used to define the dielectric boundary. Our results are consistent with a previous GB-HCT study on Fab 17/9 antibody salt bridges [33]. However, the most energetically favorable salt bridge distance (at which PMF is set to 0) from 1.1 Å Hn radii simulation seemed to land further away from TIP3P's compared to other GB simulations, which might indicate further deviation from EXP simulation structures. Therefore we used cluster analysis to compare salt bridge geometry among different simulations.
Figure 2.
Potential of mean force (PMF) for small peptide Arg-Glu salt bridge distances in different solvent models, at 300K. Error bars in each set were obtained by comparing PMF generated using the first and second half of data.
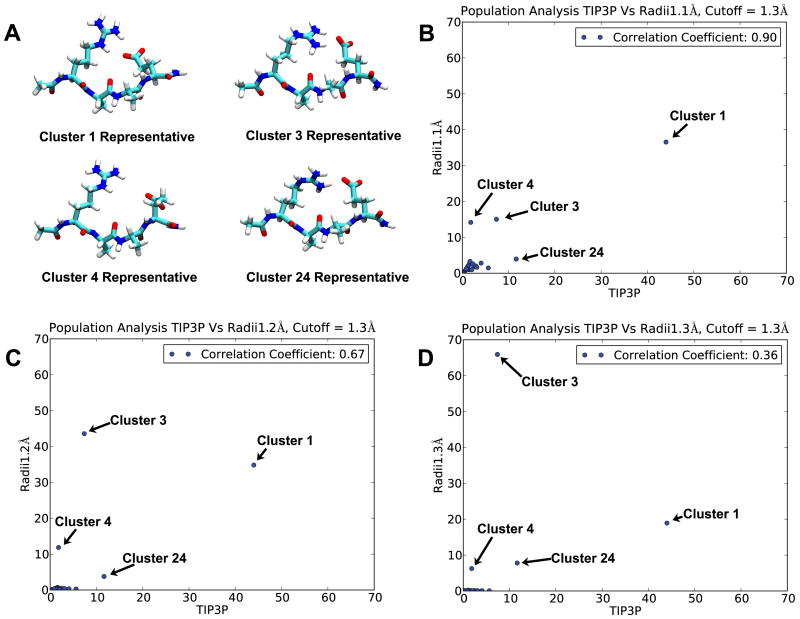
Cluster analysis was performed on a combined trajectory including structures from EXP simulation, GB 1.1Å Hn simulation, GB 1.2Å Hn simulation and GB 1.3Å Hn simulation (18 000 structures each), using salt bridge geometry as the clustering criterion (see Methods for details). Structures sampled in different simulations would fall into the same cluster if their pairwise RMSD is below the cutoff. Using combined trajectory permits direct comparison of structural distributions among different simulations. Figure 3B-D illustrates the distribution of simulation structures in different clusters, with each GB simulation plotted against EXP simulation. Overall, when Hn radii were modified from 1.3 Å (standard mbondi2) to 1.1 Å, the correlation coefficient between GB and EXP structural distributions, increased from 0.36 to 0.90. We labeled the four largest clusters for further comparison, and their representative structures are shown in Figure 3A. Most prominent changes, as we decrease Hn radii, are the increase of cluster 1 population, and the decrease of cluster 3 population. Similar to a previous study on the same system [29], our results (figure 3D) suggest that GB simulation with 1.3 Å Hn has most populated structures (cluster 3) that differ from those in EXP simulation (cluster 1). In addition, our results suggest that 1.1 Å Hn GB simulation's most populated structures are similar to those most populated in EXP simulation (they are all in cluster 1, figure 3B). 1.3 Å Hn GB simulation significantly changed salt bridge geometry preference as compared to EXP simulation; Arg Hε atom mostly isn't involved in forming salt bridge with Glu (cluster 3 and 24 compared to cluster 1). It is worth noticing that cluster 4 population is higher in 1.1 Å Hn GB simulation, in which the salt bridge is broken, but the change is much less significant compared to change in cluster 3. All smaller clusters show better GB-EXP correlation when Hn radii is smaller. Therefore, cluster analysis results demonstrate that the 1.1 Å Hn GB simulation agrees better with EXP simulation. This also emphasizes the necessity of multi-dimensional geometry comparison: although the most populated structures in 1.3 Å Hn GB simulation and EXP simulation have very different salt bridge geometries (figure 3), they have very small difference in the more simplistic distance measurement (figure 2).
Figure 3.
Cluster analysis results. Cluster analysis was done on combined trajectory including EXP simulation, GB 1.1 Å Hn simulation, GB 1.2 Å Hn simulation and GB 1.3 Å Hn simulation trajectories. Representative structures of four largest clusters (cluster 1, cluster 3, cluster 4 and cluster 24) are shown in figure A. The structural distribution of each GB simulation is plotted against EXP's in figure B, C and D, with the axes indicating the percentage of structures that fall into a given cluster. Ideally if a certain GB model is 100% correlated with EXP, all clusters should be equally populated by GB and EXP structures (all data points would be on the diagonal) indicating that the GB simulation provides an excellent reproduction of salt bridge behavior in EXP.
Since Poisson Boltzmann (PB) implicit solvent method was used as a touchstone for GB methods in previous studies [39, 40], we also explored the influence of changing radii on PB calculation. Instead of doing costly computations on PB REMD, we compared “lowest energy profile” [17] for different methods (figure 4). Since we only looked at structures with low energies, to reconstruct the “energy landscape” along the coordinate of salt bridge distance, the precision is lower than if we considered all structures to do a PMF profile (figure 2), and the absolute energy barrier value is likely less realistic. However, the averaged curves here show a similar trend as PMFs in figure 2: reducing Hn radii systematically decreases salt bridge strength. If we set GB 1.1 Å Hn radii as the standard, since it shows the best agreement to TIP3P data in figure 2, PB 1.3 Å Hn radii does equally poorly as GB 1.3 Å Hn radii, if not worse. This result suggests caution in using PB as a reference for evaluating GB quality. At least calibrating salt bridge strength by fitting to PB calculations is insufficient, since PB is itself highly sensitive to intrinsic radii that define the molecular surface. Similarly, Zhu et al. [60] found previously that the GB method that best reproduces PB results is not the best in terms of folding experiment.
Figure 4.
Lowest energy profile of GB or PB implicit solvent models using 1.1 Å or 1.3 Å Hn radii. Each point on a curve represents the average energy of 20 lowest energy structures whose salt bridge distances fall in corresponding distance range (bin size 0.1 Å). Each curve's minimum was zeroed for easier comparison. Error bars in each set were obtained by comparing PMF generated using the first and second half of data.
Applying radii changes to HIVPR simulation
After testing in the small peptide model system, we further assayed the impact of this change on the ability of GB to accurately model the structure and dynamics of a larger protein, using HIVPR as a model since we have previously reported extensive simulations using both GB and EXP models [42-44, 61, 62]. We used the D25N mutant, which is also widely used in X-ray and NMR studies because it retains native-like fold and binds to natural substrate without initiating the cleavage event [52, 53]. In our experience, flap deformation is observed in HIVPR with either Asp or Asn at the catalytic site, however, D25N system is statistically less stable than the wild-type system (figure S1), which is consistent with experimental finding that D25N mutation decreases protease dimer stability [63]. We hypothesized that deformation on the > 10 ns time scale was due to GB salt bridge artifacts. We therefore compared HIVPR GB simulations with 1.3 Å or 1.1 Å Hn radii (60ns each) to 400ns EXP simulation.
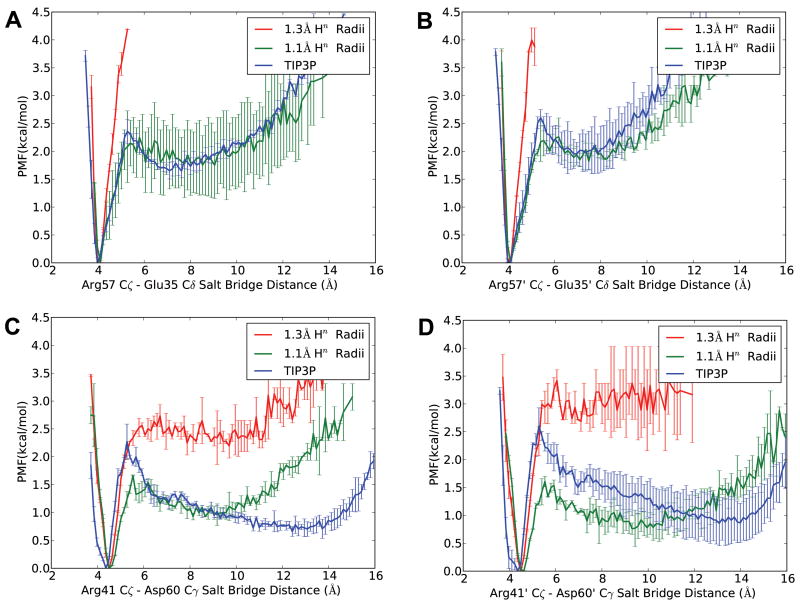
PMF profiles of 4 salt bridges near the flap region were calculated directly from distance populations in different trajectories and are shown in figure 5. Compared to TIP3P EXP MD data, GB MD using original Hn radii gave dramatically stronger salt bridges in all four cases, with over-stabilization in Arg57-Glu35 pairs on both monomers being more predominant (figure 5A, 5B); atom pair distances are always within 6 Å, so there is no data at distances for which the salt bridge is broken. After decreasing radii to 1.1 Å, Arg57-Glu35 pairs more closely reproduced the TIP3P curve, while comparisons of Arg41-Asp60 pairs on both monomers didn't provide as clear agreement. Interestingly, PMFs for Arg41-Asp60 pairs generated with 1.1 Å Hn radii were consistent in energy barrier, while a shift of 0.5 kcal/mol was observed in both 1.3 Å and TIP3P PMFs, which rendered energy comparison ambiguous. This is attributable to inadequate conformational sampling in both simulations, which is a common problem encountered in EXP simulation of macromolecules. Thus, HIVPR salt bridge PMFs here demonstrated that 1.3 Å Hn radii GB simulation gave much stronger salt bridges than TIP3P. However, to better assess whether 1.1 Å Hn radii would “rescue” HIVPR GB simulations, we need to look at MD trajectories for detail.
Figure 5.
PMF of salt bridges involving Arg in HIVPR simulation, showing salt bridge distances between Arg57_Cζ and Glu35_Cδ on each monomer (figure A and B), and between Arg41_Cζ and Asp60_Cγ on each monomer (figure C and D). Error bars in each set were obtained by comparing PMF generated using the first and second half of data.
Flap RMSD versus time are plotted in figure 6 (right). Flaps RMSD in simulations with 1.3 Å Hn radii (standard mbondi2) went as high as 20 Å towards the end, which indicates a large deviation of flap conformation from that observed in the crystal (figure 1) and is consistent with the last frame snapshot (figure 6B). Notice that the flap deformation is similar to what we observed in previous GB simulations with mbondi2 (see figure S1). Flap RMSD in EXP simulation remained almost unchanged throughout 400 ns simulation length. The RMSD to closed flap conformation (black curve) is always below its RMSD to semiopen conformation (red curve), implying that its flap conformation remains close to the closed crystal structure all the time, which is consistent with its last frame snapshot (figure 6D). This stability on the >100 ns timescale is likely due to kinetic trapping, since multiple conformations should be populated under these conditions [62]. An improved GB model with lower viscosity might significantly aid modeling of large conformational fluctuations like flap handedness switch or flap opening [44], again reinforcing our goal of obtaining a more accurate GB model.
Figure 6.
Salt bridge distance and flap RMSD for HIVPR simulations. A-B: 1.3 Å radii GB simulation. C-D: TIP3P EXP simulation. E-F: 1.1 Å radii GB simulation. Salt bridge distance: for each simulation, distances between salt bridge atom pairs (Arg57_Cζ to Glu35_Cδ, Arg41_ Cζ to Asp60_Cγ on one monomer first, then those on the other monomer) are plotted in orange, red, blue and cyan, respectively. Flap RMSD: HIVPR is overlapped with either closed crystal structure (black line, PDB ID 1HVR), or semiopen crystal structure (red line, PDB ID 1HHP). Low values for the black line indicate that flaps are in closed state, while low values for the red line indicate that flaps are in semiopen state. The final frame of each simulation is shown above RMSD curves.
In contrast, when we reduce GB simulation Hn radii to 1.1 Å, the flaps sampled multiple flap handedness switching events, indicated by a change in the crystal structure corresponding to the lower RMSD, and transient flap-opening events, during which RMSD steadily increases to more than 10 Å then decreases back to values sampled prior to opening, in 60 ns simulation length. At the end of the simulation one flap of the protease is open while the other one is closed (figure 6F), which is a common transition state in HIVPR simulations [44] and is similar to experimental observations [64]. If we compare salt bridge versus time with EXP (figure 6 left), it can be seen that salt bridges in the 1.1 Å Hn radii simulation broke more frequently than EXP, which could result from significantly higher viscosity in EXP simulation for these solvent-exposed side chains. It is also worth noting that these salt bridge distances in simulation don't seem to correlate with flap RMSDs directly. Therefore, we hypothesize that, although elbow salt bridges were shown to contribute to flap opening rate in HIVPR GB simulations, they themselves are not able to cause flap opening. Instead, they may act by increasing/decreasing the chance of flap opening upon formation/breaking.
Conclusion
Here we present our finding that Hn (Hn: Hε and 4 Hη on Arg side chain) intrinsic radii in mbondi2 should be reduced for GB simulations with ff99SB/GB-OBC. It was previously suggested that a hydrogen atom's radius in GB simulation should be smaller when the electronegativity of its bonding partner is greater [39]. Our results in a small-peptide system and in a macromolecular system both verified the approach of reducing Hn radii. Therefore, differentiating the intrinsic radii of Hn atoms from those of backbone hydrogen atoms may be necessary in order to achieve better GB simulation results, and we suggest considering 1.1 Å Hn radii for peptide or protein simulations with ff99SB/GB-OBC.
Moreover, we found that the overestimation of salt bridge strength exists in PB calculations as well. Therefore, optimizing intrinsic radii may be needed for all implicit solvent models. To optimize intrinsic radii, using explicit solvent simulation data as the standard, as performed previously [65], could be preferable.
Supplementary Material
Acknowledgments
This research was funded by NIH (GM61678 and GM079383). This research utilized resources at the New York Center for Computational Sciences at Stony Brook University/Brookhaven National Laboratory which is supported by the U.S. Department of Energy under Contract No. DE-AC02-98CH10886 and by the State of New York. YS thanks Carmenza Martinez and James Maier for helpful discussions.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Constanciel R, Contreras R. Self-Consistent Field-Theory of Solvent Effects Representation by Continuum Models - Introduction of Desolvation Contribution. Theor Chim Acta. 1984;65:1–11. [Google Scholar]
- 2.Still WC, Tempczyk A, Hawley RC, Hendrickson T. Semianalytical Treatment of Solvation for Molecular Mechanics and Dynamics. J Am Chem Soc. 1990;112:6127–9. [Google Scholar]
- 3.Qiu D, Shenkin PS, Hollinger FP, Still WC. The GB/SA continuum model for solvation. A fast analytical method for the calculation of approximate Born radii. J Phys Chem A. 1997;101:3005–14. [Google Scholar]
- 4.Alder BJ, Wainwright TE. Studies in Molecular Dynamics. 1. General Method. Journal of Chemical Physics. 1959;31:459–66. [Google Scholar]
- 5.Rahman A. Correlations in Motion of Atoms in Liquid Argon. Physical Review A - General Physics. 1964;136:405–11. [Google Scholar]
- 6.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. Journal of Chemical Physics. 1983;79:926–35. [Google Scholar]
- 7.Bashford D, Case DA. Generalized Born Models of Macromolecular Solvation Effects. Annu Rev Phys Chem. 2000;51:129–52. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 8.Tsui V, Case DA. Theory and applications of the generalized Born solvation model in macromolecular Simulations. Biopolymers. 2000;56:275–91. doi: 10.1002/1097-0282(2000)56:4<275::AID-BIP10024>3.0.CO;2-E. [DOI] [PubMed] [Google Scholar]
- 9.Feig M, Brooks CL. Recent advances in the development and application of implicit solvent models in biomolecule simulations. Curr Opin Struc Biol. 2004;14:217–24. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 10.Chen J, Brooks CL, III, Khandogin J. Recent advances in implicit solvent-based methods for biomolecular simulations. Curr Opin Struc Biol. 2008;18:140–8. doi: 10.1016/j.sbi.2008.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ponder JW, Case DA. Force fields for protein simulations. Protein Simulations. 2003;66:27–85. doi: 10.1016/s0065-3233(03)66002-x. [DOI] [PubMed] [Google Scholar]
- 12.Guvench O, MacKerell AD. Comparison of Protein Force Fields for Molecular Dynamics Simulations. Methods in Molecular Biology. 2008;443:63–88. doi: 10.1007/978-1-59745-177-2_4. [DOI] [PubMed] [Google Scholar]
- 13.Hess B, van der Vegt NFA. Hydration thermodynamic properties of amino acid analogues: A systematic comparison of biomolecular force fields and water models. J Phys Chem B. 2006;110:17616–26. doi: 10.1021/jp0641029. [DOI] [PubMed] [Google Scholar]
- 14.Shell MS, Ritterson R, Dill KA. A test on peptide stability of AMBER force fields with implicit solvation. J Phys Chem B. 2008;112:6878–86. doi: 10.1021/jp800282x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Penev E, Ireta J, Shea JE. Energetics of infinite homopolypeptide chains: A new look at commonly used force fields. J Phys Chem B. 2008;112:6872–7. doi: 10.1021/jp800058f. [DOI] [PubMed] [Google Scholar]
- 16.Matthes D, de Groot BL. Secondary Structure Propensities in Peptide Folding Simulations: A Systematic Comparison of Molecular Mechanics Interaction Schemes. Biophysical Journal. 2009;97:599–608. doi: 10.1016/j.bpj.2009.04.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Comparison of multiple amber force fields and development of improved protein backbone parameters. Proteins-Structure Function and Bioinformatics. 2006;65:712–25. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Onufriev A, Bashford D, Case DA. Exploring protein native states and large-scale conformational changes with a modified generalized born model. Proteins-Structure Function and Bioinformatics. 2004;55:383–94. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 19.Case DA, Cheatham TE, Darden T, Gohlke H, Luo R, Merz KM, et al. The Amber biomolecular simulation programs. Journal of Computational Chemistry. 2005;26:1668–88. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wang JM, Cieplak P, Kollman PA. How well does a restrained electrostatic potential (RESP) model perform in calculating conformational energies of organic and biological molecules? Journal of Computational Chemistry. 2000;21:1049–74. [Google Scholar]
- 21.Cornell WD, Cieplak P, Bayly CI, Gould IR, Merz KM, Ferguson DM, et al. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules (vol 117, pg 5179, 1995) J Am Chem Soc. 1996;118:2309. [Google Scholar]
- 22.Terada T, Shimizu K. A comparison of generalized Born methods in folding simulations. Chemical Physics Letters. 2008;460:295–9. [Google Scholar]
- 23.Hawkins GD, Cramer CJ, Truhlar DG. Pairwise solute descreening of solute charges from a dielectric medium. Chemical Physics Letters. 1995;246:122–9. [Google Scholar]
- 24.Mongan J, Simmerling C, McCammon JA, Case DA, Onufriev A. Generalized Born model with a simple, robust molecular volume correction. Journal of Chemical Theory and Computation. 2007;3:156–69. doi: 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Luca S, Yau WM, Leapman R, Tycko R. Peptide conformation and supramolecular organization in amylin fibrils: Constraints from solid-state NMR. Biochemistry. 2007;46:13505–22. doi: 10.1021/bi701427q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Markwick PRL, Bouvignies G, Blackledge M. Exploring multiple timescale motions in protein GB3 using accelerated molecular dynamics and NMR spectroscopy. J Am Chem Soc. 2007;129:4724–30. doi: 10.1021/ja0687668. [DOI] [PubMed] [Google Scholar]
- 27.Best RB, Hummert G. Optimized Molecular Dynamics Force Fields Applied to the Helix-Coil Transition of Polypeptides. J Phys Chem B. 2009;113:9004–15. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Roe DR, Okur A, Wickstrom L, Hornak V, Simmerling C. Secondary structure bias in generalized born solvent models: Comparison of conformational ensembles and free energy of solvent polarization from explicit and implicit solvation. J Phys Chem B. 2007;111:1846–57. doi: 10.1021/jp066831u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Okur A, Wickstrom L, Simmerling C. Evaluation of Salt Bridge Structure and Energetics in Peptides Using Explicit, Implicit, and Hybrid Solvation Models. Journal of Chemical Theory and Computation. 2008;4:488–98. doi: 10.1021/ct7002308. [DOI] [PubMed] [Google Scholar]
- 30.Amaro RE, Cheng XL, Ivanov I, Xu D, McCammon JA. Characterizing Loop Dynamics and Ligand Recognition in Human- and Avian-Type Influenza Neuraminidases via Generalized Born Molecular Dynamics and End-Point Free Energy Calculations. J Am Chem Soc. 2009;131:4702–9. doi: 10.1021/ja8085643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Brooks BR, Brooks CL, Mackerell AD, Nilsson L, Petrella RJ, Roux B, et al. CHARMM: The Biomolecular Simulation Program. Journal of Computational Chemistry. 2009;30:1545–614. doi: 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chen JH, Im WP, Brooks CL. Balancing solvation and intramolecular interactions: Toward a consistent generalized born force field. J Am Chem Soc. 2006;128:3728–36. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Geney R, Layten M, Gomperts R, Hornak V, Simmerling C. Investigation of salt bridge stability in a generalized born solvent model. Journal of Chemical Theory and Computation. 2006;2:115–27. doi: 10.1021/ct050183l. [DOI] [PubMed] [Google Scholar]
- 34.Chocholousova J, Feig M. Implicit solvent simulations of DNA and DNA-protein complexes: Agreement with explicit solvent vs experiment. J Phys Chem B. 2006;110:17240–51. doi: 10.1021/jp0627675. [DOI] [PubMed] [Google Scholar]
- 35.Felts AK, Gallicchio E, Chekmarev D, Paris KA, Friesner RA, Levy RM. Prediction of protein loop conformations using the AGBNP implicit solvent model and torsion angle sampling. Journal of Chemical Theory and Computation. 2008;4:855–68. doi: 10.1021/ct800051k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bondi A. Van Der Waals Volumes and Radii. Journal of Physical Chemistry. 1964;68:441–51. [Google Scholar]
- 37.Sugita Y, Okamoto Y. Replica-exchange molecular dynamics method for protein folding. Chemical Physics Letters. 1999;314:141–51. [Google Scholar]
- 38.Baker NA. Improving implicit solvent simulations: a Poisson-centric view. Curr Opin Struc Biol. 2005;15:137–43. doi: 10.1016/j.sbi.2005.02.001. [DOI] [PubMed] [Google Scholar]
- 39.Tsui V, Case DA. Molecular dynamics simulations of nucleic acids with a generalized born solvation model. J Am Chem Soc. 2000;122:2489–98. [Google Scholar]
- 40.Onufriev A, Case DA, Bashford D. Effective Born radii in the generalized Born approximation: The importance of being perfect. Journal of Computational Chemistry. 2002;23:1297–304. doi: 10.1002/jcc.10126. [DOI] [PubMed] [Google Scholar]
- 41.Okur A, Strockbine B, Hornak V, Simmerling C. Using PC clusters to evaluate the transferability of molecular mechanics force fields for proteins. Journal of Computational Chemistry. 2003;24:21–31. doi: 10.1002/jcc.10184. [DOI] [PubMed] [Google Scholar]
- 42.Hornak V, Okur A, Rizzo RC, Simmerling C. HIV-1 protease flaps spontaneously close to the correct structure in simulations following manual placement of an inhibitor into the open state. J Am Chem Soc. 2006;128:2812–3. doi: 10.1021/ja058211x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Galiano L, Ding F, Veloro AM, Blackburn ME, Simmerling C, Fanucci GE. Drug Pressure Selected Mutations in HIV-1 Protease Alter Flap Conformations. J Am Chem Soc. 2009;131:430–1. doi: 10.1021/ja807531v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hornak V, Okur A, Rizzo RC, Simmerling C. HIV-1 protease flaps spontaneously open and reclose in molecular dynamics simulations. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:915–20. doi: 10.1073/pnas.0508452103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Ryckaert JP, Ciccotti G, Berendsen HJC. Numerical-Integration of Cartesian Equations of Motion of a System with Constraints - Molecular-Dynamics of N-Alkanes. Journal of Computational Physics. 1977;23:327–41. [Google Scholar]
- 46.Darden T, York D, Pedersen L. Particle Mesh Ewald - an N.Log(N) Method for Ewald Sums in Large Systems. Journal of Chemical Physics. 1993;98:10089–92. [Google Scholar]
- 47.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. A Smooth Particle Mesh Ewald Method. Journal of Chemical Physics. 1995;103:8577–93. [Google Scholar]
- 48.Crowley MF, Darden TA, Cheatham TE, Deerfield DW. Adventures in improving the scaling and accuracy of a parallel molecular dynamics program. Journal of Supercomputing. 1997;11:255–78. [Google Scholar]
- 49.Toukmaji A, Sagui C, Board J, Darden T. Efficient particle-mesh Ewald based approach to fixed and induced dipolar interactions. Journal of Chemical Physics. 2000;113:10913–27. [Google Scholar]
- 50.Berendsen HJC, Postma JPM, Vangunsteren WF, Dinola A, Haak JR. Molecular-Dynamics with Coupling to an External Bath. Journal of Chemical Physics. 1984;81:3684–90. [Google Scholar]
- 51.Lam PYS, Jadhav PK, Eyermann CJ, Hodge CN, Ru Y, Bacheler LT, et al. Rational Design of Potent, Bioavailable, Nonpeptide Cyclic Ureas as Hiv Protease Inhibitors. Science. 1994;263:380–4. doi: 10.1126/science.8278812. [DOI] [PubMed] [Google Scholar]
- 52.Tyndall JD, Pattenden LK, Reid RC, Hu SH, Alewood D, Alewood PF, et al. Crystal structures of highly constrained substrate and hydrolysis products bound to HIV-1 protease. Implications for the catalytic mechanism. Biochemistry. 2008;47:3736–44. doi: 10.1021/bi7023157. [DOI] [PubMed] [Google Scholar]
- 53.Altman MD, Nalivaika EA, Prabu-Jeyabalan M, Schiffer CA, Tidor B. Computational design and experimental study of tighter binding peptides to an inactivated mutant of HIV-1 protease. Proteins. 2008;70:678–94. doi: 10.1002/prot.21514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ciesla M, Dias SP, Longa L, Oliveira FA. Synchronization induced by Langevin dynamics. Physical Review E. 2001;6306 doi: 10.1103/PhysRevE.63.065202. [DOI] [PubMed] [Google Scholar]
- 55.Simmerling C, Elber R, Zhang J. MOIL-View - A Program for Visualization of Structure and Dynamics of Biomolecules and STO - A Program for Computing Stochastic Paths. Modelling of Biomolecular Structures and Mechanisms. 1995:241–465. [Google Scholar]
- 56.Spinelli S, Liu QZ, Alzari PM, H HP, Poljak RJ. The three-dimensional structure of the aspartyl protease from the HIV-1 isolate BRU. Biochimie. 1991;73:1391–6. doi: 10.1016/0300-9084(91)90169-2. [DOI] [PubMed] [Google Scholar]
- 57.Rocchia W, Sridharan S, Nicholls A, Alexov E, Chiabrera A, Honig B. Rapid grid-based construction of the molecular surface and the use of induced surface charge to calculate reaction field energies: Applications to the molecular systems and geometric objects. Journal of Computational Chemistry. 2002;23:128–37. doi: 10.1002/jcc.1161. [DOI] [PubMed] [Google Scholar]
- 58.Humphrey W, Dalke A, Schulten K. VMD: Visual molecular dynamics. Journal of Molecular Graphics. 1996;14:33–8. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 59.Hunter JD. Matplotlib: A 2D graphics environment. Computing in Science & Engineering. 2007;9:90–5. [Google Scholar]
- 60.Zhu J, Alexov E, Honig B. Comparative study of generalized Born models: Born radii and peptide folding. J Phys Chem B. 2005;109:3008–22. doi: 10.1021/jp046307s. [DOI] [PubMed] [Google Scholar]
- 61.Layten M, Hornak V, Simmerling C. The open structure of a multi-drug-resistant HIV-1 protease is stabilized by crystal packing contacts. J Am Chem Soc. 2006;128:13360–1. doi: 10.1021/ja065133k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ding F, Layten M, Simmerling C. Solution structure of HIV-1 protease flaps probed by comparison of molecular dynamics simulation ensembles and EPR experiments. J Am Chem Soc. 2008;130:7184–5. doi: 10.1021/ja800893d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sayer JM, Liu F, Ishima R, Weber IT, Louis JM. Effect of the active site D25N mutation on the structure, stability, and ligand binding of the mature HIV-1 protease. J Biol Chem. 2008;283:13459–70. doi: 10.1074/jbc.M708506200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Prabu-Jeyabalan M, Nalivaika EA, Romano K, Schiffer CA. Mechanism of substrate recognition by drug-resistant human immunodeficiency virus type 1 protease variants revealed by a novel structural intermediate. Journal of Virology. 2006;80:3607–16. doi: 10.1128/JVI.80.7.3607-3616.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Swanson JMJ, Adcock SA, McCammon JA. Optimized radii for Poisson-Boltzmann calculations with the AMBER force field. Journal of Chemical Theory and Computation. 2005;1:484–93. doi: 10.1021/ct049834o. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.