A Representation and Classification Scheme for Tree-Like Structures in Medical Images: Analyzing the Branching Pattern of Ductal Trees in X-ray Galactograms

Abstract

We propose a multistep approach for representing and classifying tree-like structures in medical images. Tree-like structures are frequently encountered in biomedical contexts; examples are the bronchial system, the vascular topology, and the breast ductal network. We use tree encoding techniques, such as the depth-first string encoding and the Prüfer encoding, to obtain a symbolic string representation of the tree's branching topology; the problem of classifying trees is then reduced to string classification. We use the tf-idf text mining technique to assign a weight of significance to each string term (i.e., tree node label). Similarity searches and k-nearest neighbor classification of the trees is performed using the tf-idf weight vectors and the cosine similarity metric. We applied our approach to characterize the ductal tree-like parenchymal structure in X-ray galactograms, in order to distinguish among different radiological findings. Experimental results demonstrate the effectiveness of the proposed approach with classification accuracy reaching up to 86%, and also indicate that our method can potentially aid in providing insight to the relationship between branching patterns and function or pathology.

I. Introduction

SEVERAL structures in the human physiology follow a tree shaped morphology; examples of such structures are the dendritic extensions of neurons [1], the intrathoracic airway trees [2], the blood vessel system [3], and the breast ductal network [4] (see Fig. 1). Medical imaging modalities such as magnetic resonance imaging (MRI), computed tomography (CT), and X-ray mammography have made available large collections of 2-D and 3-D images, in which the spatial arrangement of such tree-like structures is visualized. A challenging issue when analyzing the morphology of these tree-like structures is to extract descriptive features that correspond to topological patterns and discriminative characteristics; these features capture properties such as the branching frequency, the tortuosity, and the spatial distribution of branching [3], [5]. To perform this type of analysis, a preprocessing step is usually required: the tree is traced and extracted from the image, using manual, semi-automated or fully automated procedures [6]. Computerized image analysis techniques can then be applied to compute the desired features. In medical image analysis, these features are usually associated with function or pathology and can be used to assist medical diagnosis. Examples of such analyses have been reported in the literature: regional changes in vessel tortuosity have been studied to identify early tumor development in the human brain [5] and lung structure and function has been investigated using 3-D analysis of pulmonary airway trees [2], [6]. Similarly, examining the morphology of the ductal network can potentially provide valuable insight to the risk and the development of breast cancer, and assist in diagnosing abnormalities [7], [8], [15].

Fig. 1.

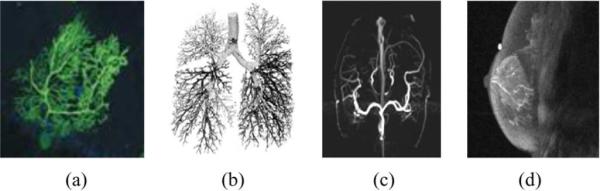
Examples of tree-like structures in medical images: (a) a dendritic brain neuron, (b) airway tree of the lungs, (c) vessel system, and (d) the breast ductal network.

In this paper, we propose a multistep approach for characterizing and classifying tree-like structures in medical images. The proposed approach uses tree encoding schemes to obtain a symbolic string representation of the tree-like structures; the problem of classifying trees is then reduced to string classification where node labels comprise the string terms. We use text mining techniques to assign a significance weight to each string term (i.e., node label), in order to identify tree branching patterns that are discriminative among groups of images. Our goal is to develop effective descriptors of tree-like structures that can be used for performing similarity searches and classification. For the purpose of illustrating our technique, we apply it to the analysis of breast ductal trees in clinical X-ray galactograms, in order to distinguish among cases of women with reported galactographic findings and normal cases. In general, our technique is independent of the imaging modality and the clinical relevance of the application; therefore, it can also be applied to other types of tree-like structures in biomedical images. Our experimental results demonstrate the effectiveness of the proposed method in automatically characterizing and classifying tree-like structures in medical images. These methods can potentially provide insight to the relationship between branching topology and function or pathology.

II. BACKGROUND

In this section, basic concepts of trees, tree modeling, tree branching descriptors, and imaging of tree structures are briefly reviewed.

Tree-like structures are physical structures that may be modeled using trees. In particular, we focus on structures modeled by directed rooted trees, defined as directed acyclic graphs (DAGs) in which there exists only one path between any two nodes [9]. Each node has one or no parents, while the node at the top of the tree that has no parents is identified as the root of the tree. A binary tree is defined as a tree in which each node has at most two successors or child nodes. When the nodes of the tree are assigned labels, then the tree is referred to as a labeled rooted tree.

In this paper we consider tree-like structures encountered in biomedical imaging applications and we demonstrate an application to trees representing the breast ductal network in mammographic images. In particular, we consider breast images obtained by X-ray galactography.

Galactography is an imaging procedure that can visualize the breast ductal network. During this procedure, X-ray mammography is performed after injecting a contrast agent into the lactiferous ducts [14]–[16]. Galactography can be useful for visualizing early symptoms of papilloma or ductal ectasia, which may cause spontaneous nipple discharge without showing recognizable change in screen-film X-ray mammograms. In our earlier studies [4], [17] galactographic images were used to manually extract the breast ductal tree-like structures in order to perform branching pattern analysis.

The breast duct anatomy has been analyzed to understand normal breast development [8] and to distinguish between groups of healthy and diseased women [10], [11], [15]. Taking into consideration that breast cancer is one of the leading causes of cancer-related mortality worldwide and that it originates in ductal and lobular epithelium, analysis of the breast ductal anatomy could potentially provide insight for understanding cancer development and spread; animal studies have shown evidence that the ductal branching can be affected by hormonal factors that correlate with the risk of developing breast cancer [22]. Moreover, studies have shown that the architecture of the ductal network is a discriminative predictor for benign and malignant lesions of the breast, even in absence of additional information [15].

In order to evaluate ductal morphology with respect to breast cancer symptoms, Bakic et al. proposed a 3-D simulated model of the ductal network based on ramification matrices [4] and a quantitative approach to classify galactograms based on ductal branching properties [11]. The elements of a ramification matrix represent the probabilities of branching at various levels of a tree [11], [12]. More specifically, a ramification (R) matrix represents a descriptor of branching structures at the topological level. The branches (edges) between nodes are identified in a tree and the R-matrix elements are computed as follows [13]:

• 1)all terminal branches are assigned a bifurcation label of 1;
• 2)a “parent” branch whose “children” have bifurcation labels i and j are labeled by max(i,j) if i ≠ j or by(i+1) if i = j;
• 3)the labeling procedure continues until the root branch is reached whose label is called the Strahler number of the tree structure.

The R matrix of a tree with Strahler number is s a lower triangular matrix, defined as

$$R_{s-1,s}=\left[r_{k,j}=\frac{b_{k,j}}{a_k},k\in (2,s),j\in (1,k)\right]$$ (1)

where is equal to the number of branches with label k For j > k, b_k,j is the number of pairs of branches with labels k and j, while for j = k, b_k,j is the number of pairs of branches both labeled k − 1 descending from a node with bifurcation number k. Therefore, r_k,j = b_k,j/a_k = p(b_k,j|a_k is the probability that a branch with label k will bifurcate into branches with the appropriate labels.

A detailed description of the R-matrix approach for the classification of galactographic trees can be found in [11]. In this paper, we compare our proposed methodology to the R-matrix approach, and show that our method compares favorably to R-matrices. While our method is evaluated specifically on binary trees, it could potentially be extended to k-way trees by replacing the use of pairs of children in the labeling with child sets of size k or by treating higher-order splits as a series of bifurcations. However, such an extension of our method is beyond the scope of the present paper and will be more thoroughly investigated in our future studies.

More recently, Wang and Marron [24] have defined metrics on trees that may be used in conjunction with statistical analysis techniques defined on Euclidean spaces, such as PCA, to perform topological analysis of tree-like structures within medical and other domains.

III. METHODS

Our methodology is based on combining tree encoding schemes with text mining techniques. The methodological steps included in our approach are as follows.

• 1)Preprocessing: Segmenting the tree-like structures from the rest of the tissue.
• 2)Characterization: Encoding and representing trees in a form conducive to storage, indexing and retrieval.
• 3)Similarity searches: Given a collection of tree structures and a query tree, find the trees that are most similar to the query.
• 4)Classification: Given classes of labeled tree structures, build a model that correctly identifies the class of a new (previously unseen) tree.

A. Preprocessing

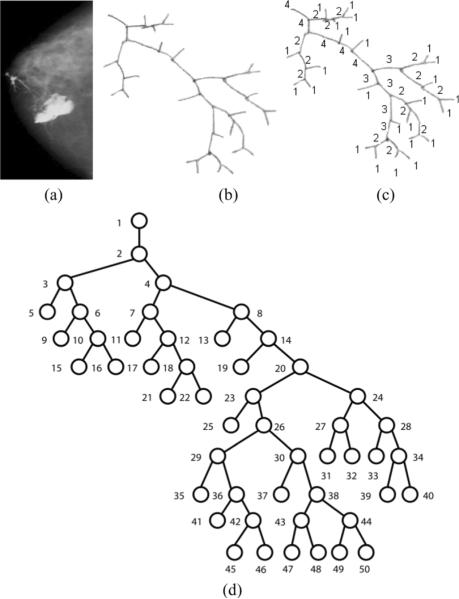
Certain preprocessing steps are necessary before the tree-like structures are available for analysis. First, the structure outline needs to be traced and segmented from the rest of the tissue or background in the image. Then, the tree-like structures are reconstructed by identifying points of branching and resolving potential ambiguities which could violate definition of a DAG (such as anastomoses [8], occurring mostly as a result of 2-D acquisition artifacts). In the application presented here, we perform tracing and reconstruction of the breast ductal tree manually, using the nipple as the root [12] (see Fig. 2). Although more advanced and fully-automated methods could potentially be implemented, such an approach is out of the scope of this paper; our main focus is the representation, classification and similarity analysis of tree-like structures.

Fig. 2.

Segmentation of a ductal tree, showing (a) a galactogram with a contrast-enhanced ductal network, (b) part of the galactogram showing enlarged the ductal network, and (c) the manually traced network of larger ducts from the contrast-enhanced portion of the galactogram.

B. Characterization

Two trees are considered isomorphic if they differ only by the order of their children, maintaining the same parent-child relationships. This can be problematic for encoding. In order to avoid such tree isomorphism problems after the tree structure has been extracted, we construct the breadth-first canonical form (BFCF) of the tree [20]. The BFCF is constructed based on the bifurcation labels of each node in the tree (see Section II); starting from the leaves, the canonical tree is assembled from the root down by recursively making the child with the smaller bifurcation number the left child of the current node in the canonical tree. Following canonicalization, the next step is to label the nodes (or branches) of the tree. In the application presented here, we preferred to use consecutive increasing integers assigned in a breadth-first manner. This labeling approach creates a potentially more appropriate representation scheme for our particular application, compared to depth-first approaches, by dealing better with cases where branches at the lower levels may not be visible due to image acquisition problems or the use or lack of contrast agents. Using breadth-first labeling, a missed branch will only cause changes in the encoding at or below the level at which the branch is missed, whereas a depth-first approach could potentially change the labeling at all levels of the tree. Fig. 3(a)–(d) shows the canonicalization and labeling procedures applied to a hand-traced ductal tree.

Fig. 3.

(a) A clinical X-ray galactogram visualizing the breast ductal network for a case with no reported radiological findings, (b) the corresponding manually traced ductal tree, (c) the same tree with bifurcation labels, and (d) the tree normalized to a canonical form.

Starting with a labeled tree, string encoding schemes can be applied; here we compare the performance of two different encodings: the depth-first string encoding and the Prüfer encoding. By using either one of the proposed encoding schemes, the problem of classifying the trees is reduced to string classification where node labels comprise the string terms. These characterization strings capture properties of the branching patterns and the topological structure of the corresponding tree.

The depth-first string encoding (DFSE) is an encoding scheme which constructs a nonunique string representation for a tree by visiting each node following a preorder depth-first traversal. During this process each node is represented in the string by its label. These encoding strings can be treated as signatures representing the original trees. As an example, the depth-first string encoding obtained for the hand traced labeled tree in Fig. 3(d) is [1 2 3 5 6 9 10 15 16 47 11 12 17 18 21 22 8 13 14 19 20 23 25 26 29 35 36 41 42 45 46 30 37 38 43 47 48 44 49 50 24 27 31 32 28 33 34 39 40]. It has been shown that DFSE provides a one-to-one correspondence between a rooted labeled tree and the obtained string representation if a symbol is used to represent a backtrack up the tree after visiting a leaf [20].

A more sophisticated tree encoding scheme that reflects branching frequencies of the tree nodes is the Prüfer encoding. The Prüfer encoding scheme constructs a unique string representation for each tree-like structure [21]. The algorithm visits each node of the tree following a preorder traversal. During this process the encoding (characterization) string is constructed, using, for each nonroot node, the label of its parent to represent it. Another approach that may be used to construct the Prüfer encoding is to iteratively remove the leaf with the smallest labeling and append it to the string representation until one node remains. In the case of a breadth-first labeled canonical tree, these approaches produce the same string in reverse order, as the leaf with the smallest labeling is always the left child of its parent node. The process of constructing the DFSE and Prüfer encodings is shown in Fig. 4(a), while the uniqueness properties of the encodings are demonstrated in Fig. 4(b).

Fig. 4.

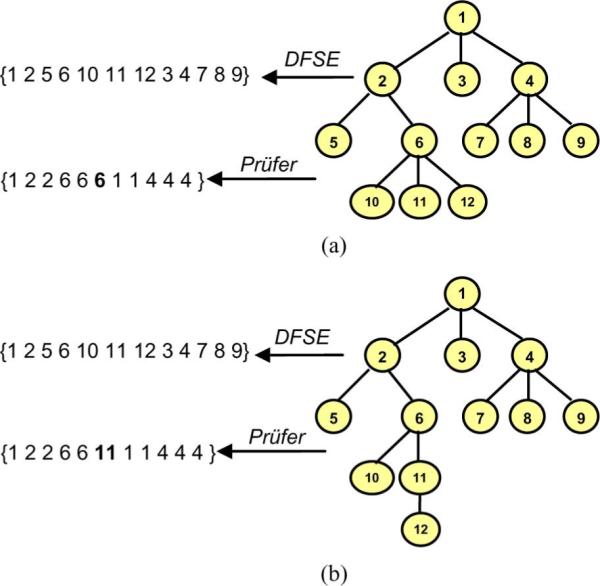
(a) A simple tree represented with a string based on the Prüfer encoding scheme. (b) moving a leaf changes the Prüfer encoding but not DFSE, contrasting the uniqueness properties of the encodings.

Prüfer, in his proof of Cayley's theorem regarding the number of labeled trees on n vertices, showed that there exists a 1–1 correspondence between (n − 2)-length sequences of integers from the set {1, 2, …, n} and labeled trees on n vertices [21]. Further, if an integer k occurs exactly m times in a sequence corresponding to a tree T, then the vertex T in with label k has degree m + 1. The greater the maximum degree of a tree, the more a node's label will occur in the code. As an example, the Prüfer encoding of a ductal tree illustrated in Fig. 3(d) is [1 2 3 3 6 6 10 10 2 4 7 7 12 12 18 18 4 8 8 14 14 20 23 23 26 29 29 36 36 42 42 26 30 30 38 43 43 38 44 44 20 24 27 27 24 28 28 34 34]. Employing Prüfer encoding results in obtaining unique characterization strings for each tree [21].

Both the DFSE and the Prüfer encoding schemes capture important information with respect to the spatial arrangement of the structure as well as the branching patterns of the nodes and are used to represent the initial trees in further analysis.

C. Vector Normalization and Weighting

In order to analyze patterns in the tree-like structures after representing them using strings, we utilize text mining techniques. We employ the tf-idf text mining technique [23] to assign a weight of significance to each string term (i.e., tree node label), indicating tree nodes that form discriminative branching patterns. The string representations constructed by applying the depth-first string encoding or the Prüfer encoding can be viewed as document vectors consisting of labeled terms. Using tf-idf weighting, each term in the document vector (that is, each node label in the tree's encoded string) can be assigned a weight determined by its relative frequency within the document against its frequency among all documents. The new representation becomes a vector with the corresponding weight at each term's feature position d_j = (w_1j, w_2j, …, w_tj), where t is the number of terms in document d_j. The tf-idf weighting has the advantage over R-matrices of emphasizing uncommon branching patterns, which are more likely to be discriminative indicators of pathology.

More specifically, the main idea of tf-idf weighting is that

• 1)more frequent terms in a “document” are more important, i.e., more indicative of the topic (such as the branching pattern of a tree-like structure)
• 2)we may want to normalize term frequency (tf) across the entire corpus
• 3)terms that appear in many different “documents” are less indicative of overall topic.

The weights derived by this approach are given by the following equation:

$$w_{ij}=t{f}_{ij}id{f}_i=t{f}_{ij}{\log }_2\left(\frac{N}{d{f}_i}\right)$$ (2)

where f_ij is the frequency of term i in document j; tf_ij is f_ij/max{f_ij}; df_i is the document frequency of i = number of documents containing term i; and idf_i is the inverse document frequency of term i = log₂ (N/df_i) and N is the total number of documents.

D. Similarity Searches and Classification

We perform similarity searches and classification by employing the cosine similarity distance metric on the string representations. As shown in the previous step, each term i in a document j is given a real-valued weight, w_ij, thus each tree's string representation can be expressed as a t-dimensional vector: d_j = (w_1j, w_2j, …, w_tj), where t is the number of different terms or size of the “vocabulary” or dimension. There are many ways to tell whether pairs of these vectors are similar; here we use the cosine value of the vectors, which is called the cosine similarity measure and is computed as follows:

$$\frac{\overrightarrow{d}j•\overrightarrow{q}}{\mid \overrightarrow{d}j\mid \cdot \mid \overrightarrow{q}\mid }=\frac{\sum _{i=1}^t(w_{ij}\cdot w_{iq})}{\sqrt{\sum _{i=1}^t{w_{ij}}^2\cdot \sum _{i=1}^t{w_{iq}}^2}}$$ (3)

where q is the query document and d_j is document j.

IV. Results

We considered 54 X-ray galactograms performed at Thomas Jefferson University Hospital and the Hospital of the University of Pennsylvania in the period between June 1994 and August 2001, from which the ductal trees were manually delineated and extracted. There were an average of 67 nodes per tree, of which approximately 30 were internal nodes and approximately 37 were terminal nodes. An example of a galactogram along with the corresponding hand-traced tree is shown in Fig. 3(a)–(c). These images were acquired from a total of 31 women with ages ranging from 28 to 75 years at exam date (mean age 47.1 years). From these images, 39 corresponded to women with no reported galactographic findings (NF) and 15 to women with reported findings (RF). Ages of women with no reported findings ranged from 28 to 74 (mean age 43.2), while ages of women with reported findings ranged from 43 to 75 (mean age 54.0). Of the 15 cases with reported findings, malignancy was found in two. The dataset analyzed in this paper includes 25 images from 15 patients from our previous R-matrix analysis of clinical galactograms [11].

We obtained the canonical trees, then assigned unique positive integer labels ascending in breadth-first order. The labeling started from the root of each tree, assigning the integer “1,” and continued in an increasing manner until all nodes were labeled. We applied the DFSE and the Prüfer encoding to obtain the string representations corresponding to the original ductal trees. Fig. 3(e) and (f) shows examples of such characterization strings. We further employed tf-idf weighting to assign a weight of significance to each node label within these strings. In each of these two cases, we considered both classes of ductal trees (NF and RF) as one group (i.e., forest) of trees and applied the tf-idf weighting to this combined dataset of encoding strings. When applying the tf-idf weighting the unequal lengths of the encoding strings were handled by padding the end of the characterization strings with a very small value of 1.00e⁻⁰¹³to avoid numerical errors when calculating the cosine similarity distance. By performing the tf-idf weighting, we obtained two datasets (one from the depth first string encoding and one from the Prüfer encoding) of tf-idf weights indicating the significance of each encoding string term (i.e., node label) in each characterization vector. Using the obtained tf-idf weight vectors we performed similarity searches and classification experiments based on the cosine similarity distance.

A. Similarity Searches

For similarity searches, we calculated the pairwise cosine distance matrix for all the tf-idf vectors. We considered each tree and its corresponding tf-idf vector as the query subject and retrieved the k most similar trees based on the cosine distance matrix. Considering the small size of our datasets, the k parameter ranged from 1 to 5. We report the percentage of relevant trees among the retrieved trees (i.e., precision) averaged over all the similarity queries performed. As relevant trees we consider the trees belonging to the same class (NF or RF) as the query tree. To compensate for the unbalanced class sizes of our dataset, we randomly under-sampled the NF class to the size of the RF class (15) and averaged the results over 100 sampling iterations.

B. Classification

For classification, we performed leave-one-out k-nearest neighbor experiments. Again, we randomly under-sampled the NF class to balance the size of our classes; random sampling has been shown to result in more accurate measurements of kNN classification accuracies than traditional deterministic sampling techniques in the literature [26]. For each test tree we retrieved the k closest neighbor trees (i.e., tf-idf vectors), based on the cosine similarity distance; we assigned the test tree the class that appeared most frequently among its neighbors. Ties were broken using the k + 1th nearest neighbor. Considering the size of our dataset, the parameter k ranged from 1 to 5. Table II illustrates the classification accuracy obtained when using the depth first string encoding and the Prüfer encoding. As shown in Table II, again Prüfer encoding outperformed DFSE on average by approximately 15%.

TABLE II.

Obtained Accuracy for the Classification Experiments Based on the Cosine Similarity Distance Metric When Using the Depth-First String Encoding and the Prüfer Encoding

Depth-First String Encoding
k	Classification Accuracy
	NF	RF	Total
1	44.89 %	42.00 %	43.44 %
2	73.11 %	69.78 %	71.44 %
3	44.22 %	49.11 %	46.67 %
4	68.67 %	67.78 %	68.22 %
5	45.33 %	66.00 %	55.67 %

Prüfer Encoding
k	Classification Accuracy
	NF	RF	Total
1	62.44 %	60.78 %	61.61 %
2	84.67 %	86.33 %	85.50 %
3	68.67 %	73.33 %	71.00 %
4	73.00%	87.00 %	80.00 %
5	62.56 %	74.33 %	68.44 %

These results are comparable to those obtained on galactograms by human experts [25], with our results showing lower sensitivity (RF accuracy: 86% versus 94%) but much higher specificity (NF accuracy: 85% versus 55%). Our results outperform previous experimental results reported in the literature, in which R-matrix elements computed from the breast ductal trees were used to distinguish among the two classes (NF versus RF) in a subset of the same dataset of galactographic images [11]. Our results also outperform the R-Matrix approach applied to the entire dataset used in this paper, having classification accuracies of 66% and 38% for NF and RF classes, respectively. However, we were able to raise the accuracy of the R-matrix approach to 81% (88% NF, 71% RF) by applying our kNN classifier using the R-matrix coefficients as features.

We also computed receiver operating characteristic (ROC) curves, which plot a test's true positive rate against false positive rate. ROC analysis does not suffer due to unbalanced class sizes [27]. The curves for the Prüfer and DFSE datasets are shown in Fig. 5. We create these curves by classifying each tree as NF if its nearest NF neighbor is within a thresholded cosine distance; if the distance is larger than the threshold, the tree is labeled as RF. This process is repeated for 100 equally spaced threshold levels over the interval of cosine distance values present in the data. By performing leave-one-out experiments, we compute the true positive rate (TPR) and the false positive rate (FPR), plotted on the y and x axes, respectively, in Fig. 5.

Fig. 5.

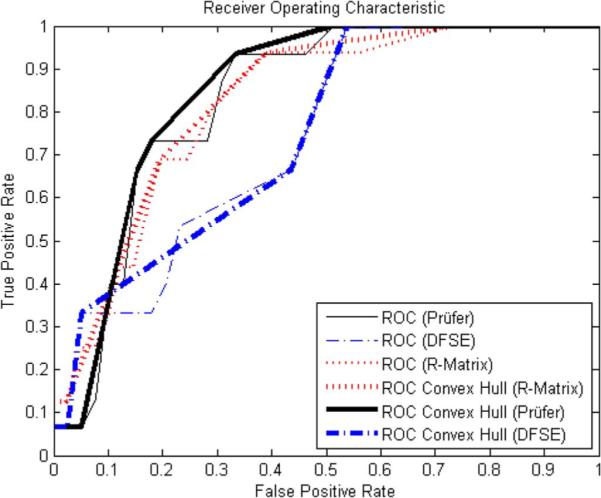
Receiver operating characteristic curves plotting classification TPR against FPR for Prüfer, DFSE, and R features.

The area underneath the ROC curve was 0.83 when using the Prüfer encoding to represent the trees, 0.74 when using the depth-first string encoding, and 0.82 when using R-matrix coefficients with the k-nearest neighbor classifier presented in this paper.

Finally, we visually examined 8 cases that the classifier consistently misclassified. Due to our random sampling procedure on a binary classification problem, we consider an image consistently misclassified if its predicted class was incorrect in at least half of the runs in which it appeared. We observed that NF trees misclassified as RF tended to have deeper left canonical subtrees, similar to the overall canonical structure of correctly classified RF trees, while RF trees misclassified as NF tended to have deeper right canonical subtrees, similar to the overall canonical structure of correctly classified NF trees. Representative examples of misclassified trees are shown in Fig. 6. Note that, as the canonical tree is built with Strahler numbers, which represent branching probabilities at various levels of the tree, this may indicate that true (i.e., correctly classified) NF trees are more likely to branch than RF trees. We also noted that the misclassified trees tended to be difficult to visualize and trace, suggesting that misclassifications may be due to error in the manual tracing of the ducts (Fig. 6).

Fig. 6.

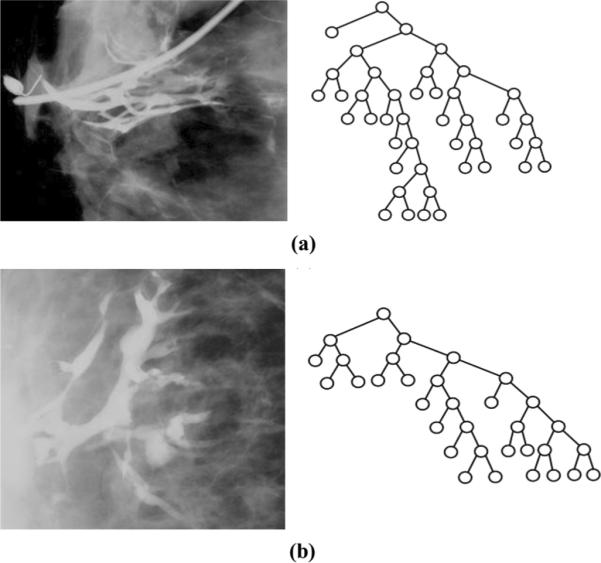
Examples of misclassified (a) NF and (b) RF images and canonical trees.

V. CONCLUSION

We present a methodology for characterizing and classifying tree-like structures in medical images. Our approach combines symbolic graph representation with text mining techniques. We use string encoding algorithms, such as the depth-first string encoding and the Prüfer encoding to construct a unique characterization string for each tree-like structure. We further perform tf-idf weighting, to assign a significance weight to each string term (i.e., node label). Our methodology was applied to breast ductal trees manually extracted from clinical X-ray galactograms. The images were divided into two groups; those with no reported galactographic findings (NF) and those with reported findings (RF). We performed similarity searches and classification experiments based on the cosine similarity distance metric. The experimental results illustrate the potential of the proposed tree characterization and classification framework to be employed for the analysis of tree-like structures in medical images. Our best results outperformed previous results obtained by a state-of-the-art method applied to the same dataset. Moreover, our approach has the advantage of constructing characterization strings that uniquely represent the tree structures and can be considered as signatures for the corresponding original trees; these signatures can also be used for indexing medical image databases where images visualizing tree-like structures need to be stored and managed. Although here we performed the string encoding process manually, one possible direction for future work is the use of kernel learning techniques, such as those described in [28], to automatically determine compact encodings. Extending canonicalization to multi-way trees is another possible area of future work. Finally, another possibility is to develop features that represent other branching properties, such as branch length, angle, and tortuosity. The proposed methodology has the potential to assist in investigating associations between branching patterns of tree-like structures in medical images and corresponding function or pathology.

TABLE I.

Obtained Precision for Similarity Search Experiments Based on the Cosine Similarity Distance Metric When Using the Depth-First String Encoding and the Prufer Encoding

Depth-First String Encoding
k	Precision
	NF	RF	Total
1	100.00 %	96.67 %	98.33 %
2	83.97 %	71.67 %	77.82 %
3	70.09 %	67.04 %	68.56 %
4	63.68 %	61.67 %	62.67 %
5	62.14 %	61.33 %	61.74 %

Prüfer Encoding
k	Precision
	NF	RF	Total
1	100 %	100 %	100 %
2	89.32 %	83.33 %	86.32 %
3	79.77 %	77.04 %	78.40 %
4	73.82 %	71.67 %	72.75 %
5	69.49 %	70.67 %	70.08 %