Different motion cues are used to estimate time-to-arrival for frontoparallel and looming trajectories

Abstract

Estimation of time-to-arrival for moving objects is critical to obstacle interception and avoidance, as well as to timing actions such as reaching and grasping moving objects. The source of motion information that conveys arrival time varies with the trajectory of the object raising the question of whether multiple context-dependent mechanisms are involved in this computation. To address this question we conducted a series of psychophysical studies to measure observers’ performance on time-to-arrival estimation when object trajectory was specified by angular motion (“gap closure” trajectories in the frontoparallel plane), looming (colliding trajectories, TTC) or both (passage courses, TTP). We measured performance of time-to-arrival judgments in the presence of irrelevant motion, in which a perpendicular motion vector was added to the object trajectory. Data were compared to models of expected performance based on the use of different components of optical information. Our results demonstrate that for gap closure, performance depended only on the angular motion, whereas for TTC and TTP, both angular and looming motion affected performance. This dissociation of inputs suggests that gap closures are mediated by a separate mechanism than that used for the detection of time-to-collision and time-to-passage. We show that existing models of TTC and TTP estimation make systematic errors in predicting subject performance, and suggest that a model which weights motion cues by their relative time-to-arrival provides a better account of performance.

Introduction

The ability to compute time-to-collision is critical to a number of different tasks encountered in everyday situations. Both catching and avoiding an oncoming object require the observer to estimate not only where the object is traveling, but also when it will reach its destination. This is especially relevant in the case of objects traveling directly towards the observer, which are potentially hazardous if not accurately detected. But observers often need to estimate the arrival times of objects traveling on non-collision courses as well. When deciding whether to cross a road, for example, it is important to be able to estimate how long an approaching car will take to reach the intersection, even when this point still lies some distance from the observer.

Computationally, the estimation of time-to-arrival for an object moving with frontal plane crossings (either head-on trajectories, time-to-contact, TTC, or on passage courses, time-to-passage, TTP) and medial plane crossings (“gap closures”, GC) are strikingly similar. It has been proposed that a prominent source of information for TTC judgments is the estimation of tau by the ratio of an object’s size to its rate of expansion (Hecht & Savelsbergh, 2004, Lee, 1976). Although this provides a reliable estimate of TTC in many situations, it has been shown that observers incorporate a number of addition sources of information, including binocular disparity (Gray & Regan, 1998, Gray & Regan, 2004, Rushton & Wann, 1999), vertical velocity (Brouwer, Lopez-Moliner, Brenner & Smeets, 2006), and models of gravity (McIntyre, Zago, Berthoz & Lacquaniti, 2001, Zago & Lacquaniti, 2005).

One extension of tau, termed ‘tau-margin’ was formulated by Bootsma & Oudejans (Bootsma & Oudejans, 1993) to encompass changes in both angular size (looming) and the angular gap size (φ and , respectively). They noted that the tau-margin, or time-to-arrival, can be specified as:

$$\frac{1}{{\tau }_m}=\frac{d\left(\ln \phi \right)}{\mathit{dt}}-\frac{d\left(\ln \theta \right)}{\mathit{dt}}$$

This general solution simplifies to the TTC condition as proposed by Lee (1976) when the object moves on a head-on trajectory (d /dt=0), and to the simple 2D gap closure condition when the object does not expand (dφ/dt=0). Psychophysically, Bootsma & Oudejans showed that observers are sensitive to the combination of these optical variables, though with unequal weighting. A variation of tau-margin based on expansion and angular bearing, termed composite tau, was proposed by Bootsma & Craig (2002). They found that observers were sensitive to both the expansion and bearing components of object motion trajectories, including during observer self-motion. However, tau components based on expansion and bearing are both based on frontal plane crossings, so it is unclear whether observers would use the same information when judging medial plane crossings.

The formulation of tau is based on a first-order description of object velocity, and thus does not account for accelerations. Lee et al (Lee, Young, Reddish, Lough & Clayton, 1983) found that observers performed interceptive motor actions based on the linear tau estimate, even when presented with accelerating objects. In medial plane crossings (gap closures), Benguigui, Ripoll & Broderick (2003) found that subjects were in general poor at accounting for accelerations, lending support to the suggestion that judgments of gap closure are also based on a first-order tau estimate. A similar result was reported in estimates of time-to-passage (TTP), in which an object moved in depth but not on a collision course to the observer (Kaiser & Hecht, 1995, Kaiser & Mowafy, 1993). Together, these results suggest that time-to-arrival judgments are in general based on combination of unambiguous first-order velocity estimates. However, few studies have addressed the implications or use of a combined-cue tau computation for estimating arrival time for all motion conditions.

A significant question therefore is whether the computation of time-to-contact, time-to-passage and gap-closure are performed as part of a broader, 3D mechanism which computes time-to-arrival regardless of where the collision point lies, or whether the brain has a separate mechanism devoted to detecting objects moving on a collision course with the observer (compared to gap closure, for example). This distinction is complicated by the fact that for a number of common visual tasks, the predictions of the tau-margin model are similar to those based on angular or expansion velocity information alone.

The presence of separate mechanisms for looming (TTC) and gap-closure is supported by a recent functional imaging study by Field and Wann showing differences in the brain areas activated during TTC and gap closure tasks (Field & Wann, 2005). They found that TTC specifically activated sensorimotor networks involved in reach-to-grasp movements. This suggests that the brain may utilize specific cortical networks for TTC estimation in the case of head-on collisions, rather than implementing the general tau-margin computation.

To address whether human observers use a single or multiple mechanisms for time-to-arrival detection, we developed an experiment in which we manipulated the cues available to subjects while estimating gap closure, TTC and TTP. Specifically, we used time-to-arrival tests in which irrelevant motion (in a dimension not related to the task) was added to the stimulus. In the gap closure task, a depth motion component was added to the stimuli, whereas for TTC and TTP tasks, a horizontal motion component was added, manipulating the perceptual information directly available to the observer while maintaining the actual arrival times. These stimuli provide test cases in which current models of time-to-arrival estimation make different predictions. We measured observer sensitivities and biases (the preference for selecting an object with irrelevant motion information) and compared them to noise-constrained time-to-contact models to show different cue-dependences for the estimation of gap closure, TTC and TTP.

Materials and Methods

Subjects

Twelve subjects, ages 18-36 (mean age 23.8, sd=5.3, 6 male, 6 female), participated in the experiments. All subjects had normal or corrected to normal vision and were recruited from the undergraduate and graduate populations at Boston University, Marquette University and the surrounding areas. Two subjects, FC and SB, were authors while all other subjects were experienced psychophysical subjects, but naïve to the purposes of the experiments. All subjects gave written consent before participating in accordance with the Institutional Review Board Committees on research involving human subjects at Boston University and Marquette University.

Apparatus

Participants viewed the visual display from a distance of 60 cm, with head position fixed by a chin and forehead rest. Stimuli were displayed on a 23” Apple Cinema Display and were generated in Matlab using the Psychophysical Toolbox (Brainard, 1997, Pelli, 1997) and OpenGL libraries. Stimuli were viewed binocularly, though motion-in-depth was indicated only by looming motion cues (no stereo information was given).

Stimulus

The stimulus contained two spherical objects positioned along the horizontal midline on either side of a central fixation mark. Objects had a mean luminance of 28 cd/m² on a background of luminance 0.3 cd/m², and were labeled “1” and “2” throughout the trial. The motion of each object was calculated so that it moved to cross the medial plane ($\stackrel{.}{x}$ as shown in Figure 1, moving toward the fixation mark; Experiment 1, “gap closure”), or the frontal plane ($\stackrel{.}{z}$, moving directly toward the subject; Experiment 2, time-to-contact, or moving parallel to the observer’s line of sight Experiment 3, time-to-passage). Note that we use GC, TTC and TTP to refer to the experimental condition, though in all cases subjects were making a time-to-arrival judgment, with the arrival point defined by the condition.

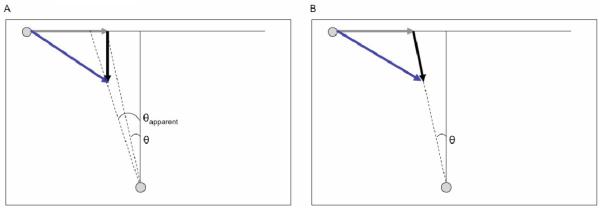
Figure 1.

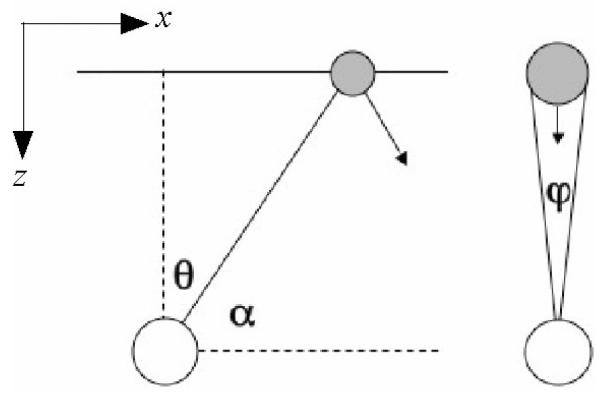
Optical variables computed and used by the model for estimating time-to-arrival.

In each case, subjects viewed the objects for 500 ms with object speeds calculated so that the first-arriving object reached the collision point one second after stimulus onset. The later-arriving object’s speed was determined such that it reached the collision point 50, 100, 300, 500 or 700 ms later. The eccentricity of each object was chosen randomly (between 2.8 and 9.5°) on each trial to randomize both the distances between the objects and collision point as well their speeds (by changing the distance traveled while maintaining a fixed time-to-arrival). Objects had an initial size of ~1.5°, and the expansion rates in the TTC condition depended on the time to arrival: the first arriving object (1 sec after stimulus onset) had a mean expansion rate of 2.9° sec⁻¹, with expansion rates slowing for later arriving objects, ranging from 2.7° sec⁻¹ for 50ms to 1.2° sec⁻¹ for 700ms. Note that these are averages across trials, however, and that randomization of the objects initial location made relying on speed information alone inaccurate.

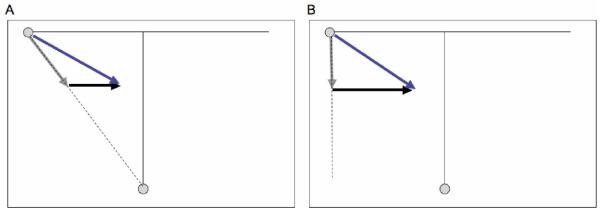
In each experiment, subjects performed an additional condition in which an irrelevant motion vector was added to the trajectory of one of the objects (selected randomly on each trial). For Exp 1 (gap closure), this consisted of a looming motion vector implemented in one of two ways. In the pure-depth looming condition, the additional motion vector was added as a motion-in-depth component perpendicular to the object’s horizontal trajectory ($\stackrel{.}{z}$, Figure 2A). This increased the object’s apparent 3D velocity, but did not affect the horizontal motion component ($\stackrel{.}{x}$), and therefore did not change the time at which the object would cross the medial plane. However, by having a motion-in-depth ($\stackrel{.}{z}$) component, the angular speed ($\stackrel{.}{\theta }$) of the object was decreased. In contrast, in the towards-observer looming condition, an irrelevant looming motion component was added in the direction of the observer (Figure 2B). This kept angular speed ($\stackrel{.}{\theta }$) constant, but added a horizontal motion component to the object’s trajectory, causing it to move faster towards the fixation in world-centered coordinates ($\stackrel{.}{x}$).

Figure 2.

Stimulus schematic for Exp 1 (gap closure) with depth motion components (bold black line) added to the horizontal motion vectors (gray). (A) Pure-depth looming added motion perpendicular to the horizontal component, thus decreasing the angular speed of the object. (B) Towards-observer looming added motion in the direction of the observer thus maintaining angular position and speed.

For Exps 2 & 3, an irrelevant horizontal motion vector was added to the object vectors (Figure 3). In both cases, the relevant motion component was motion-in-depth, so adding a horizontal component did not change the true arrival time of the object to the frontal plane of the observer.

Figure 3.

Irrelevant motion conditions for (A) Exp 2 (time-to-contact) and (B) Exp 3 (time-to-passage). In both cases, the irrelevant motion vector was a horizontal motion component (bold black line). The original object trajectory is shown with a dashed line.

During each trial, subjects were instructed to report which object would have passed the medial plane (i.e., the fixation mark, Exp 1), or passed through the subject’s frontal (depth) plane (Exps 2 & 3) first. Subjects were told which experimental condition was being tested, but were not instructed about whether there would be irrelevant motion cues added. Data were collected in a pseudo-randomized sequence of constant stimulus blocks. Each block consisted of 50 trials per level, with 5 levels per block. In the basic discrimination tasks, percent correct performance was examined as a function of the difference in arrival time between the sooner and later arriving object, between 50 and 700 ms. In the irrelevant motion conditions, percent correct performance was examined as a function of the velocity of the irrelevant motion, chosen based on pilot data (five levels between 0 to 20 cm/sec of looming velocity for GC, 0 to 8 cm/sec of horizontal velocity for TTC and 0 to 20 cm/sec of horizontal velocity for TTP). The difference in arrival time between the objects was held constant at 300 ms for all irrelevant motion conditions. For the irrelevant motion TTP condition, blocks consisted of 25 trials per speed to keep separate results for positive and negative velocities (positive velocities were perturbations towards the observer, negative away from the observer) while still collecting 50 trials per data point. Data were analyzed and compared to various optical computations (see Model below) both in terms of performance (proportion of trials answered correctly) and bias (proportion of trials where the response was to select the object that had the irrelevant motion vector added).

Model

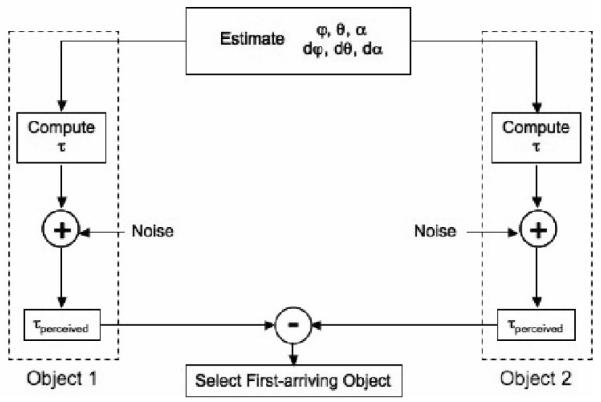
To quantitatively compare subjects’ performance to potential confounds in the computations of time-to-arrival, we developed a simple model framework (Figure 4). The model involves estimation of the optical variables for looming (φ) and gap angle (θ), as well as a third angle, denoted by α, which characterizes the angular difference between the object’s location and the observer’s depth plane. Although α is simply the complement of θ, it has the computationally useful property of not changing sign, nor approaching zero during the time course of the object’s trajectory.

Figure 4.

Model framework for comparing predictions of different time-to-arrival computations. Each branch represents the computation of time-to-arrival for one object, with the final stage being a comparison of the two estimates in order to perform the 2AFC task, i.e., which object arrives first?.

After estimating each angle and their derivatives for every pair of frames, the model estimated time-to-arrival for each object by one of several computations, detailed below. The time estimate was perturbed by an additive Gaussian noise, whose variance was determined assuming an equal variance Gaussian signal detection model. The standard deviation of the noise (and corresponding variance) was estimated by applying a least-squares cumulative Gaussian fit to subjects’ performance as a function of the difference in arrival times when the irrelevant motion was not present. Since subjects performed a 2AFC task, and noise was applied to both time-to-arrival estimates, the fitted sigma was divided by $\sqrt{2}$ and used for the noise estimate applied to each objects time-to-arrival.

Performance was examined for five computations of time-to-arrival (Table 1). For the gap closure task, predicted performance was computed on the basis of angular motion alone, and for the tau-margin formulation presented by Bootsma & Oudejans (1993), with the angular term based on θ (the angle between the object and the observer’s line of sight). For the TTC task, we compared performance based on a looming-only computation and τ_margin (using α instead θ to reflect the change in trajectory endpoint and therefore a change in the angle being closed by the objects), and a weighted version of the τ_margin formula, called τweighted. The weights for τweighted were determined based on the relative τ components, such that w_α=((1/τ_α)/(1/τ_α+1/τ_φ))². Note, however, that this formulation is atypical: since the dα/dt term is always negative for TTP estimates, the weights here are not bounded between 0 and 1. Furthermore, squaring the terms, which was done to rectify the signs, is not theoretically justified. We present this model, therefore, as an example of a well-performing model, and not as a justifiable hypothesis of the underlying mechanism. Finally, the TTP task was compared to the same three models as TTC, as well as to global tau (e.g. (Tresilian, 1991).

Table 1.

Computations of time-to-arrival (τ) used with the model as a comparison to subject performance. Note that in the TTC/TTP tasks where objects move towards the observer’s depth plane, rather than fixation, α is the gap being closed, and is used in place of θ for τ_margin.

Computation	Equation
Angular motion only	${\tau }_{\mathrm{angular}}=\frac{\theta }{d\theta /\mathit{dt}}$
Looming motion only	${\tau }_{\mathrm{loom}\mathrm{ing}}=\frac{\phi }{d\phi /\mathit{dt}}$
Tau-margin	$1/{\tau }_{\mathrm{margin}}=\frac{d\theta /\mathit{dt}}{\theta }-\frac{d\phi /\mathit{dt}}{\phi }$
Global tau	${\tau }_{\mathrm{global}}=\frac{\theta }{d\theta /\mathit{dt}}$
Weighted tau-margin	$1/{\tau }_{\mathrm{weighted}}=w_1\frac{d\phi /\mathit{dt}}{\phi }+w_2\frac{d\alpha /\mathit{dt}}{\alpha }$

Model performance was obtained by simulating the exact trials that were presented to the psychophysical subjects. For each trial, the optical variables φ, θ and α were computed, as well as their differences (to approximate the derivatives) for each pair of frames. The time-to-arrival was then estimated for each pair of frames according to the equations in Table 1, and mean was taken across time. Noise was added to each averaged time-to-arrival estimate, then the time-averaged estimates for each object were compared in order to select a first-arriving object. Performance was measured as the proportion of trials in which the model correctly selected the object that arrived first, and bias was measured as the proportion of trials in which the model selected the object that had the irrelevant motion vector added to its trajectory. The model was run separately for each subject so that the mean and standard deviation (across simulated observers) was comparable to the psychophysical data.

Results

In each experiment, we first measured the ability of subjects to detect which of the two objects would reach its collision point first as a function of the true difference in arrival time. We then performed the irrelevant motion conditions with a fixed difference in arrival time between the objects of 300 ms. It has been proposed that subjects may be able to estimate time-to-arrival for both looming and gap closure tasks from a single computation (Bootsma & Oudejans, 1993). An implication of the single-model implementation is that the estimation of time-to-arrival should depend on both looming and angular motion cues, no matter which task is being performed. To test the hypothesis that a single mechanism underlies 3D time-to-arrival estimation, we added irrelevant motion cues to the gap closure (GC), time-to-collision (TTC) and time-to-passage (TTP) tasks.

In the basic discrimination task, performance was similar among the three time-to-arrival judgments, with discrimination rates increasing with the difference in arrival times (Figure 5). There was a slight difference among tasks, with TTC having the highest detection rates and gap closure the lowest. A 2-way (3×5) ANOVA with factors for task type and difference in arrival time showed significant main effects of task type (F_2,165=6.97, p=0.001) and difference in arrival times (F_4,165 =130.07, p<0.001)¹. A post-hoc Tukey-Kramer multiple comparisons analysis showed significant differences (p<0.05) between TTC and gap closure (TTC performance was 5.35% higher, with 95% confidence intervals, CI, of 1.9 to 8.8%) and between TTP and gap closure (TTP 3.9% higher with CI=0.4 to 7.4%), but no significant difference between TTC and TTP (TTC 1.4% higher, CI=−2.0 to 4.9%).

Figure 5.

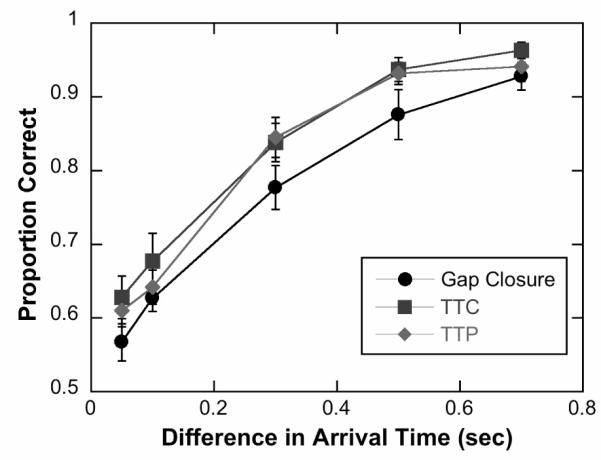
Mean performance across subjects for each of the three task conditions, gap closure (Exp 1, filled circles), time-to-contact (Exp 2, filled squares) and time-to-passage (Exp 3, filled diamonds). Error bars correspond to s.e.m. across subjects.

Performance was fit to a cumulative Gaussian function, resulting in best-fit sigma values of 283 ms for TTC, 304 ms for TTP, and 415 ms for GC. These standard deviations were used to constrain the ideal observer model: the noise applied to the estimate of each object’s time-to-arrival was normally distributed with a standard deviation equal to the best-fit sigma divided by $\sqrt{2}$ to account for the 2AFC task. One explanation for the relatively poorer GC performance is that since the objects did not approach the observer in those trials, the objects had a smaller mean size (over the course of the trial) than in TTC and TTP making them somewhat harder to detect.

Experiment 1: Gap closure

We first tested whether subjects in the gap closure task were susceptible to the addition of looming motion. We compared two types of depth motion components to determine the underlying cues being used in this task: pure-depth motion, in which the motion vector was added perpendicular to the object’s horizontal motion (changing the object’s angular speed, but not it’s true arrival time), and towards-observer looming (maintaining the angular speed present in the GC stimuli which did not have irrelevant motion added, but changing the object’s true world-centered speed and arrival time). We found that performance in the pure-depth condition dropped as larger looming velocities were added at a rate of 0.46% correct per cm/sec of looming velocity (Figure 5; linear regression slope: t=−2.84, p=0.006). In the towards-observer looming, on the other hand, there was no change in performance as looming velocity was added (Figure 6; slope: t=−0.14, p=0.88).

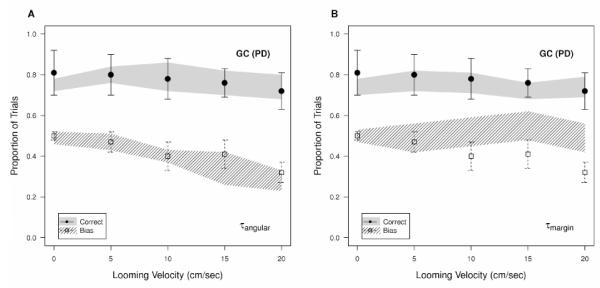
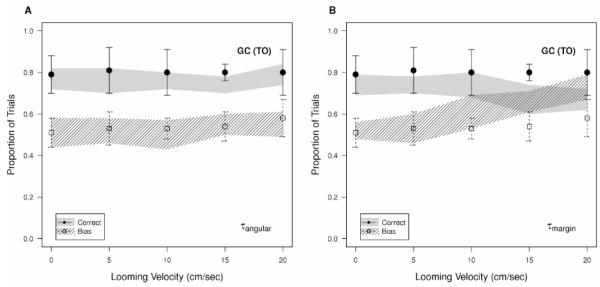
Figure 6.

Comparison of performance (solid circles for human subjects, solid shaded area for the model) and bias (open squares for human subjects, dashed region for model) in the gap closure pure depth looming motion condition. Human psychophysical data is compared to (A) a model based on angular velocity alone, and (B) a model using the τ_margin formulation. Error bars and shading are ±1 standard deviation across subjects and model simulations respectively.

A single, 3D mechanism sensitive to both looming and angular motions could predict the change in performance in the pure-depth condition in one of two ways. If subjects used an estimate of the object’s 3D velocity, then they would be biased to choose the object that had the irrelevant motion added, since it had a higher 3D speed. On the other hand, if subjects relied only on angular motion cues (rather than the true, world-centered motion), then they would underestimate the arrival time of the object since its angular speed decreased, and thus be biased against choosing the object with the irrelevant velocity component. Since either bias would result in a decrease in performance, both could explain the drop in performance as the irrelevant velocity increased. We tested this by calculating bias as the proportion of trials in which observers chose the object with irrelevant velocity (Figure 6).

In the pure-depth condition, there was a consistent decrease in bias, indicating that subjects became less likely to pick the object with irrelevant (looming) motion added as the velocity of the irrelevant motion increased. In the towards-observer condition, there was a slight increase in bias as looming motion was added. A careful analysis of our stimuli revealed that the increase in bias is likely due to a small (~5%) increase in angular speed in the towards-observer condition. This arose as a result of the way in which the horizontal offset was calculated on each frame, after the irrelevant looming stimulus had already been applied. Thus, the same horizontal offset at the end of the stimulus (after the object had approached the observer) produced a larger angular position shift than it did at the beginning of the stimulus.. If the difference in performance is due to this additional angular velocity, then an ideal observer model based exclusively on angular motion should match the biases for both irrelevant motion conditions (as we indeed see in Figure 6).

To quantitatively assess what cues could have driven observer performance in the irrelevant motion conditions, we performed simulations using the same stimuli that were presented to the subjects with time-to-arrival computed based on angular motion only (τangular) or angular and looming motion (τ_margin). In the pure depth condition, it is difficult to distinguish performance between the computations on the basis of % correct, since there is only a small change (~10%) in the human performance (Figure 6, closed circles). However, the two computations make significantly different predictions in terms of bias (Figure 6, open squares): τ_margin predicts that subjects should be unaffected by the presence of the irrelevant (looming) motion vector, whereas the use of angular motion alone (τangular) captures (though slightly overestimating) the decreasing bias shown by observers.

In the towards observer condition, in which the irrelevant looming motion is added as a vector directly towards the observer, we see a similar result. Although both models slightly underestimate performance, τ_margin predicts a drop in performance as looming motion is added, mirroring the strong bias towards selecting the object with the looming vector. However, τangular predicts a relatively constant performance, with only a very slight increase in bias due to looming, and providing a much more accurate account of subject performance.

The results from these tasks, combined with the quantitative predictions of both computations, strongly suggest that subjects were not significantly affected by the presence of looming in the stimuli and instead based their responses almost exclusively on the angular velocity of the object.

Experiment 2: Time-to-contact

To determine the cues used by subjects in the TTC task, we added an irrelevant horizontal motion component to the looming trajectory of one object. This did not change the arrival time of the object, and subjects were instructed (in all cases) to report which object passed through their depth plane first, regardless of whether it moved directly on a collision course.

The addition of horizontal motion in the TTC task caused a significant decrease in performance (Figure 7). A linear regression analysis of the change in performance as a function of angular velocity showed a significant effect of horizontal motion with a mean decrease of 1.4% per cm/sec (t=−3.15, p=0.002), indicating that the discrimination of TTC was sensitive to angular motion.

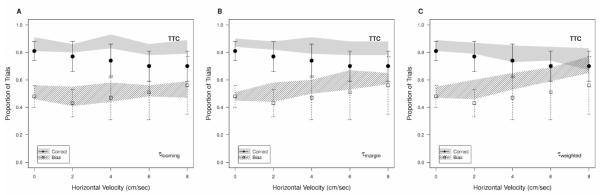
Figure 7.

Comparison of performance (solid circles for human subjects, solid shaded area for the model) and bias (open squares for human subjects, dashed region for model) in the gap closure towards observer looming motion condition. Human psychophysical data is compared to (A) a model based on angular velocity alone, and (B) a model using the τ_margin formulation. Error bars and shading are ±1 standard deviation across subjects and model simulations respectively.

We compared performance when estimating arrival time from τlooming, based on the looming motion only (from Lee 1976), τ_margin, incorporating both looming and angular motion (Bootsma & Oudejans 1993), and τweighted. None of the models fully captured the magnitude of the performance drop as horizontal motion was added to the TTC stimulus (Figure 8), though τweighted did show a decreasing performance trend. The models provided a reasonably accurate approximation of the bias, which increased modestly as the horizontal velocity component was added.

Figure 8.

Comparison of performance (solid circles for human subjects, solid shaded area for the model) and bias (open squares for human subjects, dashed region for model) in the TTC task with irrelevant angular motion added. Human psychophysical data is compared to (A) a model based on looming velocity alone, (B) a model using the τ_margin formulation, and (C) a model using the τ weighted formulation. Error bars and shading are ±1 standard deviation across subjects and model simulations respectively.

Experiment 3: Time-to-passage

As in the TTC task, we examined whether estimates of TTP would be affected by the inclusion of additional irrelevant horizontal motion. Since the objects moved on passage courses, we were interested whether there was a difference between adding horizontal motion that made the object’s trajectory approach the observer more closely, a horizontal motion towards the center of the display (positive velocities), compared to adding horizontal motion that put the object on a trajectory moving further away from the observer (negative velocities). The subjects’ average performance in the TTP task is shown in Figure 9. A 2-way (5×2) ANOVA with speed and direction of the added velocity as factors showed significant main effects for both speed (F_{(4, 102)}=8.21, p<0.001) and direction (F_{(1, 102)}=16.68, p<0.001), with positive velocities (those causing the object to move closer to the observer) easier to detect than negative velocities (Figure 9, solid circles). As in TTC, the effect of irrelevant horizontal motion (positive or negative), suggests that TTP responses were heavily affected by the addition of angular motion. Subjects’ performance also showed an elevation in bias (tendency to choose the object with horizontal motion added) as the horizontal velocity increased.

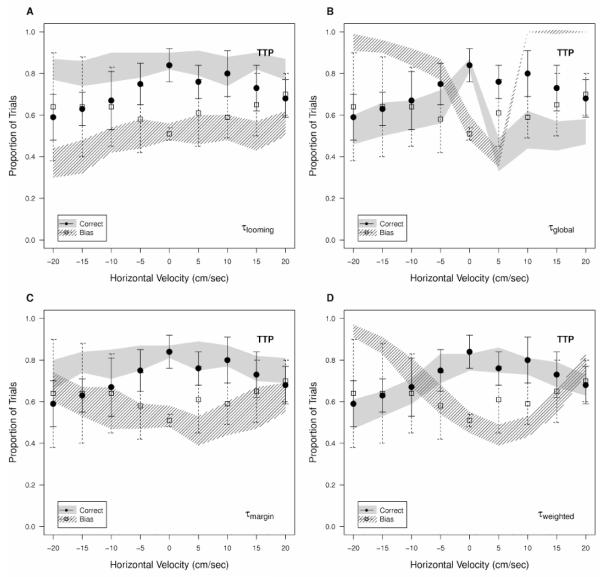
Figure 9.

Comparison of performance (solid circles for human subjects, solid shaded area for the model) and bias (open squares for human subjects, dashed region for model) in the TTC task with irrelevant angular motion added. Human psychophysical data is compared to (A) a model based on looming velocity alone, (B) a model based on global τ, (C) a model using the τ_margin formulation, and (D) a model using the τweighted formulation. Error bars and shading are ±1 standard deviation across subjects and model simulations respectively.

We again compared subject performance to model performance based on several different forms of TTP computation: looming only, τ_margin, τweighted, as well as global tau, which has been proposed as a means of estimating passage time during observer motion. Estimating time-to-arrival on the basis of looming alone, even though the objects were not directly approaching the observer, provided a highly accurate estimate of TTP in our stimuli. However, both the level and form of the response was inconsistent with subjects’ performance on the task, making it unlikely subjects relied on this cue. The computation of global tau also presented problems: although accurate when no horizontal velocity was present (in which case the object’s trajectory was parallel to the observer’s line of sight), it proved highly inaccurate for trajectories that included both depth and a horizontal velocity shifting the trajectory relative to the observer’s midline.

Instead, a combination of estimates based on looming and angular motion cues provided the best account of subject performance. The tau-margin computation captured the drop in performance as horizontal velocity was added, but greatly underestimated subjects’ performance decrease. That is, although the tau-margin model was computing fairly accurate arrival time estimates, subjects were much more error prone. The τweighted computation predicted both the decrease in performance as horizontal motion was added, as well as the asymmetry shown by increased performance for small, positive horizontal velocities (in which the object moved on a near collision path).

Similar results were found in the ability of the models to account for subject bias (Figure 9, open squares). The looming-only computation produced relatively unbiased performance, and failed to account for the increased likelihood of subjects to choose the object with horizontal motion as the speed of the irrelevant motion increased. Global tau predicted the opposite: when one object had a horizontal motion vector, it was selected dramatically more often. The tau margin formulation produced a compromise that provided a more accurate match to subject performance, with the bias gradually increasing as the horizontal motion vector increased. The weighted tau model, which most accurately estimated performance (though not bias), predicted an elevated bias with horizontal motion, but made systematic errors (specifically, overestimating the bias as the horizontal motion caused the object to move away from the observer very rapidly, i.e., velocities < -10 cm/sec), and suggests that other factors are likely to play a role, especially in extreme cases where the object poses no threat to the observer.

Discussion

Our psychophysical results demonstrate that subjects are able to estimate time-to-arrival for time-to-contact (TTC), time-to-passage (TTP), and gap closure with similar accuracy. Performance on the basic TTC and TTP tasks was not statistically different, whereas gap closure performance was significantly lower than both TTC and TTP. However, in performing these tasks, subjects appeared to utilize different optical cues when making time-to-arrival estimates, suggesting that they do not rely on a single, 3D time-to-arrival mechanism.

The irrelevant motion conditions were designed such that they did not affect the actual arrival times (except for the towards-observer gap closure condition), and thus any change in performance with the addition of irrelevant motion would suggest that subjects were obliged to use the irrelevant cue, even in situations where it provided no useful information in solving the task. Results from a variation of the gap closure task in which a looming vector (in the direction of the observer) was added to one object’s trajectory revealed that subject performance was not affected by the presence of looming motion cues. When the additional motion vector was added as a pure depth component (parallel to the observer’s line-of-sight, in which the looming object had a small reduction in angular speed), performance decreased as subjects became less likely to select the looming object. Model simulations showed that these performance and bias trends were quantitatively consistent with the use of angular motion alone, rather than a combination of angular and looming motion.

Results from TTC and TTP tasks, on the other hand, showed that observers were sensitive to angular motion induced by irrelevant horizontal motion (perpendicular to the line of sight). Subjects’ performance decreased in both tasks as a horizontal motion vector was added to one object’s trajectory. A comparison of performance and bias on both tasks to several time-to-arrival computational models suggest that performance was not likely to be governed by the use of looming alone or global tau. Instead, better performance was achieved by the use of combined cue models, such as tau-margin or weighted tau-margin computations. However, even in those cases the models failed to fully account for subjects’ performance. The tau-margin model did not fully capture the decrease in performance on the TTP task as horizontal motion was added, and the weighted tau-margin computation greatly overestimated subject bias for objects moving away from the observer.

Several factors may explain the discrepancies between these models and subject performance on the TTP task. First, we assumed a constant amount of noise in all trials, calibrated based on subjects’ individual performance estimating TTP with no horizontal velocity. If, instead, noise increases proportionally to angular velocity, then the performance of the tau-margin computation would be lower for the larger horizontal velocity conditions, and more similar to subject performance. Secondly, the main failing of the weighted tau-margin computation was an overestimation of the bias for conditions in which one object had a horizontal motion velocity moving it away from the observer’s line of sight. If human subjects use a cost function for selecting the first arriving object that includes a bias for selecting objects that are more like to collide with them, this could help reduce the overestimation of bias by this model.

Both the weighted and unweighted tau-margin computations suggest the possibility of a single mechanism available for estimating time-to-arrival regardless of the frame of reference. However, the results from the gap closure task suggest that it is not used in the case of an object moving towards a point located some distance in front of the observer, with angular motion alone being the likely relevant computation in this case. Thus, while TTC and TTP judgments are both reasonably consistent with the use of tau-margin, the pattern of subjects’ performance across conditions supports the use of two separate mechanisms: an angular motion mechanism for estimating arrival time for objects crossing the observer’s line of sight, and a tau-margin mechanism for objects passing through the observer’s depth plane.

Highlights.

• Estimates of time-to-arrival at the medial plane relies on angular motion alone.

• Estimates of time-to-arrival in at the frontal plane (TTC/TTP), on the other hand, depend on both angular and looming motion.

• Model results support a weighted tau computation for TTC/TTP.

• Suggests different time-to-arrival mechanisms depending on the object trajectory.