A dynamical model for generating synthetic Phonocardiogram signals

Abstract

In this paper we introduce a dynamical model for Phonocardiogram (PCG) signal which is capable of generating realistic synthetic PCG signals. This model is based on PCG morphology and consists of three ordinary differential equations and can represent various morphologies of normal PCG signals. Beat-to-beat variation in PCG morphology is significant so model parameters vary from beat to beat. This model is inspired of Electrocardiogram (ECG) dynamical model proposed by McSharry et al. and can be employed to assess biomedical signal processing techniques.

I. Introduction

Phonocardiogram (PCG) signal contains valuable information about electromechanical activity of human’s heart as it provides a quantitative and graphical representation of the heart sounds. There are two dominant and audible components of heart sounds, namely S1 and S2, and in some cases two more components, S3 and S4, and murmurs. These sounds are due to opening and closure of heart valves and also are a consequence of turbulent blood flow and vibrating cardiovascular structures. Some attempts have been made in recent years on modeling and synthesizing PCG signals. In general, these models can be divided in two groups: statistical and mathematical models. Statistical models are based on statistical properties of PCG, such as higher order spectra [1], [2]. The main drawback of the statistical models is that they ignore signal morphology. Therefore, they cannot be used for synthesizing realistic signals. In contrast, mathematical models are based on signal morphology and try to represent PCG time and frequency characteristics (e.g. [3], [4], [5]). In some other works, matching pursuit algorithm is used for analysis and synthesis of the phonocardiogram, but no explicit models are proposed [6], [7], [8].

In 2003, McSharry et al. [9] introduced an appropriate dynamical model for Electrocardiogram (ECG) signal based on its morphology which is capable of generating synthetic ECG signals. Lack of a dynamical model for generating artificial PCG signal and inspired by McSharry’s model for ECG we propose a dynamical model for PCG signal with ability of generating synthetic signal.

This paper is organized as follows. In Section ΙΙ the ECG dynamical model proposed by McSharry et al. is reviewed briefly. PCG morphology and proposed dynamical model are discussed in Section ΙΙΙ and investigated in Section ΙV. Section V concludes and discusses the future works for which the proposed dynamical model may be useful.

II. Review of ecg dynamical model

In 2003, McSharry et al. proposed a dynamical model for generating realistic synthetic ECG signal using a set of state equations that generates a three-dimensional (3-D) trajectory in a 3-D state space with coordinates (x, y, z). The model consists of a circular limit cycle of unit radius in the (x, y) plane around which the trajectory is pushed up and down as it approaches the P, Q, R, S and T points in the ECG. Quasi-periodicity of the ECG is reflected by the movement of the trajectory around the attracting limit cycle. The dynamical equations of motion are given by a set of three ordinary differential equations in Cartesian coordinates:

$$\{\begin{array}{l}\stackrel{.}{x}=\gamma x-\omega y\hfill \\ \stackrel{.}{y}=\gamma y+\omega x\hfill \\ \stackrel{.}{z}=-\sum _{i\in \{P,Q,R,S,T\}}{a}_i\mathrm{\Delta }{\theta }_{i}exp\left(-\frac{\mathrm{\Delta }{{\theta }_i}^2}{{{2b}_i}^2}\right)-(z-z_0)\hfill \end{array}$$ (1)

where $\gamma =1-\sqrt{x^2+y^2}$, Δθ_i = (θ − θ_i)mod 2π, θ = atan2 (y, x) is the four quadrant arctangent of the elements of x and y, ranging over [−π, π], and ω is the angular velocity of the trajectory as it moves around the limit cycle, and is related to the beat-to-beat heart rate as ω = 2πf. The baseline wander of the ECG is modeled with the parameter z₀ that is assumed to be a relatively low amplitude sinusoidal component coupled with the respiratory frequency f₂ using

$$z_0(t)=Asin(2\pi f_{2}t)$$ (2)

where A= 0.15 mV.

By neglecting the baseline wander term (z − z₀) in (1), and integrating ż equation, it can be seen that each component of the ECG waveform is modeled with a Gaussian kernel which has three parameters θ_i, a_i, b_i.

Values of the model parameters (θ_i, a_i, b_i) for each ECG beat can be obtained by fitting a curve made of sum of five Gaussian kernels to it. Typical values of these parameters for the P, Q, R, S and T points taken from [9] are shown in Table 1. The times and angles are relative to the position of the R-peak since it is always assumed to have zero phase and the ECG contents lying between two consecutive R-peaks are assumed to have a phase between 0 and 2π (or − π and π). Thus, the phase signal θ is available by simply detecting the R-peaks.

Table 1.

Typical parameters of the synthetic ECG model [9]

Index (i)	P	Q	R	S	T
Time (secs)	−0.2	−0.05	0	0.05	0.3
θi(radians)	$-\frac{\pi }{3}$	$-\frac{\pi }{12}$	0	$\frac{\pi }{12}$	$\frac{\pi }{2}$
ai	1.2	−5	30	−7.5	0.75
bi	0.25	0.1	0.1	0.1	0.4

The dynamic state equations proposed by McSharry et al. can also be written in polar coordinates as follows [10]:

$$\{\begin{array}{l}\stackrel{.}{r}=r(1-r)\hfill \\ \stackrel{.}{\theta }=\omega \hfill \\ \stackrel{.}{z}=-\sum _{i\in \{P,Q,R,S,T\}}\frac{{\alpha }_i\omega }{{b_i}^2}\mathrm{\Delta }{\theta }_{i}exp\left(-\frac{\mathrm{\Delta }{{\theta }_i}^2}{2{b_i}^2}\right)-(z-z_0)\hfill \end{array}$$ (3)

Above the a_i term in (1) are replaced with:

$$a_i=\frac{{\alpha }_i\omega }{{b_i}^2}i\in \{P,Q,R,S,T\}$$ (4)

where a_i are the peak amplitude of Gaussian kernels used for modeling each component of the ECG.

These new set of equations have some benefits compared to (1). The first equation in (3) shows the circular behavior of the generated trajectory by the model, which for any initial value of r ≥ 1 reaches to a steady state of r = 1 representing the limit cycle. The phase parameter θ has an explicit representation and indicates the angular location of the P, Q, R, S and T waves (Table 1). On the other hand, the second and third equations in (3) are independent from r, making the first equation redundant. Therefore the first equation may be excluded as it has no effect on the synthetic ECG.

III. PCG Model Description

A. Phonocardiogram Morphology

As mentioned before, a PCG beat consists of two distinct sounds, S1 and S2, sample waveforms of which are depicted in Fig. 1. Waveforms of heart sounds vary from subject to subject and beat to beat in amplitude, number of peaks and troughs, and spread in time. With all these differences, still there are some analogies among all waveforms. A closer look at the waveforms suggests the idea of damped sinusoids, since the frequency of vibration is almost constant along their waveforms. Besides, two or more Gaussian functions can model their envelope shapes. Hence considering these properties, we use Gabor kernels for modeling heart sounds. Analysis of different heart sounds shows that two Gabor kernels can represent each heart sound, S1 and S2, and in sum one heart beat of PCG signal can be modeled with four kernels as follows;

Fig. 1.

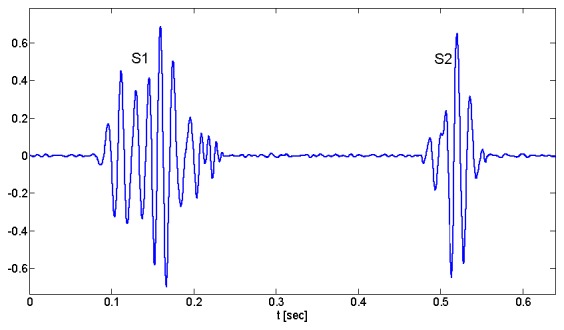
A phonocardiogram signal from a healthy person, containing the first heart sound (S1) and the second heart sound (S2).

$$Z(\theta )=\sum _{i\in \left\{S{1}^{-},S{1}^{+},S{2}^{-},S{2}^{+}\right\}}{\alpha }_i\text{e}xp\left(-\frac{{\left(\theta -{\mu }_i\right)}^2}{2{\sigma }_i^2}\right)\mathit{cos}\left(2\pi f_i\theta -{\varphi }_i\right)$$ (5)

where a_i, μ_i, and σ_i are the amplitude, center and width parameters of the Gaussian terms, and f_i, ϕ_i are frequency and phase shift of the sinusoid terms, respectively. θ is the independent parameter in radians which varies in the range [−π, π] for each beat. The −/+ superscripts indicate the two Gabor kernels which are used for modeling each heart sound.

B. Phonocardiogram Dynamical Model

Like McSharry’s model for ECG [9], the dynamic model for PCG generates a trajectory in a three-dimensional (3-D) state space with coordinates (x,y,z) that projection of the 3-D trajectory on (x,y) plane moves around a limit cycle of unit radius. Each revolution on this circle corresponds to one heart beat. Waveform of phonocardiogram signal is produced using the motion of the trajectory in the z direction. The dynamical equations of the trajectory of the model are given by a set of three ordinary differential equations,

$$\{\begin{array}{l}\stackrel{.}{r}=r(1-r)\hfill \\ \stackrel{.}{\theta }=\omega \hfill \\ \stackrel{.}{z}=-\sum _{i\in \{S{1}^{-},S{1}^{+},S{2}^{-},S{2}^{+}\}}\left(\frac{{\alpha }_i}{{\sigma }_i}\left({\theta }_i-{\mu }_i\right)\text{e}xp\left(-\frac{{\left(\theta -{\mu }_i\right)}^2}{2{\sigma }_i^2}\right)\mathit{cos}(2\pi f_i\theta -{\varphi }_i)+2\pi {\alpha }_i{f}_i\text{e}xp\left(-\frac{\left(\theta -{\mu }_i\right)}{2{\sigma }_i^2}\right)\mathit{sin}(2\pi f_i\theta -{\varphi }_i)\right)\hfill \end{array}$$ (6)

where θ = atan2(y, x) is the four quadrant arctangent of the real parts of the elements of x and y, with (− π ≤ θ ≤ π), and ω the angular velocity of the trajectory as it moves around the limit cycle and is related to beat-to-beat heart rate by $\omega (t)=\frac{2\pi }{R(t)}$ where R(t) represents the time series generated by the RR-process using the ECG signal. Considering ω constant, and integrating the third equation in (6), we reach to equation (5).

The equations of motion given by (6) are integrated numerically using a fourth-order Runge-Kutta method with a fixed time step Δt = 1/f_s where f_s is the sampling frequency of the synthetic PCG signal. Thus, both beat-to-beat heart rate and sampling frequency of the synthetic PCG signal can be adjusted.

A trajectory generated by (2) in three dimensions is depicted in Fig. 2. The z variable of this trajectory, when plotted versus time, represents the synthetic PCG signal with realistic morphology (Fig. 3).

Fig. 2.

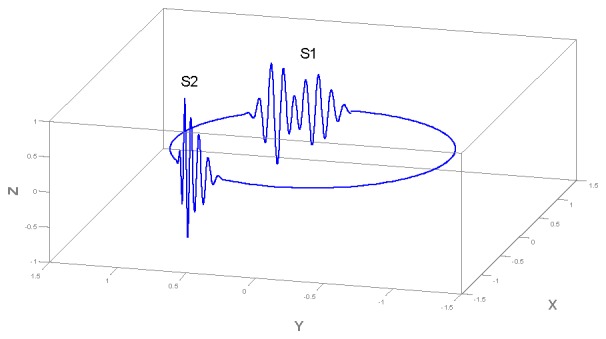
Typical trajectory generated by the dynamical model (2) in the 3-D space given by (x,y,z). Each entire movement around this trajectory is equivalent to one heart beat.

Fig. 3.

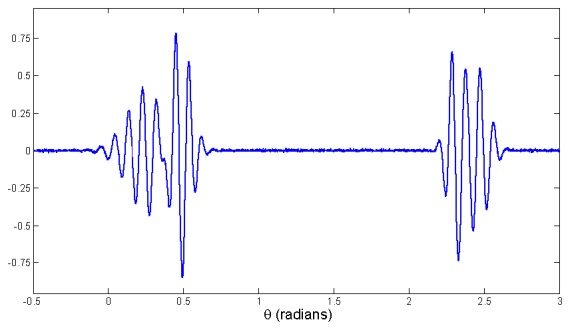
A PCG beat including two heart sounds, S1 and S2, generated by dynamical model.

There is a close relationship between events in electrocardiogram and phonocardiogram. For example, S1 occurs slightly after R-peak in ECG. To extract heart beats from PCG, a robust approach is by means of simultaneously recorded ECG signal; the middle point of each R-to-R distances is considered as the ending point of the previous beat and starting point of next beat and so PCG beats become distinguishable. The phase signal θ for each PCG beat is the same phase signal of the synchronous ECG.

PCG, in contrast to ECG, is less quasi-periodic and variation of PCG model parameters from beat to beat is significant and a little change in one parameter can probably generate an invalid heart sound waveform. So it is not convenient to represent these parameters by their mean values. But to give a visual perception of model parameters, Table 1 shows their mean values which are achieved by the analysis of normalized PCG of a healthy subject.

IV. Results

Synthetic heart sound waveform for one heart beat section is illustrated in Fig. 3. Observational uncertainty is considered by adding White Gaussian Noise to synthetic signal, yielding a similar signal to a section of real PCG from a normal human (Fig. 4.).

Fig. 4.

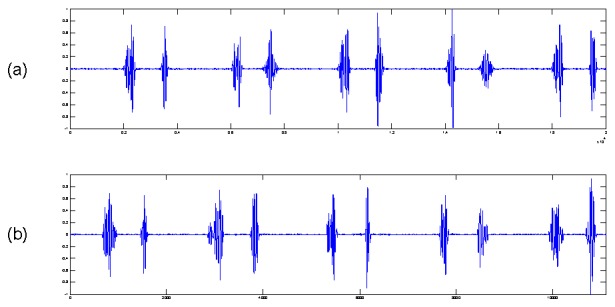
Comparison between (a) synthetic PCG with additive white Gaussian noise, and (b) real PCG from a healthy person.

V. Conclusion and future works

In this paper a new dynamical model for phonocardiogram has been introduced which is capable of synthesizing PCG signals with realistic morphologies. Model parameters may be chosen to generate various valid morphologies for synthesized heart sound waveforms. Sampling frequency and beat-to-beat intervals can also be chosen.

Having access to a realistic PCG provides a benchmark for testing numerous biomedical signal processing techniques.

A number of applications are perceivable for the model,

1. By fitting the model to the morphology of various normal PCGs, and extracting their model parameters, a database of realistic PCGs could be created.

2. The synthetic PCG could be used to evaluate the effectiveness of different techniques for denoising, heart sounds segmentation and compression.

3. Model-based PCG processing framework can be introduced in a similar way to ECG model-based processing framework (e.g. [10], [11], [12], [13]).

4. By finding a pattern or relation among model parameters of a normal heart sound, abnormal morphologies could be detected.

It is hoped that this model will be of interest for testing biomedical signal processing algorithms applied to PCG signals with different sampling frequencies and noise levels.

Table 2.

Mean value of the pcg model parameters given by (2)

Index (i)	S1−	S1+	S2−	S2+
ai	0.4250	0.6875	0.5575	0.4775
μi (radians)	$\frac{\pi }{12}$	$\frac{3\pi }{19}$	$\frac{3\pi }{4}$	$\frac{7\pi }{9}$
σi	0.1090	0.0816	0.0723	0.1060
fi	10.484	11.874	11.316	10.882
ϕi (radians)	$\frac{3\pi }{4}$	$\frac{9\pi }{11}$	$\frac{7\pi }{8}$	$\frac{3\pi }{4}$