Abstract
The bony labyrinth in the temporal bone houses the sensory systems of balance and hearing. While the overall structure of the semicircular canals and cochlea is similar across therian mammals, their detailed morphology varies even among closely related groups. As such, the shape of the labyrinth carries valuable functional and phylogenetic information. Here we introduce a new, semilandmark-based three-dimensional geometric morphometric approach to shape analysis of the labyrinth, as a major improvement upon previous metric studies based on linear measurements and angles. We first provide a detailed, step-by-step description of the measurement protocol. Subsequently, we test our approach using a geographically diverse sample of 50 recent modern humans and 30 chimpanzee specimens belonging to Pan troglodytes troglodytes and P. t. verus. Our measurement protocol can be applied to CT scans of different spatial resolutions because it primarily quantifies the midline skeleton of the bony labyrinth. Accurately locating the lumen centre of the semicircular canals and the cochlea is not affected by the partial volume and thresholding effects that can make the comparison of the outer border problematic. After virtually extracting the bony labyrinth from CT scans of the temporal bone, we computed its midline skeleton by thinning the encased volume. On the resulting medial axes of the semicircular canals and cochlea we placed a sequence of semilandmarks. After Procrustes superimposition, the shape coordinates were analysed using multivariate statistics. We found statistically significant shape differences between humans and chimpanzees which corroborate previous analyses of the labyrinth based on traditional measurements. As the geometric relationship among the semilandmark coordinates was preserved throughout the analysis, we were able to quantify and visualize even small-scale shape differences. Notably, our approach made it possible to detect and visualize subtle, yet statistically significant (P = 0.009), differences between two chimpanzee subspecies in the shape of their semicircular canals. The ability to discriminate labyrinth shape at the subspecies level demonstrates that the approach presented here has great potential in future taxonomic studies of fossil specimens.
Keywords: cochlea, inner ear, primate, Procrustes, semicircular canals, semilandmarks, shape space
Introduction
The bony labyrinth inside the petrous portion of the temporal bone houses the sense organs of hearing and balance. Characterized in therian mammals by three semicircular canals and a coiled cochlea (Luo et al., 2011) its morphology is highly conserved. Nevertheless, the detailed morphology varies even among closely related taxa and carries valuable functional, developmental and phylogenetic information (e.g. Spoor & Zonneveld, 1998; Schmelzle et al., 2007; Lebrun et al., 2010). Interspecific variation of the cochlea and semicircular canals among extant species has been associated with differences in sound perception and locomotor behaviour, respectively (Spoor et al., 2002a,b; Spoor et al., 2007; Spoor & Thewissen, 2008; Kirk & Gosselin-Ildari, 2009; Coleman & Colbert, 2010; Malinzak, 2010). Moreover, shape differences among labyrinths have been linked with differential development of the cranial base and brain (Spoor & Zonneveld, 1998; Jeffery & Spoor, 2004, 2006). As such, morphometric analyses of the bony labyrinth contribute to our basic understanding of the form-function relationship of two sensory systems, help infer the locomotor repertoire and hearing capability of fossil taxa (Fleischer, 1976; Ni et al., 2010; Silcox et al., 2009; Spoor et al. 1994, 2002a; Walker et al., 2008), give an insight into patterns of basicranial integration, and provide evidence for the taxonomic attribution and phylogenetic relationships of specific fossil specimens (Spoor, 1993; Hublin et al., 1996; Spoor et al., 2002a,b; Ladevèze et al., 2010; Lebrun et al., 2010; Macrini et al., 2010; Ekdale & Rowe, 2011).
Prior to the introduction of computed tomography (CT) the bony labyrinth could only be studied using the destructive and time-consuming techniques of dissection, casting and serial sectioning. Initial studies, most prominently Hyrtl (1845) and Gray (1907, 1908), explored the diversity of the mammalian labyrinth both qualitatively and quantitatively. Subsequently, however, the research focus largely shifted towards specific functional aspects of either the cochlea or the semicircular canals (Fleischer, 1973; Curthoys et al., 1977; Ramprashad et al., 1984; Blanks et al., 1985; Matano et al., 1985; Curthoys & Oman, 1987), although some further comparative work continued to be done (Yamada & Yoshizaki, 1959; Takahashi, 1971, 1976). It was the improved spatial resolution of medical CT that in the 1990s triggered a renewed interest in a wider comparative approach because the bony labyrinth of a wide range of extant and extinct mammalian taxa could now be investigated non-destructively (Ketten & Wartzok, 1990; Luo & Ketten, 1991; Spoor et al., 1994, 2002a,b, 2003; Hublin et al., 1996; Spoor & Zonneveld, 1998). Given the available image spatial resolution, smaller species could still not be included but, more recently, size limitations was removed when high-resolution microCT became widely available (Rook et al., 2004; Schmelzle et al., 2007; Sipla, 2007; Spoor et al., 2007; Georgi & Sipla, 2008; Walker et al., 2008,Silcox et al., 2009; Ladevèze et al., 2010; Lebrun et al., 2010; Macrini et al., 2010; Ni et al., 2010; David, 2011; Ekdale & Rowe, 2011). Over the last years, magnetic resonance imaging (MRI) has also been employed to study the bony labyrinth in a comparative context (Cox & Jeffery, 2008, 2010; Jeffery & Cox, 2010).
Early morphometric analyses of the bony labyrinth based on medical CT had to be limited to linear and angular measurements in the plane of scanning because the slice thickness and interslice distance rendered the third dimension too inaccurate (Spoor & Zonneveld, 1995). However, modern top-of-the-range medical CT, and especially microCT, produces image data sets which allow for full 3D metric analysis. Many quantitative studies based on such high-quality datasets still mostly employ basic linear measurements and angles (Rook et al., 2004; Schmelzle et al., 2007; Spoor et al., 2007; Ladevèze et al., 2010; Macrini et al., 2010; Ni et al., 2010; Ekdale & Rowe, 2011) but several more advanced analytical methods have been developed. Christensen et al. (2003) designed a method to obtain automatic volume, length and angle measurements of the bony labyrinth using a 3D deformable inner ear atlas. With clinical applications in mind, it is geared towards mapping differences between individuals of a single species (modern humans) and is less suitable for comparative studies analysing a wide range of labyrinth shapes. Georgi & Sipla (2008) employed elliptical Fourier analysis to quantify each semicircular canal individually but as 2D projections are used, this approach does not capture any out-of-plane morphology (torsion) or the spatial relationship among the three canals. In contrast, a number of recent studies have introduced methods to analyse the semicircular canals jointly and in 3D, as a major step forward in efforts to infer semicircular canal physiology in extant and fossil taxa (Ifediba et al., 2007; Cox & Jeffery, 2008; Bradshaw et al., 2010; David et al., 2010; Malinzak, 2010). Their approach is based on the computation of central streamlines of the canals and sometimes the utricle, extracted from virtual labyrinths. Finally, in a comparative study, Lebrun et al. (2010) use landmark-based geometric morphometric analysis to investigate to what extent the morphology of the bony labyrinth conveys information about the evolutionary history of strepsirrhine primate taxa. As such, it is the most sophisticated morphometric study of the bony labyrinth to date. However, a limiting factor is the type and number of landmarks used to describe the complex shape of the semicircular canals and cochlea, as most landmarks employed are type III (Bookstein, 1991) and are dependent on reference orientations based on other parts of the labyrinth. For example, the ‘superior-most point’ of the anterior canal depends on the orientation of the plane of the lateral semicircular canal to establish what is most superior. These landmarks are not truly homologous; two specimens with, for example, identical anterior canals but differently oriented lateral canals will have their superior-most point of the anterior canal placed differently. This issue is particularly important as only four or five landmarks are used for the cochlea and each semicircular canal, which is in itself insufficient to describe more complex morphologies, including the torsion and asymmetrical arc shapes of the semicircular canals.
Building on previous studies and following exploratory efforts (Gunz et al., 2009b) we introduce here a comprehensive geometric morphometric (GM) approach to shape analysis of the bony labyrinth, based on 3D semilandmarks. Two considerations were particularly important when we designed the measurement protocol. First, the 3D landmarks to be analysed should give a comprehensive representation of the overall size and shape of the labyrinth, including those aspects that are known to be either functionally or phylogenetically important. Secondly, the protocol should be flexible so that it can be used in combination with different 3D visualization methods and spatial resolutions.
The dataset of 3D landmarks introduced here pertains to the semicircular canals, the cochlea and the oval window. These are the components of the bony labyrinth that are well defined in terms of shape and size, and are functionally related to the sense organs of hearing and balance. The overall morphology of the vestibule largely reflects the spatial placement and size of the base of the cochlea, the oval window and the apertures of the canals (including their ampullae).
Each semicircular canal is quantified by two sets of landmarks and semilandmarks (Gunz et al., 2005) placed along its arc, one following the centroid of its lumen (midline curve) and a second one along the outermost margin of the canal, furthest away from the vestibule (outer curve). The reason for this approach is to bracket the in vivo location of the membranous semicircular duct inside the bony canal. When semicircular canal morphology is analysed from a functional perspective, it is the centroid of the duct along the arc that should be considered, as it represents the streamline of the endolymph circuit. How much of the cross-sectional area of the bony canal is occupied by the duct varies widely among mammalian taxa, but it runs consistently along the outermost margin of the canal (e.g. see Gray, 1907, 1908 for a diverse range of species). In those taxa where it occupies most of the bony canal, the centroid of the latter is a good approximation of that of the duct. On the other end of the spectrum, and most notably observed in modern humans and phocids, the duct occupies less than 10% of the canal’s cross-sectional area, and the outermost margin of the canal is thus closer to the duct centroid (Gray, 1907; Curthoys et al., 1977; Ramprashad et al., 1984; Curthoys & Oman, 1987; Ifediba et al., 2007). Hence, when the size relationship between duct and canal lumen is not known, functional analyses are ideally done based both on the centroid and on the outermost margin of the semicircular canals, and the separate results will bracket the outcome based on the duct centroid. We follow the functional canal model of David et al. (2010), with landmarks demarcating the ampullar and slender parts of the semicircular canals and the common crus. In mammals, the utricular part of the endolymph circuit is difficult to quantify accurately using bony morphology and we do not landmark the variably shaped vestibular surface to connect the apertures of each canal. To quantify the shape and size of the cochlea we use a single curve based on the centroid of the turns, which reflects the length of the basilar membrane. The oval window is quantified by a single curve marking its well defined edge.
With respect to the second consideration, designing a measurement protocol that can be used with a range of imaging methods, it is predominantly the spatial resolution that constrains the choice of landmarks. Depending on the body size of a particular species, image datasets require a 3D spatial resolution of between 20 and 100 μm to obtain reliable surface visualization of the bony labyrinth. Such images can be obtained with μCT, μMRI or digitized histological sections and allow for accurate landmark placement both on the surface of the labyrinth and in the centre of the lumen of the semicircular canals and the cochlea. However, using high-resolution imaging methods is not always possible or practical, and medical CT or MRI can be a faster and widely available alternative, as long as the reduced image quality is taken into account (see Fig. 1 for a comparison of image quality). For example, current top-of-the-range medical CT has an in-plane spatial resolution in the range of 0.2–0.3 mm, and a minimum interslice distance of 0.1 mm, combined with a minimum slice thickness (collimation) of about 0.6 mm. As a consequence of partial volume averaging, the entire bony labyrinth of smaller mammalian species (<10 kg in body mass) is not visualized. Among larger taxa, where the labyrinth is fully visualized, the extracted surface will be substantially affected by the threshold level used and should be seen as an approximation with limited accuracy (see Spoor et al., 1993 for a discussion of the relationship between spatial resolution, thresholding and measurements of small details). On the other hand, both phantom studies and tests applied to the labyrinth have shown that the centroid of the lumen of the semicircular canals and cochlea can be measured accurately in such images, unaffected by threshold levels and with limited impact from partial volume effects (Spoor, 1993; Spoor & Zonneveld, 1995). Hence, the measurement protocol introduced here has a core set of semilandmarks of this type, so that it can be used meaningfully when images are obtained with a variety of spatial resolutions. An extended set, with additional landmarks and semilandmarks on the outer surface, can be used when sufficient image quality is available.
Fig. 1.
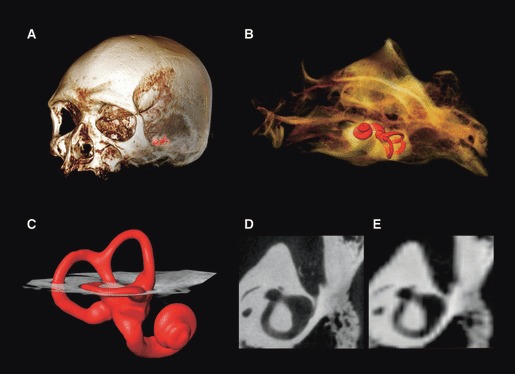
Computed tomography (CT) images of a modern human cranium; surface of the bony labyrinth is shown in red (A,B). An oblique slice through the lateral canal (C) is shown at the original resolution obtained using a microCT scanner (D), and resampled to the resolution of a medical CT scanner (E).
In the following sections we will describe and test the measurement protocol to quantify the shape of the mammalian bony labyrinth, using a sample of modern humans and chimpanzees to discuss its applications and limitations. The protocol can be applied to any 3D digital surface model of the bony labyrinth, whether derived from CT, MRI, histological sections or surface scans of fossil endocasts (e.g. Rogers, 1999). Of these, CT was used in the current study and is the method of data acquisition most commonly used in general. Preceding the description of the measurement protocol we detail an effective procedure to extract surface models of the labyrinth from CT scans, but this is not an integral part of the new method.
Materials and methods
Samples and CT scanning
The sample used in this study comprised dry crania of 50 modern humans and 30 chimpanzees, Pan troglodytes (Blumenbach, 1775) (Table 1).
Table 1.
Sample description.
| Species | Accession number | Calendar age (years) | Age (dental) | Sex | Geographic location |
|---|---|---|---|---|---|
| Homo sapiens | NF 820696 | Ad? | F | North America | |
| Homo sapiens | ULAC 12 | Ad | M | Europe | |
| Homo sapiens | ULAC 13 | Ad | F | Europe | |
| Homo sapiens | ULAC 16 | Ad | M | Europe | |
| Homo sapiens | ULAC 19 | Ad | M | Europe | |
| Homo sapiens | ULAC 33 | Ad | M | Europe | |
| Homo sapiens | ULAC 39 | Ad | F | Europe | |
| Homo sapiens | ULAC 57 | Ad | Europe | ||
| Homo sapiens | ULAC 58 | Ad | M? | Europe | |
| Homo sapiens | ULAC 60 | Ad | M | Europe | |
| Homo sapiens | ULAC 66 | Ad | Europe | ||
| Homo sapiens | ULAC 210 | Ad | Europe | ||
| Homo sapiens | ULAC 217 | Ad | Europe | ||
| Homo sapiens | ULAC 218 | Ad | F | Europe | |
| Homo sapiens | ULAC 223 | Ad | M | Europe | |
| Homo sapiens | ULAC 225 | Ad | F? | Europe | |
| Homo sapiens | ULAC 235 | Ad | M | Asia | |
| Homo sapiens | ULAC 257 | Ad | M | Africa | |
| Homo sapiens | ULAC 258 | Ad | M | Africa | |
| Homo sapiens | ULAC 261 | Ad | M | Africa | |
| Homo sapiens | ULAC 307 | Ad | Africa | ||
| Homo sapiens | ULAC 308 | Ad | Africa | ||
| Homo sapiens | ULAC 316 | Ad | Africa | ||
| Homo sapiens | ULAC 318 | Ad | F | Africa | |
| Homo sapiens | ULAC 319 | Ad | F | Africa | |
| Homo sapiens | ULAC 324 | Ad | F | Africa | |
| Homo sapiens | ULAC 335 | Ad | M | Africa | |
| Homo sapiens | ULAC 336 | Ad | F | Africa | |
| Homo sapiens | ULAC 343 | Ad | F? | Africa | |
| Homo sapiens | ULAC 770 | Ad | F | Africa | |
| Homo sapiens | ULAC 812 | Ad | M | Africa | |
| Homo sapiens | ULAC 813 | Ad | M? | Africa | |
| Homo sapiens | ULAC 814 | Ad | F? | Africa | |
| Homo sapiens | ULAC 868 | Ad | F | Asia | |
| Homo sapiens | ULAC 904 | Ad | M | Asia | |
| Homo sapiens | ULAC 909 | Ad | M | Asia | |
| Homo sapiens | ULAC 920 | Ad | F | Asia | |
| Homo sapiens | ULAC 953 | Ad | M | North America | |
| Homo sapiens | ULAC 954 | Ad | M | North America | |
| Homo sapiens | ULAC 955 | Ad | M | North America | |
| Homo sapiens | ULAC 958 | Ad | M | Central America | |
| Homo sapiens | ULAC 959 | Ad | F | Central America | |
| Homo sapiens | ULAC 961 | Ad | M | South America | |
| Homo sapiens | ULAC 962 | Ad | F | South America | |
| Homo sapiens | ULAC 968 | Ad | F | South America | |
| Homo sapiens | ULAC 978 | Ad | M | South America | |
| Homo sapiens | ULAC 985 | Ad | M? | South America | |
| Homo sapiens | ULAC 996 | Ad | F | South America | |
| Homo sapiens | ULAC 998 | Ad | M | South America | |
| Homo sapiens | ULAC 1040 | Ad | M | South America | |
| Pan troglodytes troglodytes | AMNH 54330 | Ad? | M | Central Africa | |
| Pan troglodytes troglodytes | AMNH 90191 | Ad? | F | Central Africa | |
| Pan troglodytes troglodytes | AMNH 90293 | Ad? | F | Central Africa | |
| Pan troglodytes troglodytes | AMNH 119770 | Ad? | M | Central Africa | |
| Pan troglodytes troglodytes | AMNH 167341 | Ad? | M | Central Africa | |
| Pan troglodytes troglodytes | AMNH 167343 | Ad? | F | Central Africa | |
| Pan troglodytes troglodytes | AMNH 167344 | Ad? | M | Central Africa | |
| Pan troglodytes troglodytes | AMNH 167346 | Ad? | M | Central Africa | |
| Pan troglodytes troglodytes | AMNH 201469 | Ad? | F | Central Africa | |
| Pan troglodytes verus | Leipzig 11775 | 15.39 | Ad | F | Western Africa |
| Pan troglodytes verus | Leipzig 11776 | 12.38 | Juv M2 | F | Western Africa |
| Pan troglodytes verus | Leipzig 11778 | 18.93 | Ad | F | Western Africa |
| Pan troglodytes verus | Leipzig 11779 | 12.57 | Juv M2 | M | Western Africa |
| Pan troglodytes verus | Leipzig 11780 | 25.39 | Ad | F | Western Africa |
| Pan troglodytes verus | Leipzig 11781 | 25.39 | Ad | M | Western Africa |
| Pan troglodytes verus | Leipzig 11782 | Juv M2 | M | Western Africa | |
| Pan troglodytes verus | Leipzig 11790 | 9.61 | Juv M2 | F | Western Africa |
| Pan troglodytes verus | Leipzig 11792 | 12.30 | Juv M2 | F | Western Africa |
| Pan troglodytes verus | Leipzig 11796 | Juv M2 | M | Western Africa | |
| Pan troglodytes verus | Leipzig 11800 | 22.62 | Ad | F | Western Africa |
| Pan troglodytes verus | Leipzig 11903 | 19.47 | Ad | M | Western Africa |
| Pan troglodytes verus | Leipzig 13430 | Ad | M | Western Africa | |
| Pan troglodytes verus | Leipzig 13433 | 7.61 | Juv M1 | M | Western Africa |
| Pan troglodytes verus | Leipzig 13437 | 11.39 | Juv M2 | F | Western Africa |
| Pan troglodytes verus | Leipzig 13439 | 22.88 | Ad | F | Western Africa |
| Pan troglodytes verus | Leipzig 14991 | 7.96 | Juv M1 | F | Western Africa |
| Pan troglodytes verus | Leipzig 15008 | Ad | M | Western Africa | |
| Pan troglodytes verus | Leipzig 15012 | 18.64 | Ad | M | Western Africa |
| Pan troglodytes verus | Leipzig 15013 | Ad | F | Western Africa | |
| Pan troglodytes verus | Leipzig 15019 | Ad | M | Western Africa |
NF, Norris Farms, Illinois; ULAC, University of Leipzig Anatomy Collection; AMNH, American Museum of Natural History; Leipzig, MPI EVA Leipzig; Ad, adult; Juv M1, Juvenile with M1 erupted; Juv M2, juvenile with M2 erupted.
The human sample (University of Leipzig anatomy collection and Norris Farms in Illinois, USA) encompasses a wide geographic range from Africa (n = 16), the Americas (n = 14), Asia (n = 5) and Europe (n = 15). Based on museum records or inscriptions on the crania, the sample includes females (n = 15), males (n = 22), and individuals of unknown sex (n = 13). All are adult, based on the full eruption of the maxillary M3.
The chimpanzee sample includes the common Central African subspecies, P. t. troglodytes (n = 9, American Museum of Natural History) and the Western African subspecies, P. t. verus (n = 21, Taï chimpanzee collection, Côte d’Ivoire; Boesch & Boesch-Achermann, 2000; Boesch et al., 2006, housed at the Max Planck Institute for Evolutionary Anthropology in Leipzig, MPI-EVA). The sample contains both females (n = 15) and males (n = 15) ranging from juvenile (M1 erupted, 7.6 calendar years) to adult (maxillary M3 fully erupted).
All specimens were scanned with high-resolution microCT systems, with a voxel size between 0.062 and 0.109 mm. Specimens from Leipzig were scanned with the BIR ACTIS 225/300 housed at MPI-EVA; specimens from Norris Farms and the American Museum of Natural History were scanned with the OMNI-X HD600 at the Center for Quantitative Imaging at Pennsylvania State University. The slices were reconstructed as 1024 × 1024 or 2048 × 2048, 8- or 16-bit TIFF images.
avizo 6.1-6.3 (Visualization Sciences Group) and geomagic studio 12 (geomagic, Inc.) were used to extract and landmark the 3D digital surface models of the bony labyrinth. mathematica 8 (Wolfram Research, Inc.) was used to process the landmark coordinates. In addition to the protocols given below, we provide the software-specific instructions, as well as a specific template for avizo and amira (Supporting Information Data S1). However, the steps described can be performed with many commonly used packages.
Extraction of 3D surface models
The method of surface extraction used here employs the Isosurface module of avizo. It calculates the 3D surface directly from the matrix of 8- or 16-bit grey-scale voxels, providing better surface visualization than the standard segmentation procedure of using voxels binary marked in the stack of images. However, as only a single threshold value is used to define the bony surface, the Isosurface module is most useful when dealing with high-resolution CT scans of labyrinths with a homogeneous filling of air, liquid or fine-grained rock matrix. In the present study the right labyrinth of each cranium was analysed, unless local damage favoured the use of the left one.
In the first step of the extraction protocol the boundaries of the labyrinth are identified in the orthogonal planes of the original image stack, and using the coordinates a tightly cropped data volume is obtained. As labyrinths of the same side need to be obtained for the analyses (right in this study) the volumetric data are mirrored if necessary.
Secondly, the labyrinth is visualized, using a threshold which best represents its surface. In high-resolution CT scans, with small voxel sizes compared with the main structures of the labyrinth, this can largely be done visually, but selecting an appropriate threshold can be informed by calculating half maximum height (HMH) levels between the otic capsule and the lumen in several locations (Spoor et al., 1993; Spoor & Zonneveld, 1995). Surfaces that are not part of the labyrinth, on the outside of the data volume, are removed with a range of surface editing tools. The oval and round windows, the apertures of the cochlear and vestibular ducts, as well as various foramina associated with innervation and vascularization are segmented such that no structures extrude beyond the surface of the labyrinth. When only the labyrinth remains, a surface is generated; here we used STL ascii format (Fig. 2A). Given that in avizo (and most other software tools) a surface has no thickness, it does not matter if one thresholds the ‘outside’ surface of the bone or if one inverts the grey-scale image to threshold the ‘inside’ of the labyrinth. Scans of natural endocasts of the labyrinth, which sometimes occur in the fossil record, can therefore be used without any modification of the protocol below.
Fig. 2.
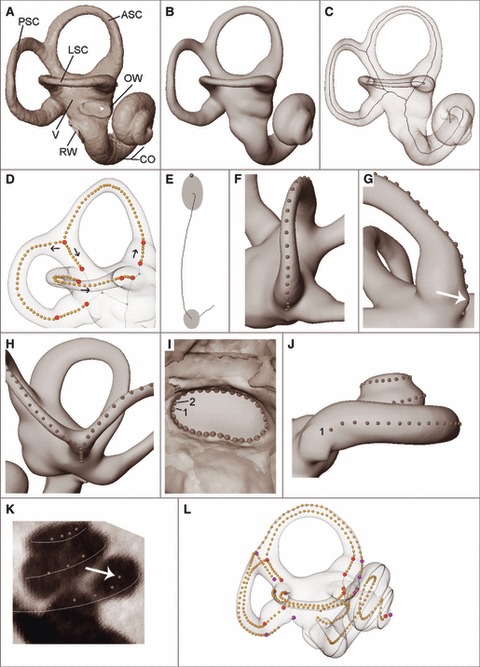
(A) Surface of the bony labyrinth with anterior, lateral and posterior semicircular canal (ASC, LSC, PSC), oval window (OW), round window (RW), cochlea (CO) and vestibule (V). (B) The same surface, closed and smoothed. (C) Midline skeleton. (D) 3D coordinates measured along medial axis; arrows show the measurement direction for each curve. (E) Cross-section through ASC showing a coordinate on the tip of the oval farthest away from the vestibule. (F) Outer curve along a semicircular canal. (G) Semilandmarks of the outer curve are not placed on the irregular fill-in of the foramen for the posterior ampullar nerve (white arrow). (H) Semilandmarks on the common crus. (I) Coordinates along the OW, measured clockwise from 1. (J) Coordinates along the cochlea outline; 1 – cochlear side of RW. (K) Midline of the cochlea measured using slices perpendicular to the outer cochlear curve as a guide (white arrow shows landmark with which the slice is aligned). (L) Raw coordinate measurements. Interior landmarks are in red, exterior landmarks in purple, and semilandmarks in orange.
Thirdly, using dedicated surface editing software (geomagic), the surface is closed and if necessary smoothed, using settings that do not reduce (‘shrink’) the size of the semicircular canals and cochlea (Fig. 2B).
Measurement protocol
Landmark data
The midline skeleton of the smoothed surface of the labyrinth is computed by thinning the encased volume, thus creating midline curves of the semicircular canals (Fig. 2C). A midline curve of the cochlea obtained this way is frequently inaccurate, even for high-resolution CT scans, and is therefore not used. Instead we create a manual midline skeleton of the cochlea.
A series of landmarks and semilandmarks are placed on the surface, on the midline curve of the semicircular canals resulting from its skeletonization, and on oblique slices through the original volume of the cochlea in the following sequence:
On the midline curve of every semicircular canal, a landmark is placed at the junction between the slender part and ampulla, and on the ‘Y-junction’ formed by the anterior and posterior canals and the common crus, as well as at the apertures of the ampullae, the common crus and the slender part of the lateral canal into the vestibule (landmarks 1-9, Table 2). For the extended protocol (see below) additional corresponding landmarks are placed on the outer curves (landmarks 11–19 in Table 2).
Approximately 40 semilandmarks are placed in sequence along the midline curve of the anterior, lateral and posterior semicircular canals, as well as the common crus (Fig. 2D). The exact number of semilandmarks is not important, as the curves will be resampled later (see below). The starting and ending points of each canal are defined as the junction with the vestibule, and the common crus is treated as a separate line segment. The anterior canal curve therefore stops at landmark 3; the posterior canal curve starts at landmark 3.
Approximately 40 semilandmarks are placed on the outer surface of each semicircular canal along a curve farthest away from the vestibule. Where the canals are oval (vs. round) in cross-section, the semilandmarks follow the vertex of the oval (Fig. 2E). The starting and ending points of each outer canal curve are where the canal lumen meets the vestibule (Fig. 2F). If the foramen of the ampullar nerve is positioned in the path of the outer curve, landmarks should not be placed on the fill-in of the foramen, as this is frequently irregularly shaped (Fig. 2G). Instead, the semilandmarks stop at the canal side edge of the foramen, followed by the landmark at the junction with vestibule as the endpoint (landmarks 11, 16, 17). As with the points along the midline curve, the outer curve of the common crus is treated as a separate line segment. Semilandmarks are placed down the common crus on the medial-most side, as a compromise between outer curves based on the posterior canal and the anterior canal individually (Fig. 2H). The outer curves of the anterior and posterior canals therefore end and start at the Y-junction these canals form with the common crus (landmark 13).
Approximately 40 semilandmarks are placed along a curve around the outline of the oval window, proceeding clockwise from the posterior-most point on the long axis (Fig. 2I).
Approximately 100 semilandmarks are placed along a curve on the surface to represent the outline of the cochlea, maximizing the distance from the modiolus (Fig. 2J). The first landmark is placed on the inferior (cochlear) margin of the round window, followed by a series of landmarks proceeding up the turns of the cochlea, and a final point at the cupula (landmark 20; Table 2 and Fig. 3). These semilandmarks are taken only to aid in identifying the position of the midline curve of the cochlea, rather than for analysis.
Semilandmarks are placed along the midline of the cochlea (Fig. 2K). To aid in the placement of these coordinates, first generate an avizo lineset from the semilandmarks on the outline of the cochlea using mathematica 8 (Supporting Information Data S2). Create slices through the smoothed surface that are perpendicular to the linesets. The first semilandmark is placed on the inferior (cochlear) side of the round window, and a series of coordinates proceeds up the turns of the cochlea (at least one landmark every 45°), with a final one at the helicotrema (landmark 10; Table 2 and Fig. 3).
Table 2.
Landmarks.
| Standard landmark set | |
| 1 | ASC to vestibule (midline) |
| 2 | ASC ampulla to slender part of ASC (midline) |
| 3 | CCR to ASC & PSC (midline) |
| 4 | CCR to vestibule (midline) |
| 5 | Slender part of PSC to ampulla (midline) |
| 6 | PSC ampulla to vestibule (midline) |
| 7 | Slender part of LSC to vestibule (midline) |
| 8 | Slender part of LSC to ampulla (midline) |
| 9 | LSC ampulla to vestibule (midline) |
| 10 | Helicotrema |
| Extended landmark set | |
| 11 | ASC to vestibule (outline) |
| 12 | ASC ampulla to slender part of ASC (outline) |
| 13 | Common crus (CCR) to ASC & PSC (outline) |
| 14 | CCR to vestibule (outline) |
| 15 | Slender part of PSC to ampulla (outline) |
| 16 | PSC ampulla to vestibule (outline) |
| 17 | Slender part of LSC to vestibule (outline) |
| 18 | Slender part of LSC to ampulla (outline) |
| 19 | LSC ampulla to vestibule (outline) |
| 20 | Cupula of cochlea |
ASC, anterior semicircular canal; LSC, lateral semicircular canal; PSC, posterior semicircular canal; CCR, common crus.
Fig. 3.

Standard (A) and extended (B) set of landmarks (interior: blue; exterior: red – cf. Table 2) and semilandmarks (orange) for statistical shape analysis.
Depending on the quality and resolution of the CT scan, it takes around 15–30 min to segment the labyrinth, and approximately another 30 min to measure all coordinates. Data collection from inner ears with good and homogeneous contrast (usually air-filled) therefore usually takes less than an hour per specimen. For specimens that are filled with matrix (as is often the case with fossils) the segmentation step can take significantly longer.
Curve lengths and enclosed area
The landmark and semilandmark coordinates (Fig. 2L) are subsequently processed in mathematica. For every curve we approximate its length based on a cubic spline interpolation computed through these (semi)landmark coordinates; these computations can be performed on the raw coordinate measurements, as this step does not require every curve to have the same number of points (in contrast to the shape analysis described below). We compute the streamline lengths following the outer curve and midline curve of the anterior, posterior and lateral semicircular canals (abbreviated ASCol, ASCml, PSCol, PSCml, LSCol, LSCml, respectively). The streamlines of the anterior and posterior canals both include the points along the common crus. As the aim of the present study is to introduce a landmark protocol of the labyrinth rather than present a biophysical analysis of the canal system (David et al., 2010) we did not, at this stage, evaluate the individual components of each canal (i.e. the slender and ampullar parts, and the common crus). However, with the landmarks defined on the canal curves, the individual lengths can be calculated. The midline curve of the cochlea represents the length of the basilar membrane.
So as to approximate the enclosed planar area of each semicircular canal (Hullar, 2006), we close each curve by connecting the endpoints and projecting it onto a best-fit plane using a least-squares criterion – all points are projected onto the plane spanned by the first two eigenvectors of the covariance matrix computed from the curve coordinates. We then compute the area enclosed by each two-dimensional polygon. Below we abbreviate the outer and midline enclosed areas of the anterior, posterior and lateral canals as ASCop, ASCmp, PSCop, PSCmp, LSCop and LSCmp. The enclosed planar area of the oval window is abbreviated OWp.
Quantifying shape with geometric morphometrics
To quantify the shape of the labyrinth we use geometric morphometric (GM) methods (Bookstein, 1991; Rohlf & Marcus, 1993; Slice, 2007; Mitteroecker & Gunz, 2009). GM comprises a set of techniques that make it possible to quantify shape and form based on 2D or 3D coordinate data (Slice, 2007; Mitteroecker & Gunz, 2009). The shape of an object is defined as the information that is independent of position, orientation and scale, whereas form comprises information about shape and size. GM relies on two core techniques: (i) the so-called ‘Procrustes superimposition’ converts the raw coordinates to shape variables by standardizing for position and orientation, as well as scaling each specimen to the same size (Rohlf & Slice, 1990), and (ii) thin-plate spline (TPS) interpolation provides a powerful way to visualize the shape differences between two forms (Bookstein, 1989, 1991). TPS deformation grids or surface warps show how one would have to deform a reference configuration to arrive at a target shape. The TPS interpolation function is computed based on the (semi)landmark coordinates of a reference and target shape; the space ‘in-between’ the (semi)landmarks is interpolated. The notion of smoothness is approached by minimizing the ‘bending energy’ of the deformation, a scalar quantity computed as the integral of the squared second derivatives of that deformation. Intuitive visualizations of shape differences between two forms in 2D are possible using TPS deformation grids. For 3D data one can also use the TPS algebra to warp a 3D surface from the reference configuration to the target configuration. Instead of warping the grid points of the deformation grid, one simply warps the vertices of a triangulated surface model (Gunz et al., 2005; Gunz & Harvati, 2007; Mitteroecker & Gunz, 2009). TPS visualizations have two major advantages: (i) they are independent of the Procrustes registration (see above) and (ii) subtle shape differences can be exaggerated to make them easier to interpret. The TPS formalism is also central to the semilandmark algorithm (Bookstein, 1997; Gunz et al., 2005) and the estimation of missing data in morphometrics (Gunz, 2005; Gunz et al., 2009a).
As GM methods require all specimens to have the same number of measurement points, the curves are first resampled to the same point count (Fig. 3C). To arrive at the same number of semilandmarks in the same order on each specimen, we start with points that are spaced equidistantly along each curve. To this end we approximate the length of each curve based on a cubic spline interpolation computed through the semilandmark coordinates measured on the curve; we then distribute a predefined number of semilandmarks evenly spaced along the curve. We distribute 32 semilandmarks along each curve quantifying the midline and exterior shape of the respective semicircular canals, eight semilandmarks respectively along the midline and the outline of the common crus, 62 semilandmarks along the midline curve of the cochlea, and 22 semilandmarks along the outline of the oval window [a total of 312 (semi)landmarks per specimen]. For each semicircular canal we place the same number of semilandmarks in the ampullar part (four semilandmarks) and in the slender part (28 semilandmarks) (Fig. 3C). The number of semilandmarks was chosen to reflect the shape of the measured structures. To assess the effects of this arbitrary choice, we repeated all analyses twice, using a higher and a lower density of curve-semilandmarks (584 and 146 (semi)landmarks per specimen, respectively) and obtained the same results. As the resampling of the curves is done automatically, it is possible to adjust the number of semilandmarks based on the specific requirements of a research project. Figure 4 shows that the number of curve semilandmarks used in this study, is suitable for the size range encountered among primates: the bony labyrinths of a brown mouse lemur (Microcebus rufus) and a male gorilla illustrate the two extremes of the extant primate size range.
Fig. 4.
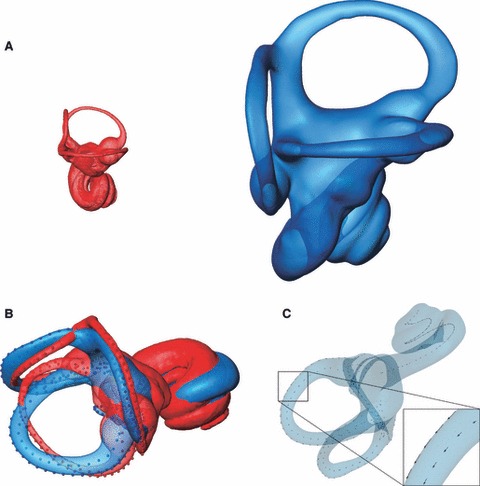
(A) Bony labyrinths of a brown mouse lemur (red) and a male gorilla (blue). Surfaces are to scale to illustrate the size range among primates. (B) Procrustes superimposition removes scale, orientation and position from the landmarks and semilandmarks; the remaining shape information can be analysed using multivariate statistics. (C) To ensure geometric homology, semilandmarks are allowed to slide along the respective curves until the thin-plate spline bending energy between each specimen and the average shape of the sample is minimal. The semilandmarks of the gorilla specimen shown in (A) slide with respect to the average shape in a large primate sample. The short arrows indicate that the semilandmarks shift only slightly.
Here we use two sets of landmarks and semilandmarks: (i) a standard set of 198 coordinates that primarily quantify the midline skeleton of the bony labyrinth, together with an outline of the oval window (Fig. 3A) and (ii) an extended set of 312 coordinates that also includes landmarks and curves on the outside of the semicircular canals (Fig. 3B,C).
The semilandmarks are initially placed evenly along the curve. However, as discussed in Bookstein (1997), this equidistant spacing is arbitrary and might create visualization artifacts (Gunz et al., 2005) when shape differences are visualized using thin-plate spline warping (as in this paper). We therefore use the sliding semilandmark algorithm described in Gunz et al. (2005, 2009a) to discard information derived from the arbitrary spacing of semilandmarks along the curves. Semilandmarks are allowed to slide along the respective curves so as to minimize the thin-plate spline bending energy between each specimen and the mean shape of the entire sample (see below). The spacing of semilandmarks is produced as a by-product of the statistical analysis itself (Mitteroecker & Gunz, 2009). This ensures that the curve semilandmarks can be considered geometrically homologous across the entire sample. To linearize the minimization problem, the semilandmarks are allowed to slide on local tangents to the curve, not the curve itself. To ensure that the semilandmarks do not slide off the curves, the sliding is done iteratively; after each iteration, semilandmarks are projected back onto the respective curves. Figure 4C illustrates how the semilandmarks slide along the curves of a gorilla labyrinth, so as to minimize the bending energy between this specimen and the average shape of a large primate sample. It is evident from this figure that the positions of the semilandmarks shift only subtly. For most applications and statistical analyses, the difference between analysing the unslid equidistant points and the slid semilandmarks will therefore be negligible. It is, however, recommended to slide the semilandmarks. First, sliding removes potential visualization artefacts (Gunz et al., 2005). More importantly, sliding the semilandmarks increases the flexibility of the measurement protocol when dealing with partially complete specimens, such as fossils that have missing parts, or where parts are filled with matrix. Regions that cannot be measured can be treated as ‘missing data’ (Gunz et al., 2009a). Such missing landmarks and semilandmarks are allowed to slide freely (without being constrained to a curve), and therefore do not influence the semilandmarks measured on observable parts of the labyrinth. The same approach allows us to incorporate a ‘free floating’ cochlear curve: given that the cochlea curve is not delimited by a fixed landmark at its vestibular side, the first semilandmark of the cochlea midline curve is treated as ‘missing’ data and allowed to move without being constrained to a curve (Gunz & Harvati, 2007; Gunz et al., 2009a). All technical and algebraic details about semilandmarks are discussed in Gunz et al. (2005); a detailed explanation of the missing data algorithm can be found in Gunz et al. (2009a).
Statistical analysis
After semilandmark sliding, all data are analysed using standard geometric morphometric methods (for comprehensive reviews see Slice, 2007 and Mitteroecker & Gunz, 2009). The coordinates are converted to shape variables using generalized least squares Procrustes superimposition (Rohlf & Slice, 1990), standardizing position, orientation and scale across the entire sample. The Procrustes shape coordinates are then analysed using principal component analysis (PCA) to explore the large-scale patterns of shape variation. For analyses in shape space, the Procrustes shape variables of each specimen are written as a row vector. The eigenvectors of the variance-covariance matrix of this data matrix are the principal components. PCA is the standard multivariate technique for exploratory data analysis.
Following Mitteroecker & Bookstein (2011) we also use between-group principal component analysis (bgPCA) to find axes in shape space that separate three a priori defined groups: humans, P. t. troglodytes and P. t. verus. To this end we first compute a covariance matrix of the group means and then project all specimens into the space spanned by the first two eigenvectors of this covariance matrix (for three groups there are only two eigenvectors with corresponding non-zero eigenvalues). Between-group PCA overcomes several limitations of linear discriminant analysis (LDA; sometimes also referred to as canonical variates analysis – CVA). As in LDA, the aim of bgPCA is to find axes in shape space that best separate groups. The advantage of bgPCA over LDA is that the axes remain orthogonal and that bgPCA can be computed for data that are not of full rank (i.e. when there are more variables than cases). Moreover, bgPCA does not require the group covariance matrices to be the same. See Mitteroecker & Bookstein (2011) for a detailed technical description of these issues.
We use permutation tests (Good, 2000) on Procrustes distance (Gunz et al., 2005; Mitteroecker & Gunz, 2009) to test for significant shape differences between group means. We compute the Procrustes distances between two group means, randomly reassign group-labels 10 000 times, and then count how many times the mean Procrustes distances between these scrambled groups are equal to, or larger than the actual distance. Dividing these counts by the number of permutations yields the exact P value (e.g. for 85 of 10 000 permutations, the P value is 85/10 001 = 0.00849915).
Visualization of mean shape differences
To visualize the shape differences among our groups, we first compute group mean shapes by averaging the respective Procrustes shape coordinates in mathematica. We then use a thin-plate spline (TPS) interpolation (Bookstein, 1989, 1991) based on the landmark and semilandmark coordinates to warp a template surface to each group mean (Gunz & Harvati, 2007; Skinner et al., 2008, 2009).
Measurement error and repeatability
To assess the intra-observer measurement error, as well as the effect of different thresholds during the segmentation step, one observer (M.R.) digitized three modern human specimens multiple times (Fig. 5). For this error study we selected ULAC 258, a specimen that falls close to the modern human average shape (see below), ULAC 920, the specimen with the overall shortest length of the semicircular canals, and ULAC 996, the specimen with the overall longest length of the semicircular canals. For each specimen we used three different thresholds to create the isosurfaces in avizo. These are the threshold considered to give the best surface reconstruction, and the lowest and highest thresholds possible which would still result in an intact visualization of the labyrinth (i.e. without obliterating parts of the canals or cochlea, or creating connections across the otic capsule).
Fig. 5.
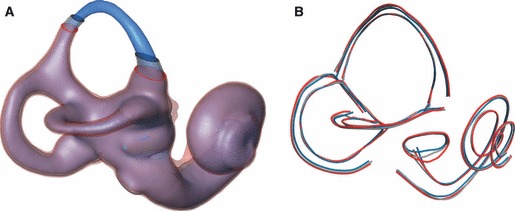
(A) One modern human specimen segmented three times using different threshold values (blue: low; grey: normal, red: high). (B) Repeated measurements on the three segmentations in (A); the coordinates along respective curves are connected by line segments. Note that blue, grey and red midline curves overlap, i.e. they are not affected by the threshold (colour codes as in A).
To illustrate how the image spatial resolution affects our measurements, we resampled the microCT scan of a modern human temporal bone (specimen ULAC 258) to the resolution of a modern medical CT scanner (from a voxel size of 90 μm to a voxel size of 300 μm). We then extracted the medial axis from a segmentation of the labyrinth in avizo (Fig. 6).
Fig. 6.
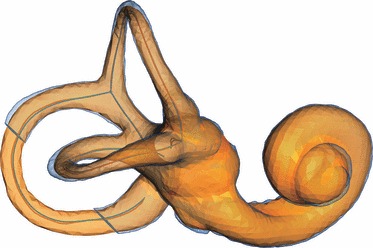
The labyrinth of a modern human segmented from the original microCT scan (blue), and from a scan that was resampled to the resolution of a medical CT scanner (orange). Whereas the ‘outside’ surfaces differ, the respective medial axes are virtually identical; i.e. the effect of image spatial resolution on the shape of the medial axis is negligible here.
Results
Measurement error
Figure 5 visualizes how different thresholds affect the segmentation: as expected, the thickness of the canals increases with an increase in the air/bone threshold (from the low threshold in blue to the high threshold in red). This effect is visible on all measurements taken on the outside of the surface. Measures of the oval window, the outer ‘streamline lengths’, as well as the outer enclosed planar areas are affected by the threshold used for the segmentation (Fig. 10A). The midline curves in the semicircular canals and the cochlea, however, are not affected by different thresholds. Correspondingly, the effect of the maximum possible variation in thresholds on midline ‘streamline length’ and midline enclosed planar area (Fig. 10B) is negligible.
In Procrustes shape space, the repeated measurements plot closely together in the PCA shown in Fig. 9A. The shape differences among repeated measurements of the same specimen at different thresholds are significantly smaller than the shape differences between that specimen and the individual most similar in shape; for all three specimens that were measured multiple times, the largest Procrustes distances between repeats was less than half the Procrustes distance between the respective specimen and its nearest neighbour in shape space.
Mean shape comparisons
We found striking differences between humans and chimpanzees in the shape of their semicircular canals, and very subtle differences in semicircular canal shape between the two chimpanzee groups (Figs 7 and 8). The shape differences between the group means (Fig. 7) are easier to interpret when two average shapes are superimposed (Fig. 8). The anterior semicircular canal is relatively larger and taller in H. sapiens than in P. troglodytes. Although the overall shape of the lateral semicircular canal is similar in H. sapiens and Pan troglodytes, the lateral canal is relatively smaller in humans than in chimpanzees. In lateral view the plane of the lateral semicircular canal in modern humans is tilted more anteroinferiorly than in P. troglodytes. The posterior semicircular canal is relatively larger and wider anteroposteriorly in H. sapiens than in P. troglodytes and shows a higher degree of torsion. The shape of the posterior semicircular canal in humans is rounder than in chimpanzees, where a more oval-shaped posterior semicircular canal is pinched in inferiorly. Subtle differences can be seen between the mean shapes of P. t. troglodytes and P. t. verus (Fig. 8B). The anterior semicircular canal in P. t. troglodytes is taller than in P. t. verus, and the width of the lateral semicircular canal is larger in P. t. troglodytes than in P. t. verus. The posterior semicircular canal, however, is slightly wider in P. t. verus than in P. t. troglodytes.
Fig. 7.
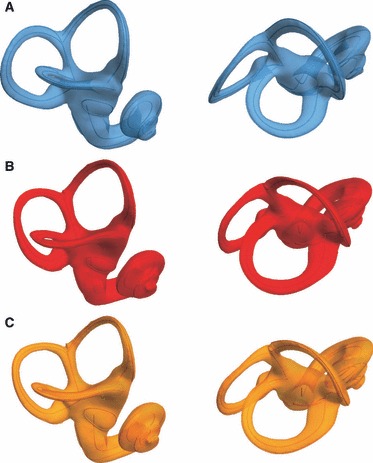
Mean shapes in two orientations. (A) Homo sapiens average shape. (B) Pan troglodytes troglodytes, (C) Pan troglodytes verus.
Fig. 8.

Group mean shapes superimposed. (A) Homo sapiens (blue) and Pan troglodytes average (red). (B) P. t. troglodytes (red) and Pan troglodytes verus (black curves and semi-transparent grey surface).
Shape space
The scores along the first two principal component (PC) axes in Procrustes shape space show a clear separation between H. sapiens and the two chimpanzee groups, both for the standard landmark and semilandmark set (Fig. 9A) and the extended (semi)landmark set (not shown here, as the PCA plot looks almost identical). Pan t. troglodytes and P. t. verus completely overlap in the subspace of the first two PCs, which together explain 55% of the total sample variation. However, if we use between-group PCA to look for dimensions in shape space that separate the three group means, we find that all three groups form non-overlapping clusters in shape space (Fig. 9B). This finding is confirmed by permutation tests based on Procrustes distances from the mean. The mean shape differences between all groups are statistically significant (P < 0.001 for all pairwise comparisons; both for the standard set of 198 (semi)landmarks, and the extended set of 312 (semi)landmarks; these results are also significant after Bonferroni correction).
Fig. 9.
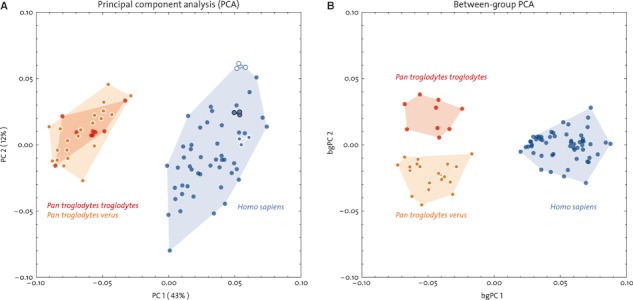
(A) Principal component analysis (PCA) of the standard (semi)landmark set (cf. Fig. 3A) in shape space. Three modern humans were measured three times; repeated measurements plot closely together in shape space (triangles). (B) Between-group PCA shows that there is no overlap among the three groups in shape space.
Discussion
Measurement error and thresholding
As expected, measurements taken on the outer surface of the bony labyrinth are affected by the choice of the threshold used during segmentation and the image spatial resolution, whereas measurements on the midline skeleton are not affected (Figs 5 and 6). The same caveat applies to the measurements of the ‘streamline lengths’ of the outer semicircular curves (ASCol, LSCol, PSCol) and the respective outer enclosed planar areas (ASCop, LSCop, PSCop, and OWp) (Fig. 10A). It is worth noting, however, that in this study we intentionally used extremely low and high thresholds to evaluate their influence on our measurements. Using more sensible thresholds, the effect would be less pronounced than in Fig. 10A. Nevertheless, the extended (semi)landmark protocol (Fig. 3B) is best used when high-resolution CT scans are available, as the impact of thresholding on the (semi)landmark positions on the “outer” surface will be limited compared to the size of the labyrinth. On the other hand, samples comprising lower resolution scans (e.g. medical CT scans) can be analysed reliably using the standard (semi)landmark set (Fig. 3A). In general we recommend that studies that rely on exact measurements of surface variables (e.g. functional studies of OW size) use the local half maximum height (HMH) level to find appropriate threshold values (for a detailed discussion see Spoor et al., 1993 and Kirk & Gosselin-Ildari, 2009).
Fig. 10.
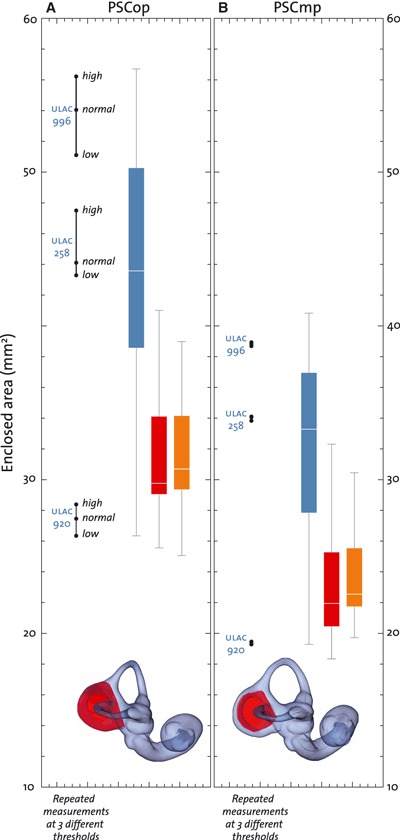
Enclosed planar areas of the posterior semicircular canal (A: PSCop; B: PSCmp). Group colour codes as in Fig. 7. The ranges of the three groups almost completely overlap. However, PSCop and PSCmp are on average significantly larger in modern humans than in both chimpanzee groups. Repeated measurements of three specimens at different thresholds show that only outside measurements are affected by the threshold value. The effect of different thresholds on PSCmp is negligible.
Shape differences among groups
The differences between humans and chimpanzees are most prominent in the relative sizes and shapes of the anterior, lateral and posterior semicircular canals (Fig. 8A). These findings are in line with previous metric studies based on linear distances and angular measurements (Spoor, 1993; Spoor & Zonneveld, 1998). Moreover, we report subtle, yet statistically significant, differences between P. t. troglodytes and P. t. verus in the shape of their semicircular canals (Fig. 8B). Even when only the standard (semi)landmark set is used, we found complete separation of the three groups in Procrustes shape space (Fig. 9B). It is beyond the scope of the current paper to consider the factors underlying the subtle shape differences found between P. t. troglodytes and P. t. verus but the ability to discriminate labyrinth shape at the subspecies level demonstrates that the approach presented here has great potential in future taxonomic studies of fossil specimens.
Conclusions
To our knowledge this is the most comprehensive measurement protocol of the bony labyrinth to date. We have demonstrated that our novel 3D GM approach makes it possible to capture and visualize large-scale species differences, as well as subtle shape differences between two subspecies of Pan troglodytes. This new method of quantifying bony labyrinth shape provides a powerful discriminatory tool for systematic biologists. Moreover, our metric approach is suitable for comparative and functional analyses of the inner ear. We hope that this detailed step-by-step description of the protocol, along with our landmark and semilandmark template which is available to other researchers (Supporting Information Data S3), will facilitate future comparative studies of the mammalian bony labyrinth.
Acknowledgments
We are grateful to the following people for access to specimens: C. Boesch, C. Feja, C. Hill, T. Ryan and K. Spanel-Borowski. We thank H. Temming, A. Winzer and P. Schönfeld for their CT scanning of the collections housed in Leipzig. We thank the Ivorian authorities, especially the Ministry of the Environment and Forests and the Ministry of Research, as well as the Swiss Research Center Abidjan for making the long-term study of the chimpanzees in the Taï National Park in Côte d’Ivoire possible, and the University of Zürich for years of careful curation of the skeletal material and U. Schwarz for doing the same at the MPI EVA in Leipzig. The helpful comments of two referees improved the manuscript.
Supporting Information
Data S1. Protocols with Avizo/Amira instructions added, and Avizo/Amira template.
Data S2. Mathematica script for conversion of Avizo/Amira landmark-sets to Avizo/Amira linesets.
Data S3. Surface and landmarks of a modern human specimen in Avizo/Amira format.
As a service to our authors and readers, this journal provides supporting information supplied by the authors. Such materials are peer-reviewed and may be re-organized for online delivery, but are not copy-edited or typeset. Technical support issues arising from supporting information (other than missing files) should be addressed to the authors.
References
- Blanks RH, Curthoys IS, Bennett ML, et al. Planar relationships of the semicircular canals in rhesus and squirrel monkeys. Brain Res. 1985;340:315–324. doi: 10.1016/0006-8993(85)90928-x. [DOI] [PubMed] [Google Scholar]
- Boesch C, Boesch-Achermann H. The Chimpanzees of the Tai Forest: Behavioural Ecology and Evolution. Oxford: Oxford University Press; 2000. [Google Scholar]
- Boesch C, Kohou G, Néné H, et al. Male competition and paternity in wild chimpanzees of the Taï forest. Am J Phys Anthropol. 2006;130:103–115. doi: 10.1002/ajpa.20341. [DOI] [PubMed] [Google Scholar]
- Bookstein FL. Principal warps: thin-plate splines and the decomposition of deformations. IEEE Trans Pattern Anal Mach Intell. 1989;V:567–585. [Google Scholar]
- Bookstein FL. Morphometric Tools for Landmark Data: Geometry and Biology. Cambridge: Cambridge University Press; 1991. [Google Scholar]
- Bookstein FL. Landmark methods for forms without landmarks: morphometrics of group differences in outline shape. Med Image Anal. 1997;1:225–243. doi: 10.1016/s1361-8415(97)85012-8. [DOI] [PubMed] [Google Scholar]
- Bradshaw AP, Curthoys IS, Todd MJ, et al. A mathematical model of human semicircular canal geometry: a new basis for interpreting vestibular physiology. J Assoc Res Otolaryngol. 2010;11:145–159. doi: 10.1007/s10162-009-0195-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen GE, He J, Dill JA, et al. Automatic measurement of the labyrinth using image registration and a deformable inner ear atlas. Acad Radiol. 2003;10:988–999. doi: 10.1016/s1076-6332(03)00121-1. [DOI] [PubMed] [Google Scholar]
- Coleman MN, Colbert MW. Correlations between auditory structures and hearing sensitivity in non-human primates. J Morphol. 2010;271:511–532. doi: 10.1002/jmor.10814. [DOI] [PubMed] [Google Scholar]
- Cox PG, Jeffery N. Geometry of the semicircular canals and extraocular muscles in rodents, lagomorphs, felids and modern humans. J Anat. 2008;213:583–596. doi: 10.1111/j.1469-7580.2008.00983.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox PG, Jeffery N. Semicircular canals and agility: the influence of size and shape measures. J Anat. 2010;216:37–47. doi: 10.1111/j.1469-7580.2009.01172.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curthoys IS, Oman CM. Dimensions of the horizontal semicircular duct, ampulla and utricle in the human. Acta Otolaryngol. 1987;103:254–261. doi: 10.3109/00016488709107791. [DOI] [PubMed] [Google Scholar]
- Curthoys IS, Blanks RH, Markham CH. Semicircular canal radii of curvature (R) in cat, guinea pig and man. J Morphol. 1977;151:1–15. doi: 10.1002/jmor.1051510102. [DOI] [PubMed] [Google Scholar]
- David R. Le système des canaux semi-circulaires des archosaures: anatomie, morphométrie, morphologie fonctionnelle, évolution. Paris: Museum National d’Histoire National; 2011. PhD thesis. [Google Scholar]
- David R, Droulez J, Allain R, et al. Motion from the past. A new method to infer vestibular capacities of extinct species. CR Palevol. 2010;9:397–410. [Google Scholar]
- Ekdale EG, Rowe T. Morphology and variation within the bony labyrinth of zhelestids (Mammalia, Eutheria) and other therian mammals. J Vertebr Paleontol. 2011;31:658–675. [Google Scholar]
- Fleischer G. Studien am Skelett des Gehörorgans der Säugetiere, einschließlich des Menschen. Säugetierkundliche Mitteilungen. 1973;21:131–239. [Google Scholar]
- Fleischer G. Hearing in extinct cetaceans as determined by cochlear structure. J Paleontol. 1976;50:133–152. [Google Scholar]
- Georgi JA, Sipla JS. Balance: comparative and functional anatomy in aquatic reptiles and birds. In: Thewissen JGM, Nummela S, editors. Sensory Evolution on the Threshold, Adaptations in Secondarily Aquatic Vertebrates. Berkley: University of California Press; 2008. pp. 233–256. [Google Scholar]
- Good PI. Permutation Tests: A Practical Guide to Resampling Methods for Testing Hypotheses. New York: Springer; 2000. [Google Scholar]
- Gray AA. The Labyrinth of Animals. Vol. 2. London: Churchill; 1907. [Google Scholar]
- Gray AA. The Labyrinth of Animals: Including Mammals, Birds, Reptiles and Amphibians. London: Churchill; 1908. [Google Scholar]
- Gunz P. Statistical and Geometric Reconstruction of Hominid Crania: Reconstructing Australopithecine Ontogeny. Vienna: University of Vienna; 2005. PhD dissertation. [Google Scholar]
- Gunz P, Harvati K. The Neanderthal ‘chignon’: variation, integration, and homology. J Hum Evol. 2007;52:262–274. doi: 10.1016/j.jhevol.2006.08.010. [DOI] [PubMed] [Google Scholar]
- Gunz P, Mitteroecker P, Bookstein FL. Semilandmarks in three dimensions. In: Slice DE, editor. Modern Morphometrics in Physical Anthropology. New York: Kluwer Academic/Plenum Publishers; 2005. pp. 73–98. [Google Scholar]
- Gunz P, Mitteroecker P, Neubauer S, et al. Principles for the virtual reconstruction of hominin crania. J Hum Evol. 2009a;57:48–62. doi: 10.1016/j.jhevol.2009.04.004. [DOI] [PubMed] [Google Scholar]
- Gunz P, Spoor F, Tilgner R, et al. The Neanderthal bony labyrinth reconsidered, introducing a new geometric morphometric approach. Am J Phys Anthropol. 2009b;138(S48):142. [Google Scholar]
- Hublin JJ, Spoor F, Braun M, et al. A late Neanderthal associated with Upper Palaeolithic artefacts. Nature. 1996;381:224–226. doi: 10.1038/381224a0. [DOI] [PubMed] [Google Scholar]
- Hullar TE. Semicircular canal geometry, afferent sensitivity, and animal behavior. Anat Rec A Discov Mol Cell Evol Biol. 2006;288:466–472. doi: 10.1002/ar.a.20304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyrtl J. Vergleichend-anatomische Untersuchungen über das innere Gehörorgan des Menschen und der Säugethiere: Mit neun Kupfertafeln. Prague: Verlag von Friedrich Ehrlich; 1845. [Google Scholar]
- Ifediba MA, Rajguru SM, Hullar TE, et al. The role of 3-canal biomechanics in angular motion transduction by the human vestibular labyrinth. Ann Biomed Eng. 2007;35:1247–1263. doi: 10.1007/s10439-007-9277-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffery N, Cox PG. Do agility and skull architecture influence the geometry of the mammalian vestibulo-ocular reflex? J Anat. 2010;216:496–509. doi: 10.1111/j.1469-7580.2010.01211.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffery N, Spoor F. Prenatal growth and development of the modern human labyrinth. J Anat. 2004;204:71–92. doi: 10.1111/j.1469-7580.2004.00250.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffery N, Spoor F. The primate subarcuate fossa and its relationship to the semicircular canals part I: prenatal growth. J Hum Evol. 2006;51:537–549. doi: 10.1016/j.jhevol.2006.07.003. [DOI] [PubMed] [Google Scholar]
- Ketten DR, Wartzok D. Three-dimensional reconstructions of the dolphin ear. In: Thomas J, Kastelein R, editors. In Sensory Abilities of Cetaceans: Laboratory and Field Evidence. New York: Plenum Press; 1990. pp. 81–105. [Google Scholar]
- Kirk EC, Gosselin-Ildari AD. Cochlear labyrinth volume and hearing abilities in primates. Anat Rec. 2009;292:765–776. doi: 10.1002/ar.20907. [DOI] [PubMed] [Google Scholar]
- Ladevèze S, de Muizon C, Colbert M, et al. 3D computational imaging of the petrosal of a new multituberculate mammal from the Late Cretaceous of China and its paleobiologic inferences. CR Palevol. 2010;9:319–330. [Google Scholar]
- Lebrun R, De León MP, Tafforeau P, et al. Deep evolutionary roots of strepsirrhine primate labyrinthine morphology. J Anat. 2010;216:368–380. doi: 10.1111/j.1469-7580.2009.01177.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luo Z, Ketten DR. CT scanning and computerized reconstructions of the inner ear of multituberculate mammals. J Vertebr Paleontol. 1991;11:220–228. [Google Scholar]
- Luo ZX, Ruf I, Schultz JA, et al. Fossil evidence on evolution of inner ear cochlea in Jurassic mammals. Proc R Soc B. 2011;278:28–34. doi: 10.1098/rspb.2010.1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macrini TE, Flynn JJ, Croft DA, et al. Inner ear of a notoungulate placental mammal: anatomical description and examination of potentially phylogenetically informative characters. J Anat. 2010;216:600–610. doi: 10.1111/j.1469-7580.2010.01224.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malinzak MD. Experimental Analyses of the Relationship between Semicircular Canal Morphology and Locomotor Head Rotations in Primates. Department of Biological Anthropology and Anatomy, Duke University; 2010. PhD dissertation. [Google Scholar]
- Matano S, Kubo T, Niemitz C, et al. Semicircular canal organ in three primate species and behavioral correlations. Fortschr Zool. 1985;30:677–680. [Google Scholar]
- Mitteroecker P, Bookstein F. Linear discrimination, ordination, and the visualization of selection gradients in modern morphometrics. Evol Biol. 2011;38:100–114. [Google Scholar]
- Mitteroecker P, Gunz P. Advances in geometric morphometrics. Evol Biol. 2009;36:235–247. [Google Scholar]
- Ni X, Flynn JJ, Wyss AR. The bony labyrinth of the early platyrrhine primate Chilecebus. J Hum Evol. 2010;59:595–607. doi: 10.1016/j.jhevol.2010.06.008. [DOI] [PubMed] [Google Scholar]
- Ramprashad F, Landolt JP, Money KE, et al. Dimensional analysis and dynamic response characterization of mammalian peripheral vestibular structures. Am J Anat. 1984;169:295–313. doi: 10.1002/aja.1001690306. [DOI] [PubMed] [Google Scholar]
- Rogers SW. Allosaurus, crocodiles, and birds: evolutionary clues from spiral computed tomography of an endocast. Anat Rec. 1999;257:162–173. doi: 10.1002/(SICI)1097-0185(19991015)257:5<162::AID-AR5>3.0.CO;2-W. [DOI] [PubMed] [Google Scholar]
- Rohlf FJ, Marcus LF. A revolution in morphometries. Trends Ecol Evol. 1993;8:129–132. doi: 10.1016/0169-5347(93)90024-J. [DOI] [PubMed] [Google Scholar]
- Rohlf FJ, Slice D. Extensions of the Procrustes method for the optimal superimposition of landmarks. Syst Zool. 1990;39:40–59. [Google Scholar]
- Rook L, Bondioli L, Casali F, et al. The bony labyrinth of Oreopithecus bambolii. J Hum Evol. 2004;46:349–356. doi: 10.1016/j.jhevol.2004.01.001. [DOI] [PubMed] [Google Scholar]
- Schmelzle T, Sánchez-Villagra MR, Maier W. Vestibular labyrinth diversity in diprotodontian marsupial mammals. Mammal Study. 2007;32:83–97. [Google Scholar]
- Silcox MT, Bloch JI, Boyer DM, et al. Semicircular canal system in early primates. J Hum Evol. 2009;56:315–327. doi: 10.1016/j.jhevol.2008.10.007. [DOI] [PubMed] [Google Scholar]
- Sipla JS. The Semicircular Canals of Birds and Non-Avian Theropod Dinosaurs. Department of Anatomical Sciences, Stony Brook University; 2007. PhD dissertation. [Google Scholar]
- Skinner MM, Gunz P, Wood BA, et al. Enamel-dentine junction (EDJ) morphology distinguishes the lower molars of Australopithecus africanus and Paranthropus robustus. J Hum Evol. 2008;55:979–988. doi: 10.1016/j.jhevol.2008.08.013. [DOI] [PubMed] [Google Scholar]
- Skinner MM, Gunz P, Wood BA, et al. Discrimination of extant Pan species and subspecies using the enamel-dentine junction morphology of lower molars. Am J Phys Anthropol. 2009;140:234–243. doi: 10.1002/ajpa.21057. [DOI] [PubMed] [Google Scholar]
- Slice DE. Geometric morphometrics. Annu Rev Anthropol. 2007;36:261–281. [Google Scholar]
- Spoor CF. The Comparative Morphology and Phylogeny of the Human Bony Labyrinth. Utrecht: Universiteit Utrecht; 1993. PhD dissertation. [Google Scholar]
- Spoor F, Thewissen JGM. Balance: comparative and functional anatomy in aquatic mammals. In: Thewissen JGM, Nummela S, editors. Sensory Evolution on the Threshold, Adaptations in Secondarily Aquatic Vertebrates. Berkeley: University of California Press; 2008. pp. 257–284. [Google Scholar]
- Spoor F, Zonneveld F. Morphometry of the primate bony labyrinth: a new method based on high-resolution computed tomography. J Anat. 1995;186(Pt 2):271–286. [PMC free article] [PubMed] [Google Scholar]
- Spoor F, Zonneveld F. Comparative review of the human bony labyrinth. Yearbook Phys Anthropol. 1998;41:211–251. doi: 10.1002/(sici)1096-8644(1998)107:27+<211::aid-ajpa8>3.3.co;2-m. [DOI] [PubMed] [Google Scholar]
- Spoor CF, Zonneveld FW, Macho GA. Linear measurements of cortical bone and dental enamel by computed tomography: applications and problems. Am J Phys Anthropol. 1993;91:469–484. doi: 10.1002/ajpa.1330910405. [DOI] [PubMed] [Google Scholar]
- Spoor F, Wood B, Zonneveld F. Implications of early hominid labyrinthine morphology for evolution of human bipedal locomotion. Nature. 1994;369:645–648. doi: 10.1038/369645a0. [DOI] [PubMed] [Google Scholar]
- Spoor F, Bajpai S, Hussain ST, et al. Vestibular evidence for the evolution of aquatic behaviour in early cetaceans. Nature. 2002a;417:163–166. doi: 10.1038/417163a. [DOI] [PubMed] [Google Scholar]
- Spoor F, Esteves F, Tecelão Silva F. The bony labyrinth of Lagar Velho 1. In: Zilhão J, Trinkaus E, Duarte C, et al., editors. The Lapedo Child, A Gravettian Human Skeleton from the Abrigo do Lagar Velho. Lisbon: Trabalhos de Arqueologia, 22, Instituto Portugues de Arqueologia; 2002b. pp. 287–292. [Google Scholar]
- Spoor F, Hublin JJ, Braun M, et al. The bony labyrinth of Neanderthals. J Hum Evol. 2003;44:141–165. doi: 10.1016/s0047-2484(02)00166-5. [DOI] [PubMed] [Google Scholar]
- Spoor F, Garland T, Krovitz G, et al. The primate semicircular canal system and locomotion. Proc Natl Acad Sci U S A. 2007;104:10808–10812. doi: 10.1073/pnas.0704250104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi H. [Comparative anatomical studies of bony labyrinths of the inner ears in Canidae] Kaibogaku Zasshi. 1971;46:85–98. [PubMed] [Google Scholar]
- Takahashi H. [Comparative anatomical study of the bony labyrinth of the inner ear of primates] Kaibogaku Zasshi. 1976;51:366–387. [PubMed] [Google Scholar]
- Walker A, Ryan TM, Silcox MT, et al. The semicircular canal system and locomotion: the case of extinct lemuroids and lorisoids. Evol Anthropol. 2008;17:135–145. [Google Scholar]
- Yamada M, Yoshizaki F. Osseous labyrinth of Cetacea. Sci Rep Whales Res Inst, Tokyo. 1959;14:291–304. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


