Uniform Transmural Strain in Pre-Stressed Arteries Occurs at Physiological Pressure

Abstract

Residual deformation (strain) exists in arterial vessels, and has been previously proposed to induce homogeneous transmural strain distribution. In this work, we present analytical formulations that predict the existence of a finite internal (homeostatic) pressure for which the transmural deformation is homogenous, and the corresponding stress field. We provide evidence on the physical existence of homeostatic pressure when the artery is modeled as an incompressible tube with orthotropic constitutive strain-energy function. Based on experimental data of rabbit carotid arteries and porcine coronary arteries, the model predicts a homeostatic mean pressure of ~90 mmHg and 70–120 mmHg, respectively. The predictions are well within the physiological pressure range. Some consequences of this strain homogeneity in the physiological pressure range are explored under the proposed assumptions.

INTRODUCTION

The existence of residual stress in arteries is widely accepted and constitutive models are formulated accordingly (e.g. see Rachev and Greenwald 2003 for a review). To account for residual stress, Chuong and Fung (1986) modeled the artery as an open sector of a cylinder that is first closed and then axially stretched to form the artery. This method, usually called the opening angle method, has the advantage of an elegant mathematical formulation and will be adopted here.

The reason for the existence of residual stress in arteries is an open question. Chuong and Fung (1986) proposed that residual stresses exist to reduce transmural stress gradients. An alternative hypothesis was offered by Takamizawa and Hayashi (1987) who suggested that the residual stress homogenizes the circumferential strain. Liu and Fung (1989) confirmed this hypothesis as an adaptation principle in hypertension. Both approaches can be considered applications of the Principle of Homeostatis, which recognizes the self-regulatory nature of physiological systems. The first precise formulation of this idea is credited to Claude Bernard (1878), who asserted that all ‘vital mechanisms’ preserve ‘constant the conditions of life in the internal environment’. Bernard’s insight was developed most notably by Cannon (1929). Both authors were concerned exclusively with the self-regulatory nature of the fluid matrix of the body, termed homeostasis by Cannon. Cannon recognized that this concept of self-regulation had the potential to be extended to ‘other materials and environmental states, whose homeostasis is essentially important for optimal activity of the organisms’. This homeostatic idea has been adapted to the biomechanics of the arterial wall (see reviews by Kassab and Navia 2006, and Kassab 2008).

Here, we focus on the relation between residual stress and the homeostatic principle. We hypothesize that when a residually pre-strained cylinder is inflated, there exists a pressure at which the strain is transmurally homogeneous and that this pressure is the mean arterial blood pressure. Here, we shall test this hypothesis with previously measured carotid (Fung et al. 1979) and coronary data (Lu et al. 2003, Wang et al. 2006).

METHODS

Deformation of a Vessel

Let (R,Θ, Z) denote the cylindrical coordinates of the sector of an incompressible annular sector of artery with opening angle α (Fig. 1a), denoted as zero stress state (ZSS), and (r,θ, z) be the cylindrical coordinates of in a deformed configuration of the vessel (Fig. 1b), denoted as loaded state, the deformation gradient tensor, F, is (e.g. Chuong and Fung 1986):

$$\mathbf{F}=\text{diag}\left(\frac{R}{k{\lambda }_{z}r},\frac{kr}{R},{\lambda }_z\right)=\text{diag}\left({\lambda }_R,{\lambda }_{\mathrm{\Theta }},{\lambda }_z\right),r^2=\frac{R^2-R_1^2}{k{\lambda }_z}+r_1^2,k=\frac{2\pi }{2\pi -\alpha }$$ (1.1)

Figure 1.

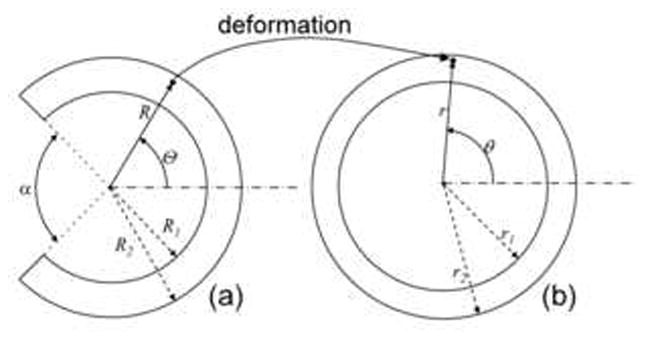
Deformation of arterial wall from open sector (zero-stress reference configuration) (a) to loaded state (b) under inner and outer constant hydrostatic pressures applied on the faces.

(R, r: radial coordinate at ZSS and loaded state, respectively) where λ_z(≥ 1) is the axial pre-stretch. For convenience, we define dimensionless radial coordinate x ≡ r²/R², such that the inner deformed surface of the deformed vessel is $x_1\equiv r^2\left(R_1\right)/R_1^2$, and the outer surface is

$$x_2=\frac{r^2\left(R_2\right)}{R_2^2}=\frac{\gamma +k{\lambda }_z{x}_1}{k{\lambda }_z(\gamma +1)},\gamma =\frac{R_2^2}{R_1^2}-1.$$ (1.2)

It can be further derived that

$$x-\frac{1}{k{\lambda }_z}=\frac{R_1^2}{R^2}\left(x_1-\frac{1}{k{\lambda }_z}\right).$$ (1.3)

It is clear that when x₁ or $r_1^2/R_1^2$ equals 1/kλ_z, the transmural deformation gradient is uniform:

$$\mathbf{F}=\text{diag}({\lambda }_R,{\lambda }_{\mathrm{\Theta }},{\lambda }_z)=\text{diag}\left(\sqrt{\frac{1}{k{\lambda }_z}},\sqrt{\frac{k}{{\lambda }_z}},{\lambda }_z\right).$$ (1.4)

i.e., the vessel reaches homeostatic state. In the next sections, we will explore the conditions for the existence of the homeostatic state.

Pressure-Radius Relationship

Since the passive response of arteries is of interest, we model the vessel wall as hyperelastic material with strain energy-function W = W(F) (see a standard reference of Ogden 1997), along with the assumption of incompressibility. The Cauchy stress σ, is σ = −qI+F ∂W/∂F, whose non-zero components in axisymmetric deformations are:

$${\sigma }_{rr}=-q+\frac{R}{k{\lambda }_{z}r}\frac{\partial W}{\partial {\lambda }_R},{\sigma }_{\theta \theta }=-q+\frac{kr}{R}\frac{\partial W}{\partial {\lambda }_{\mathrm{\Theta }}},{\sigma }_{zz}=-q+{\lambda }_z\frac{\partial W}{\partial {\lambda }_z}$$ (2.1)

and therefore

$${\sigma }_{\theta \theta }-{\sigma }_{rr}=\frac{kr}{R}\frac{\partial W}{\partial {\lambda }_{\mathrm{\Theta }}}-\frac{R}{k{\lambda }_{z}r}\frac{\partial W}{\partial {\lambda }_R}=2x{\widehat{W}}^{\prime }(x),$$ (2.2)

where, using the notation (1.1) and the definition of x, Ŵ′(x) ≡ W(λ_R (x), λ_Θ(x), λ_z) ∈ C² (0, ∞) and the prime notation denotes differentiation. The equilibrium equations in θ and z directions are satisfied identically, and that in the r (radial) direction is dσ_rr/dr + (σ_rr − σ_θθ)/r = 0 subject to boundary conditions σ_rr(r₁)=−P₁ and σ_rr(r₂)=−P₂. Integration of this radial equilibrium equation using the trivial identity dx/dr= 2rR⁻² (1 − kλx) yields

$$P_1-P_2=P(x_1)={\int }_{r_1}^{r_2}\left(\frac{kr}{R}\frac{\partial W}{\partial {\lambda }_2}-\frac{R}{k{\lambda }_{z}r}\frac{\partial W}{\partial {\lambda }_1}\right)\frac{dr}{r}={\int }_{x_1}^{x_2}\frac{{\widehat{W}}^{\prime }(x)}{1-k{\lambda }_{z}x}dx$$ (2.3)

From here on, we only consider vessels with stress free external boundary, i.e., P₂=0, thus P₁=P (x₁). Equation (2.3) determines the deformed inner radius x₁ for prescribed pressure P₁. The corresponding transmural stresses can then be derived as:

$$\{\begin{array}{l}{\sigma }_{rr}(x)=\beta +{\int }_{x_2}^x\frac{{\widehat{W}}^{\prime }(x)}{1-k{\lambda }_{z}x}dx\hfill \\ {\sigma }_{\theta \theta }(x)={\sigma }_{rr}(x)+2x{\widehat{W}}^{\prime }(x)\hfill \\ {\sigma }_{zz}(x)={\sigma }_{rr}(x)+{\lambda }_z\frac{\partial W}{\partial {\lambda }_z}-{\lambda }_R\frac{\partial W}{\partial {\lambda }_R}\hfill \end{array}$$ (2.4)

where β is a constant (zero in this case to satisfy the boundary condition).

A question arises of whether the internal pressure P(x₁) is well-defined when the vessel reaches homeostatic state, i.e., when x₁ =1/kλ_z. It will now be shown that not only is (2.3) well-defined when x₁ =1/kλ_z but also it is continuous there. First, note that trivially it follows from (1.3) that:

$$\begin{array}{l}{x}_2>x_1\text{when}{x}_1<1/k{\lambda }_z;\\ x_2=x_1\text{when}{x}_1=1/k{\lambda }_z;\\ x_2<x_1\text{when}{x}_1>1/k{\lambda }_z.\end{array}$$ (2.5)

Since

$$\frac{dP}{{dx}_1}=\frac{1}{1-k{\lambda }_z{x}_1}(W^{\prime }(x_2)-W^{\prime }(x_1)).$$ (2.6)

P is therefore differentiable at x₁ =1/kλ_z, and therefore continuous, since it follows from L’Hospital’s Rule that

$$\frac{dP}{{dx}_1}(1/k{\lambda }_z)=\frac{\gamma }{k{\lambda }_z(\gamma +1)}{W}^{″}(1/k{\lambda }_z).$$ (2.7)

In addition to the differentiability assumption made previously, it is further assumed that Ŵ(x) is a strictly convex function; i.e., Ŵ″ (x)>0. The necessity of this assumption to ensure physically realistic behaviour of arterial tissue in response to mechanical forces has been discussed in Holzapfel et al. (2000). It follows then from (2.6) that P is a monotonically increasing function of x₁.

Homeostatic Pressure

In the previous section, the value x₁ =1/kλ_z was discussed as being the only possible singular value of x₁ in the definition of the pressure difference given in (2.3); and it was shown that the pressure is in fact continuous there. The value x₁ =1/kλ_z does, however, have a characteristic that distinguishes it from all other values: it follows from (1.3) that when x₁ =1/kλ_z, the deformation is transmurally homogeneous of the form (1.4). The radial equilibrium equation then yields:

$$-q=\frac{2}{k{\lambda }_z}{\widehat{W}}^{\prime }\left(\frac{1}{k{\lambda }_z}\right)lnr+c_1,c_1=\text{constant}.$$ (3.1)

The corresponding radial stress σ_rr is therefore given by:

$${\sigma }_{rr}(r)=\frac{2}{k{\lambda }_z}{\widehat{W}}^{\prime }(\mathrm{\Omega })\times lnr+\sqrt{\mathrm{\Omega }}\frac{\partial W}{\partial {\lambda }_R}\left(\sqrt{\frac{1}{k{\lambda }_z}},\sqrt{\frac{k}{{\lambda }_z}},{\lambda }_z\right)+c_1,\mathrm{\Omega }=\frac{1}{k{\lambda }_z}.$$ (3.2)

An imposition of the boundary conditions yields the blood pressure for the vessel to reach homeostatic state, denoted P_h, as:

$$P_h=P(\mathrm{\Omega })=2\mathrm{\Omega }{\widehat{W}}^{\prime }(\mathrm{\Omega })ln\left(\frac{r_2}{r_1}\right)$$ (3.4)

Noting at homeostatic state that x₂ = x₁ =1/kλ_z, we get r₂/r₁ = R₂/R₁, and thus P_h can be determined by the zero-stress geometry, radii R₁ and R₂ and the opening angle index k, as:

$$P_h=P(\mathrm{\Omega })=2\mathrm{\Omega }{\widehat{W}}^{\prime }(\mathrm{\Omega })ln\left(\frac{R_2}{R_1}\right)$$ (3.5)

The key hypothesis here is that the residual stresses attempt to maintain the artery in a state of transmurally homogeneous strain at a certain physiological blood pressure. This then is a variation on the uniform strain hypothesis of Takamizawa and Hayashi (1987), who proposed that ‘the artery undergoes a uniform circumferential strain throughout the wall in the physiological loading state’.

Stress Distribution at Homeostatic Pressure

The constant strain fields (1.4) are accompanied by stress fields that are slowly varying functions of the radial coordinate in a logarithm form. As can be derived from (3.2), the radial stress is:

$${\sigma }_{rr}(r)=2\mathrm{\Omega }{\widehat{W}}^{\prime }(\mathrm{\Omega })\times ln\left(\frac{r}{r_1}\right)-P_h$$ (4.1)

and the hoop (circumferential) stress is:

$${\sigma }_{\theta \theta }(r)={\sigma }_{rr}(r)+2\mathrm{\Omega }{\widehat{W}}^{\prime }(\mathrm{\Omega })=2\mathrm{\Omega }{\widehat{W}}^{\prime }(\mathrm{\Omega })\times \left[1+ln\left(\frac{r}{r_1}\right)\right]-P_h$$ (4.2)

whose values on the inner and outer walls are respectively

$${\sigma }_{\theta \theta }^{in}=-P_h\left[1-\frac{1}{ln(r_2/r_1)}\right],\text{and}{\sigma }_{\theta \theta }^{\mathit{out}}=\frac{P_h}{ln(r_2/r_1)}$$ (4.3)

At homeostatic strain state, the hoop stress gradient is essentially the same as that for the radial stress, given that the difference is simply a constant 2ΩŴ′(Ω), as it follows from (3.5) and (4.2) that σ_θθ (r) = σ_rr (r)+P_h everywhere. The outer hoop stress ${\sigma }_{\theta \theta }^{\mathit{out}}$ is always tensile. There is a critical arterial thickness ratio for the hoop stress, r₂/r₁=R₂/R₁ = e ≈ 2.72 at which the inner hoop stresses is 0 and the outer hoop stress is P_h, respectively. In reality, the thickness ratio of artery is much less than this value, such that the hoop stress is tensile throughout the wall.

Orthotropic Constitutive Model

The standard mathematical model of anisotropic passive arterial response was introduced by Fung and co-workers (e.g. Chuong and Fung 1986) as:

$$W=\frac{c}{2}(exp(Q)-1),$$ (5.1)

where Q is a quadratic function of components of the Green-Lagrange strain E = (F^TF−I)/2. For an axisymmetric deformation of interest, the quadratic function has the form:

$$Q=b_1{E}_{\mathrm{\Theta }\mathrm{\Theta }}^2+b_2{E}_{ZZ}^2+b_3{E}_{RR}^2+2\left(b_4{E}_{\mathrm{\Theta }\mathrm{\Theta }}{E}_{ZZ}+b_5{E}_{RR}{E}_{ZZ}+b_6{E}_{\mathrm{\Theta }\mathrm{\Theta }}{E}_{RR}\right).$$ (5.2)

The derivative of W with respect to the variable x is given by:

$$W^{\prime }(x)=\frac{c}{2}exp(Q)\left[b_1{k}^2{E}_{\mathrm{\Theta }\mathrm{\Theta }}-b_3{E}_{RR}\frac{1}{k^2{\lambda }_z^2{x}^2}+b_5\frac{E_{ZZ}}{k^2{\lambda }_z^2{x}^2}+\frac{b_6}{2}\left(\frac{1}{k^2{\lambda }_z^2{x}^2}-k^2\right)\right]$$ (5.4)

Re-evaluation of this derivative at the homogeneous deformation state, x = 1/(kλ_z), leads to the following homeostatic pressure:

$$P_h=\frac{c}{2k^2{\lambda }_z^2}ln\left(\frac{R_2}{R_1}\right)exp(Q_h)\left[\begin{array}{l}{b}_1{k}^3(k-{\lambda }_z)+b_3(k{\lambda }_z-1)+b_4{k}^3{\lambda }_z\left({\lambda }_z^2-1\right)+b_{5}k{\lambda }_z\left(1-{\lambda }_z^2\right)+b_{6}k{\lambda }_z\left(1-k^2\right)\end{array}\right]$$ (5.6)

where

$$Q_h=\frac{1}{4k^2{\lambda }_z^2}\left[\begin{array}{l}{b}_1{k}^2{(k-{\lambda }_z)}^2+b_2{k}^2{\lambda }_z^2{({\lambda }_z-1)}^2+b_3{(1-k{\lambda }_z)}^2+2b_4{k}^2{\lambda }_z(k-{\lambda }_z)\left({\lambda }_z^2-1\right)+2b_{5}k{\lambda }_z\left(1-k{\lambda }_z\right)\left({\lambda }_z^2-1\right)+2b_{6}k\left(1-k{\lambda }_z\right)(k-{\lambda }_z)\end{array}\right]$$ (5.7)

An alternative approach for formulation of strain-energy density functions for soft fibrous tissues with anisotropic material behaviour is possible (e.g., Weinberg et al. 2007) but will not be considered here.

Mechanical Data

We use two sets of experimental data to test the above derived formulations. The first data were acquired by Fung et al. (1979) on rabbit carotid arteries. The second data include triaxial mechanical test of eight porcine left anterior descending (LAD) arteries (Lu et al. 2003). Briefly, LAD segments, 3–4 cm long and numbered as L1-L8, were dissected from fresh porcine hearts. Each specimen was mounted to test axial stretch and inflation in an organ bath at room temperature. After the vessels were preconditioned (cyclically loaded to minimize the viscous response), short rings (1–2 mm) were cut from the proximal and distal LAD artery for measurement of the inner and outer radius R₁ and R₂ and opening angle α for the zero-stress state (Fig. 1a), as listed in Table 1. During the experiment, the axial stretch λ_z was varied from 1.2 to 1.4 in increments of 0.1, and the internal pressure was continuously varied from 0 to 200 mmHg at constant λ_z. The outer radius r₂ of the deformed vessel and the axial force were recorded. The inner radius r₁ was calculated by the incompressible condition.

Table 1.

Homeostatic pressure P_h (in mmHg) for porcine left anterior descending arteries (LAD), estimated based on Fung model (5.1). The experimental data are taken from Lu et al. (2003) and Wang et al. (2006).

vessel	vessel geometry				material parameters							Ph
	R2	R1	α	k	c	b1	b2	b3	b4	b5	b6
L1	3.08	2.46	182.4	1.73	11.64	1.03	2.09	0.38	0.37	0.02	0.06	69.5
L2	6.20	5.44	256.6	3.48	5.94	1.27	2.78	0.62	0.45	0.13	0.13	79.0
L3	11.0	10.4	317.8	8.52	4.16	1.58	2.66	0.73	0.3	0.03	0.08	108.8
L4	5.37	4.76	262.5	3.69	11.45	1.00	2.16	0.52	0.39	0.04	0.06	72.1
L5	2.20	1.85	194.0	2.17	4.43	1.48	5.15	0.24	0.25	0.46	0.01	95.2
L6	3.56	3.10	261.6	3.66	13.87	0.66	4.9	0.12	0.48	0.07	0.01	119.5
L7	7.40	7.05	303.8	6.39	4.26	0.92	7.84	2.42	0.31	0.2	0.32	90.4
L8	3.52	3.07	213.0	2.45	13.86	1.26	1.89	0.52	0.27	0.05	0.14	71.6
											mean	88.3

R₁ and R₂ (mm): inner and outer radius of zero-stress state; α (degree): opening angle; k: opening angle index (Eq. 1.1); c (kPa) and {b₁~b₆}: dimensionless material parameters in Eq. (5.2).

RESULTS

We tested the anisotropic prediction of P_h for rabbit carotid arteries (Fung et al. 1979). In the current notation, the geometrical and residual stress data where R₁ = 3.92mm, R₂ = 4.52mm, k = 2.52 and λ_z = 1.02. The material parameters in Eqs. (5.1) and (5.2) were given by Chuong and Fung (1986) as c = 22.4kPa, 1{b₁ ~ b₆}= {1.0672, 0.4775, 0.0499, 0.0903, 0.0585, 0.0042}. These values lead to homeostatic pressure of P_h = 11kPa (~80mmHg) which is well within the normal physiological range of blood pressure for rabbits (see, for example, Rees et al. 1989).

The porcine LAD using an orthotropic Fung model (5.1), whose material parameters c and {b₁-b₆} were previously fitted to biaxial tests (Wang et al. 2006), and are given in Table 1 for completeness. The homeostatic pressure P_h was calculated for each LAD artery by Eq. (5.6) with physiological axial stretch λ_z = 1.35, and the results are given in Table 1. It is shown that the value of P_h ranges from range of 70 to 120 mmHg, with a mean value of 88 mmHg, which is also within the normal physiological range.

DISCUSSION

The review article of Rachev and Greenwald (2003) summarizes the evolution of the concept that tubular structures (e.g. arteries) are residually strained and stressed. It is now widely accepted that mathematical models of arteries should incorporate some measure of this residual stress in order to accurately and reliably predict the response of arteries to mechanical forces. Here, we show an important consequence of residual stress is the existence of homeostatic uniform transmural strain at physiological blood pressure.

The validation of existence of physiological homeostatic pressure P_h of rabbit carotid arteries and porcine LAD in anisotropic models is significant as the predicted homeostatic pressure P_h is consistent with both the experimental data for the residual stretch and the experimentally-based anisotropic mathematical models. It should be noted that the homeostatic pressure physiologically is not necessary the peak pressure, which is typically near 120 mmHg for human carotids and porcine LAD. Rather, it appears to be the mean pressure which is more accurately captured by the anisotropic as opposed to the isotropic models (data not shown).

It has been hypothesized that residual stresses may also result from growth and remodeling of arterial tissue and osmotic pressures (Guo et al., 2007). Regardless of the mechanism of residual stress and strain, an important consequence may be to maintain the artery in a state of homogeneous strain at mean blood pressure. This is a generalisation of the uniform strain hypothesis of Takamizawa and Hayashi (1987), who proposed that ‘the artery undergoes a uniform circumferential strain throughout the wall in the physiological loading state’. It is a generalization because it is suggested here that the full strain field is homogeneous and not just the circumferential component. Other investigations of the relation between residual strains and strain distribution include the study of Kaazempur-Mofrad et al. (2003) who determined the effect of residual strains on the cyclic stress and strain distributions in the large arteries as they undergo phasic pressure changes.

This theory of homogeneous strain at mean blood pressure may hold under compensatory pathological conditions such as hypertension. This stipulation is not new as Fung and Liu (1989) proposed that the increase in opening angle and accompanying residual stress serves to maintain uniform stress and strain gradients in hypertension. The increase in residual stress in blood vessels in response to hypertension has been well documented (see the review in Fung 1993). Thus, even though the elevation of mean blood pressure in hypertension causes the residual stresses to be increased, we speculate that the vessel will still attempt to maintain homogenous strain at this condition. Using engineering systems terminology, this is an example of ‘sub-optimization’, where a subsystem is optimised to the detriment of the overall system depending on the magnitude of the perturbation.

The opening angle method, together with an axial pre-stretch, is used here. One novelty is that an elegant relation is obtained between the mean blood pressure and the residual stress that implies homogeneous strain. This equation relates the blood pressure to both the thickness of the arterial wall and the residual stress. This relation can be inverted to obtain the in vivo residual stress state, provided the corresponding strain-energy function is known.

The derived relation between blood pressure and residual stress can be used to validate the constitutive model: a simple substitution of a proposed strain-energy function with typical values assumed for the residual stress should yield a value for the blood pressure close to 90 mmHg. This was illustrated with an example strain-energy function from the literature. An additional interesting utility of this formulation is as a constitutive constraint, with one of the model parameters determined from this relation. This could be particularly useful for a parameter that is difficult to determine experimentally.

Critique of Model

Arteries are composite structures, containing three histologically different layers (i.e., intima, media and adventitia). For normal artery at physiological pressures, however, the media of the artery dominates the mechanical response (e.g., Ogden and Schulze-Bauer 2000). Consequently, a single-layer artery model has been assumed here to strike a balance between physical realism and mathematical complexity necessary to introduce the concept of homeostatic strain and to deduce the consequence on physiologic loading (pressure). Clearly, this establishes a foundation for additional layers of complexity in future works. A homeostatic strain hypothesis for multiple layer composite models will be considered as well as the effect of smooth muscle tone in future studies.

We also note that the opening angle method adopted here has limitations; e.g., the torsional residual stresses are not considered and an assumption that residual stresses are homogeneous in the axial direction. Regardless, the major experimentally observed components of the residual stress are adequately captured by this well-accepted approach. Alternative approaches can be considered in future studies to further test the hypothesis advanced here.

Conclusion and Significance

In conclusion, it was shown that there exists a finite internal pressure at which the strain is homogeneous for an artery. A model of literature data shows that this pressure is approximately the mean blood pressure. This assumption is broadly compatible with representative existing models of arterial response to mechanical forces and has implications for growth, remodelling and disease.

• A homeostatic pressure exists for which the transmural vessel strain is homogenous.

• The homeostatic pressure is equivalent to the mean blood pressure.

• Consequences of strain homogeneity are explored under the proposed assumptions.