Updated energy budgets for neural computation in the neocortex and cerebellum

Abstract

The brain's energy supply determines its information processing power, and generates functional imaging signals. The energy use on the different subcellular processes underlying neural information processing has been estimated previously for the grey matter of the cerebral and cerebellar cortex. However, these estimates need reevaluating following recent work demonstrating that action potentials in mammalian neurons are much more energy efficient than was previously thought. Using this new knowledge, this paper provides revised estimates for the energy expenditure on neural computation in a simple model for the cerebral cortex and a detailed model of the cerebellar cortex. In cerebral cortex, most signaling energy (50%) is used on postsynaptic glutamate receptors, 21% is used on action potentials, 20% on resting potentials, 5% on presynaptic transmitter release, and 4% on transmitter recycling. In the cerebellar cortex, excitatory neurons use 75% and inhibitory neurons 25% of the signaling energy, and most energy is used on information processing by non-principal neurons: Purkinje cells use only 15% of the signaling energy. The majority of cerebellar signaling energy use is on the maintenance of resting potentials (54%) and postsynaptic receptors (22%), while action potentials account for only 17% of the signaling energy use.

Introduction

Over the past decade, there have been a number of models published employing a ‘bottom–up' approach to the estimation of energy costs associated with neural computation in the cerebral cortex (Attwell and Laughlin, 2001; Lennie, 2003), the olfactory bulb (Nawroth et al, 2007), and the cerebellum (Howarth et al, 2010). These models use data on the cell's morphology and the ion fluxes underlying synaptic potentials, maintenance of resting potentials and the propagation of action potentials, in order to estimate the energy cost of the various processes underlying neural computation, and have demonstrated that most of the brain's energy is used for electrical signaling purposes.

It is not feasible to model the voltage-gated ion fluxes underlying the action potentials in all cell types in all the brain areas considered, because data are not available on the magnitude and location of all the voltage-gated channels responsible, so these models typically followed the approach of Attwell and Laughlin (2001) by first calculating the minimum Na⁺ entry needed to produce the voltage change occurring during the action potential (given by the voltage change occurring multiplied by the capacitance of the area of cell being considered). This value was then quadrupled to take account of the fact that there is temporal overlap in the current flowing inward through Na⁺ channels and outward through K⁺ channels, increasing the Na⁺ influx needed to produce the action potential. This fourfold increase was originally estimated for squid giant axon (Hodgkin, 1975). While these models provide interesting conclusions regarding the division of signaling energy use between the various processes occurring within a brain area or a specific cell type, recent work has suggested, both experimentally (Alle et al, 2009; Carter and Bean, 2009) and theoretically (Sengupta et al, 2010), that action potentials within mammalian neurons are more energetically efficient than previously thought. This is because the temporal overlap between Na⁺ and K⁺ currents during an action potential is much less than was estimated by Hodgkin (Alle et al, 2009; Carter and Bean, 2009), so that the factor by which the minimum charge entry (needed to polarize the membrane through the voltage of the action potential) must be multiplied to obtain the actual Na⁺ entry ranges from as low as 1.04 (for cerebellar granule cells: Sengupta et al, 2010) to 2 (for Purkinje cells: Carter and Bean, 2009) compared with the value of 4 (Hodgkin, 1975), which has been commonly used. Previous models (Attwell and Laughlin, 2001; Nawroth et al, 2007; Howarth et al, 2010) have, therefore, overestimated the energy cost of action potentials in mammalian neurons.

In this paper, we present an update to the previously published estimate of the energy use associated with neural computation in the cerebral cortex (Attwell and Laughlin, 2001) and cerebellum (Howarth et al, 2010), taking into account the new data available on the energy use of action potentials. We also provide an interactive spreadsheet that allows readers to do their own calculations of the energy used on different subcellular mechanisms in the cerebral cortex, and for all the cell types in the cerebellum.

Materials and methods

Calculation of ATP Usage

Most signaling-related energy in the brain is expended on pumping of Na⁺ ions out of cells (Siesjo, 1978; Attwell and Laughlin, 2001). The signaling energy expended on different cellular processes in the rat cerebral and cerebellar cortical grey matter was estimated as previously described (Attwell and Laughlin, 2001; Howarth et al, 2010). Briefly, published anatomical and electrophysiological data were employed to calculate the ATP used to reverse the Na⁺ influx producing excitatory synaptic currents and action potentials, the Na⁺ influx occurring at the resting potential, the Ca²⁺ entry driving neurotransmitter release, and the ATP expended on other less energy consuming processes inherent in CNS information processing. Measured ion fluxes were converted into values for ATP consumption using the fact that the Na⁺/K⁺-ATPase consumes one ATP per 3 Na⁺ extruded, while 3 Na⁺/Ca²⁺ exchange followed by Na⁺ extrusion uses 1 ATP per Ca²⁺ extruded. Similarly, the ATP needed to restore Ca²⁺ to intracellular stores, and expended on transmitter and vesicle recycling, were estimated (Attwell and Laughlin, 2001). The energy expended on restoring Cl⁻ gradients after inhibitory transmission was previously estimated to be <1% of that needed to restore an equivalent change of the Na⁺ gradient and so was ignored (Howarth et al, 2010). Full details of how to do the calculations have been described previously (Howarth et al, 2010).

The multiplication factor of 4 previously used to take account of the simultaneous activation of Na⁺ and K⁺ channels during an action potential was modified as follows. For cells in the cerebral cortex, a factor of 1.24 was used (Carter and Bean, 2009). For cerebellar cells, we used the following values. For Purkinje cells, Golgi cells and molecular layer interneurons a factor of 2 was used (measured for Purkinje cells by Carter and Bean, 2009), for granule cells, a factor of 1.04 was used (for simplicity, we used the modeling by Sengupta et al (2010) based on a Hodgkin–Huxley description of the voltage-gated Na⁺ current; a more complex model is now available for the interested reader: Magistretti et al, 2006; Diwakar et al, 2009), and for mossy fibers and climbing fibers a factor of 1.3 was used (based on measurements of hippocampal mossy fibers: Alle et al, 2009). The full calculations are presented in the Supplementary Spreadsheet, which allows the reader to manipulate the parameters and investigate their effect on energy use.

Energy Consumption by Subcellular Processes

Within a given cell type, the energy calculated to be used on various subcellular processes is presented below. The following categories are used:

• Resting potential: the energy used to pump out Na⁺ to maintain the resting potential of the cell

• Action potential: the energy required to reverse the ion entry needed to charge the cell membrane during the action potential.

• Postsynaptic receptors: includes the energy used to reverse the glutamate-evoked Na⁺ and Ca²⁺ fluxes through N-methyl-D-aspartate (NMDA) and non-NMDA receptors and the energy usage on G-protein signaling.

• Neurotransmitter recycling: includes energy usage on the uptake, metabolic processing, export to neurons, and repackaging of neurotransmitters and their metabolic products.

• Presynaptic Ca²⁺ entry and vesicle cycling: includes energy required to reverse the Ca²⁺ influx triggered by presynaptic action potentials and energy usage on the vesicular release and endocytosis mechanisms.

Results

Cerebral Cortex

We recalculated the energy budget for the cerebral cortex presented by Attwell and Laughlin (2001), incorporating recently published data (Carter and Bean, 2009) demonstrating that action potentials in cortical pyramidal neurons use less energy than was assumed by Attwell and Laughlin (2001) based on an estimate by Hodgkin (1975). The ‘sodium entry ratio' in these neurons (calculated as the sodium entry during an action potential divided by the theoretical minimum sodium entry necessary) was 1.24 (Carter and Bean, 2009), that is, only 24% more than the theoretical minimum. This is much smaller than the 300% excess sodium entry, which was measured in squid giant axon (Hodgkin, 1975) and was assumed in previous calculations of cerebral cortical energy use (Attwell and Laughlin, 2001). As described previously (Attwell and Laughlin, 2001), we assume for simplicity that all neurons in the cortex are glutamatergic, as 90% of cells and synapses are glutamatergic (Abeles, 1991; Braitenberg and Schüz, 1998). Neurons are assumed to fire at an average firing rate of 4 Hz (Attwell and Laughlin, 2001) and have an Na⁺ entry overlap factor of 1.24 (Carter and Bean, 2009).

Energy Consumption by Subcellular Processes in the Cerebral Cortex

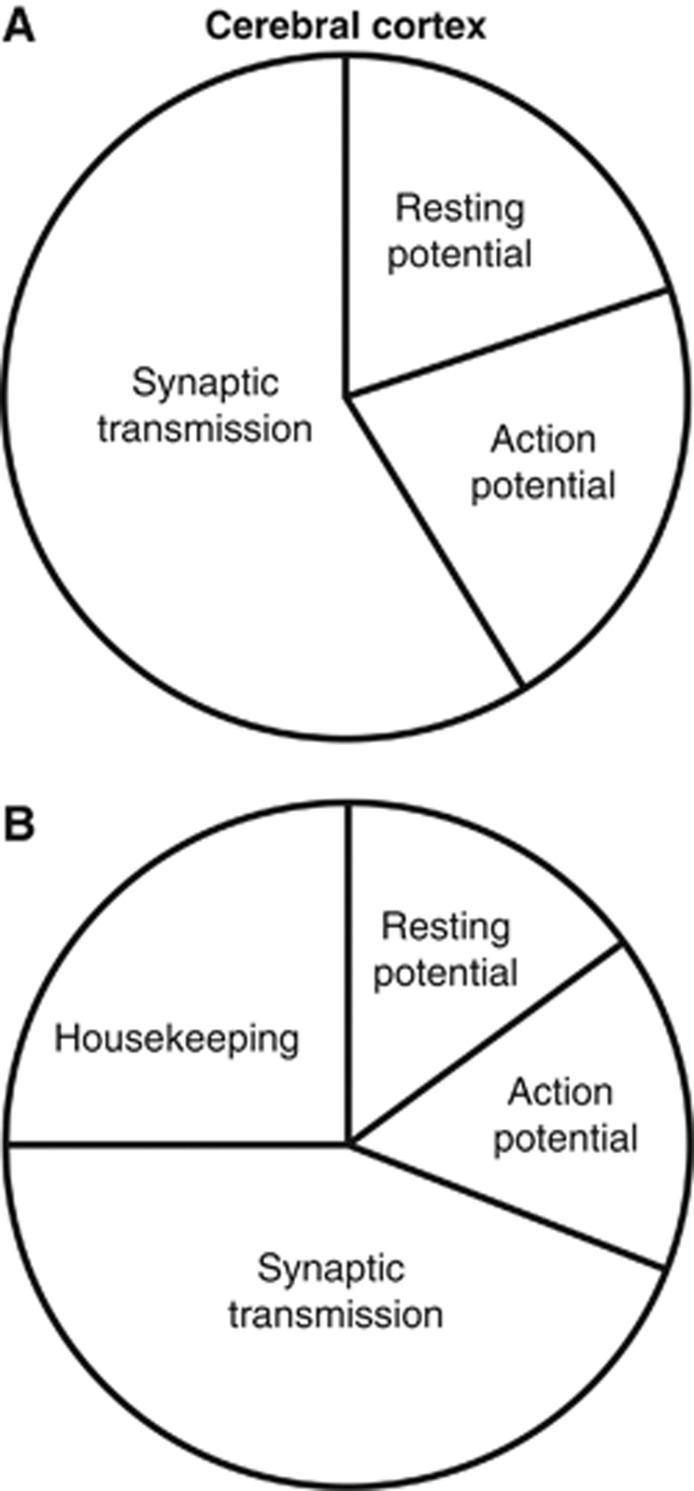
Incorporating the discovery that action potentials in cortical pyramidal cells are more energetically efficient (Carter and Bean, 2009) than was suggested by work on squid giant axon (Hodgkin, 1975), the fraction of cerebral cortical signaling energy used on action potentials is predicted to be less than previously calculated (21% versus 47% in Attwell and Laughlin, 2001), with an increased fraction of the energy usage now going on postsynaptic receptors (50% versus 34%). The percentage energy use on resting potentials (20% versus 13%) is also increased as a consequence of the lower percentage energy use on action potentials (Figure 1A). Only a small fraction of energy use goes on neurotransmitter recycling and presynaptic effects of Ca²⁺ (4% and 5%, respectively; Figure 1A). Thus, the majority of energy use is now predicted to be on postsynaptic receptors, which account for 50% of the energy use.

Figure 1.

Predicted signaling energy use for cerebral cortex. (A) Energy distribution among subcellular processes for the cerebral cortex. Resting potentials account for ∼20% of the total energy use, action potentials 21%, and synaptic processes 59% (including postsynaptic receptors (50%), neurotransmitter recycling (4%), and presynaptic Ca²⁺ entry and vesicle cycling (5%)). (B) As panel A, but including non-signaling energy use, assumed to be 6.81 × 10²² ATP/s/m³, that is, 1/3 of the neuronal signaling energy, so that housekeeping tasks are assumed to account for 25% of the total energy use. On this basis, resting potentials use 15%, action potentials 16%, and synaptic processes 44% of the total energy use.

Housekeeping energy use on non-signaling tasks, such as turnover of macromolecules, axoplasmic transport and mitochondrial proton leak (Attwell and Laughlin, 2001; Nawroth et al, 2007), which are not included in these calculations, has previously been shown to account for between 25% (rodent cortical grey matter: Attwell and Laughlin, 2001) and 50% (whole brain: Kety, 1957; Sokoloff, 1960; Siesjo, 1978; Astrup et al, 1981; Ames et al, 1992; Ames and Li, 1992; Rolfe and Brown, 1997) of total energy use. Figure 1B shows the predicted distribution of total cortical energy expenditure if one assumes that the energy use on housekeeping tasks is equivalent to ∼1/3 of the signaling energy use (i.e., 25% of the total use, and equivalent to 6.79 μmol ATP/g/min). The estimated total energy use including housekeeping energy is then 27.2 μmol ATP/g/min, which is similar to the total rate of energy use measured in the grey matter of rat (33 to 50 μmol ATP/g/min: Sokoloff et al, 1977). Uncertainty in the energy used on housekeeping tasks is the most likely cause of the difference between the predicted and measured values for energy use (Kety, 1957; Sokoloff, 1960; Siesjo, 1978; Astrup et al, 1981; Ames et al, 1992; Ames and Li, 1992; Rolfe and Brown, 1997).

Cerebellar Cortex

Previously, the signaling energy used on each cell type in the cerebellar cortex was analyzed, with all the cells firing action potentials at their measured physiological rates (except for the granule cell for which an estimated mean firing rate of 3 Hz was used (Howarth et al, 2010)). Here, we present an updated version of these calculations, incorporating recently published data (Alle et al, 2009; Carter and Bean, 2009; Sengupta et al, 2010) suggesting that action potentials are more energetically efficient than was previously assumed.

Energy Consumption by Cerebellar Cell Type

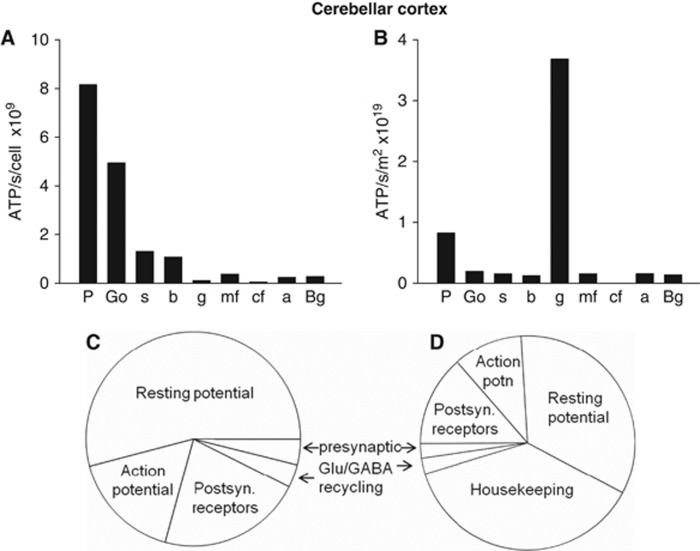
In agreement with both our previous findings, and those of Niven et al (2007), larger cells were found to use significantly more ATP/s per cell than small cells (Figure 2A). This reflects the fact that larger areas of membrane mediate larger ion fluxes, which require more ATP to be pumped back. Thus, each of the largest cerebellar neurons, the Purkinje cells, uses 8.19 × 10⁹ molecules of ATP/s, which is far greater than the 1.32 × 10⁸ molecules of ATP/s used by each of the smallest, granule, neurons (Figure 2A). However, when multiplied by the number of neurons present, the 274-fold higher density of granule cells results in them dominating the energy use of the whole cerebellar cortex (Figure 2B), consuming 67% of the total signaling energy, while the principal Purkinje neurons use only 15% of the total.

Figure 2.

Predicted signaling energy use for cerebellar cortex. (A) Cellular distribution of predicted energy use (ATP used per cell). a, astrocyte; b, basket cell; Bg, Bergmann glia; cf, climbing fiber; g, granule cell; Go, Golgi cell; mf, mossy fiber; P, Purkinje cell; s, stellate cell. (B) Cellular distribution of energy use, taking density of cells into account (ATP use per class of cell). (C) Energy distribution among subcellular processes (summed over all cell types, weighted by cell densities). Resting potentials account for ∼54% of the total energy use, action potentials 17%, postsynaptic receptors 22%, neurotransmitter recycling (ATP used in glia and on packaging transmitter into vesicles in the releasing cell) 3%, and presynaptic Ca²⁺ entry and vesicle cycling 4%. (D) As panel C, but including non-signaling energy use, assumed to be 7.7 μmol ATP/g/min (20.5–12.8 μmol ATP/g/min, see text). Housekeeping tasks then account for 38% of the energy use, resting potentials 34%, action potentials 10%, postsynaptic receptors 14%, neurotransmitter recycling (ATP used in glia and on packaging transmitter into vesicles in the releasing cell) 2%, and presynaptic Ca²⁺ entry and vesicle cycling 2%.

The predicted total signaling energy consumption for the cerebellar cortex is 12.8 μmol ATP/g/min, reduced by 22% from the value of 16.5 μmol ATP/g/min derived using the less efficient assumption for action potential energy consumption (Howarth et al, 2010), but still similar in magnitude to the value for total energy consumption measured in conscious rats of 20.5 μmol ATP/g/min (Sokoloff et al, 1977). Housekeeping energy use on non-signaling tasks, which are not included in these calculations, may account for the ∼40% difference between the predicted and measured energy use since previous studies have estimated housekeeping energy to account for between 25% (rodent cortical grey matter: Attwell and Laughlin, 2001)) and 50% (whole brain: Kety, 1957; Sokoloff, 1960; Siesjo, 1978; Astrup et al, 1981; Ames et al, 1992; Ames and Li, 1992; Rolfe and Brown, 1997) of total energy use.

Energy Consumption by Subcellular Processes in the Cerebellum

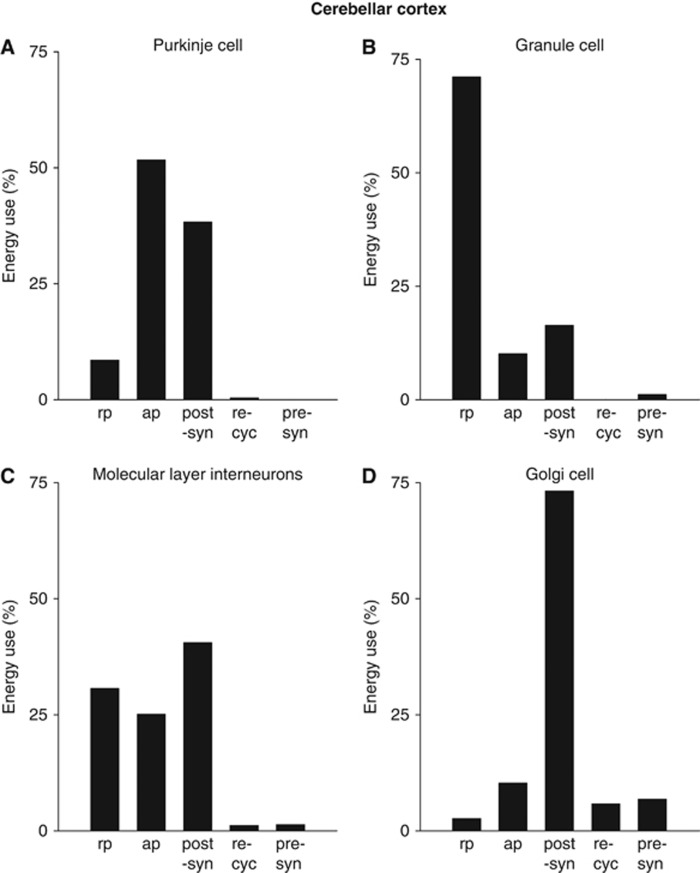
The subcellular distribution of energy use varies dramatically between different neuron types in the cerebellar cortex (Figure 3). Even after incorporating a more energy efficient action potential into the calculations, the principal output neurons of the cerebellum, the Purkinje cells, still use the majority (90%) of their signaling energy on action potentials (52%) and postsynaptic receptors (38%), and only a small fraction (9%) on maintenance of the resting potential (Figure 3A). This reflects the fact that these cells receive a large number of synaptic inputs (∼26,000 active inputs: Howarth et al, 2010) and fire action potentials at a high rate. With the discovery that action potentials in Purkinje cells are more energetically efficient (Carter and Bean, 2009) than was suggested by work on squid giant axon (Hodgkin, 1975), the fraction of Purkinje cell signaling energy used on action potentials is predicted to be less than previously calculated (52% versus 68% in Howarth et al, 2010), with an increased fraction of the energy usage now going on postsynaptic receptors (38% versus 26%). For the much smaller granule cells, which each receive a far smaller number of excitatory synaptic inputs (∼4: Eccles et al, 1967), but have to maintain the resting potential of a very long (∼4.5 mm) axon, most of the signaling energy (Figure 3B) goes on the resting potential (71%, a significantly larger percentage than the previously calculated value of 55%: Howarth et al, 2010). Recent modeling studies have suggested that the temporal overlap between Na⁺ and K⁺ currents during a cerebellar granule cell action potential is negligible, resulting in an overlap factor of only 1.04, implying an extremely energy efficient action potential (Sengupta et al, 2010). As a result, granule cells are predicted to use only a small fraction of their energy on action potentials (10% Figure 3B), much less than the previous prediction that 31% of granule cell signaling energy use is on action potentials (Howarth et al, 2010). Of the inhibitory interneurons, basket and stellate cells use similar fractions of energy on the resting potential, action potentials, and postsynaptic receptors (Figure 3C), while Golgi cells use most of their energy (73%) on postsynaptic receptors (Figure 3D), in agreement with previous estimations (Howarth et al, 2010).

Figure 3.

The subcellular distribution of cerebellar energy use by cell type. (A) Purkinje cells. Most energy is used on action potentials and postsynaptic receptors. (B) Granule cells. Most energy is used to maintain the resting potential along the long parallel fibers. (C, D) Inhibitory neurons use most energy on postsynaptic receptors and action potentials. (C) Molecular layer interneurons. (D) Golgi cells. ap, action potentials; post-syn, postsynaptic receptors; pre-syn, presynaptic Ca²⁺ entry and vesicle cycling; re-cyc, transmitter recycling (ATP used on glial uptake of transmitter and its metabolic processing, and on packaging transmitter into vesicles in the releasing cell); rp, resting potential.

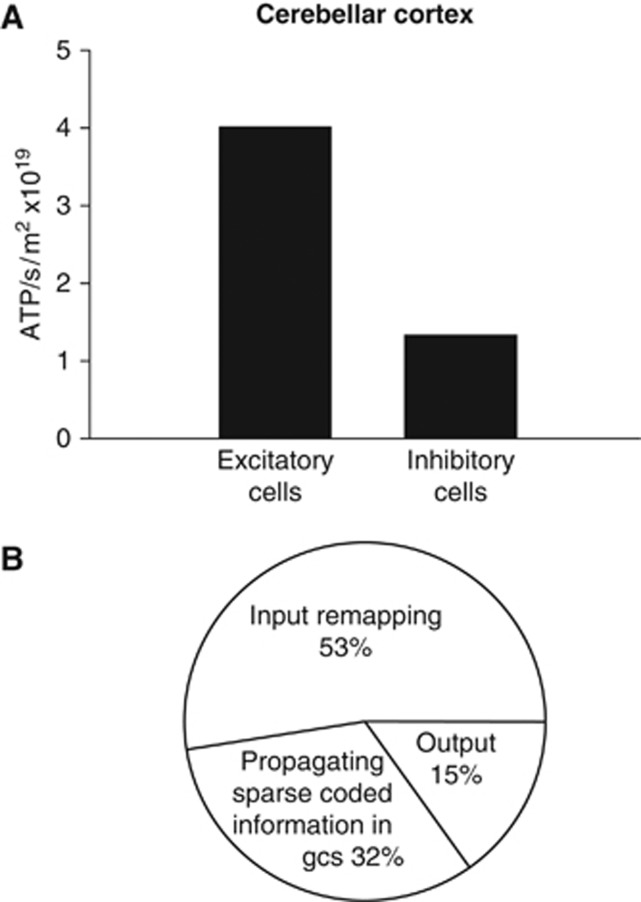
The distribution of signaling energy expenditure on subcellular tasks in the whole cerebellar cortex was calculated by summing the energy used on all processes over all cells, weighted by their area density (Figure 2C). Compared with previous predictions (Howarth et al, 2010), action potentials account for a smaller fraction of energy use as expected (17% of signaling energy versus the 36% previously reported), while the percentage energy use on both resting potentials (54% versus 42%) and postsynaptic receptors (22% versus 17%) is increased as a consequence. Only a small fraction of energy use goes on neurotransmitter recycling and presynaptic effects of Ca²⁺ (Figure 2C). Comparing these predictions for the cerebellar cortex with predictions for the cerebral cortex (Figure 1A) shows that a much greater fraction of energy is predicted to be used on maintenance of resting potentials in the cerebellum (54% versus 20% in cerebral cortex), while a smaller fraction is used on action potentials (17% versus 21% in cerebral cortex) and postsynaptic receptors (22% versus 50% in cerebral cortex). Thus, in the cerebral cortex postsynaptic receptors are the main (50%) signaling energy consumer, unlike in cerebellar cortex where the main energy use is on maintenance of resting potentials (54%) due to the high cost of maintaining the resting potentials of granule cells. Summing the signaling energy use over different neurons in the cerebellar cortex, inhibitory neurons are predicted to use 25% of the signaling energy, and excitatory neurons to use 75% (Figure 4A).

Figure 4.

Predicted energy use on different aspects of cerebellar computation. (A) Comparison of energy use by excitatory and inhibitory neurons. (B) Energy use on different stages of cerebellar computation.

Figure 2D shows the predicted distribution of total cerebellar energy expenditure if one assumes that housekeeping tasks are responsible for the difference between the predicted signaling energy use (12.8 μmol ATP/g/min), and the total energy use measured in the cerebellum of conscious rats (20.5 μmol ATP/g/min: Sokoloff et al, 1977).

Estimation of Energy Use by the Three Stages of Cerebellar Computation

Varying the firing rate of the granule cells alone results in large changes to the cerebellar energy expenditure predictions (e.g., doubling the rate from 3 to 6 Hz increased the total predicted signaling energy consumption by 17%) while varying the assumed firing rate of Purkinje cells alone had little effect on energy consumption (doubling the rate of simple spikes from 50 to 100 Hz increased the consumption by 8%). Thus, as reported previously (Howarth et al, 2010), the total signaling energy use need not correlate well with the firing rate of the principal neurons in this part of the brain.

One can conceptualize the retrieval of motor patterns from the cerebellar cortex as occurring in three stages (Tyrell and Willshaw, 1992): remapping from mossy fiber input action potentials to action potentials in the granule cell somata (using energy in mossy fibers, granule cell dendrites and somata, Golgi cells, and granular layer astrocytes); propagation of remapped information to Purkinje cells as a sparse code (using energy in the granule cell axons, molecular layer interneurons, and Bergmann glia); and computation by Purkinje cells of an output signal (using energy in the Purkinje cells). By summing the energy used in the different cell types participating in these different stages of cerebellar computation, the relative amounts of ATP used on these processes were predicted to be 53%:32%:15% (Figure 4B). Thus, most cerebellar cortical signaling energy is used on intra-cerebellar processing of the incoming information, rather than on computation of the output signal by the principal Purkinje neurons. This conclusion has been strengthened by the inclusion of more energy efficient action potentials within the cerebellum, as energy use on Purkinje cells is predicted to account for only 15% of cerebellar signaling energy use, compared with 18% as predicted previously (Howarth et al, 2010).

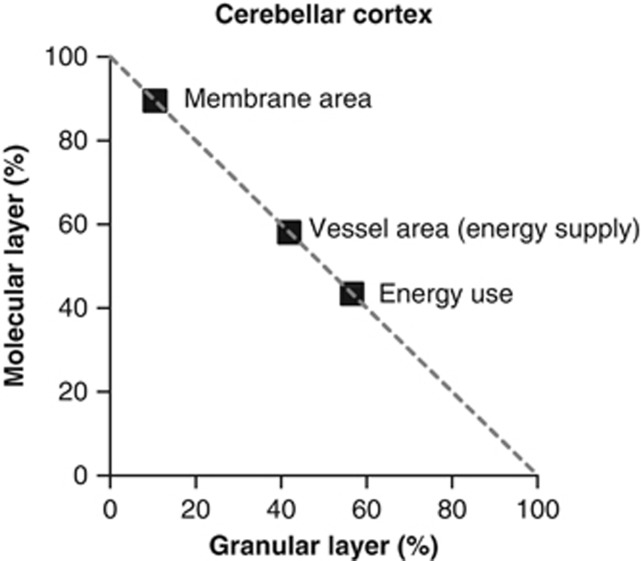
Cerebellar Energy Use Correlates Better with Energy Supply than Cellular Membrane Area

The predicted laminar distribution of energy use across the cerebellar cortex was calculated by summing the energy consumed in the parts of the neurons and glial cells in the molecular layer and the granular layer (Figure 5, including half of the Purkinje cell somata in each layer). For local tasks such as reversing the ion entry generating synaptic currents, there is no ambiguity over attributing ATP use to a particular layer. For the Na⁺ entry generating action potentials, when Na⁺ enters at the axon hillock, or wherever else there are Na⁺ channels, it will diffuse through the cell, and ATP will be consumed at the locations where there are Na⁺/K⁺-ATPase pumps to pump the Na⁺ out of the cell. Usually, these are spread more uniformly over the cell than are the Na⁺ channels. Thus, Na⁺ entry at the axon hillock will produce ATP use not only at the axon hillock but also in the soma and even the proximal dendrites. This is of no consequence for calculating the total ATP use of the cell, but for the analysis of energy use in the different cerebellar layers we, for simplicity, assumed that the ATP use was proportional to the charge needed to alter the membrane voltage in each local region.

Figure 5.

Laminar distribution of cerebellar energy use correlates better with energy supply than with cellular membrane area. Distribution of predicted energy use, calculated membrane area, and measured blood vessel surface area between the molecular and granular layers. Data for membrane area and blood vessel surface area are taken from Howarth et al (2010).

The granular layer is predicted to use 57% of the total ATP consumption, and the molecular layer 43% (Figure 5), a ratio of 1.33. As a result of including the greater energy efficiency of action potentials, the laminar distribution of energy use is reversed compared with previous calculations where the molecular layer was predicted to use more signaling energy than the granular layer (54% versus 46%, respectively, Howarth et al, 2010).

Neuronal size and connectivity differ dramatically between the granular and molecular layers. The granular layer is made up of many tiny granule cells receiving very few input synapses while the molecular layer comprises a much smaller number of large Purkinje cells receiving a large number of inputs. One might imagine the amount of membrane area present to be a factor which confers information processing power on an area of the brain. Energy use might also be expected to correlate with membrane area, since energy is largely spent on pumping ions back across membranes. Membrane area was calculated from the dimensions of the cells in each layer (see Howarth et al, 2010) and was found to be 8.6-fold larger in the molecular layer than in the granular layer (Figure 5); nevertheless, the energy used in the molecular layer is predicted to be less than in the granular layer (Figure 5). Is there, instead, a match between energy use and energy supply? To test how the laminar distribution of energy use was served by the energy supply provided by blood vessels, the previously published laminar distribution of isolectin B4-labeled blood vessels (taken as a measure of the surface area available for oxygen diffusion and glucose transport in each lamina, see Figure 4C in Howarth et al, 2010) was compared with the estimated laminar distribution of energy use. The vessel surface area was divided between the layers with 58%±3% and 42%±3% (n=3 rats, P<0.02) in the molecular and granular layers, respectively (Figure 5; Howarth et al, 2010). Hence, there is a better correlation between the distribution of energy supply and predicted energy use in each layer than between the membrane area and the predicted energy use in each layer (Figure 5).

Discussion

This work updates our previous estimation of energy use associated with neural computation in the cerebral cortex (Attwell and Laughlin, 2001) and cerebellum (Howarth et al, 2010), incorporating recently published data demonstrating that action potentials are more energy efficient than previously assumed (Alle et al, 2009; Carter and Bean, 2009; Sengupta et al, 2010). Updating the models in this way supports most of the major conclusions of the original papers.

Effect of Assuming Energetically Efficient Action Potentials

To calculate the energy used on action potentials within the cerebral or cerebellar cortex, the minimum charge entry needed to charge the cell capacitance to the peak of the action potential is multiplied by an ‘overlap factor,' which accounts for the fact that the Na⁺ and K⁺ currents producing action potentials overlap in time (Attwell and Laughlin, 2001; Howarth et al, 2010) so that extra Na⁺ entry is needed to oppose the K⁺ efflux, and needs to be pumped out, consuming ATP. However, recent work (Alle et al, 2009; Carter and Bean, 2009; Sengupta et al, 2010) has suggested that these currents have less temporal overlap than originally thought (Hodgkin, 1975).

The value of the ‘overlap factor' is variable between brain areas and between different cells within a particular brain area. A more energetically efficient action potential results from a decreased ‘overlap factor,' and this results in action potentials accounting for a smaller proportion of the signaling energy used by a brain area or individual cell type. As the action potential approaches 100% energetic efficiency (i.e., there is no temporal overlap between the Na⁺ and K⁺ currents), the ‘overlap factor' approaches the value of 1, resulting in the minimum possible energy being used on action potential production. Such a reduction in the predicted energy use on action potentials, and consequently in the total predicted signaling energy, implies that housekeeping tasks can account for a larger percentage of the total energy use (since the total measured energy use for a brain area remains unchanged).

For the cerebral cortex, the Na⁺ entry underlying action potentials has been recalculated by multiplying the minimum charge entry needed to charge the cell capacitance by a factor of 1.24 (Carter and Bean, 2009) rather than by 4 (Hodgkin, 1975) as used in the model by Attwell and Laughlin (2001). Assuming more energy efficient action potentials reduces the total cost of action potentials by 69% and results in a 32% decrease in the predicted signaling energy expenditure for the cerebral cortex as a whole, from 30 μmol ATP/g/min (Attwell and Laughlin, 2001) to 20.4 μmol ATP/g/min. This is somewhat less than the measured total energy use of 33 to 50 μmol ATP/g/min in different cortical regions (Sokoloff et al, 1977), which would allow the housekeeping energy to be higher than the 25% suggested previously (Attwell and Laughlin, 2001). The most important effect of decreasing the energy used by action potentials in the cerebral cortex is that the distribution of ATP use on the subcellular processes underlying information processing is altered, with the highest percentage of ATP use now being on synaptic currents rather than on action potentials.

For cerebellar cells, the Na⁺ entry underlying action potentials has been recalculated by multiplying the minimum charge entry needed to charge the cell capacitance by a factor of 1.3 for mossy fibers and climbing fibers (based on measurements in hippocampal mossy fibers: Alle et al, 2009), 1.04 for granule cells (based on a modeling study: Sengupta et al, 2010), and 2 for Purkinje cells, Golgi cells and molecular layer interneurons (based on measurements from Purkinje cells: Carter and Bean, 2009), rather than by 4 for all cell types (Hodgkin, 1975) as used in previous models (Attwell and Laughlin, 2001; Howarth et al, 2010). Assuming more energy efficient action potentials reduces the total cost of action potentials by 64%, and results in a 22% decrease in the predicted signaling energy expenditure for the cerebellar cortex as a whole (from 16.5 μmol ATP/g/min (Howarth et al, 2010) to 12.8 μmol ATP/g/min, allowing housekeeping energy to be higher than suggested previously as the total measured energy use (Sokoloff et al, 1977) is unchanged). The distribution of ATP use on subcellular processes is also altered, with a higher percentage of ATP use being on processes other than action potentials, predominantly synaptic currents and maintaining the granule cell resting potential. Importantly, the previous conclusion that energy use is not mainly on principal cell firing is further reinforced by the fact that action potential costs are lower than previously estimated (Howarth et al, 2010).

Assuming an overlap factor of 2 (Carter and Bean, 2009) rather than 4 for Purkinje cells and Golgi cells results in a 50% decrease in energy use on action potentials in the Purkinje cell compared with previous estimates (Howarth et al, 2010), and a 34% decrease in the total signaling energy use per Purkinje cell (reduced from 1.24 × 10¹⁰ molecules ATP/s (Howarth et al, 2010) to 8.19 × 10⁹ molecules ATP/s). Energy use on Golgi cell action potentials also decreases by 50%, resulting in an ∼10% decrease in energy use per Golgi cell (from 5.50 × 10⁹ molecules ATP/s (Howarth et al, 2010) to 4.97 × 10⁹ molecules ATP/s).

The distribution of energy use across different subcellular mechanisms in granule cells is most dramatically affected by the reduction of energy use on action potentials. Assuming an overlap factor of 1.04 for granule cells (Sengupta et al, 2010) decreases the energy used on action potentials by 74% compared with previous estimates (Howarth et al, 2010), resulting in a 23% decrease in signaling energy use per granule cell (reduced from 1.72 × 10⁸ molecules ATP/s (Howarth et al, 2010) to 1.32 × 10⁸ molecules ATP/s). An overlap factor of 1.04 implies very little temporal overlap occurring between the Na⁺ and K⁺ currents. However, this value should be used cautiously because it is based on a model of a rat granule cell (Maex and De Schutter, 1998) produced by adapting a model of an in vitro turtle granule cell (Gabbiani et al, 1994), and corrections for temperature carried out when producing that model resulted in a five-fold speeding of voltage-gated ion channel kinetics (Maex and De Schutter, 1998) so these data may not truly represent physiological conditions in rodents. If correct, an overlap factor of 1.04 for granule cell action potentials may be considered an extreme case where the action potentials are almost 100% energetically efficient. As such, it is reassuring that none of the major conclusions of Howarth et al (2010) were altered significantly when using this assumption.

If a more conservative overlap factor of 1.6 is employed for the granule cell calculations (based on measurements of CA1 pyramidal neurons: Carter and Bean, 2009), the total predicted signaling energy use for the cerebellar cortex becomes 13.3 μmol ATP/g/min, a 3.9% increase compared with the 12.8 μmol ATP/g/min predicted with the assumption of a highly efficient granule cell action potential and a 19% decrease compared with the previous estimate of 16.5 μmol ATP/g/min (Howarth et al, 2010). This more conservative estimate of granule cell action potential efficiency results in the energy use per granule cell increasing by 6% to 1.4 × 10⁸ molecules ATP/s. While the majority of granule cell signaling energy is then still predicted to be used on maintaining the resting potential (68% compared with 71%), the cost of action potential propagation increases from 10% to 15% and the energy used on postsynaptic receptors falls slightly from 17% to 16%. For the cerebellar cortex as a whole, use of a more conservative estimate of the energy efficiency of the granule cell action potential results in a small increase of the percentage of total energy use on action potentials (from 17% to 20%) and a correspondingly small fall in the percentage energy use on both resting potentials (from 54% to 52%) and postsynaptic receptors (from 22% to 21%). Importantly, the conclusion that the majority of energy use, both in the cerebellar cortex as a whole and for granule cells in particular, is on maintenance of resting potentials and not on action potential propagation remains true even if the less extreme increase in action potential efficiency is assumed.

Energy Use During Different Cortical States

The calculations performed throughout this paper have assumed physiologically occurring firing rates for all the neurons concerned taken, wherever possible, from data on awake animals. However, it is worth noting that the energy use of the cortex will depend on the cortical state at any particular time. For example, during sleep, cortical neuronal activity is, in general, decreased, hence, there would be a decrease in the energy use. For instance, the average firing rate of neurons in the barrel cortex is significantly lower during sleep (3.8 Hz) compared to when the animal is running in a textured environment (7.8 Hz) (Vijayan et al, 2010). Hence, one might expect ∼50% less energy to be used on action potential and synaptic signaling in the barrel cortex during sleep compared to when the animal is awake and running, while the energy use on the resting potential and housekeeping tasks would remain unchanged, thus altering the percentage of ATP used on different tasks in the energy budget. Similarly, the energy use of the cortex on action potentials and synaptic signaling will increase under conditions of epilepsy when the firing rate of neurons is increased.

Complicating estimation of the changes in the percentage of energy use assigned to each mechanism in the energy budget is the fact that a change of action potential frequency may lead to a change in the release probability for presynaptic terminals (as a result of presynaptic facilitation or depression) or to a change of postsynaptic ion entry per action potential (as a result of desensitization of postsynaptic receptors). In addition, for a specific neural cell type, the properties of the underlying membrane currents may result in the shape of the action potential changing with firing frequency, with altered overlap of the inward Na⁺ and outward K⁺ currents, thus altering the energy used on the production of each action potential. However, it is difficult to estimate how the sodium entry per action potential will change with a change in firing frequency. For example, the Purkinje cell action potential becomes smaller and broader as the action potential firing frequency increases and, while a broadening of the action potential would suggest that sodium entry should be reduced (because the outward K⁺ current is mainly activated after the Na⁺ current has inactivated); preliminary experiments by Carter and Bean (2009) suggest that this is counteracted by a decrease in the peak of the action potential which reduces Na⁺ channel inactivation. Over a range of firing rates up to 300 Hz, the sodium entry ratio was found to change very little (Carter and Bean, 2009), suggesting that the energy used per action potential remains roughly constant. Thus, further work is required to assess the frequency dependence of the sodium entry per action potential for different cell types.

Energy Use by Different Cell Types within the Cerebral Cortex

In the long term, it would be highly desirable to produce a detailed energy budget for the cerebral cortex, like that for the cerebellar cortex, based on the measured anatomy, electrical properties and synaptic connectivity of the different cell types in all the cortical layers. At present, there are insufficient data available in the literature to do this. However, based on the morphology of different types of cortical cell we can make the following observations. In general, cells with shorter dendrites and axons will receive less input synapses (and thus use less energy on postsynaptic currents) and will propagate their action potentials a shorter distance. Thus, pyramidal cells, which have extensive dendritic trees and axons that typically extend for centimeters and branch extensively, are expected to use more energy per cell than layer 4 spiny stellate cells, which have shorter dendrites and axons. Nevertheless, even this general conclusion can be modified by different values for the conductance per synapse onto the different cell types and by differences in action potential firing rate, and (as noted above for the cerebellum) when weighted by the number of cells of each type present the relative energy use per class of cell can differ dramatically from the relative energy use per individual cell in each class.

Principal Neurons Do Not Consume the Most Signaling Energy

This work predicts that the principal neurons in the cerebellum, the Purkinje cells, use only a small fraction of the energy consumed by the cerebellar cortex, while the granule cells dominate the signaling energy use (Figure 2B). For the cerebellar cortex, energy use is predicted to be split between excitatory and inhibitory cells in a roughly 3:1 ratio, which is very similar to previous predictions (Figure 4A). Each Purkinje cell consumes 62 times more energy than each granule cell (Figure 2A), because of the larger ion fluxes across its much larger membrane. In addition, although each inhibitory neuron is metabolically costly compared with each granule cell, when the number of cells is taken into account, inhibitory cells use far less energy than excitatory cells.

Energy Use Associated with the Different Stages of a Computational Algorithm

If one divides cerebellar computation into three stages, remapping from mossy fiber input action potentials to action potentials in the granule cell somata, propagation of the remapped information to Purkinje cells, and computation by Purkinje cells of an output signal (Tyrell and Willshaw, 1992), the relative ATP use on these processes is 53%:32%:15% (Figure 4B). Thus, the assumption of greater energy efficiency of action potentials in mammalian neurons further reinforces the idea that most ATP is consumed by the granule cells, and not by the principal output neurons. If this were true in other brain areas it would reinforce the idea that most energy use reflects the input to and information processing occurring within a brain area rather than the output from that area (Logothetis et al, 2001; Kocharyan et al, 2008).

Sensitivity of Predictions to Remaining Assumed Parameters

As discussed in Howarth et al (2010), there are several parameters for which there is little information available in the literature and, for these parameters, assumptions have had to be made. One of the major assumptions previously made (Attwell and Laughlin, 2001; Howarth et al, 2010) was that the minimum ion entry required to charge the cell capacitance during an action potential should be multiplied by 4 (Hodgkin, 1975). As discussed above, this assumption has now been corrected to reflect recent findings on the energy used by action potentials (Alle et al, 2009; Carter and Bean, 2009; Sengupta et al, 2010). There are, however, still several parameters, which are based on assumptions. As discussed in Howarth et al (2010), our predictions for cerebellar energy use are most sensitive to uncertainties in the values of three parameters, as summarized in Table 1. First, making the assumption that, after learning, 85% of parallel fiber-Purkinje cell synapses are silent (Isope and Barbour, 2002) results in a 72% decrease in the predicted cerebellar cortical energy use compared with the assumption that all synapses are active. Currently, we assume that synapses are silent because of an absence of presynaptic glutamate release. If we instead assumed that synapses are silent due to an absence of postsynaptic receptors (in the presence of glutamate release), this would lead to only a 2% increase in predicted energy use for the cerebellar cortex. Second, we assume that the resting membrane properties of the axon are different to the soma; however, if instead we assumed that they are the same (per unit area) this would result in a 3.5-fold increase in the predicted energy use (to much greater than the measured total energy use of the cerebellar cortex, indicating that such an assumption must be wrong). Finally, there is no good measurement in the literature for the mean firing rate of the granule cell. Increasing the firing rate by 1 Hz from the estimated value of 3 Hz would result in a 1.1% increase in the total predicted energy use for the cerebellar cortex.

Table 1. Effect of significant parameter uncertainties on the predicted energy use.

Parameter	Assumption	Change to assumption	Effect on predicted total energy use
Number of parallel fiber-Purkinje cell synapses which are silent	85% of synapses are silent after learning	Assume all synapses are active	Increases from 12.8 to 17.6 μmol ATP/g/min (38% increase)
	Synapses are silent due to absence of glutamate release	Assume synapses are silent due to absence of postsynaptic glutamate receptors in the presence of glutamate release	Increases to 13.1 μmol ATP/g/min (2% increase)
Resting membrane properties of granule cell axon	Resting membrane properties of axon different to soma, calculated from hippocampal space constant measurements	Assume resting membrane properties of axon are the same as those of the soma	Increases from 12.8 to 44.9 μmol ATP/g/min (a 3.5-fold increase)
Granule cell mean firing rate	Assume a time averaged firing rate of 3 Hz	Increase the firing rate by 1 Hz	Increases by 0.7 μmol ATP/g/min (a 1.1% change)

A further variable for which little is known is the true cost of housekeeping tasks such as protein and lipid synthesis and trafficking of organelles and molecules around the cell. Estimates for the proportion of energy used on housekeeping tasks (in both the cerebellum and the cortex) vary from 25% (rodent cortical grey matter: Attwell and Laughlin, 2001) to 50% (whole brain: Kety, 1957; Sokoloff, 1960; Siesjo, 1978; Astrup et al, 1981; Ames et al, 1992; Ames and Li, 1992; Rolfe and Brown, 1997). Including this range of values would result in a range of estimates for total energy use for the cerebral cortex of 27.2 to 40.7 μmol ATP/g/min, compared with the measured total energy use of 33 to 50 μmol ATP/g/min in different cortical regions (Sokoloff et al, 1977), and for the cerebellar cortex of 17.1 to 25.6 μmol ATP/g/min, compared with the measured value of 20.5 μmol ATP/g/min (Sokoloff et al, 1977). Further work is needed to accurately define these parameters.

The authors declare no conflict of interest.