Amorphous diamond-structured photonic crystal in the feather barbs of the scarlet macaw

Abstract

Noniridescent coloration by the spongy keratin in parrot feather barbs has fascinated scientists. Nonetheless, its ultimate origin remains as yet unanswered, and a quantitative structural and optical description is still lacking. Here we report on structural and optical characterizations and numerical simulations of the blue feather barbs of the scarlet macaw. We found that the sponge in the feather barbs is an amorphous diamond-structured photonic crystal with only short-range order. It possesses an isotropic photonic pseudogap that is ultimately responsible for the brilliant noniridescent coloration. We further unravel an ingenious structural optimization for attaining maximum coloration apparently resulting from natural evolution. Upon increasing the material refractive index above the level provided by nature, there is an interesting transition from a photonic pseudogap to a complete bandgap.

Photonic structures of diverse forms have evolved and have been exploited in the biological world to achieve structural coloration (1–5) including ordered structures such as thin films, multilayers, diffraction gratings, and photonic crystals. Ordered photonic structures can produce iridescent structural colors whose coloration mechanisms have been intensively studied and are well understood. For instance, iridescent coloration by photonic crystals is due to their direction-dependent partial photonic bandgaps (6–8). In addition to the ordered categories, there exists another important class of photonic structures that possess only short-range order, namely, amorphous photonic structures (9) that can produce noniridescent coloration. The best known example is the spongy keratin structure in parrot blue feather barbs whose color origin has fascinated scientists (10–16).

Incoherent scattering, such as Rayleigh (10) or Mie scattering (1, 11, 14), was proposed first. Raman opposed the hypothesis of Mie scattering based on his optical observations (12). Dyck challenged the Rayleigh model (13) by the fact that measured reflection spectra disobeyed the prediction of the Rayleigh law and suggested a hypothesis of coherent scattering. Prum and coworkers confirmed convincingly the hypothesis of coherent scattering by performing a Fourier analysis (15) and small-angle X-ray scattering (16). Their results indicated that the sponge possesses short-range order that leads to coherent scattering and the noniridescent coloration.

Although noniridescent coloration by the sponge can be conceptually understood by coherent scattering, some fundamental questions remain still to be answered. Here we study the spongy structure in the blue feather barbs of the scarlet macaw (Ara macao) through structural characterization, spectral measurement, and numerical simulation. We aim to uncover the ultimate physical origin of the noniridescent coloration and to give a quantitative description of the structure and its optical response. Our results may help us obtain an in-depth understanding of the ingenious strategies of structural coloration and design in nature but also offer valuable inspirations for artificial design and fabrication of novel photonic media and devices.

The scarlet macaw belongs to a family of Psittacidae (true parrot) native to humid evergreen forests found in the American tropics. Scarlet macaws are large and perhaps the most magnificent of the macaw species. The base plumage is red with yellow accents on blue wings. The red and yellow colors are produced by pigments. Blue feathers under study were obtained from the Shanghai Zoo, Shanghai, China. Microstructure of the blue feathers was characterized by optical microscopy and scanning electron microscopy (SEM).

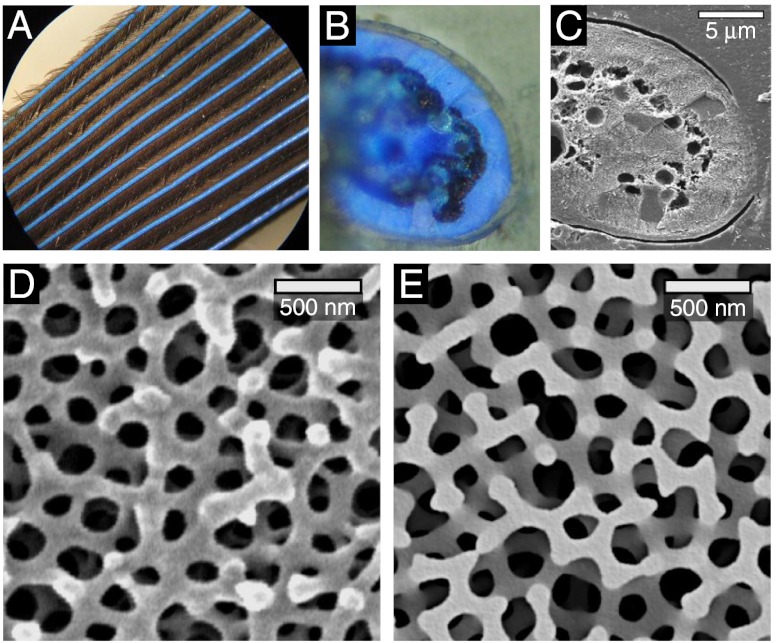
Unlike many other birds, the blue coloration of scarlet macaw feathers stems from feather barbs rather than barbules (Fig. 1A). The blue coloration does not change with perspective angle, a noniridescent characteristic, different from iridescent coloration produced by ordered photonic crystals (6–8). The outer layer of barbs is a cortex of keratin, transparent and about 0.5 μm thick (Fig. 1B). The central medullary part beneath the cortex is filled up with a spongy structure embedded with large hollow vacuoles, about a few micrometers in diameter. Comparing cross-sectional SEM images with optical microscopic images (Fig. 1 B and C), there exists a one-to-one correspondence between coloration and structure: The part occupied by the spongy structure displays a blue color. Dark regions in the optical image are due to light absorption by melanin granules around the hollow vacuoles.

Fig. 1.

(A) Optical micrograph of scarlet macaw blue feather barbs. Barbs rather than barbules display a vivid noniridescent blue color. (B) Optical micrograph of the transverse cross-section of a blue barb under 100× magnification. (C) Corresponding cross-sectional SEM image of the barb. (D) Close-up cross-sectional SEM image of the spongy keratin structure. (E) Cross-sectional image of an artificially generated model structure based on an atomic model of amorphous silicon (17).

Close-up SEM images show that the spongy structure consists of a well-defined three-dimensional network of keratin rods (Fig. 1D), closely analogous to the configuration of amorphous silicon (17), termed rod-connected amorphous diamond-structured photonic crystal (RAD-PC). The average diameter of the keratin rods is about 85 nm in the center and about 120 nm at the points where rods are joined together. The average rod length d (node-to-node distance) is about 170 nm. From SEM images, we can determine the volume fraction of keratin in the spongy structure, about 38%. We will show later that this particular volume fraction is an optimal coloration design, a result of evolution, not an accident.

To verify that the sponge is indeed a RAD-PC, a model RAD-PC was constructed on the basis of the atomic positions of idealized tetrahedrally coordinated amorphous silicon (17). In generating this model, the rod length of the RAD-PC was scaled up to the observed average value, d = 170 nm. Nearest-neighbor sites were connected by rods of circular cross section, and the rod diameter was set to be smaller in the center and increase continuously away from the center according to a simple sine function in order to conform to SEM observations. From Fig. 1E, the spongy structure in blue barbs is strikingly similar in morphology to the artificially generated construction. Comparison of vertex coordinates also shows close similarities. In the genuine and artificial structures, fourfold coordination dominates. We can thus affirm by direct appearance of Fig. 1 D and E that the spongy structure in the blue barbs is a RAD-PC.

As known in the field of photonic crystals (18–20), there has been a quest for photonic crystals with a large complete photonic bandgap. Photonic crystals with various symmetries and topologies have been tried and inspected through tremendous theoretical and experimental effort (21). Photonic crystals with a diamond symmetry were demonstrated to be most promising candidates (21), among which rod-connected ones (with rods connecting the four nearest-neighbor sites in the diamond lattice) present the champion photonic bandgaps (22). Interestingly, recent numerical studies showed that even after breaking long-range order, the resulting RAD-PCs made of silicon still retain a large complete isotropic photonic bandgap and also display interesting light confinement (23, 24). The fabrication of these structures is, however, still a great challenge in the visible and near-infrared regimes (21).

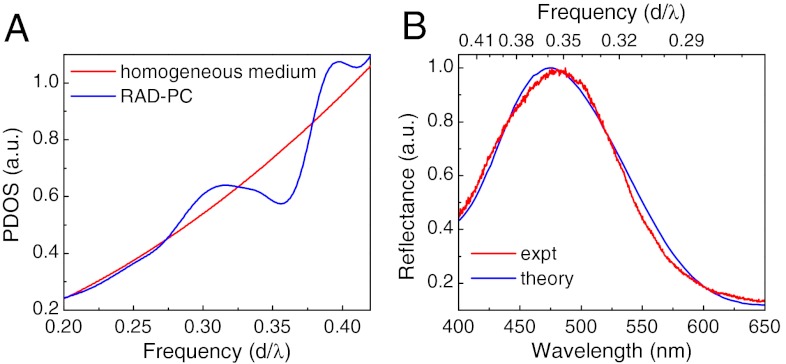
For periodic photonic structures possessing short- and long-range order (e.g., photonic crystals) their optical response is controlled by their photonic band structures (20). Structural coloration by photonic crystals can be ascribed to partial photonic bandgaps (6–8), and iridescence can be understood by the fact that these bandgaps are direction-dependent. In amorphous photonic structures, however, photonic band structures are ill defined due to the absence of long-range order. To explore the ultimate physical origin of the noniridescent coloration, we calculated instead the photon density of states (PDOS) of a model RAD-PC by the finite-difference time-domain (FDTD) spectral method (25). The PDOS of a system describes the number of photonic states available at each frequency and is a fundamental quantity that determines optical transport and quantum behavior. In our simulations, a cubic supercell of (11.5d)³ with 1,000 nodes was used to construct the model RAD-PC. Perfectly matched layer absorbing boundary conditions (26) in three dimensions were used. The refractive index of the rods was taken to be 1.54, a value typical of keratin. A prominent dip positioned at the reduced frequency 0.356d/λ appears in the calculated PDOS of the RAD-PC (Fig. 2A), distinctly different from a homogeneous medium where its PDOS scales quadratically with frequency. In amorphous and liquid metals, there exist similar dips in the electronic density of states, termed electronic pseudogaps (27), that can give rise to unusual thermal stability and electronic transport properties. The dip revealed in the PDOS of the RAD-PC is the photonic analog, dubbed photonic pseudogap. In photonic crystals, photonic bandgaps have zero PDOS, and their edges are direction-dependent due to long-range order (20). In contrast, the photonic pseudogap in a RAD-PC is isotropic with nonzero PDOS. Physically, this photonic pseudogap stems from strong scattering due to the short-range order. On the other hand, the corresponding ordered structure, the rod-connected diamond-structured photonic crystal, does not possess an isotropic photonic pseudogap.

Fig. 2.

(A) Calculated PDOS for the model RAD-PC as a function of reduced frequency d/λ, where d is the rod length and λ is the vacuum wavelength. The PDOS for a homogeneous medium with refractive index n = 1.23, a volume-weighted average, is also given for comparison. (B) Normalized calculated and measured reflection spectra under normal incidence. The calculations were based on observed d = 170 nm.

To show that a photonic pseudogap can give rise to noniridescent coloration, we calculated the reflection spectrum of a slab of the model RAD-PC by the FDTD method (Fig. 2B) under normal incidence. In the simulations, the slab has a thickness of 1.96 μm and extends infinitely along the other two directions by imposing periodic boundary conditions. The measured reflection spectrum of a single blue barb by microoptical spectroscopy is also given for comparison. Agreement between theory and experiment is excellent. For the rod length d = 170 nm, the corresponding photonic pseduogap is centered at 478 nm, excellently matching the predicted reflection peak at 474 nm. This correspondence suggests, unambiguously, that the photonic pseudogap is responsible for the blue structural coloration of the feather barbs.

Noniridescence can be understood by the fact that the photonic pseudogap is isotropic, and light is hence scattered evenly in all directions because there is no preferred orientation in the RAD-PC. In other kinds of amorphous photonic structures, such as the random-close-packing structure of chitin nanoparticles (28) and the disordered bicontinuous structure of chitin (29) found in the scales of longhorn beetles, we found similar photonic pseudogaps by numerical simulation. Thus, photonic pseudogaps may universally be the ultimate physical origin of the noniridescent coloration by amorphous photonic structures.

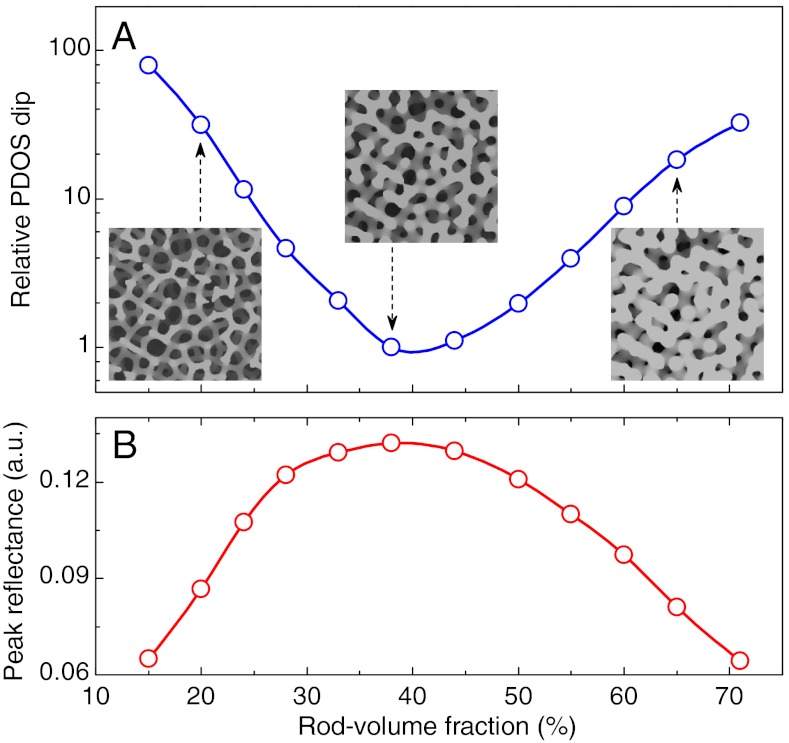
As aforementioned, the choice of a 38% volume fraction of keratin in the spongy structure may not be by accident. To unravel the implication of this volume fraction, we calculated the PDOS for the model RAD-PC as well as the reflection spectrum of a slab of the RAD-PC as a function of rod-volume fraction. With increasing rod-volume fraction, the relative dip in the PDOS decreases monotonically until reaching a minimum at about 40% (Fig. 3A). With further rod-volume fraction increases, the relative dip increases monotonically. The reflectance behaves opposite to the relative PDOS. At the rod-volume fraction of 40%, the peak reflectance is the highest and falls off for other rod-volume fractions (Fig. 3B). The adoption of this rod-volume fraction by feather barbs to attain the highest brightness of the blue coloration is a nontrivial optimization, apparently a result of natural evolution.

Fig. 3.

(A) Calculated relative PDOS dip for the model RAD-PC for different rod-volume fractions. Insets are cross-sectional images of the model RAD-PC with volume fractions of 20%, 38%, and 65%. (B) Calculated peak reflectance for the RAD-PC slab with various volume fractions. Circles are calculated data, and the lines are a guide to the eye.

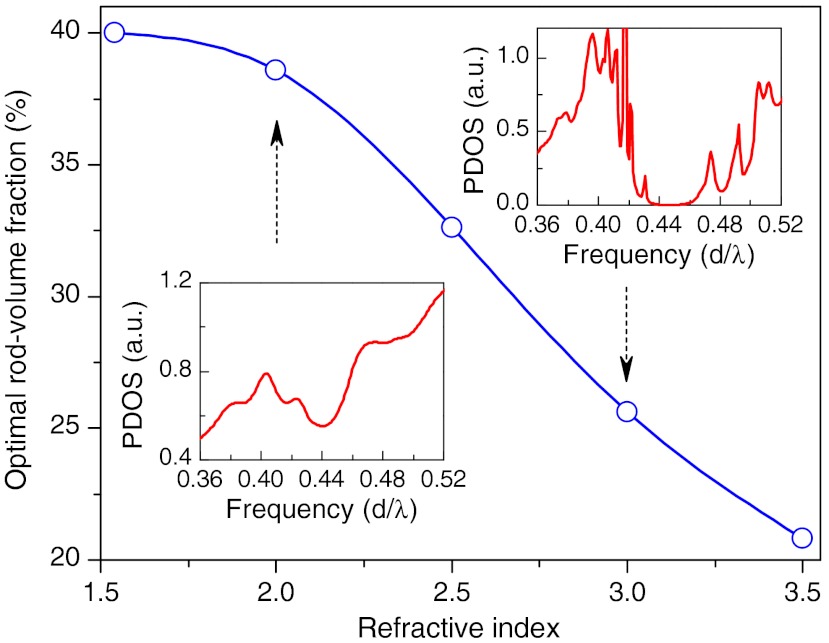
The RAD-PC in the blue feather barb possesses a photonic pseudogap rather than a complete photonic bandgap that would require a much higher refractive index than that of keratin; however, this structure can serve as a design protocol to realize artificial photonic crystals with a complete isotropic photonic bandgap by increasing the refractive index of the rods together with reoptimization of the rod-volume fraction. To show this possibility, we calculated the optimized rod-volume fraction that produces the optimal photonic pseudogap or complete photonic bandgap for different rod refractive index as shown in Fig. 4. Our simulations show that a complete isotropic photonic bandgap can open up for the rod refractive index n larger than about n = 2.3, below which only a photonic pseudogap exists.

Fig. 4.

Calculated optimal rod-volume fraction of RAD-PCs as a function of the refractive index of the rods. Insets show the PDOS for two cases: one with a photonic pseudogap at refractive index n = 2, and the other with a complete photonic bandgap at n = 3. The threshold for a complete photonic bandgap in these amorphous structures is n ∼ 2.3.

Synthetically, such RAD-PCs with a complete isotropic photonic bandgaps in the visible or infrared range could be fabricated by using the feather barbs as templates or through phase separation (16, 30). In addition to their unique structural features, RAD-PCs may exhibit many interesting, and even unusual, optical properties owing to the existence of an isotropic photonic pseudogap or a complete isotropic photonic bandgap. These could be exploited in photonic devices. Moreover, based on these natural or artificial RAD-PCs, some fundamentally interesting problems could be tackled—e.g., the original proposal for realizing the Anderson localization of light within a frequency window of a photonic pseudogap or a complete photonic bandgap in amorphous photonic crystals (19). (This is one of the two originally proposed applications for photonic crystals; but, it has not yet been demonstrated experimentally.) Unusual light transport properties could be studied as well.