A scaling law derived from optimal dendritic wiring

Abstract

The wide diversity of dendritic trees is one of the most striking features of neural circuits. Here we develop a general quantitative theory relating the total length of dendritic wiring to the number of branch points and synapses. We show that optimal wiring predicts a 2/3 power law between these measures. We demonstrate that the theory is consistent with data from a wide variety of neurons across many different species and helps define the computational compartments in dendritic trees. Our results imply fundamentally distinct design principles for dendritic arbors compared with vascular, bronchial, and botanical trees.

One of the main roles of dendrites is to connect a neuron to its synaptic inputs. To interpret neural connectivity from morphological data, it is important to understand the relationship between dendrite shape and synaptic input distribution (1–4). As early as the end of the 19th century (5), it was suggested that dendrites optimize connectivity in terms of cable length and conduction time costs, and a number of recent studies have supported the idea that optimal wiring explains dendritic branching patterns using simulations (6–8) or by reasoning from first principles (1, 2, 9, 10). However, although dendrite length is the most common measure for molecular studies of dendritic growth (11), its relationship to dendritic branching and the number of synaptic contacts has not been elucidated. Understanding this relationship should provide crucial constraints for circuit structure and function. Here we directly test the hypothesis that neurons wire up a space in an optimal way by studying the consequences for dendrite length and branching complexity. We derive a simple equation that directly relates dendrite length with the number of branch points, dendrite spanning volume, and number of synapses.

Results

Relating Total Dendritic Length to Optimal Wiring.

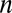We assume that a dendritic tree of total length connects target points distributed over a volume (Fig. 1A). Each target point occupies an average volume . A tree that optimizes wiring will tend to connect points to their nearest neighbors, which are on average located at distances proportional to . We need at least such dendritic sections to make up the tree. The total length of these sections sums up to

Fig. 1.

Consequences of optimal wiring for the predicted relationships between dendrite length, number of target points, and number of branch points. (A) n target points (red) are distributed in a spherical volume and connected to optimize wiring to a tree (black) with total length . (B) Relation between number of target points distributed in a spherical volume of 1,000,000 μm³ and total dendrite length of resulting synthetic dendrites connecting these points to a root in the center, for different (red) and predicted lower bound (black). (C) Synthetic dendritic trees with different 3D arrangements (Bottom Inset), spherical (black), inhomogeneous (green), off-center root (red), and cubic (blue), were generated and the number of branch points, 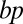was plotted vs. number of target points and their dependence on the balancing factor of the growth algorithm. The relationships are constant between all these parameters for a wide range of values. Top Inset shows that the ratio between branch points and target points is fixed for each given balancing factor. Error bars are for shuffled trees of all conditions. One hundred trees were grown for each individual condition. (D) Dendrite length vs. number of branch points in the model. Parameter in the equation is obtained in C, using average of 0.5. (E) The number of electrotonic compartments as it scales with the number of puncta. For 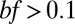the fitted power is almost perfectly 2/3.

This result shows that a 2/3 power law relationship between and (12) provides a lower bound for the total dendritic length, where is a proportionality constant. Approximating the volume around each target point by a sphere, then , and each dendritic section corresponds to the radius of a sphere, giving

(SI Text and Fig. S1). Importantly, assuming a constant ratio between the number of branch points, bp and the number of target points (which is addressed later), this assumption also results in a 2/3 power law between wiring length and the number of branch points. Supporting these intuitive derivations of power laws, there have been several proofs (12, 13) that in a minimum spanning tree in dimensions—the canonical model of a tree constructed to minimize wiring length— scales as a power of the number of target points or branch points. In summary, the wiring minimization hypothesis predicts a 2/3 power law between and bp and a 2/3 power law between and . By contrast, a process that randomly connects target points without optimizing wiring yields a power law with exponent 1. More interestingly, a canonical model of biological fractal trees previously introduced by West et al. (14) predicts a 4/3 power law between and or bp (for simple proof see SI Text and Fig. S2).

To study the scaling properties of neuronal dendritic trees, we took advantage of synthetic dendrites generated using an extension of the minimum spanning tree (MST) algorithm that we have previously shown can reproduce a wide range of dendrite morphologies (6–8). In addition to minimizing the total length to connect a set of target points to a tree as discussed above, this procedure introduces a cost to minimize all path lengths from any target point toward the root along the tree. This additional cost is parameterized with the balancing factor bf, and we previously showed that bf values between 0.1 and 0.85 reproduce realistic dendritic morphologies (Materials and Methods). When target points were randomly distributed within a spherical volume and connected to a tree to minimize these costs, we found that Eq. 1 provides a tight lower bound for total dendritic length, particularly for low bf (Fig. 1B). With increasing bf the exponent in the power law increased from 0.66 to 0.72 for bf = 0.9, the maximal realistic balancing factor. The respective mean square errors between the curves from the model and our predicted equation increased from 1% to 5.2% as bf was increased.

Relationship Between Number of Branch Points and Target Points.

The number of branch points grew proportionally to the number of target points (Fig. 1C) with proportionality constant bp/n. Such a proportional relationship is not surprising: It occurs in simple n-ary trees as well as in randomly generated trees (15). However, the particular value of the proportionality constant emerges as another direct consequence of optimal wiring as shown previously by Steele et al. (13), for the simplest case of bf = 0 (SI Text and Fig. S3)—although no analytical formula exists to compute it and it must be derived empirically. Surprisingly, we found that bp/n was independent of the geometrical arrangement of target point distributions. Specifically, the ratio did not change regardless of whether target points were distributed inhomogeneously, the root was displaced from the center of the sphere, or the physical boundaries of the sphere were replaced by those of a cube (Fig. 1C). However, the ratio depended in a linear manner on the model parameter bf (Fig. 1C, Top Inset), which we have previously shown to vary between different classes of dendrites (8). Importantly therefore, when two of the three quantities bp, , or bf are known, the third can therefore be inferred independently of tree conditions or metric scale. The 2/3 power is therefore equally present between bp and in the model (Fig. 1D), with powers ranging from 0.66 to 0.72 and a mean square error below 2% between the prediction and the model for all bf. To summarize, our algorithm that was shown previously (8) to reproduce many realistic neuronal morphologies, confirms the presence of the 2/3 power law between and and between and bp in synthetic trees.

We next tested whether the morphological power law relationship also has functional consequences. Using a model for scaling of dendritic diameters (6), we determined the passive electrotonic properties of the dendritic trees in our sample. The number of independent electrical compartments (Fig. 1E, fitted power: 0.67 for bf = 0.2) and total electrotonic length (Fig. S4) were also found to scale with the number of puncta governed by a 2/3 power law when bf > 0 (Materials and Methods and SI Text).

General Applicability of the 2/3 Power Law.

To test for the presence of our predicted power law in real neuronal morphologies, we analyzed all available dendritic trees of all different cell types from the NeuroMorpho database (16). In these reconstructions, it is unclear what the target points of the dendrites are, but branch points can unambiguously be counted. We therefore plotted the wiring length of these cells against the number of branch points (Fig. 2). The power that best described the trends between dendrite length and number of branch points obtained for all cell types individually is very close to 2/3, 0.72 ± 0.10, and residual norms confirmed the goodness of fit (Fig. 2, Right). We replaced by bp in Eq. 1 and compensated for the decrease in points by using the bp/n ratio derived from the simulations in Fig. 1C to obtain our lower bound for dendrite length (Fig. 2, Left, black line). Although providing a lower bound, the resulting equation well described the data (with a root mean square error of 6.4%) and was very similar to the best fit (Fig. 2, Left, red line) with a power of 0.70 (SI Text and Fig. S5).

Fig. 2.

General applicability of optimal space-filling power law relations. Shown is the relation between total dendrite length and number of branch points for all reconstructions from the morphological database www.neuromorpho.org (16). It strictly follows the predicted equation in all cases; Different datasets cover their respective range of length and complexity. The number of branch points and total length were normalized by the volume , which the dendrite covers (because the volume covered by the spanning fields of the dendrites was variable). Differences in balancing factor cause a vertical offset while conserving the characteristic 2/3 power law trend shown (black line) for corresponding to . Each datapoint is one neuron, with the color corresponding to neuronal type. Best fit (red line) has a power of 0.70. Upper Right shows distributions of power for the best fit of the 74 individual datasets that consisted of more than 10 reconstructions. Lower Right shows the distribution of residuals for each fit.

Relation Between Dendritic Length and Number of Synapses in Real Neurons.

So far, we have discussed that neurons optimize wiring length to connect up target points without specific reference to what the target points are. The obvious candidates are the synapses the dendrite receives from its presynaptic targets. To experimentally assess the scaling of wiring with synapse number is challenging: During development, axons and dendrites grow in parallel and synapse locations are therefore not static and predefined, but move around and are a result of neurite outgrowth itself. To avoid this problem, we studied the space-filling growth process during neurogenesis in the adult animal in periglomerular (PG) neurons of the olfactory bulb, which integrates neurons into an existing circuit where axonal inputs and network architecture are presumably fixed. Reconstructions of these neurons show that the dendritic branching complexity, as expressed by the number of branch points bp, increases during maturation (17) (Fig. 3 A and B, red). However, the immature dendrite already covers the full target volume—on average 178,000 μm³—at an early stage (Fig. 3 A and B, black; summary in Fig. 3C), approximately filling the spherical glomerulus with a 35-μm radius, and this volume does not change significantly during the increase in branching complexity. Synapse locations were labeled using GFP-tagged PSD95 markers (18) and reconstructed in conjunction with the entire dendritic trees. Because synapse numbers are known in this dataset, the volume is well defined, and the complexity of the dendrites increases during maturation, these data are ideal to test our predictions. The relationship between and for both real (18) and synthetic PG dendrites (Fig. 3D) is bounded by the 2/3 power law (with a root mean square error of 1.8%), confirming our prediction. Additionally, in the reconstructed PG neurons the number of branch points bp increased with the number of synaptic puncta with a constant ratio bp/n, which matched that predicted by our analysis of synthetic dendrites (Fig. 3D, Inset). This result indicates a quantitative match between synaptic puncta and target points of the minimum spanning tree algorithm. To test the qualitative use of synaptic puncta as target points, we further grew synthetic trees directly onto synapse locations obtained from the experiment. Using a bf = 0.2, chosen to match the number of branch points, most of the real tree structure was accounted for by the location of the synapses, indicating that they are connected optimally in the real dendrite with this choice for bf (Fig. 3E, black and red trees, respectively; SI Text and Fig. S6). We therefore conclude that the target points for synaptic contacts within the dendritic tree structure predicted by our algorithm correspond closely to the location of putative synapses observed in real PG neurons.

Fig. 3.

Power law relationships governing the dendritic geometry of newly born periglomerular cells in the adult olfactory bulb. (A) Consecutive reconstructions of a newborn periglomerular neuron (17) separated by 12-h time steps starting at 10 d after origin. Note that dendritic complexity increases without an increase in total volume occupied. (B) Quantitative analysis of the same neuron shows that the dendritic volume (convex hull; similar results obtained using a distance hull) that it spans remains fixed (black), whereas the branching complexity increases (red). (C) Corresponding population data (17) for two distinct time points during the maturation show that there is no change in spanning volume (10 d, n = 24 neurons; 45 d, n = 9 neurons; 180 d, n = 8 neurons), same y axis as B. (D) Total dendrite length vs. number of synaptic puncta n in experimental data (black circles, n = 47 neurons) (18, 40) including immature (14 d), mature (45 d), and very old (180 d) cells as well as young cells (14 d) grown in a sensory-enriched environment. All data follow the same trend expressed by and were normalized to a volume of 1,000,000 μm³. Inset shows ratios between number of branch points 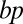and number of synaptic puncta . (E) Reconstructions of a real PG cell at three different ages (red cells, Left to Right) and the corresponding GFP-marked synaptic puncta (green circles; neurons from ref. 18). Corresponding synthetic PGs (black) were grown on the same synaptic locations while optimizing the wiring. (Bottom) Sholl intersection diagrams, which count the number of intersections to a sphere of increasing size around the soma (41), quantify the topological similarity for the three different maturation levels, comparing the real reconstructions (red) and the synthetic counterparts (black), and show a good overlap (8.7% error).

Discussion

We have derived from first principles a simple equation that relates the most fundamental measures of dendrite branching: the total length, the number of branch points, the spanning volume, and the number of synapses. We show that this equation holds for all dendrite and axon reconstructions available in the neuromorpho.org database, including over 6,000 reconstructions from 140 datasets. This power law relationship shows that dendrites grow to fill a target space in an optimal manner and, similar to a minimum spanning tree, use the least amount of wiring to reach all synaptic contacts. For the example of newborn neurons in the adult olfactory bulb, we show that the power law also holds and describes how synapse locations define dendritic morphology.

Although caution must be applied to their interpretation (19), power laws often describe fundamental scaling properties in biology (14, 20) and in particular in the brain (21–26). Many of these studies build on the fundamental principle that cable length and brain volume follow an inverse cubic power (27). We have extended this work by demonstrating a 2/3 power relationship between cable length and synapse number and provide an exact lower bound for the cable length of a dendrite when its synapse number and its spanning volume are known. We show that this power law holds not only for dendritic trees generated using our minimum spanning tree algorithm (8), but also for a wide range of real neurons. Also, our calculations predict an equation with a 1/2 power law for planar dendrites within a given surface, and both data and model are consistent with this notion (SI Text and Fig. S7). These facts strengthen the validity of our algorithm as a method for construction of dendritic trees and suggest that it captures a fundamental principle of the growth of dendritic trees. This constructive algorithmic approach is in contrast to other analysis methods for determining space filling by neuronal processes (2–4, 28). The power law relationship thus provides an important additional constraint that must be fulfilled by other methods for generating dendritic trees. What is the underlying biological mechanism for growing optimal trees? We speculate that the molecular machinery used in dendritic pathfinding implements a developmental program computationally equivalent to a minimum spanning tree algorithm. For instance, the Dscam protein family in Drosophila (29, 30) prevents dendrites from one neuron from bundling and crossing over, features that would be incompatible with minimal wiring.

The 2/3 power law we have found for neuronal dendrites challenges the well-known model by West et al. (14) of allometric scaling based on optimal flow through the tree, which predicts a 4/3 power. This difference indicates that tree structures of dendrites are functionally distinct from distribution networks such as vasculatures for which that model has been shown to work (14) and that design constraints other than resource distribution may be important determinants of dendritic shape. At the very least, the assumption of invariant terminal units in the West et al. model (14) does not seem to hold for dendritic trees, which implies that the growth algorithm for vascular, bronchial, and botanical trees is distinct from that of neurons.

The structural constraints on dendritic morphology we have demonstrated are likely to have implications for the computations implemented by neural circuits. First, we have demonstrated that the power law is reflected in the passive integrative properties of neurons such as functional compartmentalization, meaning that it places constraints on information processing. Furthermore, an interesting consequence of minimizing wiring to target synapses is that synapses that are close together are more likely to be linked by the same stretch of dendrite and therefore involved in a local computation (31–33), such that geometry is a key determinant of information processing. There is increasing evidence that such sophisticated local processing may be carried out within the dendritic tree (34, 35), with nonlinear interactions between synaptic inputs shaping the output of the neuron (36–39). We therefore predict it will be fruitful to study how the scaling laws of wiring and branching place constraints on the overall computational power of single neurons.

Materials and Methods

Wiring Algorithm.

Optimal wiring was implemented as previously described (6) to minimize both total cable length and the cost for path lengths from any target point along the tree toward the root (6). The second cost is weighted by the balancing factor bf, the only parameter required by the wiring algorithm: . These methods have been successfully used for a wide variety of dendrites (8, 39) and all algorithms are available in the TREES toolbox (8, 39).

Morphological Modeling of Simplified Trees.

Various simplified 2D and 3D geometries were used in Fig. 1C and Figs. S2D and S7C (Top Insets):

• (a) A “circular” and “spherical” arrangement with a root in the center and target points homogeneously randomly distributed.

• (b) Corresponding “inhomogeneous” arrangements, similar to the circular arrangement except that the target points were distributed in an inhomogeneous manner.

• (c) The “off-center” arrangement, similar to the circular arrangement except that the root was displaced from the center.

• (d) Corresponding “square” and “cubic” arrangements confined to boundaries with straight lines to form a square.

The target points were then connected for all cases in the same way as previously described. For the electrotonic analysis, a quadratic diameter taper according to ref. 6 (using the function “quaddiameter_tree” of the TREES toolbox) was mapped onto the dendrites, and sample specific membrane resistances of and axial resistances of 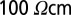were used.

Anatomical Analysis of Other Cell Types.

All data from the NeuroMorpho database (www.neuromorpho.org; version as of October 7, 2011) (16) were used for Fig. 2. These data include 142 datasets and 6,577 reconstructions (6 were discarded because the files could not be read) of dendrites and axons. Of the 142 datasets, 74 datasets had enough reconstructions (at least 10) to fit the power law. Dendritic spanning volumes were estimated using the convex hull of the dendritic tree. To fit a power law to the data, the number of branch points and total length were first normalized by their respective volume. Then the log of the data was used in a linear regression. From simulation in Fig. 1D a slightly inhomogeneous power distribution above 2/3 was expected with the power increasing slightly with higher bf. The power in the fitted power law including all 6,577 reconstructions from NeuroMorpho was 0.70 (Fig. 2), which is consistent with this result.

Anatomical Reconstructions of PG Neurons.

Reconstructions of mouse PG neurons were obtained from a published dataset (17, 18, 41). Briefly, in these studies, neurons were infected with a GFP or PSD95-GFP marker gene, the latter labeling putative synapse locations, by viral injection into newborn PG cells. These cells were left to migrate toward their specific glomerulus for 10 d and subsequently 3D image stacks were collected through a craniotomy in 12-h intervals, using a two-photon microscope. Reconstructions of tree morphologies and synapse locations were obtained from these image stacks, using Neurolucida (Mbf Bioscience). The morphologies were imported into our Matlab software package, the TREES toolbox (8, 40), and further analyzed.