Surface roughness directed self-assembly of patchy particles into colloidal micelles

Abstract

Colloidal particles with site-specific directional interactions, so called “patchy particles”, are promising candidates for bottom-up assembly routes towards complex structures with rationally designed properties. Here we present an experimental realization of patchy colloidal particles based on material independent depletion interaction and surface roughness. Curved, smooth patches on rough colloids are shown to be exclusively attractive due to their different overlap volumes. We discuss in detail the case of colloids with one patch that serves as a model for molecular surfactants both with respect to their geometry and their interactions. These one-patch particles assemble into clusters that resemble surfactant micelles with the smooth and attractive sides of the colloids located at the interior. We term these clusters “colloidal micelles”. Direct Monte Carlo simulations starting from a homogeneous state give rise to cluster size distributions that are in good agreement with those found in experiments. Important differences with surfactant micelles originate from the colloidal character of our model system and are investigated by simulations and addressed theoretically. Our new “patchy” model system opens up the possibility for self-assembly studies into finite-sized superstructures as well as crystals with as of yet inaccessible structures.

Nature has mastered the self-assembly of simple basic subunits into complex, functional structures with outstanding precision. Examples include biological membranes and viruses, which exhibit excellent control over the assembled structures with respect to their functionalities, shapes or sizes. However, the interactions between the building blocks, in the case of viruses, the protein subunits, are often complex and it remains challenging to identify the key elements for guiding and controlling the self-assembling process. By mimicking such self-assembly processes on a colloidal scale, insights into the paramount elements that control the assembly can be obtained in situ and applied to build up superstructures with new and desirable properties.

Colloidal particles with site-specific directional interactions, so called “patchy particles”, are promising candidates for bottom-up assembly routes towards such complex structures with rationally designed properties (1–3). The size and geometry of the patches together with the shape of the interparticle potential are expected to determine the formed structures and phases, which may range from empty liquids (4) and crystals (5–7) to finite-sized clusters (1, 2, 8–11), and lead to novel collective behavior (12).

Recent experimental approaches to assemble colloidal particles at specific sites include hydrophobic-hydrophilic interactions (6, 7, 13–15), and lock-and-key recognition mechanisms (16). With a wide variability of colloidal shapes available today, the ultimate challenge is to identify general methods to render specific areas of the colloids attractive or repulsive, while not depending on a specific choice of material or surface chemistry (17). Ideally, the attraction strength and range is tunable and interactions are reversible to allow the formation of equilibrium structures.

Results and Discussion

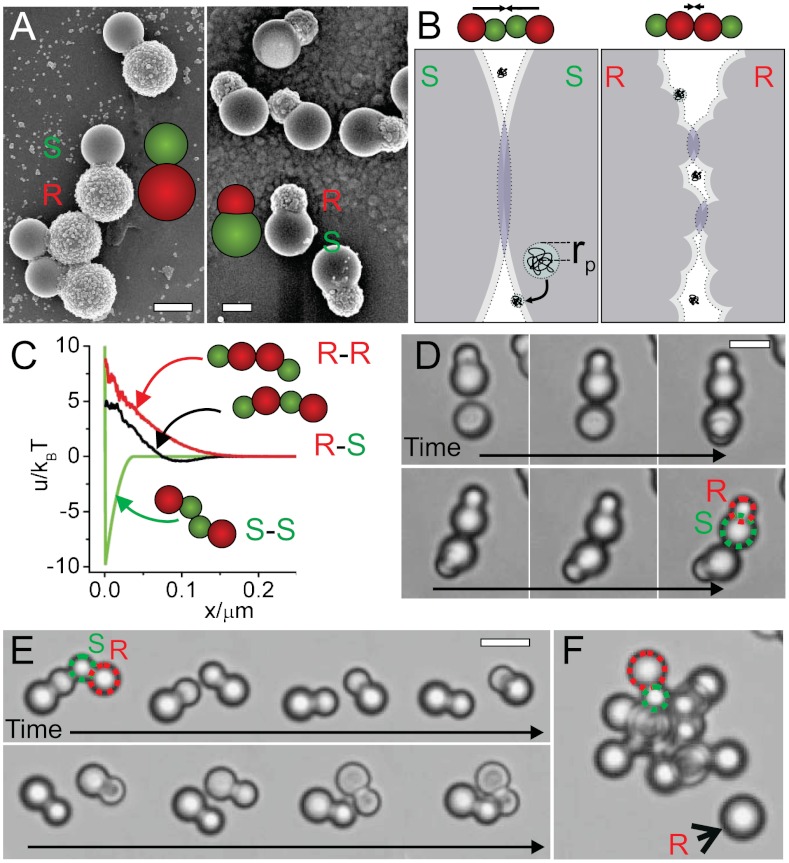
Our approach to achieve patchy particles employs depletion interactions between particles that have locally different surface roughness, as for example shown in Fig. 1A. Depletion attraction arises in dispersions of colloidal particles when a second, smaller type of non-adsorbing colloid or macromolecule, also termed depletant, is introduced in the suspension (18–20). The center of mass of the depletant cannot approach the surface of the larger colloidal particles closer than its radius r_p, restricting the volume available to it (see Fig. 1B). The volume around the colloidal particles unavailable to the depletant is called the exclusion volume.

Fig. 1.

Patchy particles by roughness specific depletion interactions. (A) Colloidal model systems consisting of one sphere with a smooth and one sphere with a rough surface. Scale bars are 2 µm. (B) In the presence of small depletants (here depicted as polymers with radius r_p) the colloidal particles are surrounded by a layer inaccessible to the depletant (dotted line). If colloidal particles approach such that their excluded volumes overlap, the depletant gains entropy, which results in a net attraction between the colloids. The resulting depletion attraction is proportional to the overlapping excluded volume (blue regions). For two rough spheres the overlap volume is significantly reduced compared to that for smooth particles. Small arrows represent the effective forces on both colloids. (C) Depletion potentials obtained from simulations between two smooth, two rough and one smooth and one rough side of our colloids, and polymer of size r_p = 19 nm (ρ_p = 0.038 ρ_overlap) as a function of the distance x between the surfaces of the colloids (for details, see SI Text). (D) Snapshots from a movie showing the breaking of a bond between the smooth sides of two particles and later reformation of the bond. Dextran polymer with radius r_p = 19 nm was used at a concentration of ρ_p = 0.4 ρ_overlap. Scale bar is 5 µm. (E) Rough spheres as indicated by the black arrow are left out of the colloidal micelles formed from the particles with one attractive patch. (F) Bond formation between the larger smooth sides of two particles and subsequent rearrangement due to the flexible bond (Dextran polymer, r_p = 8.9 nm, ρ_p = 0.20 ρ_overlap,, 0 mM NaCl). Scale bar is 5 µm.

When the surfaces of two large colloids come closer together than the diameter of the depletant, 2r_p, their exclusion volumes overlap and the volume accessible to the depletant increases by the amount of this overlap volume ΔV. Hence the entropy of the depletant, increases, and an effective attractive potential is induced between the two larger colloids (18–20). The depletion potential is roughly proportional to the number density of the depletant ρ_p and the overlap volume ΔV as u_AO = -ρ_p k_BT ΔV. Here, k_B is Boltzmann’s constant and T is the temperature. Smooth surfaces have larger overlap volumes than incommensurate rough surfaces, and thus are more strongly attracted towards each other. Experimentally, this effect was first described for plates and cylinders by Stroock and co-workers (21, 22) and Mason and co-workers (23, 24) and exploited to achieve side-specific attraction between platelets by introducing roughness on only one of the two sides (24). Roughness was also shown to suppress the depletion driven attraction between mesoscopic bilayers consisting of colloidal rods (25).

We employ this surface roughness specific depletion interaction to create particles with distinct attractive sites on curved surfaces. Our patchy particles are anisotropic polystyrene dimers that consist of one rough and one smooth sphere as shown in Fig. 1A. For this, we prepared rough cross-linked polystyrene particles from linear polystyrene spheres by seeded emulsion polymerization. During polymerization, roughness is achieved through adsorption of smaller polystyrene spheres at the surface. Using these particles in a seeded emulsion polymerization yields rough spheres with a smooth protrusion after phase separation (26–29). The synthesis protocol is sketched schematically in Fig. S1. The final particles with a small smooth patch shown in the Fig. 1A (Left) have a protrusion radius of 1.11 μm (smooth side, colored in green, polydispersity (pd) 2.9%), seed radius of 1.46 μm (rough side, colored in red, pd 2.2%) and are 4.9 μm in length (pd 2.9%). SEM images show that small particles of 185 nm (pd 16%) are partially immersed into the seed particle (Fig. S1B) effectively creating roughness on a scale of only a hemisphere of the secondary nucleated particles as depicted schematically in Fig. 1B. The protrusion size is continuously tunable by adjusting the monomer concentration during synthesis (26–29). Colloidal particles with protrusions larger than the seed particles (protrusion radius 1.66 μm, pd 3.4 %; seed particle radius 1.2 μm, pd 4.2%; roughness diameter 182 nm, pd 22%; long axis 4.70 μm, pd 3.2%) were synthesized as well to demonstrate the effect of particle geometry on the assembled structures (Fig. 1A, Right).

We calculated the effective pair potential of spherical particles between two smooth, two rough, and one smooth and one rough side, whose size and roughness were modeled after the experimentally employed colloids with small patch size (see SI Text for details). We found the depletion potential to be suppressed more strongly for a depletant that is significantly smaller than the roughness inducing small hemispheres, in analogy with studies by Zhao and Mason for flat interfaces (23). While it is reasonable to expect that surface roughness will also influence depletion attractions between spherical surfaces, it has not been demonstrated previously and it is not obvious whether the difference will be significant enough to create site-selective, patchy interactions between spherical (parts of) colloidal particles.

We experimentally demonstrate site-specific attraction using nonionic dextran polymers with radii r_p = 8.9 nm and r_p = 19 nm as depletant. As shown in Fig. 1C significant attraction on the order of -10 k_BT between only the smooth sides of the colloids can be obtained, while attraction between rough and smooth sides and two rough sides is negligible. Optical microscopy reveals that both polymers induce specific binding between the smooth sides of the colloids. Fig. 1E shows timeframes of a movie in which two particles with anisotropic roughness reversibly bind and unbind at their smooth patches (Movie S1 shows the binding and unbinding event in full). Typically, single bonds last for about 10 min. Even though the rough sides of the colloids are larger than the smooth patches which for spheres implies a significantly stronger attraction, the roughness reduces the depletion potential sufficiently to suppress attraction between the larger rough sides. The alternative colloidal system with large smooth sides and small rough parts is shown in Fig. 1D. Clearly, depletion interactions create flexible bonds between the patches and thus allow for three-dimensional rearrangements of the bound particles.

The time required to observe such an unbinding event can be calculated using Kramers’ approach (30) and taking the influence of lubrication stresses on the diffusion coefficient into account (31) (SI Text). The pair potential is a superposition of an Asakura-Oosawa depletion potential and a screened Coulomb potential. We employed 20 mM NaCl to decrease long-ranged electrostatic repulsions, which may reduce the effect of the roughness on the depletion potential. As a result, the minimum of the effective pair potential is significantly lowered and on the order of -10 k_BT (Fig. S5). From numerical integration we find the escape time in the case of one bond to be 630 s, in good agreement with experiments.

At higher depletant concentrations and thus stronger attractions, the roughness anisotropic colloidal particles spontaneously organize into clusters, in which the attractive parts constitute the core of the aggregate and the non-attractive rough sides are located at the outside. Representative images of colloidal clusters containing n = 1 to n = 12 particles are shown in Fig. 2A. Note that the colloids are free to move within the limitations of the bonds and particularly the rough parts are free to sample the accessible volume around the core of the clusters. See Fig. 2B for images of a cluster consisting of five dimers with various orientations of the rough sides. This flexibility in the cluster shape is due to the relatively small cone angle of the particles, which is ≈17°. For larger cone angles, simulations on cone-shaped particles found clusters with precise convex structures for n ≤ 17 (10, 11). Additionally, in analogy with experiments on depletion driven clusters of spheres (32), for n > 6 the smooth sides within the core are found at various iso-energetic configurations in MC simulations and Free Energy calculations. Thus, Fig. 2A only shows one of the possible configuration for each cluster size.

Fig. 2.

Colloidal micelles. (A) Typical cluster shapes obtained from colloids with attractive small smooth, and large rough (non-attractive) side containing n = 1 to n = 12 patchy particles. Upper rows show experimentally observed clusters of colloids with small, smooth side are presented. The lower, colored rows show clusters obtained from Monte Carlo simulations on dimers consisting of a rough and a smooth sphere. The smooth spheres interact by an attractive depletion potential (green) and the rough spheres interact with a hard-sphere potential (red). The interactions between rough and smooth spheres are assumed to be hard-sphere-like. In experiments and simulations, the smaller attractive sides are located at the core of the clusters, reminiscent of micelles. Snapshots for experiments and MC simulations taken after the cluster size distribution stopped evolving significantly. (B) Clusters consisting of n = 5 colloids with a small smooth patch exhibit a variety of cluster structures because the rough parts can freely explore the available volume around the center. (C) Average number of bonds per particle as a function of cluster size n. Data shown is taken after 10⁸ MC cycles, for u = -9.85k_BT, r_p = 19 nm and colloids with small patch size. Scale bars are 5 µm.

These clusters are reminiscent of surfactant micelles, where the colloids specifically bind at their smaller smooth sides inside the clusters just like the hydrophobic parts of surfactants attract each other. The larger, rough sides of the particles are located outside of the clusters similar to the hydrophilic head group of surfactant micelles. These interactions together with their overall cone-like shape make our colloids a realization of “colloidal surfactants” (29), which in analogy to molecular surfactants form “colloidal micelles”. Similar micelle-like clusters have been observed by Granick et al. for colloidal Janus-particles, whose surfaces are half hydrophilic and half hydrophobic (13, 14). These systems can be seen as the simplest analog of molecular surfactants, where hydrophobic and hydrophilic regions being combined in a single object cause micelle formation. Here, we present a new class of hybrid rough-smooth particles that spontaneously assemble into micelles by depletion interaction. While the origin of the driving forces for the formation of superstructures is different for the two model systems, they lead to similar, micelle-like assemblies due to their well-defined hybrid character.

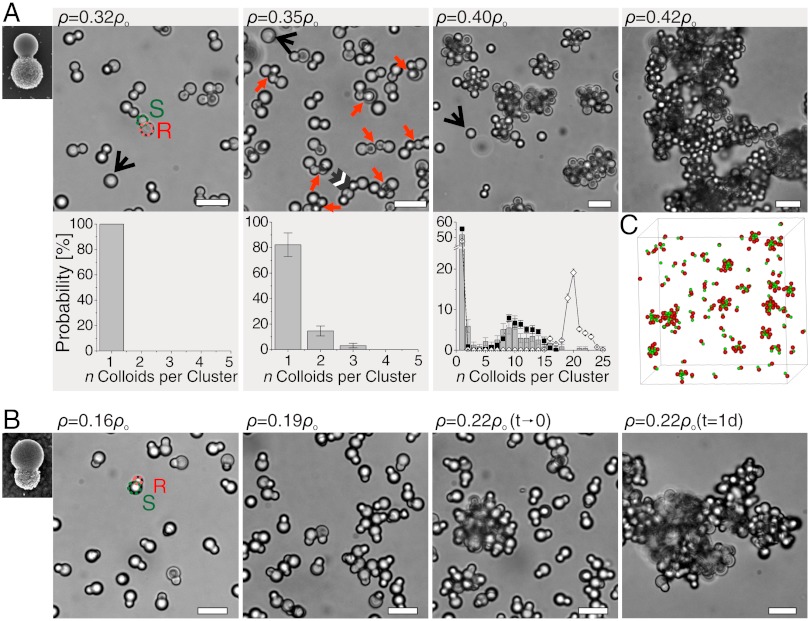
The strength of the patchy attractions and thus the average number of particles in a cluster can be tuned by the polymer concentration as illustrated by Fig. 3. At low polymer concentrations ρ_p(r_p = 19 nm) = 0.32ρ_overlap, no indication of attraction between the colloidal particles is observed as illustrated in Fig. 3A (see Fig. S7 for experiments with polymer r_p = 8.9 nm in radius). Here, 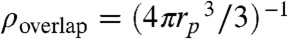is the polymer overlap concentration. An increase in the polymer concentration to ρ_p(r_p = 19 nm) = 0.35ρ_overlap leads to small clusters, consisting mainly of two to three colloids. The binding between the particles occurs selectively at their smaller smooth sides. Based on short movies, we indicate binding between smooth sides by red arrows, and binding between a rough and a smooth side by a black/white arrow. We define the probability to observe a cluster consisting of n colloids as 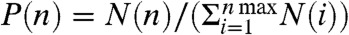, where N(n) is the total number of observed clusters of size n per sample. At this polymer concentration we find P(n) to decrease exponentially with the colloidal cluster size which is expected if the number of bonds per cluster c(n) increases linearly with n. Colloidal micelles are obtained at a slightly higher polymer concentration of ρ_p(r_p = 19 nm) = 0.38ρ_overlap. The cluster size distribution shows a significant number of single colloidal particles, equivalent to a critical micelle concentration (cmc) in surfactant systems. In this experiment the critical colloidal micelle concentration is given by the volume fraction 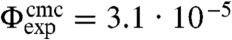. A second characteristic feature of the cluster size distribution is a peak around n = 10, the most probable cluster size.

Fig. 3.

Cluster size distributions with increasing interaction strength and different geometry. (A) Transmission light microscopy images of colloidal clusters from colloids with small attractive patch at increasing dextran polymer concentrations and corresponding cluster size distributions for experiments (bars, r_p = 19 nm), and direct MC simulations (u = -9.85k_BT, r_p = 19 nm, after 10⁸ MC cycles, filled circles) and free energy calculations (open diamond). Single particles are present in solution at ρ_p = 0.32ρ_overlap. Small clusters with an exponentially decaying size distribution for ρ_p = 0.35ρ_overlap. Bonds between smooth patches are indicated by red arrows, and black/white arrow indicates binding between smooth and rough sides of the particles. For ρ_p = 0.40ρ_overlap a clear peak in the cluster size distribution appears around n = 10. Black arrows point out rough spheres. Cluster distributions shown below the microscopy images corroborate that experiments and MC simulations are in agreement. However, the distributions are not in equilibrium yet as free energy calculations yield a significantly different cluster distribution (u = -9.85 k_BT (open diamond)). Above a critical aggregation concentration site-specificity is lost. Images for ρ_p = 0.32ρ_overlap, ρ_p = 0.35ρ_overlap and ρ_p = 0.42ρ_overlap taken two days after sample preparation, with the first two being in equilibrium. Image for ρ_p = 0.40ρ_overlap taken after four days, when the cluster size distribution did not evolve significantly anymore. Scale bars are 10 µm. (B) Transmission light microscopy images for colloids with large attractive patch at increasing attraction strength (r_p = 8.9 nm). Single particles are present in solution at ρ_p = 0.16ρ_overlap. Small, stable clusters form at a slightly higher polymer concentration ρ_p = 0.19ρ_overlap. Larger polymer concentrations lead to clusters that slowly grow over time: ρ_p = 0.20ρ_overlap. Above ρ_p = 0.22ρ_overlap the rough sides become attractive as well and the site-specificity of the attraction is lost. Images taken four days after preparation. Scale bars are 10 µm. (C) Snapshot of a typical MC simulation showing colloidal clusters as well as free particles (u = -9.85 k_BT, r_p = 19 nm).

The selective attraction of smooth surfaces at intermediate polymer concentrations can be demonstrated even more convincingly by the use of rough spheres with a diameter larger than the rough side of the anisotropic particles, namely 3.2 μm. The large single rough spheres, indicated by a black arrow in Figs. 1F and 3 are clearly excluded from the clusters despite their larger diameter, which for smooth spheres would relate to an increased depletion potential. See also Movie S2 for a rough sphere approaching a colloidal micelle without sticking, and Movie S3 for a full field view of a typical sample containing colloidal micelles.

Above a critical polymer concentration (ρ_p(r_p = 19 nm) > 0.42ρ_overlap), the site specificity of the attraction is lost. While the stronger attraction between the smooth sides still favors binding between smooth surfaces over binding between rough sides, no discrete clusters are observed, as the attractive interactions between the rough sides cannot be neglected anymore. At very high polymer concentrations (ρ_p(r_p = 19 nm) > 0.45ρ_overlap), aggregation or gel formation occurs (Fig. 3A).

Here, we note that the geometry of the colloids determines the cluster topology: employing colloids with smooth patches larger than the rough seed particles as shown in Fig. 1B leads at increasing polymer concentration first to small clusters of n = 1 to n = 4 colloids, see panel below ρ_p(r_p = 8.9 nm) = 0.19ρ_overlap in Fig. 3B. Subsequently, at stronger depletion attractions induced by ρ_p(r_p = 8.9 nm) = 0.20ρ_overlap “inverse” colloidal micelles are formed which grow without limit due to the insufficient steric protection by the rough sides. In the extreme case of smooth spheres only, growth limitations can solely be achieved by controlling the number of colloids (32). With decreasing patch size and increasing steric repulsion, or in other words a larger cone angle, we expect the cluster size distribution to shift to lower values that might even favor certain cluster sizes. (10, 11). The lower limit of the patch size is set by the physical origin of the site-specific attraction: the smooth patch size needs to be significantly larger than the scale of the roughness in order to create a sufficient difference in attraction between the patches and the rough sides. Again, above a certain polymer concentration, here ρ_p(r_p = 8.9 nm) > 0.22ρ_overlap, also the rough sides become attractive and lead to gel-like aggregates.

We also find this sensitive dependence of the cluster size distribution on the attractive potential in direct Monte Carlo (MC) simulations in a canonical ensemble (NVT). The smooth side of the particles is modeled as a sphere of diameter σ_s interacting by an attractive Asakura-Oosawa-Vrij depletion potential (18–20) (colored in green) and the rough sides as a sphere of diameter σ_r with a hard-sphere interaction (colored in red). Interactions between the two different spheres are presumed to be hard-sphere-like. Van der Waals interactions are negligible due to electrostatic repulsions between and steric stabilization of the colloids. To take the neglected screened electrostatic repulsions into account, depletion potentials with contact values around u = -10 k_BT were employed. The simulated clusters and cluster size distributions are in excellent agreement with experiments as shown in Figs. 2 and 3C for u = -9.85 k_BT, respectively. This implies that the observed clusters are robust with respect to the details of the interaction potentials, but sensitive to the second virial coefficient, and may be modeled by other attractive potentials as well (6). Just like in the experiments, the onset of clustering occurs abruptly with increasing bond energy. For u = -8.9 k_BT we do not find colloidal micelles, in contrast to the characteristically peaked cluster distribution shown in Fig. 3C for u = -9.85 k_BT The sharp transition from free monomers to colloidal micelles and larger aggregates is also consistent with the observation of gas–liquid and gas–solid transitions in colloidal spheres with short-range depletion interactions (18).

However, the cluster size distributions obtained from experiments and direct MC simulations do not agree with numerical free energy calculations on single clusters, which show strong preference for specific cluster sizes larger than those that readily formed via self-assembly, see Fig. 3 and Figs. S3 and S4 and SI Text. Clusters in experiments and direct MC simulations are prevented to reach full equilibrium by the short ranged, strong attractions between the patches which give rise to extremely long equilibration times. In contrast to small clusters where only one bond has to be broken to detach a colloid and thus exchange times τ of about 10 min, each particle in the colloidal micelles has to break on average 5 bonds with a bond energy u ≈ -10 k_BT—an event that, according to the Kramers’ escape time, occurs typically every τ = 10¹² years. Already for 2 bonds, the exchange time increases to 95 days. Sequential breaking of bonds is not likely to occur either, because particle diffusion is restricted by the remaining bonds and thus quickly leads to reformation of the bond. These long lifetimes for particles bound to more than one other particle are consistent with our experimental observations. From this we may conclude that once a particle is trapped in a micelle it will stay there indefinitely.

This irreversibility seems to be inconsistent with the observation of a background of free monomers, the cmc. However, to a good approximation, as we will show below, the cmc depends on the average number of bonds in a cluster times the bond energy. We find that the average number of bonds first increases roughly linearly and then becomes a constant function of the average cluster size n beyond n = 8 (see Fig. 2C). Close to this cluster size, the peak in the size distribution is found as shown in Fig. 3. The strength of a bond is set by the experimental conditions (depletant, ionic strength, colloidal surface properties) and thus, the cmc becomes a constant for cluster sizes beyond around n = 8, irrespective of the non-equilibrium nature of the clusters. The behavior agrees with simulations on spheres interacting via a long-ranged Janus potential (2, 9).

To quantify the experimental observations we derive a formula for the critical micelle concentration considering the coexistence between single particles and clusters. The number density of unbound colloids is ρ₁ = N(1)/V. If ΔF is the free energy to reversibly detach a particle from the cluster, the probability to find a colloid unbound is p(1) = N(1)/N_t = e^-ΔF/k_BT, with N_t the total number of particles. There are two contributions to the free energy ΔF: the work associated with breaking the bonds, Δu, and an entropic contribution -TΔS = -k_BT ln Ω₀/Ω_c which accounts for the difference in the number of configurations between a single particle, Ω₀ and the cluster state, Ω_c. Thus, we can write the number density of single particles as: ρ₁ = p(1)N_t/V = N_t/V·Ω₀/Ω_c exp[Δu/k_BT]. If we assume that detachment from a cluster liberates predominantly translational configurations, thus neglecting rotational contributions, the ratio of configurations Ω₀/Ω_c is equal to the ratio of the volumes available to the centers of mass of the particles in the two states. Assuming that monomers behave like an ideal gas, and that the fraction of free particles is small compared to the fraction of colloids in clusters, we can write Ω₀/Ω_c ≈ V/N_tv_av, where v_av is the volume available for the center of mass of a particle in a cluster. Thus, 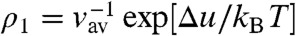. For our colloidal particles, this volume is equal to the volume available to the smooth spheres in a potential of range ξ. This result implies that a smaller available volume should be compensated by stronger bonds in order to maintain a constant density of single particles ρ₁, an intuitive result with an important consequence for the cluster life time, as we will show later. To illustrate the physical meaning of ν_av, for a square well potential and a cluster consisting of n = 2 colloids we have ν_av(n = 2) = 4πR²ξ for ξ ≪ R. In the limiting case of large clusters, we presume ν_av(n≫1) = ξ³. Then, the critical colloidal micelle concentration is given by

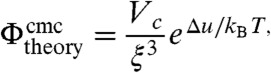[1]

where V_c is the volume of a colloidal particle. The cmc depends on the interaction range ξ in analogy to the critical density of the phase transition between liquid and gas. We employ Δu = c(n)u/(n - 1) in analogy to the definition of the cmc in surfactant micelle systems, where c(n) is the number of bonds in a cluster of size n. We take c(n)/(n - 1) = 2.4, which is roughly the average number of bonds per particle in a cluster with energy u = -10 k_BT found in direct MC simulations. Since the cmc depends sensitively on the bond energy and the average number of bonds per particle as well as on the estimate of the interaction range, this value is expected to be accurate within an order of magnitude. We obtain 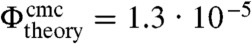, in good agreement with the experimentally found value of 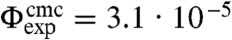. Note that in case of surfactant micelles, V_c is the volume of a surfactant molecule and v_av = v_s is the molecular volume of the solvent, which recovers the expression for the cmc of a surfactant solution (33). While the factor V_c/ξ³ is of order unity for surfactants, for colloids the value of V_c/ξ³ is significantly larger on the order of 10⁶.

Thus, in order to have a cmc at all, i.e. 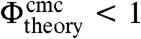, or, in more general terms, to spontaneously assemble into superstructures, significantly stronger bond energies between colloids with short-ranged interactions than between surfactant molecules are required. This implies, in turn, that according to the analysis of the escape time, equilibration times for these types of superstructures are dramatically longer. The reason for this is that the escape time of a particle is a strongly nonlinear function of the bond energy and the number of bonds of a particle in a cluster. This points to a fundamental and significant challenge in the field of equilibrium self-assembly with colloids as building blocks in situations where the difference between the available volume of the aggregated state and the dilute (monomer) state is large. This is generally the case for colloids with short-ranged interaction energies on the order of -10 k_BT per particle. In principle, it is not impossible to overcome this problem, as abundant non-equilibrium processes in biological systems show. Conceivable solutions to equilibrate colloidal systems are to apply periodic variations of the attraction strength by for example temperature sensitive depletants or single-stranded DNA, or by input of external (free) energy for instance through external fields. Equilibration problems are not expected for patchy particles with smaller patch sizes, because of fewer bonds per particles being formed.

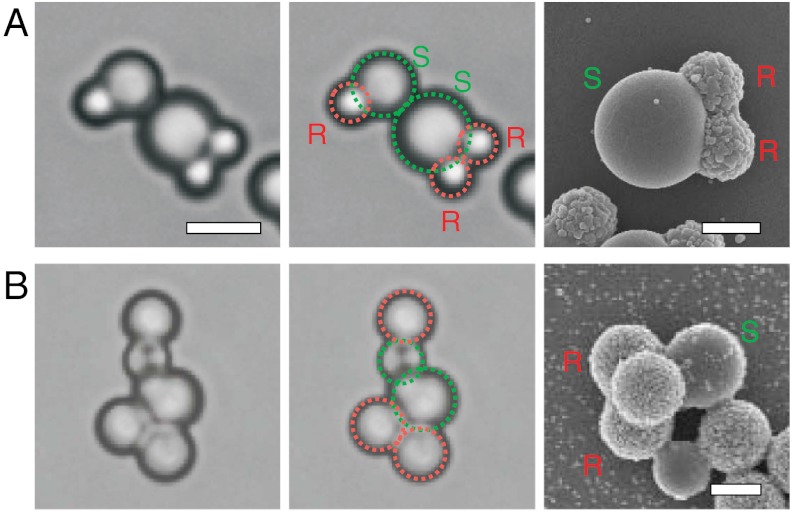
Besides the one-patch model particles presented here, a wide variety of synthetic routes for colloids with more complex patterns of rough and smooth surfaces is readily available in literature (28, 34–40). In particular, we emphasize that size, number and even the angle between patches can be controlled (38–40). Our method to render smooth parts of colloidal particles specifically attractive can straightforwardly be applied to these particles due to its material independence and generality. To exemplify this flexibility we employ colloidal molecules with complex rough and smooth shapes, as shown in Fig. 4. Despite their different shape and patch size, they interact only at their smooth sides with other colloids. Due to the available variety of colloids and their straightforward assembly even between different patch sizes, we expect rapid advances in the controlled assembly of colloidal particles into superstructures with desired topology and properties.

Fig. 4.

Assembly of complex rough-and-smooth colloids. Independent of the overall complex shape, site specificity is given by the larger attraction between the smooth sides (green) than between the rough sides (red). (A) Colloids with two rough and one large smooth side and (B) with three rough and one smooth part as shown in the electron micrographs in the right panels, interact only at their smooth sides despite the larger patch size. Scale bar in left panels is 5 µm, in right panels 2 µm.

The requirement of relatively strong bonds to stabilize colloidal aggregates with short-range attractions and the concomitant impact on equilibration times transcends the one-patch model system that we study. These insights are of fundamental and practical importance in the field of colloidal and macromolecular self-assembly, including proteins as building blocks. The analogy of the rough-smooth colloids with molecular surfactants likely extends to emulsion and interface stabilization as well, for instance by adding spherical (and smooth) particles as a colloidal liquid phase. The model system can be straightforwardly employed to study the influence of the geometry of the colloidal surfactant on the preferred curvature of emulsion droplets, a concept often used in molecular surfactants.

Materials and Methods

Particle Synthesis.

Colloidal particles consisting of one smooth and one rough sphere were synthesized following a modified synthesis by Kim et al. (27). Roughness on the seed particles was obtained through adsorption of polystyrene particles nucleated during polymerization. The synthesized colloids were washed and redispersed in 0.3% w/w aqueous polyvinyl alcohol (M_w = 30–50 kg/mol).

Sample Preparation.

The samples were prepared by mixing of aqueous solution of polymer, colloidal dispersion, 20 mM NaCl, and millipore water. All components contained 7.7 mM sodium azide to prevent bacterial growth. The colloidal volume fraction was chosen to be 0.3% w/w. For depletion interaction, dextran polymers of M_w = 110 kg/mol and M_w = 500 kg/mol were dissolved in 7.7 mM aqueous sodium azide. After preparation, the samples were filled in polymer coated capillaries to prevent absorption of the particles onto the glass walls (21) and sealed with UV curable glue onto microscope slides. The microscope samples were rotated on a stage (VWR) at 10 rpm to even out effects of gravity.

Direct Monte Carlo simulations.

We use Monte Carlo simulations in the canonical ensemble (NVT) to calculate the probability distribution of the cluster size 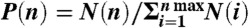, where N(n) is the number of clusters of size n in a system containing N = 1000 dumbbells at a packing fraction of 0.003. We consider the polymer to be of density ρ_p and diameter σ_p. The smooth side of the particles is modeled as a sphere of diameter σ_s interacting by an attractive Asakura-Oosawa-Vrij depletion potential (18–20) and the rough sides as a sphere of diameter σ_r with a hard-sphere interaction. Interactions between the two different spheres are also presumed to be hard-sphere-like. To take the neglected screened electrostatic repulsions into account, depletion potentials with contact values around u = -10 k_BT were employed. To improve mobility of clusters containing more than one particle, cluster moves are introduced which collectively move all particles that are part of the same cluster. Particles are considered to be part of the same cluster if the distance between their smooth spheres is less than the attraction range σ_s + σ_p.

Free Energy Calculations.

The free energy of clusters of different sizes was calculated using grand-canonical Monte Carlo (GCMC) simulations on single clusters (41). We model the particles in the same way as in the direct Monte Carlo simulations, and assume that the gas of clusters is sufficiently dilute to behave as an ideal gas. To measure the cluster free energies, we simulate single clusters, and reject all moves that would break up this cluster. Apart from translation and rotation moves, we insert and remove particles according to a standard GCMC scheme. By minimizing the free energy with respect to the number of clusters of each size we find the overall cluster size distribution.

Please refer to the SI Text online for extended details on methods.