Overview: Damage resistance of graded ceramic restorative materials

Abstract

Improving mechanical response of materials is of great interest in a wide range of disciplines, including biomechanics, tribology, geology, optoelectronics, and nanotechnology. It has been long recognized that spatial gradients in surface composition and structure can improve the mechanical integrity of a material. This review surveys recent results of sliding-contact, flexural, and fatigue tests on graded ceramic materials from our laboratories and elsewhere. Although our findings are examined in the context of possible applications for next-generation, graded all-ceramic dental restorations, implications of our studies have broad impact on biomedical, civil, structural, and an array of other engineering applications.

1. Introduction

Ceramics have become increasingly popular as dental restorative materials because of their superior aesthetics, as well as their inertness and biocompatibility. However, ceramics are brittle and subject to premature failure, especially under repeated contact loading in moist environments.¹ The financial drivers for improvements in fracture resistance of ceramics are high: the global crown and bridge (C&B) market was estimated to be $25 billion in 2010 and is expected to exceed $30 billion by 2015.² Today, about 22 – 27% C&B units are all-ceramic. Demands for more aesthetic and metal-free restorations as well as soaring precious metal prices will likely increase the number of all-ceramic prostheses.³

Clinical research and practice have revealed that full-coverage alumina-core crowns and lithium disilicate glass-ceramic bridges are susceptible to both contact-induced veneer fracture and flexure-induced bulk fracture,^4–10 while zirconia-core restorations are prone to veneer chipping^11–15 (Fig. 1). This has led to the development of monolithic zirconia restorations (e.g. BruxZir, Glidewell), in some cases reducing the restoration thickness to improve translucency and preserve tooth structure. In this case aesthetics are compromised, while the potential for hydrothermal degradation and wear of the opposing dentition is raised. Thinner restorations also increase the risk of fatigue fracture. Hence there is a need to develop an all-ceramic restorative material that exhibits superior resistance to chipping and fatigue without compromising the aesthetic advantage.

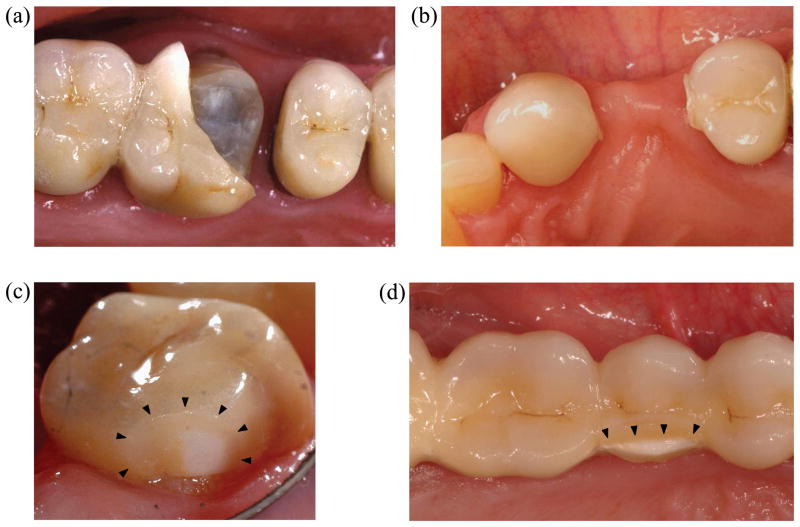
Fig. 1.

Clinical fractures in all-ceramic prostheses. (a) Cementation flexural bulk fracture in alumina-core crowns. (b) Connector flexural fracture in lithium disilicate glass-ceramic bridges. Chips and fractures in zirconia-core (c) crowns and (d) bridges. Arrows in (c) and (d) highlight chips and fractures. (Courtesy of I. Sailer and P. Guess).

Recent advances in theoretical and experimental work from our laboratory and elsewhere have demonstrated that veneer failure and bulk fracture may be substantially mitigated by controlled gradients of elastic modulus within the restoration layer^16–19 Such graded structures exhibit significantly higher resistance to fatigue sliding-contact^19–22 and flexural damage^{18, 23–25} relative to veneered and monolithic core ceramics. This is because the gradient diminishes the intensity of tensile stresses and simultaneously transfers these stresses from the layer surface into the interior, away from the source of failure-inducing surface flaws.^{17–19, 23, 26}

This article surveys results of fundamental studies on damage resistance of newly developed graded zirconia (3Y-TZP) and alumina materials in the context of dental applications. Although we draw mainly from our own studies and our focus is primarily on dental applications, the subject matter has broad impact on biomedical, civil, structural, and an array of other engineering applications. In this article, fabrication processes and the subsequent microstructural properties of functionally graded materials (FGMs) are reviewed. Examples of improved resistance to contact, flexural, and fatigue damage of graded ceramics relative to their ungraded counterparts are presented. Explicit analytical relationships for the critical loads to produce each form of damage are given. These findings provide guidelines for designing optimal ceramic structures for superior contact and flexural damage resistance.

2. Functionally graded materials

FGMs exhibit spatial variations in structure and/or composition, which have been imposed in order to obtain unprecedented properties and functionalities that cannot be realized in homogeneous materials. Although the usefulness of FGMs has been recognized since the early 1970s,²⁷ the field of FGM did not take off until the mid-1980s, probably due to a lack of suitable fabrication methods until that time. With the help of several national priority research programs in Japan^{28, 29} and Germany³⁰, a wide range of process technologies are now available: powder metallurgical process;²⁸ layer stacking;³⁰ centrifugation;³¹ glass infiltration;¹⁷ plasma spray;³² electrophoretic deposition;³³ rapid prototype color ink-jet printing;³⁴ and direct-write assembly (robocasting).³⁵ Among these processing methods, the glass infiltration technology is particularly suitable for the fabrication of all-ceramic restorations.²⁴ It combines an aesthetic, low modulus, and low hardness glass “veneer” with a high strength ceramic “core”, without a sharp interface between the materials. The lack of interface due to grading improves interfacial bond strengths, reduces residual stresses, and eliminates delaminations. The processing of these structures is simple and straightforward, and can be readily adapted to CAD/CAM technology.^{20, 22, 24} Two examples of these functionally graded ceramic dental restorative materials are glass-infiltrated zirconia and alumina.

2.1. Graded glass-zirconia structures

Elastically graded glass-zirconia structures may be produced by infiltrating the surfaces of heat-treated zirconia templates with a silica-based glass.²⁴ The merits of such an approach lie in a relatively low heat-treatment temperature for zirconia templates (compared to the sintering temperature of zirconia), and in combining glass infiltration and zirconia densification into a single process.^{18, 24} This way the glass infiltration depth can be tailored by manipulating the porosity of the zirconia templates. The grain growth³⁶ and/or destabilizing of the tetragonal zirconia phase³⁷ associated with the post-sintering heat-treatment can be prevented. The resultant structure consists of a thin, outer surface residual glass layer followed by a graded glass-zirconia layer at both the top and bottom surfaces, sandwiching a dense 3Y-TZP core (Fig. 2). The thickness of the external surface residual glass layer may vary from 5 to 80 μm and that for the graded layer may alter from 40 to 200 μm, depending on the porosity of the zirconia templates. The elastic modulus of 3Y-TZP is ~240 GPa and that for external glass is ~68 GPa. The transition of elastic modulus from the graded glass-zirconia surface (containing 45% glass) to the fine-grained 3Y-TZP core (with 0% glass) is continuous and follows a power-law relationship. The coefficient of thermal expansion (CTE) and Poisson’s ratio of the infiltrating glass are essentially the same as those of 3Y-TZP, thus no significant long-range thermal stresses are developed in the graded structure.¹⁷

Fig. 2.

SEM microstructure of functionally graded glass-zirconia materials. (a) External glass (G) and graded glass-zirconia (GZ) layers, and (b) zirocnia interior (Z).

2.2. Graded glass-alumina structures

Analogous to graded zirconias, graded glass-alumina structures may be obtained by infiltrating dense alumina surfaces with CTE-matched silica-based glasses.^{16, 38–40} Again, the resultant structure consists of a thin, outer surface residual glass layer followed by a graded glass-alumina layer, sandwiching a dense alumina core (Fig. 3). The thickness of the graded layers can vary from several tens of microns³⁸ to several thousands of microns,¹⁶ depending on the infiltrating glass compositions and infiltration temperatures. Nonetheless, the transition of elastic modulus from the graded glass-alumina surface to the alumina core is continuous, following a power-law relationship.^{16, 25}

Fig. 3.

SEM microstructure of functionally graded glass-alumina materials. (a) External glass (G) and graded glass-alumina (GA) layers, and (b) alumina interior (A).

3. Contact damage resistance of graded surfaces

One of the emerging causes of fracture of all-ceramic dental restorations is the generation of cracks due to occlusal contact and wear.^{4, 9, 41} Indentation sliding-contact of a surface with a sphere provides basic and quantitative information that typifies the contact and flexural damage sustained in dental crowns and bridges (Fig. 4).^{19, 42} We now know that occlusal like contact–slide–liftoff loading of brittle crown like structures can trigger a series of ‘partial cone cracks’ (characterized by a herringbone pattern) capable of causing failure by propagation to the core interface. Partial cone cracks arise because frictional sliding intensifies tensile stresses at the trailing edge of the occlusal contact.^43–46 Thus, partial cones occur at much lower loads than classical Hertzian cone cracks in axial testing (frictionless contact).^{19, 45} Below, we examine the resistance to sliding-contact damage of graded ceramics relative to their ungraded counterparts, as well as a commercial porcelain-veneered zirconia system. Indentation mechanics concerning the evolution of partial cones in brittle solids is reviewed.

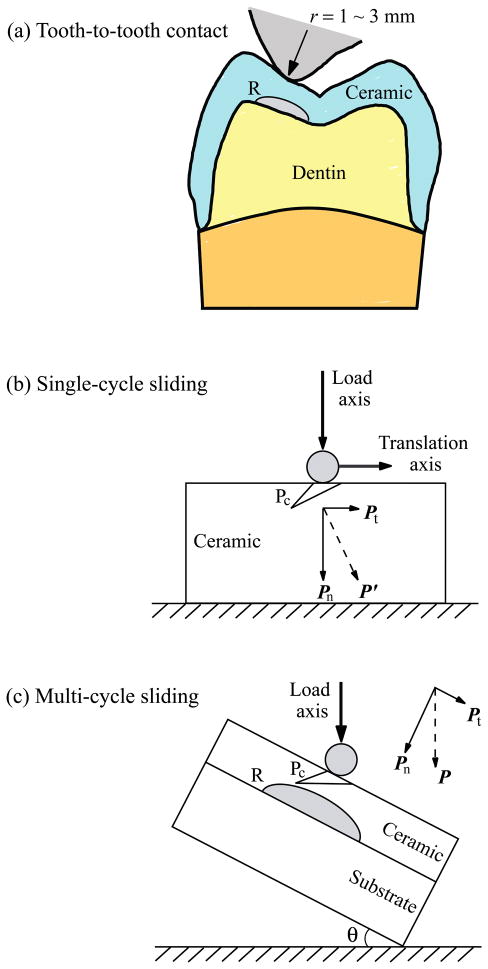
Fig. 4.

(a) Schematic of occlusion, showing that posterior tooth-tooth contact can be visualized as a spherical indenter sliding down an inclined flat surface. Experimental set-up for (b) single-cycle sliding with a translating sphere; and (c) multi-cycle off-axis fatigue loading with a 30° inclination angle. Note the superposed tangential force component in (b) and (c). The symbol P_c and R denote partial cone and flexural radial cracks, respectively.

3.1. Contact damage: single-cycle sliding

Begin with the single-cycle frictional sliding tests on the polished surfaces of elastically graded and homogeneous ceramics with a spherical tungsten carbide (WC) indenter of radius r = 1.5 mm in water (Fig. 4b). These sliding tests were designed to determine the critical normal load, P_n, for the onset of surface cracking in graded 3Y-TZP relative to ungraded and commercial porcelain-veneered 3Y-TZP. In this set of experiments, graded zirconia plates (2.5 mm thick) were fabricated by heat-treating zirconia green compacts at 1350°C for 1 h to form 3Y-TZP templates and then glass-infiltrating these templates at 1450°C for 2 h.¹⁹ The resultant surface graded layer was approximately 120 μm thick. Sintered homogeneous 3Y-TZP plates (2.5 mm thick, 1450°C for 2 h) were obtained using the same raw zirconia powder as the graded structures.

Sliding tests were run in a biaxial mode (Fig. 4b): indenter contacted the specimen surface, the load was ramped to the prescribed peak value while the specimen translated horizontally for 4 mm, at a constant velocity v = 2 mm/s. The loading rate was 2000 N/s. The normal load P_n and the tangential force P_t were monitored continuously; the steady-state coefficient of friction μ was calculated: μ = P_t/P_n. To minimize large variations of μ amongst the test specimens, all surfaces were polished down to 0.5 μm finish. For graded glass-zirconia material, the bulk of external surface glass was carefully removed by polishing using 6 μm diamond abrasives, followed by 0.5 μm finish.

Experiments of frictional sliding by a WC sphere showed that the normal load required to generate any herringbone-like partial cone cracks on elastically graded 3Y-TZP surface was P_n = 2000 N (with a coefficient of friction μ ≈ 0.1), which was over 3 times higher than that on homogeneous 3Y-TZP surface (P_n = 600 N, μ ≈ 0.1) and 40 times higher than that on porcelain-veneered 3Y-TZP surface (P_n = 50 N, μ ≈ 0.2) (Fig. 5).^{19, 22} Similar beneficial effects of modulus gradations on sliding-contact resistance have been demonstrated in fine-grained alumina infiltrated with CTE-matched silicate glass³⁹ and aluminosilicate glass.²¹

Fig. 5.

Surface view of single-cycle sliding damage in (a) graded glass-zirconia at P_n = 2000 N; (b) monolith zirconia at P_n = 600 N; and (c) porcelain-veneered zirconia at P_n = 120 N. Note: two faint incomplete ring cracks indicated by solid arrows in (b). Sliding direction from left to right of micrographs.

3.2. Contact damage: multi-cycle sliding

Now consider cyclic sliding-contact response of graded surfaces relative to their homogeneous counterparts. In an attempt to simulate the chewing motion that a molar would undergo, crown-like ceramic plates cemented to dentin-like composite supports were mounted at an inclination θ = 30° (Fig. 4c). Fatigue loading of 200 N (nominal biting force) was delivered through a spherical WC indenter (opposing cusp, 1.5 mm radius) on the specimen top surface with a contact–slide–liftoff profile, i.e. the indenter contacting the specimen surface, loading to maximum while sliding down the slope to create a wear facet ~1 mm in length, then unloading and lifting off from the specimen surface.^{20, 47–49} Sliding-contact fatigue test on polished surfaces in water showed that the graded glass-zirconia surface (with the external glass layer removed as described above) performed at least as well as its homogeneous zirconia counterpart, and both of these materials have demonstrated lifetimes that were orders of magnitude longer than porcelain-veneered zirconia.²²

While it is easy to polish off external glass from the flat specimens, it would be much more difficult to remove excess glass from the outer surface of anatomically-correct crowns and bridges. For clinical applications, this thin external glass layer is essential for aesthetics (shade options) and fracture containment, so as to preserve the anatomic features of CAD/CAM restorations, protect the underlying zirconia from the oral environment, reduce plaque formation, and prevent excessive wear of the opposing enamel. The question then arises: would a glass-rich surface compromise the toughness of a 3Y-TZP matrix, rendering the material more susceptible to chipping?

To address this question, the sliding-contact fatigue response of graded glass-zirconia surfaces with external aesthetic glass was investigated. Flat glass-zirconia graded plates with external glass (1.5 mm total thickness, 120 μm graded layer thickness, and 20 μm external glass layer thickness) were cemented to composite blocks and subjected to prolonged sliding contact up to 10 million cycles at 200 N in water.²⁰ The resistance to sliding contact fatigue of graded glass-zirconia with external glass matched that of homogeneous zirconia, and was orders of magnitude better than porcelain-veneered zirconia. Optical microscopy of cross sections perpendicular to the contact surface revealed no significant cracks in graded and ungraded zirconia following 2 million sliding cycles (Figs. 6a and b). Higher magnification SEM along the sliding direction, from the rim to the bottom of the crater, revealed a smooth transition from the external glass to the bulk zirconia (see inserts in Fig. 6a). In comparison, monolithic 3Y-TZP had a smooth wear crater at the trailing edge and a relatively coarse leading edge with minor material spalling and cracks (highlighted by the rectangular box in Fig. 6b). However, at the same sliding load, partial cone cracks propagated through an entire 1 mm porcelain veneer layer at only ~10⁵ cycles in a commercial porcelain-veneered zirconia system (LAVA, 3M ESPE) (Fig. 6c).

Fig. 6.

Cross sectional view of (a) graded glass-zirconia (GZ) with an external glass layer (G) and (b) homogeneous 3Y-TZP following sliding-contact fatigue at 200 N, 2 million cycles in water. Section view of (c) a commercial porcelain-veneered zirconia system (LAVA, 3M ESPE), showing that partial cone cracks have propagated through an entire 1 mm porcelain veneer layer after ~10⁵ sliding cycles at 200 N in water. Sliding direction from left to right of micrographs.

3.3. Indentation mechanics

We survey recent developments in the field of fracture mechanics that are most pertinent to sliding-contact damage in graded and ungraded surfaces.

3.3.1. Theories of frictional contact

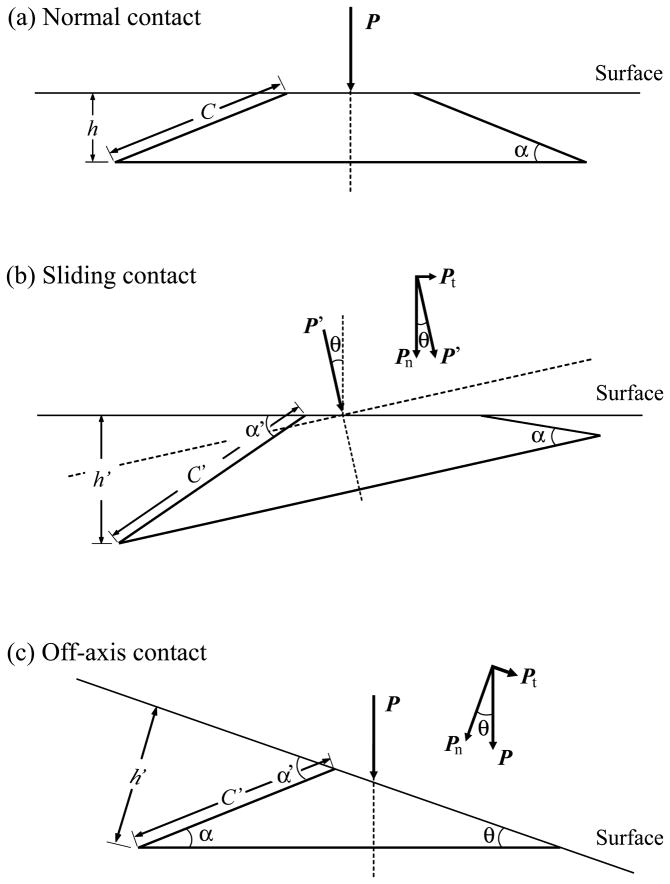
The stress fields associated with frictionless elastic contacts (μ = 0) between a rigid sphere and a flat brittle solid have been solved by Hertz.⁵⁰ The Hertzian stress field contains a large component of hydrostatic compression, considerable shear, and modest tension.^51-53 It is now well understood that cone cracks start from small-flaws on the specimen surface just outside the contact circle where the tensile stresses are greatest.⁵⁴ The embryonic cracks subsequently circumvent the contact circle as a shallow surface ring, then propagate downward and flare outward into a truncated cone configuration (Fig. 7a).⁵² The far-field approximation solution for the dimension C of a virtual cone under a normal load P_n is given by:⁵⁵

Fig. 7.

Schematic showing cone crack geometry in brittle layers with (a) normal; (b) sliding- contact; and (c) off-axis loading. Sliding direction from left to right.

$$C={(\chi {\mathit{P}}_{\text{n}}/K_{\text{c}})}^{2/3}$$ (1)

where K_c is the stress-intensity factor and χ is a crack geometry coefficient.

With the actual penetration depth of a virtual cone h = C sin α (α is the inclination angle of the cone in respect to the specimen surface) (Fig. 7a), we have:

$$h={(\chi {\mathit{P}}_{\text{n}}/K_{\text{c}})}^{2/3}sin\alpha$$ (2)

When the indenting sphere is laterally translated across a brittle surface, friction at the contact intensifies the tensile stresses at the trailing edges of the contact circles, resulting in the generation of a series of distorted classical cone cracks, i.e. partial cone cracks (Fig. 7b).⁴⁶ A theoretical model for the formation of the partial cone cracks has been put forward by Lawn et al.⁵⁶ The effects of the tangential loading are to increase the magnitude of the resultant load and to alter its direction with respect to the surface normal, Fig. 7b. At a critical load, cone crack forms but with its axis oriented in the direction of the resultant load P’. The solution for this oriented cone crack depth h’ can be expressed as:⁴⁵

$$h’={(\chi {\mathit{P}}_{\text{n}}/K_{\text{c}})}^{2/3}{(1+{\mu }^2)}^{1/3}sin\alpha ’$$ (3)

The inclination angle α’ of the rotated cone on its steepest side:

$$\begin{array}{l}\alpha ’=\alpha +\theta \\ =\alpha +arctan\mu \end{array}$$ (4)

where θ = arctan μ.

Now consider an inclined load configuration where the specimen surface normal is tilted for an angle θ in respect to the loading axis (Fig. 7c), equivalent to loading a maxillary molar on the buccal incline surface and sliding downward to the centric occlusal position (Fig. 4a). θ represents the cuspal angulation. At a critical load, a cone crack forms with its orientation (the cone axis) in the direction of applied load P (Fig. 7c). Again, the penetration depth h’ and the inclination angle α’ of the resultant cone crack can be quantified by equations (3) and (4).⁴⁷

Explicit equations (3) and (4) quantitatively predict the penetration depth and inclination angle of cone cracks for biaxial (load–slide–liftoff) loading. For a given normal load P_n, a larger friction results in a larger cone crack (C’) with a steeper inclination angle (α’) and deeper penetration depth (h’). These analyses indicate that cone cracks would initiate at a lower load in the sliding-contact relative to the normal frictionless loading.

3.3.2. Resistance to frictional contact of graded surface

Theory for frictional sliding contact on elastically graded surface by a rigid stamp, which may be flat, parabolic, semicircular or wedge-shaped, has been developed for the power-law variation in Young’s modulus with respect to depth.^57-59 Theory predicts that when the modulus increases with depth, peak values of near contact tensile stresses, responsible for surface cone cracking, are spread further into the interior compared with a homogeneous material. This is because the underlying material has a higher elastic modulus than the surface and can thus bear higher stress.²¹ These analyses indicate that controlled gradients of elastic modulus can lead to a marked increase in the resistance of a surface to frictional sliding-contact induced partial cone fracture.

4. Flexural fracture resistance of graded interfaces

As indicated in the Introduction, all-ceramic dental crowns and bridges are susceptible to flexural bulk fracture.^60–63 Therefore, it is highly desirable to develop all-ceramic restorative systems with superior load-bearing properties and with materials robust enough for ultra-conservative restorative protocols that preserve tooth structure. Below, we examine the resistance to flexural fracture of graded ceramics relative to their ungraded counterparts. Recent advances in fracture mechanics concerning the effect of surface elastic gradients on flexural stress dissipation are reviewed.

4.1. Flexural fracture: single-cycle loading

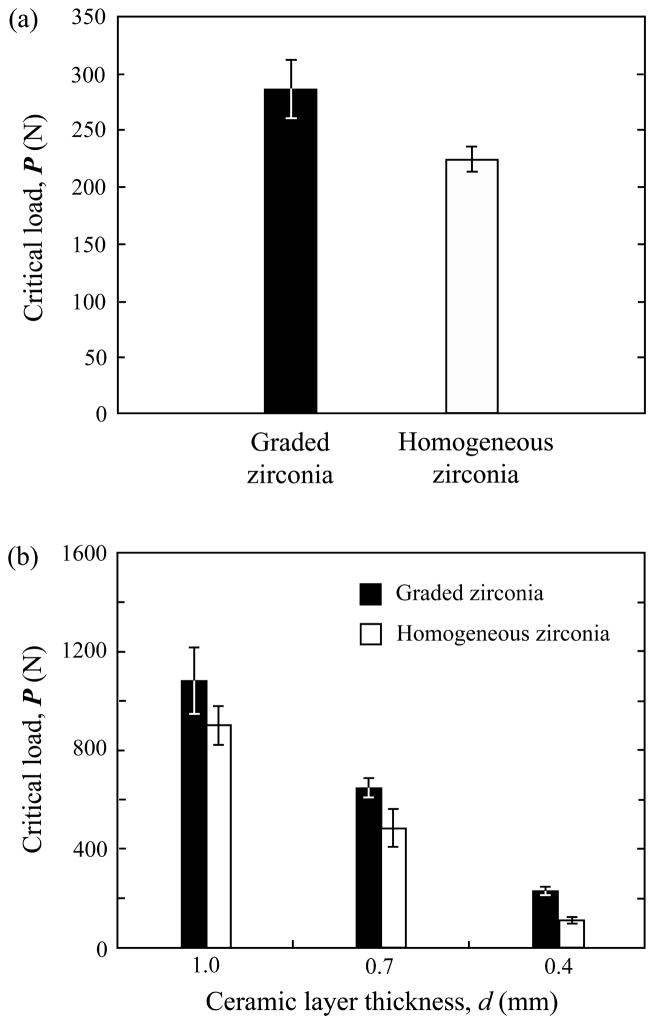
Single-cycle flexural test on graded glass-zirconia sandwich beams and their ungraded zirconia counterparts were carried out using three-point bend test.¹⁸ Graded sandwich and homogeneous zirconia beams (N = 6 for each specimen type) of dimensions 1.2 x 4 x 25 mm were prepared; loads at the fracture point for polished graded and homogeneous zirconia beams are shown in Fig. 8a. Loads required to fracture graded beams (285 ± 26 N, mean ± SD) were ~28 % higher than those for homogeneous zirconia beams (223 ± 11 N). These beams are the thinnest specimens which meet the specifications for three-point bending test as recommended by the International Organization for Standardization.⁶⁴ For thinner specimens, we adopted a ball-on-ceramic/polymer bilayer method to determine the critical fracture load of a bending plate.^{42, 65, 66} The ball-on-flat bilayer indentation flexural test produces bending stresses in the ceramic layer just like those generated by a biaxial or three-point bend test, and yet is more tolerant to the specimen dimensions, capable of testing specimens with smaller thicknesses and irregular shapes. Critical loads for the onset of fracture in graded glass-zirconia plates (N = 6 per specimen type per thickness) were 1081 ± 140, 648 ± 39, and 227 ± 20 N for d = 1.0, 0.7, and 0.4 mm, which were 17%, 25%, and 50% higher than their homogeneous zirconia counterparts (894 ± 85, 487 ± 78, and 113 ± 10 N) (Fig. 8b). Similar beneficial effects of modulus gradations on flexural fracture resistance have been demonstrated in fine-grained alumina infiltrated with CTE-matched silicate glass.^{25, 38}

Fig. 8.

Bar chart showing critical loads for flexural fracture of (a) ceramic beams subject to three-point bending; and (b) ceramic plates subject to ball-on-ceramic/polymer bilayer tests.

4.2. Flexural fracture: cyclic fatigue loading

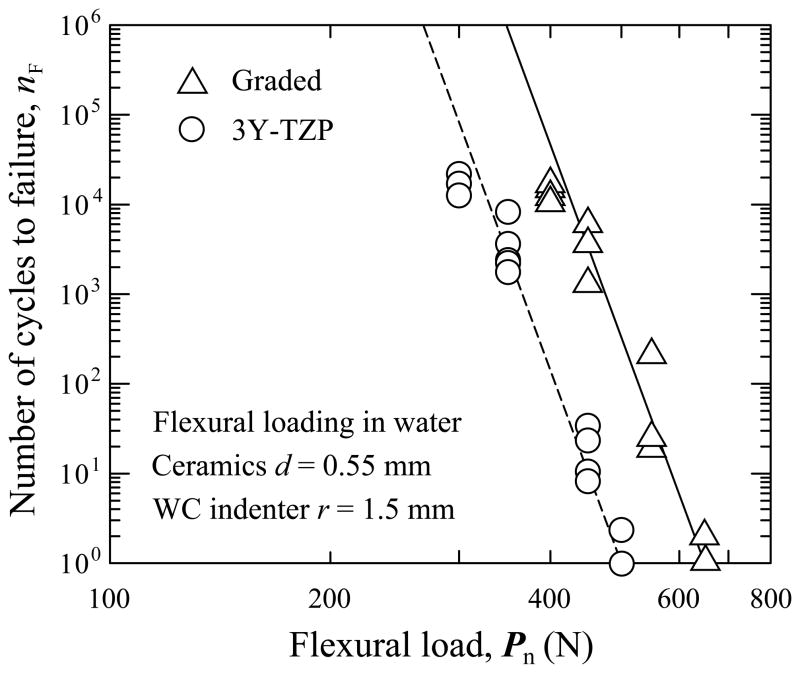
Cyclic flexural tests were conducted to determine the long-term load-bearing capacity of graded and ungraded zirconia. Thin plates (d = 0.55 mm), representing thin restorations or connectors of bridges, were bonded to dentin-like composite supports with dental cement. Ceramic/composite bilayer specimens were mounted at an angle and flexural load applied at the ceramic top surface in water (Fig. 4c). In this case, failure occurred by initiation of radial cracks at the cementation surface.⁶⁷ The current fatigue tests were designed to determine the number of cycles to failure, n_F, for a range of prescribed fatigue loads from 250 N to 800 N. Damage maps were constructed for graded glass-zirconia and homogeneous zirconia on compliant substructures (Fig. 9). A significantly higher number of cycles were required to fracture graded glass-zirconia relative to pure zirconia plates, demonstrating an improved fatigue flexural damage resistance from surface grading (Fig. 9). Similar beneficial effects of modulus gradients on fatigue fracture resistance have been demonstrated in fine-grained alumina infiltrated with CTE-matched silicate glass.³⁹

Fig. 9.

Plot of cycles to failure as function of flexural load for graded and ungraded 3Y-TZP. Failure occurs by radial fracture from the cementation surface.

4.3. Fracture mechanics analysis: composite beam theory

A general theory has been recently developed for stress analysis of simply supported graded sandwich beams subject to transverse center loads.^{18, 25} Closed-form equations have been derived to relate the bending stress distribution to elastic modulus profiles and layer thicknesses. Theory predicts that proper modulus gradients at the ceramic surface can effectively reduce and spread the maximum bending stress from the surface into the interior, away from the strength limiting surface flaws. The magnitude of such stress dissipation is governed by the thickness ratio of the beam to the graded layers as well as bulk (E_b) to surface (E_s) modulus ratio and the scaling exponent n of the power-law modulus variation.^{18, 25} A thickness ratio d_total/d_graded = 2 –10 is most effective for stress reduction.¹⁸ A low n value (0.15 < n < 0.5) coupled with a small bulk-to-surface modulus ratio (E_b/E_s = 3 – 6) is most desirable for reducing the maximum stress and transferring it into the interior, while keeping the surface stress low.²⁵

Although graded surfaces may only reduce the maximum stress by 10% – 20% and transfer the peak stress 100 μm, or in some cases only several 10s of μm, beneath the surface, the absence of large internal flaws of fine-grained ceramics, coupled with the somewhat diminished effectiveness of any such internal flaws as stress concentrators,⁵⁵ renders the graded material more flaw-tolerant and resistant to higher loads. A typical dental prosthesis has a thickness range of 0.4 – 1.5 mm. Given the thicknesses of the graded layers are 80 and 120 μm for alumina and zirconia respectively, the equivalent thickness ratio for both graded alumina and zirconia lies between 1.7 and 9.4, overlapping with the above-mentioned most desirable thickness range d_total/d_graded = 2 – 10. Thus, by grading the ceramic surface, we can significantly improve the load-bearing capacity of alumina and zirconia restorations, averting flexural bulk fracture that happens all too often in all-ceramic crowns and bridges.

5. Clinical implications

Use of zirconia in crowns and bridges has increased over recent years, owing to aesthetic and biocompatibility demands. In addition, zirconia frameworks are produced by milling of either fully sintered or partially sintered zirconia blocks, a process that is more rapid and less labor intensive relative to the lost-wax casting process for metals. Zirconia frameworks are less expensive than precious metal copings. Applying an aesthetic veneer over a zirconia framework is no more difficult than over metal. However, the fact remains that porcelain-veneered zirconia restorations suffer unexpectedly high chipping rates, regardless of manufacturer.^{11, 14, 15, 68–75} If these chipping rates could be reduced, zirconia-based all-ceramic prostheses would become more widely used, addressing a quality of life issue. Functionally graded glass-zirconia structures offer a simple remedy.

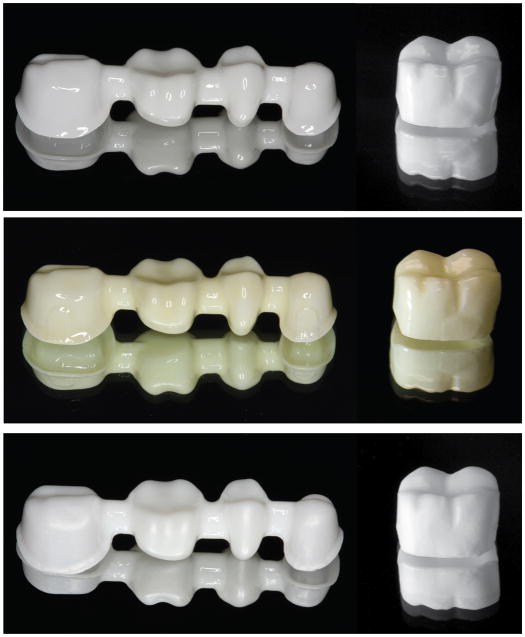
Zirconia cores are, however, only a portion of the all-ceramic restoration. Thus, we propose alternative monolithic graded glass-zirconia restorations (i.e. without porcelain veneer), which could be successfully and economically used in posterior applications to eliminate the vulnerable porcelain veneer, while providing superior strength and aesthetics. The color characterization of these graded glass-zirconia restorations is achieved by external residual glass and subsequent staining. A straightforward protocol for fabricating anatomically-correct zirconia crowns and bridges with graded surfaces has been developed. A scan file from a model crown control with standard occlusion is imported into a milling machine. This creates enlarged green zirconia templates, accounting for 25 vol.% sintering shrinkage with 50 μm cement relief. For monolithic graded glass-zirconia crowns, green templates are first heat treated at 1350°C for 1 h. The glass is then applied as a uniform slurry using the enameling technique, and fired at 1450°C for 2 h. The resulting graded structure has a thin external aesthetic glass layer at both the occlusal and cementation surfaces (Fig. 10).

Fig. 10.

Graded monolithic glass-zirconia four-unit frameworks and single crowns with white (top) and light yellow (center) shades. Similar framework and crown made from monolithic zirconia (bottom).

Experimental findings suggest that restorations made from graded glass-zirconia are orders of magnitude more resistant to sliding-contact damage than the current porcelain-veneered zirconia systems, thereby averting chips and fractures of the porcelain veneer. The graded layer also enhances the flexural fracture resistance of zirconia, allowing the utilization of thinner restorations for highly conservative restorative protocols that preserve tooth structure. Additionally, the cementation (intaglio) surface of graded restorations can be etched with hydrofluoric acid and silanized to facilitate a resin-cement bond, greatly improving the cementation strength compared to their ungraded counterparts.

The graded glass-zirconia approach has addressed an important clinical problem in connection with zirconia-based restorations—susceptibility to chipping and fracture of the veneering porcelain. The emerging problems of hydrothermal degradation and fatigue fracture related to thin monolithic zirconia restorations are also endeavored. The further development of this grading technology could potentially lead to all-ceramic restorative systems with superior long-term clinical performance. We contend that surface grading is but one step in this forward progress.