Growth and remodeling of the left ventricle: A case study of myocardial infarction and surgical ventricular restoration

Abstract

Cardiac growth and remodeling in the form of chamber dilation and wall thinning are typical hallmarks of infarct-induced heart failure. Over time, the infarct region stiffens, the remaining muscle takes over function, and the chamber weakens and dilates. Current therapies seek to attenuate these effects by removing the infarct region or by providing structural support to the ventricular wall. However, the underlying mechanisms of these therapies are unclear, and the results remain suboptimal. Here we show that myocardial infarction induces pronounced regional and transmural variations in cardiac form. We introduce a mechanistic growth model capable of predicting structural alterations in response to mechanical overload. Under a uniform loading, this model predicts non-uniform growth. Using this model, we simulate growth in a patient-specific left ventricle. We compare two cases, growth in an infarcted heart, pre-operative, and growth in the same heart, after the infarct was surgically excluded, post-operative. Our results suggest that removing the infarct and creating a left ventricle with homogeneous mechanical properties does not necessarily reduce the driving forces for growth and remodeling. These preliminary findings agree conceptually with clinical observations.

1. Introduction

Heart failure is a chronic medical condition in which the pumping efficiency is gradually reduced as the heart muscle progressively becomes weaker [42]. The single most common cause of heart failure is ischemic heart disease with acute myocardial infarction. Prognosis is poor with 40% mortality within 12 months of diagnosis, and a 10% annual mortality rate thereafter [8]. To treat heart failure, several innovative procedures were introduced within the past two decades. Cardiac resynchronization therapy [27], the Dor procedure [10, 47], myosplint [18, 34], adjustable passive constraint [25], the injection of passive material [53, 55], and surgical ventricular restoration [3, 9, 26], as shown in Figure 1, and are only a few examples. Most of these procedures were motivated by engineering intuition, but their mechanical characteristics and their long-term impact were unclear. To quantify the mechanical effects of these surgical procedures on cardiac function, patient-specific mathematical models have been proposed to predict strain and stress profiles throughout the heart [54, 58]. Since it is virtually impossible to measure regional stresses in the myocardial wall in vivo, these mathematical modeling seems to be a reasonable alternative.

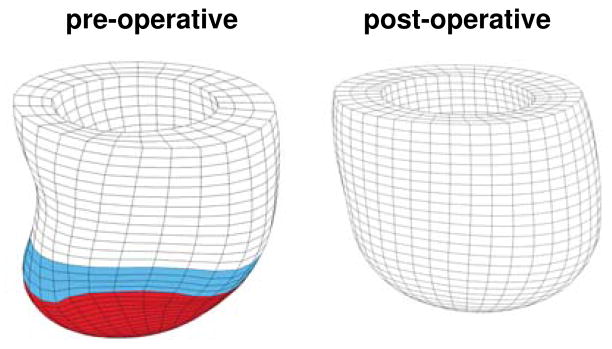
Figure 1.

Surgical ventricular restoration after myocardial infarction. Pre-operative left ventricle with apical infarct, shown in red, and boarder zone, shown in blue, left. Post-operative left ventricle with the infarct removed, right.

To date, most mathematical models focus on characterizing the acute, short-term impact of surgical procedures [19, 25]. Only recently, novel mathematical models have been proposed to study the chronic, long-term effects of clinical interventions [4, 30, 35]. Although the theoretical and computational modeling of cardiac growth is still in its infancy, and the calibration and validation of these models remain challenging [2, 28], the ultimate goal of these growth models is to provide additional insight into the driving forces for cardiac growth, and support the rational design of new treatment options [1, 37, 49].

Clinically, the structural remodeling of the left ventricle is considered a strong indicator of progressive heart failure [7, 21]. In response to volume overload, the ventricle dilates to maintain the cardiac output at its physiological level [56]. Cardiac maladaptation is accompanied by changes in left ventricular shape from prolate elliptical to spherical [29]. These chronic changes in shape, size, and function of the left ventricle should be addressed when selecting the appropriate interventional treatment to ensure not only short-term but also long-term success.

Here, we adopt a recently proposed framework for the constitutive modeling of growth in cardiac tissue [5, 13, 36]. Instead of modeling growth by assuming it is an isotropic process [30, 31, 48], we model ventricular dilation as a natural consequence of the serial deposition of sarcomeres at the cellular level [12]. The model is thus inherently mechanistic, and captures the phenomena associated with anisotropic cardiac growth across the scales. In contrast to existing formulations based on a generic elliptical model of the left ventricle [2, 30], we utilize a patient-specific model created from magnetic resonance images. Finally, rather than assuming uniform material properties for the myocardial tissue [13, 40], we model a left ventricle diagnosed with an apical infarct, and use different material properties for the infarct region and the remote region, thus adding an additional source of heterogeneity.

This manuscript is organized as follows. First, in Section 2, we briefly summarize the modeling of cardiac dilation based on a mechanistic constitutive model for growth in anisotropic soft biological tissues. Then, in Section 3, we illustrate the algorithmic implementation within an explicit nonlinear finite element setting. In Section 4, we demonstrate the features of the model by simulating growth in a patient-specific infarcted left ventricle, first with the infarct in place, than with the infarct surgically removed. Finally, in Section 5, we summarize the results and limitations of the proposed approach, and address potential clinical applications.

2. Continuum modeling of cardiac growth

In this section, we briefly summarize the kinematic equations, the equilibrium equations, and the constitutive equations of cardiac growth.

2.1. Kinematics of cardiac growth

In the geometrically exact setting, the key kinematic quantity to characterize deformation is the deformation gradient, F,

$$\mathit{F}=\frac{\partial \mathit{\chi }}{\partial \mathit{X}}$$ (1)

where χ is the deformation map between the undeformed and the deformed configuration and ∂χ/∂X denotes its spatial gradient with respect to the undeformed coordinates X. To characterize growth, we multiplicatively decompose F into an elastic part F^e and a growth part F^g [41],

$$\mathit{F}={\mathit{F}}^{\text{e}}·{\mathit{F}}^{\text{g}}$$ (2)

This concept, most known in finite elasto-plasticity [39], is widely used in multi-field modeling such as thermo-elasticity [33], poro-elasticity [38] and growth [6, 22, 32]. Motivated by physiological observations, we introduce a single scalar-valued growth multiplier ϑ, which reflects the longitudinal growth of individual heart muscle cells through serial sarcomere deposition [12]. We assume that cardiac dilation is an isochoric process characterized through growth along the fiber direction f₀ and simultaneous shrinkage orthogonal to f₀ such that the overall tissue volume remains constant [51].

$${\mathit{F}}^{\text{g}}=\vartheta {\mathit{f}}_0\otimes {\mathit{f}}_0+\frac{1}{\sqrt{\vartheta }}[\mathit{I}-{\mathit{f}}_0\otimes {\mathit{f}}_0]$$ (3)

The corresponding Jacobians J = J^e J^g follow accordingly with J = det(F), J^e = det(F^e) and, for the case of isochoric growth, J^g = det(F^g) = 1. With the definition of the growth tensor (3), we can immediately extract the elastic part of the deformation gradient F^e = F · F^g−1, which will be essential to evaluate the constitutive equations. Accordingly, we introduce the elastic right Cauchy Green deformation tensor

$${\mathit{C}}^{\text{e}}={\mathit{F}}^{\text{et}}·{\mathit{F}}^{\text{e}}$$ (4)

and the elastic Green Lagrange strains in terms of the elastic tensor F^e and the unit tensor I.

$${\mathit{E}}^{\text{e}}=\frac{1}{2}[{\mathit{F}}^{\text{et}}·{\mathit{F}}^{\text{e}}-\mathit{I}]$$ (5)

Through its rotation into the local fiber-sheet coordinate system [15, 16], we obtain the strain components in the fiber, cross-fiber, and sheet plane normal directions $E_{\text{ff}}^{\text{e}},E_{\text{ss}}^{\text{e}},E_{\text{nn}}^{\text{e}}$, and the corresponding shear components $E_{\text{fs}}^{\text{e}},E_{\text{sn}}^{\text{e}}$, and $E_{\text{fn}}^{\text{e}}$.

Remark 1

Alternative to equation (3), we could postulate an isochoric growth tensor in the following form,

$${\mathit{F}}^{\text{g}}=\vartheta {\mathit{f}}_0\otimes {\mathit{f}}_0+\frac{1}{\vartheta }{\mathit{s}}_0\otimes {\mathit{s}}_0+{\mathit{n}}_0\otimes {\mathit{n}}_0.$$

for which growth would occur along the fiber direction f₀ and simultaneous shrinkage would occur along the cross-fiber direction s₀. This formulation implies that the microstructure would remain unaffected along the sheet plane normal n₀. This formulation is based on the concept of myocardial sheets [20], where the individual muscle fibers are arranged in layers resulting in a locally orthotropic material characterization [15, 23].

2.2. Equilibrium equation of cardiac growth

In the absence of external forces, the balance of linear momentum can be expressed as

$$\text{div}(\mathit{\sigma })=\rho \ddot{\mathit{\chi }},$$ (6)

where div(·) denotes the divergence with respect to the spatial position x = χ(X,t) and σ is the Cauchy stress. In view of the computational algorithm we will apply in the sequel, we have explicitly introduced the acceleration term here, with ρ denoting the local density and χ̈ denoting the acceleration.

2.3. Constitutive equations of cardiac growth

Leaving aside the effects of active contraction [14, 50], we focus on the passive part of the constitutive equations here. We introduce the following strain energy function

$$\psi =\frac{1}{2}C[exp(b_{\text{f}}{E}_{\text{ff}}^{\text{e}2}+b_{\text{t}}(E_{\text{ss}}^{\text{e}2}+E_{\text{nn}}^{\text{e}2}+2E_{\text{sn}}^{\text{e}2})+b_{\text{fs}}(2E_{\text{fs}}^{\text{e}2}+2E_{\text{nn}}^{\text{e}2}))-1],$$ (7)

where C,b_f, b_t, and b_fs are diastolic myocardial parameters [16]. We derive the second Piola stress S^e by taking the partial derivative of ψ with respect to the elastic right Cauchy Green stretch tensor C^e, and take into account the quasi-incompressibility condition, which applies for most soft biological tissues [44, 46]. This results in the following expression [24]

$${\mathit{S}}^{\text{e}}=\rho J^{\text{e}}{\mathit{C}}^{\text{e}-1}+2{(J^{\text{e}})}^{-2/3}\text{dev}(\frac{\partial \stackrel{\sim }{\psi }}{\partial {\mathit{C}}^{\text{e}}})$$ (8)

where the dev operator is defined as follows,

$$\text{dev}(\circ )=(\circ )-\frac{1}{3}((\circ ):{\mathit{C}}^{\text{e}}){\mathit{C}}^{\text{e}-1}$$ (9)

and ψ̃ is the isochoric part of the free energy ψ. Using the kinematic equation (2), we obtain the total second Piola stress as the pull back of the elastic stress to the ungrown reference configuration

$$\mathit{S}={\mathit{F}}^{\text{g}-1}·{\mathit{S}}^{\text{e}}·{\mathit{F}}^{\text{g}-\text{t}}.$$ (10)

The total Cauchy stress σ is calculated by a classical push forward operation

$$\mathit{\sigma }=\frac{1}{J}\mathit{F}·\mathit{S}·{\mathit{F}}^{\text{t}}=\frac{1}{J}{\mathit{F}}^{\text{e}}·{\mathit{S}}^{\text{e}}·{\mathit{F}}^{\text{et}}.$$ (11)

We introduce a stress-driven evolution equation for cardiac growth [22]

$$\stackrel{.}{\vartheta }=k(\vartheta )\phi (\mathit{\sigma })$$ (12)

in terms of the scaling function k(ϑ) and the growth criterion φ(σ), where

$$k=\frac{1}{{\tau }_{\vartheta }}{\left[\frac{{\vartheta }^{max}-\vartheta }{{\vartheta }^{max}-1}\right]}^{\gamma }.$$ (13)

In the above equation, τ_ϑ denotes the adaptation speed, ϑ^max is the maximum sarcomere lengthening, and γ is the degree of nonlinearity of sarcomere deposition [12, 32]. Following thermodynamic considerations [13], we use the following growth criterion

$$\phi =max\left\{\text{tr}(J\mathit{\sigma })-p^{\text{crit}},0\right\}$$ (14)

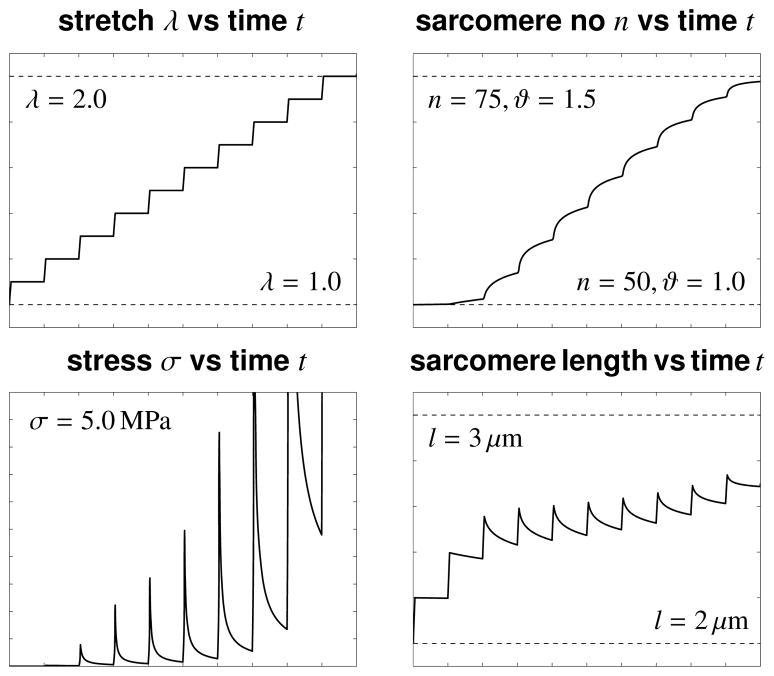
where tr (Jσ) = J σ:I denotes the trace of the Kirchhoff stress. The difference between tr(Jσ) and the critical growth threshold pressure p^crit is a physiological over-stress, which we assume to act as the driving force for growth [22, 40]. Alternatively, we could introduce cardiac growth as a strain-driven growth process [12, 13]. Figure 2 illustrates the features of our growth model for the simple model problem of uniaxial tension.

Figure 2.

Growth upon uniaxial tension. The stretch is gradually increased from λ = 1.0 to λ = 2.0, top left. For each new stretch level λ, the stress σ increases rapidly and then relaxes as the tissue grows, bottom left. Stress relaxation is caused by a serial deposition of sarcomere units in each cell. The number of sarcomeres increases from n = 50 to n = 75 as the growth multiplier increases from the ungrown state at ϑ = 1.0 to the growth limit of ϑ = ϑ^max = 1.5, top right. For each new stretch level λ, the length of the individual sarcomeres increases rapidly and then relaxes as new sarcomeres are deposited, bottom right.

Remark 2 (Definition of the stress tensor)

The definition of the second Piola stress tensor, S, in equation (10) is a natural consequence of the multiplicative decomposition of the deformation gradient tensor in equation (2). The stress definition is in complete analogy to the concept of finite strain plasticity. It implies, that the stress is attributed exclusively to the elastic part of the deformation F^e and that cardiac growth F^g does not produce stress.

Remark 3 (Evolution of growth)

The modeling of growth is conceptually similar to other types of inelastic behavior, e.g., plasticity or damage. The growth criterion φ acts similar to a yield function, and the critical growth threshold pressure p^crit is similar to the yield stress. This implies that growth is only activated if the current pressure p exceeds the critical threshold level, i.e., p = tr(Jσ) > p^crit. The scaling function k is similar to a nonlinear hardening function, characterizing the nonlinearity of the inelastic response.

3. Computational modeling of cardiac growth

While previous growth models were based on implicit computational algorithms [22, 59], here we illustrate the algorithmic realization of finite growth within an explicit nonlinear finite element setting. This will allow us to utilize commercial finite element packages such as LS-DYNA®, which are based on explicit time integration schemes. In particular, we illustrate the temporal discretization of the growth multiplier ϑ and of the deformation χ, and summarize the algorithm in an illustrative flowchart.

3.1. Explicit update of growth multiplier

Our goal is to determine the current growth multiplier ϑ for a given deformation state F_n, and a given growth multiplier ϑ_n, both at the end of the previous time step t_n. We introduce the following finite difference approximation of the first order material time derivative,

$$\stackrel{.}{\vartheta }=\frac{\vartheta -{\vartheta }_{\text{n}}}{\mathrm{\Delta }{t}_{\text{n}}}$$ (15)

where Δt_n = t − t_n > 0 denotes the current time increment. Using explicit time stepping schemes, we now reformulate the evolution equation (12) with the help of the following finite difference approximation

$$\vartheta ={\vartheta }_{\text{n}}+\frac{\mathrm{\Delta }{t}_{\text{n}}}{{\tau }_{\vartheta }}{\left[\frac{{\vartheta }^{max}-{\vartheta }_{\text{n}}}{{\vartheta }^{max}-1}\right]}^{\gamma }max\left\{\text{tr}(J\mathit{\sigma })-p^{\text{crit}},0\right\}.$$ (16)

3.2. Explicit update of deformation

For the deformation χ, we apply the following finite difference approximation of the second order time derivative,

$$\ddot{\mathit{\chi }}=\frac{\mathit{\chi }}{\mathrm{\Delta }{t}_{\text{n}}^2}-\frac{{\mathit{\chi }}_{\text{n}}}{\mathrm{\Delta }{t}_{\text{n}}}(\frac{1}{\mathrm{\Delta }{t}_{\text{n}}}+\frac{1}{\mathrm{\Delta }{t}_{\text{n}-1}})+\frac{{\mathit{\chi }}_{\text{n}-1}}{\mathrm{\Delta }{t}_{\text{n}}\mathrm{\Delta }{t}_{\text{n}-1}}$$ (17)

where χ_n and χ_n−1 are the deformation maps of the previous two time steps, and Δt_n−1 = t_n − t_n−1 denotes the last time increment. We can then reformulate the equilibrium equation (6) using this finite difference approximation.

$$\mathit{\chi }=(1+\frac{\mathrm{\Delta }{t}_{\text{n}}}{\mathrm{\Delta }{t}_{\text{n}-1}}){\mathit{\chi }}_{\text{n}}-\frac{\mathrm{\Delta }{t}_{\text{n}}}{\mathrm{\Delta }{t}_{\text{n}-1}}{\mathit{\chi }}_{\text{n}-1}+{(\mathrm{\Delta }{t}_{\text{n}})}^2\frac{1}{\rho }\text{div}({\mathit{\sigma }}_{\text{n}})$$ (18)

3.3. Algorithmic treatment of growth

Table 1 illustrates the algorithmic treatment of stress-driven transversely isotropic growth.

Table 1.

Computational algorithm for cardiac growth within an explicit finite element framework

given Fn and ϑn
calculate growth tensor ${\mathit{F}}_{\text{n}}^{\text{g}}$	(3)
calculate elastic tensor ${\mathit{F}}_{\text{n}}^{\text{e}}={\mathit{F}}_{\text{n}}·{\mathit{F}}_{\text{n}}^{\text{g}-1}$	(2)
calculate elastic Green tensor ${\mathit{C}}_{\text{n}}^{\text{e}}={\mathit{F}}_{\text{n}}^{\text{et}}·{\mathit{F}}_{\text{n}}^{\text{e}}$	(4)
calculate elastic second Piola stress ${\mathit{S}}_{\text{n}}^{\text{e}}=\partial \psi /\partial {\mathit{C}}_{\text{n}}^{\text{e}}$	(8)
calculate Cauchy stress ${\mathit{\sigma }}_{\text{n}}=1/J_{\text{n}}{\mathit{F}}_{\text{n}}^{\text{e}}·{\mathit{S}}_{\text{n}}^{\text{e}}·{\mathit{F}}_{\text{n}}^{\text{et}}$	(11)
growth criterion φ = tr(Jnσn) − pcrit	(14)
calculate growth function k(ϑn)	(13)
calculate growth multiplier ϑ	(16)
calculate deformation χ	(18)

4. Simulation of left ventricular growth

We hypothesize that cardiac growth is heterogeneously distributed with regional and transmural variations. To test our hypothesis, we implement our model in a commercial finite element program, LS-DYNA®, and perform a first prototype analysis. We create a patient-specific model of the left ventricle, identify its elastic material parameters in an inverse analysis, and quantify regional and transmural variations of growth. We compare two cases, growth in an infarcted heart, pre-operative, and growth in the same heart, after the infarct was surgically removed, post-operative.

4.1. Patient-specific model of the left ventricle

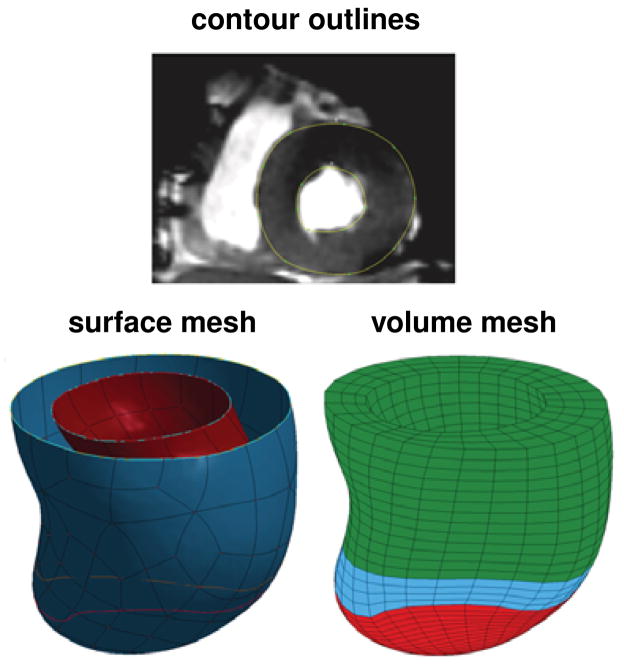
Figure 3 illustrates the stages of the model generation procedure. Figure 3, top, shows a two-dimensional magnetic resonance image of a short axis view with contours of the endocardium and epicardium, Figure 3, left, shows the three-dimensional surfaces representing the left ventricle, and Figure 3, right, shows the finite element discretization. The magnetic resonance images used in this study are based on a patient with myocardial infarction scanned before and after surgery [58]. Using image processing software, we contour the left ventricular endocardium and epicardium and create their three-dimensional surface models. From these, we create a volumetric finite element discretization, consisting of tri-linear hexahedral elements. Our finite element mesh contains 4249 elements, 4296 nodes, and 12888 degrees of freedom for the pre-operative case, illustrated in Figure 1, left, and 5100 elements, 5165 nodes, and 15495 degrees of freedom for the postoperative case, illustrated in Figure 1, right.

Figure 3.

Generation of a patient-specific left ventricular geometry. Two-dimensional magnetic resonance image with contour lines, top, surface representation of the endocardium and epicardium, left, and volume mesh of the left ventricle, right. The finite element mesh consists of 4249 elements, 4296 nodes, and 12888 degrees of freedom for the pre-operative model with distinct infarct region, shown in red, distinct borderzone, shown in blue, and a remote region shown in green.

4.2. Model parameters and prescribed loading

Figure 3, right, shows the left ventricle of a patient with an infarct in the apex region shown in red, the infarct borderzone shown in blue, and the remote region shown in green. The patient underwent magnetic resonance image examinations, one pre-operative, before surgery was performed, and one postoperative, after the infarct was excluded. For the pre-operative model, we assume that only the borderzone and the remote region are allowed to grow following the constitutive model described in Section 2, while the infarct zone itself does not grow. For the post-operative model, all regions are allowed to grow.

As illustrated in Figure 4, we prescribe homogeneous Dirichlet boundary conditions at the base of the left ventricle along the heart’s long axis. We allow the inner, endocardial nodes to move freely in the basal plane, while fixing the outer, epicardial basal nodes in all directions. The inner, endocardial surface is loaded with a uniform pressure. We increase the pressure linearly up to 12 mmHg and then keep it constant to allow the ventricle to grow.

Figure 4.

Boundary conditions and loading for pre-operative case, left, and post-operative case, right. The base of the left ventricle is fixed vertically along the heart’s long axis. Inner, endocardial basal nodes are allowed to move in the basal plane. Outer, epicardial basal nodes, are fixed in all directions. The inner, endocardial surface is loaded with a uniform pressure, which is increased linearly to 12 mmHg, and then kept constant to allow the ventricle to grow.

We identify the material parameters of the baseline elastic model by identifying the stiffnesses C in Equation (7) such that it minimizes the error between the computationally predicted diastolic left ventricular volume and the volume extracted from the corresponding magnetic resonance images. The stiffness of the infarct region C_I is set to be ten times stiffer than at the remote and borderzone region C_R [52]. Accordingly, we identify a stiffness of C_R = 0.087 KPa for the remote and border-zone regions, and C_I = 0.87 KPa for the infarct region. For the anisotropic elastic material parameters introduced in equation (7), we choose b_f = 49.25, b_t = 19.25, and b_fs = 17.44. We assign the fiber angles to vary linearly transmurally through the left ventricular wall. Their range is set from −60° to 60°, from epicardium to endocardium [17]. For the growth parameters introduced in equation (12), we choose a maximum sarcomere lengthening of ϑ^max = 1.5, an adaptation speed of τ_ϑ = 10, a critical growth threshold of p^crit = 10⁻⁴ KPa, and a growth exponent of γ = 2.0. Figure 2 illustrates the growth model for the set of elastic and growth material parameters introduced above in the context of uniaxial tension. For the temporal discretization, we apply an explicit time integration scheme and divide the time interval of interest T into 1.5 × 10⁶ time steps of 2/3 × 10⁻⁶ T. For the spatial discretization, we apply tri-linear eight-noded brick elements with full integration.

4.3. Regional and transmural variations of growth

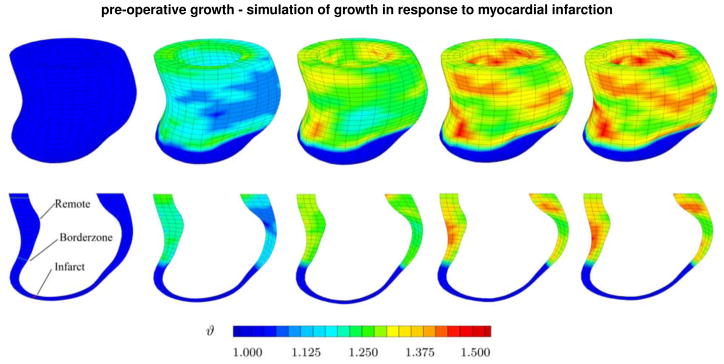
Figure 5, top, shows the spatio-temporal evolution of the growth multiplier ϑ across the left ventricle for the pre-operative case. It confirms our hypothesis as it clearly displays regional variations in growth. Although we apply a uniform loading, because of regional thickness variations and a non-growing infarct, the growth profile displays pronounced regional heterogeneities. Interestingly, the highest values of the growth multiplier are located in regions of high curvature, or rather high changes in curvature.

Figure 5.

Pre-operative growth. Spatio-temporal evolution of growth across the left ventricle of an infarcted heart. The simulations demonstrate regional variations, top row, and transmural variations, bottom row, of growth. Snap shots display the gradual increase of growth over time. Blue colors indicates no growth, ϑ = 1.0, red colors indicate that growth has reached its maximum predefined value, ϑ = ϑ^max = 1.5.

Figure 5, bottom, shows a cross section of the left ventricle to illustrate transmural variations in growth. The five snap shots indicate that in most remote and borderzone regions, growth is larger in the epiocardium, the outer wall than in the endocardium, the inner wall. Since we have modeled the infarct as non-growing tissue, the growth multiplier remains at its baseline value of ϑ = 1.0 in the apex region.

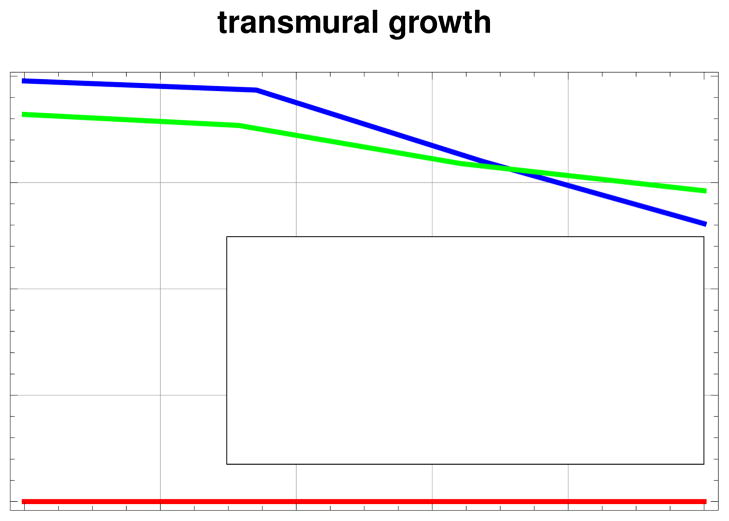
Figure 6 illustrates the transmural variation of the growth multiplier ϑ at different depths across the left ventricular wall. It confirms the observations from Figure 5, bottom. While the infarct itself does not grow, growth is heterogeneous in the borderzone and in the remote region. The borderzone has higher levels of growth in the epicardium, compared to the remote region. In the endocardium, growth magnitudes are reversed for both regions.

Figure 6.

Transmural variation of the growth multiplier ϑ at three different locations, inside the infarct, in the borderzone, and away from the infarct. The thickness is normalized.

4.4. Comparison of pre-operative and post-operative growth

Finally, we investigate whether surgical ventricular restoration has a positive impact on cardiac mechanics, as engineering intuition would suggest [3, 26]. We use data of the same patient, after the infarct was surgically excluded, and perform a computational simulation of growth. All other parameters, loading, and boundary conditions are similar to the example in the previous section. The material parameters are identified following the same procedure described in the previous section, yielding a homogeneous stiffness of C = 0.105 KPa.

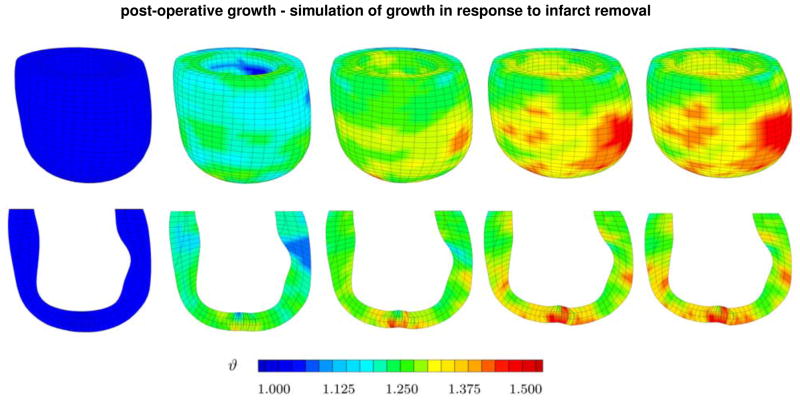
Figure 7, top, documents the spatio-temporal evolution of the growth multiplier ϑ across the left ventricle for the postoperative case. In contrast to the pre-operative case, now, the mechanical properties of the ventricle are set to be homogeneous. Surprisingly, even though excluding the infarct region avoids stress concentrations in and around the boarderzone, the simulations display pronounced regional variations of growth. In agreement with Figure 5, we observe high growth multipliers in regions of high curvature, or more precisely, regions with high changes in curvature. A typical example is the apical region where the infarct has been removed and the two boarder zones are stitched together non-smoothly. The simulation suggests that surgical ventricular restoration successfully removes constitutive heterogeneities. However, it may at the same time induce new heterogeneities of kinematic nature, which might become a trigger for ventricular growth and remodeling.

Figure 7.

Post-operative growth. Spatio-temporal evolution growth of across the left ventricle after surgical ventricular restoration. The simulations demonstrate regional variations, top row, and transmural variations, bottom row, of growth. Snap shots display the gradual increase of growth over time. Blue colors indicates no growth, ϑ = 1.0, red colors indicate that growth has reached its maximum predefined value, ϑ = ϑ^max = 1.5.

Figure 7, bottom, displays a cross section of the left ventricle to illustrate transmural heterogeneities of growth for the post-operative case. The five snap shots indicate that growth is heterogeneous, and that it initiates at the apex, where the infarct was excluded, and the left ventricle was stitched together. Although these results are just preliminary at this stage, they might provide additional insight in the long-term success of surgical ventricular restoration.

5. Discussion

Myocardial infarction is the single most common cause of heart failure. We hypothesized that mechanical non-uniformities around the infarct region initiate regional variations in cardiac growth. Our approach was to simulate cardiac growth using a novel mechanistic growth model, in which the dilation of the ventricle is characterized through the lengthening of cardiomyocytes, initiated by the serial deposition of sarcomere units. Embedded in a finite element simulation environment, our model proved capable of predicting growth of a patient-specific left ventricle in response to mechanical overload.

Our model is in excellent agreement with growth phenomena observed in dilated cardiomyopathies reported in the literature. In a recent long-term study in infarcted sheep, we have found a significant chronic fiber lengthening, accompanied by a chronic radial shortening [51], which agrees nicely with the format of our growth tensor in equation (3). In freshly isolated cardiac tissue, compared with a healthy control group, cardiomycytes from patients with dilated cardiomyopathy were reported to be 40% longer, while the cell widths displayed no statistically significant differences [11]. The length of the individual sarcomeres, however, was the same in both groups. This is in excellent agreement with the effects captured by our model with a growth multiplier ϑ increasing from ϑ^max = 1.0 to ϑ^max = 1.5, corresponding to a cell cardiomyocyte lengthening of 50%. In a 16-week long in vivo study in rabbits, the serial sarcomere number per cardiomyocyte increased chronically from 62 to 95 sarcomere units [57]. This corresponds to a growth multiplier of ϑ = 1.53, which is in excellent agreement with our model. The study further suggests that cardiomyocytes are capable to add one sarcomere per day. However, this initially linear sarcomere deposition rate decays after approximately four weeks. In our model, the sarcomere deposition rate is governed by two parameters, the sarcomere deposition time τ and the sarcomere deposition nonlinearity γ. Since we were only interested in the final converged end result of growth, the values of these parameters did not play a key role in the present analysis. We are currently in the process of identifying these parameters using longitudinal studies reported in the literature [57].

In contrast to existing growth models [12, 13], the proposed model is based on an explicit time integration scheme, see Table 1. This allows us to use explicit commercial codes. In particular, it enables us to utilize an existing algorithmic infrastructure with well-established patient-specific mesh generation modules [52], passive tissue response modules [16], and parameter identification modules [46]. We have shown that the model is portable into a commercially available finite element code, and that it captures similar phenomena as implicit codes [12, 13, 40].

The proposed model is an advancement of existing models in that it was created from patient-specific magnetic resonance images, rather than from a generic, elliptic geometry with a pre-defined uniform thickness. This is important, as our results have shown, since real geometries are not uniform, see Figure 3. It is this nonuniformity that may trigger the onset of growth as indicated in Figures 5 and 7.

While existing models assume that the material behavior is uniform across the heart [12], we have studied the impact of a non-uniform material response. This allows us to model growth not only in the context of dilated cardiomyopathies, where the heart dilates fairly uniformly, but also in the context of ischemic cardiomyopathies, where dilation is triggered locally through an infarcted region, see Figure 5.

Under a uniform loading, our model predicts significant regional and transmural variations in growth. These variations can be attributed to different wall thicknesses of our patient-specific model. Previous studies based on idealized elliptic geometries with uniform wall thicknesses were unable to capture these characteristics [13, 30]. When examining the postoperative left ventricle, where the infarcted tissue has been surgically removed and the ventricle was initially expected to display a more homogeneous state, we still observe significant regional variations in growth. Specifically, we observe highest values of growth near the stitching region where curvature changes are high, see Figure 6. Our simulation suggests that surgical ventricular restoration is capable to successfully remove constitutive heterogeneities, however, it may at the same time induce new kinematic heterogeneities, which might turn into new triggers for ventricular growth and remodeling. The ability to predict cardiac growth and remodeling might provide insight into the long-term success of surgical ventricular restoration. To build confidence in the model, it would be desirable to analyze the surgically removed infarct tissue histologically, in particular in the borderzone. It would be important to explore whether the individual cells have truly undergone the computationally predicted lengthening and thinning [51, 57]. This prototype model is only a very first step towards a better mechanistic understanding of the chronic phenomena associated with ventricular growth and remodeling. While many issues remain to be addressed before the model can be used to reliably predict cardiac dilation and the outcomes of related interventional procedures, we believe that it can already serve as a useful tool to qualitatively compare different treatment options. The next logical step would be to further calibrate and validate the mathematical model. While the calibration of the elastic baseline parameters is already partly embedded in the proposed approach, the calibration of the growth parameters presents a scientific challenge. Human data typically lack a well-defined starting point and systematic studies of ventricular growth across the scales are rare. Nevertheless, we think that computational modeling can provide valuable insight into the interplay of clinically relevant mechanical fields such as strain, stress, and growth, which are virtually impossible to measure in vivo during the chronic progression of heart failure.