Filtering artifacts from lifetime distributions when maximizing entropy using a bootstrapped model

Abstract

The maximum entropy method (MEM) has been used in many studies to reliably recover effective lifetimes from kinetics, whether measured experimentally or simulated computationally. Here, recent claims made by Mulligan et al. regarding MEM analyses of kinetics (Anal. Biochem. 421 (2012) 181–190) are shown to be unfounded. Their assertion that their software allows “analysis of datasets too noisy to process by existing iterative search algorithms” is refuted with a MEM analysis of their triexponential test case with increased noise. In addition, it is shown that lifetime distributions recovered from noisy kinetics data with the MEM can be improved by using a simple filter when bootstrapping the prior model. When deriving the bootstrapped model from the lifetime distribution obtained using a uniform model, only the slower processes are represented as Gaussians in the bootstrapped model. Using this new approach, results are clearly superior to those of Mulligan et al. despite the presence of increased noise. In a second example, ambiguity in the interpretation of Poisson kinetics in the presence of scattered excitation light is resolved by filtering the prior model.

Rooted in information theory, the maximum entropy method (MEM)¹ has been used to interpret a variety of noisy measurements for many years. Since its early applications to astronomical images [1,2], the method has proven to be valuable in biophysical studies, as when interpreting time-dependent signals in terms of a distribution of effective lifetimes [3–8]. The MEM has also been used to infer a two-dimensional distribution of activation enthalpy and entropy from ligand rebinding kinetics monitored at low temperatures [9]. The program MemExp [7,8] can be used to analyze kinetics with phases of opposite sign and a slowly varying baseline in terms of lifetime distributions and discrete exponentials. Experiments (e.g., see Ref. [10,11]) and simulations [12,13] have been interpreted using MemExp.

Here, a simple way of bootstrapping the prior model that defines the entropy of the lifetime distribution is shown to suppress unwarranted features. The approach is applied first to a test case proposed recently involving exponentials of opposite sign and then to simulated Poisson kinetics convolved with a known instrument response function. For simplicity, we assume that neither analysis requires a baseline correction and that the Poisson data involve kinetics that decay monotonically. The fit ℱ_i to datum D_i at time t_i can then be written as

$${ℱ}_i=D_0{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}d\text{log}\tau (g(\text{log }\tau )-h(\text{log }\tau ))e^{-t_i/\tau }$$ (1)

for the first test case and as

$${ℱ}_i=D_0{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}d\text{log}\tau f(\text{log }\tau ){\displaystyle {\int }_{t_o}^{\text{min}(t_i,t_f)}}\mathit{\text{dt}}\prime R(t\prime )e^{-(t_i-t\prime )/\tau }+\xi R(t_i)$$ (2)

for the second application. Each distribution is represented on a discrete set of points that are equally spaced in log τ. D₀ is a normalization constant, and scattered excitation light can be accounted for with positive values of ξ. The response function R is peaked at zero time and is appreciable only on the interval [t₀, t_f], with t₀ < 0. The zero-time shift [14,15] between the measured kinetics and instrument response is assumed to be negligible. The data are fit using a smoothed and renormalized response function.

Because the goal of a MEM calculation is to fit the data well using an “image” with maximal entropy, the function maximized is Q ≡ S − λC, where S is the entropy of the image, C is a goodness-of-fit statistic, and λ is a Lagrange multiplier. No additional Lagrange multiplier is used here to constrain normalization. For data with Gaussian noise (first test case), C is the familiar chi-square:

$$C(\mathbf{D},ℱ)={\chi }^2=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(\frac{{ℱ}_i-D_i}{{\sigma }_i}\right)}^2$$ (3)

where σ_i is the standard error of the mean. For data with Poisson noise (second test case), C is the Poisson deviance:

$$C(\mathbf{D},ℱ)=\frac{2}{N}{\displaystyle \sum _{i=1}^N}[D_i\text{ln}(D_i/{ℱ}_i)+{ℱ}_i-D_i]$$ (4)

The entropy S of image f is given by [16]

$$S(\mathbf{f},\mathbf{F})=-{\displaystyle \sum _{j=1}^M}[f_j\text{ln}(f_j/F_j)+F_j-f_j]$$ (5)

where F is the prior model used to incorporate existing knowledge into the MEM solution. Unconstrained maximization of S without regard for the fit (λ = 0) yields f_j = F_j.

Note that for Poisson data, C(D, ℱ) and S(f, F) share the same functional form to within a multiplicative constant. The symmetry in Q is apparent in Eqs. (4) and (5); the kinetics data represent a set of N points with Poisson expectations ℱ_i, whereas the MEM image is a set of M values with Poisson expectations F_j. Thus, the MEM calculation drives the fit toward the data and the image toward the prior model by minimizing the corresponding Poisson deviances.

In the first application (Eq. (1)), f includes the two distributions of lifetimes, g and h, that describe kinetics of opposite sign. In the second application (Eq. (2)), f includes the distribution of lifetimes and the scattered-light parameter ξ. For simplicity, f is referred to as the lifetime distribution. The ability to adapt F to the measured signal, to bootstrap the prior model, lends flexibility to the MEM that is lacking in other regularization methods such as those that minimize the sum of squared amplitudes [17]. This flexibility inherent in the MEM (Eq. (5)) is rather advantageous in practice because the bias introduced by regularization can be tuned by changing F. Consequently, various bootstrapping approaches have been developed [8]. By contrast, MEM analyses that define the entropy simply as S = −∑flnf assume a uniform prior model and may suffer from artifacts as a result. Similarly, regularization methods that optimize a function other than the entropy of Eq. (5) introduce a bias that cannot be reduced conveniently.

The prior model F can be derived from the data in different ways, and it is wise to assess the sensitivity of the recovered distribution f to reasonable changes in F. Beginning with a uniform F, the distribution recovered by the MEM can be blurred by convolution with a Gaussian to produce the bootstrapped prior model for the remainder of the calculation. This approach has been shown to improve results in image restoration [18] and in the analysis of kinetics [7]. When sharp and broad features coexist in the underlying distribution, so-called differential blurring can improve the results, as monitored by the goodness of fit and the autocorrelation of the residuals [7,8]. In this case, relatively sharp peaks in f are made even sharper before incorporating them into the prior model, whereas the remainder of f is blurred. Differential blurring can suppress artifactual ripples that persist when the entire lifetime distribution is blurred uniformly. Another way to modify F so as to reduce the bias of regularization in a reasonable and intuitive way is introduced in the next section.

Methods

A new means of bootstrapping the prior model was implemented in MemExp, version 4.0 (available at http://www.cmm.cit.nih.gov/memexp), as follows. A simple filter is used to suppress any potentially artifactual peak that arises at short lifetimes, for example, when scattered excitation light can be mistaken for a fast process in the kinetics. The MEM calculation is initiated using a uniform prior. Once C drops below a specified value (~1.0), the mean, area, and full width at half maximum are estimated numerically for each peak in f that is to be represented in the bootstrapped prior, that is, any feature peaked at a lifetime longer than a user-specified cutoff. Here, the cutoff was set at log τ = −1.5 for the first application and at log τ = −1.2 for the second, values chosen to exclude the earliest peak observed when using a uniform prior. The area of each peak to be included is estimated by integrating over the distribution between the local minima immediately preceding and following the peak. Of course, the g and h distributions are treated independently. For peaks that are not resolved well enough to directly calculate the half width at half maximum on either side, the half width is simply approximated as the difference between the locations of the peak and the adjacent minimum. If the peak is well separated on only one side, that half width is doubled to approximate the full width. The uniform prior is then replaced by a sum of Gaussians with the same means and areas as the peaks resolved in f (at lifetimes longer than the cutoff), with all peak widths multiplied by a user-specified constant (1.5 used here). The MEM calculation is then resumed with the entropy redefined in terms of this new prior distribution F. This ability to change F (and S) in reasonable ways helps the user to assess which features in f(log τ) are truly established by the kinetics being analyzed and which are dependent on the choice of model F.

Results

Test case I: triexponential kinetics with amplitudes that sum to zero

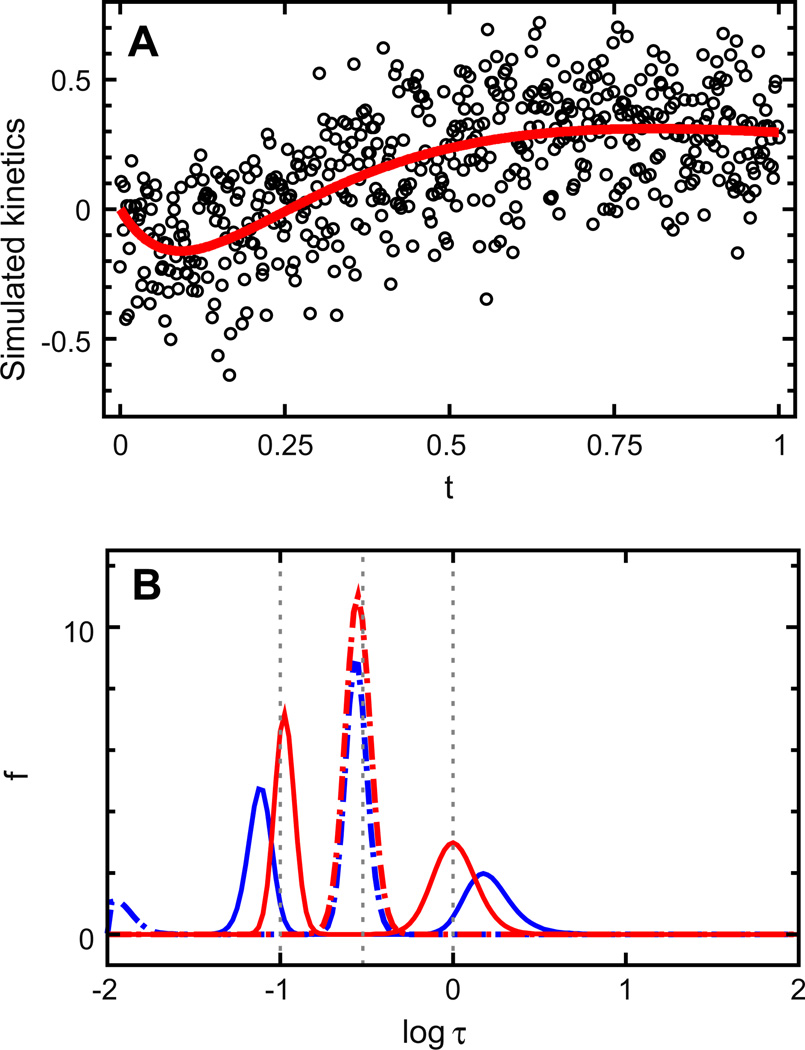
The kinetics recently purported to expose inadequacies [17] in the program MemExp, and in iterative methods in general, is revisited here. Gaussian noise with a time-independent standard error of σ = 0.2, a value greater than that used by Mulligan et al. [17], was added to the kinetics simulated at 512 points given by D(t) = e^−t − 2e^−3.333t + e^−10t (Fig. 1A). Lifetime distributions obtained with the program MemExp, version 3.0, using a uniform prior and MemExp, version 4.0, using a filtered prior are shown in Fig. 1B. D₀ was set to 1, and the “allin1” mode of MemExp was used to estimate the standard errors. Although the results of both MemExp runs compare favorably with results obtained using ALIA [17], those obtained with the adapted prior are clearly superior. Not only is the small peak at log τ ~ −2 obtained with a uniform prior suppressed when using the filtered prior, but the means of the two outer peaks improve considerably. The areas of the three peaks resolved using the filtered prior are 1.039, −2.020, and 0.951, respectively.

Fig. 1.

MemExp analysis of kinetics simulated as a sum of three exponentials with amplitudes that sum to zero. (A) Simulated data with (circles) and without (red line) Gaussian noise added. (B) Lifetime distributions recovered at χ² = 0.850 using a uniform prior model (blue) and using a model bootstrapped from the data by omitting features resolved with the uniform model peaked at log τ < −1.5 (red). Peaks shown as dot-dashed lines correspond to negative amplitudes. Vertical dotted lines indicate the “true” lifetimes.

Test case II: Poisson kinetics, deconvolution of instrument response, and scattered light

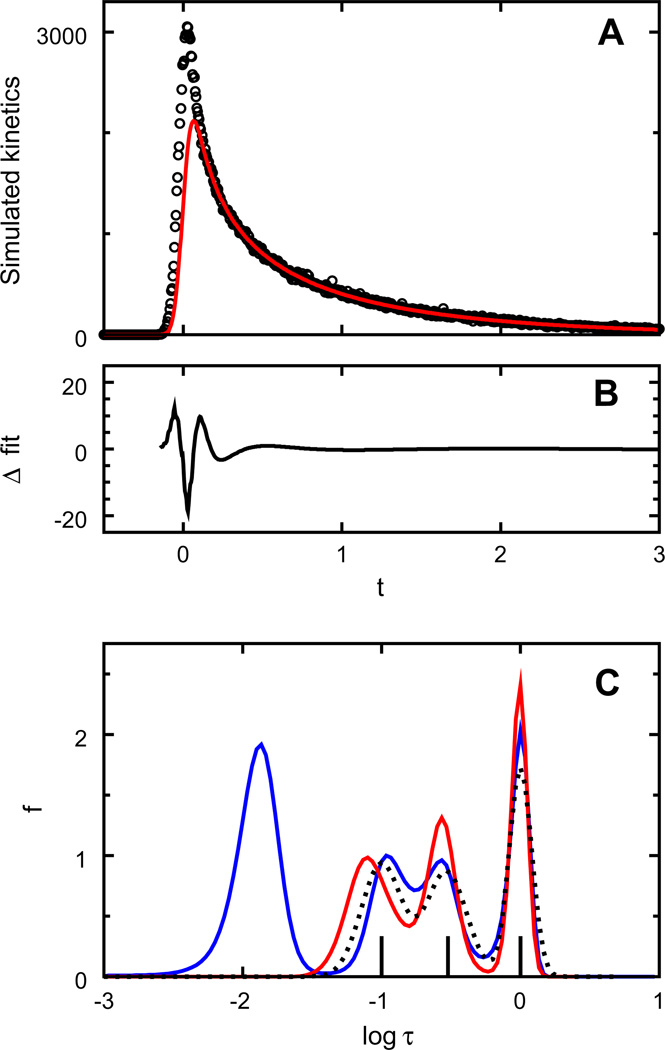
Five different data sets were simulated as a sum of three exponentials with equal amplitudes (1000) and lifetimes equal to 0.1, 0.3, and 1.0. The kinetics was convolved with a Gaussian instrument response with a full width at half maximum of 0.1, and scattered light was added with ξ = 150. Poisson noise was added to the kinetics and to the instrument response. The interval between successive time points was Δt = 0.005. Because the inversion of Eq. (2) is performed in MemExp after renormalizing the known instrument response, the normalization can be initialized to a value approximating the maximum value of the data. Here, D₀ was set to 3000. The integral of the recovered f distribution, multiplied by D₀, ultimately determines the normalization of the fit.

Each of the five data sets was numerically inverted using a uniform prior of F_j = 0.001 and using a bootstrapped prior that was filtered to omit peaks resolved at log τ < −1.2 when using the uniform prior. For three of the five kinetic traces, the use of a uniform prior resulted in lifetime distributions with three phases, in accord with the simulated data (not shown). For the other two data sets, an artifactual peak appeared at short lifetimes in the inversion using a uniform prior. Results are shown in Fig. 2 for one of these two data sets. Distributions recovered at a Poisson deviance of 1.041 are shown for the uniform and bootstrapped priors. The integral of the f distribution is 1.692 for the inversion using a uniform prior and 1.091 for the inversion using the filtered prior. The areas of the four peaks resolved using a uniform prior are 0.701, 0.322, 0.313, and 0.356. The areas of the three peaks resolved using the filtered prior are 0.387, 0.355, and 0.348. Analysis of the kinetics using the two priors leads one to correctly conclude that the additional fast process recovered with a uniform prior is not needed and that three phases of approximately equal weight describe the data. Moreover, the scattered light is estimated more accurately with the adapted prior (ξ = 141.2) than with the uniform prior (ξ = 125.1); the correct value is 150. By incorporating only the slower peaks in F, the fit at short times is influenced by the data at long times where ambiguities due to scattered light and finite pulse width are much smaller. By emphasizing the slower processes, as opposed to an assumed or estimated normalization, this approach can filter artifacts from the distribution of lifetimes.

Fig. 2.

MemExp analysis of kinetics simulated as a sum of three exponentials convolved with a Gaussian instrument response. (A) Simulated data with (circles) and without (red line) scattered light and Poisson noise added. (B) Difference in the two fits to the noisy data obtained at a Poisson deviance of 1.041. (C) Corresponding lifetime distributions recovered using a uniform prior model (blue) and using a model bootstrapped from the data by omitting features resolved with the uniform model peaked at log τ < −1.2 (red). Also shown are the bootstrapped model (dotted line) and the “true” exponentials (vertical bars).

Discussion

In their recent article, Mulligan et al. [17] advocated minimization of the sum of squared amplitudes using their program ALIA, rather than the maximization of entropy, to infer rate distributions from noisy kinetics. They stated,

“Analysis can also be hindered if the normalization of the signal must be estimated from the data given that inversion by the maximum entropy method used by MemExp is dependent on this information. Because ALIA requires no information about signal normalization, MemExp was also not provided with the normalization for this test. We found that in the case of this test dataset, MemExp was unable to produce an accurate rate spectrum.”

These claims are clearly unsubstantiated. It is more accurate to say that because MemExp was written with the goal of generality and broad applicability, the MemExp user has options, and not all options are appropriate in all cases. In particular, the user may prompt the program to estimate the normalization of the signal, D₀ in Eqs. (1) and (2). The documentation warns that this estimation is not recommended for all applications. Alternatively, the user can set D₀ to specify normalization that is known independently. Of course, the user can also choose to set D₀ = 1 to perform the inversion analogous to that performed using ALIA. With D₀ = 1, it is easily shown that the MemExp user can produce an accurate rate spectrum for the triexponential test case. Moreover, one can use MemExp to successfully obtain the rates, even when the Gaussian noise added is increased substantially (Fig. 1). Therefore, the assertion by the authors that ALIA can be used to analyze “datasets too noisy to process by existing iterative search algorithms” has not been established. The strange results they obtained using MemExp have nothing to do with the regularization choice: Eq. (5) versus ∑f². Rather, they wrote their program precluding a user-specified normalization, which can be useful in some applications, and they used MemExp in an unreasonable way. Although it is true that iterative methods are relatively slow computationally, speed is typically not a concern in the analysis of kinetics.

There are several advantages to maximizing the entropy, instead of minimizing the sum of squared amplitudes, that have been well documented for some time. As was discussed in 1990, in the absence of prior knowledge, maximizing the entropy, S = −∑flnf, imposes no correlation in simple examples such as the “kangaroo problem,” whereas minimizing ∑f² does impose correlation [19]. In the presence of prior knowledge, the entropy can be generalized to good effect by defining the entropy in terms of a prior model (Eq. (5)). The adaptation of this model to the data being analyzed can be useful in reducing artifacts and/or resolving ambiguities (Figs. 1B and 2C). In addition, evaluation of the entropy requires the natural logarithm of each amplitude, ensuring that amplitudes remain positive. Analyses that minimize the sum of squared amplitudes will be plagued by artifactual lobes in the rate spectrum of the wrong sign.

The two examples analyzed here highlight the advantage of the MEM’s flexibility to alleviate bias by adapting the prior model to the data being analyzed. Improved results are obtained in both cases simply by discarding peaks at very short lifetimes and incorporating the others into the definition of S. In the second example, qualitatively different lifetime distributions, one with three peaks and one with four peaks, can describe the noisy data equally well. The corresponding fits differ only slightly at short times (Fig. 2B) because the presence of scattered excitation light introduces ambiguity. The incorporation of the incorrect fast process (and greater signal normalization) in the distribution recovered with a uniform prior is compensated for by its incorrect (reduced) estimate of the scattered light. The incorrect fast process is clearly undesirable given that it is peaked near log τ = −2 and the data are sampled at intervals of Δt = 0.005. When faced with such an ill-posed problem, multiple interpretations of the data are possible, and use of the adaptable prior automated here can help to conveniently identify the simplest interpretation.

The recovery of a distribution of effective lifetimes from noisy kinetics data is clearly complicated whenever there is uncertainty in the value of the signal at short times. Distributions recovered by the MEM using a uniform prior (F_j = constant) can include unwarranted features if the normalization is underestimated [20]. The method introduced here is attractive because the fit at short times is guided by the data at longer times. The prior is bootstrapped so as to suppress artifacts that arise from ambiguities at short times, for example, due to scattered light. Whenever use of a filtered prior eliminates a peak at short lifetimes, as in the current examples, a simpler interpretation of the data has been found. It is always important to assess the sensitivity of the MEM result to the choice of prior distribution, and the current approach should be among those methods routinely applied.