On the origin of the unusual behavior in the stretching of single-stranded DNA

Abstract

Force-extension curves (FECs), which quantify the response of a variety of biomolecules subject to mechanical force (f), are often quantitatively fit using worm-like chain (WLC) or freely jointed chain (FJC) models. These models predict that the chain extension, x, normalized by the contour length increases linearly at small f and at high forces scale as x ∼ (1 − f^−α), where α = 0.5 for WLC and unity for FJC. In contrast, experiments on single-stranded DNA (ssDNA) show that over a range of f and ionic concentration, x scales as x ∼ ln f, which cannot be explained using WLC or FJC models. Using theory and simulations we show that this unusual behavior in FEC in ssDNA is due to sequence-independent polyelectrolyte effects. We show that the x ∼ ln f arises because in the absence of force the tangent correlation function, quantifying chain persistence, decays algebraically on length scales on the order of the Debye length. Our theory, which is most appropriate for monovalent salts, quantitatively fits the experimental data and further predicts that such a regime is not discernible in double-stranded DNA.

INTRODUCTION

The response of double-stranded DNA (dsDNA), RNA, proteins, and polysaccharides to mechanical force (f) has provided a microscopic basis for describing their elasticity.^{1, 2, 3, 4, 5, 6, 7} A number of studies have established that the measured force-extension curves (FECs) can be nearly quantitatively reproduced using standard worm-like chain (WLC) model⁸ or freely jointed chain (FJC) model.⁹ However, recent single molecule experiments on single-stranded DNA (ssDNA) showed that the measured FECs exhibit unexpected behavior that cannot be described using the WLC or FJC model. Surprisingly, over a wide range of stretching forces f and at low ionic strengths I, the chain extension normalized by the contour length of the chain, L, scales as x ∼ ln f.^{10, 11, 12}

The unusual behavior found for a range of f values in ssDNA implies that the standard polymer models that take only the elasticity of the chain are not adequate. Here, we provide a theoretical explanation of the x ∼ ln f behavior using analytical calculations and simulations by treating ssDNA as a polyelectrolyte chain. We show that the tangent correlation function from which the chain persistence length is extracted decays as a power law on scales a ≲ s ≲ λ_D (the Debye length). Such a behavior, which was not previously noticed, is a consequence of polyelectrolyte (PE) effects in ssDNA and gives rise to the x ∼ ln f behavior. We confirm the theoretical predictions using simulations, which also show excellent agreement with experimental data for ssDNA (Ref. ¹²) for I from 1 mM to 3 M. Our theory not only produces quantitative agreement with experiments, but also establishes the importance of PE effects in predicting the response of ssDNA to f.

THEORY FOR STRETCHING ssDNA INCLUDING POLYELECTROLYTE EFFECTS

Measured FECs for a broad class of biopolymers can be understood in terms of an interplay of the tensile length ξ_t = k_BT/f (k_BT is the thermal energy), the persistence length ξ_p, and the monomer length a. The resulting theory allows us to determine a priori the precise polymer model that best describes the measured FECs for a specific macromolecule.¹³ For a discrete semiflexible chain, the tangent correlation at f = 0 decays as

$$\begin{array}{c}\hfill ⟨\cos \theta \left(s\right)⟩=\exp \left(-\frac{s}{{\xi }_p}\right),\end{array}$$ (1)

where θ(s) is the angle between two tangent vectors that are separated by length s along the chain (Fig. 1a). At very high forces, $f>{\mathcal{F}}_h\equiv c{k}_{B}T{\xi }_p/a^2$, ⟨cos θ⟩ is independent of s and can be approximated as¹³

$$\begin{array}{c}\hfill ⟨\cos \theta ⟩\left(f\right)\approx \exp \left(-c\frac{{\xi }_t}{a}\right),\end{array}$$ (2)

where c is a model-dependent constant on the order of 4 for non-charged polymers. Thus, the macromolecule behaves as a FJC with x ≈ 1 − ξ_t/a ∼ 1 − f⁻¹. When $k_{B}T/{\xi }_p\le f\le {\mathcal{F}}_h$, due to the interplay of ξ_p and ξ_t, the macromolecule can be modeled by a sequence of independent segments whose length λ_K is force-dependent. In this force regime, the tangent correlation is given by¹³

$$\begin{array}{c}\hfill ⟨\cos \theta ⟩\left(f\right)\approx \exp \left(-c\frac{{\xi }_t}{{\lambda }_K}\right).\end{array}$$ (3)

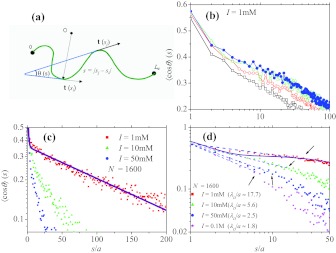
Figure 1.

(a) A cartoon of the polymer chain showing tangent vectors at s_i and s_j along the chain. The angle θ(s = |s_j − s_i|) between the two vectors is shown. The average value over all possible conformation of the chain ⟨cos θ(s)⟩ is the tangent correlation along the chain. The length scale over which ⟨cos θ(s)⟩ decays at f = 0 is the measure of the chain persistence length. (b) At I = 1 mM, all the curves with various N values (from bottom to top N = 100, 200, 800, 1600) show that there are strong finite size effects. Only when N exceeds 1600 do the curves converge. (c) ⟨cos θ(s)⟩ in log-linear scale for N = 1600 and at various I. The solid line is a double exponential fit using ⟨cos θ⟩ = (1 − β) exp (− s/λ₁) + β exp (− s/λ₂),²⁴ with β ≈ 0.358 and λ₁ ≈ 1.02a and λ₂ ≈ 179.11a. (d) To identify the power law behavior the data in (c) are shown as a log-log plot. The curves at various ionic strength clearly show that ⟨cos θ(s)⟩ decays as a power law on scale s ⩽ λ_D. The arrows correspond to λ_D. The solid line is the double exponential fit.

Thus, ${\lambda }_K=\sqrt{c{\xi }_t{\xi }_p}$ and x ≈ 1 − ξ_t/λ_K ∼ 1 − f^−1/2, which is the well-known WLC behavior.^{8, 14}

Exponential decay of ⟨cos θ(s)⟩ in uncharged polymers (Eq. 1) results from the sequential transmission of interactions along the chain backbone. However, in polyelectrolytes such as ssDNA, direct repulsive interactions between any pair of monomers within a scale ∼λ_D could alter Eq. 1. It has already been shown that deviations from Eq. 1 could occur even in stiff chains without intramolecular interactions.¹⁵ The PE effects can profoundly change the nature of FECs. Because the anticipated decay of ⟨cos θ⟩ in PEs, which is slower than in uncharged polymers, affects FEC, we propose that the intrinsic (f = 0) tangent correlation on scales s ≲ λ_D in polyelectrolytes should decay as

$$\begin{array}{c}\hfill ⟨\cos \theta \left(s\right)⟩\approx C{\left(\frac{s}{a}\right)}^{-\gamma },\text{for}a\le s\lesssim {\lambda }_D,\end{array}$$ (4)

were C and γ are functions of a/λ_D ∝ I^1/2. Note that, in the complete screening limit λ_D/a ≪ 1, the correlation equation must reduce to the exponential form, thus $⟨\cos \theta (s=a)⟩\equiv C_0=\exp (-a/{\xi }_p^0)$, with ${\xi }_p^0$ being the bare persistence length; C₀ is, thus, the lower limit for C.

Just as for macromolecules with short-ranged interactions between the monomers, the FEC for PEs should quantitatively match the prediction of the FJC model as long as $f>{\mathcal{F}}_h^{PE}$. We determine ${\mathcal{F}}_h^{PE}$ by equating Eqs. 2, 4 at s = a yielding

$$\begin{array}{c}\hfill {\mathcal{F}}_h^{PE}=c\frac{k_{B}T}{a\ln C^{-1}}.\end{array}$$ (5)

In the complete screening limit ${\mathcal{F}}_h^{PE}$ in Eq. 5 reduces to ${\mathcal{F}}_h$ for uncharged polymers described above.

In the regime where the force is high enough such that every segment on the order of λ_D is independent of each other, the chain can be modeled as a FJC with force-dependent λ_K segments, with the tangent correlation due to the tensile energy being given in Eq. 3. By equating the rhs's of Eqs. 4, 3 at s = λ_K we have the solution for λ_K(f),

$$\begin{array}{c}\hfill {\lambda }_K=\frac{c}{\gamma W\left(\frac{c{C}^{*}}{\gamma }\frac{k_{B}T}{fa}\right)}\frac{k_{B}T}{f},\end{array}$$ (6)

where C* = C^−1/γ and W(z), the Lambert omega function,¹⁶ is the inverse of z = We^W. The equation for the FEC for polyelectrolytes becomes

$$\begin{array}{c}\hfill x\approx 1-\frac{{\xi }_t}{{\lambda }_K}=1-\frac{\gamma }{c}W\left(\frac{c{C}^{*}}{\gamma }\frac{k_{B}T}{fa}\right),\end{array}$$ (7)

or equivalently,

$$\begin{array}{c}\hfill f\approx C^{*}{e}^{-c/\gamma }\frac{k_{B}T}{a}\frac{\exp \left(\frac{c}{\gamma }x\right)}{1-x}.\end{array}$$ (8)

Thus, in the regime where x is not too close to 1, the $\exp \left(\frac{c}{\gamma }x\right)$ factor dominates in Eq. 8, which implies that f ∼ exp (x), or equivalently x ∼ ln f. The condition for observing the unusual behavior is c/γ ≫ 1. We show using simulations (see below) that when 1/γ ∼ (λ_D/a)^0.36, this condition is satisfied for λ_D ≫ a or at low ionic strengths, just as observed in experiments.^{10, 11, 12}

SIMULATIONS

In order to validate the theoretical predictions we first performed Monte Carlo (MC) simulations of a PE chain with bending rigidity and screened electrostatic repulsions between the monomers, a model that is appropriate for ssDNA. The chain Hamiltonian is given by

$$\begin{array}{c}\hfill \frac{{\mathcal{H}}_c}{k_{B}T}=-\frac{{\xi }_p^0}{a}\sum _{i=0}^N\frac{{\mathbf{b}}_i{\mathbf{b}}_{i+1}}{a^2}+\frac{q^2}{2}{\lambda }_B\underset{j=i+1}{\sum _{i=0}^N}\frac{e^{-\frac{r_{ij}}{{\lambda }_D}}}{r_{ij}}-\frac{\mathbf{f}}{k_{B}T}\sum _{i=0}^N{\mathbf{b}}_i,\end{array}$$ (9)

where N is the number of monomers, b_i is the ith bond vector (Fig. 1a), r_ij is the distance between beads i and j, λ_B = 0.7 nm is the Bjerrum length,¹⁷ and q = a exp (0.0338 + 1.36I^2/5) nm⁻¹ with I measured in molarity units (M), and q is the effective charge number per monomer in monovalent solutions.¹⁸ Here a = 0.55 nm and ${\xi }_p^0=0.65$ nm, which are similar to the parameters for ssDNA/RNA.^{10, 11, 12, 13, 19, 20} The Debye length is related to I (in M) as ${\lambda }_D=1/\sqrt{8\pi {\lambda }_{B}0.602I}$ in monovalent solutions.¹⁸

Sampling of chain conformations is done using the Metropolis scheme with the crankshaft and pivot moves.^{18, 21} Starting from an initial conformation, the chain is equilibrated for at least 10⁶ MC steps before the actual sampling starts. The long range nature of the electrostatic interactions, even though dampened by the Debye-Huckel factor, is computationally demanding. To circumvent this problem, we use a matrix to store all the pairwise interactions and only update the pairs whose distances are changed by the MC moves. To expedite the computations we introduce a cut-off distance of 20λ_D, which is large enough such that it does not introduce any errors. We checked the accuracy by comparing FECs and the tangent correlation data at I = 1 and 20 mM with cutoffs of 10 and 20λ_D and no cutoff, and found virtually no discrepancies. With these two enhancements the sampling can be sped up by a factor of at least 5 for large N.

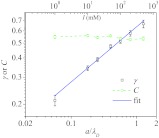
We calculated the tangent correlation for the model polyelectrolyte for I ranging from 1 to 500 mM. To reduce finite size effects, we simulated for each I several replicas of the chain with different lengths N, starting from 100 and doubling it every time, until the results for ⟨cos θ(s)⟩ are independent of chain length (N ⩾ 800) (see Fig. 1b for data at I = 1 mM). The smaller I is (the longer λ_D) the stronger are the finite size effects. Hence, at low ionic strengths N has to be sufficiently large to obtain converged results. From Fig. 1c, it is clear that ⟨cos θ(s)⟩ decays exponentially at large s as commonly accepted.^{17, 22, 23, 24} However, the curvatures at small values of s (especially, as salt concentration decreases) suggest that the tangent correlation function qualitatively changes for PEs. The data in Fig. 1d in a log-log scale clearly show the postulated power law (Eq. 4) at all values of I. The range over which the power law decay is observed is from s/a = 1 up to a few λ_D’s, which is more robust than we conservatively anticipated. Note that the fit using Eq. (6(a)) in Ref. 24 with a double exponential form, although good for large s (Fig. 1c, solid line), does not reproduce the true behavior in this regime (Fig. 1d, solid line). Thus, the simulations validate Eq. 4. We fit the initial power law decay to extract C and γ as functions of I (or λ_D). As shown in Fig. 2, γ ≈ 0.64(a/λ_D)^0.36, whereas C is almost a constant for the range of I considered here.

Figure 2.

The values of C and γ extracted from the simulation data of ⟨cos θ(s)⟩ for PE chains with N = 1600 using Eq. 4.

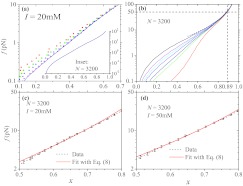
In order to ascertain the range over which the x ∼ ln f behavior is observed using our PE model, we performed simulations of a chain under tension using I = 20 mM and N = 100, 200, …, 3200. As shown in Fig. 3a, the FECs are almost independent of chain length at f ≳ 5 pN but are clearly N-dependent for f < 5 pN. At even smaller forces, i.e., f < 0.5 pN, the discrepancies between the N = 1600 and N = 3200 curves are still discernible, which imply strong finite size effects. Nevertheless, the prominent feature of the curves is the x ∼ ln f behavior which spans almost 3 decades in force (0.1 pN ⩽ f ⩽ 50 pN) for all values of N, which becomes increasingly transparent as N increases. Figure 3b shows the FECs of a chain with N = 3200 at several ionic strengths from 1 mM to 3000 mM. For reference we also show the analytic fit¹³

$$\begin{array}{c}\hfill x\approx 1-{\xi }_t/\sqrt{{\lambda }_K^2+a^2},\end{array}$$ (10)

with α = 2 and c = 4 in the x > 1/2. It can be seen that the x ∼ ln f regime is visible in most of the curves although it is narrower with increasing ionic strength. Moreover, all the curves converge at f ≈ 50 pN, or x ≈ 0.89, which can be analytically fit using Eq. 10. This implies that all the chains start to enter the FJC regime and electrostatic interactions among the monomers and the ionic conditions play an insignificant role in the high stretching limit. Thus, the observed unusual FEC (x ∼ ln f) is pronounced over a few decades in force f, and is surprisingly found to be a consequence of the previously unnoticed power law decay of ⟨cos θ(s)⟩ (Eq. 4) at short distances.

Figure 3.

(a) Force-extension curves (FECs) for various N values at I = 20 mM. The N values from top to bottom are 100, 200, 400, 1600, and 3200 (solid line). The inset shows the FEC for N = 3200. (b) FECs for a PE chain with N = 3200 at various values of I. The values of I from bottom to top are 1, 10, 20, 50, 100, 200, and 3000 mM. The dashed line is plotted using $x\approx 1-{\xi }_t/\sqrt{{\lambda }_K^2+a^2}$ Eq. 10. (c) and (d) Fits using Eq. 8 to simulation data for a chain with N = 3200 at I = 20 and 50 mM, respectively. See text for the values of the parameters.

ANALYSIS OF EXPERIMENTAL DATA

Next we tested the validity of Eq. 8 by fitting it to the simulated FECs with only C* and c/γ as two adjustable parameters. Because of the approximation made in deriving the equation, we restrict the fitting region to be 0.5 < x < 0.8. Indeed, as shown by the solid lines in Figs. 3c (I = 20 mM) and 3d (I = 50 mM), Eq. 8 fits the data in the region with reasonable accuracy. At I = 20 mM, the fitted value for c/γ is ∼4.01 and for C* is ∼1.78. If we reconcile the fitted γ with the value obtained through independent simulation for the tangent correlation at the same I in Fig. 2, we get c = 1.7 and C ≈ 0.80 (C is larger than the direct-fit value of 0.54). Similar values were also obtained at I = 50 mM.

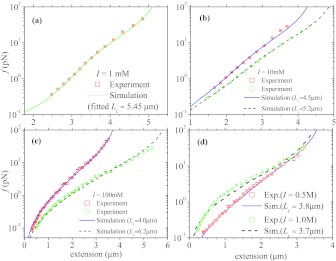
Now we use the theory and simulation results to analyze the stretching data of ssDNA by fitting the FECs. Figure 4 shows the fit of experimental FECs of ssDNA (Ref. ¹²) at a few representative ionic strengths I using simulated FECs of our PE model, with the contour length L_cas the only adjustable parameter. The simulation results quantitatively reproduce the experimental FECs. The fits at other I from 1 mM to 3000 mM are also excellent. It should be emphasized that the sole adjustable parameter L_c varies from one FEC to another and is very close to the values obtained from the rule from simulated curves at various I, x(f = 50 pN) ≈ 0.89 (see Fig. 3b).

Figure 4.

Single-parameter (using the contour length L_c as the fit parameter) fits of simulated FECs to experimental data of ssDNA in Na⁺ solutions.¹² The high quality of the fits for I = 1 mM (a), 10 mM (b), 100 mM (c), 500 mM and 1000 mM (d) indicates that electrostatic interactions play a dominant role in the stretching of ssDNA.

DISCUSSIONS

It should be noted that the Hamiltonian 9 only takes into account the intrinsic bending rigidity of the polymer and the screened electrostatic interactions as in the Debye-Huckel theory. The ssDNA molecules used in experiments¹² were specially treated to prevent base-paring interactions, so it is reasonable not to include them in our model. The high quality of the fits using our theory strongly suggests that long-ranged interactions predominantly due to PE effects give rise to the x ∼ ln f behavior. It further validates our arguments that the logarithmic dependence of extension on the force is intimately related to the power law decay in the tangent correlation at small arc-length separations in the absence of force. Thus, we can readily use the values of C and γ in Fig. 2, that have been extracted from direct simulations of the tangent correlation, as predictions characterizing the decay of tangent correlation of ssDNA.

We can also use the approximate stretching equation 7 with c = 1.7 and L_c obtained from the assumption x(f = 50 pN) ≈ 0.89, and adjust C and γ to fit to the experimental FECs. Using this procedure we also obtained good agreement with the values obtained from a direct fit of Eq. 4 to the simulation data of tangent correlation. The fitted values of C to the experiment data are somewhat higher than those obtained using the direct fit, but it also stays almost a constant for all the range of I considered. Thus, the analytical theory with only C and γ as parameters suffices to fit the experimental data over a wide range of salt concentration.

Logarithmic dependence of ssDNA upon stretching has been reported in earlier single molecule experiments.¹⁰ However, in fitting the experimental FECs, they used a different model, namely, the extensible FJC with electrostatic interactions that are similar to ours in Eq. 9. As noted here, they also showed that the entropic worm-like chain model²⁵ failed to fit the experiment data and tended to give unphysical persistence length. However, as pointed out elsewhere,¹³ both the discreteness (which is not present in the WLC model, but is in our model and the one by Dessinges et al.¹⁰) and the bending stiffness play important roles in the elastic properties of biomolecules in usual ranges of stretching force. Moreover, we have seen that at low ionic strengths, the PE effects in ssDNA are very strong in the range of force less than about 10 pN (I-dependent). In this range of forces the nature of FECs is mainly determined by the electrostatic interactions. At the force higher than 10 pN, the semiflexibility of the chain should play an important role and the WLC model^{8, 14} can be used to describe quantitatively the FECs.

Finally, it is interesting to wonder why the x ∼ ln f dependence has not been observed in dsDNA, which is also an excellent model polyelectrolyte. In dsDNA, the intrinsic persistence length (∼50 nm in monovalent salts) is usually much larger than the Debye length, λ_D. Hence, the range over which the initial power law decay of the tangent correlation can be observed is far too small. For all practical purposes, ⟨cos θ(s)⟩ exhibits the standard exponential decay for all s. As a result, dsDNA behaves as a WLC with polyelectrolyte effects playing only a minor role especially when the salt concentration is high.^{8, 26} Thus, the x ∼ ln f behavior cannot be observed in practice in monovalent solutions even though in theory such a regime must exist. In a recent paper, ssDNA in divalent cations such as Mg^{2 +} or Ca^{2 +} shows even a stronger dependence of extension x on f than x ∼ ln f.²⁷ In order to address these issues, we need to develop a better description of ion-PE interactions.

CONCLUSIONS

In summary, we have shown that the unusual stretching behavior of ssDNA is due to polyelectrolyte effects whose origins can be traced to a previously unnoticed power law decay of the tangent correlation function in PEs in the absence of force on length scales comparable to the Debye length. Using theoretical arguments and simulations of a minimal model for a PE we demonstrated that at forces (10–50 pN) the FEC is given by x ∼ ln f. Our theory quantitatively explains the measured FEC (Ref. ¹²) (x ∼ ln f). The simple analytic expression for FECs can be used to predict the response of force in other single-stranded RNA and DNA as well as synthetic polyelectrolytes.

Note added in proof : While this paper was under review we received a preprint by M. J. Stevens, D. B. McIntosh, and O. Saleh reporting simulations that illustrate the relevance of crumpled structures at short length scales in polyelectrolytes in leading to the observed scaling x ∼ ln f. The physics underlying the origin of x ∼ ln f in both the treatments are similar.